A Lightweight Public Verifiable Multi Secret Sharing Scheme Using Short Integer Solution

Abstract

In this paper we introduce a multi secret sharing (MSS) scheme based on lattice conception. Lattice constitutes the core of many cryptographic constructions. The advantage of using lattice, which our scheme will inherit, is twofold: first is that the hardness of lattice problems is well understood. We will show that breaking our scheme leads to a solution for the robust Short Integer Solution problem. Hence, the presented scheme’s security is guaranteed by leveraging lattice based conceptions. Second advantage is that working with lattice is simple and, consequently, execution is fast. A main problem with previous schemes is that they mostly are based on numerical assumptions which are slow and need much throughput. Inheriting simplicity and fastness make our scheme an excellent choice to implement in facilities with limit computational power and resources. In secret sharing schemes, typically in any protocol, dishonest participants and dealer can cheat during execution. To mitigate these concerns we augment our scheme with verifiability properties, say verifiable and public verifiable secret sharing. Verifiability prevents the dealer to share wrong shares and public verifiability forces participants to submit their sub-shares correctly. In MSS schemes, releasing some public values which are used in recovering step is inevitable. At the end, a comprehensive comparison by a table in the conclusion section shows that the presented scheme has minimum number of public values among MSS schemes.

1 Introduction

Secret sharing is defined as a method to share a secret between many participants such that an authorized subset of them can recover the secret by submitting their shares. In this process each of the participants is given a private information which is called share or private share. The set of the subsets of authorized participants is called access structure and is denoted by Γ. If all of the elements which belong to an access structure have cardinal t, then we call this scheme a (t, n)-threshold secret sharing scheme. In this definition n denotes the number of participants. Secret sharing was introduced by Shamir [1] and Blakeley [2] independently. Shamir presented a (t, n)-threshold scheme based on interpolation. In his scheme every $t-1$ participant cannot obtain any information about the secret (in view of information theory). Secret sharing plays an important role in many cryptographic protocols such as Multi-Party Protocols [3], distributed signature [4, 5], E-Voting [6], etc. hence many researchers were motivated to work in this area [7–10].

Firs type of secret sharing has four major shortcomings that should be addressed. Before delving into details, we outline these important shortcomings,

• 1. They share one secret, but in many situations we need to share more than one secret.

• 2. Dealer can distribute wrong shares among the participants. Consequently, different subsets of participants recover different values.

• 3. In recovering phases, malicious parties can submit wrong information to attain the other parties secret shares.

• 4. Most of secret sharing schemes are based on numerical assumptions.

Scholars introduced multi secret sharing scheme to resolve the first shortcoming. He and Dawson [11] present the first MSS Scheme in which many secrets are shared while just one share is assigned to each participants. Their scheme has a restriction in recovering phase. In fact, in their scheme recovering the secrets should be done in a predetermined order otherwise it endangers security of unrecovered secrets which is undesirable. In their scheme some public values are publishes by the dealer. These public values are used in recovering the secrets process. Typically, in recovering stage, parties compute specific values regarding the target secret called sub-share. This process is done by an algorithm that takes the shares and index of the target secret and outputs the corresponding sub-share. Using these produced sub-shares and published public values the target secret can be recovered. After their scheme other schemes have presented to remove the constraint on recovering order and reducing the number of public values [12]. Less public values would be an advantage because it has direct impact on efficiency.

Another important improvement, which addresses the second drawback, is verifiability. Verifiable secret sharing schemes have introduced by Chor et al. [13]. In this kind of schemes, dealer cannot deceive the participants and assign them wrong shares. The exact definition of verifiable secret sharing scheme is presented in the next section. Harn [7] proposed a MSS scheme that enjoys verifiability property. After presenting a verifiable MSS (VMSS) almost all of the new MSS schemes are equipped with this property and it has become an inseparable part of secret sharing schemes, especially MSS.

The third drawback is related to cheating participants. In recovering process, cheating parties should not be permitted to submit wrong shares. Otherwise, they can see other parties sub-shares, which jeopardizes the security of the scheme. In order to overcome this drawback, public verifiable secret sharing scheme was proposed [14]. In this scheme, by using mathematical conceptions they presented a secret sharing which is public verifiable. In public verifiable secret sharing schemes participants using a specific protocol prove their shares validity.

Most of the secret sharing are based on numerical assumptions, e.g. RSA assumption, Factorization, Dicrete Logarithm, etc. Shor in 1994 presented a quantum algorithm that solves the factorization problem in polynomial time [15]. This paper shows vulnerability of previous protocols that use numerical assumptions. Consequently, previous secret sharing schemes will collapse after advent of quantum computers. Therefore researchers have been seeking new candidates that can resist against quantum algorithms. Another disadvantage of using numerical based protocols is that they impose heavy computations to protocol executioner. This factor has adverse influence on performance. In many cases we have not access to much resource to implement heavy schemes. It shows our demand to lightweight schemes which, obviously, cannot be reached by numerical based schemes.

Aforementioned shortcomings motivated researchers to use lattice in secret sharing schemes [16, 17]. Informally, lattice is a discrete subgroup of ${\mathbb {R}}^n$ or equivalently integer combination of a few independent vectors in ${\mathbb {R}}^n$. Many computational problems are related to the lattice conception [18, 19], e.g. finding shortest vector problem (SVP), closest vector problem (CVP), shortest independent vector problem (SIVP), Short Integer Solution (SIS) and many other problems. This problems are believed to be hard and the best algorithm for solving them need exponential time. For instance, it is proved that CVP is a NP-Hard (non-deterministic polynomial-time hard) problem. Therefore, until $NP\ne P$ no one can solve CVP problem in polynomial time (P stands for the class of problems that have polynomial time solution). In other word, cryptographic constructions which are formed base on CVP cannot be broken in polynomial time until $NP=P$ holds . Robustness of lattice based cryptography has made it to one of the nominees in post quantum cryptography [20]. Moreover, the operations which are used in lattice are fast and simple. These specifications have caused using lattice widely in new cryptographic constructions which are robust and lightweight [21–23].

In this paper, we present an MSS scheme and verifiable versions (verifiable and public verifiable) of it based on SIS to address the four stated shortcomings. In the presented scheme secrets can be shared among the participants such that they can recover any secret in an undetermined order while participants get one share. The scheme inherits good features of lattice such as simplicity, fastness and security. It is fast and lightweight in comparison to previous schemes which are chiefly based on number theoretic assumptions. As a consequence, executing this scheme is easy and it can be implemented in computers with low throughput capacity such as smart phones. Another benefit of using lattice is that the introduced scheme is reliable because its security is based on well-studied problem SIS. We demonstrate that breaking our scheme leads to solving the hard lattice problem SIS. As a result, our scheme will resist against quantum algorithms. The presented scheme is verifiable. Hence, dealer cannot give incorrect shares. In order to add public verifiability property to the scheme, we have modified Vadim’s identification protocol and leveraged it the scheme. Only the participants who have submitted correct sub-share can satisfy a third party that they have submitted the correct value. Verifiable versions, VMSS and PVMSS, makes this scheme a good option to be used in sophisticated protocols that trustworthy of parties are questionable. As a final advantage, to the best of our knowledge the presented scheme has the least number of public values.

The paper is structured as follows: in the Sect. 2 we introduce lattice concepts that are needed at the rest of this paper, presenting a scheme and assessing its security is next. Verifiable versions constitutes main core of the Sect. 4. The final section is dedicated to conclusion.

2 Preliminaries

In this section we review some concepts and introduce some notations which are needed in this paper. The notation $\in _r$ means choosing uniformly from a finite set. we will use the rot function which is defined as follows,

$$rot^j(A)=[a_{j+1},a_{j+2},\ldots ,a_n,a_1,\ldots ,a_j]$$

Definition 1

Suppose $b_1,b_2,\ldots ,b_m$ are m linearly independent vectors in ${{\mathbb {R}}}^n\,(m\le n)$. The lattice that generated by these vectors is linear integer combination of them,

$${\mathcal {L}}(b_1,b_2,\ldots ,b_m)=\left\{ \sum _{i=1}^{m}z_ib_i|z_i\in {{\mathbb {Z}}}\right\}$$

The vectors $b_1,b_2,\ldots ,b_m$ are a basis for the lattice. Basis is not unique and it can be shown that $B^{\prime}$ is another basis for ${\mathcal {L}}(B)$ if and only if $B^{\prime}=BU$ where U is an appropriate unimodular matrix.

Many problem such as shortest vector problem (SVP), closest vector problem (CVP) and the other well-known problems [24] play an important role in lattice theory. Many version of this problems are assessed. One of these versions is approximation version. In approximation version we have a function f along with the principal problem, and the aim is to find an answer which its norm is at most f times bigger than the exact answer. For instances, in approximation problem $SVP_{n^2}$ our goal is to find a vector in lattice which has norm at most $n^2$ time bigger than the shortest vector in lattice.

One specific problem is SIS which concludes the core of our scheme you can see its definition below.

Definition 2

[25] Suppose a matrix $A\in {\mathbb {Z}}^{m\times n}_p$ is given, find two vector $x,x'\in {\mathbb {Z}}^n$ such that $Ax\equiv Ax'({\text{mod}}\, p)$, and $\parallel x\parallel , \parallel x'\parallel \le 10n^{1.5}$.

SIS can be interpreted as finding a short solution for linear equation system $AX=Y({\text{mod}}\, p)$. For $n=[4m\log m]$ and some integer $p=\widetilde{\varTheta }(m^3)$ solving SIS can be reduced to solving $SIVP_{\widetilde{O}(n^2)}$ [25]. Vadim presented an identification scheme based on SIS problem [25]. This scheme is depicted in the following table. For more details interested readers are referred to the original paper. In this protocol Prover wants to convince the Verifier that he knows $\omega \in \{0,1\}^n$ where $Aw({\text{mod}}\, p)$ is public.

In secret sharing schemes two desirable goal are identifying fraudulent dealer and participants.

Definition 3

[14] A verifiable secret sharing scheme consists of a secret sharing scheme and a additional algorithm Verify such that participants can verify their shares: $\exists u\,\,\,\forall M\in \varGamma \,\,\, s.t.\,\,\, if\,\,\, \forall i\in M:Verify(s_i)=1\,\,\, then\,\,\, the\,\,\, participants$ who belongs to M recover u and $u=s$ (s is the secret) if dealer was honest.

Verifiability makes sure that participants recover same secret regardless of which authorized subset of participants are executing recovering process.

Definition 4

[14] A public verifiable secret sharing is a secret sharing such that participants can prove validity of their submitted sub-shares.

In public verifiable secret sharing scheme if a participant submits a wrong share, he/she cannot proof that the submitted value is valid.

3 Multi Secret Sharing Scheme

We use the lattice conceptions to introduce a threshold MSS scheme whose security is based on SIS problem. In presented scheme participants can recover any secret in any stage without compromising security of other secrets. Lets walk into the details of the scheme.

3.1 Share Distribution

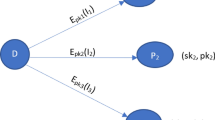
Dealer shares r secrets $S_1, S_2, \ldots ,S_r\in {{\mathbb {Z}}}_{q}^{m}$ among s participants $P_1,\ldots ,P_s$ in such a way that every $t \,\, (t\le s)$ participant can recover the secrets in an unordered manner. Dealer computes the private shares and public values as follows:

• 1. He/She chooses $d_i\in _r\{0,1\}^n,1\le i\le s$ and a random matrix $A_{m\times n}\in {\mathbb {Z}}_q^{m\times n}$ where $n=[4m\log m]$.

• 2. Chooses $Q_1(x),\ldots ,Q_{n}(x)\in _r {\mathbb {Z}}_q[x]$ of degree $s-1$ such that $d_i=[Q_1(i),\ldots ,$ $Q_{n}(i)]$

• 3. Sends $d_i$ to the ith participant, $1\le i\le s$, as their private share.

• 4. Publishes the values $S_i+Arot^i(\overline{Q}(0))$ ($\overline{Q}(x):=[Q_1(x),\ldots ,Q_{n}(x)]$) for $1\le i\le r$ and $\overline{Q}(-1),\ldots ,\overline{Q}(-s+t)$.

Sharing process is very simple and this facts makes the scheme applicable and efficient.

3.2 Secret Reconstruction

Now, we explain recovering secret process. Assume t participants, $P_{1}, P_{2},\ldots ,P_{t}$, collaborate to recover S _j , hence they compute and submit related sub-shares. The sub-share of $P_{i}$ corresponding to the secret S _j is:

$$Arot^j(d_{i})=Arot^j(\overline{Q}(i))$$

S _j can be recovered using these sub-shares and the public values. In the first step they compute $Arot^j(\overline{Q}(0))$ by interpolation:

$$\begin{aligned}Arot^j(\overline{Q}(0))&=\left( \sum _{i=1}^{t}\frac{(t!/i)(s-t)!}{(1-i)\cdots (-1)(t-i)!(i+s-t)!/i!}Arot^j(d_i)\right. \\ &\quad +\left. \sum _{i=-1}^{-s+t}\frac{t!(-1)\cdots (i-1)(i+1)\cdots (-s+t)}{(1-i)\cdots (t-i)(-1-i)\cdots (-1)(+1)\cdots (-s+t-i)}Arot^j\overline{Q}(i)\right) \\ & =A\left( \sum _{i=1}^{t}\frac{(t!/i)(s-t)!}{(1-i)\cdots (-1)(t-i)!(i+s-t)!/i!}rot^j\overline{Q}(i)\right. \\ &\quad +\left. \sum _{i=-1}^{-s+t}\frac{t!(-1)\cdots (i-1)(i+1)\cdots (-s+t)}{(1-i)\cdots (t-i)(-1-i)\cdots (-1)(+1)\cdots (-s+t-i)}rot^j\overline{Q}(i)\right) \end{aligned}$$

Consequently, S _j can be extracted easily with a minus operation;

$$S_j=\left( S_j+Arot^j(\overline{Q}(0))\right) -Arot^j(\overline{Q}(0))$$

As you can see, every subset of authorized participants can recover every secret in each stage without any constraint on the order of secret recovering. Clearly, all of this operation can be done in a efficient way which is one of the most desirable feature in any cryptographic protocol.

3.3 Security

In this section we will prove that the presented scheme is secure in term of constructing any subset of secrets does not cause constructing any other unrecovered secrets. We show that this scheme inherits its robustness from SIS problem.

Notice that If we look at recovering stages separately, it can be considered as a perfect secret sharing which means deficiency of any sub-share causes disability to recovering the secret similar to Shamir’s scheme [1]. Therefore, we can conclude that this scheme is secure if we can show that computing the sub-shares corresponding to unrecovered secret from the revealed sub-shares is computationally impossible. We can rewrite this problem in mathematical terminology as follows:

Problem 3.3

Suppose a matrix $A\in {\mathbb {Z}}_q^{m\times n}$ and $d\in \{0,1\}^n$ are chosen uniformly. Given $\{Arot^i(d)|i\in I\}$ where $card(I)m<n$, the aim is computing $Arot^j(d)$ such that $j\notin I$.

We will show that SIS problem can be reduced to the above problem. It means if there exists an adversary which solves the above problem, it is possible to build an adversary which solves the SIS problem.

Theorem 1

Assume that there exists an adversary $adv_1$ such that solves the Problem 3.3, then there exists an algorithm $adv_2$ such that given $\{Arot^i(d)|i\in I\}$, where $card(I)m<n$, computes d.

Proof

The adversary $adv_2$ invokes $adv_1$ and feeds it with $\{Arot^i(d)|i\in I\}$ and gets $Arot^j(d)$ afterwards $adv_2$ feeds $\{Arot^i(d)|i\in I\}\cup Arot^j(d)$ to $adv_1$ and builds another one. Repeating this procedure provides a system of linear equations which its solution is d. Then by solving this system of linear equations d can be extracted. $\hfill\square$

Theorem 2

Given $\{Arot^i(d)|i\in I\}$ where $card(I)m<n$ and $d\in _r\{0,1\}^n$, whit a high probability there exists $d'\in \{0,1\}^n$ such that

$$\{Arot^i(d)|i\in I\}=\{Arot^i(d')|i\in I\}$$

Proof

For simplicity assume that $I={1,2,\ldots ,k}$. Without loss of generality we can assume that $\left( Ad,\ldots ,Arot^k(d)\right) \in {{\mathbb {Z}}}^{km}_q$ is distributed uniformly in ${{\mathbb {Z}}}^{km}_q$. Therefore, the probability of collision is at least $1-{2^{km\log q}}/{2^n}$. Therefor, with a high probability there is a $d'$ such that $\{Arot^i(d)|i\in I\}=\{Arot^i(d')|i\in I\}$ holds. $\hfill\square$

Theorem 3

If there exists an algorithm $adv_1$ that solves the Problem 3.3, then we can solve SIS problem with high probability.

Proof

Suppose we have an algorithm $adv_1$ that solves the Problem 3.3. According to Theorem 1 there is an algorithm $adv_2$ such that if we feed $\{Arot^i(d)|i\in I\}$ to $adv_2$ the output would be d. In addition, in Theorem 2 we have proven that with a high probability there exist another $d'\in \{0,1\}^n$ such that $\{Arot^i(d)|i\in I\}=\{Arot^i(d')|i\in I\}$, hence output of $adv_2$ on $\{Arot^i(d)|i\in I\}$ with probability ${1}/{2}\left( 1-{2^{km\log q}}/{2^n}\right)$ would be $d'$ where $\{Arot^i(d)|i\in I\}=\{Arot^i(d')|i\in I\}$, so $A(d-d')=0$. In other words we have found a small vector $d-d'\in \{-1,0,1\}^n$ which satisfies the equation $Ax=0$. This means the SIS problem is solved. $\hfill\square$

In proving the security we stated a problem which solving it is equivalence to breaking our scheme. Then we demonstrate that solving this problem leads to a solution to SIS problem. Hence, we can conclude that the presented scheme is robust until SIS is intractable. In addition, we know that lattice is one of the approaches in post quantum cryptography. These facts conclude that the presented scheme resists possible quantum attacks.

4 Verifiable Versions of the Scheme

This section deals with introducing verifiable version of presented scheme. One of the must important issues in secret sharing scheme is verifiability [13]. Participants or dealer cannot always be trusted because the participants can submit wrong sub-share to discover the other participants shares and the dealer may share wrong shares among the participants in such way that different set of authorized participants recover different values. Thus a scheme should be resistant against deceiver participants and dealer.

4.1 Robustness Against Fraudulent Dealer

Here, we introduce verifiable version of the scheme that satisfying the Definition 3. In fact it is a manner to identify fraudulent dealer. Suppose the shares are distributed by the dealer. The participants easily can verify their shares. First of all they submit $Ad_i$ for $i=1,2,\ldots ,s$ alongside the public values $\overline{Q}(-1),\ldots ,\overline{Q}(-s+t)$ we obtain $2s-t$ points on the equation $A\overline{Q}(x)$, in addition $\overline{Q}(x)$ consists of n polynomials of degree s, so if the shares were distributed correctly, using every s values from $\{\overline{Q}(-1),\ldots ,\overline{Q}(-s+t)$, $Ad_i$ for $i=1,2,\ldots ,s\}$ and applying interpolation we should be able to compute the other $s-t$ values, otherwise the shares haven’t been distributed correctly. This method assure the participants that they have been received the correct shares and any t participants in each stage recover the same value.

4.2 Robustness Against Fraudulent Participants

Sometimes, a fraudulent participant can submit a wrong sub-share amid the secret recovering process. This would help him/her to attain the other participants share. Consequently he/she can recover the secret by others’ sub-share and his/her correct sub-share. Therefore we need a procedure which prevents participants to submit wrong sub-shares. Therefore we introduce PVMSS version of our scheme in this section. In our scheme using simple procedure any participants has to prove that he/she has submitted correct sub-share corresponding to the target secret.

Suppose in share distribution dealer publishes $Ad_i$ for $i=1,2,\ldots ,s$ alongside the public values. Publishing these values is crucial for verifying process. Hence, the ith participant in recovering the jth secret should be able to prove that he has submitted the correct sub-share, say $Arot^j(d_i)$. We showed Vadim’s authentication scheme (2) and the following chart is a modified version of it. In this procedure any participant can prove that he has submitted the correct sub-share. Suppose he has submitted W as his sub-share. If he delivers right value, he can convince verifier that $W=Arot^j(d_i)$ as follows,

Theorem 4

Participants can not convince the verifier while they have submitted wrong sub-shares.

Here is the sketch of proof. We refrain to go trough the details.

Proof

A simple comparison between Vadim’s scheme and the modified version shows that cheating probability in this process is at most half of probability of success of each adversary in Vadim scheme, because the relation $(*)$ satisfies iff $W=Arot^j(d_i)({\text{mod}}\, p)$. In addition, we can reduce this probability exponentially by repeating the process to make sure that a submitted sub-share is correct with a high probability. $\hfill\square$

5 Conclusion

To overcome the four shortcomings, which are listed in the introduction section, we present an MSS scheme based on SIS problem. First of all, it is a MSS scheme which means we can share many secrets while one share is assign to each participants. Assigning one share to participants makes managing participants’ share in terms of saving, sending, etc. easy. Furthermore, in recovering stage, we have no constraint on recovering secrets order and authorized participants can reconstruct any secret in any stage. Hence, the first shortcoming is resolved.

Regarding the second and third shortcomings, we enforced our scheme with verifiability, VMSS and PVMSS. The presented scheme is VMSS which means participants can check validity of their shares and it prevents dealer to distribute wrong shares. Moreover, pledging participants to submit correct sub-shares in each stage is another treasured advantage of verifiability, say PVMSS, because they cannot submit a fake value to see others sub-shares.

In order to tackle the fourth flaw, lattice conception SIS is leveraged. Using SIS as a basic primitive has two benefits. First, unlike the previous schemes that are based on numerical assumptions and need heavy mathematical operations, our scheme uses simple operations and, consequently, has less running time. This feature makes it a better choice to implement in facilities with limit resources. Second, its security is backed by the hardness of SIS problem. We proved that breaking the presented scheme leads to solving SIS problem. Adding this proof to the fact that lattice based cryptography is one of the approach in post quantum cryptography concludes that the presented scheme is beyond the boarder of possible quantum attacks.

One important factor in efficiency of a MSS scheme is the number of public values. In any MSS scheme releasing a number of public values is inevitable. In this paper, we tried to give a scheme with minimum number of public values while it captures the aforementioned properties. To the best of our knowledge, the presented scheme has the least number of public values. To demonstrate this claim a comprehensive comparison between our scheme and the other well-known MSS schemes is showed through the following table. In the Table n, m and t denote the number of participants, secrets and threshold respectively (Table 1).

Table 1 Comparing to the other MSS schemes

All in one, we have introduced an efficient lightweight secret sharing scheme that resolves the four mentioned shortcomings while it has least number of public values among the MSS schemes and resists against quantum attacks.