An Authentication and Key Agreement Mechanism for Multi-domain Wireless Networks Using Certificateless Public-Key Cryptography

Abstract

With rapid growth of mobile wireless networks, handheld devices are popularly used by people and many mobile applications have been rapidly developed. Mutual authentication and key agreement are very important security mechanisms in wireless network systems for preventing unauthorized network access, server impersonation attack and malicious attacks of the subsequent session message. Considering the limited computing capability of smart cards or mobile devices, the security scheme design suitable for these mobile devices is a nontrivial challenge. This paper presents an authentication and key agreement mechanism for multi-domain wireless networks using certificateless public key cryptography. Based on the computational Diffie–Hellman assumption and the random oracle model, we show that the proposed scheme is secure against an uncertified user and a malicious registration server simultaneously. As compared with the recently proposed schemes, our scheme enjoys less computational cost on the basis of BLS short signature scheme and has higher security level by exploiting the certificateless public key cryptography system. Moreover, our scheme can be used to mutual authentication and key agreement between members of distinct domains where all the servers use different system parameters. Efficiency analysis of related the security and computation overheads are given to demonstrate that our scheme is well suited for mobile devices with limited computing capability.

1 Introduction

Due to rapid growth in popularity of the Internet and wireless communications, many wireless E-commerce and business applications provide rapid and convenient resource accessing services to users. In order to provide security services in wireless networks, mutual authentication and key agreement are very important mechanisms in wireless network systems for preventing unauthorized network access, server impersonation attack and malicious attacks of the subsequent session message. The general approach to construct authentication and key agreement scheme is to use a public key infrastructure (PKI) in which a trusted authority, called certification authority, issues certificates to bind users and their public keys. However, the PKI is costly to use as it involves certificate revocation, storage, distribution, and verification. In order to overcome the above mentioned problem, identity-based cryptography (IBC) was firstly introduced by Shamir [1] in 1984. The main practical benefit of IBC is in greatly reducing the need for, and reliance on, the public key certificates. But IBC has the particularity to involve trusted authorities called private key generator (PKG) whose task is to compute users’ private key from their identity information. The PKG can generate the secret keys of all its users, so private key escrow becomes an inherent problem in IBC. Moreover, secret keys must be sent over a secure channel, which makes secret key distribution a daunting task [2].

To fill the gap between traditional cryptography and identity-based cryptography, Al-Riyami and Paterson proposed a new paradigm called certificateless public key cryptography (CL-PKC) [3]. It is intended to solve the key escrow issue which is inherent in identity-based cryptography, while at the same time, eliminate the use of certificates as in the conventional PKI, which is generally considered to be costly to use and manage. Currently, many CL-based cryptographic schemes have been proposed such as signature schemes [4–6] and authenticated key agreement protocols [7–9]. In addition, on the basis of BLS short signature scheme [10], some CL-based signatures schemes [11, 12] are proposed for low-bandwidth channels and/or low-computation power, such as PDAs or cell phones.

Now, handheld devices are popularly used by people and many mobile applications have been rapidly developed. Considering the limited computing capability of smart cards or mobile devices, the security scheme design based on traditional public-key systems is a nontrivial challenge because most cryptographic algorithms require many expensive computations. In 2006, Das et al. [13] proposed an efficient ID-based remote user authentication scheme with smart cards using bilinear pairings. Goriparthi et al. [14] showed that their scheme is insecure against forgery attack resulting in an adversary can always pass the authentication. Recently, Giri and Srivastava [15] proposed an improved scheme to withstand the forgery attack. Unfortunately it was shown by Tseng et al. [16, 17] that this scheme has too expensive computational cost for smart cards with limited computing capability. In addition, in [16] they showed that both [13] and [15] do not provide mutual authentication and key exchange between the user and the server and proposed a solution; in [17] Tseng et al. showed that [15] is unable to be used for a multi-server environment and proposed a more efficient scheme. However, all of schemes above face the key escrow issue as a result of adopting identity-based cryptography system. Moreover, their schemes assume that a single PKG will be responsible for issuing secret keys to members of a large-scale network or assume that different PKGs will share common system parameters and differ only in the master private key.

In this paper, we propose a mutual authentication and key exchange scheme using certificateless public key cryptography. The smart card is a low power computing device while a server is regarded as a powerful node. We shift the computational burden to the powerful node and reduce the computational cost required by smart cards. Compared with other secure schemes for wireless network regarding the security and computation overheads, we believe that our scheme is more efficient and more suitable for handheld devices with low computational capabilities on wireless communication. Our scheme has the following merits: (1) Users needn’t submit their passwords to the registration server and they can freely choose and change their password without any assistance from the server; (2) The bilinear pairing operations to be computed only at the server side, and our scheme adopts CL-based short signatures to further induce the user computational cost. This makes our scheme especially attractive for the applications with a powerful server and number of handheld devices with low computational capabilities. (3) The scheme can be used to mutual authentication and key agreement between members of distinct domains using different system parameters. (4) The scheme is secure against an uncertified user and a malicious registration server simultaneously under the computational Diffie–Hellman assumption [18, 19] in the random oracle [20]. (5) The scheme satisfies the enhanced partial forward secrecy and key control security attributes.

The remainder of this paper is organized as follows. The preliminaries for bilinear pairings and security definitions are given in the next section. The formal models of authentication and key agreement mechanism for multi-domain wireless networks using certificateless public key cryptography is described in Sect. 3. Section 4 describes a concrete CL-based mutual authentication and key agreement scheme for multi-domain wireless networks. The security analysis and discussions of the proposed scheme are presented in Sect. 5. In Sect. 6, the performance comparison among the proposed scheme and the recently proposed schemes is presented. Section 7 gives our conclusions.

2 Preliminaries

In this section, the mathematical preliminaries required to understand the authentication and key agreement mechanism presented in the sect. 4 are introduced. Using the notation of Boneh & Franklin [18], let $G_{1}$ be an additive group of prime order $q$ and $G_{2}$ be a multiplicative group of the same order $q$. Assume the existence of a map $\hat{{e}}$ from $G_{1}\times G_{1}$ to $G_{2}$. Typically, $G_{1}$ will be a subgroup of the group of points on an elliptic curve over a finite field, $G_{2}$ will be a subgroup of the multiplicative group of a related finite field and the map $\hat{{e}}$ will be derived from either the Weil or Tate pairing on the elliptic curve. The mapping $\hat{{e}}$ must be efficiently computable and has the following properties.

• 1. Bilinearity: $\hat{{e}}({ aP}, { bQ}) = \hat{{e}}(P, Q)^{ab}$ for all $P, Q\in G_{1}, a, b\in Z_q^*$.

• 2. Non-degeneracy: There exists $P$ and $Q\in G_{1}$ such that $\hat{{e}}(P, Q) \ne 1_{G2}$.

• 3. Computability: There is an efficient algorithm to compute $\hat{{e}}(P, Q)$ for all $P, Q \in G_{1}$.

  The security of our scheme described here relies on the hardness of the following problems.

Definition 1

Discrete Logarithm Problem (DLP): Given $Q \in G_{1}$ where $P$ is a generator of $G_{1}$, find an element $a \in Z_q^*$ such that aP = Q.

Definition 2

Computational Diffie–Hellman problem (CDHP) in $G_{1}$: Given (P, aP, bP), where $a, b \in Z_q^*$, compute abP.

3 Formal Models of Authentication and Key Agreement Mechanism

In the section, we present the generic model and security model of an authentication and key agreement mechanism for multi-domain wireless networks using certificateless public key cryptography. Smart cards are used to aid users to memorize their secret keys and some public parameters. Meanwhile, smart cards perform some cryptographic operations, such as generate login messages, authenticate the service server and so on. In our scheme, there are three entities involved in this scheme: the user with a smart card, the registration server and the service server, where the user and the registration server in a same domain, and the service server may be in a different domain.

3.1 Generic Model

The model of an authentication and key agreement mechanism for multi-domain wireless networks using certificateless public key cryptography consists of the following six algorithms:

The Setup Algorithm: On input of a security parameter $k$, the registration server (RS) uses this algorithm to produce its master public/private key pair. It also outputs some public parameters params which are the global public parameters for the system. Similarly, the service server (SS) obtains his private key and public parameters prms, if RS and SS in a same domain, $params = prms$.

The Registration Algorithm: On input of the system’s public parameters params and master pricate key of RS, the user U submits his identity ${ ID}_{U}$ to the RS, RS performs the registration algorithm to generate the user’s private key. Finally, RS loads related public information and the user’s private key into a smart card, and issues it to the user.

The Login Algorithm: On input of the user’s identity, user’s password and SS’s identity, the smart card performs the login algorithm to produce a login message $\upsigma$.

The User Authentication Algorithm: On input of the system’s public parameters of RS and SS, user’s public key and the login message $\upsigma$, the SS runs the user authentication algorithm to check whether the message $\upsigma$ is valid. If the validation does not hold, this algorithm outputs ”Reject”. Otherwise, the SS uses his private key to produce an authentication message.

The Server Authentication Algorithm: On input of the user’s password and the authentication message, the user runs the server authentication algorithm to check whether the authentication message is valid. If the validation holds, this algorithm outputs “Accept”. Otherwise, it outputs “Reject”.

Key Agreement Algorithm: On input of the both parties identity, user’s password and the message exchanged, the user runs the key agreement algorithm to produce a session key. Symmetrically, the SS runs this algorithm to produce a same session key.

3.2 Security Model

In this section, we discuss the definition of the security of an authentication and key agreement mechanism for multi-domain wireless networks using certificateless public key cryptography. The security of our scheme depends on the user authentication algorithm and the server authentication algorithm, where the former algorithm uses the CL-based short signature algorithm and the latter is implemented by running an authenticated key agreement protocol.

For certificateless cryptosystems, the widely accepted notion of security was defined by Al-Riyami and Paterson in [3]. According to their definitions as well as the definitions in [21], there are two types of adversary with different capabilities:

Type I Adversary: This type of adversary $A_{I}$ models a dishonest user who does not have access to the master private key of registration server but has the ability to replace the public key of any entity with a value of his choice.

Type II Adversary: This type of adversary $A_{II}$ models a malicious registration server who has access to the master private key but cannot perform public keys replacement.

Generally, there are five oracles which can be accessed by the adversaries according to the game specifications which will be given later.

• 1. Create-User: On input an identity ${ ID}_{U}$, if ${ ID}_{U}$ has already been created, nothing is to be carried out. Otherwise, the oracle runs the login algorithms to obtain the password $s_{U}$ and public key ${ PK}_{U}$. In this case, ${ ID}_{U}$ is said to be created. In both cases, ${ PK}_{U}$ is returned.

• 2. Public-Key-Replace: On input an identity ${ ID}_{U}$ and a user public key ${ PK}_U^{\prime }$, the original user public key of ${ ID}_{U}$ is replaced with ${ PK}_U^{\prime }$.

• 3. Password-Extract: On input an identity, it returns the corresponding user password $s_{U}$. Note that $s_{U}$ is the password value associated with the original public key ${ PK}_{U}$. This oracle does not output the password value associated with the replaced public key ${ PK}_U^{\prime }$.

• 4. Private-Key-Extract: On input an identity ${ ID}_{U}$, if ${ ID}_{U}$ has already been created, nothing is to be carried out. Otherwise, the oracle runs the registration algorithms to obtain the private key $D_{U}$. In both cases, $D_{U}$ is returned.

• 5. Sign: On input an identity ${ ID}_{U}$ and a time stamp $T$, returns a valid login message.

3.2.1 The Security of the User Authentication

In our scheme, the user authentication uses the CL-based short signature algorithm, and the standard notion of security for a signature scheme is called existential unforgeability against adaptive chosen message attack defined by Goldwasser, Micali and Revist [22]. We modify their notion slightly to adapt for our user authentication scheme. In our security model, we define two games, one for $A_{1}$ and the other for $A_{2}$.

Definition 3

If no polynomially bounded adversary $A_{1}$ has a non-negligible advantage in the following game, $A_{1}$ without knowing the user’s private key and password cannot generate the valid login message $\upsigma$, so that the service server can authenticate the user U.

Game

• Initial: The challenger $C$ runs the setup algorithm with a security parameter $k$ and sends the system parameters to the adversary $A_{1}$.

• Probing: In the probing phase, $A_{1}$ adaptively access all the oracles defined in Section 3.2 in a polynomial number of times.

• Forge: $A_{1}$ outputs a forgery $\sigma ^{*}$ for ${ ID}_{U}$ that is not produced by the Sign oracle, where the private key of ${ ID}_{U}$ is not asked, we say $A_{1}$ wins the game if the result of user authentication algorithm is not “Reject”.

The advantage of $A_{1}$ is defined as the probability that it wins.

Definition 4

If no polynomially bounded adversary $A_{2}$ has a non-negligible advantage in the following game, $A_{2}$ without knowing the user’s password cannot generate the valid login message $\sigma$, so that the service server can authenticate the user U.

Game

• Initial: The challenger $C$ runs the setup algorithm with a security parameter $k$ and sends the system parameters and RS’s private key to the adversary $A_{2}$.

• Probing: $A_{2}$ performs the same step just like in the Definition 3 except that the $A_{2}$ need not to adaptively access the Private-Key-Extract and Public-Key-Replace oracles.

• Forge: $A_{2}$ outputs a forgery $\sigma ^{*}$ for ${ ID}_{U}$ that is not produced by the Sign oracle, he cannot ask the password corresponding to ${ ID}_{U}$ and wins the game if the result of user authentication algorithm is not “Reject”.

The advantage of $A_{2}$ is defined as the probability that it wins.

3.2.2 The Security of the Server Authentication

In our scheme, the server authentication is implemented by running an authenticated key agreement protocol, and many key agreement protocols provide proof that adopts the extended formulation by Blake-Wilson [23] of the Bellare-Rogaway model [20]. In that model, the players do not deviate from the protocol and the adversary, whose capabilities are modelled through a pre-defined set of oracle queries, is not a player, but does control all the network communications. We use his model to test the security strength of our server authentication scheme.

In the BR model [20], each party involved in a session (run) of a protocol is treated as an oracle. An adversary can access the oracle by issuing the allowed queries. An oracle $\Pi _{i,j}^s$ denotes an instance $s$ of party $i$ involved with a partner party $j$ in a session where the instance of party $j$ is $\Pi _{j,i}^t$. The oracle $\Pi _{i,j}^s$ given an input message executes the prescribed protocol $\Pi$ and produces the output by $\Pi (1^{k},i,j,{ PK}_i, { SK}_i, P_j, conv_{i,j}^s, x) = (m,\delta _{i,j}^s, \sigma _{i,j}^s)$ where $x$ is the input message; $m$ is the output message; $1^{k}$ is the security parameter; ${ PK}_{i}$ is the public key information of party $i$; ${ SK}_{i}$ is the private key information of party $i$; $P_{j}$ is the public key of $j$; $\delta _{i,j}^s$ is the decision of the oracle, and $\sigma _{i,j}^s$ is the generated session key. Upon completion, $\Pi$ updates the conversation transcript $conv_{i,j}^s$ as $conv_{i,j}^s.x.m$. Here, $x.m$ denotes the concatenation of two strings, $x$ and $m$.

In the first phase, the adversary $A_{i}(i=1,2)$ can adaptively access the Create-User, Public-Key-Replace, Password-Extract and Private-Key-Extract oracles in a polynomial number of times, where $A_{2}$ doesn’t need to access Private-Key-Extract and Public-Key-Replace oracles. In addition, they can make the following queries:

• $\hbox {Send}(\Pi _{i,j}^s, x)$. $\Pi _{i,j}^s$ executes $\Pi (1^{k},i,j,{ PK}_i, { SK}_i, P_j, conv_{i,j}^s, x)$ and responds with $m$ and $\delta _{i,j}^s$. If the oracle $\Pi _{i,j}^s$ does not exist, it will be created. The Send query allows an adversary to send a message to any oracle $\Pi _{i,j}^s$, such that $i$ believes the message has been sent from $j$. The adversary may initiate protocol runs using such queries.

• $\hbox {Reveal}(\Pi _{i,j}^s)$. $\Pi _{i,j}^s$ reveals the private output $\sigma _{i,j}^s$ of the session if the oracle accepts. The Reveal query allows an adversary to ask an oracle $\Pi _{i,j}^s$ to reveal the session key it currently holds.

• $\hbox {Test}(\Pi _{i,j}^s)$. Allows an adversary to query an oracle $\Pi _{i,j}^s$ to output $\sigma _{i,j}^s$, which is either a true session key or a randomly generated key. The adversary then must guess if the key is real or not.

An oracle may be in one of the following states (it cannot be in more than one state).

• Accepted: If the oracle has decided to accept a session key, after receipt of properly formatted messages.

• Rejected: If the oracle has decided to not to accept and aborts the run of the protocol.

• *: If the oracle has yet to decide whether to accept to reject for this run of the protocol. We assume that there is some time out on this state.

• Opened: If a Reveal query has been performed against this oracle for its last run of the protocol (its current session key is revealed).

• Corrupted: If the oracle has responded to a corrupt query and revealed or replaced its private key. An oracle $\Pi _{i,j}^s$ is also corrupted if its public key is replaced in $\Pi _{j,i}^t$ (using the Replace query).

• Controlled: If the oracle has responded to a Coin query.

In the first phase, the adversary $A_{i}(i=1,2)$ can issue any number of queries to a set of oracles. When it has decided it has collected enough information, $A_{i}$ ends the first phase. In the second phase, $A_{i}$ issues a Test query to a fresh oracle $\Pi _{i,j}^s$, defined as follows.

Definition 5

(fresh oracle). An oracle $\Pi _{i,j}^s$ is fresh if (1) $\Pi _{i,j}^s$ has accepted (it knows the partner $j$); (2) $\Pi _{i,j}^s$ is unopened (has not been issued the Reveal query); (3) party $i$ is not both controlled and corrupted; (4) party $j\ne i$ is not corrupted; (5) there is an unopened oracle $\Pi _{j,i}^t$ which has had a matching conversation to $\Pi _{i,j}^s$.

After $A_{i}$ has issued the Test query, oracle $\Pi _{i,j}^s$, as a challenger, randomly chooses $b\in \{0, 1\}$ and responds with the session key $\sigma _{i,j}^s$ if $b=0$. Otherwise, it returns a random sample generated according to the distribution of the session secret $\sigma _{i,j}^s$. The adversary must guess the value of $b$ by issuing a prediction bit $b'$, and thus the advantage is defined to be

$$\begin{aligned} Adv(A_{i}) = {\vert }P[b' = b] -1/2{\vert } \end{aligned}$$

Definition 6

(benign adversary). An adversary is called a benign adversary if it faithfully conveys messages between two oracles $\Pi _{i,j}^s$ and $\Pi _{j,i}^t$.

In the face of a benign adversary, a secure authenticated key agreement protocol [24] is defined as follows:

Definition 7

A protocol is a secure AK, that is to say, our server authentication scheme is secure if:

• 1. In the presence of the benign adversary on $\Pi _{i,j}^s$ and $\Pi _{j,i}^t$, both oracles always accept holding the same session key $\sigma$, and this key is distributed uniformly at random on $\{0, 1\}^{k}$; and for every adversary $A_{i}(i=1,2)$:

• 2. If two oracles $\Pi _{i,j}^s$ and $\Pi _{j,i}^t$ have matching conversations and both $i$ and $j$ are uncorrupted, then both accept and hold the same session key $\sigma$;

• 3. $Adv(A_{i})$ is negligible.

4 Proposed Scheme

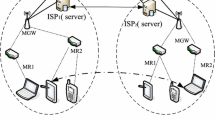
Here, we first present the multi-domain environment where all members of distinct domains use different system parameters. For each domain environment, there are a central registration server, $n$ service servers and many legal users. The multi-domain environment is depicted in Fig. 1. In many user authentication schemes [15, 25, 26], the server must keep a system secret to verify the user’s login message. If a user wants to access multiple servers, the user must register with each server individually and remember several identifiers and the corresponding secrets. In order to solve this problem, Tseng et al. [17] proposed a pairing-based user authentication scheme for a multi-server environment in distributed networks, but they scheme assumes that different servers will share common system parameters and differ only in the master private key. Moreover, all of schemes above are insecure against a malicious registration server.

Fig. 1

The multi-domain environment

In the following, we present our authentication and key agreement mechanism for multi-domain wireless networks using certificateless public key cryptography. Unlike other schemes [15, 25, 26], in our proposed scheme each service server does not keep the system private keys to authenticate users. Users do not need to register with each service server individually and remember several identifiers and the corresponding secrets. Compared to the schemes [17], our scheme can be used to mutual authentication and key agreement between members of distinct domains using different system parameters, and our scheme is secure against an uncertified user and a malicious registration server simultaneously. Thus, our proposed scheme is well suitable for the multi-domain environment in distributed networks. The details of algorithms in the proposed scheme are given as follows:

4.1 Setup Phase

Suppose $G_{1-i}$ is an additive cyclic group of prime order $q_{i}$, and $G_{2-i}$ is a multiplicative cyclic group of the same order. We assume that solving CDHP is hard in group $G_{1-i}$. Suppose $P_{i}$ is a generator of $G_{1-i}$. There exists a bilinear pairing map $\hat{{e}}_i$ from $G_{1-i}\times G_{1-i}$ to $G_{2-i}$ and cryptographic hash functions $H_{1-i}\, :\, \{0,1\}^{n} \rightarrow G_{1-i},\,H_{2-i}\, :\, \{0,1\}^{n}\times G_{1-i} \times \{0,1\}^{n}\times G_{1-i} \rightarrow G_{1-i}$ and $H_{3-i}\, :\, G_{1-i} \times G_{1-i} \rightarrow Z_{q_i}^*$. A server selects a random number $s_{i} \in Z_{q_i}^*$ as the private key and computes the public key $P_{{ pub}-i}=s_{i} P_{i}$. Suppose RS obtains his private key $s_{1}$ and system public parameters are $<G_{1-1},\,G_{2-1},\hat{{e}}_1, q_{1},P_{1},P_{{ pub}-1},H_{1-1}, H_{2-1},H_{3-1}>$, and SS chooses his private key $s_{2}$ and system public parameters are $<G_{1-2},G_{2-2}, \hat{{e}}_2, q_{2}, P_{2}, P_{{ pub}-2}, H_{1-2}, H_{2-2}, H_{3-2} >$. This phase is executed only once.

4.2 Registration Phase

The registration phase is depicted in Fig. 2. A user U first generates his username ${ ID}_{U}$, then he submits his identity ${ ID}_{U}$ to the registration server RS for registration. The registration server RS perform the following steps:

• 1. The registration server RS computes $Q_{U}= H_{1-1} ({ ID}_{U})$.

• 2. RS uses his private key $s_{1}$ to computes $D_{U}=s_{1}Q_{U}$.

• 3. RS loads $\hat{{e}}_1, P_{1}, P_{{ pub}-1}, H_{1-1}, H_{2-1}, H_{3-1}, D_{U}, Q_{U}$ and ${ ID}_{U}$ into a smart card and issues the smart card to the user U. The server stores the ${ ID}_{U}$ into its database.

Fig. 2

The registration phase

4.3 Mutual Authentication and Key Agreement Phase

This phase is executed whenever a user wants to log into the remote server to access the services. This phase is further divided into login, user authentication, server authentication and key agreement phases. In the login phase, user sends a login request to the SS. The SS first authenticates the user and then authenticates itself to the user. Finally, they establish a common session key after mutual authentication for the security of subsequent session message. Figure 3 depicts the mutual authentication and key agreement phase between the user U and the service server SS.

[Login phase]

In the login phase, if the user U wants to access the SS with the identity ${ ID}_{{ SS}}$, U inserts his smart card into the terminal, for the first time, the smart card asks the user U to enter his password, U selects his password $s_{U} \in Z_{q_1}^*$, and then the smart card computes U’s public key ${ PK}_{U}=s_{U} P_{1}$, the smart card stores $s_{U}$ and ${ PK}_{U}$. Otherwise, the user enters his identity ${ ID}_{U}$, his password and the service identity ${ ID}_{{ SS}}$. The smart card performs the following steps:

• 1. The smart card computes $Q'=H_{1-1} ({ ID}_{U})$ and ${ PK}'=s_{U} P_{1}$, and then checks if $Q'=Q_{U}$ and ${ PK}'={ PK}_{U}$. If they are correct, it continues next step, otherwise, terminates the operation

• 2. The smart card acquires the system public parameters of SS and the current time stamp $T_{1}$, then selects one random nonce $x \in Z_{q_1}^*$, computes $R_{1} =xP_{2},\,W=H_{2-1} ({ ID}_{U}, { PK}_{U}, T_{1},\,R_{1})$ and $V=D_{U}+s_{U} W$.

• 3. Finally, the smart card sends the login message $\sigma = ({ ID}_{U}, { ID}_{{ SS}}, T_{1}, R_{1}, V)$ to the service server SS, the login message can be viewed as a signature $(R_{1}, V)$ on the message $({ ID}_{U}, { ID}_{{ SS}}, T_{1})$.

[User Authentication Phase]

As receives the login message $({ ID}_{U},\,T_{1},\,R_{1},\,V)$ at time $T_{2}$. The service server SS performs the following operations to verify the login message.

• 1. The SS first verifies the validity of ${ ID}_{U}$ and ${ ID}_{{ SS}}$, then verifies the time interval between $T_{2}$ and $T_{1}$. If $(T_{2}-T_{1})\leqq \Delta t$, the SS proceeds to the next step. Otherwise, the login message is rejected. Here $\Delta t$ denotes the expected valid time interval for transmission delay.

• 2. The SS computes $W=H_{2-1} ({ ID}_{U}, { PK}_{U}, T_{1}, R_{1})$.

• 3. The SS accepts the login message if and only if the following equation holds: $\hat{{e}}_1 (P_1 ,V)=\hat{{e}}_1 (Q_U, P_{{ pub}-1}) \hat{{e}}_1 (W,{ PK}_U)$, otherwise the SS rejects it.

• 4. If the login message is correct, the SS acquires the current time stamp $T_{3}$ and selects one random nonce $y\in Z_{q_2}^*$, then computes $R_{2} = yP_{1}, { KB}_{1} = { yPK}_{U},\,{ KB}_{2} = s_{2} R_{1}$ and ${ Auth}=H_{3-2} ({ KB}_{1}, { KB}_{2})$. Finally, the SS sends $(R_{2}, T_{3}, { Auth})$ to the user U.

[Server Authentication Phase]

As receives the authentication message $(R_{2}, T_{3}, { Auth})$ at time $T_{4}$. The user U verifies the validity of the time interval between $T_{3}$ and $T_{4}$ for transmission delay. If $T_{3}$ is valid, the user authenticates the service server SS by checking whether ${ Auth} = H_{3-2} ({ KA}_{1}, { KA}_{2})$, where ${ KA}_{1} = s_{U} R_{2}$ and ${ KA}_{2}=xP_{{ pub}-2}$. It is obvious that ${ KA}_{1}=s_{U}R_{2} = ys_{U}P_{1}={ yPK}_{U}={ KB}_{1}$ and ${ KA}_{2}=xP_{{ pub}-2}=s_{2}xP_{2}=s_{2} R_{1}={ KB}_{2}$.

[Key Agreement Phase]

After mutual authentication between the user U and the service server SS, they respectively computes the session key $MK_{A}=H(K_{{ AB}} {\vert }{\vert } { KA}_{1} {\vert }{\vert } { KA}_{2})$ and $MK_{B}=H(K_{{ AB}} {\vert }{\vert } { KB}_{1} {\vert }{\vert } { KB}_{2}) = MK_{A} = MK_{{ AB}}$, where $K_{{ AB}} ={ ID}_{U} {\vert }{\vert } PK_{U} {\vert }{\vert } T_{1} {\vert }{\vert } R_{1} {\vert }{\vert } { ID}_{{ SS}} {\vert }{\vert } P_{{ pub}-2} {\vert }{\vert } T_{3} {\vert }{\vert } R_{2}$ and $H$ is a key derivation function. Thus, we come to the conclusion that the two communication entities successfully established a common session key $MK_{{ AB}}$.

Fig. 3

The mutual authentication and key agreement phase

In the following, we present the correctness of the verification equation in user authentication phase.

$$\begin{aligned}&\hat{{e}}_1 (Q_U ,P_{{ pub}-1} )\hat{{e}}_1 (W,PK_U ) =\;\hat{{e}}_1 (P_1 ,s_1 Q_U +s_U W) \\&\quad =\hat{{e}}_1 (P_1 ,D_U +s_U W)=\hat{{e}}_1 (P_1 ,V) \end{aligned}$$

4.4 Password Change Phase

This phase is invoked whenever the user U wants to change his password. This phase does not require any interaction with the servers and works as follows:

• 1. U inserts the smart card into the terminal and enters his identity ${ ID}_{U}$ and password $s_{U}$. The smart card computes $Q'=H_{1-1} ({ ID}_{U})$ and ${ PK}'=s_{U}P_{1}$, and then checks if $Q'=Q_{U}$ and ${ PK}'= PK_{U}$. If they are correct, it continues next step, otherwise, terminates the operation.

• 2. The smart card allows U to submits a new password $s_U^{\prime }$, then the smart card computes ${ PK}_U^{\prime } =s_U^{\prime } P_{{ pub}-1}$.

• 3. The smart card stores new $s_{U^{\prime }}$ and ${ PK}_U^{\prime }$.

5 Security Analysis

Based on the discrete logarithm problem and computational Diffie–Hellman problem in the random oracle model, we show that the proposed scheme offers mutual authentication, known session key security, key-compromise impersonation, unknown key share, enhanced partial forward secrecy and key control security attributes.

5.1 Providing Mutual Authentication

On one hand, we show that the service server can authenticate the user. In our scheme, the login messages $({ ID}_{U},\,T_{1},\,R_{1},\,V)$ is viewed as a signature $(R_{1},\,V)$ on the message $({ ID}_{U}, { ID}_{{ SS}}, T_{1})$. We respectively prove that type I adversary without knowing the private key of the user U in following Theorem 1 and type II adversary without knowing the password of the user U in following Theorem 2 cannot forge a valid signature on the message $({ ID}_{U}, { ID}_{{ SS}}, T_{1})$.

On the other hand, we prove that the user U can authenticate the service server. In our scheme, after user authentication phase, the service server generates the authentication message $(R_{2}, T_{3}, Auth)$, the user can compute and verify the Auth value by running an instance of our authenticated key agreement protocol. We respectively prove that type I adversary without knowing the private key of the user U in following Theorem 3 and type II adversary without knowing the password of the user U in following Theorem 4 cannot compute the Auth value.

Theorem 1

In the random oracle model, we assume we have an adversary called $A_{1}$ succeeds during the game of Definition 3 with an advantage $Adv (A_{1})$ when asking at most $q_{i}\,H_{i}\,\hbox {queries}(i=1,2)$, at most $q_{c}$ Create-User queries, $q_{p}$ Password-Extract queries, $q_{r}$ Public-Key-Replace queries, $q_{k}$ Private-Key-Extract queries and $q_{s}$ Sign queries. Then, there exists a distinguisher $C$ that can solve the Computational Diffie–Hellman problem with an advantage $Adv(C)^{CDH} > ((q_1 -q_k )(q_1 -q_s )/(q_{_1 }^2 (q_1 -1)))\cdot Adv(A_1)$.

Proof

Let $P$ be the generator of $G_{1}$.We assume the distinguisher $C$ receives a random instance (P, aP, bP) of the Computational Diffie–Hellman problem. His goal is to computeabP. $C$ will run $A_{1}$ as a subroutine and act as $A_{1}$’s challenger in the game of Definition 3. To maintain consistency between queries made by $A_{1},\,C$ keeps the following lists: $L_{i}$ for $i = 1,2$ of data for query/response pairs to random oracle $H_{i}$; $L_{u}$ of the queries made by $A_{1}$ to the Create-User oracle and $L_{s}$ of the queries generated by $A_{1}$ to the Sign oracle. At the beginning of the game, $C$ gives $A_{1}$ the system parameters of RS and SS, we define RS’s system public parameters are $<G_{1},G_{2},\hat{{e}},q,P,P_{{ pub}},H_{1},H_{2},H_{3}>$ and SS’s system public parameters are $<G_{1-2},G_{2-2},\hat{{e}}_2, q_{2}, P_{2}, P_{{ pub}-2}, H_{1-2}, H_{2-2}, H_{3-2}>$, where $P_{{ pub}} =aP$ is the input of the CDH problem.

Create-User: On a new Create-User query for user U, $C$ chooses a random number $s_{U}\in Z_q^*$ and computes ${ PK}_{U}=s_{U} P$. Then, he adds $({ ID}_{U}, s_{U}, PK_{U})$ into the list $L_{u}$ and returns ${ PK}_{U}$ to $A_{1}$.

$\mathbf {H}_{1}$ queries: $C$ chooses a random number $i_{b}\in \{1,2,{\ldots },q_{1}\}$ first. $A_{1}$ asks a polynomially bounded number of $H_{1}$ queries on identities of his choice. At the $i_{b}$-th $H_{1}$ query, $C$ sets $w= \bot ,\,{ ID}_{b}={ ID}_{U}$ and $H_{1}({ ID}_{U})=bP$. For others queries, $C$ chooses a random number $w\in Z_q^*$, and sets $H_{1} ({ ID}_{U}) = wP$. In both cases, then $C$ will puts the pair $({ ID}_{U}, w, H_{1}({ ID}_{U}))$ in list $L_{1}$ and answers $H_{1}({ ID}_{U})$.

$\mathbf {H}_{2}$ queries: $C$ searches an element $({ ID}_{U}, PK_{U}, T_{1}, R_{1}, W)$ in the list $L_{2}$. If such an element is found, $C$ answers $W$, otherwise he answers $A_{1}$ by a random number $W\in G_{1}$ and puts the $({ ID}_{U}, PK_{U}, T_{1}, R_{1}, W)$ into list $L_{2}$.

Public-Key-Replace: $A_{1}$ can request to replace public key ${ PK}_{U}$ of a user U with new public key ${ PK}_U^{\prime }$ chosen by $A_{1}$ itself. $C$ replaces the original public key ${ PK}_{U}$ with ${ PK}_U^{\prime }$ if ${ ID}_{U}$ has been created. Otherwise, $C$ executes Create-User query to generate $({ ID}_{U}, s_{U}, PK_{U})$, then sets ${ PK}_{U}=PK_U^{\prime }$ and adds $({ ID}_{U}, s_{U}, PK_U^{\prime })$ to the $L_{u}$. Here, to replace a public key, the password value corresponding to the new public key is not required.

Password-Extract: On a Password-Extract query of ${ ID}_{U}$, We assume that Create-User query for ${ ID}_{U}$ has been asked. $C$ will check the list $L_{u}$ and return $s_{U}$ to $A_{1}$.

Private-Key-Extract: On a Private-Key-Extract query of ${ ID}_{U}$, We assume that $H_{1}$ query for ${ ID}_{U}$ has been asked. If ${ ID}_{U} = { ID}_{b}$, then $C$ fails and stops. Otherwise, $C$ searches a pair $({ ID}_{U}, w, H_{1}({ ID}_{U}))$ corresponding to ${ ID}_{U}$ in the list $L_{1}$, then computes $D_{U} = wP_{{ pub}}$ and returns $D_{U}$ as the answer.

Sign queries: We will assume that $A_{1}$ makes the Create-User(${ ID}_{1}$) query before it makes a Sign query for identities ${ ID}_{1}$. We have the following two cases to consider.

• Case 1: ${ ID}_{1} \ne { ID}_{b}$. $C$ obtains the private key $D_{1}$ and password $s_{1}$ corresponding to ${ ID}_{1}$ by running the Private-Key-Extract query and Password-Extract query algorithms. Then $C$ acquires the current time stamp $T_{1}$, selects one random nonce $x\in Z_q^*$, computes $R_{1} = xP_{2},\,W=H_{2} ({ ID}_{1}, PK_{1}, T_{1}, R_{1})$ and $V=D_{1} + s_{1} W$. $C$ returns the login message $({ ID}_{1},\,{ ID}_{{ SS}},\,T_{1},\,R_{1},\,V)$ to $A_{1}$.

• Case 2: ${ ID}_{1} ={ ID}_{b}$. $C$ fails and stops.

At last, $A_{1}$ outputs a valid forgery $\sigma ^{*}=({ ID}_{A},\,{ ID}_{{ SS}},\,T^{*},R^{*},V^{*})$, where the private key of ${ { ID}}_{A}$ is not asked. If ${ ID}_{A} \ne { ID}_{b},\,C$ aborts. Otherwise, he obtains the $s_{A}$ and ${ PK}_{A}$ by running the Password-Extract query and Create-User query algorithms, then $C$ computes $W^{*} =H_{2}({ ID}_{A}, PK_{A}, T^{*}, R^{*})$, we can have $V^{*} = \theta + s_{A}W^{*}$ (where $\theta =V^{*}-s_{A}W^{*}$ is $C$ candidate for the CDH problem). Finally, $C$ checks that $\hat{{e}}(P,V)=\hat{{e}}(bP,aP)\hat{{e}}(W^{*},PK_A)$, if so, $C$ answers 1, else answers 0.

We now have to assess $C$’s probability of success. Note that $C$ fails if $A_{1}$ has asked a Private-Key-Extract query on ${ ID}_{b}$, we know that the probability for $C$ not to fail is $(q_{1}-q_{k})/q_{1}$; Further, $C$ fails if $A_{1}$ has asked a Sign query on ${ ID}_{b}$, we know that the probability for $C$ not to fail is $(q_{1}-q_{s})/q_{1}$; At last, $C$ fails if $A_{1}$ does not choose to be challenged on the pair $({ ID}_{A}, { ID}_{{ SS}})$ with ${ ID}_{A} ={ ID}_{b}$, among those $q_{1}$ identities and at least one of them will be the subject of a Private-Key-Extract or Sign query from $A_{1}$, so $C$ does not fail with a probability greater than $1/(q_{1}-1)$. Taking into account all the probabilities that $C$ will not fail its simulation, the value of $Adv(C)$ is calculated as follows:

$$\begin{aligned}&Adv(C)^{CDH(G_1 ,P)} \\&\quad > ((q_1 -q_k )/q_1 )\cdot ((q_1 -q_s )/q_1 )\cdot (1/(q_1 -1))\cdot Adv\,(A_1 ) \\&\quad =((q_1 -q_k )(q_1 -q_s )/(q_{_1 }^2 (q_1 -1)))\cdot Adv\,(A_1 ) \end{aligned}$$

Theorem 2

In the random oracle model, we assume we have an adversary called $A_{2}$ succeeds during the game of Definition 4 with an advantage $Adv (A_{2})$ when asking at most $q_{i}\,H_{i}\, \hbox {queries}(i = 1,2)$, at most $q_{c}$ Create-User queries, $q_{p}$ Password-Extract queries, $q_{k}$ Private-Key-Extract queries and $q_{s}$ Sign queries. Then, there exists a distinguisher $C$ that can solve the Computational Diffie–Hellman problem with an advantage $Adv(C)^{CDH} > ((q_c -q_k )(q_c -q_s )/(q_c^2 (q_c -1)))\cdot Adv\,(A_2 )$.

Proof

Let $P$ be the generator of $G_{1}$.We assume the distinguisher $C$ receives a random instance (P, aP, bP) of the Computational Diffie–Hellman problem. His goal is to computeabP. $C$ will run $A_{2}$ as a subroutine and act as $A_{2}$’s challenger in the game of Definition 4. To maintain consistency between queries made by $A_{2},\,C$ keeps the following lists: $L_{i}$ for $i= 1,\,2$ of data for query/response pairs to random oracle $H_{i}$; $L_{u}$ of the queries made by $A_{2}$ to the Create-User oracle and $L_{s}$ of the queries generated by $A_{2}$ to the Sign oracle. At the beginning of the game, $C$ gives $A_{2}$ the private key $s$ of RS and system parameters of RS and SS, we define RS’s system public parameters are $<G_{1},G_{2},\hat{{e}},q,P,P_{{ pub}},H_{1},H_{2}, H_{3}>$ and SS’s system public parameters are $<G_{1-2},G_{2-2},\hat{{e}}_2,q_{2},P_{2},P_{{ pub}-2},H_{1-2}, H_{2-2},H_{3-2}>$.

Create-User: On a new Create-User query for user U, $C$ chooses one random numbers $i_{b}\in \{1, 2,{\ldots },q_{c}\}$ first. At the $i_{b}$-th query, $C$ sets $s_{U}=\bot ,\,{ ID}_{b}={ ID}_{U}$ and ${ PK}_{U}=aP$. For others queries, $C$ chooses a random number $s_{U}\in Z_q^*$ and computes ${ PK}_{U}=s_{U} P$. In both cases, $C$ adds $({ ID}_{U}, s_{U}, PK_{U})$ into the list $L_{u}$ and returns ${ PK}_{U}$ to $A_{2}$.

$\mathbf {H}_{1}$ queries: $C$ chooses a random number $w\in Z_q^*$, and sets $H_{1} ({ ID}_{U}) = wP$. Then $C$ puts the pair $({ ID}_{U}, w, H_{1} ({ ID}_{U}))$ in list $L_{1}$ and answers $H_{1} ({ ID}_{U})$.

$\mathbf {H}_{2}$ queries: $C$ searches an element $({ ID}_{U}, PK_{U}, T_{1}, R_{1}, h_{2}, W)$ in the list $L_{2}$. If such an element is found, $C$ answers $W$, otherwise $C$ chooses a random number $h_{2} \in Z_q^*$, and sets $W=h_{2} P+bP$. Then $C$ puts the pair $({ ID}_{U}, PK_{U}, T_{1}, R_{1}, h_{2}, W)$ in list $L_{2}$ and answers $W$.

Password-Extract: On a Password-Extract query of ${ ID}_{U}$, We assume that Create-User query for ${ ID}_{U}$ has been asked. If ${ ID}_{U} = { ID}_{b}$, then $C$ fails and stops. Otherwise, $C$ searches a pair $({ ID}_{U}, s_{U}, PK_{U})$ corresponding to ${ ID}_{U}$ in the list $L_{u}$, then return $s_{U}$ to $A_{2}$.

Sign queries as in the proof of the Theorem 1.

At last, $A_{2}$ outputs a valid forgery $\sigma ^{*} = ({ ID}_{A},\,{ ID}_{{ SS}},\,T^{*},\,R^{*},\,V^{*})$, where the password of ${ ID}_{A}$ is not asked. If ${ ID}_{A} \ne { ID}_{b},\,C$ aborts. Otherwise, he runs the $H_{2}$ simulation algorithm to obtain $W^{*} = h_{2} P+bP$, we can have $V^{*}=D_{A}+a(h_{2} P+bP)$ and $\theta =V^{*}$ $-D_{A}-h_{2} aP$ (where $\theta$ is $C$ candidate for the CDH problem). Finally, $C$ Check that $\hat{{e}}(P,V)=\hat{{e}}(Q_A ,P_{{ pub}} )\hat{{e}}(W^{*},aP)$, if so, $C$ answers 1, else answers 0.

We now have to assess $C$’s probability of success. Note that $C$ fails if $A_{2}$ has asked a password query on ${ ID}_{b}$. We know that the probability for $C$ not to fail is $(q_{c}-q_{p})/q_{c}$; Further, $C$ fails if $A_{2}$ has asked a Sign query on ${ ID}_{b}$, we know that the probability for $C$ not to fail is $(q_{c}-q_{s})/q_{c}$; At last, $C$ fails if $A_{2}$ does not choose to be challenged on the pair $({ ID}_{A}, { ID}_{{ SS}})$ with ${ ID}_{A} = { ID}_{b}$, among those $q_{c}$ identities and at least one of them will be the subject of a Password-Extract or Sign query from $A_{2}$, so $C$ does not fail with a probability greater than $1/(q_{c}-1)$. Taking into account all the probabilities that $C$ will not fail its simulation, the value of $Adv (C)$ is calculated as follows:

$$\begin{aligned}&Adv(C)^{CDH(G_1 ,P)} \\&\qquad > ((q_c -q_p )/q_c )\cdot ((q_c -q_s )/q_c )\cdot (1/(q_c -1))\cdot Adv\,(A_2) \\&\qquad =((q_c -q_k )(q_c -q_s )/(q_c^2 (q_c -1)))\cdot Adv\,(A_2 ) \end{aligned}$$

Theorem 3

The server authentication scheme is secure, provided that $H_{1}$ is random oracles and the Computational Diffie–Hellman problem is hard. Specifically, assume that the Type-I adversary $A_{1}$ has non-negligible advantage $Adv(A_{1})$ in computing authentication value Auth, making at most $q_{c}$ Create-User queries, $q_{p}$ Password-Extract queries, $q_{r}$ Public-Key-Replace queries and $q_{k}$ Private-Key-Extract queries. Let $q_{n}$ be the total number of the oracles that $A_{1}$ creates. Then there exists an algorithm $C$ solve the CDH problem with an advantage $1/q_{n}\cdot Adv(A_{1})$.

Proof

Condition 1 follows from the assumption that the two oracles follow the protocol and $A_{1}$ is benign. In this case, both oracles accept (since they both receive correctly formatted messages from the other oracle) holding the same authentication value $Auth$(since ${ KA}_{1} = { KB}_{1}$ and ${ KA}_{2} = { KB}_{2}$).

Condition 2 follows from the fact that if the two oracles are uncorrupted, then they cannot be impersonated, and if they are partners then each has received properly formatted messages from the other. So they will both accept holding the same authentication value Auth. In the following, we show that the Condition 3 is also satisfied.

We shall slightly abuse the notation $\Pi _{A,{ SS}}^n$ to refer to the $n$-th one among all the $q_{n}$ participant instances in the game, instead of the $n$-th instance of participant $A$. As $n$ is only used to help identify oracles, this notation change will not affect the soundness of the model.

Let $P_{2}$ be the generator of $G_{1-2}$. We assume the simulator $C$ receives a random instance ($P_{2}, aP_{2}, bP_{2}$) of the Computational Diffie–Hellman problem. His goal is to compute and output $abP_{2}$. $C$ will run $A_{1}$ as a subroutine to solve the CDH problem with non-negligible probability. To maintain consistency between queries made by $A_{1},\,C$ keeps the following lists: $L_{1}$ for query/response pairs to random oracle $H_{1}$ and $L_{u}$ of the queries made by $A_{1}$ to the Create-User oracle. At the beginning of the game, $C$ gives $A_{1}$ the system parameters of RS and SS, we define RS’s system public parameters are $<G_{1}, G_{2}, \hat{{e}}, q, P, P_{{ pub}}, H_{1}, H_{2}, H_{3}>$ and SS’s system public parameters are $<G_{1-2}, G_{2-2}, \hat{{e}}_2, q_{2}, P_{2}, P_{{ pub}-2}, H_{1-2}, H_{2-2}, H_{3-2}>$, where $P_{{ pub}-2} = aP_{2}$ is the input of the CDH problem.

Create-User, Public-Key-Replace, Password-Extract queries as in the proof of the Theorem 1.

$\mathbf {H}_{1}$ queries: $C$ chooses a random number $w\in Z_q^*$, and sets $H_{1} ({ ID}_{U}) = { wP}$, then $C$ will puts the pair $({ ID}_{U}, w, H_{1} ({ ID}_{U}))$ in list $L_{1}$ and answers $H_{1} ({ ID}_{U})$.

Private-Key-Extract: On a Private-Key-Extract query of ${ ID}_{U}$, We assume that $H_{1}$ query for ${ ID}_{U}$ has been asked. $C$ searches a pair $({ ID}_{U}, w, H_{1} ({ ID}_{U}))$ corresponding to ${ ID}_{U}$ in the list $L_{1}$, then computes $D_{U} = wP_{{ pub}}$ and returns $D_{U}$ as the answer.

Send queries: $C$ chooses a random number $\pi \in \{1,2, {\ldots }, q_{n} \}$ first. For any oracle $\Pi _{A,{ SS}}^n$, at the $\pi$-th Send query, $C$ answers by $R_{1} = bP_{2}$. For others queries, $C$ chooses a random number $d_{i}\in Z_q^*$ and answers $d_{i}P_{2}$.

Test queries: At some point in the simulation, $A_{1}$ will ask a single Test query of some oracle. If $A_{1}$ does not choose the guessed oracle $\Pi _{A,{ SS}}^\pi$ to ask the Test query, then $C$ aborts.

Output: At the end of the game, the algorithm $A_{1}$ outputs an authentication value Auth of the form $H_{3-2}(K_{1}, K_{2})$, where $K_{1}, K_{2}\in G_{1}$.

Solving the CDH Problem: $C$ outputs $K_{2}$ as its guess for the value $abP_{2}$.

Now we evaluate the probability that $C$ does not abort. Note that $C$ fails if $A_{1}$ does not choose the guessed oracle $\Pi _{A,{ SS}}^\pi$ to ask the Test query, we know the adversary has chosen the $\pi$-th oracle as the test oracle with a probability $1/q_{n}$. We have

$$\begin{aligned} \textit{Adv(C does not abort)} > 1/q_{n} \end{aligned}$$

Note that participant SS has the public key $P_{{ pub}-2} = aP_{2}$. Given a message $bP_{2}$, part of the agreed authentication value Auth is $abP_{2}$. So if the adversary computes the correct session key with non-negligible probability $Adv(A_{1})$, then $C$ answers the CDH problem correctly with probability with $1/q_{n}\cdot Adv(A_{1})$, contradicting to the hardness of the CDH problem.

Theorem 4

The server authentication scheme is secure, provided that $H_{3-2},\,H_{1}$ is random oracles and the Computational Diffie–Hellman problem is hard. Specifically, suppose the Type-II adversary $A_{2}$ against the scheme with non-negligible probability $Adv(A_{2})$ and in the attack $H_{3-2}$ has been queried $q_{h}$ times at most and $q_{n}$ oracles have been created. Then there exists an algorithm $C$ solve the CDH problem with an advantage $2(q_c -q_p )Adv(A_2 )/(q_c \cdot q_n )$.

Proof

The proof follows along similar lines to the proof of Theorem 3. We assume the simulator $C$ receives a random instance (P, aP, bP) of the Computational Diffie–Hellman problem. His goal is to compute abP. $C$ will run $A_{2}$ as a subroutine to solve the CDH problem with non-negligible probability. To maintain consistency between queries made by $A_{2},\,C$ keeps the following lists: $L_{1}$ for query/response pairs to random oracle $H_{1}$; $L_{u}$ of the queries made by $A_{2}$ to the Create-User oracle and $L_{h}$ of some of the queries made by $A_{2}$ to the $H_{3-2}$ oracle. At the beginning of the game, $C$ gives $A_{2}$ the system parameters and private key $s$ of RS, we define RS’s system public parameters are $<G_{1}, G_{2}, \hat{{e}}, q, P, P_{{ pub}}, H_{1}, H_{2}, H_{3}>$ and SS’s system public parameters are $<G_{1-2}, G_{2-2}, \hat{{e}}_2, q_{2}, P_{2}, P_{{ pub}-2}, H_{1-2}, H_{2-2}, H_{3-2}>$.

The algorithm $C$ selects one random integers $\tau$ from $\{1,2,{\ldots },q_{n}\}$ and works by interacting with $A_{2}$ as follows:

Create-User, Password-Extract queries as in the proof of the Theorem 2.

$\mathbf {H}_{1}$ queries: $C$ chooses a random number $w\in Z_q^*$, and sets $H_{1} ({ ID}_{U}) = wP$, then $C$ will puts the pair $({ ID}_{U}, w, H_{1} ({ ID}_{U}))$ in list $L_{1}$ and answers $H_{1} ({ ID}_{U})$.

$\mathbf {H}_{3-2}$ queries: Upon receiving a $H_{3-2}$ query, $C$ first searches $L_{h}$ for the tuple with $(K_{1}, K_{2}, h)$, where $K_{1}, K_{2}\in G_{1}$. If the requested input is already on the list, then the corresponding $h$ is returned, otherwise a random $h\in \{0,1\}^{n}$ is responded and a new entry is inserted into the list $L_{h}$.

Send queries: For any oracle $\Pi _{A,{ SS}}^n$, at the $\tau$-th Send query, $C$ answers by $R_{2} = bP$. For others queries, $C$ chooses a random number $d_{i}\in Z_q^*$ and answers $d_{i}P$.

Reveal queries: Upon receiving a Reveal query, $C$ outputs the appropriate session key, except if $A_{2}$ asks the oracle $\Pi _{A,{ SS}}^\tau$ to ask the Test query, then $C$ aborts.

Test queries: At some point in the simulation, $A_{2}$ will ask a single Test query of some oracle. If $A_{2}$ does not choose the guessed oracle $\Pi _{A,{ SS}}^\tau$ to ask the Test query, then $C$ aborts; otherwise, $C$ randomly picks a value $\beta$ from the session key space and responds to $A_{2}$ with $\beta$.

Output: At the end of the game, the algorithm $A_{2}$ outputs its guess.

Solving the CDH Problem: $C$ picks a tuple of the form $(K_{1}, K_{2}, h)$ from $L_{h}$ and returns $K_{1}$ as the response to the CDH challenge.

Now we evaluate the probability that $C$ does not abort, Note that $C$ fails if $A_{2}$ has asked a Private-Key-Extract query on ${ ID}_{b}$. We know that the probability for $C$ not to fail is $(q_{c}-q_{p})/q_{c}$; Further, if the test session is the $\tau$-th oracle, then the simulation goes through. The probability that the simulator has chosen the right session is $1/q_{n}$, because a randomly chosen oracle is the initiator of the test session is $1/q_{n}$. We have

$$\begin{aligned} Adv\left( \textit{C does not abort} \right)&> (q_c -q_p)/q_c \;\cdot \;1/q_n \\&= (q_c -q_p )/ (q_c \cdot q_n ) \end{aligned}$$

According to the simulation of the Send query, the test oracle $\Pi _{A,{ SS}}^\tau$ must have obtained the value $R_{2} = bP$. The oracle should hold an authentication value Auth of the form $H_{3-2}(K_{1}, K_{2})$, in which $K_{1} =abP$.

Let $\hat{H}$ be the event that abP as $K_{1}$ has been queried to $H_{3-2}$. Because $H_{3-2}$ is a random oracle, we have $P[A_{2} \hbox {wins}{\vert } \lnot \hat{H}] = 1/2$. Then

$$\begin{aligned} \hbox {P}\left[ {A_2 \hbox {wins}} \right]&= \hbox {P}\left[ {A_2 \hbox {wins}|\lnot \hat{{H}}} \right] \hbox {P}\left[ {\lnot \hat{{H}}} \right] +\hbox {P} \left[ {A_2 \hbox {wins}|\hat{{H}}} \right] \hbox {P}\left[ {\hat{{H}}} \right] \\\quad&\le \hbox { P}\left[ {A_2 \hbox {wins}|\lnot \hat{{H}}} \right] \hbox {P}\left[ {\lnot \hat{{H}}} \right] +\hbox {P}\left[ {\hat{{H}}} \right] \\&= 1/2 \left( {\hbox {P}\left[ {\lnot \hat{{H}}} \right] } \right) +\hbox {P}\left[ {\hat{{H}}} \right] \\&= 1/2+1/2\left( {\hbox {P}\left[ {\hat{{H}}} \right] } \right) \end{aligned}$$

It follows that $P[\hat{H}] \ge 2 Adv(A_{2})$. Combining all the above results, we have that $C$ solves the CDH problem with probability at least $2(q_c -q_p )Adv(A_2 )/(q_c \cdot q_n)$, contradicting to the hardness of the CDH problem.

5.2 Further Security Considerations

In this section we will heuristically argue that the authentication and key agreement scheme satisfies the following security properties.

• 1. Known session key security (KSKS): The session key of our protocol varies with every protocol run since it is established according to the values of the protocol entities’ ephemeral private keys ($x$ and $y$) in the specific session. Hence, if one session key is compromised this does not mean that any other session keys are compromised.

• 2. Key-compromise impersonation (KCI): The proposed key agreement scheme is resistant to key-compromise impersonation because the key is computed using asymmetric information. We have the following two cases to consider.

  Case 1. :

  Suppose that adversary is the Type-I adversary $A_{1}$ who knows A’s password $s_{A}$ and private key $D_{A}$. If the $A_{1}$ wishes to impersonate SS and sends messages to A, he knows $s_{A},\,D_{A},\,R_{1},\,y$ and $R_{2}$. From this the $A_{1}$ can compute $K_{{ AB}}$ and ${ KA}_{1}=s_{A}R_{2}={ yPK}_{A} = { KB}_{1}$, but it can’t compute the ${ KA}_{2} = xP_{{ pub}-2}$ or ${ KB}_{2}=s_{2}R_{1}$.

  Case 2. :

  Suppose that adversary is the Type-II adversary $A_{2}$ who knows A’s password $s_{A}$, A’s private key $D_{A}$ and RS’s master private key $s$. he also can’t compute the ${ KA}_{2} =xP_{{ pub}-2}$ or ${ KB}_{2}=s_{2}R_{1}$ as $A_{1}$ even though he knows $s$.

• 3. Unknown key share (UKS): An entity A cannot be coerced into sharing a key with C when in fact A thinks she is sharing a key with SS. If A wants to share a key with SS, A uses SS’s public key $P_{{ pub}-2}$ and identifier ${ ID}_{{ SS}}$ in computing the session key. Thus, C must obtain the corresponding private key in order to compute the key. Note that incorporating parties’ identities in the computation of a session key generally avoids the unknown key share (UKS) attack [27].

• 4. Enhanced partial forward secrecy (EPFS): If the password and private key of user A is compromised, previously established session keys will still remain unknown to an adversary due to the key derivation function $H(K_{{ AB}}{\vert }{\vert } { KA}_{1} {\vert }{\vert } { KA}_{2})$, in which ${ KA}_{2}=xP_{{ pub}-2}={ KB}_{2}=s_{2}R_{1}$. As the adversary does not know the ephemeral value $x$ or $s_{2}$, she must compute $x$ or $s_{2}$ from $R_{1} = xP_{2}$ and $P_{{ pub}-2}= s_{2}P_{2}$ respectively which is the discrete logarithm problem. If the private key of SS is compromised, previously established session keys will still remain unknown to an adversary due to the key derivation function $H(K_{{ AB}} {\vert }{\vert } { KB}_{1} {\vert }{\vert } { KB}_{2})$, in which ${ KB}_{1} = { yPK}_{A}=s_{A}R_{2} = { KA}_{1}$. As the adversary does not know the ephemeral value $y$ or $s_{A}$, she must compute $y$ or $s_{A}$ from $R_{2} = yP_{1}$ and ${ PK}_{A}=s_{A}P_{1}$ respectively which is the discrete logarithm problem. But in [16] if the private key of the service server is compromised by an attacker, then the attacker can obtain the previous session key.

• 5. Key control (KC): Since each party contributes a fresh ephemeral key as one of the input used to compute the session key, one of the parties cannot force the session key to be some preselected value. But in [16] only user contributes a fresh ephemeral key as one of the input used to compute the session key, and the user can force the session key to be some preselected value. Hence, we conclude that the scheme [16] does not satisfy key control security attribute.

6 Protocol Comparison

In this section, we compare the efficiency of our scheme with Tseng et al.’s scheme [16] regarding the security and computation overheads not including precomputation overheads required by different phases.

We use the following notations to analyze the computational complexity for our scheme and some existing previous schemes.

• $t_{a}$ is the time for addition of two elements in the additive group $< G_{1},+>$.

• $t_{m}$ is the time for point scalar multiplication on the additive group $< G_{1},+ >$.

• $t_{g}$ is the time for $x\in Z_q^*$ times multiplication in the multiplicative group $< G_{2},\times >$.

• $t_{e}$ is the time for bilinear pairing operation.

• Y and N denote that the property holds and does not hold in the scheme respectively.

As we all know, a bilinear pairing operation is very time-consuming than other operations [18, 19]. Table 1 summarizes the performance result of the proposed scheme in terms of the computational costs for the registration phase, the mutual authentication phase and the password change phase, respectively. Moreover, we use notations EPFS, KC and SAMRS as abbreviations for whether the scheme satisfy enhanced partial forward secrecy and key control security attribute and whether the scheme is secure against a malicious registration server respectively.

Table 1 A comparison of efficiency

As shown in the Table 1, both schemes do not require expensive bilinear pairing operation on the user side, which makes them more efficient than others schemes [13, 15]. Compared with the Tseng et al.’s scheme, our scheme enjoys higher security level and less operation cost. Hence, consider the wireless user with limited computing capability and communication security it may be that our authentication and key agreement scheme is more applicable.

7 Conclusions

In this paper, we have proposed an authentication and key agreement mechanism for multi-domain wireless networks using certificateless public key cryptography. We have shown that the proposed scheme is secure against an uncertified user and a malicious registration server simultaneously under the computational Diffie–Hellman assumption in the random oracle. By exploiting the certificateless public key cryptography system, our scheme successfully eliminates the key escrow issue which is inherent in identity-based cryptography. In the proposed scheme, we shift the computational burden to the server; moreover, our scheme adopts CL-based short signatures to further induce the user computational cost. As a result, the computational cost required by the user is reduced to be well suited for smart cards. As compared with the recently proposed schemes, our scheme has better performance in term of the security and computation overheads.