Abstract
The authenticated key agreement (AKA) protocol is an important cryptographic mechanism, which allows two users to establish a session key for future communication. Recently, the certificateless public key cryptography received wide attention since it could solve the certificate management problem in the traditional public key cryptography and solve the key escrow problem in the identity-based public key cryptography. In this paper, we present a strongly secure certificateless authenticated key agreement (CLAKA) protocol without pairing suitable for smart media and mobile environments, which is provably secure in the extended Canetti–Krawczyk (eCK) model and is secure as long as each party has at least one uncompromised secret. Compared with previous CLAKA protocols, our protocol has advantages over them in security or efficiency.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To solve the certificate management problem in the traditional public key cryptography, Shamir [17] proposed the concept of identity-based public key cryptography (ID-based PKC) in 1984. There is no certificate is required in ID-based PKC since the user’s public key is his identity such as name, e-mail address, telephone number et al. However, the user’s private key is generated by key generation centre (KGC) in the ID-based PKC. Then the ID-based PKC has to face with the key escrow problem, i.e. the KGC knows user’s private key. To solve the problem, Al-Riyami et al. [1] proposed the concept of the certificateless public key cryptosystem (CLPKC). In CLPKC, a user’s private key is comprised of partial secret and a secret value, which are generated by the KGC and the user separately. Then, the CLPKC could solve the key escrow problem in the ID-based PKC. Since Al-Riyami et al.’s work, many cryptographic mechanisms in certificateless setting have been proposed.
Authenticated key agreement (AKA) protocol is a cryptographic mechanism, through which two users can generate a shared session key over an open network. As an important protocol of the CLPKC, certificateless authenticated key agreement (CLAKA) protocol has been studied widely. After the pioneering work of Al-Riyami et al., many CLAKA protocols [14, 15, 18–21, 23] using pairings have been proposed to satisfy different applications. From the theoretical analysis [7] and experimental results [6] we know that the pairing operation is a very complicated operation. To improve efficiency, several pairing-free CLAKA protocols [8–10, 12] have been proposed. The authors also demonstrated that their protocols are provably secure in formal models. Bellare et al. [3] proposed the first formal model for AKA protocols. After that, several extended models have been proposed [2, 4, 5]. Among them, the Canetti-Krawczyk (CK) model [5] is considered as the most promising one. To capture more desirable security properties, LaMacchia et al. [13] presented a more strong security model—the extended Canetti-Krawczyk (eCK) model for AKA protocols. In 2009, Lippold et al. [14] proposed the eCK model for CLAKA protocols. They also proposed the first CLAKA protocols using paring, which is provably secure in the eCK model for CLAKA protocols. Yang et al. [22] found that these pairing-free CLAKA protocols [8–10, 12] are not secure in the eCK model. To improve security, Yang et al. proposed a new pairing-free CLAKA protocol and demonstrated it is provably secure in the eCK model. In Yang et al.’s protocol, nine elliptic curve scalar multiplication operations are needed to generate a session key. To improve performance, He et al. [11] proposed an efficient protocol. However, He et al.’s protocol is not secure in Lippold et al.’s model since the adversary could compute the session key if he get the initiator’s partial private key and the ephemeral private key and the responder’s secret value and the ephemeral private key. In this paper, we present a strongly secure CLAKA without pairing, which is provably secure in the eCK model and is secure as long as each party has at least one uncompromised secret. Compared with previous ID-based AKA protocols, our protocol has advantages over them in security or efficiency.
The remainder of this paper is organized as follows. Section 2 describes some preliminaries. In Section 3, we propose our CLAKA protocol. The security analysis of the proposed protocol is presented in Section 4. In Section 5, performance analysis is presented. Finally, in Section 6 we conclude the result.
2 Preliminaries
2.1 Background of elliptic curve group
Let the symbol E/F p denote an elliptic curve E over a prime finite field F p , defined by an equation
and with the discriminant
The points on E/F p together with an extra point O called the point at infinity form a group
G is a cyclic additive group in the point addition “+” defined as follows: Let P, Q ∈ G, l be the line containing P and Q (tangent line to E/F p if P = Q), and R, the third point of intersection of l with E/F p . Let l′ be the line connecting R and O. Then P “+” Q is the point such that l′ intersects E/F p at R and O. Scalar multiplication over E/F p can be computed as follows:
Let the order of G be n. The following problems are commonly used in the security analysis of many cryptographic protocols.
Computational Diffie-Hellman (CDH) problem
Given a generator P of G and (aP, bP) for unknown a, b ∈ R Z * n , the task of CDH problem is to compute abP.
2.2 Security model for CLAKA protocols
Lippold et al. proposed the eCK model for CLAKA protocols based on Swanson’s work. We will give an introduction to Lippold et al.’s model. The details of the eCK model for CLAKA can be found in [14].
Let U = {U
1, U
2, …, U
n
} be a set of parties. The protocol may be run between any two of these parties. For each party there exists an identity based public key that can be derived from its identity. There is a KGC that generates a party’s partial private key according to his identity. Additionally, a party generates their own secret values and public keys. The adversary  is modeled as a probabilistic polynomial-time Turing machine and has full control of the communication network over which protocol messages are exchanged. Let ∏
x
i,j
denote x th protocol session which is run between the party U
i
(the initiator) and the partner party U
j
(the responder). We say that a session sk
x
i,j
enters an accepted state when it computes a session key sk
x
i,j
. The session sk
x
i,j
is assigned a partner identity pid = (ID
i
, ID
j
). Let comms denote the transcript of the messages exchanged between the initiator and the responder during the session. Two sessions sk
x
i,j
and ∏
y
j,i
are called matching if they have the same comms and pid. The game runs in two phases. During the first phase of the game, the adversary
is modeled as a probabilistic polynomial-time Turing machine and has full control of the communication network over which protocol messages are exchanged. Let ∏
x
i,j
denote x th protocol session which is run between the party U
i
(the initiator) and the partner party U
j
(the responder). We say that a session sk
x
i,j
enters an accepted state when it computes a session key sk
x
i,j
. The session sk
x
i,j
is assigned a partner identity pid = (ID
i
, ID
j
). Let comms denote the transcript of the messages exchanged between the initiator and the responder during the session. Two sessions sk
x
i,j
and ∏
y
j,i
are called matching if they have the same comms and pid. The game runs in two phases. During the first phase of the game, the adversary  is allowed to issue the following queries in any order:
is allowed to issue the following queries in any order:
-
Send(∏ x i,j , m): The adversary sends the message m to party i in session ∏ u i,j on behalf of party j and gets response from i according to the protocol specification. In the case of one-round protocols, party i behaves as follows:
-
m = λ: Party i generates an ephemeral value and responds with an outgoing message only.
-
m ≠ λ If party i is a responder, it generates an ephemeral value for the session and responds with an outgoing message m and a decision indicating acceptance or rejection of the session. If party i is an initiator, it responds with a decision indicating accepting or rejecting the session.
-
RevealMasterKey: The adversary is given the master secret key.
-
RevealSessionKey(∏ u i,j ): If the session has not accepted, it returns ⊥, otherwise it reveals the accepted session key.
-
RevealPartialPrivateKey(i): The adversary is given party i’s partial private key.
-
RevealSecretValue(i): If party i has been asked the ReplacePublicKey query, it returns ⊥. Otherwise, the adversary is given party i’s secret value.
-
ReplacePublicKey(i, pk): The adversary replaces party i’s public key with the value chosen by himself.
-
RevealEphemeralKey(∏ x i,j ): The adversary is given the ephemeral secret key used in ∏ x i,j .
-
-
Once the adversary  decides that the first phase is over, it starts the second phase by choosing a fresh session ∏
x
i,j
and issuing a Test(∏
x
i,j
) query, where the fresh session and test query are defined as follows:
decides that the first phase is over, it starts the second phase by choosing a fresh session ∏
x
i,j
and issuing a Test(∏
x
i,j
) query, where the fresh session and test query are defined as follows:
-
Definition 1 (Fresh session) [14]. A session ∏ x i,j is fresh if (1) ∏ x i,j has accepted; (2) ∏ x i,j is unopened (not being issued the RevealSessionKey query); (3) the session state at neither party participating in this session is fully corrupted; (4) there is no opened session ∏ y j,i which has a matching conversation to ∏ x i,j .
Test(∏ x i,j ): The input session ∏ x i,j must be fresh. A bit b ∈ {0, 1} is randomly chosen. If b = 0, the adversary is given the session key, otherwise it randomly samples a session key from the distribution of valid session keys and returns it to the adversary.
After the Test(∏ x i,j ) query has been issued, the adversary can continue querying except that the test session ∏ x i,j should remain fresh. At the end of the game, the adversary
 outputs a guess bit b′.
outputs a guess bit b′.  wins if and only if b′ = b.
wins if and only if b′ = b.  ’s advantage to win the above game, denoted by
’s advantage to win the above game, denoted by  , is defined as:
, is defined as: 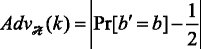 , where k is a security parameter.
, where k is a security parameter.There are two kinds of adversaries in the CLAKA protocol, i.e. the Type I adversary
 and the Type II adversary
and the Type II adversary  . The adversary
. The adversary  is not able to access the master key but he could replace public keys at his will. The adversary
is not able to access the master key but he could replace public keys at his will. The adversary  represents a malicious KGC who generates partial private keys of users.
represents a malicious KGC who generates partial private keys of users.  could access to the master key, but he is not able to replace public keys.
could access to the master key, but he is not able to replace public keys. -
Definition 2 (Strong Type I secure key agreement protocol) [14]. A CLAKA protocol is Strong Type I secure if every probabilistic, polynomial-time adversary
 has negligible advantage in winning the above game subject to the following constraints:
has negligible advantage in winning the above game subject to the following constraints:-
 may corrupt at most two out of three types of secrets per party involved in the test session,
may corrupt at most two out of three types of secrets per party involved in the test session, -
 is allowed to replace public keys of any party; however, this counts as the corruption of one secret,
is allowed to replace public keys of any party; however, this counts as the corruption of one secret, -
 may not reveal the secret value of any identity for which it has replaced the certificateless public key,
may not reveal the secret value of any identity for which it has replaced the certificateless public key, -
 is allowed to ask session key reveal queries even for session keys computed by identities where
is allowed to ask session key reveal queries even for session keys computed by identities where  replaced the identity’s public key,
replaced the identity’s public key, -
 is allowed to replace public keys of any party after the test query has been issued.
is allowed to replace public keys of any party after the test query has been issued.
-
-
Definition 3 (Strong Type II secure key agreement protocol) [14]. A CLAKA protocol is Strong Type II secure if every probabilistic, polynomial-time adversary
 has negligible advantage in winning the above game subject to the following constraints:
has negligible advantage in winning the above game subject to the following constraints:-
 is given the master secret key s at the start of the game,
is given the master secret key s at the start of the game, -
 may corrupt at most one additional type of secret per party participating in the test query,
may corrupt at most one additional type of secret per party participating in the test query, -
 is allowed to replace public keys of any party; however, this counts as the corruption of one secret,
is allowed to replace public keys of any party; however, this counts as the corruption of one secret, -
 may not reveal the secret value of any identity for which it has replaced the public key,
may not reveal the secret value of any identity for which it has replaced the public key, -
 is allowed to ask session key reveal queries even for session keys computed by identities where he replaced the identity’s public key,
is allowed to ask session key reveal queries even for session keys computed by identities where he replaced the identity’s public key,
 is allowed to replace public key of any party after the test query has been issued.
is allowed to replace public key of any party after the test query has been issued. -
3 Our protocol
In this section, we propose a new CLAKA protocol which is secure against the Type I/II adversary. Our protocol consists of five polynomial time algorithms, i.e. Setup, PartialPrivateKeyExtract, SetSecretValue, SetPublicKey and Key − Agreement. The detail of these algorithms is described as follows.
-
Setup: Given security parameter k, KGC does the following steps to generate the system parameters and the mast key.
-
(1)
KGC chooses a k -bit prime p, generates an elliptic curve E over finite field F p , generates a group G of elliptic curve points on E with prime order n and determines a generator P of G.
-
(2)
KGC chooses the master key mk = s ∈ Z * n and computes the master public key P pub = s ⋅ P.
-
(3)
KGC chooses three cryptographic secure hash functions H 1 : {0, 1}* × G → Z * n H 2 : {0, 1}* × G × G × G → Z * n and H 3 : {0, 1}* × {0, 1}* × G × G → {0, 1}k.
-
(4)
KGC publishes params = {F p , E p , G, P, P pub , H 1, H 2, H 3} as system parameters and secretly keeps the master key s.
-
(1)
-
PartialPrivateKeyExtract: Given params, mk, and identity ID of a user, KGC generates a random number r ID ∈ Z * n , computes R ID = r ID ⋅ P, h ID = H 1(ID, R ID ) and s ID = r ID + h ID s mod n. Then KGC returns the partial private key D ID = (s ID , R ID ) to the user.
The user can validate D ID by checking whether the equation s ID ⋅ P = R ID + h ID ⋅ P pub holds. The partial private key is valid if the equation holds and vice versa.
-
SetSecretValue: Given params, the user with identity ID picks a random number x ID ∈ Z * n , computes P ID = x ID ⋅ P and sets x ID as his secret value.
-
SetPublicKey: Given params and x ID , the user with identity ID computes P ID = x ID P and sets P ID as his public key.
-
Key − Agreement: Assume that an entity A with identity ID A has partial private key D A , secret value x A and public key P A and an entity B with identity ID B has partial private key D B , secret value x B and public key P B . If they want to establish a session key, as shown in Fig. 1, the following steps will be executed.
-
1)
A chooses a random number t A ∈ Z * n and computes T A = t A ⋅ P, then A sends M 1 = {ID A , R A , T A } to B.
-
2)
After receiving M 1, B chooses a random number t B ∈ Z * n and computes T B = t B ⋅ P, h A = H 1(ID A , R A ), k A = H 2(ID A , R A , P A , P pub ), k B = H 2(ID B , R B , P B , P pub ), K 1 BA = (t B + k B x B + s B )(T A + k A P A + R A + h A P pub ), K 2 BA = t B ⋅ T A , and the session key sk = H 3(ID A ‖ID B ‖T A ‖T B ‖K 1 BA ‖K 2 BA ). At the last, B sends M 2 = {ID B , R B , T B } to A.
-
3)
Upon receiving M 2, A computes h B = H 1(ID B , R B ), k A = H 2(ID A , R A , P A , P pub ), k B = H 2(ID B , R B , P B , P pub ), K 1 AB = (t A + k A x A + s A )(T B + k B P B + R B + h B P pub ), K 2 AB = t A ⋅ T B and the session key sk = H 3(ID A ‖ID B ‖T A ‖T B ‖K 1 AB ‖K 2 AB ).
$$ \begin{array}{l}{K}_{AB}^1=\left({t}_A+{k}_A{x}_A+{s}_A\right)\left({T}_B+{k}_B{P}_B+{R}_B+{h}_B{P}_{pub}\right)\\ {}=\left({t}_A+{k}_A{x}_A+{s}_A\right)\left({t}_B+{k}_B{x}_B+{s}_B\right)P\\ {}=\left({t}_B+{k}_A{x}_B+{s}_B\right)\left({t}_A+{k}_B{x}_A+{s}_A\right)P\\ {}=\left({t}_B+{k}_B{x}_B+{s}_B\right)\left({T}_A+{k}_A{P}_A+{R}_A+{h}_B{P}_{pub}\right)={K}_{BA}^1\end{array} $$(5)and
$$ {K}_{AB}^2={t}_A{t}_BP={t}_B{t}_AP={K}_{BA}^2 $$(6)Thus, the correctness of the protocol is proved.
-
1)
4 Security analysis
In this section, we will show our protocol is provably secure in the eCK model. We treat H 1, H 2 and H 3 as three random oracles [3]. For the security, the following theorems are provided.
Theorem 1
If there exists an adversary that has an advantage against our CLAKA protocol  , the challenger
, the challenger  can use this adversary to solve the CDH problem. We show that the success probability of any adversary against the protocol is limited by
can use this adversary to solve the CDH problem. We show that the success probability of any adversary against the protocol is limited by  , where
, where  is the advantage that the challenger gets in solving the CDH problem given security parameter k using the adversary.
is the advantage that the challenger gets in solving the CDH problem given security parameter k using the adversary.
Proof
From the correctness analysis our protocol, we know that matching sessions compute the same session keys. Like Lippold et al. [14] did, we also do not distinguish two types of adversaries. We will use the similar method proposed by Lippold et al. to show the proposed CLAKA protocol is provably secure in the eCK model.
We assume that an adversary  against our protocol has a non-negligible advantage
against our protocol has a non-negligible advantage  in winning the game outlined in Section 2.2, where k is the security parameter. Let n
0 and n
1 denote the maximum number of sessions that any one party may have and the maximum number of distinctive honest parties that
in winning the game outlined in Section 2.2, where k is the security parameter. Let n
0 and n
1 denote the maximum number of sessions that any one party may have and the maximum number of distinctive honest parties that  activates separately. Since H
3 is modeled as a random oracle, then
activates separately. Since H
3 is modeled as a random oracle, then  has only three possible ways to distinguish the tested session key from a random string.
has only three possible ways to distinguish the tested session key from a random string.
-
Guessing attack:
 correctly guesses the session key.
correctly guesses the session key. -
Key-replication attack: The adversary
 forces a non-matching session to have the same session key with the test session. In this case, the adversary
forces a non-matching session to have the same session key with the test session. In this case, the adversary  can simply learn the session key by querying the non-matching session.
can simply learn the session key by querying the non-matching session. -
Forging attack: Assume that ∏ X I,J is the test session. At some point in its run, the adversary
 queries H
3 on the value (ID
A
‖ID
B
‖T
A
‖T
B
‖K
1
AB
‖K
2
AB
) in the test session owned by party I communicating with party J. Clearly, in this case
queries H
3 on the value (ID
A
‖ID
B
‖T
A
‖T
B
‖K
1
AB
‖K
2
AB
) in the test session owned by party I communicating with party J. Clearly, in this case  computes the values K
1
AB
and K
2
AB
itself.
computes the values K
1
AB
and K
2
AB
itself.
From the similar analysis in [16], we know that the success probability of the guessing attack and the key-replication attack is negligible. Thus, we cannot get an advantage in winning the game against our protocol unless it queries the H
3 oracle on the session key through the forging attack. Then, using the adversary  , we could construct a challenger
, we could construct a challenger  to solve the CDH problem. Let
to solve the CDH problem. Let  be the advantage that the challenger
be the advantage that the challenger  gets in solving the CDH problem given the security parameter k using the adversary
gets in solving the CDH problem given the security parameter k using the adversary  . Before the game starts, the challenger
. Before the game starts, the challenger  tries to guess the test session and the strategy that the adversary
tries to guess the test session and the strategy that the adversary  will adopt.
will adopt.  randomly selects two indexes I, J ∈ {1, 2, …, n
1}, where I ≠ J.
randomly selects two indexes I, J ∈ {1, 2, …, n
1}, where I ≠ J.  also chooses X ∈ {1, 2, …, n
0} and thus determines the test session ∏
X
I,J
, which is correct with probability larger than \( \frac{1}{n_0{n}_1^2} \).
also chooses X ∈ {1, 2, …, n
0} and thus determines the test session ∏
X
I,J
, which is correct with probability larger than \( \frac{1}{n_0{n}_1^2} \).  aborts the game whenever it finds that it has missed its guess. Otherwise, the game proceeds as usual. According to the fresh session definition,
aborts the game whenever it finds that it has missed its guess. Otherwise, the game proceeds as usual. According to the fresh session definition,  has the following nine choices for
has the following nine choices for  ’s strategy:
’s strategy:
-
1)
The adversary may neither learn the secret value of I nor the secret value of J.
-
2)
The adversary may neither learn the ephemeral private key of I nor the ephemeral private key of J.
-
3)
The adversary may neither learn the secret value of J nor replace the public key of J and may also not learn the partial private key of I.
-
4)
The adversary may neither learn the ephemeral private key of J nor the secret value of I.
-
5)
The adversary may neither learn the ephemeral private key of I nor the secret value of J.
-
6)
The adversary may neither learn the secret value of I nor replace the secret value of I and may also not learn the partial private key of J.
-
7)
The adversary may neither learn the ephemeral private key of J nor the partial private key of I.
-
8)
The adversary may neither learn the ephemeral private key of I nor the partial private key of J.
-
9)
The adversary may neither learn the partial private key of I nor of the partial private key J.
-
Strategy 1. In this strategy,
 could get I’s partial private key s
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.
could get I’s partial private key s
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.  also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
Y
J,I
, where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),
also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
Y
J,I
, where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  . To achieve the goal,
. To achieve the goal,  sets the public key P
I
of I to aP and the public key P
J
of J to bP.
sets the public key P
I
of I to aP and the public key P
J
of J to bP.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where \( Q=\frac{1}{k_I{k}_J}\left({K}_{I,J}^1-\left({t}_I+{s}_I\right)\left({T}_J+{k}_J{P}_J+{R}_J+{h}_J{P}_{pub}\right)-{k}_I\left({t}_J+{s}_J\right){R}_I\right) \). As soon as
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where \( Q=\frac{1}{k_I{k}_J}\left({K}_{I,J}^1-\left({t}_I+{s}_I\right)\left({T}_J+{k}_J{P}_J+{R}_J+{h}_J{P}_{pub}\right)-{k}_I\left({t}_J+{s}_J\right){R}_I\right) \). As soon as  finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. -
Strategy 2. In this strategy,
 could get I’s secret value x
I
and.
could get I’s secret value x
I
and.  also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),
also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  . To achieve the goal,
. To achieve the goal,  sets the ephemeral public key T
I
of ∏
X
I,J
to aP and the ephemeral public key T
J
of ∏
Y
J,I
to bP, where ∏
Y
J,I
is ∏
X
I,J
’s matching session.
sets the ephemeral public key T
I
of ∏
X
I,J
to aP and the ephemeral public key T
J
of ∏
Y
J,I
to bP, where ∏
Y
J,I
is ∏
X
I,J
’s matching session.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(K
2
I,J
, P) holds,
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(K
2
I,J
, P) holds,  is able to identify valid queries. As soon as
is able to identify valid queries. As soon as  finds such a query,
finds such a query,  aborts the game and returns K
2
I,J
as solution of the CDH challenge. The probability that
aborts the game and returns K
2
I,J
as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. -
Strategy 3. In this strategy,
 could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.
could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.  also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
Y
J,I
’s , where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),
also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
Y
J,I
’s , where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  .
.  sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.
sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.  sets the public key P
J
of J to bP.
sets the public key P
J
of J to bP.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where \( Q=\frac{1}{k_J}\left({K}_{I,J}^1-\left({t}_I+{k}_I{x}_I\right)\left({T}_J+{k}_J{P}_J+{R}_J+{h}_J{P}_{pub}\right)-\left({t}_J+{s}_J\right)aP\right) \). As soon as
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where \( Q=\frac{1}{k_J}\left({K}_{I,J}^1-\left({t}_I+{k}_I{x}_I\right)\left({T}_J+{k}_J{P}_J+{R}_J+{h}_J{P}_{pub}\right)-\left({t}_J+{s}_J\right)aP\right) \). As soon as  finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. -
Strategy 4. The strategy is symmetric to Strategy 3, its probability of success is equal to the probability of success for Strategy 3. To save space, we will not give the detail here.
-
Strategy 5. In this strategy,
 could get I’s partial private key s
I
and secret value x
I
.
could get I’s partial private key s
I
and secret value x
I
.  also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
Y
J,I
, where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),
also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
Y
J,I
, where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  . To achieve the goal,
. To achieve the goal,  sets the ephemeral public key T
I
of the test session ∏
X
I,J
to aP and the public key P
J
of J to bP.
sets the ephemeral public key T
I
of the test session ∏
X
I,J
to aP and the public key P
J
of J to bP.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where \( Q=\frac{1}{k_J}\left({K}_{I,J}^1-\left({k}_I{x}_I+{s}_I\right)\left({T}_J+{k}_J{P}_J+{R}_J+{h}_J{P}_{pub}\right)-\left({t}_J+{s}_J\right){T}_I\right) \). As soon as
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where \( Q=\frac{1}{k_J}\left({K}_{I,J}^1-\left({k}_I{x}_I+{s}_I\right)\left({T}_J+{k}_J{P}_J+{R}_J+{h}_J{P}_{pub}\right)-\left({t}_J+{s}_J\right){T}_I\right) \). As soon as  finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. -
Strategy 6. The strategy is symmetric to Strategy 5, its probability of success is equal to the probability of success for Strategy 5. To save space, we will not give the detail here.
-
Strategy 7. In this strategy,
 could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.
could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.  also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),
also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  .
.  sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
.
sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
.  sets the ephemeral public key T
J
of ∏
Y
J,I
to bP.
sets the ephemeral public key T
J
of ∏
Y
J,I
to bP.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
1
I,J
− (t
I
+ k
I
x
I
)(T
J
+ k
J
P
J
+ R
J
+ h
J
P
pub
) − (k
J
x
J
+ s
J
)aP. As soon as
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
1
I,J
− (t
I
+ k
I
x
I
)(T
J
+ k
J
P
J
+ R
J
+ h
J
P
pub
) − (k
J
x
J
+ s
J
)aP. As soon as  finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. -
Strategy 8. The strategy is symmetric to Strategy 7, its probability of success is equal to the probability of success for Strategy 7. To save space, we will not give the detail here.
-
Strategy 9. In this strategy,
 could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.
could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
X
I,J
.  also could get J’s secret value x
J
and ephemeral private key t
J
of the session ∏
Y
J,I
, where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),
also could get J’s secret value x
J
and ephemeral private key t
J
of the session ∏
Y
J,I
, where ∏
Y
J,I
is ∏
X
I,J
’s matching session. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  .
.  sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.
sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.  also sets J’s partial public key R
J
to bP − h
J
P
pub
and H
1(ID
J
, R
J
) ← h
J
, where h
J
is a random number.
also sets J’s partial public key R
J
to bP − h
J
P
pub
and H
1(ID
J
, R
J
) ← h
J
, where h
J
is a random number.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
1
I,J
− (t
I
+ k
I
x
I
)(T
J
+ k
J
P
J
+ bP) − (t
J
+ k
J
x
J
)aP. As soon as
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
1
I,J
− (t
I
+ k
I
x
I
)(T
J
+ k
J
P
J
+ bP) − (t
J
+ k
J
x
J
)aP. As soon as  finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
.
-
5 Comparison with previous protocols
For the convenience of evaluating the computational cost, we define some notations as follows.
-
T mul : The time of executing a scalar multiplication operation of point.
-
T add : The time of executing an addition operation of point.
-
T h : The time of executing a one-way hash function.
We will compare the efficiency of our protocol with two latest CLAKA protocols without pairing, i.e. Yang et al.’s protocol [22] and He et al.’s protocol [11]. Table 1 shows the comparison among pairing-free CLAKA protocols in terms of efficiency and security model. Yang et al.’s protocol is implemented in general group. To give fair comparison, we transform it to the elliptic cure group described in Section 2.1. From Table 1, we know that Yang et al.’s protocol [22] and our protocol has advantage in security to He et al.’s protocol [3] since Yang et al.’s protocol [22] and our protocol are provably secure in the eCK model and is secure as long as each party has at least one uncompromised secret. Besides, our protocol has better performance than Yang et al.’s protocol. Moreover, our protocol just needs a more hash function operation than He et al.’s protocol. We conclude that our protocol is more suitable for practical applications.
6 Conclusion
To improve performance, many pairing-free CLAKA protocols have been proposed. In this paper, we proposed a new pairing-free CLAKA protocol and proved its security in the eCK model. The analysis shows our protocol has advantages over previous CLAKA protocols in security or efficiency.
References
Al-Riyami S, Paterson KG (2003) Certificateless public key cryptography. In: Proc. of ASIACRYPT 2003, LNCS 2894, Springer-Verlag, pp 452–473
Bellare M, Pointcheval D, Rogaway P (2000) Authenticated key exchange secure against dictionary attacks. In: Proc.of the EUROCRYPT 2000. LNCS, Springer-Verlag, Vol. 1807, pp 139–55
Bellare M, Rogaway P (1993) Entity authentication and key distribution. In: Proc. of the CRYPTO 1993. LNCS, Springer-Verlag, Vol. 773, pp 232–49
Bellare M, Rogaway P (1995) Provably secure session key distribution: the three party case. In: Proc. of the 27th ACM symposium on the theory of computing, ACM, pp 57–66
Canetti R, Krawczyk H (2001) Analysis of key-exchange protocols and their use for building secure channels. In: Proc. of the EUROCRYPT 2001. LNCS, Springer-Verlag, Vol. 245, pp 453–74
Cao X, Kou W (2010) A pairing-free identity-based authenticated Key agreement scheme with minimal message exchanges. Inf Sci 180:2895–2903
Chen L, Cheng Z, Smart NP (2007) Identity-based key agreement protocols from pairings. Int J Inf Secur 6:213–241
Geng M, Zhang F (2009) Provably secure certificateless two-party authenticated key agreement protocol without pairing. In: Proc. of International Conference on Computational Intelligence and Security, pp 208–212
He D, Chen Y, Chen J, Zhang R, Han W (2011) A new two-round certificateless authenticated key agreement protocol without bilinear pairings. Math Comput Model 54(11–12):3143–3152
He D, Chen J, Hu J (2012) A pairing-free certificateless authenticated key agreement protocol. Int J Commun Syst 25(2):221–230
He D, Padhye S, Chen J (2012) An efficient certificateless authenticated key agreement protocol. Comput Math Appl 64(6):1914–1926
Hou M, Xu Q (2009) A two-party certificateless authenticated key agreement protocol without pairing. In: Proc. of 2nd IEEE International Conference on Computer Science and Information Technology, pp 412–416
LaMacchia BA, Lauter K, Mityagin A (2007) Stronger security of authenticated key exchange. In: Proc. of the ProvSection 2007. LNCS, Springer-Verlag , Vol. 4784, pp 1–16
Lippold G, Boyd C, Nieto J (2009) Strongly secure certificateless key agreement. In: Pairing 2009, pp 206–230
Mandt T, Tan C (2008) Certificateless authenticated two-party key agreement protocols. In: Proc. of the ASIAN 2006, LNCS, Springer-Verlag, Vol. 4435, pp 37–44
Ni L, Chen G, Li J, Hao Y (2011) Strongly secure identity-based authenticated key agreement protocols. Comput Electr Eng 37:205–217
Shamir A (1984) Identity-based cryptosystems and signature protocols. Proc. CRYPTO1984, LNCS, Vol. 196, pp 47–53
Shao Z (2005) Efficient authenticated key agreement protocol using self-certifed public keys from pairings. Wuhan Univ J Nat Sci 10(1):267–270
Shi Y, Li J (2007) Two-party authenticated key agreement in certificateless public key cryptography. Wuhan Univ J Nat Sci 12(1):71–74
Swanson C (2008) Security in key agreement: Two-party certificateless protocols, Master Thesis, University of Waterloo
Wang S, Cao Z, Dong X (2006) Certificateless authenticated key agreement based on the MTI/CO protocol. J Inf Comput Sci 3:575–581
Yang G, Tan C (2011) Strongly secure certificateless key exchange without pairing. In: Proc. of 6th ACM Symposium on Information, Computer and Communications Security, pp 71–79
Zhang L, Zhang F, Wua Q, Domingo-Ferrer J (2010) Simulatable certificateless two-party authenticated key agreement protocol. Inf Sci 180:1020–1030
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (grant number 2013R1A1A2059864).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Tu, H., Kumar, N., Kim, J. et al. A strongly secure pairing-free certificateless authenticated key agreement protocol suitable for smart media and mobile environments. Multimed Tools Appl 74, 6365–6377 (2015). https://doi.org/10.1007/s11042-015-2470-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-015-2470-3





 outputs a guess bit b′.
outputs a guess bit b′.  wins if and only if b′ = b.
wins if and only if b′ = b.  ’s advantage to win the above game, denoted by
’s advantage to win the above game, denoted by  , is defined as:
, is defined as: 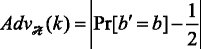 , where k is a security parameter.
, where k is a security parameter. and the Type II adversary
and the Type II adversary  . The adversary
. The adversary  is not able to access the master key but he could replace public keys at his will. The adversary
is not able to access the master key but he could replace public keys at his will. The adversary  represents a malicious KGC who generates partial private keys of users.
represents a malicious KGC who generates partial private keys of users.  could access to the master key, but he is not able to replace public keys.
could access to the master key, but he is not able to replace public keys. has negligible advantage in winning the above game subject to the following constraints:
has negligible advantage in winning the above game subject to the following constraints: may corrupt at most two out of three types of secrets per party involved in the test session,
may corrupt at most two out of three types of secrets per party involved in the test session, is allowed to replace public keys of any party; however, this counts as the corruption of one secret,
is allowed to replace public keys of any party; however, this counts as the corruption of one secret, may not reveal the secret value of any identity for which it has replaced the certificateless public key,
may not reveal the secret value of any identity for which it has replaced the certificateless public key, is allowed to ask session key reveal queries even for session keys computed by identities where
is allowed to ask session key reveal queries even for session keys computed by identities where  replaced the identity’s public key,
replaced the identity’s public key, is allowed to replace public keys of any party after the test query has been issued.
is allowed to replace public keys of any party after the test query has been issued. has negligible advantage in winning the above game subject to the following constraints:
has negligible advantage in winning the above game subject to the following constraints: is given the master secret key s at the start of the game,
is given the master secret key s at the start of the game, may corrupt at most one additional type of secret per party participating in the test query,
may corrupt at most one additional type of secret per party participating in the test query, is allowed to replace public keys of any party; however, this counts as the corruption of one secret,
is allowed to replace public keys of any party; however, this counts as the corruption of one secret, may not reveal the secret value of any identity for which it has replaced the public key,
may not reveal the secret value of any identity for which it has replaced the public key, is allowed to ask session key reveal queries even for session keys computed by identities where he replaced the identity’s public key,
is allowed to ask session key reveal queries even for session keys computed by identities where he replaced the identity’s public key, is allowed to replace public key of any party after the test query has been issued.
is allowed to replace public key of any party after the test query has been issued.
 correctly guesses the session key.
correctly guesses the session key. forces a non-matching session to have the same session key with the test session. In this case, the adversary
forces a non-matching session to have the same session key with the test session. In this case, the adversary  can simply learn the session key by querying the non-matching session.
can simply learn the session key by querying the non-matching session. queries H
3 on the value (ID
A
‖ID
B
‖T
A
‖T
B
‖K
queries H
3 on the value (ID
A
‖ID
B
‖T
A
‖T
B
‖K
 computes the values K
computes the values K
 could get I’s partial private key s
I
and ephemeral private key t
I
of the test session ∏
could get I’s partial private key s
I
and ephemeral private key t
I
of the test session ∏ also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏ ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  . To achieve the goal,
. To achieve the goal,  sets the public key P
I
of I to aP and the public key P
J
of J to bP.
sets the public key P
I
of I to aP and the public key P
J
of J to bP.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where 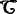 finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
.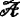 could get I’s secret value x
I
and.
could get I’s secret value x
I
and.  also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),
also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  . To achieve the goal,
. To achieve the goal,  sets the ephemeral public key T
I
of ∏
sets the ephemeral public key T
I
of ∏ uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(K
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(K
 is able to identify valid queries. As soon as
is able to identify valid queries. As soon as  finds such a query,
finds such a query,  aborts the game and returns K
aborts the game and returns K
 is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏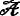 also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏ ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  .
.  sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.
sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.  sets the public key P
J
of J to bP.
sets the public key P
J
of J to bP.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where  finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. could get I’s partial private key s
I
and secret value x
I
.
could get I’s partial private key s
I
and secret value x
I
.  also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏
also could get J’s partial private key s
J
and ephemeral private key t
J
of the session ∏ ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  . To achieve the goal,
. To achieve the goal,  sets the ephemeral public key T
I
of the test session ∏
sets the ephemeral public key T
I
of the test session ∏ uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where  finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏ also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),
also could get J’s partial private key s
J
and secret value x
J
. Given a CDH problem instance (P, aP, bP),  ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  .
.  sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
.
sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
.  sets the ephemeral public key T
J
of ∏
sets the ephemeral public key T
J
of ∏ uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
 finds such a query,
finds such a query, 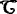 aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
. could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏
could get I’s secret value x
I
and ephemeral private key t
I
of the test session ∏ also could get J’s secret value x
J
and ephemeral private key t
J
of the session ∏
also could get J’s secret value x
J
and ephemeral private key t
J
of the session ∏ ’s task is to compute abP using the adversary
’s task is to compute abP using the adversary  .
.  sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.
sets I’s partial public key R
I
to aP − h
I
P
pub
and H
1(ID
I
, R
I
) ← h
I
, where h
I
is a random number.  also sets J’s partial public key R
J
to bP − h
J
P
pub
and H
1(ID
J
, R
J
) ← h
J
, where h
J
is a random number.
also sets J’s partial public key R
J
to bP − h
J
P
pub
and H
1(ID
J
, R
J
) ← h
J
, where h
J
is a random number.  uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
uses a proper pairing to check whether the queries of the adversary to the H
3 oracle are validity by checking whether the equation e(aP, bP) = e(Q, P) holds, where Q = K
 finds such a query,
finds such a query,  aborts the game and returns Q as solution of the CDH challenge. The probability that
aborts the game and returns Q as solution of the CDH challenge. The probability that  is able to find a solution to the CDH challenge is
is able to find a solution to the CDH challenge is  .
.