Outage Capacity for Secondary Users Due to Bandwidth Fluctuations: Multicarrier Versus Single Carrier

Abstract

In this work we study the channel capacity from the point of view of a secondary user that shares the bandwidth of the channel with a primary user using dynamic spectrum access in cognitive radio.The secondary user sees bandwidth fluctuations (i.e, at any given time the bandwidth can be available or not) that impact its channel capacity. We study the outage capacity for the secondary user considering two scenarios in which the secondary user uses either a single carrier modulation for the case in which bandwidth fluctuates over the complete transmission band, and a multicarrier modulation for the case in which bandwidth fluctuations are over various transmission subbands. We derive expressions for the outage capacity of the secondary user for both single carrier and multicarrier. Results show that: (1) The outage capacity for single carrier can be higher than for multicarrier, but with a higher outage probability for single carrier than for multicarrier. In fact, a low value of outage probability for single carrier requires a duty cycle for the secondary user close to one, but this has the problem that it leaves a very short duty cycle for the primary user. (2) Although for the secondary user the outage capacity for multicarrier is smaller than for single carrier, for multicarrier lower values of the outage probability can be achieved even for short values of the duty cycle of the secondary user, allowing larger duty cycle values of the primary user. (3) For multicarrier, the outage capacity is more sensitive to changes in the duty cycle than to changes in the outage probability. To obtain a larger outage capacity with low values of both the outage probability and the duty cycle, it requires the use of a large number of subbands.

1 Introduction

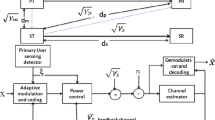
Recently, several communication systems have been proposed in which two groups of users with two different priorities share the channel bandwidth in a random fashion. One example of this situation is in dynamic spectrum access for cognitive radio (DSA-CR), in which the set of primary users (PUs) use the channel bandwidth at will, but the set of secondary users (SUs) must wait until the channel bandwidth is available [1, 2]. From the point of view of the SUs, the bandwidth is shared with the PUs in a random fashion. Hence, the channel seen by the SUs is a channel with random fluctuations in the available bandwidth. Operation in additive white Gaussian noise (AWGN) but under random fluctuations in the available bandwidth results in a capacity that is a random process. Studying the channel capacity and the outage capacity under this operating conditions can provide insight on the design of communications system working in this regime.

In this work we study the outage capacity from the point of view of a SU that share the bandwidth of the channel with a PU using DSA-CR (for specific mechanisms to sense and share the channel see for example [3] [4]). We explore two scenarios in which the SU uses either a single carrier (SC) modulation for the case where bandwidth fluctuations is over the complete band, and a multicarrier (MC) modulation for the case where bandwidth fluctuations are over various subbands. We derive expressions for the outage capacity due to bandwidth fluctuations for both SC and MC and proceed to make a comparison between them. For the MC case the expression for the outage capacity is a function of the outage probability, the number of carriers and the duty cycle of the SU.

The following definitions and notation are used through the paper:

• Capacity $\mathcal{{C}}$: The information-theoretical channel capacity.

• Random capacity ${\mathcal{{C}}}_{{\text {rand}}}(t)$: The instantaneous capacity of a channel with random fluctuations in the available bandwidth.

• Averaged capacity $\mathcal{{C}}_{{\text {avg}}}$: The ${\mathcal{{C}}}_{{\text {rand}}}(t)$ averaged over the random bandwidth effects.

• Outage capacity $\mathcal{{C}}_{{\text {out}}}$: The ${\mathcal{{C}}}_{{\text {rand}}}(t)$ falls below $\mathcal{{C}}_{{\text {out}}}$ with a given outage probability $\mathcal{{P}}_{{\text {out}}}$.

In Sect. 2 we provide the expressions for ${\mathcal{{C}}}_{{\text {rand}}}(t)$, its mean value $\mathcal{{C}}_{{\text {avg}}}$, its correlation function $R_{{\mathcal{{C}}}_{{\text {rand}}}}(\tau )$, and its variance $\sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}}$. In Sect. 2 we also provide the expressions for $\mathcal{{C}}_{{\text {out}}}$. In Sect. 3 we study the differences in terms of $\mathcal{{C}}_{{\text {out}}}$ when the SU uses either SC or MC, and provide some numerical results. Section 4 provides the conclusions.

2 Capacity Expressions

2.1 Channel Capacity

Following the Shannon-Hartley theorem [5], the capacity of a Gaussian channel can be written as

$$\begin{aligned} C\left( P,W,N_o\right) = W \; \log _2\left( 1+ \frac{P}{N_o \; W}\right) , \end{aligned}$$

(1)

in bits per second (bps),where $W$ is the channel bandwidth, $P$ is the average signal power, and $N_o/2$ is the (two-sided) power spectrum density of the noise. Equation (1) indicates that a noiseless Gaussian channel $(N_o -> 0)$ offers infinite capacity, but in a real situation $(N_o > 0)$ we have a finite capacity. Then, we can compare two arbitrary channels with capacities $C\left( P_1,W_1,N_o\right)$ and $C\left( P_2,W_2,N_o\right)$. For instance, if we assume two channels, $1$ and $2$, such that $W_2 = 2 W_1$, and we expect that $C\left( P_2,W_2,N_o\right) = 2 C\left( P_1,W_1,N_o\right)$, then we must have:

$$\begin{aligned} C_2\left( P_2,W_2,N_o\right)&= W_2 \; \log _2\left( 1+ \frac{P_2}{N_o \; W_2}\right) = 2 W_1 \; \log _2\left( 1+ \frac{P_2}{N_o \; 2 W_1}\right) \nonumber \\&= 2 C\left( P_1,W_1,N_o\right) = 2 W_1 \; \log _2\left( 1+ \frac{P_1}{N_o \; W_1}\right) (\hbox {iff }\, P_2=2P_1) , \nonumber \\ \end{aligned}$$

(2)

in other words, when the bandwidth of the Gaussian channel increases N times, from $W_1$ to $W_N = N W_1$, it make sense to expect that the new capacity be $N$ times the original one. In this case the average power must also be augmented with the same factor $N$, i.e. from $P_1$ to $P_N = N P_1$.

2.2 Random Capacity for SC

Let us now assume that $W$ varies in time in a bursty fashion. In this work we model bursty operation multiplying $W$ by a bursty function $b(t)$. The random process (r.p.) $b(t)$ takes the values $1$ or $0$ depending if $W$ is available to the SU or not, respectively.¹ Random capacity is defined as

$$\begin{aligned} {\mathcal{{C}}}_{{\text {rand}}}(t) \mathop {=}\limits ^{\bigtriangleup }C\left( Pb(t),Wb(t),N_o\right) = W b(t) \; \log _2\left( 1+ \frac{P b(t)}{N_o \; W b(t)}\right) . \end{aligned}$$

(3)

We assume that the r.p. $b(t)$ is wide sense stationary (w.s.s.), and that the fluctuation rate of $b(t)$ is slower than the data frame transmission rate. We denote $p_0$ and $p_1$ as the probabilities that $b(t)=0$ and $b(t)=1$ at any random value of time $t$, respectively. The $b(t)$ has mean $\mathcal{E}_{b}\{ b(t) \} = p_1$, autocorrelation $R_b(\tau ) = \mathcal{E}_{b}\{ b(t) b(t+\tau ) \}$, and variance $\sigma ^2_b = R_b(0) - R_b(\infty )$, where $\mathcal{E}_{b}\{\cdot \}$ is the expected value operator with respect to $b$.

By noticing that

$$\begin{aligned} {\mathcal{{C}}}_{{\text {rand}}}(t) = \left\{ \begin{array}{ll} C\left( P,W,N_o\right) , &{}\quad \mathrm{for}\, b(t)=1, \\ 0 , &{}\quad \mathrm{for}\, b(t)=0, \\ \end{array}\right. \end{aligned}$$

(4)

we can rewrite

$$\begin{aligned} {\mathcal{{C}}}_{{\text {rand}}}(t) = b(t) \; C\left( P,W,N_o\right) \;. \end{aligned}$$

(5)

The mean value of ${\mathcal{{C}}}_{{\text {rand}}}(t)$ is

$$\begin{aligned} \mathcal{{C}}_{{\text {avg}}}&= \mathcal{E}_{b}\{{\mathcal{{C}}}_{{\text {rand}}}(t) \} = p_1 \; C\left( P,W,N_o\right) \;, \end{aligned}$$

(6)

and the autocorrelation of ${\mathcal{{C}}}_{{\text {rand}}}(t)$ is

$$\begin{aligned} R_{{\mathcal{{C}}}_{{\text {rand}}}}(\tau )&= R_b(\tau ) \; C^2\left( P,W,N_o\right) . \end{aligned}$$

(7)

The statistics of $b(t)$ depends on the specific communication scenario we want to analyze. For example, for a $b(t)$ produced by a Poisson process we can use the random telegraph waveform in [6]. Figure 1 depicts one possible realization of $b(t)$.

Fig. 1

One realization of the r.p. $b(t)$

When $p_1=\frac{1}{2}$, the probability that $k$ transitions occur in a time interval of length $T$ is given by the Poisson distribution

$$\begin{aligned} P(kT) = \frac{(aT)^k}{k\mathrm{!}} \exp {(-aT)}, \end{aligned}$$

(8)

where $a$ is the average number of transitions per second. Hence, the autocorrelation of $b(t)$ is [6]

$$\begin{aligned} R_b(\tau )&= \mathrm{Prob}(b(t)=1,b(t+\tau )=1) = p_1 \mathrm{Prob}(k\, \hbox { even}, T=\mid \tau \mid ) \nonumber \\&= \frac{p_1}{2} [1 + \exp {(-2a \mid \tau \mid })]. \end{aligned}$$

(9)

Notice that the discontinuity points of $b(t)$ have Poisson distribution only in the particular case with $p_1=p_0=0.5$. For other values of $p_1$ and $p_0$, the r.p. $b(t)$ is modelled as a Markov process [7]. In this general case $b(t)$ is asymptotically stationary with mean $p_1$ , and autocorrelation [8]

$$\begin{aligned} R_b(\tau ) = (p_1)^2 + p_1 p_0 \exp (-\mu _1 (1+\frac{\mu _1}{\mu _0}) |\tau |), \end{aligned}$$

(10)

where $\mu _0$ is the transition probability from $b(t)=0$ to $b(t)=1$, and $\mu _1$ is the transition probability from $b(t)=1$ to $b(t)=0$.

Substituting $R_b(\tau )$ in (10) into (7) we get

$$\begin{aligned} R_{{\mathcal{{C}}}_{{\text {rand}}}}(\tau )&= C^2\left( P,W,N_o\right) \; \left[ (p_1)^2 + p_1 p_0 \exp (- \mu _1 (1+\frac{\mu _1}{\mu _0}) |\tau |) \right] . \quad \end{aligned}$$

(11)

In particular, the variance of ${\mathcal{{C}}}_{{\text {rand}}}(t)$ is

$$\begin{aligned} \sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}}&= R_{{\mathcal{{C}}}_{{\text {rand}}}}(0) - R_{{\mathcal{{C}}}_{{\text {rand}}}}(\infty ) = C^2\left( P,W,N_o\right) \; (p_1 (1-p_1)). \end{aligned}$$

(12)

2.3 Random Capacity for MC

When considering $N$ channels with bandwidth, power and power spectral density, $W_i, P_i, N_{o,i} = N_o, i = 1, 2, \ldots , N$, and each channel having its own $b_i(t), i=1,2,\ldots ,N$, the aggregated random capacity is

$$\begin{aligned} {\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}(t)&\mathop {=}\limits ^{\bigtriangleup }&\sum _{i=1}^{N} {\mathcal{{C}}}_{{\text {rand}},i}(t) = \sum _{i=1}^{N} b_i(t) \; C\left( P_i,W_i,N_o\right) , \end{aligned}$$

(13)

where we have assumed that $W_i=W/N$ and (according to (2)) $P_i=P/N$, therefore $P = \sum _{i=1}^{N} Pi$ and $W = \sum _{i=1}^{N} Wi$,

If the set $\{ b_i(t) \}$ are independent and identically distributed (i.i.d.), then expression (13) can be written as

$$\begin{aligned} {\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}(t)&= \sum _{i=1}^{N} b_i(t) \frac{W}{N} \; \log _2\left( 1+ \frac{P}{N_o \; W}\right) = \sum _{i=1}^{N} b_i(t) \; \frac{C\left( P,W,N_o\right) }{N} \end{aligned}$$

(14)

The mean value of ${\mathcal{{C}}}_{{\text {rand}}}^{{\text {(}}N)}(t)$ is

$$\begin{aligned} \mathcal{{C}}_{{\text {avg}}}^{{\text {(N)}}}&= \mathcal{E}_{b_1,b_2,\ldots ,b_N}\left\{ \sum _{i=1}^{N} b_i(t) \; \frac{C\left( P,W,N_o\right) }{N} \right\} = p_1 \; C\left( P,W,n_o\right) = \mathcal{{C}}_{{\text {avg}}}, \end{aligned}$$

(15)

i.e., both SC and MC have the same $\mathcal{{C}}_{{\text {avg}}}$, but the autocorrelation function for MC is

$$\begin{aligned} R_{{\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}}(\tau )&= \mathcal{E}_{b_1,b_2,\ldots ,b_N}\{{\mathcal{{C}}}_{{\text {rand}}}(t) {\mathcal{{C}}}_{{\text {rand}}}(t+\tau ) \} \nonumber \\&= \mathcal{E}_{b_1,b_2,\ldots ,b_N}\left\{ \sum _{i=1}^{N} b_i(t) \; \frac{C\left( P,W,N_o\right) }{N} \sum _{j=1}^{N} b_j(t+\tau ) \; \frac{C\left( P,W,N_o\right) }{N} \right\} \nonumber \\&= \left[ N \; R_b(\tau ) \; + \; N \; (N-1) \; p_1^2 \right] \; \frac{C^2\left( P,W,N_o\right) }{N^2} , \end{aligned}$$

(16)

where for $i <> j$ we have used $\mathcal{E}_{b_1,b_2,\ldots ,b_N}\{ b_i(t) b_j(t+\tau ) \}= (1 \cdot 1) (p_1 \cdot p_1) + (1 \cdot 0) (p_1 \cdot p_0) + (0 \cdot 1) (p_0 \cdot p_1) + (0 \cdot 0) (p_0 \cdot p_0)=p_1^2$. Notice that we can write () as

$$\begin{aligned} R_{{\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}}(\tau )&= \frac{1}{N} \; R_{\mathcal{{C}}_{{\text {rand}}}}(\tau ) \; + \; \frac{N-1}{N} \; \mathcal{{C}}^2_{{\text {avg}}} \end{aligned}$$

(17)

In particular, the variance of ${\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}(t) = R_{{\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}}(0) -R_{{\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}}(\infty )$ can be written as

$$\begin{aligned} \sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}} = \frac{ \sigma ^2_{\mathcal{{C}}_{{\text {rand}}} } }{N} \end{aligned}$$

(18)

2.4 Outage Capacity for SC

Clearly ${\mathcal{{C}}}_{{\text {rand}}}(t)$ fluctuates around ${\mathcal{{C}}}_{{\text {avg}}}$ with a variance $\sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}}$. We are also interested in calculating what is the outage probability that ${\mathcal{{C}}}_{{\text {rand}}}(t)$ falls below a certain minimum value called outage capacity. Following the definition of outage capacity in [9], in our case we define the outage capacity ${\mathcal{{C}}}_{{\text {out}}}$ related to the outage probability $\mathcal{{P}}_{{\text {out}}}$ using the following expression:

$$\begin{aligned} \mathrm{Prob}({\mathcal{{C}}}_{{\text {rand}}}(t) \; < \; {\mathcal{{C}}}_{{\text {out}}})&= \mathcal{{P}}_{{\text {out}}}. \end{aligned}$$

(19)

In (19), $\mathcal{{P}}_{{\text {out}}}$ indicates the probability that the system can be in outage, i.e. the probability that the system cannot successfully decode the transmitted symbols, and ${\mathcal{{C}}}_{{\text {out}}}$ is the data rate which is successfully decoded with probability $1-\mathcal{{P}}_{{\text {out}}}$ [10]. In general, the probability density function (p.d.f.) of ${\mathcal{{C}}}_{{\text {rand}}}(t)$ is difficult to calculate, so calculation of ${\mathcal{{C}}}_{{\text {out}}}$ using (19) is complicated. Similarly to the methodology used in [11], to calculate ${\mathcal{{C}}}_{{\text {o}}ut}$ we will use the Chebyshev’s inequality [7] that establishes a bound in the probability of ${\mathcal{{C}}}_{{\text {rand}}}(t)$ being outside an interval $(\mathcal{{C}}_{{\text {avg}}}-\delta ,\mathcal{{C}}_{{\text {a}}vg}+\delta )$

$$\begin{aligned} \mathrm{Prob}(|{\mathcal{{C}}}_{{\text {rand}}}(t) \; - \; \mathcal{{C}}_{{\text {avg}}}| \; \ge \; \delta ) \; \le \; \sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}} \; / \; \delta ^2. \end{aligned}$$

(20)

Since we are considering both $\mathrm{Prob}({\mathcal{{C}}}_{{\text { rand}}}(t) \; \ge \; ({\mathcal{{C}}}_{{\text {avg}}}+\delta ))$ and $\mathrm{Prob}({\mathcal{{C}}}_{{\text {rand}}}(t) \; \le \; ({\mathcal{{C}}}_{{\text {avg}}}-\delta ))$ we chose [11]

$$\begin{aligned} (\sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}} \; / \; \delta ^2) = 2\mathcal{{P}}_{{\text {out}}} \qquad \mathrm{and } \qquad \delta \; = \; \mathcal{{C}}_{{\text {avg}}} \; - \; {\mathcal{{C}}}_{{\text {o}}ut}, \end{aligned}$$

(21)

From (20) and (21) the following inequality is obtained

$$\begin{aligned} {\mathcal{{C}}}_{{\text {out}}} \ge \mathcal{{C}}_{{\text {avg}}} - \sqrt{\sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}} \; / \; (2\mathcal{{P}}_{{\text {out}}})}. \end{aligned}$$

(22)

Since (22) is an approximation, to avoid negative capacity values the following definition is used

(23)

where $\mathrm{max}(x,y)$ takes the maximum between $x$ and $y$. An expression similar to (23) will be used for MC.

3 Analysis SC Versus MC and Numerical Results

We are interested in studying the differences when the SU uses either SC or MC. For this purpose, we define

$$\begin{aligned}&{\mathcal{{C}}}_{{\text {SC}}}(t) \mathop {=}\limits ^{\bigtriangleup }{\mathcal{{C}}}_{{\text {rand}}}(t), \quad \mathcal{{C}}_{{\text {avg-SC}}} \mathop {=}\limits ^{\bigtriangleup }\mathcal{{C}}_{{\text {avg}}}, \quad \sigma ^2_{{\text {SC}}} \mathop {=}\limits ^{\bigtriangleup }\sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}}, \end{aligned}$$

(24)

$$\begin{aligned}&{\mathcal{{C}}}_{{\text {MC}}}(t) \mathop {=}\limits ^{\bigtriangleup }{\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}(t) , \quad \mathcal{{C}}_{{\text {avg-MC}}} \mathop {=}\limits ^{\bigtriangleup }\mathcal{{C}}_{{\text {avg}}}^{{\text {(N)}}}, \quad \sigma ^2_{{\text {MC}}} \mathop {=}\limits ^{\bigtriangleup }\sigma ^2_{{\mathcal{{C}}}_{{\text {rand}}}^{{\text {(N)}}}}. \end{aligned}$$

(25)

Figure  2 depicts an example of ${\mathcal{{C}}}_{{\text {avg}}}$ and realizations of ${\mathcal{{C}}}_{{\text {SC}}}(t)$ and ${\mathcal{{C}}}_{{\text {MC}}}(t)$.

Fig. 2

Example of ${\mathcal{{C}}}_{{\text {avg}}}$ and realizations of ${\mathcal{{C}}}_{{\text {SC}}}(t)$ and ${\mathcal{{C}}}_{{\text {M}}C}(t)$

We have found that $\mathcal{{C}}_{{\text { avg-SC}}}=\mathcal{{C}}_{{\text {avg-MC}}}$. We now may ask the following questions: (1) Which system, SC or MC, have less variance due to the bursty operation?, and (2) What are the implications in terms of outage capacity?

Equation (18) provides the answer for the first question, i.e., ${\mathcal{{C}}}_{{\text {MC}}}(t)$ has a variance that is $N$ times smaller than the variance of ${\mathcal{{C}}}_{{\text { SC}}}(t)$. This is illustrated in Fig. 3.

Fig. 3

Examples of $\sigma ^2_{{\text {SC}}}$ and $\sigma ^2_{{\text {MC}}}$

Next, we investigate the difference in outage capacity produced by this difference in variances. Using (23) as a baseline, let us define

(26)

(27)

We recall that (26) and (27) were derived using the Chebyshev’s inequality. From the definition in (13) we can see that the p.d.f. of ${\mathcal{{C}}}_{{\text {MC}}}^{{\text {(N)}}}(t)$ is approximately symmetric and take a variety of values (see Fig. 4b), but from the definition in (5) we see that the p.d.f. of ${\mathcal{{C}}}_{{\text { SC}}}^{{\text {(N)}}}(t)$ takes only two values (see Fig. 4a). Hence, we expect (26) to be a poor approximation for ${\mathcal{{C}}}_{{\text {out-SC}}}$ and (27) to be a good approximation for ${\mathcal{{C}}}_{{\text {out-MC}}}$.

Fig. 4

Example of histograms for ${\mathcal{{C}}}_{{\text {SC}}}^{{\text {(N)}}}(t)$ and ${\mathcal{{C}}}_{{\text {MC}}}^{{\text {(N)}}}(t)$

To find an “exact” value for ${\mathcal{{C}}}_{{\text {out-SC}}}$, consider the expression

$$\begin{aligned} \mathrm{Prob}({\mathcal{{C}}}_{{\text {SC}}}(t) \; < \; {\mathcal{{C}}}_{{\text {out-SC}}}) = \mathcal{{P}}_{{\text {out}}}, \end{aligned}$$

(28)

however, for the SC case it is clear that

$$\begin{aligned} {\mathcal{{C}}}_{{\text {SC}}}(t) = \left\{ \begin{array}{ll} C\left( P,W,N_o\right) , &{} \mathrm{with\, probability\, p_1,} \\ \psi \in ( \; 0 \;,\; C\left( P,W,N_o\right) \; ), &{} \hbox {with probability zero}, \\ 0 , &{} \hbox { with probability } 1-p_1, \\ \end{array}\right. \end{aligned}$$

(29)

From (28) and (29) we conclude that

$$\begin{aligned} \mathcal{{C}}_{{\text {out-SC}}} \mathop {=}\limits ^{\bigtriangleup }\left\{ \begin{array}{ll} \alpha \; C\left( P,W,N_o\right) , &{} \quad \hbox {for}\,\mathcal{{P}}_{{\text {out}}} = (1-p_1)\,\hbox {and}\, 0 < \alpha \le 1, \\ \hbox {not defined} , &{} \quad \hbox {for}\,\mathcal{{P}}_{{\text {out}}}\,<>\,(1-p_1) \\ \end{array}\right. . \end{aligned}$$

(30)

From (30) we conclude that a low $\mathcal{{P}}_{{\text {out}}}$ requires a value of $p_1$ close to one, i.e., a duty cycle of the SU close to one, but this has the problem that it leaves a very short duty cycle for the PU. Figure 5 shows an example of $C\left( P,W,N_o\right) , {\mathcal{{C}}}_{{\text {avg}}}$ and ${\mathcal{{C}}}_{{\text {out-SC}}}$ using both the “exact” value in (30) with $\alpha =1$ (i.e. $\hbox {Cout-SC} = \hbox {C}\,\,(\hbox {P, W, No})$), and the approximation in (26).

Fig. 5

Examples of $C\left( P,W,N_o\right) , {\mathcal{{C}}}_{{\text {avg}}}$ and ${\mathcal{{C}}}_{{\text {out-SC}}}$

For the MC case we can investigate the relation between ${\mathcal{{C}}}_{{\text {out-MC}}}$ and $\mathcal{{P}}_{{\text {out}}}$ for different $p_1$ using the relations in (21) to write the expression

$$\begin{aligned} \mathrm{Prob}({\mathcal{{C}}}_{{\text {MC}}}(t) \; < \; {\mathcal{{C}}}_{{\text {out-MC}}})&\le \frac{\sigma ^2_{{\text {MC}}} }{(\mathcal{{C}}_{{\text {avg-MC}}} - {\mathcal{{C}}}_{{\text {out-MC}}} )^2}. \end{aligned}$$

(31)

Recall that $\mathcal{{C}}_{{\text {avg}}} = p_1 \; C\left( P,W,N_o\right)$, and that if $N >> 1$ then $\sigma ^2_{{\text {MC}}} << 0$. Hence, low values of $\mathcal{{P}}_{{\text {out}}}$ can be achieved for both large and small values of the duty cycle $p_1$. A small value of the duty cycle of the SU allows a larger duty cycle values of the PU, but it may require the estimation of a large number $N$ of $\{ b_i(t) \}$. Figure 6 depicts an example of $C\left( P,W,N_o\right) , {\mathcal{{C}}}_{{\text {avg}}}$ and the approximation for ${\mathcal{{C}}}_{{\text {out-MC}}}$ in (27).

Fig. 6

Examples of $C\left( P,W,N_o\right) , {\mathcal{{C}}}_{{\text {avg}}}$ and ${\mathcal{{C}}}_{{\text {out-MC}}}$

To further investigate the effect of $p_1, \mathcal{{P}}_{{\text {o}}ut}$ and $N$ in ${\mathcal{{C}}}_{{\text {out-MC}}}$, Fig. 7 plot ${\mathcal{{C}}}_{{\text {out-MC}}}$ in (27) for different conditions. As expected, increasing $N$ increases ${\mathcal{{C}}}_{{\text {out-MC}}}$. However, there is a diminishing return, i.e., the benefit of increasing $N$ diminishes as $N$ grows. Moreover, the ${\mathcal{{C}}}_{{\text {out-MC}}}$ is more sensitive to changes in $p_1$ than in $\mathcal{{P}}_{{\text {out}}}$. Besides, for low values of both $p_1$ and $\mathcal{{P}}_{{\text {out}}}$ large values of $N$ need to be considered.

Fig. 7

The ${\mathcal{{C}}}_{{\text {out-MC}}}$ for different values of $p_1$, $\mathcal{{P}}_{{\text {out}}}$, and $N$

4 Conclusion

In this work we have studied the outage capacity from the point of view of a SU that shares the bandwidth of the channel with a PU using DSA-CR. We have derived expressions for the outage capacity due to bandwidth fluctuations for both SC and MC and proceeded to make a comparison between them. Our analysis indicated the following:

• The ${\mathcal{{C}}}_{{\text {MC}}}(t)$ has a variance that is $N$ times smaller than the variance of ${\mathcal{{C}}}_{{\text {SC}}}(t)$.

• The ${\mathcal{{C}}}_{{\text {out-SC}}}$ can be high but with a high $\mathcal{{P}}_{{\text {out}}}$. A low value of $\mathcal{{P}}_{{\text {out}}}$ requires a value of $p_1$ close to one, but this has the problem that it leaves a very short duty cycle for the PU.

• The ${\mathcal{{C}}}_{{\text {out-MC}}}$ is lower than ${\mathcal{{C}}}_{{\text {out-SC}}}$, but low values of $\mathcal{{P}}_{{\text {out}}}$ can be achieved even for large duty cycle values of the primary user. However, it may require the estimation of a large number of $\{ b_i(t) \}$.

• For low values of both $\mathcal{{P}}_{{\text {out}}}$ and $p_1$, large values of $N$ need to be considered to get a reasonable value of ${\mathcal{{C}}}_{{\text {out-MC}}}$ However, the benefit of increasing $N$ diminishes as $N$ grows.

• The ${\mathcal{{C}}}_{{\text {out-MC}}}$ is more sensitive to changes in $p_1$ than in $\mathcal{{P}}_{{\text {out}}}$ .

For future work more studies with other types of channels and other distributions of $b(t)$ can be considered.