Energy Balanced Model for Lifetime Maximization in Randomly Distributed Wireless Sensor Networks

Abstract

In this paper, an energy balanced model (EBM) for lifetime maximization for a randomly distributed sensor network is proposed. The lifetime of a sensor network depends on the rate of energy depletion caused by multiple factors, such as load imbalance, sensor deployment distribution, scheduling, transmission power control, and routing. Therefore, in this work, we have developed a mathematical model for analysis of load imbalance under uniform and accumulated data flow. Based on this analysis, we developed a model to rationalize energy distribution among the sensors for enhancing the lifetime of the network. To realize the proposed EBM, three algorithms—annulus formation, connectivity ensured routing and coverage preserved scheduling have been proposed. The proposed model has been simulated in ns-2 and results are compared with Energy-Balanced Transmission Policy and Energy Balancing and unequal Clustering Algorithm. Lifetime has been measured in terms of the time duration for which the network provides satisfactory level of coverage and data delivery ratio. EBM outperform both the existing models. In our model the variance of residual energy distribution among the sensors is lower than other two models. This validated the essence of energy rationalization hypothesized by our model.

1 Introduction

Wireless sensor network is a set of small and intelligent entities which are responsible for their organization, configuration and working in order to provide sensing services assigned to them [1]. The services provided by a sensor network belong to broad spectrum of real time applications. Surveillance in battlefields and buildings for stopping possible intrusion and theft, monitoring vehicular traffic and for pest management in agricultural fields etc. are some of the vital applications [2]. In spite of its wide applicability, research in this area has its own challenges. One of the main challenges in WSN is to maximize the lifetime of the network by conserving energy and without compromising the coverage and connectivity in the realistic environments [3].

Energy management is a critical task in wireless sensor networks due to severely power limited sensors. The limitation of power is because of the two operating factors. First, sensors consume lots of energy while operating with full intensity which cannot be supported by a small battery for longer duration. Secondly, battery cannot be replenished in a sensor network due to inaccessibility of physical locations [4]. In the literature, many solutions exist for energy balancing in the wireless senor network. These solutions balance energy consumption among different sensors in the network while they are at work [5]. However, performance of a sensor network primarily depends on the deployment scheme. But at the same time, these solutions also suffer from the inherent discrepancy in the deployment itself. There are two kinds of deployment schemes; deterministic deployment and random deployment. In the former, sensors are deployed in pre-calculated manner in the sensing region. In the latter, sensors are not deployed in so called well calculated manner. However, if situation is not very hostile, some estimation can be carried out before deployment [6]. Different sensors bear different load in randomly deployed networks. Due to this fact, sensors near the sink lose their energy earlier and thus network suffers from the problem of connectivity [7].

In this paper, we propose an energy balanced model for wireless sensor network. We assume that for a large wireless sensor networks in hostile environment sensors are deployed randomly. However, this random deployment can be realized by following normal distribution from its center to the boundaries. We analyze the energy consumption in transmission and sensing by all the sensors. In the paper, we have used energy consumption and load interchangeably. Load analysis has been performed for uniform data flow and accumulated data flow. In the current work, we intend to fairly equalize the energy consumption by all the sensors deployed in sensing region using adaptive sensing, adjusting transmission range and density control of sensors. To realize the proposed energy model, supporting algorithms for annulus formation, connectivity ensured routing and coverage preserved scheduling are developed. We have carried out extensive simulations to validate the applicability of EBM.

2 Related Work

In the literature, most of the research works on energy balancing models for wireless sensor networks deal with the planned networks. Therefore, researchers have not focused on energy balancing in these networks since such networks either do not require energy balancing necessarily or do not provide much opportunity for energy balancing. But, in randomly deployed networks, energy balancing is one of the key requirements due to unpredicted topology. Powell et al. have proposed a spreading technique to balance the energy among sensors of the same slice. The authors divided the whole sensing region in many slices. The technique has also been validated through simulation for data monitoring and propagating task by applying the probabilistic data propagation algorithm with optimal parameters [8]. Energy-Balanced Transmission Policy (EBTP) has been proposed based on controlled transmission power by Azad and Kamruzzaman in [9]. Authors have proposed that imbalance in energy consumption causes early demise of some of the sensors which ultimately leads to the problems of coverage and connectivity in the network. The analysis has been performed by taking concentric circles around the sink and load is balanced by decreasing the transmission range of different sensors near the sink. Efthymiou et al. [10] have suggested an algorithm for energy balancing in the sensor network through routing.

Sardouk et al. in [11], have proposed a scheme to maximize the lifetime of the network based on the cooperation among different sensors. This scheme considers information importance based communication for energy efficient data processing. In [12], Bouabdallah et al. have suggested a protocol that finds multiple paths for traffic generated by sensors to balance energy in the network. It is proved analytically that choosing multiple paths for sensors to forward data conserves energy to maximize the lifetime of a network. A scalable and distributed algorithm is presented for routing of data by Chang and Tassiulas [13]. This routing technique is based on linear programming formulation used for choosing next hop. Chiasserini and Garetto proposed a scheme that schedules redundant sensors to go in sleep mode for saving the battery power and maximizing the lifetime of the network [14]. An energy estimation approach has been suggested in [15], where authors claimed that their approach enables mobile agents to predict the remaining energy of all sensors in their clusters. Additionally, they have also presented a routing scheme to balance the energy among sensors using mobile agents. In [16] authors have developed an clustering algorithm which selects a sensor as cluster head based on remaining energy, node degree, density, etc. This algorithm provides opportunity to each sensor to become a cluster head to balance the energy consumption among all the sensors. Heuristic based routing technique to control transmission power of all sensors has been suggested in [17]. Authors in [18] have proposed load balanced clustering algorithm. This algorithm considers parameters such as radius of cluster based on distance and distribution, node degree and remaining energy of sensors to form clusters.

Energy Balancing and unequal Clustering Algorithm (EBCAG) using gradient routing has been presented in [19]. EBCAG assigns grades to each sensor of the network. A grade is the minimum number of hop-counts required to reach the sink. After assigning grades, unequal clusters have been created to achieve fairly balanced energy depletion among all the sensors. Descending gradient based forwarding strategy has been used by each cluster members to forward data to the sink. Algorithms for efficient cluster head selection and cluster formation have also been provided.

Our motivation for this paper rests on the laxity of researchers for not addressing the problem of energy imbalance inadequately. A few of researchers addressed this problem once the distribution of sensors had been assumed. This assumption poses lots of limitations due to uneven load. Some others addressed the problem by assuming routing as one of possible candidates for energy balancing. Therefore, in this work, we have made an attempt to address the problem of energy imbalance by using adaptive sensing and transmission without compromising coverage and connectivity. This approach does not only fairly equalize the energy consumption by different sensors but also improves lifetime of network.

3 Problem Description

Problems of coverage and connectivity are critical for randomly distributed wireless sensor networks. Connectivity is measured in terms of successful packet transmission to the sink. However this could not be the only metric for measurement of connectivity; how efficiently connection is established also matters. At the same time optimized coverage for the region is required for quality of service. While addressing the problem of coverage and connectivity, issue of energy consumption and balancing is mostly ignored. Some efforts have been made by researchers to address the problem of energy balancing independent of coverage and connectivity. Therefore, to increase the lifetime of the network, one needs to balance the energy consumption among sensors with maintaining satisfactory coverage and connectivity. The problem is formulated as follows:

Sensors in a wireless senor network primarily perform two tasks; sensing and transmission. For sensing, we assume that each sensor takes $E_s$ units of energy per unit time. According to free space path loss model, the received power $P_{r}$ at a distance $d$ from a sensor is given by following equation

$$\begin{aligned} P_{r} =P_{t} \left( {\frac{\lambda }{4\pi d}} \right) ^{2}G_{t} G_{r} \end{aligned}$$

(1)

where $P_{t}$ represents the transmission power used by a sensor, $\lambda$ is the wavelength of signal, and $G_{t} ,and \; G_{r}$ are antenna gains for transmitting and receiving sensors respectively. We note that power consumed in sensing is directly proportional to the square of distance (1). We have

$$\begin{aligned} E_{s_{1} }&\propto r_{1}^2\end{aligned}$$

(2)

$$\begin{aligned} \hbox { and } E_{s_{2} }&\propto r_{2}^2 \end{aligned}$$

(3)

where, $E_{s_{1} }$ and $E_{s_{2} }$ are energy consumed by sensors $s_{1}$ and $s_{2}$ with sensing ranges $r_{1}$ and $r_{2}$ respectively. From (2) to (3), we get.

$$\begin{aligned} \frac{E_{s_{1} } }{E_{s_{2} } }=\frac{r_{1}^2 }{r_{2}^2 } \end{aligned}$$

(4)

Another task performed by a sensor is transmission of accumulated data. We assume that $E_{t}$ is the energy consumed per unit time in transmission between two sensors separated by distance $t$. The path loss formula given in (1) is also applicable for this case, therefore, we have

$$\begin{aligned} \frac{E_{t_{1} } }{E_{t_{2} } }=\frac{t_{1}^2 }{t_{2}^2 } \end{aligned}$$

(5)

We assume that sensing region is circular in shape having radius $R$. Further, we also assume that data generated by each sensor in a sensing region follows binomial distribution and routed to the sink which is situated in the center of the region. Our objective, in this work is to fairly equalize the total energy consumption of each sensor over a specified period of time. We consider that the energy consumed during time $T$ in sensing and transmission by $i$th sensor are $E_{i}^{s}$ and $E_{i}^{t}$ respectively. Therefore, the total energy consumed during time $T$ by $i$th sensor can be expressed as

$$\begin{aligned} E_{i}^s +E_{i}^t =E_{i}^T \quad \forall i=1\ldots N \end{aligned}$$

(6)

where, $N$ is total number of sensors deployed. Our objective is to keep $E_{i}^T$ fairly equal for all sensors, i.e. $E_{1}^T =E_{2}^T =\cdots =E_{N-1}^T =E_N^T$. Further, in the paper the energy $E_{i}^{T}$ is also referred to as load on $i$th sensor. While achieving this objective we are required to maintain a satisfactory coverage and connectivity in the sensing region. The notations used in EBM are given in Table 1.

Table 1 Notation table

4 Mathematical Analysis of Load on Sensors

We present a mathematical model for energy balancing based on uniform data flow and accumulated data flow. Load analysis has been performed for both uniform and accumulated data flow. In the following section, we analyze the distribution pattern of sensors and its impact on the load.

4.1 Load Analysis Under Uniform Data Flow

Without losing the generality of problem, we assume that sensing region is circular in shape with radius $R$. It is also assumed that sink is situated at the center of sensing region. In view of the assumptions, it is clear that data sensed in the entire region ultimately reach the center of circle. In this approach, sensors near the center deplete their energy faster. Therefore, for fair distribution of sensors or load, we have divided sensing region in concentric circles with approximately equal spacing (cf. Fig. 1). Using this model, we analyze how the rate of flow of data exerts transmission load on sensors in each concentric circle towards the sink.

Fig. 1

Increasing load under uniform data flow

Let total amount of data to be carried through each annulus from outer most to the sink is $L$. Let spacing between each concentric circle is decreasing by a very small factor $\delta$ from outside to inside. Radii of circles from outside to inside can be given by $R,\delta R,\,\delta ^{2}R$ and so on. Area of outer most annulus is given by $\pi (R^{2}-\delta ^{2}R^{2})$. In the same way we can calculate the area of other annulus as follows: $\pi (\delta ^{2}R^{2}-\delta ^{4}R^{2}),\pi (\delta ^{4}R^{2}-\delta ^{6}R^{2})$ and so on. We assume that sensors are distributed uniformly in each annulus and the load in an annulus is equally distributed among sensors in that annulus. Load in each annulus is given by the following formula.

$$\begin{aligned} \textit{load}=\frac{\textit{amount}\;\textit{of} \;\textit{data} \; \textit{in} \;\textit{the} \;\textit{annulus}}{\textit{area}\; \textit{of} \;\textit{the} \;\textit{annulus}} \end{aligned}$$

(7)

Let $X$ is a random variable such that $X(n)$ represents the probability that data is generated in $n$th annulus (from outside to inside) by following uniform distribution. The probability $X(n)$ can be calculated as follows.

$$\begin{aligned} X\left( n \right) =\frac{\pi (\delta ^{2n}R^{2}-\delta ^{2n+2}R^{2})}{\pi R^{2}},\quad 0<\delta <1\; and \;n\ge 0 \end{aligned}$$

(8)

Theorem 1

X is geometrically distributed.

Proof

Probability of data generation in $n$th annulus is given by $X\left( n \right) =\frac{\pi \left( {\delta ^{2n}R^{2}-\delta ^{2n+2}R^{2}} \right) }{\pi R^{2}}$. By solving the expression on right hand side of the Eq. (8), we get following series $\left( {1-\delta ^{2}} \right) ,\delta ^{2}\left( {1-\delta ^{2}} \right) ,\,\delta ^{4}\left( {1-\delta ^{2}} \right) ,$... for different possible values of $n$. This is a geometrically distributed series with parameter $\left( {1-\delta ^{2}} \right)$: hence the result. $\square$

Theorem 2

Geometric distribution $X\left( n \right)$ in limiting case can be expressed by exponential distribution.

Proof

We assume that $q=1-\delta ^{2}$ is very small and $mq=\mu ,$ where $m$ is supposed to be large and $x=\frac{n}{m}$. From Eq. (8), we have

$$\begin{aligned} \begin{aligned}&\displaystyle \mathop \sum \limits _{n=0}^\infty q\left( {1-q} \right) ^{n}=1\\&\displaystyle \mathop \sum \limits _{n=0}^\infty \mu \left( {1-\frac{\mu }{m}} \right) ^{m\frac{n}{m}}\frac{1}{m}=1 \end{aligned} \end{aligned}$$

as $m\rightarrow \infty$, and by applying $\left( {1-z} \right) ^{m}\approx e^{-zm}$, we have

$$\begin{aligned} \mathop \int \limits _0^\infty \mu e^{-\mu x}dx=1 \end{aligned}$$

(9)

where $\mu =m(1-\delta ^{2})$. From Eq. (9), it is clear that data generated in all annuli is exponentially distributed from outside to inside. $\square$

Theorem 3

The probability density function of load on sensors given in Eq. (9) yields to Gaussian distribution in limiting case from inner to outer annulus.

Proof

We assume that $Y$ is a random variable where $Y=1/X$, and Y follows Poisson distribution. The probability density function $f_{y} (n)$ for Y can be given as

$$\begin{aligned} f_{y} (n)=\frac{\left( {m\left( {1-\delta ^{2}} \right) } \right) ^{n}e^{-m(1-\delta ^{2})}}{n!} \end{aligned}$$

(10)

Let $m(1-\delta ^{2})=\mu$ and $x=n=\mu \left( {1+\varepsilon } \right) \;\mu \gg 1\; and\; \varepsilon \ll 1$

Since $m$ converges to $\mu$ and $x!\approx \sqrt{2\pi x}\left( {\frac{e}{x}} \right) ^{-x}as \ x\rightarrow \infty$, we have

$$\begin{aligned} f_{y} (n)&= \frac{(\mu )^{\mu (1+\varepsilon )}e^{-\mu }}{\sqrt{2\pi }e^{-\mu (1+\varepsilon )}\left[ {\mu (1+\varepsilon )} \right] ^{\mu \left( {1+\varepsilon } \right) +\frac{1}{2}}}\\&= \frac{e^{-\mu \varepsilon }\left[ {(1+\varepsilon )} \right] ^{-\mu \left( {1+\varepsilon } \right) -\frac{1}{2}}}{\sqrt{2\pi \mu }}\\&= \frac{e^{-\mu \varepsilon ^{2}/2}}{\sqrt{2\pi \mu }} \end{aligned}$$

By substituting the value of $\varepsilon$, the probability density function $f_{GU} (x)$ of the load on sensors under uniform data flow can be expressed as

$$\begin{aligned} f_{GU} \left( x \right)&= \frac{e^{-(x-\mu )^{2}/2\mu }}{\sqrt{2\pi \mu }}\nonumber \\&= \frac{e^{-\left( {x-m\left( {1-\delta ^{2}} \right) } \right) ^{2}/2m(1-\delta ^{2})}}{\sqrt{2\pi m(1-\delta ^{2})}} \end{aligned}$$

(11)

$\square$

The distribution of load in the various annuli has been analyzed by simulating (7) and (11). For $m=$100,000 and $p=.99$, the distribution of load in various annuli has been show in Fig. 2.

Fig. 2

Load curve Under uniform data flow

The result in Fig. 2 shows that the distribution of load on sensors from inner to outer annulus follows folded Gaussian distributed in limiting case. Sensors are deployed as per Eq. (11) with appropriate mean and variance to equalize the load in network.

4.2 Load Analysis Under Accumulated Data Flow

In this section, we analyze the load on each sensor under accumulated data flow. Sensors are distributed according to Gaussian distribution as described in previous section by Eq. (11) to compensate for excessive load on sensors in the inner annulus under uniform data flow model. It is assumed that sensors are generating data following binomial distribution with parameter $t$. Let the area of each annulus is sufficiently large to accommodate a large number of sensors to cover it. Probability mass function of data generated by $r$ out of $n$ sensors is given by

$$\begin{aligned} f_B (r)=\frac{n!}{r!(n-r)!}t^{r}(1-t)^{n-r} \end{aligned}$$

(12)

Let $t=\frac{\mu }{s}$, where $s$ is assumed to be large and $t$ is small. According to the law of rare events, we obtain

$$\begin{aligned} f_P \left( r \right) =\frac{1}{r!}\mu ^{r}e^{-\mu } \end{aligned}$$

(13)

Expression (13) represents a probability mass function for Poisson distribution. Data generated from each annulus is assumed to follow Poisson process. Under accumulated data flow model, we have to analyze the load on each sensor in each annulus. It is apparent from the Fig. 3 that inner annuluses have to carry not only their own data but also data generated from outer annuluses. We have assumed that for a large number of annulus this data distribution follows Gaussian distribution as proved in theorem 3. Therefore, probability density function of the load on sensors can be given as

$$\begin{aligned} f_{GA} (x)=\frac{e^{-(x-\mu )^{2}/2\mu }}{\sqrt{2\pi \mu }} \end{aligned}$$

(14)

Fig. 3

Accumulated data flow

4.3 Load Equalization

Before equalization of load, we need to simulate Eq. (7) to show the distribution of load in the various annuli. Result obtained through is depicted in Fig. 4 for $t=0.1$ and $s=$ 100,000 using Eq. (12) for generation of data by sensors. It shows that due to accumulated data flow from outer annulus to the sink, load on sensors in inner annulus increases rapidly.

Fig. 4

Load curve under accumulated data flow

Now we present a scheme to equalize the load on sensor in different annulus. In the inner annulus, sensors transmit more packets in comparison to those in outer annulus. We have analyzed the impact of increasing data load on sensors. It was observed that the load follows folded Gaussian distribution.

We have presented the load curve for accumulated data in Fig. 5. From the figure, the area of an annulus is calculated by multiplying height of load curve (red line) over annulus with the width of annulus. For equalizing the load, we take rectangles of equal area throughout the curve. These areas can be kept equal if we increase the width with increasing distance from the origin as shown in Fig. 5. However, in this discussion annulus number represents the number of sensors in that annulus. Therefore, by changing the width of annulus we are varying the sensing range or transmission range of the sensors in the annulus. The area of annulus can be changed by either controlling the sensing or transmission range. Sensing range of sensors can be controlled by scheduling the sensors. Transmission range of a sensor can be controlled by designing appropriate routing protocols. We have used adaptive sensing and transmission method for equalizing excessive load on sensors. To accomplice this objective we present scheduling and routing algorithms in the next section.

Fig. 5

Equalizing load in each annulus

5 Proposed Algorithms

In this section, supporting algorithms for energy balancing are presented. These algorithms include creation of annulus in the sensing region (cf. Fig. 6), connectivity ensured routing and coverage preserved scheduling.

Fig. 6

Annulus formation

5.1 Annulus Forming Algorithm (AFA)

We assume that $R_{i}$ is the transmission range of a sensor in $i$th annulus. The width of an annulus is assumed to be twice of the transmission range of sensor in that annulus. Therefore, it is important to determine the value of $R_{i}$. We derive transmission range $R_{i}$for sensors according to their distance from the sink by using $L_{i} R_{i} =L_{i-1} R_{i-1} \forall i\ge 1$ or $R_{i} =\frac{L_{i-1} R_{i-1} }{L_{i} }$. The value of $L_{i}$ is computed from (14) as

$$\begin{aligned} L_{i} =\frac{e^{-(A_{i} -\mu )^{2}/2\mu }}{\sqrt{2\pi \mu }} \end{aligned}$$

(15)

In the Eq. (15) $A_{i}$ is the annulus number determined using the following function.

$$\begin{aligned} A_{i} =\left\{ \begin{array}{ll} \frac{h_{i} }{2} &{}\quad \textit{if} \;h_{i} \; is \;even \\ \frac{h_{i} -1}{2} &{}\quad \textit{if} \;h_{i} \; is \;odd \\ \end{array} \right. \end{aligned}$$

(16)

where $h_{i}$ is the minimum number of hop counts from sink to $i$th sensor. To find $h_{i}$, sink node sends a Hello packet to its neighboring sensors with hop count 0. All the sensor nodes, which receive the Hello packet, increase the hop count by 1 and broadcast the packet further. A sensor node sends Hello packet if it has lower hop count than the previously received packet and remembers the packet that has lowest hop counts, i.e. $h_{i}$. Every sensor node finalizes its annulus number after elapsed of a period sufficient to deliver a Hello packet from sink to the farthest sensor node. A sensor stores the identity of all the sensors which have sent it the hello packet. This information is used in routing of the data packets. In Fig. 7, we have depicted the fields of a node of Hello list.

Fig. 7

Fields of a node of Hello list

Broadcasting of the Hello packet by sensors may result in collision of packets. To avoid the collisions a sensor has to wait for a random period before sending the Hello packet. This waiting time is determined by using a parameter $\xi _{i}\; for\;i=1,2,\ldots N$ that depends on the hop count. We assumed that waiting times for the sensors are exponentially distributed. Therefore, waiting time is given by $W_{i} =\xi _{i}\; e^{-\xi _{i} t}$, where $t$ is a uniform random variable with interval [0, 1]. We assume that waiting time of sensor is inversely proportional to hop count, i.e. a node having Hello packet with minimum hop count value should wait for minimum period. The parameter $\xi _{i}$ depends on the density of sensors in nearby region. If density is high, sensors must wait for longer period for avoiding possible collisions and therefore, $\xi _{i} \propto \frac{1}{\eta _{i} }$, where $\eta _{i}$ is the density of sensors in $i$th annulus. Density of sensors decreases from the inner to outer annulus and can be expresses as follows, if the sensors are deployed using Eq. (11)

$$\begin{aligned} \eta _{i}\propto \frac{1}{\frac{e^{-\left( {h_{i} -m\left( {1-\delta ^{2}} \right) } \right) ^{2}/2m(1-\delta ^{2})} }{\sqrt{2\pi m(1-\delta ^{2})}}}\end{aligned}$$

(17)

$$\begin{aligned} \xi _{i} =C\frac{e^{-\left( {h_{i} -m\left( {1-\delta ^{2}} \right) } \right) ^{2}/2m(1-\delta ^{2})} }{{h_{i} \sqrt{2\pi m(1-\delta ^{2})}}} \end{aligned}$$

(18)

where, $C$ is a normalizing constant that depends on the number of sensors in the region. Therefore, the waiting time for a sensor can be given as follows

$$\begin{aligned} W_{i} =C\frac{e^{{-\left( {h_{i} -m\left( {1-\delta ^{2}} \right) } \right) ^{2}/2m(1-\delta ^{2})} }}{h_{i} \sqrt{2\pi m(1-\delta ^{2})}}e^{-C\frac{e^{{ {-\left( {h_{i} -m\left( {1-\delta ^{2}} \right) } \right) ^{2}/2m(1-\delta ^{2})} }}}{h_{i} \sqrt{2\pi m(1-\delta ^{2})}}t} \end{aligned}$$

(19)

The algorithm for annulus formation is presented below:

5.2 Connectivity Ensured Routing Algorithm (CERA)

We present a routing algorithm to realize Energy Balancing Model proposed to rationalize the energy consumption by the sensors. The algorithm is designed to deliver a packet from a sensor to the sink using minimum number of hops. To forward packets a sensor selects a next hop sensor from its Hello List. While selecting next hop sensor from the Hello List, sensors from lower level annulus are preferred over sensors from same annulus. For rationalization of energy among sensors, from an annulus a sensor with the highest residual energy is selected.

5.3 Coverage Preserved Scheduling Algorithm (CPSA)

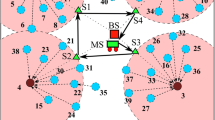
In this section, we present coverage preserved scheduling algorithm for EBM to further rationalize energy. The algorithms for routing and connectivity rationalize energy consumed in transmission only. However, energy consumed in sensing also needs to be rationalized. A large number of sensors are deployed in the sensing region to achieve satisfactory coverage that results in redundancy. We propose coverage preserved scheduling algorithm which sets off redundant sensors for a specific period. Identification of redundant sensors while preserving coverage is critical for scheduling. Therefore, in the proposed algorithm, we have developed a relative coordinate system that helps in identifying redundant sensors. In the relative coordinate system, we determine the relative coordinates of a sensor with respect to known coordinates of two sensors. In this system, we designate any sensor to be located at origin $(0,0)$. We choose another sensor which is assumed to be located on x-axis at distance $d$ from the sensor at origin. Therefore, the coordinate of this sensor is $(d,0)$. By using the geometry, now we can determine the relative coordinate of any other sensor by using the coordinates, i.e. $(0,0)$ and $(d,0)$ of the two known sensors (cf. Fig. 8).

Fig. 8

Coordinates assignments

In the Fig. 8, we have designated a sensor $O$ at $(0,0)$ and chosen another sensor A with coordinates $(d,0)$. With help of this, the relative coordinate of sensor $B$ is calculated as

$$\begin{aligned} \textit{ON}=\hbox {a}=\hbox { OB }\cos (\textit{BON})\end{aligned}$$

(20)

$$\begin{aligned} \textit{BN}=\hbox {b}=\hbox { OB }\sin (\textit{BON}) \end{aligned}$$

(21)

Where the angle $\textit{BON}$ is given by $\cos \left( {\textit{BON}} \right) =\frac{\textit{BO}^{2}+\textit{ON}^{2}-\textit{BN}^{2}}{2.\textit{BO}.\textit{ON}}$. Similarly, we can calculate the coordinates of other sensors in the network. Once, the relative coordinates of all the sensors are known, we can determine redundant sensors by using concept of geometry as follows.

We consider a sensor with coordinate $(m,n)$ and sensing range $r_{1}$. Now choose its neighboring sensor within sensing range having coordinate $(p,q)$ and sensing range $r_{2}$. The coverage of these sensors can be expressed by the equation of circles as

$$\begin{aligned} \left( {x-m} \right) ^{2}+\left( {y-n} \right) ^{2}&= r_{1} ^{2}\end{aligned}$$

(22)

$$\begin{aligned} \left( {x-p} \right) ^{2}+\left( {y-q} \right) ^{2}&= r_{2} ^{2} \end{aligned}$$

(23)

Now we can determine intersection points of these two circles by solving the above equations. Similarly, we can determine intersection points of sensor at $\left( {m,n} \right)$ with its all neighboring sensors. Now middle points of all pairs of consecutive intersection points are determined. If every middle points are covered by at least one neighboring sensor, the sensor $\left( {m,n} \right)$ is fully covered and therefore, considered to be redundant.

The algorithms for annulus formation, connectivity ensured routing and coverage preserved scheduling are backbone of the proposed EBM. HELLO packets are used in annulus formation in AFA algorithm. HELLO packets add to overheads in terms of energy consumption in WSNs. But at the same time, information gathered by exchange of Hello Packets is used in routing. In other word no additional packets are required for route discovery. Second, formation of annulus is also used for transmission power control by adjusting the transmission range in each annulus. Therefore, the energy consumed in transmission of Hello packets in annulus formation is a gain in energy saving in terms of route discovery and transmission power control.

6 Performance Analysis

In this section, we evaluate the performance of EBM via simulation in terms of distribution of energy consumption among the sensors, lifetime measurement in terms of data delivery and coverage, and number of Hello packets received by different sensors.

6.1 Simulation Environment

EMB model is simulated using network simulator ns-2. We have assumed that all the sensors have same transmission range and same sensing range. The sensing range varies from $r_s =25\;to\;35$ m and the transmission range varies from $r_{t} =25\;to\;35$ m. Data packet length is assumed to be $30$ bytes. Transmission power consumed in each packet transmission is $10\,\upmu$ J/bit. Power consumed in receiving of a data packet is $0.9\,\upmu$ J/bit and power consumed by a sensor in idle mode is $0.05\,\upmu$ J/bit. Energy consumed in sensing is $1$ mJ/s. Energy consumed in sleep mode of sensors is infinitesimally small and its value is $1.5$ nJ/s. Initial energy of each sensor is assumed to be $1.5$ J and transmission bit rate is $40$ kbps. Sensing field is assumed to be a circular region of radius $R=500$ m. We assume that width of last annulus is $50$ m. Sink is situated at the center of sensing field. The number of sensors deployed in sensing field is taken to be $N=$ 1,500.

6.2 Annulus Formation

In the analysis of load in case of uniform data flow, we assume a large number of annuli in the field. Since transmission range of sensors is taken in the range from $25\;m$ to $35\;m$, we cannot take a large number of annulus in this case. However, radio transmission range of sensors changes with width of annulus. It is assumed that distribution of sensors in the sensing field follows Gaussian distribution. Our main objective is to rationalize energy but at the same time to maintain full coverage. Therefore, there should be sufficient number of sensors in the outermost annulus to provide complete coverage. Let assume that number of sensors required for this purpose is $k$. Therefore, by following Gaussian distribution, it can be expressed as under.

$$\begin{aligned} \mathop \int \limits _{R_{15} }^R \left( {\frac{1}{\sqrt{2\pi \sigma }}e^{-\left( {x-\mu } \right) ^{2}/2\sigma ^{2}}} \right) dx=k/N \end{aligned}$$

(24)

where, $R_{15}$ and $R$ are inner and outer radii of outmost annulus respectively. AFA is run with above simulation parameters. Result of this simulation is shown in Figs. 9 and 10.

Fig. 9

Number of Hello packets received at individual sensors

Fig. 10

Numbers of sensors in each annulus

In Fig. 9, the number of Hello packets received by different sensors is shown. About 35 % of sensors received 4 $Hello$ packets. Analytically the average value ought to be 3.78 for all sensors. About 30 % of sensors received 3 Hello packets. As the sensors are deployed randomly, some of sensors receive no Hello Packet.

Figure 10 depicts the number of sensors in each annulus. By using Eq. (24) with For $\mu =0$ analytically we found that the number of sensors in outermost annulus should be 100 when total 1,500 sensors are considered. The result in Fig. 10 shows that there are 98 sensors in the outermost annulus. There is a marginal variation in the two results.

6.3 Connectivity Measurement

This section analyses the performance of CERA through simulation. We assumed that every sensor in each annulus generates data by following Poisson distribution with rate parameter 20 packets/s. The connectivity is measured in term of fractions of packet transmitted successfully to sink. We call this fraction as data delivery ratio and it is defined as

$$\begin{aligned} Data\;Delivery\;Ratio=\frac{Number\;of\;Packets\;successfully\;received\;at\;sink}{Number\;of\;Packets\;Generated} \end{aligned}$$

The results of simulations for data delivery ration are shown in Fig. 11. We observed that the delivery ratio increases exponentially with the increasing number of sensors. Data delivery ratio starts saturating after $0.8$ for $r=25$ m and after $0.9$ for $r=35$ m. With increasing transmission range, data delivery ratio increases rapidly and less number of sensors are required to achieve satisfactory ratio.

Fig. 11

Data delivery ratio for various transmission ranges

Figure 12 shows average number of hop counts that a packet takes to reach the sink. It is observed that with increasing number of sensors, the hop counts decrease rapidly. It is due to the fact that CERA first finds a sensor in lower annulus to forward the packet to the sink. If such a sensor is not found, it looks for a forwarding sensor in its own annulus. This increases the number of hops for a packet to reach the sink.

Fig. 12

Average hop counts of successful delivery

6.4 Coverage Measurement

In this section the performance of CPSA is measured in terms of percentage of coverage obtained for varying number of sensors and different sensing ranges. Results in Fig. 13 show that higher level of coverage is obtained when sensors are not scheduled since sensors use maximum sensing range. However, with scheduling, the same level of coverage is obtained.

Fig. 13

Coverage with scheduling (CPSA) and without scheduling (NS no scheduling)

In Fig. 14, shows the percentage of average number of sleeping sensors after scheduling. It is apparent from the figure that with increasing sensing range, percentage of sleeping sensors also increases. For the larger number of sensors, the percentage of sleeping sensors increases rapidly.

Fig. 14

Percentage of sleeping sensors after scheduling

6.5 Distribution of Residual Energy

In this section, performance of EBM in terms of distribution of residual energy among sensors at the end of different simulation period has been measured. We have run simulation for total of 200 s. Distribution of residual energy is measured in four intervals of 50 s each. It is assumed that sensors generate data by Poisson distribution with rate parameter of $20$ packets per second. The simulation results are shown in Fig. 15. The results obtained from this simulation are compared with the models of energy balancing EBTP and EBCAG. From the results, it is observed that the distribution of sensors for residual energy follows Gaussian curve. Average is taken to count the number of sensors with a specific energy value. At t = 50 s, there are about 800 sensors with residual energy of $0.8000\;Joules$ which is mean value of residual energy in EBM. In case of EBTP and EBCAG, the spread of sensors around mean is faster than EBM. From this, we conclude that in EBM rationalization of energy regardless of simulation time is better than EBTP and EBCAG.

Fig. 15

Energy with sensors at a t = 50 s, b t = 100 s, c t = 150 s, d t = 200 s

6.6 Lifetime Measurement

A sensor network is assumed to be alive for a duration to which it provides satisfactory service. In this work, lifetime of sensor network in terms of the time duration for which satisfactory coverage and data deliver ratio achieved.

In Fig. 16 shows simulation results for comparison of data delivery ratio among EBM, EBTP and EBCAG. In our simulation we have considered data delivery ratio above 80 % as satisfactory level. It is quite evident from the figure that the lifetime of EMB is better than with other two models. This can be attributed to the fact that in EBM, sensors near the sink remain alive for longer duration since redundant sensors are set off for a specific period by CPSA, and sensor with higher residual energy is selected as next hop and transmission range is controlled by CERA. In case of EBTP and EBCAG, sensors near the sink exhaust their energy early since they bear excessive load of forwarding, and absence of energy efficient next hop selection and scheduling. For satisfactory data delivery ratio, the lifetime obtained using EBM is almost double of EBTP and 50 % higher than EBCAG.

Fig. 16

Comparison of data delivery ratio among EBM, EBTP and EBCAG

In Fig. 17 simulation results of lifetime in terms of coverage provided for 280 s is shown. In our simulation we have considered coverage above 90 % as satisfactory level. EBM provides better satisfactory coverage for longer duration in comparison to EBTP and EBCAG. The reason behind this improvement is that CPSA sets off redundant sensors in the sensing field for a specific period. For satisfactory coverage EBM provides about 50 and 35 % longer network lifetime as compared to that of EBTP and EBCAG respectively.

Fig. 17

Comparison of lifetime in terms of coverage for EBM, EBTP, and EBCAG

7 Conclusion

The energy balanced model for wireless sensor network presented in this paper, reaffirm the significance of energy rationalization for providing satisfactory coverage and enhancing lifetime of the network. Energy loss in transmission of HELLO packets for formation of annuli compensated by energy gain in route discovery is a proved as a novel contribution of the model through simulation results. Distribution of sensors in annuli, scheduling of sensors and selection of next hop sensor based on residual energy for forwarding of packets are the prime contributors in rationalizing energy among the sensors in the network. The model does not only rationalize the energy but it saves energy by adjusting transmission range in each annulus using transmission power control additionally. The significant increase in lifetime of the network using EBM as compared to EBTP and EBCAG proves the effectiveness of the proposed model. In the future research, authors will explore the idea of using game theory for rationalization of residual energy among sensors in WSNs.