1 Introduction

Nowadays, wireless relay nodes are highly useful in connecting nodes located in rural areas [1] and expanding wireless service coverage [2]. Using relays, wireless relay systems can provide reliable transmissions when the distance between a source node and a destination node is sufficiently long and the transmission power is limited. Current and emerging applications, such as Internet TV, roadside to vehicle communication, wireless down-link broadcasting, satellite imaging require content to be downloaded quickly and reliably from a host over possibly unknown channels. The throughput-delay tradeoff is discussed for two-way relay systems. On the other hand, in the high throughput regime (or under a long delay constraint), we can show that encoding and forwarding at a relay node plays a crucial role in improving performance efficiency. This paper considers two-way single-relay multi-user wireless networks in which two multi-user single-hop networks are linked by a single relay node.

Network coding (NC) is a recently introduced paradigm to efficiently disseminate data in wireless networks, where data flows coming from multiple sources are combined to increase throughput, reduce delay, and enhance robustness. In contrast to the traditional store and forward approach [3], it implements a store, code, and forward technique, where each node stores incoming packets in its own buffer and transmits the combined data. The combining is performed over some finite Galois field.

Wireless Local Area Networks (WLANs) using the IEEE 802.11 series of standards have experienced an exponential growth in the recent past [4–8]. The MAC layer of many wireless protocols resembles that of IEEE 802.11. Hence, while we focused on this protocol, it is evident that the results easily extend to other protocols with similar MAC layer operation. The IEEE 802.11 presents two options [4], namely the Distributed Coordination Function (DCF) and the Point Coordination Function (PCF). PCF is generally a complex access method that can be implemented in an infrastructure based network. The mechanism of DCF is based on Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA). We focus on DCF in this paper.

Many works of random access protocols assume that each node always has data packets to be transmitted, i.e., their queues are saturated. An efficient and accurate analytical model to evaluate the saturated throughput for the CSMA/CA protocol with the binary slotted exponential back-off algorithm was proposed in [5]. This is employed as a MAC protocol in the IEEE 802.11 standard [4]. However, it is important to show analytical models on the unsaturated conditions in order to obtain a fundamental understanding of the behavior of random access protocols and provide reference performances of the throughput and delay according to the offered traffic. We developed analytical models for the CSMA/CA protocol with and without XOR-based network coding for single-relay multi-user wireless networks assuming asymmetric bidirectional flows.

1.1 Contributions

We focus on the interaction between Medium Access Control (MAC) and network coding. We consider a single-relay multi-user wireless network configuration in order to capture the effects of each protocol component and quantify the performance degradation due to packet collisions and random transmission schedules.

This work builds a strong connection between the theory of network coding and wireless system design. Particularly, the system presented in this paper was the first to show that network coding can be cleanly integrated into the wireless network stack to deliver practical and measurable gains. This work provides a practical design for wireless network coding. The key difference from past work is to take an opportunistic approach to algorithm and system design.

In the NC system, we consider the network coding schemes of [9] for all data transmission. According to these algorithms, whenever only one buffer (the number of buffers is two in our network scenario) at relay node has a packet, the relay node broadcasts its packet with probability \(\theta \) (the forwarding factor) over the channel whereas nothing is transmitted with probability \(1- \theta \).

The main questions we consider in this paper are 1) whether network coding offers delay gains, and 2) how to design relay node parameters that minimize average and maximum delay, and what is the complexity of this task. When using NC at the relay node in Monte-Carlo simulations, significant improvements are shown in packet delay and throughput of the network as a function of \(\theta \). Our notion of delay is motivated from real-time applications with progressively refined input. However, our notion of delay is relevant to a much more general class of applications. For instance, the network coding schemes decrease the packet delay of the system up to \(30\,\%\) with trade off of the offered Quality of Service (QoS) in terms of throughput. This is in addition to \(35\,\%\) improvement in the Packet Loss Ratio (PLR) and \(60\,\%\) reduction in the Average number of transmission per packet. Similar improvements are achieved in all other examples of network topology.

The main contributions of this paper are the introduction of:

  1. 1.

    The first attempt to analyze the performance of network coding in CSMA/CA with two-hop unbalanced bidirectional traffic in two-way relay wireless networks. We derived closed-form expressions for delay and throughput, with and without network coding, by solving queuing systems for the buffer behavior at the relay node, even if the buffers on nodes are non-saturated. The results show that the network coding can enhance the achievable regions in two directional delay, especially with a symmetric network structure. These descriptions can develop new analytical models for other random access protocols and evaluate the effects of wireless link qualities or queue capacity on delay and throughput, with and without network coding.

  2. 2.

    A low complexity, decentralized combination and transmission technique with the forwarding factor \(\theta \) to improve the performance of network. We evaluate the impact of the forwarding factor.

  3. 3.

    A highly accurate model for IEEE 802.11 DCF protocol in a single hop setting under both saturated and non-saturated traffic loads. One can evaluate the performance through the proposed analytical models without any computer simulations, regardless of whether the queue at the relay node is saturated or not. In our considered network topology, we provide an analytical model to confront the hidden node problem in ad hoc networks.

The rest of this paper is organized as follows: In Section 2, previous approaches to IEEE 802.11 protocol analysis under saturation and non-saturation cases and network coding for the link layer are reviewed. Section 3 explains the CSMA/CA systems and network topology for two-hop wireless relay networks. Section 4 presents the network model with and without network coding for performance analysis. Section 5 shows an extended Markovian model characterizing the MAC layer under non-saturated traffic conditions, presenting modifications that account for transmission errors and analyzes the two-hop network due to the hidden node problem. In Sect. 6, we explain the performance analysis of the network by focusing on expressing exact packet delay and rough throughput for two access mechanisms with and without network coding. In Sect. 7, we present simulation results where typical MAC layer parameters for IEEE 802.11 are used to obtain exact packet delay and rough throughput values as a function of various system level parameters under network coding and two access mechanisms. Finally, Section 8 is devoted to conclusions and directions to future works.

2 Related Works

The seminal paper of Bianchi [5] is the first paper to describe the binary exponential back-off mechanism of the DCF protocol within a single node as a two dimensional Discrete Time Markov Chain (DTMC). Bianchi’s Markov chain, while providing a closed form solution, lacks two important features specified by the IEEE 802.11b standard. These are retransmission limits and back-off counter freezing. Variations of Bianchi’s Markov chain were proposed to describe the IEEE 802.11 protocol more accurately and adhere to the standard. Wu [10] and Chatzimisios [11] included the retransmission limit where a packet is dropped after reaching a maximum number of retransmissions but they did not consider the non-saturated case. Babich [12], Zhang [13] and Xiao [14] improved the analysis by adding the back-off counter freezing probability to their models and they did not assume dropping the situation after reaching a maximum number of retransmissions. Gupta [15] and Kao [16] proposed an analytical model to calculate the network throughput and delay of dedicated control channel protocols that are designed to schedule multiple packets to be transmitted on different data channels simultaneously.

Rui et al. [17] addressed the full-duplex relaying. Some expressions for outage and average capacity of a two-hop cooperative system with a full-duplex relay are derived under an independent but not identically distributed Rayleigh fading environment. In [18], the authors presented a novel MAC protocol based on IEEE 802.11, called C-MAC, which is able to support the basic building block of the cooperative system but they did not analyze their protocol. Ke et al. [19] proposed a new backoff mechanism, called Smart Exponential-Threshold-Linear (SETL) Backoff Mechanism, to enhance the system performance of contention-based wireless networks. Thus, the backoff mechanism is one of the most important parts in the modeling of a protocol.

In the literature, three main approaches were used to account for the non-saturation load assumption. Some Markovian models like Engelstad [20] and Malone [21] use additional states to model the behavior of a tagged node when it does not have any packets to send. Another approach used by Zhai [22] and Tickoo [23] scales the transmission probability of a saturation model by the probability of having at least one packet in the queue. Another approach used to model the non-saturation performance estimates the number of active contending nodes implicitly in the model, as in [24] and [25]. There is a major weakness in all of mentioned papers. The weakness is that the authors did not consider a realistic protocol to access the medium in their models. In their models, the nodes retransmit the packets till they are successfully transmitted. This means they did not consider dropping the packets in their models. A packet is dropped when it reaches the last backoff stage and experiences another collision.

One topic that has not been studied thoroughly in the literature is the interaction between the opportunistic wireless network coding and the MAC protocol. Most of the existing studies are theoretical and make several assumptions about the structure of the network or the channel access scheme. For example, Liu et al. [26] have derived theoretical bounds for the achievable throughput of network coding in large ad-hoc networks. More recently, Chaporkar et al. [27] investigated adaptive network coding and scheduling for wireless ad-hoc networks. They demonstrated that wireless network coding can perform less effectively than non-coded packet transmission since wireless broadcast can reduce spatial reuse. In another related work that identified the same problem, the authors propose an algorithm that determines whether transmitting coded or uncoded packets is the optimal decision regarding the status of the transmission buffer [28]. In [29], Asterjadhi et al. considered practical dissemination algorithms exploiting network coding for data broadcasting in ad hoc wireless networks. For an efficient design, they analyzed issues related to the use of network coding in realistic network scenarios. A simulation study by Fasolo et al. [30] presented results that highlight the sub-optimal performance of existing 802.11-based MAC protocols and network coding. Although several limitations of existing MAC protocols for network coding have been identified, none of the aforementioned works introduced any enhancements that address these problems.

Sagduyu et al. [31], showed the achievable throughput region and throughput optimization in random access mode employing network coding over wireless linear multi-hop networks for several source packet transmission schemes in the case of saturated queues. Le et al. [32] proposed a fundamental coding structure and clarified the encoding number of packets by taking into consideration the physical wireless environments. They also showed that the maximum number of coding flows was fewer than expected because many of the wireless transmissions interfered with each other. Argyriou [33] proposed the use of opportunistic acknowledgments (OACKs) for overheard packets which are obtained from opportunistic listening.

In [34], the authors developed algorithms that explored the delicate trade-off between waiting and transmitting using network coding. Cloud et al. [35] designed a cross-layer approach to aid in developing a cooperative solution using multi-packet reception (MPR), network coding, and MAC. They constructed a model for the behavior of the IEEE 802.11 MAC protocol and applied it to key small canonical topology components and their larger counterparts. Hasegawa et al. [36] proposed a scheme jointly applying packet aggregation and XOR-based network coding. This is called bidirectional packet aggregation and coding (BiPAC), for bidirectional voice over IP (VoIP) flows in wireless linear multi-hop networks and demonstrated the increase of supportable VoIP sessions through the implementation to IEEE 802.11 networks.

Fouli et al. [37] investigated network coding in access point-to-multi-point (PMP) broadcast networks. These are centralized networks with a number of user nodes communicating individually through a central access point (AP). Most importantly, they are concerned with the queuing effects on delay within a switch, particularly at high loads. To simplify the analysis, they ignored upstream channel arbitration and focused on queuing delay at the AP.

Hsu et al. [38] proved that the decision at relay node to wait for the next coding opportunity can reduce the number of transmissions, whereas it incurs a penalty in terms of packet delay. In this paper, the authors proposed an on-line algorithm for making transmit/wait decisions at the relay nodes. The algorithm minimizes the total system cost which includes both the number of transmissions as well as packet delay. The newest work in this field has been done by Antonopoulos et al. [39]. The authors introduced a network coding-aided energy efficient MAC protocol which coordinates the transmissions among a set of relay nodes which act as helpers in cooperative Automatic Repeat reQuest-based (ARQ-based) wireless networks. Using network coding methods, the energy efficiency of the network increases without compromising the system performance in terms of QoS.

In this paper, we focus on the delay analysis of IEEE 802.11 based wireless networks for reliable packet transmissions in wireless relay systems and study its throughput-delay tradeoff. The results of this paper are two-fold. The first is modeling and characterizing the impact of network coding on the packet delay in IEEE 802.11. The second is considering this impact both in saturated and non-saturated cases.

3 Problem Statement and System Model

In this section, we describe the CSMA/CA systems, both with and without network coding, on two-hop wireless relay networks with bidirectional unbalanced traffic, system design parameters, and evaluation parameters. The list of the notation of all symbols which have been used in this paper is summarized in Table 1.

Table 1 The notation of all symbols that have been used
Full size table

3.1 MAC Protocols

We considered two different MAC protocols based on CSMA, which is currently the most widely used medium access mechanism in wireless ad hoc networks.

  1. 1.

    IEEE 802.11b [4]: this scheme is an improvement over the basic IEEE 802.11b, where an acknowledgment mechanism is implemented. The packet is retransmitted, after a back-off period, when there is no acknowledgment from the intended receiver. Using this mechanism, only collisions at the addressed receiver can be detected. Also, this strategy does not solve the hidden terminal problem.

  2. 2.

    IEEE 802.11b with RTS/CTS handshake [4]: To further improve the performance, we considered the previous scheme with an additional RTS/CTS handshake. These control messages are introduced to alleviate the hidden node problem. The CTS is only transmitted by the node addressed in the packet header. As for the previous schemes, this strategy can not detect collisions at all the overhearing nodes.

3.2 Network Topology

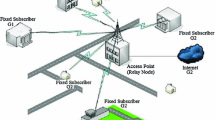
This paper deals with two-hop wireless relay access systems that consist of one relay node \(\mathbf{R}\) and two end node groups 1 and 2 as illustrated in Fig. 1. Let us assume that node \(\mathbf{R}\) and all the end nodes are fixed base stations (subscriber) but are not mobile-phones or wireless terminals powered by an internal battery. All nodes have one transceiver with an omnidirectional antenna. The transmission from any user towards the AP is a point-to-point transmission while the transmission from the AP back to the users is a broadcast PMP transmission. Therefore, a node can be either transmitting or receiving, but not both simultaneously. We assume that all nodes in an end node group and node \(\mathbf{R}\) are in transmission range but any node in a group is out of transmission range to all nodes in another group. Furthermore, no interference is incurred on the receiver of a node in a group due to the transmissions in another group. For example, if node \(\mathbf{R}\) (Access Point) is on the roof of a department in a university, the end node groups are within a blind zone of each other, and so on. We also assume that the buffer capacity is infinite for all nodes in the system in order to analyze the delay. We can assume some departments in a university as two separate groups that want to make a video conference or VoIP. As seen in Fig. 1, three users in group 1 can transfer their packets to four users in group 2 via relay node on the roof of a building.

Fig. 1
figure 1

Single-relay multi-user wireless networks which have two multi-user single-hop wireless networks via the relay node \(\mathbf{R}\)

Full size image

Let us consider only the bidirectional traffic via node \(\mathbf{R}\) and assume that there is no closed traffic inside groups 1 and 2. Node \(\mathbf{R}\) is an EF repeater and does not have the source of traffic. Node \(\mathbf{R}\) directs packets from a source in group 1 to its destination in group 2 and vice versa. The buffer at node \(\mathbf{R}\) is a first-in first-out (FIFO) queue. If there are always packets in the buffer, the buffer is called saturated, otherwise it is called non-saturated. Node \(\mathbf{R}\) generally undergoes any unbalanced traffic between groups 1 and 2. The traffic unbalance is caused by a difference in arrival rate of new packets among end nodes or a difference in the number of nodes between groups 1 and 2. A system without network coding is called a non-NC system while that with network coding is called an NC system.

We suppose that all nodes employ the IEEE 802.11 protocol. We assume constant length packets and that all packets will begin their transmissions only at the beginning of a slot. The system is time slotted and all nodes are synchronized. Let us define a packet transmitted from a node in group \(v\) as packet \(v\) for any \(v\in \{1,2\}\). For convenience, \(\bar{v}\in \{1,2\}\) is defined as the complementary element of \(v\in \{1,2\}\). The node transmits a packet with probability \(\tau _v\) and they are the same for all nodes in group \(v\). The transmission probability of relay \(\mathbf{R}\) is denoted by \(\tau _R\).

Figure 2 illustrates the ACK packet transmissions for non-NC and NC systems. As shown in Fig. 2, if the coding packet is transmitted from node \(\mathbf{R}\) and received correctly at both the destinations, two ACK packets are transmitted from both the destinations. This is a simple model for the ACK packet transmissions in which an additional ACK sub slot is attached to the total slot. We should emphasize that the address of destination nodes are put in the header of coded packet. RTS/CTS access mechanism is to overcome the hidden node problem so the users in two groups have to use this mechanism. However, two groups are in the range of transmission of relay node, in our network scenario the relay node does not need to use RTS/CTS access mechanism to send its packet and it uses the basic access mechanism to send a packet and receive the ACK frame. In two access mechanisms, the destination user just sends ACK frame to relay node. The relay node uses RTS frame to determine the destination node and puts its address in the header of coded packet.

Fig. 2
figure 2

The ACK packet transmission for NC system under base access mechanism. a Non network coding packet transmission. b Network coding packet transmission

Full size image

Node \(\mathbf{R}\) transmits the head of its buffer with probability \(\tau _R\) for non-NC systems if its buffer is nonempty. In NC systems \(\mathbf{R}\) has two virtual buffers 1 and 2. If \(\mathbf{R}\) receives packet \(v\) successfully, \(\mathbf{R}\) stores the pointer of the packet in virtual buffer \(v\). Any end node stores the packets received from the same group in the packet pool, which is a buffer to store undirected packets heard by opportunistic listening [40], to decode the coding packets transmitted from \(\mathbf{R}\). Node \(\mathbf{R}\) gets a transmission opportunity with probability \(\tau _R\) if its buffer is nonempty. In such a case, if both the virtual buffers are nonempty, the packet is encoded from two packets corresponding to the heads of virtual buffers by operating a bitwise XOR and is called a coding packet. If a virtual buffer is nonempty and another is empty, the relay node will transmit with probability \(\theta \) (forwarding factor) whereas nothing is transmitted with probability \(1-\theta \). This approach is called probabilistic network coding. If the destination receives a coding packet from \(\mathbf{R}\) successfully, it can decode the desired packet by operating the bitwise XOR of the received coding packet and the packet in the packet pool. If a node receives two or more packets at the same slot, a collision occurs. We clarify the effect of the system design parameters \(n_v\) (number of members in group \(v\)), \(W\) (minimum size of contention window), \(\theta \) and \(q\) (whereby \(q\) is the probability of having at least one packet to be transmitted in the buffer) on the delay.

It is assumed that the nodes in group 2 are connected with Internet backbone working as an access point (AP) in the case of IEEE 802.11. The user nodes in group 1 are assumed to exploit some bidirectional communication services such as VoIP, TV conference, P2P, etc. It is one of the important issues to achieve fairness between uplink and downlink data flows rather than fairness among all user nodes as discussed in [41] for single-hop wireless IEEE 802.11 networks.

3.3 Problem Description

The use of traditional access mechanisms such as CSMA-like protocols, when multiple nodes transmit, may suffer from a high number of collisions and dropped packets. Packets collisions and scheduling mechanisms are two main factors which should be taken into account when using network coding in a MAC protocol. Both collisions and scheduling are the direct consequence of the random (CSMA-like) channel access that were adopted in this study. Collisions impact the performance as fewer packets are collected. Packet scheduling refers to the way in which different nodes take turns in transmitting, which is dictated by the MAC rules. The transmission order is important when network coding is used at higher layers as it influences the way encoded packets are created, i.e., which packets are mixed together. In this paper we focus on the analysis of random access schemes as used by IEEE 802.11. We provide an analysis of the combined use of the NC and MAC layer in a multi-hop, with relay node. We then design a cross-layer solution that decreases delay subject to the constraint of fairness between flows, rather than between nodes, for a multi-hop network structure. Our solution uses cooperation between nodes and takes into account the interaction among NC, and MAC. In such PMP architectures, network coding can use the basic broadcast architecture to turn unicast transmissions into more efficient broadcast transmissions, as depicted in Fig. 3. This figure illustrates the wireless two-way relay network in which bidirectional data transfer takes place between end nodes \(G1\) and \(G2\) when the assistance of the relay node \(\mathbf{R}\) is investigated. The transmission protocol, is considered which consists of the following two phases: the multiple access (MA) phase, during which \(G1\) and \(G2\) transmit to \(\mathbf{R}\), and the broadcast (BC) phase during which \(\mathbf{R}\) transmits to \(G1\) and \(G2\). The network coding method is employed at relay node in such a way that \(G1\, (G2)\) can decode the message of \(G2\) \((G1)\), given that \(G1\, (G2)\) knows its own messages. Network coding hence achieves the packet exchange in only three packet transmissions, using 50 % less downstream bandwidth.

Fig. 3
figure 3

The two way relay network with two phase (MA and BC phase)

Full size image

The wireless two-way relay network with NC is applicable to a number of access-metro network architectures such as WLANs (e.g., infrastructure-mode WiFi), broadband satellite networks, and cellular access networks (e.g., long term evolution (LTE) and WiMAX). The investigation of localized traffic in PMP networks is urged by the enormous growth of traffic generated by applications that stand to benefit from local packet exchanges, including user-generated high-definition video, video and voice conferencing, peer-to-peer, as well as video gaming.

4 Network Coding Model

Network coding is modeled by considering the ability of a given node to combine multiple packets together. We use COPE [40] as a case study. COPE inserts a coding shim between the IP and MAC layers and uses the broadcast nature of the wireless channel to opportunistically code packets from different nodes using a simple XOR operation. The wireless channel enables each node to overhear packets that can be used to help decode any subsequently received encoded packets. In the proposed model, each encoded packet is sent by relay node and it can be decoded by the intended recipients. Consistent with COPE’s implementation, each packet is sent as a broadcast transmission on the channel at the first opportunity, without delay, and each information flow does not exercise congestion control. Finally, neither the complexity of the coding or decoding operations nor any other aspects of the NC implementation found in [40] are considered since their contributions to the overall network performance is small.

In this section, we focus on the network coding model for the RTS/CTS access mechanism. It should be emphasized that it is calculated using a similar manner for the basic access mechanism.

The probability in a time slot that only one station in group \(v\) transmits is introduced as:

$$\begin{aligned} \varGamma _v=n_v\tau _v(1-\tau _v)^{n_v-1}, \end{aligned}$$
(1)

where \(\tau _v\) is the transmission probability of a packet for a user in group \(v\) and will be computed in Eq. 16 and the probability in a time slot that no stations in group \(v\) transmit is introduced as:

$$\begin{aligned} \gamma _v=(1-\tau _v)^{n_v}. \end{aligned}$$
(2)

4.1 CSMA/CA Protocol Without Network Coding

We assume queue states at relay node \(\mathbf{R}\) as sequences of packets \(\fancyscript{V}_1^n=v_1v_2...v_n (v_i\in \{1,2\})\) in the output queue and the empty queue state as \(\fancyscript{V}_1^n=0\). The queue state in the \(k\)-th slot is denoted as \(V_k\) for any \(k\ge 0\) and let us define the initial state as \(V_0 = 0\). Figure 4 illustrates the Markov chain of \(V_k\), where self-transitions are not drawn. The steady-state probability of a state \(\fancyscript{V}_1^n\) is denoted as \(Q(\fancyscript{V}_1^n)\) and the number of packets \(v\) in state \(\fancyscript{V}_1^n\) is denoted as \(n_v(\fancyscript{V}_1^n)\).

Fig. 4
figure 4

The Markov chain of buffer states in \(\fancyscript{V}_1^n\) at node \(\mathbf{R}\) for systems without network coding

Full size image

The state transition that packet \(v\) is transmitted but \(\bar{v}\) is not when the output queue at relay node \(\mathbf{R}\) is empty corresponds to \(\lambda _{0,v}\) in Fig. 4, which is expressed as:

$$\begin{aligned} \lambda _{0,v} = \eta _{sv}, \end{aligned}$$
(3)

where \(\eta _{sv} = \varGamma _v\gamma _{\bar{v}}P_{SX}\) and \(P_{SX}\) is the hidden node probability. Computation of \(P_{SX}\) will be presented later in Sect. 5.3.

The probability of packet collision when the relay node wants to send packet \(v\) to group \(\bar{v}\) is expressed as:

$$\begin{aligned} P_{CollR-v-nonNC} = 1-\gamma _{\bar{v}}. \end{aligned}$$
(4)

This is due to the relay node and at least one of the users in group \(\bar{v}\) simultaneously send their packets.

Similarly, based on the queue behavior at relay node \(\mathbf{R}\), the other state transition probabilities shown in Fig. 4 are expressed as:

$$\begin{aligned} \lambda _v&= \eta _{sv}(1-\tau _R), \nonumber \\ \mu _v&= \tau _R\gamma _{\bar{v}} + P_{drop-v}, \end{aligned}$$
(5)

where \(P_{drop-v} = P_{CollR-v-nonNC}^{m+1}\), \(m\) is the maximum number of retransmissions for a packet, and \(\tau _R\) is the probability that the relay node will attempt transmission in a slot time and it will be computed later in Sect. 5.1.

The utilization factor with respect to packets \(v\) when the output queue is nonempty at relay node \(\mathbf{R}\) is defined as

$$\begin{aligned} \rho _v = \frac{\lambda _v}{\mu _v}, \end{aligned}$$
(6)

Lemma 1

In the non-saturated condition for relay node \(\mathbf{R}\), the steady-state probabilities of queue states are introduced as:

$$\begin{aligned} Q(0)&= \frac{(1-\tau _R)(1-\rho _1 - \rho _2)}{(1-\tau _R) + \tau _R(\rho _1 + \rho _2)},\nonumber \\ Q(v)&= \frac{\rho _vQ(0)}{(1-\tau _R)}, \nonumber \\ Q(\fancyscript{V}_1^n)&= \frac{\rho _1^{n_1(\fancyscript{V}_1^n)}\rho _2^{n_2(\fancyscript{V}_1^n)}Q(0)}{(1-\tau _R)}. \end{aligned}$$
(7)

Lemma 2

If the output queue at relay node \(\mathbf{R}\) is non-saturated, the steady-state probabilities of the numbers of packets in the output queue at relay node \(\mathbf{R}\) are as follows:

$$\begin{aligned} P_v(0)&= Q(0)\bigg [ \frac{1-\tau _R(1-\rho _{\bar{v}})}{(1-\tau _R)(1-\rho _{\bar{v}})}\bigg ], \nonumber \\ P(n)&= \frac{(\rho _1 + \rho _2)^n}{(1-\tau _R)}P(0); n>0. \end{aligned}$$
(8)

The proof of Lemmas 1 and 2 will be included in “Appendices 1 and 2”, respectively.

Remark 1

The probability of \(q\) for relay node \(\mathbf{R}\) is equal to : \(q = [1-Q(0)]\).

4.2 CSMA/CA Protocol with Network Coding

We assume queue states at relay node \(\mathbf{R}\) as pairs \((n_1,n_2)\) of numbers of packets in the virtual queues 1 and 2. The queue state in the \(i\)-th slot is defined as \(\varphi _i = (\varphi _{1,i}, \varphi _{2,i})\) for any \(i \ge 0\) and let us define the initial state \(\varphi _0 = (0, 0)\). Figure 5 depicts the Markov chain of \(\varphi _i\), where self-transitions are not shown. The steady-state probability of a state \((n_1,n_2)\) is denoted as \(P(n_1,n_2)\).

Fig. 5
figure 5

The Markov chain of the queue states process \(\varphi _i \) in the system with network coding

Full size image

The state transition probabilities \(\lambda _{0,v}\) and \(\lambda _v\) in Fig. 5 are expressed as Eqs. 3 and 5, respectively, as in the case of the without network coding protocol. The state transition from \(\varphi _i = (n_1,n_2)\) to \(\varphi _{i+1} = (n_1-1,n_2-1)\) in Fig. 5 means that both packets in a coded packet are successfully received at both destination nodes. When relay node \(\mathbf{R}\) simultaneously transmits a packet with at least one of the users in groups (1 or 2), the collision will occur. This probability is equal to:

$$\begin{aligned} P_{CollR-NC} = 1-\gamma _v\gamma _{\bar{v}}. \end{aligned}$$
(9)

The corresponding state transition probability \(\mu _v\) and \(\mu \) are introduced as:

$$\begin{aligned} \mu _v&= \theta \tau _R\gamma _{\bar{v}} + P_{drop-v}, \nonumber \\ \mu&= \tau _R\gamma _v\gamma _{\bar{v}} + P_{drop}, \end{aligned}$$
(10)

where \(\theta \) is the forwarding factor and \(P_{drop} = P_{CollR-NC}^{m+1}\).

The transition \(\mu _{0,v}\) means that the packet \(v\) in a coded packet is successfully received but \(\bar{v}\) is not and is equal to:

$$\begin{aligned} \mu _{0,v} = \tau _R(1-\gamma _v)\gamma _{\bar{v}}. \end{aligned}$$
(11)

Lemma 3

For any \(v\in \{1,2\}\), the steady-state probabilities of the numbers of packets in virtual queue \(v\) are as follows:

$$\begin{aligned} P_v(0)&= \frac{(1-\rho _v)(1-\tau _R)-\rho _v\tau _RP(0,0)}{1-\tau _R}, \nonumber \\ P_v(n)&= \rho _v^n\bigg [\frac{(1-\rho _v)[(1-\tau _R)+\tau _RP(0,0)]}{1-\tau _R}\bigg ]. \end{aligned}$$
(12)

If one of the queues in relay node is saturated and the other is non-saturated, (i.e. \(\rho _1<1\) and \(\rho _2 \ge 1\)) therefore \(P(0,0) = 0\) and hence \(\lambda _{1,1}\) is equal to \(\lambda _1\) from Eq. 50 in “Appendix 3”. The detailed balance equations related to virtual buffer 1 are obtained as:

$$\begin{aligned}&\displaystyle P_1(n+1) = \rho _1P_1(n), \nonumber \\&\displaystyle \sum \limits _{n=0}^\infty P_1(n) = 1 \Rightarrow P_1(0) = 1-\rho _1, P_1(n) = \rho _1^n(1-\rho _1). \end{aligned}$$
(13)

Lemma 4

The steady-state probability of state \(P(0,0)\) is introduced as:

$$\begin{aligned} P(0,0) = \frac{(1-\tau _R)(1-\rho _1)(1-\rho _2)}{1-\tau _R(1-\rho _1)(1-\rho _2)}. \end{aligned}$$
(14)

The proof of Lemmas 3 and 4 will be included in “Appendices 2 and 4”, respectively.

Remark 2

The probability of \(q\) for relay node \(\mathbf{R}\) using network coding is equal to : \(q = [1-P(0,0)]\).

5 Network Models and Parameters

This section develops a simple model that gives insight into cross-layer design of wireless networks by using NC, and various MAC approaches. We identify each network element’s fundamental behavior and model them using simple, intuitive methods so that various performance measures can be evaluated and design trade-offs can be weighed. Subsequent sub-sections identify specific behaviors of these elements and describe the abstractions and simplifications needed to make the model tractable. The scenario considered consists of a wireless error-free packet network that is operated in fixed-length time-slots. Each node is half-duplex (i.e., cannot receive and transmit in the same time-slot), and only one packet can be sent per time-slot by relay node.

5.1 Markovian Model Characterizing the MAC Layer Under Non-saturated Traffic Conditions

The access technique employed by the desired source corresponding to the 802.11 DCF, with or without the RTS/CTS mechanism, is analyzed in non-saturated traffic conditions and takes into account multiple simultaneous communications between different node pairs. In this section, we present the basic rationale of the proposed bi-dimensional Markov model useful for evaluating the delay of the CSMA/CA under non-saturated traffic conditions. We made the following assumptions: the number of terminals is finite, the channel is free of errors, and packet transmission is based on two MAC protocols as introduced in Sect. 3.1. For conciseness, we will limit our presentation to the ideas needed for developing the proposed model. The interested reader can refer to [4, 5] for many details on the operating functionalities of the CSMA/CA.

The proposed non-saturated model extends the model presented in [5, 42]. In this paper, it is assumed that a station may store the next packet in a single packet buffer. Thus, the proposed model is slightly more aggressive than the non-saturated one presented in [21]. In addition, the model proposed hereafter is developed by neglecting the post back-off performed by the source after a successful transmission.

A two-dimensional Markov process \((s(t), \pi (t))\) can now be defined, based on three assertions:

  1. 1.

    the probability \(\tau \) that a station will attempt transmission in a time slot is variable across all time slots;

  2. 2.

    the probability \(P_{Coll}\) that any transmission experiences a collision is independent of the number of collisions already suffered;

  3. 3.

    \(q\) is the probability of having at least one packet transmitted in the buffer.

It is modeled by the Markov chain depicted in Fig. 6, where \(m\) is the maximum back-off stage, or the maximum number of retransmissions, \(P_{eq}\) is the conditional probability that the source generally encounters errors, i.e., a collision (assumed independent of the number of collisions suffered by the packet in the previous attempts), \(W_i\) is the contention window size at the \(i-\)th transmission attempt. \(W = W_0\) represents the minimum contention window. We recall that a back-off time counter is initialized depending on the number of failed transmissions for the transmitted packet. It is chosen in the range of \([0,W_i - 1]\) following a uniform distribution. At the first transmission attempt, i.e., for \(i = 0\), the contention window size is set equal to a minimum value \(W_0 = W\), and the process \(s(t)\) takes on the value \(s(t) = i = 0\).

Fig. 6
figure 6

Markov chain for the contention model in non-saturated traffic conditions

Full size image

One major deviation from Bianchi’s model [5] is the inclusion of \(P_f\) which represents the probability that the channel is frozen and a node in the back-off state does not decrement its back-off counter \((P_d = 1-P_f)\).

The back-off stage \(i\) is incremented in unitary steps after each unsuccessful transmission up to the maximum value \(m\), while the contention window is doubled at each stage up to the maximum value \(CW_{max} = 2^mW\). The back-off time counter is decremented as long as the channel is sensed idle and stopped when a transmission is detected. The station transmits when the back-off time counter reaches zero. After reaching these limits the packet will be discarded if it is not successfully transmitted.

On the basis of this assumption, collisions can occur with probability \(P_{Coll}\) on the transmitted packets. In this scenario, a packet is successfully transmitted if there is no collision (this event has probability \(1 - P_{Coll}\)).

Unlike Bianchi’s model [5], the simplicity of such a model can also be retained in non-saturated conditions by introducing a new state, labeled \(I\), accounting for the following two situations:

  • Immediately after a successful transmission, the buffer of the transmitting station is empty;

  • The station is in an idle state with an empty buffer until a new packet arrives at the buffer for transmission.

If a collision occurs, the back-off stage is incremented so the new state can be \((i+1, k)\) with probability \(P_{eq}/W_{i+1}\), since a uniform distribution between the states in the same back-off stage is assumed.

The Markov process of Fig. 6 is governed by the following transition probabilities:

$$\begin{aligned} P_{i,k|i,k+1}&= P_d, \quad \qquad k\in [0,W_i-2], i\in [0,m] \nonumber \\ P_{i,k|i,k}&= 1- P_d, \quad k\in [1,W_i-1], i\in [0,m] \nonumber \\ P_{0,k|i,0}&= q(1-P_{eq})/W_0, \qquad k\in [0,W_0-1], i\in [0,m-1] \nonumber \\ P_{0,k|m,0}&= q/W_0 , \qquad k\in [0,W_0-1] \nonumber \\ P_{i,k|i-1,0}&= P_{eq}/W_i, \quad k\in [0,W_i-1], i\in [1,m] \nonumber \\ P_{I|i,0}&= (1-q)(1-P_{eq}), \quad i\in [0,m-1] \nonumber \\ P_{I|m,0}&= 1-q, \nonumber \\ P_{0,k|I}&= q/W_0, \qquad k\in [0,W_0-1] \nonumber \\ P_{I|I}&= 1-q. \end{aligned}$$
(15)

The first equation in Eq. 15 states that, at the beginning of each slot time, the back-off time is decremented if the channel was sensed free. If the channel was not sensed free, the state will stay in it according to the second equation.The third equation accounts for the fact that after a successful transmission, a new packet transmission starts with back-off stage 0 with probability \(q\), in case there is a new packet in the buffer to be transmitted. The fourth equation deals with successful or unsuccessful transmissions in the last stage and the need to reschedule a new contention stage, if there is a new packet in the buffer to transmit. The fifth equation depicts unsuccessful transmissions and the need to reschedule a new contention stage. The sixth equation deals with the practical situation in which after a successful transmission, the buffer of the station is empty, and as a consequence, the station transits in the idle state \(I\) waiting for a new packet arrival. The seventh equation is for the last stage, regardless of whether the packet is being transmitted successfully or not. The eighth equation models the situation in which a new packet arrives in the node buffer and a new back-off procedure is scheduled. Finally, the ninth equation models the situation in which there are no packets to be transmitted and the station is in the idle state.

The next line of pursuit consists of finding a solution to the stationary distribution: \(\pi _{i,k}=\lim _{t\rightarrow \infty }P[s(t)=i,\pi (t) =k], \forall k\in [0,W_i-1], \forall i\in [0,m]\), that is, the probability of a station occupying a given state at any discrete time slot.

Proposition 1

\(\tau \), the probability that a station starts a transmission in a randomly chosen time slot can be expressed as:

$$\begin{aligned} \tau&= \pi _{0,0}\frac{1-P_{eq}^{m+1}}{1-P_{eq}} \nonumber \\&= \frac{2qP_d\left( 1-P_{eq}^{m+1}\right) (1-2P_{eq})}{2P_d(1-q)(1-P_{eq})(1-2P_{eq})+qW(1-P_{eq})(1-(2P_{eq})^{m+1})+q(1-2P_{eq})(2P_d-1)\left( 1-P_{eq}^{m+1}\right) }.\nonumber \\ \end{aligned}$$
(16)

We will present how to calculate this proposition in “Appendix 5”.

5.2 Channel State Markov Chain

To compute the probability of \(P_f\), we consider the channel state Markov chain in Fig. 7. In this figure, \(S,\, C\), and \(I\) stand for the state of the channel having a successful transmission, a Collision, or being Idle while the considered node is backing off. In practice, a back-off state can be entered from either a transmission state or from a previous back-off state. The \(p_{ei}\) parameter presents the probability that the transmitting node finds the channel idle. Thus \(p_{ei}\) can be calculated as \(p_{ei} = P_{idle}\) and \(P_{idle}= (1-\tau _R)\gamma _1\gamma _2\) will be expressed in Sect. 5.3. Similarly, \(p_{es}\) and \(p_{ec}\) can be expressed for relay node and user group \(v\) as follows:

$$\begin{aligned} p_{es-v}&= (n_v-1)\tau _v(1-\tau _v)^{n_v-2}(1-\tau _R)\gamma _{\bar{v}}P_{SX},\nonumber \\ p_{es-R}&= (\varGamma _1\gamma _2+ \varGamma _2\gamma _1)P_{SX},\nonumber \\ p_{ec-v}&= 1- p_{ei-v}-p_{es-v}\nonumber \\ p_{ec-R}&= 1- p_{ei-R}-p_{es-R}. \end{aligned}$$
(17)

where \(P_{SX}\) is the probability that no hidden node problem takes place in the channel and will be computed in Sect. 5.3.

Fig. 7
figure 7

Channel state Markov chain

Full size image

As mentioned in Fig. 7, \(P_d= p_e.P_{I}\) where \(p_e = 1\).

Given that the number of colliding nodes is \(n_1+n_2\), the probability that no colliding node selects zero as the new back-off counter is \((1-\frac{1}{\overline{CW}})^{n_1+n_2}\). \(p_{ss}\) represents the probability that the channel stays in the \(S\) state, the probability that the channel moves from \(S\) to \(C\) is \(p_{sc}\), the probability that the channel can be Idle after \(S\) state is \(p_{si}\) and they are expressed for relay node and user group \(v\) as (they are equal):

$$\begin{aligned} p_{ss}&= (n_1+n_2)\left( \frac{1}{\overline{CW}}\right) \left( 1-\frac{1}{\overline{CW}}\right) ^{n_1+n_2-1},\nonumber \\ p_{sc}&= \sum \limits _{n=2}^{n_1+n_2}\left( \begin{array}{l} n_1+n_2 \\ n \end{array} \right) \left( \frac{1}{\overline{CW}}\right) ^n\left( 1-\frac{1}{\overline{CW}}\right) ^{n_1+n_2-n}, \nonumber \\ p_{si}&= 1- p_{sc}-p_{ss}. \end{aligned}$$
(18)

where \(\overline{CW}\) is the average back-off window size over all stages and can be expressed as:

$$\begin{aligned} \overline{CW} = \sum _{i=0}^m\frac{(1-P_{Coll})P_{Coll}^iW_i}{1-P_{drop}}, \end{aligned}$$
(19)

and \(P_{drop}\) is the probability that the packet is dropped after \(m+1\) transmissions and can be computed as \(P_{drop} = P_{Coll}^{m + 1}\). \(P_{Coll}\) can be computed from Eqs. 4 and 9 for relay node and will be calculated in Sect. 5.3 for users group \(v\).

Similarly, \(p_{cs}\), \(p_{ci}\) and \(p_{cc}\) are given as:

$$\begin{aligned} p_{cs}&= (n_1+n_2)\left( \frac{1}{\overline{CW}}\right) (1-\frac{1}{\overline{CW}})^{n_1+n_2-1}, \nonumber \\ p_{ci}&= (1-\frac{1}{\overline{CW}})^{n_1+n_2},\nonumber \\ p_{cc}&= 1- p_{cs}-p_{ci}. \end{aligned}$$
(20)

Knowing all transition probabilities, to obtain the steady-state probabilities for the channel state vector \(V = [P_I P_C P_S]\), we solve \(VP = V\), where transition matrix \(P\) of the Channel State Markov Chain can be calculated as:

$$\begin{aligned} P = \left( \begin{array}{lll} p_{ei} &{}p_{es}&{} p_{ec} \\ p_{ci} &{}p_{cs}&{} p_{cc} \\ p_{si} &{}p_{ss}&{} p_{sc} \end{array} \right) . \end{aligned}$$
(21)

When a packet is successfully received by a node we can consider some attempts to transmit it. For any subsequent success at the \(i + 1{st}\) attempt preceded by \(i\) collisions, the channel access time \(T^{(i)}\) is calculated as follows:

$$\begin{aligned} T^{(i)} = T_{suce}+i\overline{T_{coll}}+\sum _{j=0}^i\overline{W_j}\fancyscript{D}, \end{aligned}$$
(22)

where \(\overline{W_j}\) is the average number of back-off slots selected at stage \(j\) and computed as \(\overline{W_j}= \frac{W_j-1}{2}\), \(\fancyscript{D}\) is the average slot duration that the considered node should wait before decrementing its back-off counter, \(\overline{T_{coll}} = T_{XColl1-Bas}\) or \(\overline{T_{coll}} = P_{hid1v}.T_{XColl1-RTS} + P_{nhid1v}.T_{XColl2}\) and \(T_{suce}= T_{XSucc-Bas}\) or \(T_{suce}= T_{XSucc-RTS}\), where they will be computed in Sect. 5.3.

Let us define \(T\) as one hop delay for the non-dropped packet and it can generally be written as:

$$\begin{aligned} T = \frac{1}{1-P_{drop}}\sum _{i=0}^mP_{Suce}^{(i)}\bigg [ T_{suce}+i\overline{T_{coll}}+\sum _{j=0}^i\overline{W_j}\fancyscript{D}\bigg ], \end{aligned}$$
(23)

where \(P_{Suce}^{(i)} = (1-P_{Collv-RTS})P_{Collv-RTS}^i\) for user group \(v\) and \(P_{Suce}^{(i)} = (1-P_{CollR-v-nonNC})P_{CollR-v-nonNC}^i\) and \(P_{Suce}^{(i)} = (1-P_{CollR-NC})P_{CollR-NC}^i\) for relay node \(\mathbf {R}\) which can be computed as Eqs. 36, 4 and 9, respectively.

Proposition 2

The average slot duration can be computed as:

$$\begin{aligned} \fancyscript{D} = (1-\tau )D_1 + \tau D_2, \end{aligned}$$
(24)

where \(\tau \) is the transmission probability for a node in the network.

The “Appendix 6” will show how to compute this proposition.

5.3 Network Model Based Hidden Node Problem

In this section, we analyze the two-hops network taking into account the hidden node problem. To analyze this scenario, we study the events that can take place within a considered time slot.

We first argue about the possible events which can occur in a randomly selected time slot. Consider station A in group \(v\). From A’s standpoint, there are three possibilities: (1) In the idle state, it may be counting down its back-off timer when the channel has been sensed idle or just waiting for the end of it’s neighbor’s transmission; (2) it may have started the transmission process after the back-off timer has reached zero and the transmission is successful; or (3) its transmission suffers a collision. Now we consider several conditions in a slot time for one station in group \(v\) as follows:

  • The probability that station \(A\) is idle in a considered time slot is \(1-\tau _v\). Under this condition, the probability that all other stations are all idle is:

    $$\begin{aligned} P_{idle}= (1-\tau _R)\gamma _1\gamma _2, T_{idle} = \sigma . \end{aligned}$$
    (25)

    Since all stations within group \(v\) are idle in this particular slot, station \(A\) will remain in the idle state for \(\sigma \) unit of time and decrement its back-off counter by one.

  • We consider station \(A\) as being idle and at least one station within group \(v\) transmitting. This sub-scenario can be further divided into two sub-cases: only one station (say, station \(X\)) transmits or more than one station transmits. \(P_{Xtx-1}\) as the probability that only one node is in the transmission state, based on the fact that at least one node is transmitting. \(P_{Xtx-1}\) is obtained as:

    $$\begin{aligned} P_{Xtx-1}= \frac{(n_v-1)\tau _v(1-\tau _R)(1-\tau _v)^{n_v-2}+ \tau _R(1-\tau _v)^{n_v-1}}{1-(1-\tau _R)(1-\tau _v)^{n_v-1}}. \end{aligned}$$
    (26)

    In this case, we can consider two scenarios. The first one is when none of the users in the other group \((\bar{v})\) does not transmit a packet through \(X\)’s duration. In this scenario, \(X\) will successfully transmit its packet in all access mechanisms. This will affect the time duration that station \(A\) needs to remain silent. Since station \(A\) will know the busy period of station \(X\) by receiving the data frame or the RTS frame transmitted by \(X\) which are expressed as:

    $$\begin{aligned} T_{XSucc-Bas}&= H + E[P] + \delta + SIFS + ACK + \delta + DIFS, \nonumber \\ T_{XSucc-RTS}&= RTS + \delta + SIFS + CTS + \delta + SIFS\nonumber \\&+\,H + E[P] + \delta + SIFS + ACK + \delta + DIFS, \end{aligned}$$
    (27)

    knowing the time durations for ACK frames, ACK timeout, DIFS, SIFS, EIFS, RTS, CTS, CTS timeout, \(\sigma \), average packet payload length (E[P]) and PHY and MAC headers duration (H), and propagation delay \(\delta \), all of the required parameters can be computed. The second one is when at least one of the users in group \(\bar{v}\) sends the packet to relay node. In this situation, the collision will occur. This condition is called the hidden node problem. The collision may occur during the time that station \(X\) is transmitting the RTS frame or the data packet to the intended receiver. According to two situations, we can express the duration idle time for \(A\) node by:

    $$\begin{aligned} T_{XColl1-Bas}&= H + E[P] + \delta + DIFS,\nonumber \\ T_{XColl1-RTS}&= RTS + \delta + DIFS, \nonumber \\ T_{XColl2}&= RTS \!+\! \delta \!+\! SIFS \!+\! CTS \!+\! \delta \!+\! SIFS \!+\! H \!+\! E[P] \!+\! \delta \!+\! DIFS.\qquad \end{aligned}$$
    (28)
    $$\begin{aligned} T_{Xtx-1-Bas}&= P_{nhidv-Bas}.T_{XSucc-Bas} + P_{hidv-Bas}.T_{XColl1-Bas}, \nonumber \\ T_{Xtx-1-RTS}&= P_{SX}.T_{XSucc} + P_{hid1v}.T_{XColl1} + P_{nhid1v}.P_{hid2v}.T_{XColl2}, \end{aligned}$$
    (29)

    where \(P_{SX} = P_{nhid1v}.P_{nhid2v}\). The probability of hidden node for the basic access mechanism is:

    $$\begin{aligned} P_{nhidv-Bas} = \gamma _{\bar{v}}^{T_{\bar{v}_1-Bas}} , T_{\bar{v}_1-Bas} = \lceil \frac{H + E[P]}{\alpha _{Bas}} \rceil . \end{aligned}$$
    (30)

    The probability of hidden node for RTS/CTS access mechanism is:

    $$\begin{aligned} P_{nhid1v}&= \gamma _{\bar{v}}^{T_{\bar{v}_1}} , T_{\bar{v}_1} = \lceil \frac{RTS+ \delta }{\alpha } \rceil , \nonumber \\ P_{nhid2v}&= \gamma _{\bar{v}}^{T_{\bar{v}_2}} , T_{\bar{v}_2} = \lceil \frac{RTS+ \delta + H + E[P]}{\alpha } \rceil , \end{aligned}$$
    (31)

    where \(\alpha _{Bas}\) and \(\alpha \) are the average length of a generalized time slot to be derived later for basic and RTS/CTS access mechanisms, respectively and \(P_{hidv-Bas} = 1 - P_{nhidv-Bas}, P_{hid1v} = 1 - P_{nhid1v} , P_{hid2v} = 1 - P_{nhid2v}\). The alternative sub-case is that more than one station within group \(v\) decides to transmit a packet with probabilities of \(P_{Xtx-2} = 1 - P_{Xtx-1}\) and it can keep on doing the countdown of its back-off timer after a time duration of \(T_{Xtx-2-Bas}\) and \(T_{Xtx-2-CTS}\):

    $$\begin{aligned} T_{Xtx-2-Bas}&= H + E[P] + EIFS, \nonumber \\ T_{Xtx-2-CTS}&= RTS + \delta + EIFS. \end{aligned}$$
    (32)

  • We propose that station \(A\) transmits and at least one station within group \(v\), station \(B\), transmits. Under such conditions, the probability of collision and time that \(A\) has to wait for the other transmit is:

    $$\begin{aligned} P_{Coll-A}&= \tau _v(1-(1-\tau _v)^{n_v-1}(1-\tau _R)), \nonumber \\ T_{Coll-A-Bas}&= H + E[P] + ACK\_Timeout + DIFS,\nonumber \\ T_{Coll-A-RTS}&= RTS + \delta + CTS\_Timeout + DIFS. \end{aligned}$$
    (33)

  • We assume that station \(A\) transmits and all other stations within group \(v\) (except \(A\)) are idle. In this condition, the collision may occur if at least one of the stations in the other group \((\bar{v})\) wants to transmit a packet to the relay node. For two access mechanisms, we provided the probabilities of the hidden node as mentioned in Eqs. 30 and 31 and we calculated station \(A\)’s time duration to wait for the retransmission of its packet, for the hidden node problem as follows:

    $$\begin{aligned} T_{ASucc-Bas}&= T_{XSucc-Bas} , T_{ASucc-RTS} = T_{XSucc-RTS},\nonumber \\ T_{Ahid-Bas}&= H + E[P] + \delta + ACK\_Timeout + DIFS, \nonumber \\ T_{Ahid1}&= RTS + \delta + CTS\_Timeout + DIFS, \nonumber \\ T_{Ahid2}&= RTS + \delta + SIFS + CTS + \delta \nonumber \\&+SIFS + H + E[P] + \delta + ACK\_Timeout + DIFS. \end{aligned}$$
    (34)

    Based on the above discussions, we summarize in Table 2 what could happen to station \(A\) at the considered time slot. Due to space limitations, we show all cases only for the RTS/CTS access mechanism in Table 2 and the basic access mechanism is similar to this. If we define the time duration for each case as a generalized time slot, then the average length of a generalized time slot, \(\alpha _{Bas}\) and \(\alpha \), can be expressed by:

    $$\begin{aligned} \alpha _{Bas} = \sum P_i.T_i, \alpha = \sum P_i.T_i. \end{aligned}$$
    (35)
Table 2 All cases of what may happen to station \(A\) at a considered time slot for RTS/CTS access mechanism
Full size table

According to the analytical model described above, the conditional collision probability \(P_{Coll}\) can be represented for two protocols and group \(v\) by:

$$\begin{aligned} P_{Collv-Bas}&= 1+(1-\tau _R)(1-\tau _v)^{n_v-1}(1-\tau _{\bar{v}})^{n_{\bar{v}}}(P_{hidv-Bas} - 1), \nonumber \\ P_{Collv-RTS}&= 1\!+\!(1\!-\!\tau _R)(1\!-\!\tau _v)^{n_v-1}(1\!-\!\tau _{\bar{v}})^{n_{\bar{v}}}(P_{hid1v}\!+\! P_{nhid1v}P_{hid2v} \!- \!1). \end{aligned}$$
(36)

5.4 System Design and Performance Parameters

The transmission probability \(\tau _R,\, \theta \) at relay node \(\mathbf{R},\, n_v\) and \(W\) at user nodes in group \(v\) are system design parameters to minimize the delay for single-relay multi-user wireless networks using CSMA/CA, with or without network coding protocols. This paper clarifies the relationship between such system design parameters and performance parameters such as delay packet \(T_v\) for each user node group \(v\). The channel access delay \(T_v\) is defined as the average time from the packet becoming the head of the queue from user group \(v\) until the acknowledgment frame is received from user group \(\bar{v}\).

6 Performance Analysis

6.1 Delay Analysis

This subsection analyzes the accurate delay, with and without NC protocols, for any single-relay multi-user wireless network. In delay analysis, we focus on the traffic control to achieve the fairness between the delay of user node group \(v\) for \(v\in \{1,2\}\). The traffic control to achieve per-group fairness can be extended to the case of per-node fairness as discussed later.

In this section, we focus on the analysis of delay for the RTS/CTS access mechanism. It should be emphasized that the analysis of delay is calculated using a similar manner for the basic access mechanism. For delay analysis, we derive its components. The first duration is the time that the user in group \(v\) sends a packet to the relay node and receives the acknowledgment from relay node. The second part is the waiting time in the queue of the relay node and it depends on the network coding strategy. The last duration is the time that the relay node sends the received packet in the head of its queue and receives the acknowledgment.

6.1.1 Packet Delay Without Network Coding

If the output queue at relay node \(\mathbf{R}\) is saturated, the average number of packets in the steady-state in the output queue at relay node \(\mathbf{R}\) is as follows:

$$\begin{aligned} N_R = \sum _{n=0}^\infty nP(n) = \sum _{n=1}^\infty \frac{n(\rho _1+\rho _2)^n}{1-\tau _R}P(0) = \frac{(\rho _1+\rho _2)}{(1-\tau _R)(1-\rho _1-\rho _2)^2}P(0). \end{aligned}$$
(37)

In this situation, if an innovative packet enters the buffer it has to wait a duration equal to: \(T_{QV} = N_R\cdot T_{R-\bar{v}}\), where \(T_{R-\bar{v}}\) can be calculated from Eq. 21. After that time, the packet is in the head of the buffer. The average time which one packet takes to get from group \(v\) to group \(\bar{v}\) is expressed as:

$$\begin{aligned} T_{v-nonNC} = T_{v-R} + T_{R-\bar{v}} + T_{QV} = T_{v-R} + T_{R-\bar{v}}(1+N_R), \end{aligned}$$
(38)

where \(T_{v-R}\) can be computed from Eq. 22.

6.1.2 Packet Delay with Network Coding

The average number of packets staying in the virtual queue \(v\) at relay node \(\mathbf{R}\) in the steady-state is expressed as:

$$\begin{aligned} N_{R-v} = \sum _{n=0}^\infty nP_v(n) = \frac{\rho _v(1-\tau _R+\tau _RP(0,0))}{(1-\tau _R)(1-\rho _v)}. \end{aligned}$$
(39)

The average time that one packet takes from group \(v\) to group \(\bar{v}\) can be computed by summation on all of delay and is expressed as:

$$\begin{aligned} T_{v-NC} = T_{v-R} + T_{R-\bar{v}} + N_{R-v}. T_{R-\bar{v}}= T_{v-R} + T_{R-\bar{v}}(1+N_{R-v}). \end{aligned}$$
(40)

6.2 Rough Throughput Analysis

In this subsection, we compute the rough throughput of the network in order to trade off between delay and throughput. We are now ready to calculate the normalized rough throughput \(S\) as:

$$\begin{aligned} S=\frac{E[\text {payload bits successfully transmitted in a slot}]}{E[\text {slot length}]}. \end{aligned}$$
(41)

6.2.1 Rough Throughput Without Network Coding

We can calculate the rough throughput in non NC systems using Eq. 38 as follows:

$$\begin{aligned} S_{nonNC} = \frac{(n_1+n_2)E[P]}{n_1T_{1-nonNC}+n_2T_{2-nonNC}}, \end{aligned}$$
(42)

where \(E[P]\) is the length of payload and \(n_v\) is the number of users in group \(v\).

6.2.2 Rough Throughput with Network Coding

To calculate the rough throughput in the NC system, we can use Eq. 40 and it is expressed as:

$$\begin{aligned} S_{NC} = \frac{(n_1+n_2)E[P]}{n_1T_{1-NC}+n_2T_{2-NC}}. \end{aligned}$$
(43)

7 Model Validation and Simulation Results

This section focuses on simulation results for validating the theoretical models and derivations presented in the previous sections. We have developed a C++ simulator modeling both the DCF protocol details in IEEE 802.11b and the back-off procedures of a specific number of independent transmitting stations. The simulator is designed to implement the main tasks accomplished at both the MAC and PHY layers of a wireless network in a more versatile and customizable manner than ns-2, where the lack of a complete physical layer makes a precise configuration difficult. The simulator considers an Infrastructure BSS (Basic Service Set) with a relay node and a certain number of stations which communicates only with the access point as a relay node.

For the sake of simplicity, inside each station there are only three fundamental working levels: traffic model generator, MAC and PHY layers. Traffic is generated by \(q\) parameter. Moreover, the MAC layer is managed by a state machine which follows the main directives specified in the standard [4], namely waiting times (DIFS, SIFS, EIFS), post-back-off, back-off, basic and RTS/CTS access mode. The typical MAC layer parameters for IEEE 802.11b are given in Table 3 [4, 5]. The system values are those specified for the frequency hopping spread spectrum (FHSS) PHY layer. We varied the extended range of nodes in our extension simulation which are \(1\le n_1, n_2 \le 100\) but to prove our analysis, we considered one scenario in this paper. Similar results are seen in all ranges but lower ranges show the most returns. The simulator was run 1000 times and the results were averaged. Each simulation is stopped when 60,000 packets have been processed. The number of user nodes in group 1 is \(n_1 = 10\) and the number of user nodes in group 2 is \(n_2 = 6\).

Table 3 FHSS system parameters and additional parameters to obtain numerical results [5]
Full size table

We mention the basic access for non-network coding, network coding, RTS/CTS access for non-network coding and network coding with nonNCB, NCB, nonNCRTS and NCRTS, respectively. As mentioned, using the forwarding factor \(\theta \) is one of our contributions in this paper. We explored the effect of \(\theta \) on network performance.

We depict simulated throughput and analytical rough throughput from Eqs. 42 and 43 for RTS/CTS mechanism in Fig. 8a without NC and with NC protocols, respectively. As seen in Fig. 8a, the rough throughput is not exact and it is slightly different from simulation results. This event is due to disregarding some states of analysis. Figure 8b shows simulated throughput of the network as a function of \(\theta \). As expected, the achieved throughput in RTS/CTS access mechanism is better than in the basic access mechanism due to the release hidden node problem. Also in this figure, throughput significantly reduces as \(\theta \) increases.

Fig. 8
figure 8

Throughput of network. a Simulated throughput and rough throughput for RTS/CTS mechanism as a function of \(q\). b Simulated throughput for two access mechanisms as a function of \(\theta \) with \(q_1 = 1\) and \(q_2 = 0.5\)

Full size image

We obtained the average delay to transmit a packet from one user in group \(v\) to group \(\bar{v}\) through the relay node for non NC and NC systems from simulations and using Eqs. 38 and 40, respectively.

We show the comparison of results from simulation and analysis in Fig. 9a, b. In these figures, we illustrate the delay of users, \(T_v\) for \(v \in \{1,2\}\) versus \(q\). The curves are obtained from the non-saturated group delay and from Monte Carlo simulations when the packet \(v\) is randomly transmitted from a user node in group \(v\) with probability \(\tau _v\) in a slot. The saturation case occurs when \(q=1\). The value of \(\theta \) is equal to \(0.25\). The figures show a good agreement between analytical and numerical results, confirming that \(q\) can largely decrease the delay of users.

Fig. 9
figure 9

Average channel access delay \((T_v)\). a Theoretical and simulated delay \((T_v)\) for RTS/CTS access mechanism as a function of \(q\) with and without network coding. b Theoretical and simulated delay \((T_v)\) for basic access mechanism as a function of the \(q\) with and without network coding. c Simulated average channel access delay \((T_v)\) for RTS/CTS access mechanism as a function of \(\theta \) with \(q_1 = 1\) and \(q_2 = 0.5\)

Full size image

As seen in Fig. 9a, b, the theoretical and simulated results are different for some values of \(q\). This is due to two reasons. First, we attain simulated results using the Monte Carlo method, so if the simulation is run more, more precise results will be obtained. Second, in analysis of the hidden node problem we can not consider all of the realistic cases and we dissemble some bothersome states which increase the complexity of analysis. Thus, we made some assumptions to simplify our analysis and they lead to a slight difference between the analytical and simulation results.

To investigate the dependency of the delay from \(\theta \), we have reported in Fig. 9c the average channel access delay versus the value for \(\theta \). In this figure, we show RTS/CTS access mechanism with \(q_1 = 1\) and \(q_2 = 0.5\) (saturation and unsaturation cases). When \(\theta \) grows up, the saturation and unsaturation delay increase. Because the number of users in group 1 is more than group 2, its delay is greater than group 2. With the introduction of a waiting interval before transmission by the forwarding factor, the relay node has the chance of collecting other innovative packets and sending out the coded packet. Moreover, the reduction of the number of transmissions and the characteristics of the forwarding factor help in decreasing the collision probability at the MAC layer. When \(\theta \) was close to \(1\), the relay node does not wait long enough to receive the new packet and decides to transmit the packet in its buffer immediately. The collision probability will then increase and this leads to high delay as illustrated in Fig. 9c.

To balance between the throughput and the packet delay in the network we can choose an appropriate value for \(\theta \). For this reason, we can compare the results of performance evaluation versus \(\theta \) in Figs. 8(b) and 9(c).

One of the parameters that is very important to evaluate a network is Packet Loss Ratio \((PLR)\). This parameter is equal to the number of unsuccessful packets to all transmitted packets from group \(v\). If this value is very low, the performance of the network is high. We depict the complement of \(PLR (1-PLR)\) versus \(q\) for group 1 for two access mechanisms with and without network coding in Fig. 10a. As shown in Fig. 10a, when \(q\) is very close to 1 (saturation case), the value of \(PLR\) is very high so the performance of this network is very low. When this network uses the network coding in the relay node, the value of \(PLR\) is very low and in RTS/CTS access mechanism it is lower than the basic access mechanism. The nonNCB case is the worst case in this figure.

Fig. 10
figure 10

Packet Loss Ratio \((PLR)\) for two access mechanisms. a Packet Loss Ratio \((PLR)\) for two access mechanisms as a function of \(q\) with \(\theta = 0.25\) for group 1. b Packet Loss Ratio \((PLR)\) for two access mechanisms as a function of \(\theta \) with \(q_1 = 1\) and \(q_2 = 0.5\) for group 1

Full size image

Figure 10b shows the dependence of \(PLR\) to \(\theta \) for \(q_1 = 1\) and \(q_2 = 0.5\) for basic and RTS/CTS access mechanisms for group 1. For example, a low value of \(\theta \) gives excellent performance in the case of \(q_1\) and the RTS/CTS access mechanism. Large values of \(\theta \) may, in fact, limit the performance of the network and so the value of \(PLR\) will increase for two access mechanisms. This figure has a different behavior in low and high values of \(\theta \). For example, \(\theta \) lower than 0.7 leads to a high value of \(1-PLR\) for the RTS/CTS access mechanism for \(q_1\) and at greater values the condition changes. This situation also occurs for the basic access mechanism. This is the reason stated above regarding the network delay.

Owing to the model’s key assumption of independence at each retransmission, the average number of transmissions that each station must perform in order to successfully complete a packet transmission is shown in Fig. 11a, b for two access mechanisms. Figure 11a, b shows that the number of transmissions per packet significantly increases as \(q\) increases and as \(\theta \) increases. As shown in Fig. 11a, network coding leads to a reduction in the average number of transmissions per packet for users and the network without network coding and with basic access mechanism is the worst case in this figure. Figure 11b also has the same behavior for the average number of transmissions per packet. In this figure, by increasing \(\theta \) the average number of transmissions for saturation case \((q_1=1)\) significantly increases.

Fig. 11
figure 11

Average number of transmissions per packet for two access mechanisms for group 1. a Average number of transmissions per packet as a function of \(q\) with and without network coding with \(\theta = 0.25\). b Average number of transmissions per packet as a function of \(\theta \) with \(q_1 = 1,\, q_2 = 0.5\)

Full size image

We ran extensive simulations using our simulator over a wide range of contention window sizes. Due to space limitations, we show in detail the numerical validation results for the RTS/CTS access mechanism, which show the average channel access delay. Figure 12 shows that the dependence of the delay from the maximum number of \(m\) of back-off stages or \(W_{min}\) is marginal. The figures report the cases of both NC and nonNCRTS schemes, with \(CW_{max} = 1024,\, W_{min}\) from 8 to 512, \(q_1 = 1,\, q_2 = 0.5\) and \(\theta = 0.25\) for group 1. We see that the choice of \(W_{min}\) practically affects the system delay, as long as it is lower than 64. It is observed that when we use network coding for the RTS/CTS access mechanism, the average channel access delay strongly depends on \(W_{min}\). Figure 12a reports that the average channel access delay is lower than the delay of the network without network coding (as shown in Fig. 12b). This can be considered as an important parameter of a network.

Fig. 12
figure 12

Average channel access delay \((T_v)\) for RTS/CTS access mechanism as a function of \(W_{min}\) for \(q_1 = 1,\, q_2 = 0.5\) for group 1. a The network coding case with \(\theta = 0.25\). b The non network coding case

Full size image

It should be emphasized that the extension simulations have a good agreement with analytical results, for example simulated results in Figs. 9c, 10a, 10b, 11 and 12 are similar to analytical results. Also simulation results show that the delay increases by increasing the number of stations in groups 1 and 2.

8 Conclusion and Future Works

In this paper, a novel network coding-based MAC scheme for single relay multi user wireless networks was presented. Understanding the delay behavior of network coding with a fixed number of transmitters and receivers, and a limited number of encoded symbols is a key step towards its applicability in real-time communication systems with stringent delay constraints. We succeeded in developing analytical models of the network delay on basic and RTS/CTS access mechanisms with network coding (NCRTS and NCB) for single-relay multi-user wireless networks with bidirectional data flows. The analytical models involved the effects of queue saturation and non-saturation at the relay node. To validate the accuracy of our proposed models, we extensively tested the performance estimation of the models for a wide range of \(q\), the forwarding factor \(\theta \), contention window sizes, and traffic loads. Compared to systems without network coding, substantial improvements in packet delay, throughput, PLR and average number of transmission per packet are obtained with network coding. As an example, packet delay improves up to \(30\,\%\) in terms of \(\theta \) (forwarding factor). Our experimental results show that these models lead to improvements in all system features.

As a future work we will clarify the effect of channel on the total throughput and delay in the NCRTS and NCB protocol and we will show the cooperation between NC, Multi-Packet Reception (MPR) and MAC layer in the single relay multi user wireless networks.