1 Introduction

Wireless relay nodes have been highly effectively used in connecting nodes located in rural areas [1] and expanding wireless service coverage [2]. This paper considers two way relay wireless networks in which two multi-user single-hop networks are linked by a single relay node.

In networks, multi-user interference is an important limitation. In order to alleviate it, the use of multi-packet reception (MPR) has been proposed [3, 4]. In this paper, a new cross-layer MAC/PHY design based on IEEE 802.11 wireless local area networks (WLANs) with hidden terminals will be presented. In WLANs with hidden terminals, not all terminals can hear each other and multiple RTS packets may arrive at an access point (AP) with varying time offsets complicating the issue of collision handling. Our proposed design utilizes an MPR algorithm that can minimize the number of dropped packets by resolving collisions in the PHY layer. We consider one component: a compatible MPR-aware MAC as an upgrade to IEEE 802.11 with RTS/CTS signaling. The MPR PHY detects multiple asynchronous packets while providing diversity gain. The MPR-aware MAC framework is tuned to maximally benefit from multiple packet delivery and to accept multiple RTS packets with large offsets.

In recent years, there has been a growing interest in the applications of network coding (NC) techniques in multi-hop wireless networks, where data flows coming from multiple sources are combined to increase throughput, reduce delay, and enhance robustness. In contrast to the traditional store and forward approach [5], it implements a store, code, and forward technique, where each node stores incoming packets in its own buffer and transmits the combined data. The combining is performed over some finite Galois field. We focused on the interaction between Medium Access Control (MAC), NC and MPR over a single-relay multi-user wireless network configuration in order to capture the effects of each protocol component and quantify the performance degradation due to packet collisions and random transmission schedules. Our notion of delay is motivated by real-time applications with progressively refined input. However, our notion of delay is relevant to a much more general class of applications. The MAC layer of many wireless protocols resembles that of IEEE 802.11. Hence, while we focused on this protocol, it is evident that the results easily extend to other protocols with similar MAC layer operation. The IEEE 802.11 MAC presents two options [6], namely the Distributed Coordination Function (DCF) and the Point Coordination Function (PCF). PCF is generally a complex access method that can be implemented in an infrastructure based network. The mechanism of DCF is based on Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA). We focus on DCF in this paper.

Many works of random access protocols assume that each node always has data packets to be transmitted, i.e., their queues are saturated. An efficient and accurate analytical model to evaluate the saturated throughput for the CSMA/CA protocol with the binary slotted exponential back-off algorithm was proposed in [7]. This is employed as an MAC protocol in the IEEE 802.11 standard [6]. However, it is important to show analytical models on the unsaturated conditions in order to obtain a fundamental understanding of the behavior of random access protocols and provide reference performances of the throughput and delay according to the offered traffic. We developed analytical models for the CSMA/CA protocol with and without XOR-based NC for simple single-relay multi-user wireless networks assuming asymmetric bidirectional flows.

In the NC system, we consider the network coding schemes of [8] for all data transmission. According to these algorithms, whenever only one buffer (the number of buffers is two in our network scenario) at relay node has a packet, the relay node broadcasts its packet with probability \(\theta \) (the forwarding factor) over the channel whereas nothing is transmitted with probability \(1- \theta \).

The main questions we consider in this paper are (1) whether network coding and MPR offer performance gains, and (2) how to design relay node parameters that improve average delay and throughput, and what is the complexity of this task. When using NC at the relay node with MPR scenario in Monte-Carlo simulations, significant improvements are shown in packet delay and throughput of the network as a function of \(\theta \). For instance, the network coding and MPR schemes decrease the packet delay of the system up to \(40\,\%\) with trade off of the offered quality of service (QoS) in terms of throughput. This is in addition to \(30\,\%\) improvement in the packet loss ratio (PLR) and \(45\,\%\) reduction in the Average number of transmissions per packet. Similar improvements are achieved in all other examples of network topology.

The main contributions of this paper are the introduction of:

  1. (i)

    The first attempt to analyze the performance of network coding and MPR in CSMA/CA with two-hop unbalanced bidirectional traffic in two-way relay wireless networks. One can evaluate the throughput and delay through the proposed analytical models without any computer simulations regardless of whether the queue at the relay node is saturated or not.

  2. (ii)

    A highly accurate model for IEEE 802.11 DCF protocol in a single hop setting under both saturated and non-saturated traffic loads. We derived closed-form expressions for the throughput and delay, with and without network coding in MPR scenario, by solving queuing systems for the buffer behavior at the relay node. As in the case of the two-hop unbalanced traffic, the results show that the transmission probability of the relay node is a design parameter that is crucial to improve the achievable performance of the CSMA/CA with NC and MPR approach. The results show that NC and MPR can enhance the achievable regions in two directional throughput and delay, especially with the symmetric network structure.

  3. (iii)

    A low complexity, decentralized combination and transmission technique with the forwarding factor \(\theta \) to mitigate the deadlock problem in multi-hop networks. We evaluate the impact of the forwarding factor.

  4. (iv)

    Detailed descriptions of proofs in a number of theorems and lemmas with respect to the throughput and delay, with and without NC in MPR scenario for single-relay multi-user wireless networks. These descriptions helped develop new analytical models for other random access protocols and evaluate the effects of wireless link qualities or queue capacity on throughput and delay, with and without NC in MPR scenario.

The rest of this paper is organized as follows: In Sect. 2, previous approaches to IEEE 802.11 protocol analysis under saturation and non-saturation cases and network coding with the MPR approach for the link layer are reviewed. Section 3 explains the CSMA/CA systems and network topology for two-hop wireless relay networks with MPR scenario. Section 4 presents the network model with and without network coding for performance analysis under MPR scenario. Section 5 shows an extended Markovian model characterizing the MAC layer under non-saturated traffic conditions, presenting modifications that account for transmission errors. In Sect. 6, we explain the performance analysis of the network by focusing on expressing exact packet delay and rough throughput for RTS/CTS access mechanism with and without network coding for MPR relay node. In Sect. 7, we present simulation results where the typical MAC layer parameters for IEEE 802.11 are used to obtain exact packet delay and rough throughput values as a function of various system level parameters under network coding and MPR scenario. Finally, Sect. 8 is devoted to conclusions and direction to future works.

2 Related Work

The seminal paper of Bianchi [7] is the first paper to describe the binary exponential back-off mechanism of the DCF protocol within a single node as a two dimensional Discrete Time Markov Chain (DTMC). Bianchi’s Markov chain, while providing a closed form solution, lacks two important features specified by the IEEE 802.11b standard. These are retransmission limits and back-off counter freezing. Variations of Bianchi’s Markov chain were proposed to describe the 802.11 protocol more accurately and adhere to the standard. Babich [9], Zhang [10] and Xiao [11] improved the analysis by adding the back-off counter freezing probability to their models. Gupta [12] and Kao [13] proposed an analytical model to calculate the network throughput and delay of dedicated control channel protocols that are designed to schedule multiple packets to be transmitted on different data channels simultaneously.

Rui et al. [14] addressed the full-duplex relaying. Some expressions for outage and average capacity of a two-hop cooperative system with a full-duplex relay are derived under an independent but not identically distributed Rayleigh fading environment. In [15], the authors presented a novel MAC protocol based on IEEE 802.11, called C-MAC, which is able to support the basic building block of the cooperative system. Ke et al. [16] proposed a new backoff mechanism, called the smart exponential-threshold-linear (SETL) Backoff Mechanism, to enhance the system performance of contention-based wireless networks.

One approach used to model the non-saturation performance estimates the number of active contending nodes implicitly in the model, as in [17, 18]. In [19], the authors proposed an adaptive back-off scheme and evaluated the performance of the proposed scheme for ad hoc networks. The back-off mechanism devised by them grants a node access to the channel based on its probability of collision for a transmitted frame in comparison to the nodes in the two-hop contention area.

One topic that has not been studied thoroughly in the literature is the interaction between the opportunistic wireless NC and the MAC protocol. Most of the existing studies are theoretical and make several assumptions about the structure of the network or the channel access scheme. For example, Liu et al. [20] have derived theoretical bounds for the achievable throughput of NC in large ad-hoc networks. More recently, Chaporkar et al. investigated adaptive NC and scheduling for wireless ad-hoc networks [21]. They demonstrated that wireless NC can perform less effectively than non-coded packet transmission since wireless broadcast can reduce spatial reuse. In another related work that identified the same problem, the authors propose an algorithm that determines whether transmitting coded or uncoded packets is the optimal decision regarding the status of the transmission buffer [22]. In [23], Asterjadhi et al. considered practical dissemination algorithms exploiting NC for data broadcasting in ad hoc wireless networks. For an efficient design, they analyzed issues related to the use of NC in realistic network scenarios. A simulation study by Fasolo et al. [24] presented results that highlight the sub-optimal performance of existing 802.11-based MAC protocols and NC. Although several limitations of existing MAC protocols for NC have been identified, none of the aforementioned works introduced any enhancements that address these problems.

Sagduyu et al. [25] showed the achievable throughput region and throughput optimization in random access mode employing NC over wireless linear multi-hop networks for several source packet transmission schemes in the case of saturated queues. Le et al. [26] proposed a fundamental coding structure and clarified the encoding number of packets by taking into consideration the physical wireless environments. They also showed that the maximum number of coding flows was fewer than expected because many of the wireless transmissions interfered with each other. Argyriou [27] proposed the use of opportunistic acknowledgments (OACKs) for overheard packets which are obtained from opportunistic listening. In [28], the authors developed algorithms that explored the delicate trade-off between waiting and transmitting using NC. Cloud et al. [29] designed a cross-layer approach to aid in developing a cooperative solution using MPR, NC, and MAC. They constructed a model for the behavior of the IEEE 802.11 MAC protocol and applied it to key small canonical topology components and their larger counterparts. Hasegawa et al. [30] proposed a scheme jointly applying packet aggregation and XOR-based NC. This is called bidirectional packet aggregation and coding (BiPAC), for bidirectional voice over IP (VoIP) flows in wireless linear multi-hop networks and demonstrated the increase of supportable VoIP sessions through the implementation of IEEE 802.11 networks.

Fouli et al. [31] investigated network coding in access point-to-multi-point (PMP) broadcast networks. These are centralized networks with a number of user nodes communicating individually through a central access point (AP). Most importantly, they are concerned with the queuing effects on delay within a switch, particularly at high loads. To simplify the analysis, they ignored upstream channel arbitration and focused on queuing delay at the AP.

Hsu et al. [32] proved that the decision at relay node to wait for the next coding opportunity can reduce the number of transmissions, whereas it incurs a penalty in terms of packet delay. In this paper, the authors proposed an on-line algorithm for making transmit/wait decisions at the relay nodes. The algorithm minimizes the total system cost which includes both the number of transmissions as well as packet delay. The newest work in this field has been done by Antonopoulos et al. [33]. The authors introduced a network coding-aided energy efficient MAC protocol which coordinates the transmissions among a set of relay nodes which act as helpers in cooperative Automatic Repeat reQuest-based (ARQ-based) wireless networks. Using network coding methods, the energy efficiency of the network increases without compromising the system performance in terms of QoS.

In this work, we focus on the throughput and delay analysis of IEEE 802.11 based wireless networks which use NC and MPR at the physical layer in saturated and non-saturated cases. The results of this paper are twofold. The first is on modeling and characterizing the impact of NC on the throughput and delay in IEEE 802.11. The second is considering this impact both in saturated and non-saturated cases with MPR scenario.

3 Problem Statement and System Model

In this section, we describe the CSMA/CA systems, both with and without network coding, on two-hop wireless relay networks with bidirectional unbalanced traffic and MPR relay node, system design parameters, and evaluation parameters. The list of the notation of all symbols which have been used in this paper is summarized in Table 1.

Table 1 The notation of all symbols that have been used
Full size table

3.1 Network Topology

This paper deals with two-hop wireless relay access systems that consist of one relay node \(\mathbf {R}\) and two end node groups 1 and 2, as illustrated in Fig. 1. Let us assume that node \(\mathbf {R}\) and all the end nodes are fixed base stations (subscriber) but are not mobile-phones or wireless terminals powered by an internal battery. All nodes have one transceiver with an omnidirectional antenna. The transmission from any user towards the AP is a point-to-point transmission while the transmission from the AP back to the users is a broadcast PMP transmission. Therefore, a node can be either transmitting or receiving, but not both simultaneously. We assume that all nodes in an end node group and node \(\mathbf {R}\) are in transmission range but any node in a group is out of transmission range to all nodes in another group. Furthermore, no interference is incurred on the receiver of a node in a group due to the transmissions in another group. For example, if node \(\mathbf {R}\) (Access Point) is on the roof of a department in a university, the end node groups are within a blind zone of each other, and so on. We also assume that the buffer capacity is infinite for all nodes in the system in order to analyze the delay. We can assume some departments in a university as two separate groups that want to make a video conference or VoIP. As seen in Fig. 1, three users in group 1 can transfer their packets to four users in group 2 via relay node on the roof of a building.

Fig. 1
figure 1

Single-relay multi-user wireless networks which have two multi-user single-hop wireless networks via the relay node \(\mathbf {R}\)

Full size image

Let us consider only the bidirectional traffic via node \(\mathbf {R}\) and assume that there is no closed traffic inside groups 1 and 2. Node \(\mathbf {R}\) is an EF repeater and does not have the source of traffic. Node \(\mathbf {R}\) directs packets from a source in group 1 to its destination in group 2 and vice versa. The buffer at node \(\mathbf {R}\) is a first-in first-out (FIFO) queue. If there are always packets in the buffer, the buffer is called \(saturated \), otherwise it is called \(non-saturated \). Node \(\mathbf {R}\) generally undergoes any unbalanced traffic between groups 1 and 2. The traffic unbalance is caused by a difference in arrival rate of new packets among end nodes or a difference in the number of nodes between groups 1 and 2. A system without network coding is called a \(non-NC system \) while that with network coding is called an \(NC system \).

We suppose that all nodes employ the IEEE 802.11 protocol. We assume constant length packets and that all packets will begin their transmissions only at the beginning of a slot. The system is time slotted and all nodes are synchronized. Let us define a packet transmitted from a node in group \(v\) as packet \(v\) for any \(v\in \{1,2\}\). For convenience, \(\bar{v}\in \{1,2\}\) is defined as the complementary element of \(v\in \{1,2\}\). The node transmits a packet with probability \(\tau _v\) and they are the same for all nodes in group \(v\). The transmission probability of relay \(\mathbf {R}\) is denoted by \(\tau _R\).

Figure 2 illustrates the ACK packet transmissions for non-NC and NC systems. As shown in Fig. 2, if the coding packet is transmitted from node \(\mathbf {R}\) and received correctly at both the destinations, two ACK packets are transmitted from both the destinations. This is a simple model for the ACK packet transmissions in which an additional ACK sub slot is attached to the total slot. We should emphasize that the address of destination nodes are put in the header of the coded packet. RTS/CTS access mechanism is to overcome the hidden node problem so the users in the two groups have to use this mechanism. However, the two groups are in the range of transmission of relay node. In our network scenario, the relay node does not need to use RTS/CTS access mechanism to send its packet and it uses the basic access mechanism to send a packet and receive the ACK frame. In the access mechanism, the destination user just sends the ACK frame to the relay node. The relay node uses RTS frame to determine the destination node and puts its address in the header of the coded packet.

Fig. 2
figure 2

The ACK packet transmission for NC system under base access mechanism. a Non network coding packet transmission. b Network coding packet transmission

Full size image

Node \(\mathbf {R}\) transmits the head of its buffer with probability \(\tau _R\) for non-NC systems if its buffer is nonempty. In NC systems \(\mathbf {R}\) has two virtual buffers 1 and 2. If \(\mathbf {R}\) receives packet \(v\) successfully, \(\mathbf {R}\) stores the pointer of the packet in virtual buffer \(v\). Any end node stores the packets received from the same group in the packet pool, which is a buffer to store undirected packets heard by opportunistic listening [34], to decode the coding packets transmitted from \(\mathbf {R}\). Node \(\mathbf {R}\) gets a transmission opportunity with probability \(\tau _R\) if its buffer is nonempty. In such a case, if both the virtual buffers are nonempty, the packet is encoded from two packets corresponding to the heads of virtual buffers by operating a bitwise XOR and is called a coding packet. If a virtual buffer is nonempty and another is empty, the relay node will transmit with probability \(\theta \) (forwarding factor) whereas nothing is transmitted with probability \(1-\theta \). This approach is called probabilistic network coding. If the destination receives a coding packet from \(\mathbf {R}\) successfully, it can decode the desired packet by operating the bitwise XOR of the received coding packet and the packet in the packet pool. If a node receives two or more packets at the same slot, a collision occurs. We clarify the effect of the system design parameters \(n_v\) (number of members in group \(v\)), \(W\) (minimum size of contention window), \(\theta \) and \(q\) (whereby \(q\) is the probability of having at least one packet to be transmitted in the buffer) on the delay.

It is assumed that the nodes in group 2 are connected with Internet backbone working as an access point (AP) in the case of IEEE 802.11. The user nodes in group 1 are assumed to exploit some bidirectional communication services such as VoIP, TV conference, P2P, etc. It is one of the important issues to achieve fairness between uplink and downlink data flows rather than fairness among all user nodes as discussed in [35] for single-hop wireless IEEE 802.11 networks.

3.2 Multi-packet Reception Model

MPR allows for reception, at the physical layer, of one or more simultaneously received packets. The number of simultaneous transmissions that the relay node can successfully receive without a collision is \(m_{MPR}\). In our model, CSMA/CA is strictly enforced for \(m_{MPR} = \{1, 2\}\). If a node (in group \(v\)) senses any other node (in group \(v\)) transmitting, it will follow the IEEE 802.11 DCF algorithm and not attempt to transmit again until the channel is idle. If more than one node in group \(v\) (or group \(\bar{v}\)) transmits their packets simultaneously, the collision will occur whereas if one node in group \(1\) and one node in group \(2\) simultaneously transmit the packet, the relay node can receive their packet without collision. This model uses MPR to minimize the hidden node problem.

3.3 Problem Description

The use of traditional access mechanisms such as CSMA-like protocols, when multiple nodes transmit, may suffer from a high number of collisions and dropped packets. Packets collisions and scheduling mechanisms are two main factors which should be taken into account when using network coding in an MAC protocol. Both collisions and scheduling are the direct consequence of the random (CSMA-like) channel access that were adopted in this study. Collisions impact the performance as fewer packets are collected. Packet scheduling refers to the way in which different nodes take turns in transmitting, which is dictated by the MAC rules. The transmission order is important when network coding is used at higher layers as it influences the way encoded packets are created, i.e., which packets are mixed together. In this paper, we focus on the analysis of random access schemes as used by IEEE 802.11b with RTS/CTS handshake. We provide an analysis of the combined use of NC, MPR and MAC layer in a multi-hop, with relay node. We then design a cross-layer solution that increases throughput and decreases delay subject to the constraint of fairness between flows, rather than between nodes, for a multi-hop network structure. Our solution uses cooperation between nodes and takes into account the interaction among NC, MAC, and MPR.

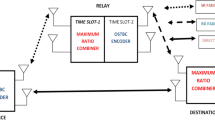
In such PMP architectures, network coding can use the basic broadcast architecture to turn unicast transmissions into more efficient broadcast transmissions, as depicted in Fig. 3. This figure illustrates the wireless two-way relay network in which bidirectional data transfer takes place between end nodes \(G1\) and \(G2\) when the assistance of the relay node \(\mathbf {R}\) is investigated. The transmission protocol, is considered which consists of the following two phases: the multiple access (MA) phase, during which \(G1\) and \(G2\) transmit to \(\mathbf {R}\), and the broadcast (BC) phase during which \(\mathbf {R}\) transmits to \(G1\) and \(G2\). The network coding method is employed at relay node in such a way that \(G1\) (\(G2\)) can decode the message of \(G2\) (\(G1\)), given that \(G1\) (\(G2\)) knows its own messages. Network coding hence achieves the packet exchange in only three packet transmissions, using 50 % less downstream bandwidth.

Fig. 3
figure 3

The two way relay network with two phase (MA and BC phase)

Full size image

The wireless two-way relay network with NC is applicable to a number of access-metro network architectures such as WLANs (e.g., infrastructure-mode WiFi), broadband satellite networks, and cellular access networks (e.g., long term evolution (LTE) and WiMAX). The investigation of localized traffic in PMP networks is urged by the enormous growth of traffic generated by applications that stand to benefit from local packet exchanges, including user-generated high-definition video, video and voice conferencing, peer-to-peer, as well as video gaming.

4 Network Coding Model

Network coding is modeled by considering the ability of a given node to combine multiple packets together. We use COPE [34] as a case study. COPE inserts a coding shim between the IP and MAC layers and uses the broadcast nature of the wireless channel to opportunistically code packets from different nodes using a simple XOR operation. The wireless channel enables each node to overhear packets that can be used to help decode any subsequently received encoded packets. In the proposed model, each encoded packet is sent by relay node and it can be decoded by the intended recipients. Consistent with COPE’s implementation, each packet is sent as a broadcast transmission on the channel at the first opportunity, without delay, and each information flow does not exercise congestion control. Finally, neither the complexity of the coding or decoding operations nor any other aspects of the NC implementation found in [34] are considered since their contributions to the overall network performance is small.

In this section, we focus on the network coding model for MPR relay node with \(m_{MPR} = 2\).

The probability in a time slot that only one station in group \(v\) transmits is introduced as:

$$\begin{aligned} \Gamma _v=n_v\tau _v(1-\tau _v)^{n_v-1}, \end{aligned}$$
(1)

where \(\tau _v\) is the transmission probability of a packet for a user in group \(v\) and will be computed in Eq. 16 and the probability in a time slot that no stations in group \(v\) transmit is introduced as:

$$\begin{aligned} \gamma _v=(1-\tau _v)^{n_v}. \end{aligned}$$
(2)

4.1 CSMA/CA Protocol Without Network Coding and \(m_{MPR} = 2\)

We assume queue states at relay node \(\mathbf {R}\) as sequences of packets \(\mathcal {V}_1^n=v_1v_2\ldots v_n (v_i\in \{1,2\})\) in the output queue and the empty queue state as \(\mathcal {V}_1^n=0\). The queue state in the \(k\)-th slot is denoted as \(V_k\) for any \(k\ge 0\) and let us define the initial state as \(V_0 = 0\). Figure 4 illustrates the Markov chain of \(V_k\), where self-transitions are not drawn. The steady-state probability of a state \(\mathcal {V}_1^n\) is denoted as \(Q(\mathcal {V}_1^n)\) and the number of packets \(v\) in state \(\mathcal {V}_1^n\) is denoted as \(n_v(\mathcal {V}_1^n)\).

Fig. 4
figure 4

The Markov chain of buffer states in \(\mathcal {V}_1^n\) at node \(\mathbf {R}\) for systems without network coding

Full size image

The state transition that packet \(v\) is transmitted but \(\bar{v}\) is not when the output queue at relay node \(\mathbf {R}\) is empty corresponds to \(\lambda _{0,v}\) in Fig. 4, which is expressed as:

$$\begin{aligned} \lambda _{0,v} = \Gamma _{v}\gamma _{\bar{v}}. \end{aligned}$$
(3)

The probability of packet collision when the relay node wants to send packet \(v\) to group \(\bar{v}\) is expressed as:

$$\begin{aligned} P_{CollR{-}v{-}nonNC} = 1-\gamma _{\bar{v}}. \end{aligned}$$
(4)

Similarly, based on the queue behavior at relay node \(\mathbf {R}\), the other state transition probabilities shown in Fig. 4 are expressed as:

$$\begin{aligned}&\lambda _v = \Gamma _{v}\gamma _{\bar{v}}(1-\tau _R), \nonumber \\&\mu _v = \tau _R\gamma _{\bar{v}} + P_{drop{-}v}, \end{aligned}$$
(5)

where \(P_{drop{-}v} = P_{CollR{-}v{-}nonNC}^{m+1}\), \(m\) is the maximum number of retransmissions for a packet, and \(\tau _R\) is the probability that the relay node will attempt transmission in a slot time and it will be computed later in Sect. 5.1.

The utilization factor with respect to packets \(v\) when the output queue is nonempty at relay node \(\mathbf {R}\) is defined as

$$\begin{aligned} \rho _v = \frac{(\lambda _v+\lambda _{v,\bar{v}})}{\mu _v}, \end{aligned}$$
(6)

Lemma 1

In the non-saturated condition for relay node \(\mathbf {R}\), the steady-state probabilities of queue states are introduced as:

$$\begin{aligned} Q(0)&= \frac{(1-\tau _R)(1-\rho _1 - \rho _2)}{(1-\tau _R) + \tau _R(\rho _1 + \rho _2)},\nonumber \\ Q(v)&= \frac{\rho _vQ(0)}{(1-\tau _R)}, \nonumber \\ Q(\mathcal {V}_1^n)&= \frac{\rho _1^{n_1(\mathcal {V}_1^n)}\rho _2^{n_2(\mathcal {V}_1^n)}Q(0)}{(1-\tau _R)}. \end{aligned}$$
(7)

Lemma 2

If the output queue at relay node \(\mathbf {R}\) is non-saturated, the steady-state probabilities of the numbers of packets in the output queue at relay node \(\mathbf {R}\) are as follows:

$$\begin{aligned} P_v(0)&= Q(0)\bigg [ \frac{1-\tau _R(1-\rho _{\bar{v}})}{(1-\tau _R)(1-\rho _{\bar{v}})}\bigg ], \nonumber \\ P(n)&= \frac{(\rho _1 + \rho _2)^n}{(1-\tau _R)}P(0); n>0. \end{aligned}$$
(8)

The proof of Lemmas 1 and 2 will be included in Appendices 1 and 2, respectively.

Remark 1

The probability of \(q\) for relay node \(\mathbf {R}\) is equal to: \(q = [1-Q(0)]\).

4.2 CSMA/CA Protocol with Network Coding and \(m_{MPR} = 2\)

We assume queue states at relay node \(\mathbf {R}\) as pairs \((n_1,n_2)\) of numbers of packets in the virtual queues 1 and 2. The queue state in the \(i\)-th slot is defined as \(\varphi _i = (\varphi _{1,i}, \varphi _{2,i})\) for any \(i \ge 0\) and let us define the initial state \(\varphi _0 = (0, 0)\). Figure 5 depicts the Markov chain of \(\varphi _i\), where self-transitions are not shown. The steady-state probability of a state \((n_1,n_2)\) is denoted as \(P(n_1,n_2)\).

Fig. 5
figure 5

The Markov chain of the queue states process \(\varphi _i \) in the system with network coding

Full size image

The state transition probabilities \(\lambda _{0,v}\) and \(\lambda _v\) in Fig. 5 are expressed as 3 and 5, respectively, as in the case of the without network coding protocol. The state transition from \(\varphi _i = (n_1,n_2)\) to \(\varphi _{i+1} = (n_1-1,n_2-1)\) in Fig. 5 means that both packets in a coded packet are successfully received at both destination nodes. When relay node \(\mathbf {R}\) simultaneously transmits a packet with at least one of the users in groups (1 or 2), the collision will occur. This probability is equal to:

$$\begin{aligned} P_{CollR{-}NC} = 1-\gamma _v\gamma _{\bar{v}}. \end{aligned}$$
(9)

The corresponding state transition probability \(\mu _v\) and \(\mu \) are introduced as:

$$\begin{aligned} \mu _v&= \theta \tau _R\gamma _{\bar{v}} + P_{drop{-}v}, \nonumber \\ \mu&= \tau _R\gamma _v\gamma _{\bar{v}} + P_{drop}, \end{aligned}$$
(10)

where \(\theta \) is the forwarding factor and \(P_{drop} = P_{CollR{-}NC}^{m+1}\).

The transition \(\mu _{0,v}\) means that the packet \(v\) in a coded packet is successfully received but \(\bar{v}\) is not and is equal to:

$$\begin{aligned} \mu _{0,v} = \tau _R(1-\gamma _v)\gamma _{\bar{v}}. \end{aligned}$$
(11)

Lemma 3

For any \(v\in \{1,2\}\), the steady-state probabilities of the numbers of packets in virtual queue \(v\) are as follows:

$$\begin{aligned} P_v(0)&= \frac{(1-\rho _v)(1-\tau _R)-\rho _v\tau _RP(0,0)}{1-\tau _R}, \nonumber \\ P_v(n)&= \rho _v^n\bigg [\frac{(1-\rho _v)[(1-\tau _R)+\tau _RP(0,0)]}{1-\tau _R}\bigg ]. \end{aligned}$$
(12)

If one of the queues in relay node is saturated and the other is non-saturated, (i.e. \(\rho _1<1\) and \(\rho _2 \ge 1\)) therefore \(P(0,0) = 0\) and hence \(\lambda _{1,1}\) is equal to \(\lambda _1\) from Eq. 40 in C. The detailed balance equations related to virtual buffer 1 are obtained as:

$$\begin{aligned} P_1(n+1)&= \rho _1P_1(n), \nonumber \\ \sum \limits _{n=0}^\infty P_1(n)&= 1 \Rightarrow P_1(0) = 1-\rho _1, P_1(n) = \rho _1^n(1-\rho _1). \end{aligned}$$
(13)

Lemma 4

The steady-state probability of state \(P(0,0)\) is introduced as:

$$\begin{aligned} P(0,0) = \frac{(1-\tau _R)(1-\rho _1)(1-\rho _2)}{1-\tau _R(1-\rho _1)(1-\rho _2)}. \end{aligned}$$
(14)

The proof of Lemmas 3 and 4 will be included in Appendices 3 and 4, respectively.

Remark 2

The probability of \(q\) for relay node \(\mathbf {R}\) using network coding is equal to: \(q = [1-P(0,0)]\).

5 Network Models

This section develops a simple model that gives insight into cross-layer design of wireless networks by using NC, and MAC protocol. We identify each network element’s fundamental behavior and model them using simple, intuitive methods so that various performance measures can be evaluated and design trade-offs can be weighed. Subsequent sub-sections identify specific behaviors of these elements and describe the abstractions and simplifications needed to make the model tractable. The scenario considered consists of a wireless error-free packet network that is operated in fixed-length time-slots. Each node in the groups is half-duplex (i.e., cannot receive and transmit in the same time-slot), and also only one packet can be sent per time-slot by relay node.

5.1 Markovian Model Characterizing the MAC Layer Under Non-saturated Traffic Conditions

The access technique employed by the desired source corresponding to the IEEE 802.11 DCF, with or without the RTS/CTS mechanism, is analyzed in non-saturated traffic conditions and takes into account multiple simultaneous communications between different node pairs. In this section, we present the basic rationale of the proposed bi-dimensional Markov model useful for evaluating the performance of the CSMA/CA under non-saturated traffic conditions. We made the following assumptions: the number of terminals is finite, the channel is free of errors, and packet transmission is based on RTS/CTS access mechanism. For conciseness, we will limit our presentation to the ideas needed for developing the proposed model. The interested reader can refer to [6, 7] for many details on the operating functionalities of the CSMA/CA.

The proposed non-saturated model extends the model presented in [7, 36]. In this paper, it is assumed that a station may store the next packet in a single packet buffer. Thus, the proposed model is slightly more aggressive than the non-saturated one presented in [37].

A two-dimensional Markov process \((s(t), \pi (t))\) can now be defined, based on three assertions:

  1. (i)

    the probability \(\tau \) that a station will attempt transmission in a time slot is variable across all time slots;

  2. (ii)

    the probability \(P_{Coll}\) that any transmission experiences a collision is independent of the number of collisions already suffered;

  3. (iii)

    \(q\) is the probability of having at least one packet transmitted in the buffer.

It is modeled by the Markov chain depicted in Fig. 6, where \(m\) is the maximum back-off stage, or the maximum number of retransmissions, \(P_{eq}\) is the conditional probability that the source generally encounters errors, i.e., a collision (assumed independent of the number of collisions suffered by the packet in the previous attempts), \(W_i\) is the contention window size at the \(i-\)th transmission attempt. \(W = W_0\) represents the minimum contention window. We recall that a back-off time counter is initialized depending on the number of failed transmissions for the transmitted packet. It is chosen in the range of \([0,W_i - 1]\) following a uniform distribution. At the first transmission attempt, i.e., for \(i = 0\), the contention window size is set equal to a minimum value \(W_0 = W\), and the process \(s(t)\) takes on the value \(s(t) = i = 0\).

Fig. 6
figure 6

Markov chain for the contention model in non-saturated traffic conditions

Full size image

One major deviation from Bianchi’s model [7] is the inclusion of \(P_f\) which represents the probability that the channel is frozen and a node in the back-off state does not decrement its back-off counter (\(P_d = 1-P_f\)).

The back-off stage \(i\) is incremented in unitary steps after each unsuccessful transmission up to the maximum value \(m\), while the contention window is doubled at each stage up to the maximum value \(CW_{max} = 2^mW\). The back-off time counter is decremented as long as the channel is sensed idle and stopped when a transmission is detected. The station transmits when the back-off time counter reaches zero. After reaching these limits, the packet will be discarded if it is not successfully transmitted.

On the basis of this assumption, collisions can occur with probability \(P_{Coll}\) on the transmitted packets. In this scenario, a packet is successfully transmitted if there is no collision (this event has probability \(1 - P_{Coll}\)).

Unlike Bianchi’s model [7], the simplicity of such a model can also be retained in non-saturated conditions by introducing a new state, labeled \(I\), accounting for the following two situations:

  • Immediately after a successful transmission, the buffer of the transmitting station is empty;

  • The station is in an idle state with an empty buffer until a new packet arrives at the buffer for transmission.

If a collision occurs, the back-off stage is incremented so the new state can be \((i+1, k)\) with probability \(P_{eq}/W_{i+1}\), since a uniform distribution between the states in the same back-off stage is assumed.

The Markov process of Fig. 6 is governed by the following transition probabilities:

$$\begin{aligned}&P_{i,k|i,k+1} = P_d, \quad k\in [0,W_i-2], i\in [0,m] \nonumber \\&P_{i,k|i,k} =1- P_d, \quad k\in [1,W_i-1], i\in [0,m] \nonumber \\&P_{0,k|i,0}=q(1-P_{eq})/W_0, \quad k\in [0,W_0-1], i\in [0,m-1] \nonumber \\&P_{0,k|m,0}=q/W_0 , \quad k\in [0,W_0-1] \nonumber \\&P_{i,k|i-1,0}=P_{eq}/W_i, \quad k\in [0,W_i-1], i\in [1,m] \nonumber \\&P_{I|i,0}=(1-q)(1-P_{eq}), \quad i\in [0,m-1] \nonumber \\&P_{I|m,0}=1-q, \nonumber \\&P_{0,k|I}=q/W_0, \quad k\in [0,W_0-1] \nonumber \\&P_{I|I}=1-q. \end{aligned}$$
(15)

The first equation in Eq. 15 states that, at the beginning of each slot time, the back-off time is decremented if the channel was sensed free. If the channel was not sensed free, the state will stay in it according to the second equation.The third equation accounts for the fact that after a successful transmission, a new packet transmission starts with back-off stage 0 with probability \(q\), in case there is a new packet in the buffer to be transmitted. The fourth equation deals with successful or unsuccessful transmissions in the last stage and the need to reschedule a new contention stage, if there is a new packet in the buffer to transmit. The fifth equation depicts unsuccessful transmissions and the need to reschedule a new contention stage. The sixth equation deals with the practical situation in which after a successful transmission, the buffer of the station is empty, and as a consequence, the station transits in the idle state \(I\) waiting for a new packet arrival. The seventh equation is for the last stage, regardless of whether the packet is being transmitted successfully or not. The eighth equation models the situation in which a new packet arrives in the node buffer and a new back-off procedure is scheduled. Finally, the ninth equation models the situation in which there are no packets to be transmitted and the station is in the idle state.

The next line of pursuit consists of finding a solution to the stationary distribution: \(\pi _{i,k}=\lim _{t\rightarrow \infty }P[s(t)=i,\pi (t) =k], \forall k\in [0,W_i-1], \forall i\in [0,m]\), that is, the probability of a station occupying a given state at any discrete time slot.

Proposition 1

\(\tau \), the probability that a station starts a transmission in a randomly chosen time slot can be expressed as:

$$\begin{aligned} \tau&= \pi _{0,0}\frac{1-P_{eq}^{m+1}}{1-P_{eq}} \nonumber \\&= \frac{2qP_d(1-P_{eq}^{m+1})(1-2P_{eq})}{2P_d(1-q)(1-P_{eq})(1-2P_{eq})+qW(1-P_{eq})(1-(2P_{eq})^{m+1})+q(1-2P_{eq})(2P_d-1)(1-P_{eq}^{m+1})}.\nonumber \\ \end{aligned}$$
(16)

We will present how to calculate this proposition in Appendix 5.

5.2 Channel State Markov Chain

To compute the probability of \(P_f\), we consider the channel state Markov chain in Fig. 7. In this figure, \(S\), \(C\), and \(I\) stand for the state of the channel having a successful transmission, a Collision, or being Idle while the considered node is backing off. In practice, a back-off state can be entered from either a transmission state or from a previous back-off state. The \(p_{ei}\) parameter presents the probability that the transmitting node finds the channel idle. Thus \(p_{ei}\) can be calculated as \(p_{ei} = P_{idle}\) and \(P_{idle} = (1-\tau _R)\gamma _1\gamma _2\). Similarly, \(p_{es}\) and \(p_{ec}\) can be expressed for relay node and user group \(v\) as follows:

$$\begin{aligned} p_{es-v}&= (n_v-1)\tau _v(1-\tau _v)^{n_v-2}(1-\tau _R), \nonumber \\ p_{es-R}&= {\left\{ \begin{array}{ll} \gamma _1\gamma _2, &{}\quad {\hbox {if}\, \hbox {NC}\, \hbox {used},} \\ \gamma _1+ \gamma _2 ,&{}\quad {\hbox {if}\, \hbox {NC}\, \hbox {not}\, \hbox {used}}\; \end{array}\right. }, \nonumber \\ p_{ec-v}&= 1- p_{ei-v}-p_{es-v} \nonumber \\ p_{ec-R}&= 1- p_{ei-R}-p_{es-R}. \end{aligned}$$
(17)

As mentioned in Fig. 7, \(P_d= p_e.P_{I}\) where \(p_e = 1\).

Fig. 7
figure 7

Channel state Markov chain

Full size image

Given that the number of colliding nodes is \(n_1+n_2\), the probability that no colliding node selects zero as the new back-off counter is \(\left( 1-\frac{1}{\overline{CW}}\right) ^{n_1+n_2}\). \(p_{ss}\) represents the probability that the channel stays in the \(S\) state, the probability that the channel moves from \(S\) to \(C\) is \(p_{sc}\), the probability that the channel can be Idle after \(S\) state is \(p_{si}\) and they are expressed for relay node and user group \(v\) as (they are equal):

$$\begin{aligned} p_{ss}&= (n_1+n_2)\left( \frac{1}{\overline{CW}}\right) \left( 1-\frac{1}{\overline{CW}}\right) ^{n_1+n_2-1}, \nonumber \\ p_{sc}&= \sum _{n=2}^{n_1+n_2}\left( \begin{array}{c} n_1+n_2 \\ n \end{array} \right) \left( \frac{1}{\overline{CW}}\right) ^n\left( 1-\frac{1}{\overline{CW}}\right) ^{n_1+n_2-n}, \nonumber \\ p_{si}&= 1- p_{sc}-p_{ss}. \end{aligned}$$
(18)

where \(\overline{CW}\) is the average back-off window size over all stages and can be expressed as:

$$\begin{aligned} \overline{CW} = \sum _{i=0}^m\frac{(1-P_{Coll})P_{Coll}^iW_i}{1-P_{drop}}, \end{aligned}$$
(19)

and \(P_{drop}\) is the probability that the packet is dropped after \(m+1\) transmissions and can be computed as \(P_{drop} = P_{Coll}^{m + 1}\). \(P_{Coll}\) can be computed from Eqs. 4 and 9 for relay node and \(P_{Coll} = \tau _v(1-(1-\tau _v)^{n_v-1}(1-\tau _R))\) for users group \(v\).

Similarly, \(p_{cs}\), \(p_{ci}\) and \(p_{cc}\) are given as:

$$\begin{aligned} p_{cs}&= (n_1+n_2)\left( \frac{1}{\overline{CW}}\right) \left( 1-\frac{1}{\overline{CW}}\right) ^{n_1+n_2-1}, \nonumber \\ p_{ci}&= \left( 1-\frac{1}{\overline{CW}}\right) ^{n_1+n_2}, \nonumber \\ p_{cc}&= 1- p_{cs}-p_{ci}. \end{aligned}$$
(20)

Knowing all transition probabilities, to obtain the steady state probabilities for the channel state vector \(V = [P_I P_C P_S]\), we solve \(VP = V\), where transition matrix \(P\) of the Channel State Markov Chain can be calculated as:

$$\begin{aligned} P = \left( \begin{array}{c c c} p_{ei} &{}p_{es}&{} p_{ec} \\ p_{ci} &{}p_{cs}&{} p_{cc} \\ p_{si} &{}p_{ss}&{} p_{sc} \end{array} \right) . \end{aligned}$$
(21)

Knowing the time durations for ACK frames, ACK timeout, DIFS, SIFS, EIFS, RTS, CTS, CTS timeout, \(\sigma \), average packet payload length (E[P]) and PHY and MAC headers duration (H), and propagation delay \(\delta \), all of the required parameters can be computed in the rest of the paper.

When a packet is successfully received by a node we can consider some attempts to transmit it. For any subsequent success at the \(i + 1\)st attempt preceded by \(i\) collisions, the channel access time \(T^{(i)}\) is calculated as follows:

$$\begin{aligned} T^{(i)} = T_{suce}+i\overline{T_{coll}}+\sum _{j=0}^i\overline{W_j}\mathcal {D}, \end{aligned}$$
(22)

where \(\overline{W_j}\) is the average number of back-off slots selected at stage \(j\) and computed as \(\overline{W_j}= \frac{W_j-1}{2}\), \(\mathcal {D}\) is the average slot duration that the considered node should wait before decrementing its back-off counter, \(\overline{T_{coll}}\) and \(T_{suce}\) as follows:

$$\begin{aligned} \overline{T_{coll}}&= \! {\left\{ \begin{array}{ll}\! H + E[P] + \delta + DIFS, &{} \quad \text {basic mechanism,} \\ RTS + \delta + DIFS, &{}\quad \text {RTS/CTS mechanism}\; \end{array}\right. }\end{aligned}$$
(23)
$$\begin{aligned} T_{suce}&= \! {\left\{ \begin{array}{ll}\! H + E[P] + 2\delta + SIFS + ACK + DIFS, &{}\quad \text {basic mechanism,} \\ RTS + 4\delta {+} 3SIFS {+} CTS {+} H {+} E[P] {+} ACK {+} DIFS, &{}\quad \text {RTS/CTS mechanism}\; \end{array}\right. } \end{aligned}$$
(24)

Let us define \(T\) as one hop delay for the non-dropped packet and it can generally be written as:

$$\begin{aligned} T = \frac{1}{1-P_{drop}}\sum _{i=0}^mP_{Suce}^{(i)}\bigg [ T_{suce}+i\overline{T_{coll}}+\sum _{j=0}^i\overline{W_j}\mathcal {D}\bigg ], \end{aligned}$$
(25)

where \(P_{Suce}^{(i)} = (1-P_{CollR{-}v{-}nonNC})P_{CollR{-}v{-}nonNC}^i\) and \(P_{Suce}^{(i)} = (1-P_{CollR{-}NC}) P_{CollR{-}NC}^i\) for relay node \(\mathbf {R}\) which can be computed as Eqs. 4 and 9, respectively and \(P_{Suce}^{(i)} = (1-P_{Collv})P_{Collv}^i\) for user group \(v\) which can be computed by \(P_{Collv} = \tau _v(1-(1-\tau _R)(1-\tau _v)^{n_v-1})\).

Proposition 2

The average slot duration can be computed as:

$$\begin{aligned} \mathcal {D} = (1-\tau )D_1 + \tau D_2, \end{aligned}$$
(26)

where \(\tau \) is the transmission probability for a node in the network.

The Appendix 6 will show how to compute this proposition.

5.3 System Design and Performance Parameters

The transmission probability \(\tau _R\), \(\theta \) at relay node \(\mathbf {R}\), \(n_v\) and \(W\) at user nodes in group \(v\) are system design parameters to improve the performance of single-relay multi-user wireless networks using CSMA/CA, with or without network coding protocols and MPR. This paper clarifies the relationship between such system design parameters and performance parameters such as delay packet \(T_v\) for each user node group \(v\) and throughput \(S\). The channel access delay \(T_v\) is defined as the average time from the packet becoming the head of the queue from user group \(v\) until the acknowledgment frame is received from user group \(\bar{v}\).

6 Performance Analysis

6.1 Delay Analysis

This subsection analyzes the accurate delay, with and without NC protocols, for any single-relay multi-user wireless network. In delay analysis, we focus on the traffic control to achieve the fairness between the delay of user node group \(v\) for \(v\in \{1,2\}\). The traffic control to achieve per-group fairness can be extended to the case of per-node fairness as discussed later.

In this section, we focus on the analysis of delay for the RTS/CTS access mechanism. For delay analysis, we derive its components. The first duration is the time that the user in group \(v\) sends a packet to the relay node and receives the acknowledgment from relay node. The second part is the waiting time in the queue of the relay node and it depends on the network coding strategy. The last duration is the time that the relay node sends the received packet at the head of its queue and receives the acknowledgment.

6.1.1 Packet Delay Without Network Coding and \(m_{MPR}=2\)

If the output queue at relay node \(\mathbf {R}\) is saturated, the steady-state probabilities of the numbers of packets \(v\) in the output queue at relay node \(\mathbf {R}\) are as follows:

$$\begin{aligned} N_R = \sum _{n=0}^\infty nP(n) = \sum _{n=1}^\infty \frac{n(\rho _1+\rho _2)^n}{1-\tau _R}P(0) = \frac{(\rho _1+\rho _2)}{(1-\tau _R)(1-\rho _1-\rho _2)^2}P(0). \end{aligned}$$
(27)

In this situation, if an innovative packet enters the buffer it has to wait a duration equal to: \(T_{QV} = N_R.T_{R-\bar{v}}\), where \(T_{R-\bar{v}}\) can be calculated from 21. After that time the packet is in the head of the buffer. The average time which one packet takes to get from group \(v\) to group \(\bar{v}\) is expressed as:

$$\begin{aligned} T_v = T_{v-R} + T_{R-\bar{v}} + T_{QV} = T_{v-R} + T_{R-\bar{v}}(1+N_R), \end{aligned}$$
(28)

where \(T_{v-R}\) can be computed from 21.

6.1.2 Packet Delay with Network Coding and \(m_{MPR}=2\)

The average number of packets staying in the virtual queue \(v\) at relay node \(\mathbf {R}\) in the steady state is expressed as:

$$\begin{aligned} N_{R-v} = \sum _{n=0}^\infty nP_v(n) = \frac{\rho _v(1-\tau _R+\tau _RP(0,0))}{(1-\tau _R)(1-\rho _v)}. \end{aligned}$$
(29)

The average time that one packet takes from group \(v\) to group \(\bar{v}\) can be computed by summation on all delays and is expressed as:

$$\begin{aligned} T_v = T_{v-R} + T_{R-\bar{v}} + N_{R-v}. T_{R-\bar{v}}= T_{v-R} + T_{R-\bar{v}}(1+N_{R-v}). \end{aligned}$$
(30)

6.2 Rough Throughput Analysis

In this subsection, we compute the rough throughput of the network in order to trade off between delay and throughput. We are now ready to calculate the normalized rough throughput \(S\) as:

$$\begin{aligned} S=\frac{E[\text {payload bits successfully transmitted in a slot}]}{E[\text {slot length}]}. \end{aligned}$$
(31)

6.2.1 Rough Throughput Without Network Coding and \(m_{MPR}=2\)

We can calculate the rough throughput in non NC systems using Eq. 28 as follows:

$$\begin{aligned} S_{nonNC} = \frac{(n_1+n_2)E[P]}{n_1T_{1-nonNC}+n_2T_{2-nonNC}}, \end{aligned}$$
(32)

where \(E[P]\) is the length of payload and \(n_v\) is the number of users in group \(v\).

6.2.2 Rough Throughput with Network Coding and \(m_{MPR}=2\)

To calculate the rough throughput in the NC system, we can use Eq. 30 and it is expressed as:

$$\begin{aligned} S_{NC} = \frac{(n_1+n_2)E[P]}{n_1T_{1-NC}+n_2T_{2-NC}}. \end{aligned}$$
(33)

7 Model Validation and Simulation Results

This section focuses on simulation results for validating the theoretical models and derivations presented in the previous sections. We have developed a C++ simulator modeling both the DCF protocol details in IEEE 802.11b and the back-off procedures of a specific number of independent transmitting stations. The simulator is designed to implement the main tasks accomplished at both the MAC and PHY layers of a wireless network. The simulator considers an Infrastructure Basic Service Set (BSS) with a relay node and a certain number of stations which communicates only with the access point as a relay node.

For the sake of simplicity, inside each station there are only three fundamental working levels: traffic model generator, MAC and PHY layers. Traffic is generated by \(q\) parameter. Moreover, the MAC layer is managed by a state machine which follows the main directives specified in the standard [6], namely waiting times (DIFS, SIFS, EIFS), post-back-off, back-off, basic and RTS/CTS access mode. The typical MAC layer parameters for IEEE 802.11b are given in Table 2 [6, 7]. The system values are those specified for the frequency hopping spread spectrum (FHSS) PHY layer. We varied the extended range of nodes in our extension simulation which are \(1\le n_1, n_2 \le 100\), but to prove our analysis, we considered one scenario in this paper. Similar results are seen in all ranges but lower ranges show the most returns. The simulator was run 1,000 times and the results were averaged. Each simulation is stopped when 60,000 packets have been processed. The number of user nodes in group 1 is \(n_1 = 10\) and the number of user nodes in group 2 is \(n_2 = 6\). We present the simulated and analytical results of RTS/CTS access mechanism in this section for \(m_{MPR}=1\) and \(m_{MPR}=2\) with and without NC.

Table 2 FHSS system parameters and additional parameters to obtain numerical results [7]
Full size table

We mention the RTS/CTS access mechanism for non-network coding and network coding with nonNCRTS and NCRTS, respectively. As mentioned, using the forwarding factor \(\theta \) is one of our contributions in this paper. We explored the effect of \(\theta \) on network performance.

We obtained the average delay to transmit a packet from one user in group \(v\) to group \(\bar{v}\) through the relay node for non NC and NC systems from simulations and using Eqs. 28 and 30, respectively. We show the comparison of results from simulation and analysis in Fig. 8a, b for \(m_{MPR}=1,2\). The curves are obtained from the non-saturated group delay and from Monte Carlo simulations when the packet \(v\) is randomly transmitted from a user node in group \(v\) with probability \(\tau _v\) in a slot. The saturation case occurs when \(q=1\). The value of \(\theta \) is equal to \(0.25\). The figures show a good agreement between analytical and numerical results, confirming that \(q\) can largely decrease the delay of users.

Fig. 8
figure 8

Average channel access delay (\(T_v\)) for RTS/CTS access mechanism. a Theoretical and simulated delay (\(T_1\)) as a function of \(q\) with and without network coding. b Theoretical and simulated delay (\(T_2\)) as a function of \(q\) with and without network coding. c Simulated average channel access delay (\(T_v\)) as a function of \(\theta \) with \(q_1 = 1\) and \(q_2 = 0.5\) and \(m_{MPR} = 1, 2\)

Full size image

To investigate the dependency of the delay from \(\theta \), we have reported in Fig. 8c the average channel access delay versus the value for \(\theta \). In this figure, we show RTS/CTS access mechanism with \(q_1 = 1\) and \(q_2 = 0.5\) (saturation and unsaturation cases) with \(m_{MPR}=1, 2\). When \(\theta \) goes up, the saturation and unsaturation delay increase. Because the number of users in group 1 is more than group 2, its delay is greater than group 2. With the introduction of a waiting interval before transmission by the forwarding factor, the relay node has the chance of collecting other innovative packets and sending out richer combinations. Moreover, the reduction of the number of transmissions and the characteristic of the forwarding factor help in decreasing the collision probability at the MAC layer. When \(\theta \) was close to \(1\), the relay node does not wait long enough to receive the new packet and decides to transmit the packet in its buffer immediately. The collision probability will then increase and this leads to high delay as illustrated in Fig. 8c. As seen in Fig. 8c, when relay node uses MPR with \(m_{MPR}=2\) the collision probability reduces and it leads to reducing the delay of the network.

One of the parameters that is very important to evaluate a network is Packet Loss Ratio \((PLR)\). This parameter is equal to the number of unsuccessful packets to all transmitted packets from group \(v\). If this value is very low, the performance of the network is high. We depict the complement of \(PLR\) (1-\(PLR\)) versus \(q\) for group 1 for RTS/CTS access mechanism with and without network coding and \(m_{MPR}=1, 2\) in Fig. 9a. As shown in Fig. 9a, when \(q\) is very close to 1 (saturation case), the value of \(PLR\) is very high so the performance of this network is very low. When this network uses the network coding in the relay node, the value of \(PLR\) is very low and in MPR scenario it is lower than when the relay node does not use MPR. The nonNCRTS case with \(m_{MPR} =1\) is the worst case in this figure.

Fig. 9
figure 9

Packet loss ratio (\(PLR\)) for RTS/CTS access mechanisms. a Packet loss ratio (\(PLR\)) as a function of \(q\) with \(\theta = 0.25\) for group 1, with and without network coding. b Packet loss ratio (\(PLR\)) as a function of \(\theta \) with \(q_1 = 1\) and \(q_2 = 0.5\) for group 1

Full size image

Figure 9b shows the dependence of \(PLR\) to \(\theta \) for \(q_1 = 1\) and \(q_2 = 0.5\) for RTS/CTS access mechanism for group 1 with \(m_{MPR} =1, 2\). For example, a low value of \(\theta \) gives excellent performance in the case of \(q_2\) and \(m_{MPR}=2\). Large values of \(\theta \) may, in fact, limit the performance of the network and so the value of \(PLR\) will increase for saturated and non-saturated scenarios. As expected, MPR scenario with \(m_{MPR}=2\) can improve PLR and by decreasing the value of \(\theta \) and \(q\), PLR will reduce.

Owing to the model’s key assumption of independence at each retransmission, the average number of transmissions that each station must perform in order to successfully complete a packet transmission is shown in Fig. 10a, b for RTS/CTS access mechanism with \(m_{MPR} =1, 2\). Figure 10a, b show that the number of transmissions per packet significantly increases as \(q\) increases and as \(\theta \) increases. As shown in Fig. 10a, network coding leads to a reduction in the average number of transmissions per packet for users and the network without network coding and \(m_{MPR}=1\) is the worst case in this figure. Figure 10b also has the same behavior for the average number of transmissions per packet. In this figure, by increasing \(\theta \) the average number of transmissions for saturation case (\(q_1=1\)) and \(m_{MPR} =1\) significantly increases.

Fig. 10
figure 10

Average number of transmissions per packet with \(m_{MPR}=1, 2\) for group 1. a Average number of transmissions per packet as a function of \(q\) with and without network coding with \(\theta = 0.25\). b Average number of transmissions per packet as a function of \(\theta \) with \(q_1 = 1\), \(q_2 = 0.5\)

Full size image

We ran extensive simulations using our simulator over a wide range of contention window sizes. Due to space limitations, we show in detail the numerical validation results for the RTS/CTS access mechanism, which show the average channel access delay. Figure 11 show that the dependence of the delay (\(T_{v}\)) from the maximum number of \(m\) of back-off stages or \(W_{min}\) is marginal. The figures report the cases of both NC and nonNCRTS schemes, with \(CW_{max} = 1{,}024\), \(W_{min}\) from \(8\) to \(512\), \(q_1 = 1\), \(q_2 = 0.5\), \(m_{MPR}=1, 2\) and \(\theta = 0.25\) for group 1. We see that the choice of \(W_{min}\) practically affects the system delay, as long as it is lower than 64. It is observed that when we use network coding for the RTS/CTS access mechanism and MPR scenario, the average channel access delay strongly depends on \(W_{min}\). Figure 11a reports that the average channel access delay with MPR and network coding scenarios is lower than the delay of the network without network coding and MPR scenarios (as shown in Fig. 11b). Thus, an appropriate \(W_{min}\) can be chosen to balance between delay and throughput of the network. This can be considered as an important parameter of a network.

Fig. 11
figure 11

Average channel access delay (\(T_v\)) for RTS/CTS access mechanism as a function of \(W_{min}\) for \(q_1 = 1\), \(q_2 = 0.5\), with and without network coding and \(m_{MPR}=1, 2\). a Average channel access delay \(T_1\) (group 1). b Average channel access delay \(T_2\) (group 2)

Full size image

We depict simulated throughput and analytical rough throughput from Eqs. 32 and 33 for RTS/CTS access mechanism in Fig. 12 with and without NC protocols and \(m_{MPR}=1, 2\). As seen in Fig. 12a, the rough throughput is not exact and it is slightly different from simulation results. This event is due to disregarding some states of analysis. Figure 12b shows simulated throughput of the network as a function of \(\theta \). As expected, the achieved throughput in the non-saturated RTS/CTS access mechanism with \(m_{MPR}=2\) is the best due to the release hidden node problem. Also in this figure, throughput significantly reduces as \(\theta \) increases.

Fig. 12
figure 12

Throughput of network for RTS/CTS mechanism and \(m_{MPR}=1, 2\). a Simulated throughput and rough throughput as a function of \(q\) with \(\theta =0.25\). b Simulated throughput as a function of \(\theta \) with \(q_1 = 1\) and \(q_2 = 0.5\)

Full size image

We define a new parameter to validate the network throughput as \(\epsilon \). This parameter is the ratio of the number of transmitted NC-packets to all transmitted packets from relay node to group nodes. Figure 13 shows that the \(\epsilon \) of the RTS/CTS access mechanism highly depends on \(\theta \) for \(q_1 = 1\) and \(q_2 = 0.5\) with \(m_{MPR} =1, 2\). For example, a low value of \(\theta \) gives excellent performance in the case of \(q_1\) and MPR scenario. Large values of \(\theta \) may, in fact, limit the throughput of the network and so the value of \(\epsilon \) will decrease for RTS/CTS access mechanism. This figure has a different behavior in low and high values of \(\theta \). For example, \(\theta \) lower than \(0.43\) leads to a high value of \(\epsilon \) for the RTS/CTS access mechanism for \(q_1\) with \(m_{MPR}= 2\) and at greater values the condition changes. This case also occurs for \(m_{MPR}= 1\). This is the reason stated above regarding the network throughput.

Fig. 13
figure 13

The value of \(\epsilon \) for RTS/CTS access mechanism as a function of \(\theta \) with \(q_1 = 1\) and \(q_2 = 0.5\) and with \(m_{MPR}=1, 2\)

Full size image

It should be emphasized that the extension simulations have a good agreement with analytical results, for example simulated results in Figs. 8c, 9a, 9b, 10, 11 and 12 are similar to analytical results. Also, simulation results show that the delay increases and the throughput decreases by increasing the number of stations in groups \(1\) and \(2\).

8 Conclusion and Future Works

In this paper, we have presented an analytical model for MPR node in two-way relay wireless networks over IEEE 802.11 protocol with and without NC that can accurately predict the performance for a wide range of scenario parameters in single relay multiuser wireless networks. We started by developing analytical models of the network performance with network coding (NCRTS) for single-relay multi-user wireless networks with MPR scenario and bidirectional data flows. The analytical models involved the effects of queue saturation and non-saturation at the relay node. Finally, we succeeded in accurately modeling the performance of IEEE 802.11 under the saturation and non-saturation assumptions using a Markov chain during back-off countdown.

To validate the accuracy of our proposed models, we extensively tested the estimation performance of the models for a wide range of \(q\), the forwarding factor \(\theta \), \(\epsilon \), contention window sizes, and traffic loads. Compared to systems without network coding and MPR scenarios, substantial improvements in packet delay, throughput, PLR and average number of transmission per packet are obtained with network coding and MPR scenarios. As an example, packet delay improves up to \(40\,\%\) and throughput improves up to \(45\,\%\) in terms of \(\theta \) (forwarding factor) in the MPR scenario with network coding. Our experimental results show that these models lead to improvements in all system features. As a future work we will clarify the effect of channel on the total throughput and delay in the NCRTS protocol in the single relay multi user wireless networks.