Secrecy Rate of Two-Hop AF Relaying Networks with an Untrusted Relay

Abstract

Two cooperative communication protocols, two-way and one-way half-duplex relayings, are investigated and then compared in the amplify-and-forward (AF) mode. The relay is assumed to play the roles of eavesdropper and relay (i.e., an untrusted relay). With a fair power constraint at each node, the secrecy rate of the one-way relaying protocol is proved to be zero strictly. For the two-way relaying protocol, the signal-to-noise ratio (SNR) threshold is derived, above which the secrecy rate is non-zero. Defining a parameter, namely mistrust level, and non-zero secrecy rate can be achieved for the one-way relaying protocol in certain range of the mistrust level at high SNR. With a fair total power constraint, no matter how unreliable the relay is, the two-way AF half-duplex relaying protocol is proved to be a better choice under high SNR.

1 Introduction

The broadcast nature of wireless communication has attracted more and more attention about the privacy and security issues. Wyner indicated that perfect secure communication is possible without relying on secret keys based on physical layer security [1]. As an extension of Wyner’s theory, security analyses on broadcast channel [2] and Gaussian wiretap channel [3] were performed respectively. Secure cooperative relaying as an excellent communication technique in the amplify-and-forward mode was also analyzed in detail [4]. The symmetric Gaussian interference channel to enhance secrecy rates in cooperative manner was investigated [5].

With better spectral efficiency, two-way relaying protocols based on amplify-and-forward have been investigated from a security point of view [6–8]. At the aspect of intensive beamforming, i.e., optimal beamforming, null-space beamforming, and artificial noise beamforming were proposed based on a two-way relay network model with an eavesdropper [8]. In the large-scale relaying field, opportunity relay selection scheme depending on the global instantaneous channels for cooperative networks with secrecy constraints was introduced [9]. Although the two-way relaying protocol can achieve a higher rate than one-way relaying protocol owing to the bidirectional nature [10, 11], its security needs more discussions. Security of communication systems with untrusted relays was examined [7, 12], where it was assured that an untrusted relay is much better than an eavesdropper. Further, an innovative high trust model was proposed [13]. Although cooperative networks with untrusted relays have received much attention by far, the secrecy rate comparison between the one- and two-way untrusted relaying protocols has not yet been investigated.

Fig. 1

Two-hop relay networks: a system model for one-way relay communications; b system model for two-way relay communications

In this paper, a two-hop AF half-duplex relaying model is proposed, where the relay is captured by the eavesdropper and disguised as a legitimate relay. For one-way relaying protocol, the secrecy rate is proved to be strictly zero with equal power constraint at each node. After introducing the mistrust level, non-zero secrecy rate can be achieved for one-way relaying protocol, and the range of the mistrust level will be derived at high SNR with non-zero secrecy rate constraint. For two-way relaying protocol, the SNR threshold is derived, above which the sum secrecy rate is non-zero. With a fair total power constraint, the two-way relaying protocol is proved to outperform the one-way relaying protocol whatever the mistrust level is under high SNR.

2 System Model

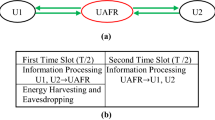
Suppose all nodes receive equal additive white Gaussian noise power $\sigma ^{2}$. As shown in Fig. 1, the channel coefficient $h_i$ is modeled as a zero-mean, independent, circularly symmetric complex Gaussian random variable with variance $d_i^{-c}$, where $d_i$ is the Euclidean distance from $S_i$ to $R, i=1,2, c$ is the channel fading exponent. Let $\gamma _i =\left| {h_i } \right| ^{2}$ for link $S_i \rightarrow R$. Suppose the channels are reciprocal. $P_1$ and $P_2$ denote the transmit powers of the nodes in one- and two-way relaying protocols, respectively, i.e., all nodes in a relaying protocol have the same transmit power.

For the one-way relaying network shown in Fig. 1a, source $S_1$ transmits information symbol $s_1^\#$ to the relay with expectation $\hbox {E}\left\{ {\left| {s_1^\# } \right| ^{2}} \right\} =1$ in the first phase. The relay receives

$$\begin{aligned} r^{\# }=\sqrt{P_1 }h_1 s_1^\# +n^{\# } \end{aligned}$$

(1)

where $n^{\# }$ is the noise received by the relay. In the second phase, the relay amplifies and forwards the received signal to the destination. The relay broadcasts the signal

$$\begin{aligned} x_R^\# =\rho _1 r^{\# } \end{aligned}$$

(2)

where $\rho _1 =\sqrt{{P_1 }/{\left( {\sigma ^{2}+P_1 \gamma _1 } \right) }}$ is the power normalization factor. The destination receives

$$\begin{aligned} y^{\# }=\rho _1 \sqrt{P_1 }h_1 h_2 s_1^\# +\rho _1 h_2 n^{\# }+v^{\#} \end{aligned}$$

(3)

where $v^{\# }$ is the noise received by the destination.

For the two-way relaying network shown in Fig. 1b, the two sources send information symbols $s_1^*$ and $s_2^*$, respectively, in the first phase. The relay receives

$$\begin{aligned} r^{*}=\sqrt{P_2 }h_1 s_1^*+\sqrt{P_2 }h_2 s_2^*+n^{*} \end{aligned}$$

(4)

where $n^{*}$ denotes the noise received by the relay. In the second phase, the relay broadcasts signal

$$\begin{aligned} x_R^*=\rho _2 r^{*} \end{aligned}$$

(5)

where $\rho _2 =\sqrt{{P_2 }/{\left( {\gamma _1 P_2 +\gamma _2 P_2 +\sigma ^{2}} \right) }}$ is the power normalization factor. Since $S_i$ knows $s_i^*(i=1,2)$, it can cancel its own data. Therefore, $S_1$ and $S_2$ get

$$\begin{aligned}&y_1^*=\rho _2 \sqrt{P_2 }h_1 h_2 s_2^*+\rho _2 h_1 n^{*}+v_1^*\end{aligned}$$

(6)

$$\begin{aligned}&y_2^*=\rho _2 \sqrt{P_2 }h_1 h_2 s_1^*+\rho _2 h_2 n^{*}+v_2^*\end{aligned}$$

(7)

where $v_1^*$ and $v_2^*$ denote the noise received by $S_1$ and $S_2$, respectively.

3 Security of Two-Hop Relay Networks

3.1 Secrecy Rate of One-Way AF Relaying Protocol

With equal power constraint at each node, the secrecy rate of one-way untrusted relaying protocol is

$$\begin{aligned} R_1^s =\left[ {\frac{1}{2}\log _2 \left( {R_{S_1 }^\# } \right) -\frac{1}{2}\log _2 \left( {R_{E_1 }^\# } \right) } \right] ^{+} \end{aligned}$$

(8)

Where $\left[ x \right] ^{+}=\max \left\{ {0,x} \right\} ,R_{S_1 }^\# =1+\frac{\rho _1^2 \gamma _1 \gamma _2 P_1 }{\rho _1^2 \gamma _2 \sigma ^{2}+\sigma ^{2}}$, and $R_{E_1 }^\# =1+\frac{P_1 \gamma _1 }{\sigma ^{2}}$.

Theorem 1

With equal power constraint at each node, the secrecy rate $R_1^s$ of one-way AF half-duplex untrusted relaying protocol is strictly zero for all ${P_1 }/{\sigma ^{2}}$.

Proof

$R_1^s =0$ can be converted to $R_{S_1 }^\# -R_{E_1 }^\# \le 0$ due to the monotonicity of logarithm function. From (8), one can get

$$\begin{aligned} R_{S_1 }^\# -R_{E_1 }^\#&= \frac{\rho _1^2 \gamma _1 \gamma _2 P_1 }{\rho _1^2 \gamma _2 \sigma ^{2}+\sigma ^{2}}-\frac{P_1 \gamma _1 }{\sigma ^{2}}\nonumber \\&= \frac{-\left( {\frac{P_1 }{\sigma ^{2}}} \right) ^{2}\gamma _2 ^{2}-\left( {\frac{P_1 }{\sigma ^{2}}} \right) \gamma _2 }{\frac{P_1 }{\sigma ^{2}}\left( {\gamma _1 +\gamma _2 } \right) +1} \end{aligned}$$

(9)

The numerator of Eq. (9) is always negative, and the corresponding denominator is positive, therefore the secrecy rate is strictly zero for all ${P_1 }/{\sigma ^{2}}$.

The assumption of theorem 1 is that the relay is an untrusted relay. Assuming there is a mistrust level $T \left( {0\le T\le 1} \right)$. If $T=0$, the relay is regarded as a legitimate relay, while if $T=1$, the relay is a complete untrusted relay. That’s to say, if $n$ subchannels are eavesdropped in total $N$ for orthogonal frequency division multiplexing (OFDM) link $S_i \rightarrow R$, and $T=n/N$ can be regarded as the mistrust level. Thus, the ergodic secrecy rate of one-way AF relaying protocol is

$$\begin{aligned} R_1^{s^{\prime }} =\left[ {\frac{1}{2}\log _2 \left( {R_{S_1 }^\# } \right) -\frac{1}{2}T\log _2 \left( {R_{E_1 }^\# } \right) } \right] ^{+} \end{aligned}$$

(10)

$\square$

Proposition

Under high SNR, the secrecy rate $R_1^{s^{\prime }}$ of the one-way AF half-duplex relaying protocol is non-zero when $0\le T<1+\frac{\log _2 \gamma _2 -\log _2 \left( {\gamma _1 +\gamma _2 } \right) }{\log _2 {P_1 \gamma _1 }/{\sigma ^{2}}}$.

Proof

Under high SNR, $\rho _1^2 \approx 1/{\gamma _1 }$, thus $R_1^{s^{\prime }} >0$ can be transformed to

$$\begin{aligned} T&< \frac{\log _2 \left( {R_{S_1 }^\# } \right) }{\log _2 \left( {R_{E_1 }^\# } \right) }=\frac{\log _2 \left( {1+\frac{P_1 }{\sigma ^{2}}\frac{\gamma _1 \gamma _2 }{\gamma _1 +\gamma _2 }} \right) }{\log _2 \left( {1+\frac{P_1 }{\sigma ^{2}}\gamma _1 } \right) } \nonumber \\&\approx \frac{\log _2 \frac{P_1 }{\sigma ^{2}}\frac{\gamma _1 \gamma _2 }{\gamma _1 +\gamma _2 }}{\log _2 \frac{P_1 }{\sigma ^{2}}\gamma _1 }=1+\frac{\log _2 \gamma _2 -\log _2 \left( {\gamma _1 +\gamma _2 } \right) }{\log _2 {\gamma _1 P_1 }/{\sigma ^{2}}} \end{aligned}$$

(11)

From Eq. (11), the upper bound of $T$ increases as ${P_1 }/{\sigma ^{2}}$ increases, i.e., in practice, OFDM communication systems can bear more subchannels eavesdropped with non-zero secrecy rate constraint under high SNR. Specially, if $\gamma _1 =\gamma _2 =\gamma$, the upper bound can be further simplified to $1-\log _2^{-1} \frac{P_1 }{\sigma ^{2}}\gamma$. $\square$

3.2 Secrecy Rate of Two-Way AF Relaying Protocol

With equal power constraint at each node, the sum secrecy rate of two sources in the two-way AF half-duplex relaying protocol is

$$\begin{aligned} R_2^s =\sum _{i=1,2} {\left[ {\frac{1}{2}\left( {\log _2 \left( {R_{S_i }^{*} } \right) -\log _2 \left( {R_{E_i }^{*} } \right) } \right) } \right] ^{+}} \end{aligned}$$

(12)

where $R_{S_i }^{*} =1+\frac{\rho _2^2 \gamma _1 \gamma _2 P_2 }{\rho _2^2 \gamma _j \sigma ^{2}+\sigma ^{2}}$, and $R_{E_i }^{*} =1+\frac{\gamma _i P_2 }{\gamma _j P_2 +\sigma ^{2}},\quad i,j=1,2$.

Theorem 2

With equal power constraint at each node, the sum secrecy rate of two sources in the two-way AF half-duplex untrusted relaying protocol is non-zero when ${P_2 }/{\sigma ^{2}}>\min \left\{ {\Gamma _1 ,\Gamma _2 } \right\}$, where $\Gamma _1$ and $\Gamma _2$ will be given in the proof section.

Proof

Let $R_{S_1 }^s \!=\!\left[ {\frac{1}{2}\left( {\log _2 \left( {R_{S_1 }^{*} } \right) \!-\!\log _2 \left( {R_{E_1 }^{*} } \right) } \right) } \right] ^{\!+\!}, R_{S_2 }^s \!=\!\left[ {\frac{1}{2}\left( {\log _2 \left( {R_{S_2 }^{*} } \right) \!-\!\log _2 \left( {R_{E_2 }^{*} } \right) } \right) } \right] ^{\!+\!}$. Equation (12) is equal to

$$\begin{aligned} R_2^s =R_{S_1 }^s +R_{S_2 }^s \end{aligned}$$

(13)

To make $R_2^s >0$, there exists one positive in $\left\{ {R_{S_1 }^s ,R_{S_2 }^s } \right\}$ at least. For $R_{S_1 }^s >0$, it can be transformed to $R_{S_1 }^{*} -R_{E_1 }^{*} >0$ due to the monotonicity of logarithm function. Thus,

$$\begin{aligned} R_{S_1 }^{*} -R_{E_1 }^{*} =\gamma _1 \gamma _2^2 \left( {\frac{P_2 }{\sigma ^{2}}} \right) ^{2}-\left( {\gamma _1 \gamma _2 +\gamma _1^2 } \right) \frac{P_2 }{\sigma ^{2}}-\gamma _1 \end{aligned}$$

(14)

Let $x={P_2 }/{\sigma ^{2}}, y=R_{S_1 }^{*} -R_{E_1 }^{*}$, and Eq. (14) can be rewritten as

$$\begin{aligned} y=\gamma _1 \gamma _2^2 x^{2}-\left( {\gamma _1 \gamma _2 +\gamma _1^2 } \right) x-\gamma _1 \end{aligned}$$

(15)

Quadratic function in Eq. (15) is concave, and the number of points of intersection on the horizontal axis depends on

$$\begin{aligned} \Delta _1 =\left( {\gamma _1 \gamma _2 +\gamma _1^2 } \right) ^{2}+4\gamma _1^2 \gamma _2^2 \end{aligned}$$

(16)

From Eq. (16), $\Delta _1$ is strictly positive, therefore $y$ has two different points of intersection on the horizontal axis, one is negative, while the other is positive. Denote the positive one as

$$\begin{aligned} \Gamma _1 =\frac{\gamma _1 \gamma _2 +\gamma _1^2 +\Delta _1^{1/2} }{2\gamma _1 \gamma _2^2 } \end{aligned}$$

(17)

This concludes that $y=R_{S_1 }^{*} -R_{E_1 }^{*} >0$ while $x={P_2 }/{\sigma ^{2}}>\Gamma _1$. Namely, if ${P_2 }/{\sigma ^{2}}>\Gamma _1 , R_{S_1 }^s >0$ can be obtained, and $R_{S_1 }^s =0$ only when ${0<P_2 }/{\sigma ^{2}}<\Gamma _1$.

Similarly, $R_{S_2 }^s >0$ can be obtained when ${P_2 }/{\sigma ^{2}}>\Gamma _2$, and $R_{S_2 }^s =0$ when ${0<P_2 }/{\sigma ^{2}}<\Gamma _2$, and $\Gamma _2$ is

$$\begin{aligned} \Gamma _2 =\frac{\gamma _1 \gamma _2 +\gamma _2^2 +\Delta _2^{1/2} }{2\gamma _2 \gamma _1^2 } \end{aligned}$$

(18)

where $\Delta _2 =\left( {\gamma _1 \gamma _2 +\gamma _2^2 } \right) ^{2}+4\gamma _1^2 \gamma _2^2$.

Further, to obtain non-zero secrecy rate of both sources, i.e., $\left\{ {R_{S_1 }^s >0,R_{S_2 }^s >0} \right\}$, the corresponding intersection should be known, such as if $\Gamma _1 >\Gamma _2$ (i.e. $\gamma _1 >\gamma _2$), the SNR range is ${P_2 }/{\sigma ^{2}}>\Gamma _1$, or else ${P_2 }/{\sigma ^{2}}>\Gamma _2$. $\square$

3.3 Secrecy Rates for One- and Two-Way AF Relaying Protocols with Fair Power Constraint

With a fair total power constraint, the total transmit power is equal for both one- and two-way relaying protocols, i.e., $P_t =2P_1 =3P_2$. The secrecy rate of the one-way relaying protocol and the secrecy sum-rate of the two-way relaying protocol with the same mistrust level $T$ are, respectively

$$\begin{aligned}&R_{1,t}^s =\left[ {\frac{1}{2}\log _2 \left( {R_{S_1 ,t}^\# } \right) -\frac{1}{2}T\log _2 \left( {R_{E_1 ,t}^\# } \right) } \right] ^{+}=\left[ M \right] ^{+} \end{aligned}$$

(19)

$$\begin{aligned}&R_{2,t}^s =\sum _{i=1,2} {\left[ {\frac{1}{2}\left( {\log _2 \left( {R_{S_i ,t}^{*} } \right) -T\log _2 \left( {R_{E_i ,t}^{*} } \right) } \right) } \right] ^{+}} =\sum _{i=1,2} {\left[ {N_i } \right] ^{+}} \end{aligned}$$

(20)

where $R_{S_1 ,t}^\# =1+\frac{\rho _3^2 \gamma _1 \gamma _2 {P_t }/2}{\rho _3^2 \gamma _2 \sigma ^{2}+\sigma ^{2}}, R_{E_1 ,t}^\# =1+\frac{\gamma _1 {P_t }/2}{\sigma ^{2}}, R_{S_i ,t}^{*} =1+\frac{\rho _4^2 \gamma _1 \gamma _2 {P_t }/3}{\rho _4^2 \gamma _j \sigma ^{2}+\sigma ^{2}}$ and $R_{E_i ,t}^{*} =1+\frac{\gamma _i {P_t }/3}{\gamma _j {P_t }/3+\sigma ^{2}}$, and the corresponding power amplification factors are, respectively

$$\begin{aligned}&\rho _3 =\sqrt{\frac{{P_t }/2}{{P_t \gamma _1 }/2+\sigma ^{2}}}\\&\rho _4 =\sqrt{\frac{{P_t }/3}{{P_t \gamma _1 }/3+{P_t \gamma _2 }/3+\sigma ^{2}}} \end{aligned}$$

Theorem 3

With equal total power constraint, i.e., $2P_1 =3P_2 =P_t$, the secrecy sum-rate of the two-way AF half-duplex relaying protocol is higher than that of the one-way AF half-duplex relaying protocol in the high SNR regime, i.e.

$$\begin{aligned} R_{2,t}^s -R_{1,t}^s >0 \end{aligned}$$

(21)

Proof

The secrecy rate of the one-way AF half-duplex relaying protocol is strictly zero when the relay is a complete untrusted node. In particular, a secrecy rate comparison between the one- and two-way AF half-duplex relaying protocols will be investigated in specific mistrust level range, where the secrecy rates of both one- and two-way relaying protocols are non-zero. In the high SNR regime, one can obtain

$$\begin{aligned}&R_{S_i ,t}^{*} =1+\frac{\rho _4^2 \gamma _1 \gamma _2 {P_t }/3}{\rho _4^2 \gamma _j \sigma ^{2}+\sigma ^{2}}\approx 1+\frac{P_t }{\sigma ^{2}}\frac{\gamma _1 \gamma _2 }{3\left( {\gamma _1 +\gamma _2 +\gamma _j } \right) } \end{aligned}$$

(22)

$$\begin{aligned}&R_{E_i ,t}^{*} =1+\frac{\gamma _i {P_t }/3}{\gamma _j {P_t }/3+\sigma ^{2}}\approx 1+\frac{\gamma _i }{\gamma _j } \end{aligned}$$

(23)

From Eqs. (22) and (23), one can obtain $R_{S_i ,t}^{*} \gg R_{E_i ,t}^{*} >1$, thus $N_i >0$ for any $T$. Therefore, $\sum \nolimits _{i=1,2} {N_i } -M>0$ is equivalent to $R_{2,t}^s -R_{1,t}^s >0$ whether $M$ is positive or not. From Eqs. (19) and (20),

$$\begin{aligned} \sum _{i=1,2} {N_i } -M=\frac{1}{2}\log _2 \frac{R_{S_1 ,t}^{*} R_{S_2 ,t}^{*} }{R_{S_1 ,t}^\# }-\frac{1}{2}T\log _2 \frac{R_{E_1 ,t}^{*} R_{E_2 ,t}^{*} }{R_{E_1 ,t}^\# }>0 \end{aligned}$$

(24)

In the high SNR regime, Eq. (24) will be simplified to

$$\begin{aligned} T\log _2 \frac{2\left( {\gamma _1 +\gamma _2 } \right) ^{2}}{\gamma _1^2 \gamma _2 {P_t }/{\sigma ^{2}}}<\log _2 \frac{2}{9}\frac{P_t }{\sigma ^{2}}\frac{\gamma _1 \gamma _2 \left( {\gamma _1 +\gamma _2 } \right) }{\left( {2\gamma _1 +\gamma _2 } \right) \left( {\gamma _1 +2\gamma _2 } \right) } \end{aligned}$$

(25)

$\log _2 \frac{2\left( {\gamma _1 +\gamma _2 } \right) ^{2}}{\gamma _1^2 \gamma _2 {P_t }/{\sigma ^{2}}}$ is negative, thus

$$\begin{aligned} T&> {\log _2 \frac{2}{9}\frac{P_t }{\sigma ^{2}}\frac{\gamma _1 \gamma _2 \left( {\gamma _1 +\gamma _2 } \right) }{\left( {2\gamma _1 +\gamma _2 } \right) \left( {\gamma _1 +2\gamma _2 } \right) }}/{\log _2 \frac{2\left( {\gamma _1 +\gamma _2 } \right) ^{2}}{\gamma _1^2 \gamma _2 {P_t }/{\sigma ^{2}}}} \nonumber \\&\approx -1-\frac{\log _2 \frac{2}{9}\frac{\left( {\gamma _1 +\gamma _2 } \right) ^{3}}{\gamma _1 \left( {2\gamma _1 +\gamma _2 } \right) \left( {\gamma _1 +2\gamma _2 } \right) }}{\log _2 {P_t }/{\sigma ^{2}}} \end{aligned}$$

(26)

Under high SNR, ${P_t }/{\sigma ^{2}}>\frac{2}{9}\frac{\left( {\gamma _1 +\gamma _2 } \right) ^{3}}{\gamma _1 \left( {2\gamma _1 +\gamma _2 } \right) \left( {\gamma _1 +2\gamma _2 } \right) }$, and Eq. (26) is strictly true for any $T$. $\square$

4 Simulation Results

Assume the distance between $S_1$ and $S_2$ meets $d_1 +d_2 =1$ with $0<d_1 ,d_2 <1$. Monte Carlo experiment with $10^{5}$ independent trials is performed to obtain the average results.

In Fig. 2, the average SNR threshold, above which the two-way relaying protocol can obtain non-zero secrecy rate, is plotted for different $d_1$ at $c=2,3,4$. Since the secrecy rate of the two-way relaying protocol is the sum secrecy rate of two sources, the corresponding SNR threshold consists of two thresholds, namely, $\hbox {E}\left[ {\Gamma _1 } \right]$ of $S_1$ and $\hbox {E}\left[ {\Gamma _2 } \right]$ of $S_2 , \hbox {E}\left[ \cdot \right]$ denotes expectation. Take $c=4$ as an example, in the extremely low SNR interval $\left[ {-80,0} \right]$, the curves show the SNR threshold of the overall system, the corresponding maximal SNR threshold is at $d_1 =d_2 =0.5$, and a higher path loss exponent leads to a lower average SNR threshold. In the interval $\left[ {0,100} \right]$, the curves show the SNR threshold of only one source, while the threshold at $d_1 =d_2 =0.5$ is minimum, and a higher path loss exponent will lead to a higher average SNR threshold.

Fig. 2

Average SNR threshold of two-way relaying protocol for different $c$

Figure 3 shows the SNR requirement versus mistrust levels in one-way relaying protocol with different secrecy rate constraints. The noise power is $\sigma ^{2}=-30$ dBm, the channel fading exponent is 3, and the SNR range is from 0 to 30 dB. For the same mistrust level and $d_1$, the source needs more transmit power to obtain higher secrecy rate. It is interesting to note that the system needs less power to meet the secrecy rate constraint under low mistrust level for $d_1 =0.5$ compared with that for $d_1 =0.75$, while it is opposite when the mistrust level is high, since the middle between the source and the destination is the better position for a higher rate, and the long distance from source will weaken the eavesdropper-source link. For secrecy rate constraint $R_{S_1 }^{s^{\prime }} =1$ bits/s/Hz, when the transmit power is small, any mistrust level will not meet the secrecy rate constraint, so the curves are not drawn in this case.

Fig. 3

Mistrust level versus transmit power with different secrecy rate constraints

Figure 4 shows the average secrecy sum-rate of the two-way relaying protocol and the average secrecy rate of the one-way relaying protocol for different SNRs. The relay is located at the middle point of the two sources (i.e., $d_1 =d_2 =0.5$). The noise power, the channel fading exponent, and the SNR range are set the same as Fig. 3. When the mistrust level is 0, the comparison of rate curves indicates that the two-way relaying protocol outperforms the one-way relaying protocol. The secrecy rates of one- and two-way relaying protocols increase overall as the total transmit power increases except that the mistrust level of one-way relaying protocol is $T=1$, and the two-way relaying protocol will have much more superiority. As expected, the secrecy rate of the one-way relaying protocol is zero when the mistrust level is 1. For any mistrust level, the two-way relaying protocol has higher secrecy rate than the one-way relaying protocol in the given high SNR range.

Fig. 4

Average secrecy rate for different mistrust levels

Under high SNR, the two-way relaying protocol is a better choice over the one-way relaying protocol, especially in the wireless sensor networks, whose relays are captured easily. When the SNR achieves a special threshold, the security of the system can be ensured without considering the mistrust level of the relay. The capture tolerability or the secrecy rate of the system can be improved by increasing the transmit power, namely, increasing transmit power makes the system tolerates more subchannels eavesdropped with secrecy rate constraint in OFDM systems.

5 Conclusions

The secrecy rates of the one- and two-way half-duplex AF relaying protocols with an untrusted relay were investigated and then compared. By increasing the transmit power, the range of the mistrust level will be extended with non-zero secrecy rate constraint for one-way relaying protocol. The one-way relaying protocol is not secure any more when the mistrust level of the relay is 1, no matter how large the transmit power is. For the two-way relaying protocol, even though the mistrust level is 1, the non-zero secrecy rate can be achieved in certain SNR threshold, which has been derived. With a fair power constraint, where the two relaying protocols have equal total transmit power, the two-way relaying protocol is always superior to the one-way relaying protocol under high SNR.