1 Introduction

With the rapid deployment of various wireless systems, the limited radio spectrum is becoming increasingly crowded. On the other hand, it is evident that most of the allocated spectrum experience low utilization. As a novel approach to enhancing the utilization efficiency of the scarce radio spectrum, cognitive radio (CR) has attracted tremendous interests recently. A key feature of the CR network is to allow an secondary user (SU) to simultaneously share a licensed spectrum as long as the secondary transmission does not interfere with the primary link. As a result, the challenge of the CR network is to protect the primary users (PUs) from harmful interference induced by the SUs as well as to meet the quality of service (QoS) demands of SUs. Multi-input multi-output (MIMO) technique, with its significantly increased transmission capacity, has become a dominating technique in next-generation wireless systems. It is thus quite natural to combine these two techniques to achieve higher spectral efficiency. This technological combination results in the so-called cognitive MIMO radio [1].

Beamforming and power control are two well-known approaches that can mitigate co-channel interference (CCI) and enhance the system capacity. Recently, joint beamforming and power control has been widely studied for CR networks as a quite promising interference suppression technique [2–5]. For such a system, it has additional challenge of keeping the operation of SUs such that the received interference at the PUs remains below a tolerable limit. In [3], the joint beamforming and power allocation for a single-input multiple-output (SIMO) multiple access channels in CR networks was considered. The problem of joint beamforming and power control for SUs when they are allowed to transmit simultaneously with PUs was studied in [4]. The objective is to optimize the network sum rate under the interference constraints of PUs, which is a non-convex problem. Iterative dual subgradient algorithm was proposed to solve such problems. In [5], the authors considered the downlink of CR systems with multiple SUs and multiple PUs. Precoding and power allocation were performed at the secondary base station (SBS) to maximize the throughput of the secondary network. The problem is difficult to solve due to its non-convex property. Then, the authors converted it into a convex optimization problem.

As multiple non-cooperative SUs share the same frequency band licensed to a PU, game theory can be naturally applied to CR networks. In recent years, game theory has been applied to solve the problem of power control for providing the maximum throughput in CR networks [6]. The authors in [7] further considered both power and rate control using a game-theoretic approach, where the SUs were considered as active players in the game. The extension to the cognitive MIMO system was considered in [1, 8, 9]. Therein, both theoretic analysis and algorithm were carefully investigated. However, the problem of joint beamforming and power allocation for cognitive MIMO systems is different from the traditional radio networks and to the best of our knowledge, few studies have been performed to look at this problem in a cognitive MIMO radio environment via game theory.

The above works were all based on the assumption of perfect channel state information (CSI) between SUs and PUs. In practice, however, perfect channel knowledge could be difficult to obtain due to the loose cooperation between PUs and SUs, as well as many other factors such as inaccurate channel estimation, limited feedback or lack of channel reciprocity. There are two common ways to model imperfect CSI: Bayesian and worst-case approaches. The worst-case approach is more suitable for characterizing instantaneous CSI with errors, assuming that the actual channel lies in the channel uncertainty region of a known nominal channel. The size of this region represents the amount of channel uncertainty. The worst-case approach has been used to design robust beamforming for SUs in a multiple-input single-output (MISO) CR system [10, 11]. In [10], the software assisted method and a geometric method were considered for single SU and single PU to find suboptimal solution for the certainty and uncertainty models. For more SUs or PUs, [12] made some approximations for the uncertainty channel model between SUs and PUs. In [13], the worst-case of uncertainty was considered and the initially nonconvex uncertainty problems are transformed into a second order cone programming (SOCP) or other convex problems, which can be solved by software. A robust distributed uplink power allocation algorithm for underlay cognitive radio networks was proposed in [14]. The objective is to maximize the sum utility of SUs when channel gains from SUs to primary base stations and interference caused by PUs to the SBS are uncertain.

Uncertainty in game theory has only recently been investigated. In [15], following the worst-case robust theory, the authors took into account the imperfectness of SU-to-PU CSI by adopting proper interference constraints. The existence and uniqueness of the NE of the robust game is studied by relying on the variational inequality theory. A distribution-free robust framework for the rate-maximization game has been proposed in [16], where the authors analyzed the social properties of the equilibrium under varying channel uncertainty bounds for the two-user case. Robust equilibrium in additively coupled games in communications networks has been presented in [17]. The objective is to present a complete analysis of the NE in robust games as compared to that of NE in nominal games with complete information.

In our earlier work [18], we studied the problem of joint beamforming and power allocation in a cognitive MIMO system under the game-theoretic framework when the CSI is known. The aim is to maximize the sum utility of SUs by jointly optimizing the beamforming vector and the power allocation vector among the SUs. Compared with the existing works, it is cumbersome to find the optimal solution to joint beamforming and power allocation through convex optimization because the objective function in the optimization problem is non-convex. Therefore, a non-cooperative game is formulated and the NE is considered as the solution of this game. However, due to the lack of cooperation between SBS and PU in practice, in this work the imperfect CSI is taken into account by the robust interference constraint. The optimization problem in the formulated robust game is converted into a SOCP problem.

The rest of this paper is organized as follows. The cognitive MIMO system is described in Sect. 2. The games formulated under perfect CSI and imperfect CSI are discussed in Sects. 3 and 4, respectively. Simulation results are presented in Sect. 5. Some concluding remarks are made in Sect. 6.

2 System Model

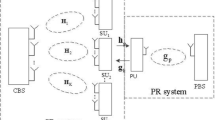
We consider a CR downlink network which shares the spectrum resource with a primary system, as illustrated in Fig. 1. Similar system models have been considered in [19]. The primary system consists of a primary base station (PBS) that transmits signals to a single PU. The secondary network has a single SBS, equipped with \(M\) antennas, serving \(K\) SUs. Throughout this paper, we assume that the PBS and the PU are equipped with a single antenna. Due to the sharing of the same frequency band, the received signal at the PU is interfered by the signals transmitted from SBS. Similarly, the received signals at the SUs are interfered by the signal transmitted from the PBS. Without loss of generality, each SU equips only one antenna. The transmitted signal vector of SUs is compactly written as

$$\begin{aligned} \mathbf{X}=\mathbf{F}\mathbf{P}\mathbf{S}, \end{aligned}$$
(1)

where \(\mathbf{S}\,{=}\,[s_1,s_2,\ldots ,s_K]^H\) denotes the transmitted signal vector, in which \(s_k\) (\(\Omega \,{=}\,1,\ldots ,K\), \(k\in \Omega \)) is the desired signal for user \(k\), \(\mathbf{F}=[\mathbf{f}_1,\mathbf{f}_2,\ldots ,\mathbf{f}_K]\) denotes the beamforming matrix, with \(\mathbf{f}_k\) being an (\(M \times K\)) beamforming vector for the \(k\)-th SU. Likewise, \(\mathbf{P}=\text{ diag }\{\sqrt{p_1},\ldots ,\sqrt{p_K}\}\) accounts for the power allocation matrix. For simplicity, we assume that all SUs are homogeneous and experience independent fading.

Fig. 1
figure 1

Cognitive MIMO system model

Full size image

The received signal at the \(k\)-th SU is given by

$$\begin{aligned} y_k&= \mathbf{h}_k^H\mathbf{X}+\sqrt{p_p}g_kx+n_k \nonumber \\&= \sqrt{{p_k}}\mathbf{h}_k^H\mathbf{f}_ks_k+\mathbf{h}_k^H \sum \limits _{i=1,i\ne k}^{K}\sqrt{{p_i}}\mathbf{f}_is_i \nonumber \\&+\sqrt{p_p}g_kx+n_k, \end{aligned}$$
(2)

where \(\mathbf{h}_k\) denotes the (\(M \times 1\)) channel vector from the SBS to the \(k\)-th SU, which is assumed to be independent and identically distributed (i.i.d.), complex Gaussian, with zero mean and unit variance, \(p_p\) denotes the transmission power of the PU, \(g_k\) represents the channel coefficient between the PBS and the \(k\)-th SU, \(x\) represents the transmitted signal from the PBS, \(n_k\) is an additive white Gaussian noise with zero mean and variance \(\sigma _k^2\). The received signal at the PU is given by

$$\begin{aligned} y_p=\sqrt{p_p}g_px+\mathbf{h}_p^H\sum \limits _{i=1}^K \sqrt{p_i}\mathbf{f}_is_i+n_p, \end{aligned}$$
(3)

where \(g_p\) denotes the channel coefficient between the PBS and the PU, \(\mathbf{h}_p\) is an (\(M \times 1\)) vector representing the channel coefficients between the SBS and the PU, \(n_p\) is an additive white Gaussian noise with zero mean and variance \(\sigma _p^2\).

The signal-to-interference-plus-noise-ratio (SINR) of the \(k\)-th SU is calculated by

$$\begin{aligned} {\textit{SINR}}_k=\frac{p_k|\mathbf{h}_k^H\mathbf{f}_k|^2}{\sum _{i=1,i\ne k}^{K}p_i|\mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+\sigma _k^2}. \end{aligned}$$
(4)

The achievable rate of the \(k\)-th SU can be expressed as

$$\begin{aligned} R_k=\log _2(1+{\textit{SINR}}_k). \end{aligned}$$
(5)

In the cognitive MIMO system, to guarantee the QoS requirements of SUs, the received SINR of each SU should be greater than a threshold \(\gamma _k\) [2], i.e.,

$$\begin{aligned} {\textit{SINR}}_k\ge \gamma _k. \end{aligned}$$
(6)

On the other hand, to guarantee the QoS of the PU, interference to the PU caused by SUs should be below a interference threshold \(I_{th}\), i.e.,

$$\begin{aligned} \sum \limits _{k=1}^{K}p_k|\mathbf{h}_p^H\mathbf{f}_k|^2\le I_{th}. \end{aligned}$$
(7)

In practice, the CSI between the SBS and the PU is often imperfect due to lack of cooperation. To take into account imperfect CSI, we adopt the following general model [11–14]. The true channel coefficient vector \(\mathbf{h}_p\) can be written as

$$\begin{aligned} \mathbf{h}_p=\hat{\mathbf{h}}_p+\Delta _p, \end{aligned}$$
(8)

where \(\hat{\mathbf{h}}_p\) is the CSI available at the SBS and \(\varvec{\Delta }_p\) is a norm-bounded uncertain vector, namely,

$$\begin{aligned} \Vert \varvec{\Delta }_p\Vert ^2\le c_p\varepsilon _p^2. \end{aligned}$$
(9)

Here, \(c_p\) and \(\varepsilon _p^2\) are uncertainty parameter and estimation error, respectively. The achievable rate of the \(k\)-th SU under imperfect CSI can be written as

$$\begin{aligned} R_k^{rob}=\log _2(1+{\textit{SINR}}'_k), \end{aligned}$$
(10)

where \({ SINR}'_k\) is the received SINR of the \(k\)-th SU under imperfect CSI.

3 Game Under Perfect CSI

To better understand the joint beamforming and power allocation game under imperfect CSI in the cognitive MIMO system, the game under perfect CSI is recalled in this section.

3.1 Game-Theoretic Formulation

Game theory is an effective tool to analyze competitive optimization problems. For the cognitive MIMO system, each SU’s transmission is a source of interference for the others. When a SU selfishly chooses a strategy to increase its own utility, it may increase the interference level of other SUs. Therefore, the strategies chosen by different SUs depend on each other. Based on the system model described above, a non-cooperative game is formulated as follows [20]:

$$\begin{aligned} G=\{\Omega ,\{\mathbf{f}_k,p_k\}_{k\in \Omega },\{u_k\}_{k\in \Omega }\} \end{aligned}$$
(11)

where \(\Omega =\{1,2,\ldots ,K\}\) is the set of the \(K\) SUs, \(\{\mathbf{f}_k,p_k\}\) is the set of admissible strategies of the \(k\)-th SU, which is non-negative. \(u_k\) is the utility function of the \(k\)-th SU in sharing spectrum with the PU and other SUs. Consequently, the utility function can be designed based on the achievable rate, i.e.,

$$\begin{aligned} u_k=\log _2(1+{\textit{SINR}}_k). \end{aligned}$$
(12)

Due to greediness, a utility function like (12) leads to an inefficient outcome, i.e., each player focuses on the forming of its own beam without nulling the interference to the PU. To prevent this selfish behavior, pricing has been used as an effective tool to give players incentives to cooperate for resource usages. Therefore, the utility function with pricing is rewritten as follows:

$$\begin{aligned} u_k=\log _2(1+{\textit{SINR}}_k)-\lambda p_k\left| \mathbf{h}_p^H\mathbf{f}_k\right| ^2, \end{aligned}$$
(13)

where \(\lambda \) is a positive constant and has an effect to reflect the potential interference to the PU. The non-cooperative game is formulated as [18]

$$\begin{aligned}&\max \,\,\sum \limits _{k=1}^K u_k \nonumber \\&\text{ s.t. }\,\, \sum \limits _{k=1}^K p_k\left| \mathbf{h}_p^H\mathbf{f}_k\right| ^2\le I_{th}, \nonumber \\&\quad \quad \sum \limits _{k=1}^K p_k\le P_T, \nonumber \\&\quad \quad {\textit{SINR}}_k \ge \gamma _k, \end{aligned}$$
(14)

Here, each SU competes against the others by choosing its beamforming vector \(\mathbf{f}_k\) and power \(p_k\) to maximize the sum utility of SUs with the following three constraints. The first constraint restricts the interference power to the PU. The second constraint is to guarantee the total transmission power from the SBS is bounded by a certain limit \(P_T\). In the third constraint, the SINR requirement for each SU is guaranteed. Consequently, the objective of the non-cooperative game is to coordinate the beamforming vector and power allocation for SUs to reach to NE.

3.2 Existence of NE

To analyze the outcome of the game, the existence of a NE is a well-known optimality criterion. In a NE point, every player is unilaterally optimal and no player can increase its utility alone by changing its own strategy. According to the fundamental game theory, the strategic non-cooperative game admits at least one NE point if for all \(k\in \Omega \),

  1. (i)

    The feasible set \(B_k=\{\mathbf{f}_k,p_k\}\) is a nonempty compact convex subset of a Euclidean space.

  2. (ii)

    The utility function \(u_k(\cdot )\) is continuous and quasi-concave on \(B_k=\{\mathbf{f}_k,p_k\}\).

Obviously, the feasible set \(B_k=\{\mathbf{f}_k,p_k\}\) is nonempty and convex, so the first condition could be satisfied. Utility function is continuous in strategy space \(B_k=\{\mathbf{f}_k,p_k\}\), thus it will be proved as quasi-concave function only. By taking the first derivative of \(u_k(\cdot )\) with respect to \(p_k\) and \(|\mathbf{f}_k|^2\), respectively, we have

$$\begin{aligned} \frac{\partial u_k}{\partial p_k}&= \frac{1}{\ln 2} \frac{|\mathbf{h}_k^H\mathbf{f}_k|^2}{\sum _{i=1,i \ne k}^K p_i|\mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+ \sigma _k^2+p_k|\mathbf{h}_k^H\mathbf{f}_k|^2}\nonumber \\&-\lambda |\mathbf{h}_p^H\mathbf{f}_k|^2,\end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial u_k}{\partial |\mathbf{f}_k|^2}&= \frac{1}{\ln 2} \frac{p_k|\mathbf{h}_k^H|^2}{\sum _{i=1,i\ne k}^K p_i|\mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+ \sigma _k^2+p_k|\mathbf{h}_k^H\mathbf{f}_k|^2}\nonumber \\&-\lambda p_k|\mathbf{h}_p^H|^2. \end{aligned}$$
(16)

Then, by setting these first derivatives to zero, we get

$$\begin{aligned} p_k&= \frac{\frac{|\mathbf{h}_k^H|^2}{ \lambda \ln 2|\mathbf{h}_p^H|^2}-\left[ \sum _{i=1,i\ne k}^{K}p_i|\mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+ \sigma _k^2\right] }{|\mathbf{h}_k^H\mathbf{f}_k|^2},\end{aligned}$$
(17)
$$\begin{aligned} |\mathbf{f}_k|^2&= \frac{\frac{|\mathbf{h}_k^H|^2}{\lambda \ln 2|\mathbf{h}_p^H|^2}-\left[ \sum _{i=1,i\ne k}^{K}p_i|\mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+ \sigma _k^2\right] }{p_k|\mathbf{h}_k^H|^2}. \end{aligned}$$
(18)

Moreover, by finding the second derivative of \(u_k(\cdot )\) with respect to \(p_k\) and \(|\mathbf{f}_k|^2\), respectively, we get

$$\begin{aligned} \frac{\partial u_k^2}{\partial ^2 p_k}=-\frac{1}{\ln 2} \frac{|\mathbf{h}_k^H\mathbf{f}_k|^4}{\left[ \sum _{i=1,i \ne k}^{K}p_i|\mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+ \sigma _k^2+p_k|\mathbf{h}_k^H\mathbf{f}_k|^2\right] ^2}, \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial u_k^2}{\partial ^2 |\mathbf{f}_k|^2}=- \frac{1}{\ln 2}\frac{p_k^2|\mathbf{h}_k^H|^4}{\left[ \sum _{i=1,i\ne k}^{K}p_i|\mathbf{h}_k^H \mathbf{f}_i|^2+p_p|g_k|^2+\sigma _k^2+p_k| \mathbf{h}_k^H\mathbf{f}_k|^2\right] ^2}. \end{aligned}$$
(20)

As \(|\mathbf{h}_k^H\mathbf{f}_k|^4\ge 0\) and \(p_k^2|\mathbf{h}_k^H|^4\ge 0\), it is easy to check that \(\frac{\partial u_k^2}{\partial ^2 p_k}\le 0\) and \(\frac{\partial u_k^2}{\partial ^2 |\mathbf{f}_k|^2}\le 0\). Consequently, the utility functions of SUs satisfy all the required conditions for the existence of at least one NE.

3.3 Uniqueness of NE

The key aspect of the uniqueness of the NE is that the best response function is a standard function. Assuming that the beamforming strategy is given. In order to prove that the NE is unique, the best response function \(BR_k(p_k)\) should be a standard function, which fulfills the following axioms [21]:

  1. (i)

    Positivity: for all \(k\in K\), \(BR_k(p_k)>0\).

  2. (ii)

    Monotonicity: if \(p_k>p'_k\), then \(BR_k(p_k)>BR_k(p'_k)\).

  3. (iii)

    Scalability: for all \(\mu >1\), \(\mu BR_k(p_k)>BR_k(\mu p_k)\).

Positivity: To ensure the normal operation of the system, the best response function must meet the positivity condition.

Monotonicity: If \(p_k>p'_k\), then \(\sum _{i=1,i\ne k}^K p_i|\mathbf{h}_k^H\mathbf{f}_i|^2<\sum _{i=1,i\ne k}^K p'_i|\mathbf{h}_k^H\mathbf{f}_i|^2\). We can get

$$\begin{aligned} {\textit{BR}}_k(p_k)-{\textit{BR}}_k(p'_k)&= \frac{\frac{|\mathbf{h}_k^H|^2}{\lambda \ln 2| \mathbf{h}_p^H|^2}-\left[ \sum _{i=1,i\ne k}^{K}p_i| \mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+\sigma _k^2\right] }{| \mathbf{h}_k^H\mathbf{f}_k|^2} \nonumber \\&-\frac{\frac{|\mathbf{h}_k^H|^2}{\lambda \ln 2| \mathbf{h}_p^H|^2}-\left[ \sum _{i=1,i\ne k}^{K}p'_i|\mathbf{h}_k^H \mathbf{f}_i|^2+p_p|g_k|^2+\sigma _k^2\right] }{|\mathbf{h}_k^H \mathbf{f}_k|^2} \nonumber \\&=\frac{\sum _{i=1,i\ne k}^{K}p'_i|\mathbf{h}_k^H \mathbf{f}_i|^2-\sum _{i=1,i\ne k}^{K}p_i|\mathbf{h}_k^H \mathbf{f}_i|^2}{|\mathbf{h}_k^H\mathbf{f}_k|^2} \nonumber \\&\ge 0. \end{aligned}$$
(21)

As a result, the monotonicity property is satisfied.

Scalability: for all \(\mu >1\), we have

$$\begin{aligned} \mu {\textit{BR}}_k(p_k)-{\textit{BR}}_k(\mu p_k)&= \mu \frac{\frac{|\mathbf{h}_k^H|^2}{\lambda \ln 2| \mathbf{h}_p^H|^2}-\left[ \sum _{i=1,i\ne k}^{K}p_i| \mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+\sigma _k^2\right] }{| \mathbf{h}_k^H\mathbf{f}_k|^2} \nonumber \\&-\frac{\frac{|\mathbf{h}_k^H|^2}{\lambda \ln 2| \mathbf{h}_p^H|^2}-\left[ \sum _{i=1,i\ne k}^{K}\mu p_i| \mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+\sigma _k^2\right] }{| \mathbf{h}_k^H\mathbf{f}_k|^2} \nonumber \\&=\frac{(\mu -1)\left[ \sum _{i=1,i\ne k}^{K}p_i| \mathbf{h}_k^H\mathbf{f}_i|^2-(p_p|g_k|^2+\sigma _k^2)\right] }{| \mathbf{h}_k^H\mathbf{f}_k|^2}. \end{aligned}$$
(22)

According to the positive requirement

$$\begin{aligned} \sum \limits _{i=1,i\ne k}^{K}p_i|\mathbf{h}_k^H\mathbf{f}_i|^2&\ge \sum \limits _{i=1,i\ne k}^{K}p_i|\mathbf{h}_k^H\mathbf{f}_i|^2+p_p|g_k|^2+\sigma _k^2\nonumber \\&> \left( p_p|g_k|^2+\sigma _k^2\right) . \end{aligned}$$
(23)

so \(\mu {\textit{BR}}_k(p_k)>{\textit{BR}}_k(\mu p_k)\ge 0\). Consequently, the scalability property is satisfied.

From the above proof, we can see that the best response function \({\textit{BR}}_k(p_k)\) is a standard function, i.e., it has only one solution. Similarly, when the power allocation strategy is fixed, we can also prove that the best response function \({\textit{BR}}_k(\mathbf{f}_k)\) is a standard function. To sum up, the NE point of the game is unique.

3.4 Joint Beamforming and Power Allocation Algorithm

In this section, we present an iterative algorithm that repeats the beamforming and power allocation steps until convergence [22]. The algorithm has two parts: First, using some initial beamforming matrix, a power vector is computed when the power allocation part operates for a certain number of iterations. Then, with this power vector, the generalized eigenvalue solver finds the optimal beamforming matrix. This set of power allocation and beamforming steps is repeated, using the power in each round and then the beamforming vectors that are calculated from the previous round, until convergence to a locally optimal pair of power and beamforming vectors is achieved.

The iterative algorithm is summarized as follows:

Set \(n=0\). Initialize powers \(p_k^{(0)}\) and beamforming vectors \(\mathbf{f}_k^{(0)}\), \(k\in \Omega \).

Step 1: At each iteration, set \(n_0=n\). Repeat{ For each user \(k\in \Omega \) calculate the interference

$$\begin{aligned} I_k^{(n)}=\sum \limits _{i\in \Omega ,i\ne k}^{K}p_i^{(n)}|\mathbf{h}_k^H\mathbf{f}_i^{(n)}|^2+ p_p^{(n)}|g_k|^2+\sigma _k^2. \end{aligned}$$
(24)

For each user \(k\in \Omega \) update power

$$\begin{aligned} p_{k+1}^{(n)}=\frac{\frac{|\mathbf{h}_k^H|^2}{ \lambda \ln 2|\mathbf{h}_p^H|^2}-I_k^{(n)}}{| \mathbf{h}_k^H\mathbf{f}_k^{(n)}|^2}. \end{aligned}$$
(25)

Set \(n=n+1\), \(\mathbf{f}_k^{(n)}=\mathbf{f}_k^{(n-1)}\) for each \(k\in \Omega \). } until \(n=n_0+N\).

Step 2: For each user compute the beamforming vector, which are generalized eigenvalue problems, i.e.,

$$\begin{aligned} \mathbf{f}_k^{(n)}=\arg \max _{\Vert x\Vert =1}\frac{x^HM_k^Sx}{x^HM_k^Ix}, \end{aligned}$$
(26)

where \(M_k^S=p_k^{(n)}|\mathbf{h}_k^H|^2\), \(M_k^I=\sum \nolimits _{i\in \Omega ,i\ne k}^{K}p_i^{(n)}| \mathbf{h}_k^H|^2+(p_p^{(n)}|g_k|^2+\sigma _k^2)\mathbf{I}\).

Step 3: Repeat Steps 1 and 2 until convergence.

3.5 Convergence of the Algorithm

For any fixed \(\lambda >0\), \(p_{k+1}^{(n)}=\frac{\frac{|\mathbf{h}_k^H|^2}{\lambda \ln 2|\mathbf{h}_p^H|^2}-I_k^{(n)}}{|\mathbf{h}_k^H\mathbf{f}_k^{(n)}|^2}\) . If \(\lambda _1>\lambda _2\), then the corresponding optimal solutions \(\hat{p}(\lambda _1)\) and \(\hat{p}(\lambda _2)\) are obtained, satisfying \(\hat{p}(\lambda _1) < \hat{p}(\lambda _2)\) regardless of the initial values. The algorithm can be implemented to obtain the fixed point of Eq. (26). Assuming that the order of power allocation is from SU 1 to SU \(K\), The process of Step1 could be regarded as a power allocation game with a coordinated utility function, as the power allocation strategy of each SU is the best response of the utility function. So the convergence in Step1 can be guaranteed.

The beamforming and power allocation algorithm can be interpreted as the best response in a beamforming and power allocation game [22]. Considering the algorithm, the power updates and beamforming updates result in an increase of the objective function. That is, the utility function satisfies \(U(\mathbf{P}^{(n+1)},\mathbf{F}^{(n+1)})\ge U(\mathbf{P}^{(n)},\mathbf{F}^{(n)})\), for \(n=0,1,\ldots \) . The local optimization of \(\mathbf{F}\) and \(\mathbf{P}\) are implemented alternately until the sum utility of SUs converges to a stable value.

4 Game Under Imperfect CSI

Under the assumption of imperfect CSI between the SBS and the PU, in order to enable the SUs to share the spectrum with the PU, we should find appropriate power and beamforming weights to distribute them among the SUs so that the sum utility of SUs is maximized and the interference created to the PU is as low as possible. This can be described by a robust game, i.e., the SUs compete with each other to maximize the sum utility under imperfect CSI.

4.1 Game-Theoretic Formulation

Adopting the worst-case CSI uncertainty model, the robust game \(G^{rob}\) can be formulated as

$$\begin{aligned}&\max _{p_k,\mathbf{f}_k}\,\,\sum \limits _{k=1}^K R_k^{rob} \nonumber \\&\text{ s.t. }\,\, \sum \limits _{k=1}^K p_k|(\hat{\mathbf{h}}_p+\mathbf{\Delta }_p)^H\mathbf{f}_k|^2\le I_{th}, \nonumber \\&\qquad \sum \limits _{k=1}^K p_k\le P_T, \nonumber \\ {}&\qquad {\textit{SINR}}_k\ge \gamma _k, \nonumber \\&\qquad \Vert \mathbf{\Delta }_p\Vert ^2\le c_p\varepsilon _p^2. \end{aligned}$$
(27)

This optimization problem is non-convex. After we make some approximations, it is clear that the objective is equivalent to maximizing \(\sum _{k=1}^K \sqrt{p_k}|\mathbf{h}_k^H\mathbf{f}_k|\) [10]. We define \(\mathbf{w}_k=\sqrt{p_k}\mathbf{f}_k\). Then, the objective function can be rewritten as \(\sum _{k=1}^K |\mathbf{h}_k^H\mathbf{w}_k|\). Similarly, the interference power can be expressed as \(\sum _{k=1}^K |({\hat{\mathbf{h}}}_p+\Delta _p)^H\mathbf{w}_k|^2\). Thus, the problem (27) can be transformed into

$$\begin{aligned}&\max _{p_k,\mathbf{f}_k}\,\,\sum \limits _{k=1}^K |\mathbf{h}_k^H\mathbf{w}_k|, \nonumber \\&\text{ s.t. }\,\, \sum \limits _{k=1}^K |({\hat{\mathbf{h}}}_p+\Delta _p)^H\mathbf{w}_k|^2\le I_{th}, \nonumber \\&\qquad \sum \limits _{k=1}^K p_k\le P_T, \nonumber \\&\qquad {\textit{SINR}}_k\ge \gamma _k, \nonumber \\&\qquad \Vert \mathbf{\Delta }_p\Vert ^2\le c_p\varepsilon _p^2. \end{aligned}$$
(28)

Now we show that the above problem can be reformulated as a second order cone program (SOCP) problem, following similar steps in [15]. Defining \(\hat{\mathbf{\Delta }}_p=\frac{1}{\sqrt{c_p}}\mathbf{\Delta }_p\), the interference constraint in (28) is equivalent to

$$\begin{aligned} \sum \limits _{k=1}^K \max _{\Vert \hat{\mathbf{\Delta }}_p\Vert \le \varepsilon _p}|(\hat{\mathbf{h}}_p+\hat{\mathbf{\Delta }}_p)^H\mathbf{w}_k|\le \sqrt{I_{th}}. \end{aligned}$$
(29)

Using the triangle inequality and the Cauchy–Schwarz inequality with \(\Vert \hat{\mathbf{\Delta }}_p\Vert \le \varepsilon _p\), it follows that

$$\begin{aligned} \sum \limits _{k=1}^K |\hat{\mathbf{h}}_p^H\mathbf{w}_k+ \hat{\mathbf{\Delta }}_p^H\sqrt{c_p}w_k|&\le \sum \limits _{k=1}^K(| \hat{\mathbf{h}}_p^H\mathbf{w}_k|+|\hat{\mathbf{\Delta }}_p^H \sqrt{c_p}\mathbf{w}_k|) \nonumber \\&\le \sum \limits _{k=1}^K|\hat{\mathbf{h}}_p^H\mathbf{w}_k|+| \hat{\mathbf{\Delta }}_p\sqrt{c_p}\mathbf{w}_k| \nonumber \\&\le \sum \limits _{k=1}^K|\hat{\mathbf{h}}_p^H\mathbf{w}_k|+ \varepsilon _p\Vert \sqrt{c_p}\mathbf{w}_k\Vert , \end{aligned}$$
(30)

where the equality is achieved when

$$\begin{aligned} \hat{\mathbf{\Delta }}_p=\varepsilon _pe^{j\phi _p}\frac{ \sqrt{c_p}\mathbf{w}_k}{\Vert \sqrt{c_p}\mathbf{w}_k\Vert }, \end{aligned}$$
(31)

\(\phi _p=\angle (\hat{\mathbf{h}}_p^H\mathbf{w}_k)\). This indicates

$$\begin{aligned} \sum \limits _{k=1}^{K}\max _{\Vert \hat{\mathbf{\Delta }}_p\Vert \le \varepsilon _p}|(\hat{\mathbf{h}}_p+\hat{\mathbf{\Delta }}_p)^H\mathbf{w}_k|&=\sum \limits _{k=1}^{K}|\hat{h}_p^H \mathbf{w}_k|+\varepsilon _p\Vert \sqrt{c_p}\mathbf{w}_k\Vert \end{aligned}$$
(32)

So (29) is equivalent to

$$\begin{aligned} \sum \limits _{k=1}^{K}|\hat{\mathbf{h}}_p^Hw_k|+\varepsilon _p\Vert \sqrt{c_p}\mathbf{w}_k\Vert \le \sqrt{I_{th}} \end{aligned}$$
(33)

Note that the arbitrary phase rotation of \(\mathbf{w}_k\) does not change the value of the objective function or the constraints. Therefore, we can assume that \(\mathbf{w}_k\), \(\mathbf{h}_k\), \(\mathbf{h}_p\) have the same phase, i.e.,

$$\begin{aligned} Re\{\mathbf{h}_k^H\mathbf{w}_k\}\ge 0,\,&Im\{\mathbf{h}_k^H \mathbf{w}_k\}=0,\,\quad \quad Im\{\hat{\mathbf{h}}_p^H\mathbf{w}_k\}=0. \end{aligned}$$
(34)

By combining (28), (33), and (34), the optimization problem can be converted into a SOCP problem, as

$$\begin{aligned}&\max _{p_k,\mathbf{f}_k}\,\,\sum \limits _{k=1}^K \mathbf{h}_k^H\mathbf{w}_k \nonumber \\&\text{ s.t. }\,\, Im\{\hat{\mathbf{h}}_p^H\mathbf{w}_k\}=0, \nonumber \\&\qquad \sum \limits _{k=1}^K (|\hat{\mathbf{h}}_p^H\mathbf{w}_k|+\sqrt{c_p}\Vert \mathbf{w}_k\Vert )\le \sqrt{I_{th}}, \nonumber \\&\qquad \sum \limits _{k=1}^K \Vert \mathbf{w}_k\Vert \le \sqrt{P_T}, \nonumber \\&\qquad {\textit{SINR}}_k\ge \gamma _k. \end{aligned}$$
(35)

Proposition 1

The joint beamforming and power allocation problem (35) is a convex optimization problem with respect to \(\mathbf{w}_k\).

Proof

According to [23], we introduce a new variable \(y_k=\log Re\{\mathbf{w}_k\}\). Thus, \(Re\{\mathbf{w}_k\}=\exp (y_k)\). The objective function in (35) is transformed to \(\sum _{k=1}^K \mathbf{h}_k^H\exp (y_k)\), which is convex with respect to \(y_k\) as the sum-exp function is a convex function. The second constraint in (35) is transformed to \(\sum _{k=1}^K (|\hat{\mathbf{h}}_p^H \exp (y_k)|+\sqrt{c_p}\Vert \exp (y_k)\Vert )\le \sqrt{I_{th}}\). The left part of the inequality is a sum-exp function with respect to \(y_k\), which is convex. The third constraint in (35) is transformed to \(\sum _{k=1}^K \Vert \exp (y_k)\Vert \le \sqrt{P_T}\). The left part of the inequality is a sum-exp function with respect to \(y_k\), which is also convex. \(\square \)

The interference generated by the PU together with the noise at the \(k\)-th SU is \(p_p|g_k|^2+\sigma _k^2=1\). The interference among different SUs has been assumed to be zero to simplify the formulation of the sum utility, i.e., \(\mathbf{h}_k^H\mathbf{w}_i=0, i\ne k\). Then, the fourth constraint in (35) can be transformed to

$$\begin{aligned} \frac{\sum _{i=1,i\ne k}^{K}|\mathbf{h}_k^H\mathbf w _i|^2+p_p|g_k|^2+\sigma _k^2}{|\mathbf{h}_k^H \mathbf{w}_k|^2}&= \frac{1}{|\mathbf{h}_k^H\exp (y_k)|^2} \nonumber \\&\le \frac{1}{\gamma _k} \end{aligned}$$
(36)

The left part of the inequality (36) is a nonnegative exponential function, which is convex with respect to \(y_k\) [23]. Since the objective function and the constraints are all convex, the problem (35) is a convex optimization problem. This completes the proof.

This optimization problem is very difficult to solve. So we will resort to numerical simulations to illustrate the convergence property of the sum utility of SUs.

4.2 Analysis of NE

Because \(Im\{\mathbf{h}_k^H\mathbf{w}_k\}=0\), \([\mathbf{h}_1^H, \ldots , \mathbf{h}_K^H]\) is not of full column rank [15]. However, the best response of each SU is a dominant strategy (Generally, if the feasible strategy for a player is a dominant strategy, regardless of the strategies of the other players, its strategy will maximize the payoff function of the players). This implies that the above robust game has a unique NE.

5 Simulation Results

In this section, simulations are conducted to examine the performance of the proposed algorithm under i.i.d. Rayleigh flat fading channels. Moreover, we show the convergence property of joint beamforming and power allocation under imperfect CSI.

5.1 Perfect CSI Case

It is assumed that the SBS has perfect CSI about the fading channel coefficients from the SBS to both the PU and SUs. For simplicity, we consider a scenario with two SUs and a single PU. We choose pricing factor as \(\lambda =0.25\), noise power as \(\sigma ^2=3e-3\) W, PU transmission power as \(P_p=0.1\) W, SU total transmission power as \(P_T=20\) W, the interference threshold as \(I_{th}=100\), the \(k\)-th SU minimum SINR constraint as \(\gamma _k=5\) dB, respectively.

In the following, we show the convergence of the joint beamforming and power allocation algorithm with respect to transmission power and beamforming weights. Figure 2 shows the convergence of transmission power for each SU, where the power initialization for each SU is the same as 0. It is observed that the transmission power converges in 5 iterations due to the preceding update of beamforming weights. Figure 3 depicts the beamforming weight for each SU when transmission powers converge to the optimal values. The initialization of beamforming weights is 1 for each SU. Moreover, Fig. 4 plots the sum utility of SUs versus the pricing factor \(\lambda \) when the interference to the PU caused by SUs is restricted. As observed from Fig. 4, the sum utility of SUs converges and decreases as \(\lambda \) increases.

Fig. 2
figure 2

Convergence of transmission power for each SU

Full size image
Fig. 3
figure 3

Convergence of beamforming weights for each SU

Full size image
Fig. 4
figure 4

Sum utility of SUs for different \(\lambda \)

Full size image

5.2 Imperfect CSI Case

In this subsection, we show the impact of channel uncertainty on sum utility of SUs by comparing the imperfect CSI case with the perfect CSI case. According to the ratio of the channel coefficient from the SBS to a SU and the one from the SBS to the PU, i.e. \(h_k/h_p\), the transmission power is allocated to each SU in a descending order. The sum utility obtained by a SOCP approximation algorithm [12] is evaluated. The estimation error is set to \(\varepsilon _p^2=\Vert \hat{\mathbf{h}}_p\Vert ^2\). Figure 5 shows the sum utility of SUs for a scenario with four SUs and a PU. The uncertainty parameter is set to \(c_p =0, 0.05, 0.2, 0.4\), respectively. When \(c_p=0\), the CSI is perfect. In addition, the noise power and the interference threshold between SUs and the PU are set to 1. Due to the CSI uncertainty, the sum utility is lower than that under perfect CSI. As the value of the uncertainty parameter increases, the sum utility becomes less. The sum utility of SUs under imperfect CSI converges with the increase of transmission power constraint of SUs.

Fig. 5
figure 5

Sum utility of SUs under imperfect CSI

Full size image

6 Conclusion

In this paper, the joint beamforming and power allocation problem for a cognitive MIMO system has been studied via game theory. Imperfect CSI between the SBS and the PU was considered. An ellipsoid model was adopted to describe the CSI uncertainty. The problem was formulated as a robust game. The uncertainty optimization problem was transformed into a SOCP problem, in an effort to maximize the sum utility of SUs. Due to the CSI uncertainty, the sum utility is lower than that under perfect CSI. Simulation results showed the convergence property of the sum utility of SUs.