1 Introduction

Transmission control protocol (TCP) in multi-hop ad hoc networks has recently attracted substantial research attentions [1–3]. TCP-Vegas is a typical enhanced TCP that uses a rate-based congestion control mechanism [4]. Generally speaking, TCP-Vegas has good performance in ad hoc networks for three reasons. First, the transmission rate is adjusted carefully by comparing with the estimated rate. Secondly, Vegas halves the congestion window (cwnd) size by identifying whether the retransmission packets belong to the current stage of congestion control. Thirdly, it emphasizes packet delay rather than packet loss as the criterion to determine the transmission rate. However, it only calculates the expected throughput using the round-trip time (RTT), which may not characterize the real throughput of the whole network due to the overlook of lower layer parameters. Besides, Vegas changes its current cwnd value based on the previous network situation, which means that this mechanism incurs latency to the computation and thus leads to the loss of accuracies and adaptations in rapidly changing environments.

Due to the potential improvements in performance, multiple studies have been made to cope with the problems of Vegas in wireless networks. An improved mechanism Vegas-W was proposed in [5], in which the cwnd is extended by a fraction with a rate control timer in the sending process, and the probing schemes have been changed to increase the window upon receiving more than one acknowledgment (ACK). However, the interaction analysis between TCP and lower protocols is needed for further improvement. Cheng etc. presented a threshold control mechanism with cross-layer response approach in [6] for improving TCP Vegas performance in IEEE 802.11 wireless networks. A model [7] based bandwidth estimation algorithm for 802.11 TCP data transmissions was developed by using feedback information from receivers.

Although these methods attained some improvements, all of them still have the inherent weaknesses of conventional TCP that stems from deferred calculations. Specifically, the calculations only reflect the past network conditions rather than the present and future ones, which makes them unsuitable for rapid changing environments. In this paper, we are inspired from the prediction algorithm [8], where the available duration of links is predicted to construct an efficient topology.

In this paper, we propose an improved TCP version based on TCP Vegas and Grey prediction named Gvegas, to deal with the problem of real throughput prediction and online congestion control. In addition, unlike other typical TCP variants, our scheme only needs revisions at the sender without involving intermediate nodes. To our best knowledge, this is the first work to consider both prediction and decision in congestion avoidance (CA) stage by predicting network condition before collision. Specifically, our contributions are summarized as follows:

In order to make the basis of congestion control more precisely for online congestion control in multihop ad hoc networks, we improve the theoretical and actual throughput model with cross-layer information sharing and grey prediction, respectively.

We model the congestion control decision as a MDP to choose the congestion window changing factor more effectively and adaptively. In addition, the action is quantified according to network state with round trip time.

We provide the performance analytic models of the improved congestion control over TCP Vegas, and utilize simulations and theoretical analysis to demonstrate the improved scheme can significantly promote the TCP performance in terms of both throughput and delay.

The remainder of this paper is organized as follows. We briefly describe some related works in Sect. 2. The main idea of the improved mechanism is introduced in Sect. 3. Section 4 formulates the cross layer model of expected throughput. Section 5 introduces the actual throughput prediction based on grey theory. Section 6 describes the RTT quantification and the exploration of cwnd changes based on Q-learning, in addition, the detailed algorithm and corresponding complexity analysis of space and time are also discussed. Section 7 numerically examines the Gvegas’s performance along with the Vegas and Newreno. Finally, Sect. 8 provides the conclusions of this paper.

2 Related works

TCP is the most widely applied transport layer protocol for reliable data transmission. Although there are many TCP versions with various congestion control schemes for different environments, such as TCP Newreno, TCP Vegas etc., some researchers have demonstrated that TCP Vegas can achieve higher throughput, fewer retransmissions and less delay than Newreno [9], because Vegas implements a more precise congestion avoidance mechanism based on packet delay rather than the packet loss. However, Vegas fails to make full use of available bandwidth to transmit packets since incorrect bandwidth estimates may occur due to unstable conditions in multi-hop wireless networks.

To detect congestion more reliably, several TCP throughput models have been proposed [10–12]. Samios et al. [10] developed a model to estimate the throughput of a Vegas flow as a function of packet loss rate, RTT, and protocol parameters. Similarly, a steady-state throughput of TCP Newreno was transferred as a function of RTT and loss behavior in [11]. The simulation results in [10, 11] show that TCP throughput model combining both packet loss and delay can achieve higher throughput. Furthermore, the throughput model of Vegas in [10] was extended by [12], which combined with the TCP segment information and TCP acknowledgement (ACK) to maximize the TCP throughput. Although these researches achieve the TCP performance improvements, they don’t fully concern the performance improvement from congestion control in wireless ad hoc environments.

Congestion control is another most significant way to improve TCP performance in wireless ad hoc networks [13]. An intelligent congestion control technique was proposed in [14] by using a neural network (NN) to regulate reliable data traffic in ad hoc wireless mesh networks. Badarla et al. [15] mainly concentrated on adapting to the changing network conditions and appropriately updating the congestion window by learning algorithm without relying on any network feedbacks. The above congestion control methods obtain some enhancements to some degree, however, they seldom explicitly consider the cross-layer network information to improve TCP performance.

Cross-layer designs allow information sharing among different layers in order to improve the functionality [13], in which some lower parameters could be considered when performing the cross layer design. Cheng et al. [6] proposed a congestion control scheme with dynamic threshold and cross layer response, in which the network performance was improved by the adaptation of congestion window size in accordance with the estimated buffer length. In [16], some typical cross layer factors were analyzed and modeled, and the TCP optimization was formulated as a Markov Decision Process (MDP). Furthermore, Xie et al. [17] presented a TCP pacing protocol by cross-layer measurement and analysis on the lower bound of the contention window to reduce packet burstiness in wireless networks.

In addition to the above schemes, TCP performance could be improved by status prediction through probabilistic approaches. For example, prediction strategies such as increasing the hold time of the topology for static scenario or increasing the HELLO generation rate for mobile scenario were proposed to promote the TCP efficiency [18]. Different from [18], congestion window was adjusted based on the estimation of network state by using the feedback information from the receiver [19].

Although, there are various cross-layer improved researches to improve the performance of multi-hop wireless networks, most of them always try to solve the basis of congestion and its control decision separately and make congestion control decision corresponding to past congestion control status which cannot really reflect the environmental conditions on time. In order to achieve overall and online optimization, this paper will promote the TCP performance towards the direction of prediction and joint cross-layer optimization.

3 Gvegas formulation

The Vegas mechanism uses the difference presented by (1) [4] between the expected (v_expect_) and actual (v_actual_) throughput to decide how to change cwnd:

$$diff = v\_expect\_- v\_actual\_= \left( {\frac{WindowSize}{BaseRTT} - \frac{SentData}{ActualRTT}} \right) \cdot BaseRTT$$
(1)

Specifically, the cwnd is either changed by adding or subtracting one packet or remains unchanged according to diff as follows:

$$cwnd = \left\{ {\begin{array}{*{20}l} {cwnd + 1,} \hfill & {diff < v\_\alpha } \hfill \\ {cwnd - 1,} \hfill & {diff > v\_\beta } \hfill \\ {unchanged,} \hfill & {other} \hfill \\ \end{array} } \right.$$
(2)

where \(v\_\alpha\) and \(v\_\beta\) are corresponding threshold values [4].

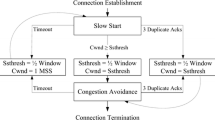
Gvegas has two parts as shown in Fig. 1. The first one, which contains expected throughput, grey prediction and residual modification model, makes the congestion control more accurate. The other one, which comprises quantification and reinforcement learning model, makes the cwnd adaptive to network changes. In the first part, v_expect_ and v_actual_ in (1) are replaced with expected and predicted values, respectively. The expected model uses cross-layer parameters to obtain throughput, and the prediction uses grey theory to predict the future throughput. In the second part, we quantify RTT into cwnd changing size, and a Q-learning algorithm is used to explore the optimal changing size for different cwnd phases.

Fig. 1
figure 1

The structure diagram of Gvegas

Full size image

3.1 Overview of grey prediction

Grey theory is a system that focuses on the uncertainty problems of small samples and poor information [20] which consists of two parts: grey prediction and grey decision. A grey system represents the cognitive degree for environment data and is widely used due to its simple and information imperfect characteristics. Typically, there are five categories of grey prediction including: (1) time series forecasting, (2) calamity forecasting, (3) seasonal calamity forecasting, (4) topological forecasting and (5) systematic forecasting [21].

GM(1,1) model [22, 23], which is one of the most widely used grey prediction models, can weaken the stochastic fluctuation in original series by accumulated generating operation (AGO), so as to dig out its inherent law, and build a one order different equation model to describe the law. The model gets the undecided coefficients of the one order grey differential equation by using least squares estimation and obtains the final prediction value by using inverse accumulated generating operation.

3.2 Overview of Q-learning

Reinforcement learning (RL) [24] is a learning system aiming to maximize a long-term performance measure with typical scenario shown in Fig. 2. In RL model, one agent can interact with its environment autonomously: it observes environment state in S, chooses one available action from A, and receives one reward in R from environment. The state-action pair in \(S \to A\) is a policy \(\pi^{ * }\) which aims to maximize the total reward \(V^{\pi } \left( {s_{t} } \right) = \sum\limits_{t = 0}^{\infty } {\gamma^{t} r_{t} }\), where the \(r_{t}\) is a received reward.

Fig. 2
figure 2

The reinforcement learning scenario

Full size image

Q-learning is a widely used RL algorithm [25]. In real applications, due to existence of uncertainty, agent cannot forecast the reward and next state when an action is performed. This will result in that the agent cannot obtain perfect \(\pi^{ * }\) by solving \(V^{\pi } \left( {s_{t} } \right)\). Therefore, Q-learning uses \(Q^{\pi } \left( {s,a} \right)\) to get the best policy: \(V^{{\pi^{ * } }} \left( s \right) = \mathop {\hbox{max} }\limits_{a \in A} Q^{{\pi^{ * } }} \left( {s,a} \right)\) and the renewal of Q value is as follows:

$$Q_{t + 1} \left( {s,a} \right) = Q_{t} \left( {s,a} \right) + \alpha \left[ {r_{t} + \gamma \mathop {\hbox{max} }\limits_{{a^{{\prime }} }} Q_{t} \left( {s^{{\prime }} ,a^{{\prime }} } \right) - Q_{t} \left( {s,a} \right)} \right]$$
(3)

where \(\alpha\) is the learning rate denoted as \(\alpha = \frac{1}{1 + visit(s,a)}\), visit(s,a) is the times of one station-action pair has been visited. s′ and a′ are the next state and action which belong to the set of S and A, respectively. Q-learning typically selects the “greedy” action a which has the highest Q(s,a) value with a probability \(\varepsilon\) (approximating 1) and selects a random action with probability 1−\(\varepsilon\).

4 Cross-layer model of TCP expected throughput

For simplicity of analysis, we assume that the main consideration of the throughput model involves the Transport Layer (TL) and Media Access Control (MAC) sub-layer.

4.1 TCP Vegas throughput model

A typical stochastic model for the steady-state throughput of TCP Vegas has been modeled by [10], as shown in (4), where Th Vegas is the throughput received, n is the expected number of consecutive Loss Free Periods (LFP) that occurs between one slow start (SS) and another slow start period, p denotes the loss event rate, W 0 is the average of cwnd during stable backlog state, T TO is the average duration of first timeout in a series of timeouts, and RTT is the average RTT.

$$Th_{Vegas} = \frac{{\left( {n + 1} \right)\left( {\frac{1 - p}{p} + W_{0} } \right) + \frac{{2p\left( {2 - p} \right)}}{{\left( {1 - p} \right)^{2} }}}}{{N_{SS2TO} RTT + D_{TO} }}$$
(4)

where N SS2TO and D TO are represented by Eqs. (5) and (6), respectively

$$N_{SS2TO} = 2\log W_{0} + \left( {n + 1} \right)\frac{1 - p}{{pW_{0} }} + \left( {1 + \frac{{nW_{0} }}{32}} \right) + \frac{9n}{8} - \frac{11}{4} + \frac{{4 - 2^{{\log W_{0} }} }}{{W_{0} }}$$
(5)
$$D_{TO} = \left( {\left( {1 - p} \right)^{2} \sum\limits_{k = 1}^{6} {\left( {\left( {2^{k} - 64k + 320} \right)\left( {2p - p^{2} } \right)} \right)^{k - 1} + \frac{64}{{\left( {1 - p} \right)^{2} }} - 321} } \right)T_{TO}$$
(6)

In order to predict the maximum achievable expected throughput for TCP-based data transmissions over IEEE 802.11 WLANs in multi-hop ad hoc networks. We extend TCP throughput model in (4) to include the characteristics of IEEE 802.11 Distributed Coordination Function (DCF) and queue management model in the subsequent subsections.

4.2 IEEE 802.11 DCF model

IEEE 802.11 DCF can be executed in either ad hoc or infrastructure-based networks and, indeed, is the typical access method implemented in most commercial wireless cards [26]. DCF contains three-times handshake as shown in Fig. 3. A sender sends a Request to Send (RTS) to a receiver after a DIFS time. Upon receiving the RTS, the receiver waits for one SIFS delay to send Clear to Send (CTS) to the sender. Then, the sender and receiver establish a link, during which the sender detects whether there is a collision before transmitting. If the answer is yes, a random back-off time will be selected by sender to build next transmission request. When the retransmission times reach the retry attempt limit, the packet will be dropped. The process time, successful delivery probability and loss probability of a packet from node to node are denoted by pt DCF , dp DCF and lp DCF , respectively.

$$pt_{DCF} = DIFS + 3 \cdot SIFS + t_{RTS} + t_{CTS} + t_{macACK}$$
(7)

The value of dp DCF is given by [7]

$$dp_{DCF} = (1 - D\_\tau )^{ncdf - 1} \cdot (1 - BER)^{dl + dh}$$
(8)

where \(ncdf\) indicates the number of competition channel data flow. \(D\_\tau\) denotes the probability of a request to send data. BER, dl, dh and CW I are the bit error rate, packet size, length of packet header and initial size of cwnd, respectively, i.e.

$$D\_\tau = \frac{2}{{CW_{I} + 1}}$$
(9)

When the retransmission times reach the retry attempt limit rl, a packet is dropped with probability given by

$$lp_{DCF} = \left( {1 - dp_{DCF} } \right)^{rl}$$
(10)
Fig. 3
figure 3

The access mechanism of DCF with RTS/CTS

Full size image

4.3 Queue management model

In this paper, we assume that Random Early Discard (RED) is used as the mechanism of queue management. The loss probability and the processing time of successfully transmitted packet at the RED stage are denoted by lp queue and pt queue , respectively. pt queue is available in real time via the feedbacks of RED protocol. lp queue is given by

$$lp_{queue} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {queue_{t}^{avg} \le queue_{t - 1}^{\hbox{min} } } \hfill \\ {1,} \hfill & {queue_{t}^{avg} \ge queue_{t - 1}^{\hbox{max} } } \hfill \\ {\frac{{queue_{t}^{avg} - queue_{t - 1}^{\hbox{min} } }}{{queue_{t - 1}^{\hbox{max} } - queue_{t - 1}^{\hbox{min} } }},} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(11)

where \(queue_{t - 1}^{\hbox{min} }\) and \(queue_{t - 1}^{\hbox{max} }\) are the minimal and maximal size of queue at time t−1. \(queue_{t}^{avg}\) indicates the average queue length at time t.

4.4 The expected throughput model

We formulate the expected throughput model by joint consideration of the term Th Vegas in (4) and the limitation of the maximum cwnd in a multihop ad hoc network. The throughput model is given by:

$$NV\_t{\text{ = min}}\left( {\frac{WindowSize}{BaseRTT},\,\frac{{\left( {n + 1} \right)\left( {\frac{{1 - p^{*} }}{{p^{*} }} + W_{0} } \right) + \frac{{2p^{*} \left( {2 - p^{*} } \right)}}{{\left( {1 - p^{*} } \right)^{2} }}}}{{N_{SS2TO} RTT^{*} + D_{TO} }}} \right)$$
(12)

where N SS2TO and D TO are defined by (5) and (6), respectively. Besides, p * and RTT * are defined by

$$p^{*} = \left( {1 - \prod\limits_{i = 1}^{hs} {\left( {1 - lp_{DCF}^{i} } \right)} } \right) + \left( {1 - \prod\limits_{i = 1}^{hs} {\left( {1 - lp_{queuequeue}^{i} } \right)} } \right) + lp_{TCPdrop}$$
(13)

and

$$RTT^{*} = \sum\limits_{i = 1}^{hs} {\left( {\left( {1 - lp_{{_{DCF} }}^{i} } \right) \cdot pt_{{_{DCF} }}^{i} } \right)} + \sum\limits_{i = 1}^{hs} {\left( {\left( {1 - lp_{queue}^{i} } \right) \cdot pt_{queue}^{i} } \right)} + \left( {1 - lp_{TCPdrop} } \right) \cdot pt_{TCP\_ACK}$$
(14)

where hs represents the sum of hops of a network connection, the p in \(N_{SS2TO}\) and \(D_{TO}\) is replaced by p *. The lp TCPdrop and pt TCP_ACK are the drop probability and processing time of TCP ACK which could be detected in real time via feedbacks of TCP protocol. The value of pt DCF , lp DCF and lp queue can be calculated by (7, 10) and (11).

5 Prediction of actual throughput based on grey model

Chapter 4 discusses the expected throughput in cross-layer model, however, the existing TCP variants also use the actual throughput of last stage in the Eq. (1) as the basis to control the congestion at next stage. This mechanism cannot cope with the real-time control and unpredictable dynamics of ad hoc networks. Thus, we propose a future actual throughput prediction scheme based on the GM(1,1) grey model [22, 23].

5.1 The grey prediction of throughput

We focus on predicting the actual throughput of the next stage by grey prediction GM(1,1) model [23] shown in Fig. 4. For simplicity, we assume that grey model predicts at discrete time interval called “stage”. The mode predicts the future network throughput at stage t + 1 to determine the cwnd changing size. In our model, the actual network throughputs of the last t stages are regarded as the input column ag o = {ag o(1), ag o(2),…,ag o(t)}, where t represents the length of input data and its minimum length is 4 for the purpose of prediction precision [23]. Accumulated Generating Operation (AGO), which will output the sequence of ag 1, aims to eliminate the randomness of ag o. In addition, ag z(t), created by Adjacent Average Generation Operation (AAGO), is the intermediate sequence to calculate the parameters of aga and agb as follows:

$$agb - aga \cdot ag^{z} \left( t \right) = ag^{0} \left( t \right)$$
(15)

where aga and agb are evolution parameter and grey action, respectively:

$$aga\,=\,\frac{{\sum\limits_{k = 2}^{t} {ag^{z} \left( k \right) \cdot \sum\limits_{k = 2}^{t} {ag^{0} \left( k \right) - \left( {t - 1} \right) \cdot \sum\limits_{k = 2}^{t} {ag^{z} \left( k \right) \cdot ag^{0} \left( k \right)} } } }}{{\left( {t - 1} \right) \cdot \sum\limits_{k = 2}^{t} {ag^{z} \left( k \right)^{2} - \left( {\sum\limits_{k = 2}^{t} {ag^{z} \left( k \right)} } \right)^{2} } }}$$
(16)
$$agb = \frac{{\sum\limits_{k = 2}^{t} {ag^{0} \left( k \right) \cdot \sum\limits_{k = 2}^{t} {ag^{1} \left( k \right)^{2} - \sum\limits_{k = 2}^{t} {ag^{1} \left( k \right)} \cdot \sum\limits_{k = 2}^{t} {ag^{1} \left( k \right) \cdot ag^{0} \left( k \right)} } } }}{{\left( {t - 1} \right) \cdot \sum\limits_{k = 2}^{t} {ag^{z} \left( k \right)^{2} - \left( {\sum\limits_{k = 2}^{t} {ag^{z} \left( k \right)} } \right)^{2} } }}$$
(17)

The throughput prediction for next stage is denoted by

$$a\hat{g}^{0} \left( {t + 1} \right) = \left( {ag^{0} \left( 1 \right) - \frac{agb}{aga}} \right) \cdot e^{ - aga \cdot t} \cdot \left( {1 - e^{aga} } \right)$$
(18)
Fig. 4
figure 4

Definition model of GM(1,1)

Full size image

5.2 Residual modification model

Residual modification model is used to correct the prediction error, which is given by

$$ar^{0} \left( k \right)\,=\,\frac{{a\hat{g}^{0} \left( k \right) - v\_actual\_\left( k \right)}}{v\_actual\_\left( k \right)},\quad k = \{ 1,2, \ldots ,t\}$$
(19)

The original sequence of prediction error is set to be the input of grey prediction model. Therefore, the prediction of error, which is defined as \(a\hat{r}^{0} \left( {t + 1} \right)\), will reduce the error between the predicted and actual throughputs. Finally, the throughput prediction with residual modification is given by

$$gv\_actual\_= a\hat{g}^{0} \left( {t + 1} \right) + a\hat{r}^{0} \left( {t + 1} \right) \cdot v\_actual\_\left( t \right)$$
(20)

5.3 Stability analysis of grey prediction

5.3.1 The condition of convergence

We analyze the stability of the grey prediction system according to Lyapunov’s second method. The definition of differential function of grey prediction is given by

$$\frac{{dx^{(1)} }}{dt} = x^{{(1){\prime }}} { = }agb - aga \cdot x^{(1)}$$
(21)

We define the positive definite function of Lyapunov as

$$V(x^{(1)} ) = (agb - aga \cdot x^{(1)} )^{2} { + }c,\left( {c > 0} \right)$$
(22)

The time derivative of V is given by

$$V(x^{(1)} )^{{\prime }} = - 2aga \cdot (agb - aga \cdot x^{(1)} ) \cdot x^{{(1)^{{\prime }} }}$$
(23)

Equation (23) can be rewritten as follows by combining with (21).

$$V(x^{(1)} )^{{\prime }} = - 2aga \cdot (agb - aga \cdot x^{(1)} )^{2}$$
(24)

According to Lyapunov’s second method [27], if aga is larger than zero, then \(V(x^{(1)} )^{{\prime }}\) is negative semi-definite, which means that the Eq. (21) has asymptotic stability about zero solutions. At the same time, the value of aga should belong to the range [−2/(t + 1),2/(t + 1)] for the sake of ensuring prediction accuracy in grey model [22]. Thus, we let the value of aga lie in the range (0, 2/(t + 1)].

5.3.2 Convergence rate of grey prediction

The solution of (21) is given by [22]

$$\hat{x}^{(1)} (t + 1) = \left( {x^{(1)} (0) - \frac{agb}{aga}} \right) \cdot \exp ( - aga \cdot t) + \frac{agb}{aga}$$
(25)

with prediction sequence \(\hat{x}^{(1)} (t + 1)\). The next stage prediction of \(x^{(0)} (t)\) can be calculated by

$$\hat{x}^{(0)} (t + 1) = \left( {x^{(1)} (0) - \frac{agb}{aga}} \right) \cdot \exp ( - aga \cdot t) \cdot (1 - \exp (aga))$$
(26)

under the relationship of \(x^{(0)} \left( {t + 1} \right) = x^{\left( 1 \right)} \left( {t + 1} \right) - x^{\left( 1 \right)} \left( t \right)\).

According to the definition, (26) can be rewritten as \(\hat{x}^{(0)} (t + 1) = \exp (aga) \cdot \hat{x}^{(0)} (t)\), which can be replaced with \(x_{t + 1} = g(x_{t} ) = \exp ( - aga) \cdot x_{t}\). We assume that the initial value of system is perturbed by \(\zeta_{0}\). Then, according to the Lyapunov exponential spectrum [27], the distance between original and interrupted values is by the following equation after N iterations

$$\zeta_{t} \cong \zeta_{0} \cdot \exp (\lambda \cdot t_{s} )$$
(27)

where t s represents continuous-time variable and \(\lambda\) is defined by

$$\lambda = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {\ln \left| {\frac{{df(x_{i} ,u)}}{dx}} \right|}$$
(28)

where N is the times of iterations, x i is the prediction value of the ith iteration.

Finally, the evaluation of the Lyapunov exponential spectrum of (28) is given by

$$\begin{aligned} \lambda & = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {\ln \left| {\frac{{df(x_{i} ,u)}}{dx}} \right|} \\ \quad & = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {\ln \left| {\frac{{dg(x_{i} ,u)}}{dx}} \right|} \\ \quad & = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {\ln \left| {\exp ( - aga)} \right|} \\ \quad & = - aga \\ \end{aligned}$$
(29)

From (29), (27) can be rewritten as \(\zeta_{t} \cong \zeta_{0} \cdot \exp ( - aga \cdot t_{s} )\). When aga∈(0,2/(t + 1)], the Lyapunov exponential spectrum \(\lambda \in [ - 2/(t + 1),0) < 0\). It means that the phase volume of system is contracted in this direction, and the movement is stable in this direction. Specifically, the distance between original and interrupted values decreases exponentially as \(\left| \lambda \right|\) increases. In other words, the convergence rate is exponential in the length of input data.

6 Mechanism of congestion control

In the process of transmission, we try to make a full use of available network capacity and follow the conditions and principles of Vegas simultaneously by combining quantification with Q-learning. From formulation (1, 12) and (20), the final diff is calculated by

$$diff = v\_expect\_- v\_actual\_= \left( {NV\_t - gv\_actual\_} \right) \cdot BaseRTT$$
(30)

6.1 RTT quantization

In order to take more proper actions according to the circumstances, we combine the throughput and the RTT quantization to control the cwnd change sizes, instead of only using the criterion of throughput. At the same time, the RTT is quantified to different degrees as the size of cwnd changes, which is described by

$$cwnd{ = }\left\{ {\begin{array}{*{20}l} {cwnd + bl{ + 1},} \hfill & {RTT \le \hbox{min} RTT} \hfill \\ {cwnd + bl + 1 - \frac{1}{{\left( {\hbox{max} RTT - \hbox{min} RTT} \right)^{2} }}\, \cdot \left( {RTT - \hbox{min} RTT} \right)^{2} ,} \hfill & {\hbox{min} RTT < RTT \le \hbox{max} RTT} \hfill \\ {wnd + bl,} \hfill & {\hbox{max} RTT < RTT} \hfill \\ \end{array} } \right. \,$$
(31)

In order to overcome the conservation of cwnd changes in traditional Vegas mechanism, minRTT and maxRTT in Eq. (31) are the minimal and maximal RTTs at each congestion control stage, respectively.

The random parameter bl is uniformly chosen in the interval \(\left[ {m_{sf} \cdot \gamma ,n_{sf} \cdot \gamma } \right]\), where γ value is −1, 0 or 1 according to throughput state,m sf and n sf are span factor which could determine the width of the range. Besides, we formulate the phase of CA as a MDP to explore the optimal value of bl for cwnd changing phases for the purpose of improving the accuracy of congestion control.

6.2 Q-learning exploration model

In the Q-learning model, we let the state S t be the different stages of cwnd changes. The action associated with a state is the value selection for bl. The return of R i (s,a i ) is set to be the value of the actual throughput. The purpose of the Q-learning is to choose the optimal action that maximizes the following Q function [28].

$$Q_{t + 1} \left( {s_{t} ,a_{t} } \right) = \left[ {1 - \alpha_{t} } \right] \cdot Q_{t + 1} \left( {s_{t} ,a_{t} } \right){ + }\alpha_{t} \cdot \left[ {R_{t + 1} + \left( {q\gamma } \right) \cdot \mathop {\hbox{max} Q_{t} \left( {s_{t + 1} ,a} \right)}\limits_{a} } \right]$$
(32)

where \(q\gamma \in \left( {0,1} \right]\) is a discount factor that denotes the relative importance of present and future rewards. Q converges to Q * with probability 1 [28] when the learning rate \(\alpha_{n}\) meets the condition \(\sum\nolimits_{i = 1}^{\infty } {\alpha_{{t\left( {i,s,a} \right)}} } = \infty ,\sum\nolimits_{i = 1}^{\infty } {\left( {\alpha_{{t\left( {i,s,a} \right)}} } \right)}^{2} < \infty\), where t(i,s,a) means that the action a is selected in state s in the ith iteration. The optimal strategy of s t is defined by \(\pi^{ *} \left( {s_{t} } \right){ = }\mathop {\text{argmax}}\limits_{{s_{t} }} Q^{*} \left( {s_{t} ,a} \right)\).

For a tradeoff between exploration and exploitation, we utilize the \(\varepsilon - greedy\) [29] action selection strategy, in which the optimal action is selected with probability of \(\varepsilon\).

6.3 Algorithm and complexity analysis

The algorithm of improved congestion avoidance control with prediction and self-adaption are summarized in Algorithm 1.

figure f

From Algorithm 1, the space and time complexities of Gvegas mainly rely on the ones of the grey model and Q-learning model. The space and time complexities of the grey prediction can be denoted by \(O_{sg} \left( t \right)\) and \(O_{tg} \left( {t - 1} \right)\), respectively. Similarly, the space and time complexity of Q-learning can be denoted by \(O_{qg} \left( {\left| S \right| \cdot \left| A \right|} \right)\) and \(O_{qg} \left( {\left| A \right|} \right)\) [29]. Therefore, the overall space complexity of Gvegas is \(O\left( {\left| S \right| \cdot \left| A \right|} \right)\), and the time complexity is \(O\left( {\hbox{max} \left( {\left| A \right|,\left( {t - 1} \right)} \right)} \right)\). In addition, there is no deployment difficulty for Gvegas which is realized only on the sender without any changes at routers and receivers.

7 Simulation results and discussions

We implement Gvegas in NS2 and verify its performance along with TCP Vegas and Newreno under different length of input data (t = 4, 5, 6, 7, 8) in three simulation scenarios: “chain”, “Reference Point Group Mobility Model (RPGM)” and “Wireless Mobile Ad Hoc Network (WMAHN)” scenarios, and each performance metric of scenario is computed by averaging results of 500 simulation runs. We assume that the Internet layer, MAC layer and queue manager use IP, IEEE 802.11 and RED protocols, respectively. All scenarios have the same MAC layer parameters given in Table 1. We set the span factor m sf  = 1, and n sf  = 3. The learning factor \(q\gamma\) and learning rate \(\alpha_{t}\) are equal to 0.95 and 0.3 [30], respectively. In addition,\(\varepsilon\) is set to be 0.8. One TCP flow in Gvegas, Vegas or Newreno is always transmitted from sender nodes 4 to receiver node 5 throughout the simulation in each scenario, and the end-to-end throughput and delay between node 4 and node 5 are collected to be the performance analysis parameters by gathering the simulation information from those two nodes. Each chain scenario simulation has a duration of 240 and 600 s for each RPGM and WMAHN scenario. For the purpose of better display, each four seconds is denoted as a timestamp in multi-hop chain scenario, and ten seconds for both RPGM and WMAHN scenario.

Table 1 MAC sub-layer parameters
Full size table

7.1 Multi-hop chain wireless network scenario

We assume that there are six nodes that have the identical transmission range of 150 meters and initial positions of those nodes are indicated in Fig. 5. In this simulation, a linear multi-hop chain is kept by all nodes with random velocities in a range [5, 8] m/s. The average throughput and delay of 500 runs among Gvegas, Vegas and Newreno are displayed by Fig. 6. In addition, the expectations of throughput and delay of 500 runs each with 240 s simulation of different prediction length of t = {4, 5, 6, 7, 8} are shown by Fig. 7.

Fig. 5
figure 5

Positions information of nodes

Full size image
Fig. 6
figure 6

The average simulation results of multi-hop chain network. a t = 4, b t = 5, c t = 6, d t = 7, e t = 8

Full size image
Fig. 7
figure 7

The expectation of throughput and delay of chain of different prediction length

Full size image

From Fig. 6, we compare the performance in terms of throughput and delay of Gvegas with those of Vegas and Newreno for different t = {4, 5, 6, 7, 8}. We can see that both the average throughput and delay of Gvegas are significantly improved compared with Vegas and Newreno, irrespective of the values of t in Fig. 6. From Fig. 7, we can further see that the throughput of Gvegas is improved more than doubled and fivefold in Vegas and Newreno, respectively. In addition, the delay of Gvegas is shorter by 42 and 90 % on average than Vegas and Newreno, respectively.

7.2 RPGM scenario

RPGM is a typical rescue type of ad hoc mobile group mode, in which each group has a logic center, and other nodes are equally distributed around the center. The group movement is represented by change of the center, including the position, velocity, direction and accelerated speed, etc.

Let a group have six nodes, each having the same transmission range of 80 m in a 800 × 600 m area. We assume that the group is formed by these six nodes randomly distributed in a sub-area of 200 × 200 m. The group’s velocity is uniformly randomly chosen in [1, 3] m/s with a random pause time when reaching a destination. The average throughput and delay of 500 simulation runs among Gvegas, Vegas and Newreno in RPGM are displayed by Fig. 8. In addition, the expectations of throughput and delay of 500 runs each with 600 s simulation of different prediction length of t = {4, 5, 6, 7, 8} are shown by Fig. 9.

Fig. 8
figure 8

The average simulation results of group ad hoc network. a t = 4, b t = 5, c t = 6, d t = 7, e t = 8

Full size image
Fig. 9
figure 9

The expectation of throughput and delay of RPGM of different prediction length

Full size image

From Fig. 8, we can see that the performance of Gvegas is greatly better than that of Vegas and Newreno in terms of both average throughput and transmission delay in RPGM. In more detail, Fig. 9 shows that Gvegas attains more throughputs than Vegas and Newreno by about 22 and 52 % on average for each t = {4, 6, 5, 7, 8}, and shorter delay by about 60 and 82 %, respectively. Because Gvegas has the capability to foresee the environment conditions in the near future, Gvegas can take reasonable actions before collision or congestion based on the prediction. As demonstrated in Sect. 5.3, the shorter the input data length of prediction is, the faster the convergence rate is. The simulation results in RPGM scenario further confirm that the curves of both throughput and delay in forecast sequence of t = 4 are more smoothly than other prediction length.

7.3 WMAHN scenario

WMAHN is a self-configuring, dynamic network in which nodes are free to move. We assume that ten nodes are randomly distributed in a square area of 300 × 300 m area and each node has the same transmission range of 80 m. In addition, we let the node’s velocity be uniformly randomly chosen in [1, 5] m/s with a random pause time in [0,5]s when arriving at a destination. The average throughput and delay of 500 simulation runs among Gvegas, Vegas and Newreno in WMAHN are displayed by Fig. 10. Furthermore, the expectations of throughput and delay of 500 runs each with 600 s simulation of different prediction length of t = {4, 5, 6, 7, 8} are shown by Fig. 11.

Fig. 10
figure 10

The average simulation results of mobile ad hoc network. a t = 4, b t = 5, c t = 6, d t = 7, e t = 8

Full size image
Fig. 11
figure 11

The expectation of throughput and delay in WMAHM of different prediction length

Full size image

From Fig. 10, we can see that the performance of Gvegas is obviously better than that of Vegas and Newreno after a few simulation times. At the beginning of simulation, Gvegas is not stable since the perception of dynamic environment is not enough for Q-learning and Grey predictor. But, the throughput and delay of Gvegas become better than Vegas and Newreno through exploration about 100 s. This is further explained in Fig. 11, which shows that the expectation of throughput of Gvegas is better than that of Vegas and Newreno by about 60 % and five times for each t = {4, 6, 5, 7, 8}, and delay shorter by about 60 and 80 %, respectively. Besides, the simulation results confirm that the curves of both throughput and delay in forecast sequence of t = 4 are more smoothly than other prediction length.

8 Conclusions

This paper uses the cross-layer throughput model to calculate the achievable throughput and predict the throughput of the next time stage based on grey theory for real-time congestion control. In addition, the quantization of RTT is performed by the optimal action exploration of Q-learning. The convergence condition and rate of grey model based on Lyapunov’s second method have shown the effectiveness of the improved method. Simulation results show that the performance of our proposed scheme greatly outperforms the Vegas and Newreno in terms of both average throughput and delay in multi-hop ad hoc networks. From simulation results and convergence analysis, we suggest that the prediction length t = 4 is a reasonable choice for typical scenarios.