1 Introduction

Accurate and reliable monthly runoff forecasting plays an important role in water resources management, such as water supply (Şen 2021), hydroelectric generation and ecological restoration. Generally, existing methods can be approximately partitioned into data-driven (Chu et al. 2021; Feng et al. 2021; Liao et al. 2020; Riahi-Madvar et al. 2021) and physical-based models (Abuzied and Mansour 2019; Abuzied and Pradhan 2020; Abuzied et al. 2016; Bournas and Baltas 2021; Budamala and Mahindrakar 2020; El Harraki et al. 2021; Liao et al. 2016). Data-based models can simulate the relationship between input and output without regard to complex mechanisms of runoff generation (Niu et al. 2019). In contrast, physical-based models take into account specific physical process and demand mass data, such as underlying surface conditions, human activity influences and climate change, which are not easily collected (Feng and Niu 2021). Unlike the physical-based models, the data-based models demand less data and can offer satisfactory forecast results. As a typical representative of data-based models, artificial neural networks (ANN) have been widely and successfully utilized in hydrology-related areas, for instance, precipitation forecasting (Nourani et al. 2009), runoff forecasting (Shu et al. 2021; Noorbeh et al. 2020), and water level forecasting (Seo et al. 2015). In recent decades, numerous ANN architectures and algorithms have been investigated in hydrological time series forecasting (ASCE-Task-Committee 2000).

Long short-term memory neural networks (LSTM) proposed by Hochreiter and Schmidhuber (1997) are a special kind of recurrent neural network (RNN) and have the merits of fast convergence and good nonlinear predictive capability. To avoid the problems of training long sequences and vanishing gradients faced by the traditional RNN, LSTM implement constant error flow via constant error carrousels within special memory cells. Referring to LSTM, many studies have been conducted on hydrological time series forecasting (Lv et al. 2020; Ni et al. 2020; Wang et al. 2021). Nevertheless, the hyperparameters of LSTM are predetermined, which has a certain impact on forecast accuracy. In general, there are two main methods to improve the forecast accuracy in previous studies. The first is to combine decomposition algorithms to decompose original time series data into several subcomponents, employ LSTM to simulate each subcomponent, and aggregate the results of each subcomponent as the final result (Lv et al. 2020). Zuo et al. (2020), for example, proposed single-model forecasting based on VMD and LSTM to predict daily streamflow 1–7 days ahead and investigated the robustness and efficiency of the proposed model for forecasting highly nonstationary and nonlinear streamflow. The second is to utilize optimization algorithms to optimize the hyperparameters of the LSTM (ElSaid et al. 2018). Yuan et al. (2018), for example, used the ant lion optimizer (ALO) to calibrate the parameters of the LSTM, and verified its effectiveness with the historical monthly runoff of the Astor River Basin. At present, there are several commonly used decomposition algorithms (Colominas et al. 2014; Roushangar et al. 2021; Shahid et al. 2020); for instance, wavelet decomposition, empirical mode decomposition (EMD) and VMD. Optimization algorithms, such as particle swarm optimization and ant colony optimization, can be seen in the literature as optimizing the parameters of neural networks (Wan et al. 2017; Yu et al. 2008). In this study, both methods are considered.

Variational mode decomposition (VMD) (Dragomiretskiy and Zosso 2014) is an entirely nonrecursive variational model that can extract modes concurrently. Via VMD, a signal can be decomposed into a sequence of subcomponents with different frequency bands and time resolutions (Fang et al. 2019). Compared to empirical mode decomposition (EMD), VMD is capable of separating tones of similar frequencies. VMD has been widely applied in many research fields, such as fault diagnosis (Zhang et al. 2017), signal processing (Wang et al. 2017), wind speed monitoring (Liu et al. 2018) and hydrological time series forecasting (Feng et al. 2020; Li et al. 2021; Sibtain et al. 2021). In this study, VMD was selected as a data preprocessing tool to decompose monthly runoff series. In recent years, an emerging swarm intelligence algorithm called the gray wolf optimizer (GWO) has been proposed, which imitates the social hierarchy and hunting behavior of gray wolves (Mirjalili et al. 2014). With its strong robustness and searching ability in solving optimization problems, the GWO has been widely and successfully applied in many fields, such as model parameter calibration (Tikhamarine et al. 2020), reservoir operation (Niu et al. 2021) and optimal power dispatch (Nuaekaew et al. 2017). Hence, in view of its strong robustness and searching ability, the GWO can be adopted to optimize the hyperparameters of LSTM.

In this paper, a hybrid model, referred to as the VMD-GWO-LSTM, is proposed for monthly runoff forecasting. According to the monthly runoff series of two real-world hydropower reservoirs in China, the proposed method is certified to be feasible. The innovation of this study can be stated as follows. (1) To decrease modeling difficulty, VMD is adopted to decompose monthly runoff series into several simple subcomponents. (2) For each subcomponent, the input–output relationships are identified by the LSTM, and the GWO method is employed to optimize the hyperparameters of the LSTM. (3) The results of the case study indicate that, compared to several traditional models, the proposed hybrid VMD-GWO-LSTM method can yield better forecast accuracy. To our knowledge, there have been few studies combining VMD, LSTM, and GWO to forecast monthly runoff, demonstrating that this study has the potential to fill this gap.

The rest of this work is organized as follows: Sect. 2 describes the details of the proposed approach; in Sect. 3, the proposed method is utilized to forecast the monthly runoff of two reservoirs; and finally, the conclusions are summarized.

2 Methodology

2.1 Variational Mode Decomposition

VMD is a novel variational method that can nonrecursively decompose a nonstationary signal into a given number of mode functions, and each individual mode is compact around its center frequency (Dragomiretskiy and Zosso 2014). To obtain each mode and its center frequency, a constrained variational problem can be expressed as follows:

$$\left\{ \begin{gathered} \mathop {\min }\limits_{{\left\{ {u_{k} (t)} \right\},\left\{ {\omega_{k} (t)} \right\}}} \left\{ {\sum\limits_{k} {\left\| {\partial_{t} \left[ {\left( {\delta (t) + \frac{j}{\pi t}} \right)*u_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|}_{2}^{2} } \right\} \hfill \\ s.t.\sum\limits_{k} {u_{k} (t) = f(t)} \hfill \\ \end{gathered} \right.$$
(1)

where t is the time step; \(u_{k} (t)\) and \(\omega_{k} (t)\) denote the k-th mode and its corresponding center frequency, respectively; \(\delta (t)\) is the Dirac distribution, * denotes the convolution calculation; and \(f\left( t \right)\) denotes the t-th data of the input signal.

To facilitate the solution, the quadratic penalty factor \(\alpha\) and the Lagrangian multiplier \(\lambda\) are introduced to transform the constrained variational problem into an unconstrained variational problem. Hence, the augmented Lagrangian structure can be expressed as follows:

$$\begin{aligned}L\left( {\left\{ {u_{k} } \right\},\left\{ {\omega_{k} } \right\},\lambda } \right) &= \alpha \sum\limits_{k} {\left\| {\partial_{t} \left[ {\left( {\delta (t) + \frac{j}{\pi t}} \right)*u_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|}_{2}^{2} \\&+ \left\| {\kern 0.1500em f(t) - \sum\limits_{k} {u_{k} (t)} } \right\|_{2}^{2} + \left\langle {\lambda (t),f(t) - \sum\limits_{k} {u_{k} (t)} } \right\rangle\end{aligned}$$
(2)

where \(\left\langle \cdot \right\rangle\) represents the inner product operation.

Equation (2) can then be solved by the alternating direction method of multipliers (ADMM) to obtain the saddle point of the augmented Lagrangian function. In the ADMM, the variables (\(\hat{u}_{k}^{n + 1}\),\(\omega_{k}^{n + 1}\) and \(\hat{\lambda }^{n + 1}\)) are continuously updated to optimize each modal component.

2.2 Long Short-term Memory Neural Networks

As a type of deep learning neural networks, the LSTM was proposed to overcome the vanishing/exploding gradient problem faced by traditional RNN (Hochreiter and Schmidhuber 1997). The LSTM takes the place of the conventional hidden unit with a memory cell and contains multiple memory blocks, each of which includes three gates: input gate, forget gate and output gate and at least one memory cell. By using the LSTM, information from the three gates can be added or deleted to the memory cell state. Based on the previous state, current memory and current input, the LSTM has the ability to decide which cells are restrained and promoted and on the basis of the three gates what information is saved and forgotten during the training process (Altan et al. 2021). The structure of the LSTM is shown in Fig. 1. For the three gates, the multiplicative input gate unit is employed to recognize new information that can be gathered in the cell; the multiplicative output gate unit is utilized to compute the information that can be propagated to the network; and the multiplicative forget gate unit is used to decide whether the last status of the cell can be forgotten (Li et al. 2018).

Fig. 1
figure 1

Schematic diagram of long short-term memory neural networks

Full size image

The calculation of the three gates and cell state can be generally expressed as follows:

$$\begin{gathered} f_{t} = \sigma \left( {W_{f} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{f} } \right) \hfill \\ i_{t} = \sigma \left( {W_{i} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{i} } \right) \hfill \\ \tilde{c}_{t} = \tanh \left( {W_{c} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{c} } \right) \hfill \\ c_{t} = f_{t} \odot c_{t - 1} + i_{t} \odot \tilde{c}_{t} \hfill \\ o_{t} = \sigma \left( {W_{o} \odot \left[ {h_{t - 1} ,x_{t} } \right] + b_{0} } \right) \hfill \\ h_{t} = o_{t} \cdot \tanh \left( {c_{t} } \right) \hfill \\ \end{gathered}$$
(3)

where \(f_{t}\), \(i_{t}\), \(o_{t}\) denote the output of the forget gate, input gate and output gate, respectively; \(\tilde{c}_{t}\) is the potential cell state; \(c_{t}\) and \(h_{t}\) denote the cell state and cell output at time t, respectively; \(W_{f}\), \(W_{i}\), \(W_{c}\) \(W_{o}\) and \(b_{f}\), \(b_{i}\), \(b_{c}\), \(b_{0}\) denote weight matrices and the corresponding bias vectors, respectively; \(x_{t}\) is the input at time t; \(\sigma\) is the sigmoid function; and \(\odot\) denotes matrix multiplication.

It is worth noting that the LSTM relies heavily on a set of hyperparameters to achieve good performance, which usually requires a certain amount of practical experience to manually select and optimize the hyperparameters. Therefore, for convenience, automatic algorithmic approaches with the ability to converge faster and gain an optimal/near optimal solution within an acceptable time can be employed to enhance the performance of the LSTM (Nakisa et al. 2018).

2.3 Gray Wolf Optimizer

The GWO algorithm is a novel swarm intelligent optimization algorithm that simulates the leadership hierarchy and predation strategy of gray wolves (Mirjalili et al. 2014). Gray wolves possess a very strict social dominant hierarchy, which can be divided into four categories: alpha wolf (α), beta wolf (β), delta wolf (δ) and omega wolf (ω). The alpha dominates the whole wolf pack and is responsible for making decisions. Beta wolves are subordinate to the alpha in the hierarchy but command delta and omega wolves as well. The hunting process of gray wolves can be divided into three stages: (i) tracking, chasing and approaching prey; (ii) hunting, surrounding and cornering the prey until it stops moving; and (iii) attacking the prey (Mirjalili et al. 2014). The GWO algorithm can be generally described as follows.

First, encircling prey is carried out by the gray wolves before the hunting process, which can be defined as follows:

$$\vec{D} = \left| {\vec{C} \cdot \vec{X}_{p} (t) - \vec{X}(t)} \right|$$
(4)
$$\vec{X}(t + 1) = \vec{X}(t) - \vec{A} \cdot \vec{D}$$
(5)
$$\vec{A} = 2\vec{a} \cdot \vec{r}_{1} - \vec{a}$$
(6)
$$\vec{C} = 2 \cdot \vec{r}_{2}$$
(7)

where t is the current iteration; \(\vec{D}\) is the distance between the gray wolf and the prey; \(\vec{X}_{P} (t)\) is the position vector of the t-th prey; \(\vec{X}(t)\) is the position vector of the t-th gray wolf; \(\vec{A}\) and \(\vec{C}\) are coefficient vectors; \(\vec{r}_{1}\) and \(\vec{r}_{2}\) are random numbers in [0,1]; and \(\vec{a}\) is a transition parameter that is linearly reduced from 2 to 0 during the iterative computation.

Then, the hunting process is implemented. After recognizing the position of the prey and encircling it, the wolves will hunt the prey, which is guided by the alpha and the beta and delta will occasionally participate. The formulas are given as follows, in which other wolves should be obeyed to update their positions:

$$\left\{ \begin{gathered} \vec{D}_{\alpha } = \left| {\vec{C}_{1} \cdot \vec{X}_{\alpha } - \vec{X}} \right| \hfill \\ \vec{D}_{\beta } = \left| {\vec{C}_{2} \cdot \vec{X}_{\beta } - \vec{X}} \right| \hfill \\ \vec{D}_{\delta } = \left| {\vec{C}_{3} \cdot \vec{X}_{\delta } - \vec{X}} \right| \hfill \\ \end{gathered} \right.$$
(8)
$$\left\{ \begin{gathered} \vec{X}_{1} = \vec{X}_{\alpha } - A_{1} \cdot \vec{D}_{\alpha } \hfill \\ \vec{X}_{2} = \vec{X}_{\beta } - A_{2} \cdot \vec{D}_{\beta } \hfill \\ \vec{X}_{3} = \vec{X}_{\delta } - A_{3} \cdot \vec{D}_{\delta } \hfill \\ \end{gathered} \right.$$
(9)
$$\vec{X}(t + 1) = \frac{{\vec{X}_{1} + \vec{X}_{2} + \vec{X}_{3} }}{3}$$
(10)

Finally, attacking prey is executed. To simulate being close to the prey, the value of \(\vec{a}\) is decreased linearly, and correspondingly, the fluctuation range of \(\vec{A}\) is also decreased within the interval of [-2a, 2a]. When \(\vec{A}\) ranges in [-1, 1], the next position of a gray wolf in any position is between its current position and the position of the prey (Mirjalili et al. 2014). Thus, the attack on the prey can be realized.

2.4 Hybrid Model for Monthly Runoff Forecasting

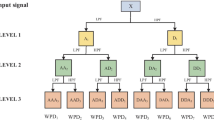
To improve the forecast accuracy of monthly runoff forecasting, a hybrid model shortened to the VMD-GWO-LSTM is proposed and illustrated in Fig. 2. The main procedure can be described as follows:

  • Step 1: Data preprocessing. VMD is utilized to decompose the original runoff sequence to obtain K subsequences with different frequencies. All subsequences that are divided into calibration and validation data are normalized to [-1, 1].

  • Step 2: Input determination. The partial autocorrelation function (PACF) is utilized to determine the input variables of each subsequence for the LSTM model.

  • Step 3: Hyperparameter optimization. For each LSTM model, the optimal parameters of the number of hidden layer neurons, the number of epochs and the learning rate are searched by the GWO, and root-mean-squared error (RMSE) is selected as the optimization criterion.

  • Step 4: Aggregation. The forecast results of all subsequences are arithmetically aggregated as the final forecast results.

Fig. 2
figure 2

The flowchart of VMD-GWO-LSTM for monthly runoff forecasting

Full size image

2.5 Evaluation Index

In this section, four evaluation indices namely, RMSE, mean absolute percentage error (MAPE), coefficient of correlation (R) and Nash–Sutcliffe efficiency coefficient (CE), are employed. Generally, the smaller RMSE and MAPE are and the higher R and CE are, the better the model performance. These indices are listed below:

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(Q_{i} - \hat{Q}_{i} )^{2} } }$$
(11)
$$MAPE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{Q_{i} - \hat{Q}_{i} }}{{Q_{i} }}} \right|} \times 100$$
(12)
$$R = \frac{{\sum\limits_{i = 1}^{n} {(Q_{i} - \overline{Q}_{i} )(\hat{Q}_{i} - \overline{\hat{Q}}_{i} )} }}{{\sqrt {\sum\limits_{i = 1}^{n} {(Q_{i} - \overline{Q}_{i} )^{2} \sum\limits_{i = 1}^{n} {(\hat{Q}_{i} - \overline{\hat{Q}})^{2} } } } }}$$
(13)
$$CE = 1 - \frac{{\sum\limits_{i = 1}^{n} {(Q_{i} - \overline{Q}_{i} )^{2} } }}{{\sum\limits_{i = 1}^{n} {(Q_{i} - \overline{Q})^{2} } }}$$
(14)

where \(n\) is the number of observed data; \(Q_{i}\) and \(\hat{Q}_{i}\) are the observed and forecasted values, respectively; and \(\overline{Q}_{i}\) and \(\overline{\hat{Q}}_{i}\) are the averages of all observed and forecasted values, respectively.

3 Case Studies

3.1 Study Area and Data

Two multipurpose reservoirs, the Xinfengjiang and Guangzhao Reservoirs located in China, were selected as case studies. The Xinfengjiang Reservoir is located on the Xinfeng River, which is the largest tributary of the Dongjiang River and a second-level tributary of the Pearl River. Located in Heyuan city, Guangdong Province, the Xinfeng River Basin has a subtropical monsoon climate. With obvious interannual and seasonal variations, the annual average precipitation is 1742.0 mm, of which approximately 76% is accounted for from April to September. The total drainage area of the Xinfeng River Basin is 5813 km2 and the upstream area of the Xinfengjiang Reservoir is 5740 km2. With an average gradient of 1.29%, the length of the river is 163 km. Mainly constituted of hills and mountains, the terrain of the Xinfeng River Basin is low in the west and high in the east. For the Xinfeng River Baisn, the mountainous area accounts for 33.6%, and the hilly area accounts for 63.5%. With 336.1 MW of installed capacity and 13.896 billion m3 of storage volume, the Xinfengjiang Reservoir is the largest reservoir in southern China. For the Xinfengjiang Reservoir, the primary goal is power generation. The Guangzhao Reservoir is located on the middle reaches of the Beipan River, which is a tributary of the Xijiang River and a second-level tributary of the Pearl River. Located on the slope of the Yunnan-Guizhou Plateau, the Beipan River Basin is connected to the hilly basin of central Guizhou Province in the east and has a subtropical plateau monsoon climate. With an obvious seasonal variation, the annual average precipitation is 1178.0 mm, of which approximately 80% is accounted for from May to September. The total drainage area of the Beipan River Basin is 26557 km2 and the upstream area of the Guangzhao Reservoir is 13548 km2. With an average gradient of 0.437%, the length of the river is 441.9 km. The terrain of the Beipan River Basin is high in the northwest and low in the southeast. For the Beipan River basin, the mountainous area accounts for 85%, and the hilly area accounts for 10%. With 1040 MW of installed capacity and 3.245 billion m3 of storage volume, the primary goal of the Guangzhao Reservoir is power generation. Hence, accurate monthly runoff forecasting is vital for these two reservoirs.

Monthly runoff series data from the Xinfengjiang and Guangzhao Reservoirs were retrieved to validate the proposed method. The monthly runoff data for the Xinfengjiang Reservoir cover 1943 to 2015 and the data for the Guangzhao Reservoir cover 1956 to 2017. For these two reservoirs, approximately 70% of the data were used for calibration, and the remaining data were used for validation.

3.2 Decomposition Results

According to VMD, the key parameter of the number of modes should be predefined, which affects the decomposed results (Wen et al. 2019). To obtain satisfactory performance, the traditional EMD method was employed to ascertain the number of subsequences. The decomposed results for the Xinfengjiang Reservoir utilizing VMD and EMD are shown in Fig. 3. There were significant differences in the acquired subcomponents for the two reservoirs, which indicate the variability of VMD and EMD in extracting intrinsic information from the original monthly runoff series.

Fig. 3
figure 3

Decomposed results of monthly runoff data in Xinfengjiang Reservoirs

Full size image

3.3 Input Determination

The selection of input variables that directly affect the forecast results, should be predetermined. As a statistical method, the partial autocorrelation function (PACF) can be employed to analyze and determine the input variables (Feng et al. 2020; He et al. 2019). In practice, the input variables are often determined by means of the PACF values in which the previous values are selected as inputs when all PACF values fall into the confidence interval. It is worth mentioning that if the number of input variables is too small, the forecast accuracy of the model will be low. Hence, the determination of the input variables is also needed based on experience or other methods. In this study, the input variables were determined by the fact that if the number of input variables was equal to or less than 2 for the first time, PACF values falling back into the confidence interval in the second time could be considered. The PACF values for the original and decomposed subsequences of the Xinfengjiang Reservoir data are shown in Fig. 4. On the basis of Fig. 4, the input variables for each sequence of Xinfengjiang Reservoir data could be determined. From Table 1, it can be easily seen that the numbers of input variables for the original and decomposed data are similar but not always the same, indicating the complex and variable features of the data from the two reservoirs.

Fig. 4
figure 4

PACF values of each series from the Xinfengjiang Reservoir

Full size image
Table 1 The selected input values of each series for the Xinfengjiang and Guangzhao Reservoirs
Full size table

3.4 Model Development

To confirm the feasibility of the proposed method, five models were employed for comparison, namely, backpropagation neural networks (BPNN), support vector machine (SVM), LSTM, VMD-LSTM and EMD-LSTM models. The details of the models are stated as follows.

  1. 1.

    BPNN, SVM and LSTM models.

    The original monthly runoff data were used to calibrate the parameters of the BPNN, SVM and LSTM models. In this study, the input variables for the three models were set based on PACF values of the original series. For the BPNN model, three layers were employed, the output nodes were set as 1, and the hidden nodes were set by a trial-and-error procedure. For the SVM model, the radial basis function was chosen as the kernel function, and the genetic algorithm was used to optimize the parameters. For the LSTM model, the number of hidden layers was 2, the output nodes were set as 1 and the hidden units for each hidden layer were set by a trial-and-error procedure. In addition, the hyperparameters, i.e., epoch and learning rate, were also set by a trial-and-error procedure.

  2. 2.

    VMD-LSTM and EMD-LSTM models.

    For the VMD-LSTM and EMD-LSTM models, there were there three main steps to be implemented. First, the original monthly runoff data were decomposed into several subsequences using VMD or EMD. Second, the standard LSTM model was employed to simulate each subsequence, and the input variables for each subsequence are listed in Table 1. Finally, the results for each subsequence were aggregated as the final results.

3.5 Forecast Results

3.5.1 Results for the Xinfengjiang Reservoir

According to the aforementioned methods, the original monthly runoff series and extracted subsequences were simulated. The detailed evaluation indices of different models over the calibration and validation periods for the Xinfengjiang Reservoir are presented in Table 2. It can be intuitively found that compared with the BPNN, SVM, LSTM, EMD-LSTM and VMD-LSTM models, VMD-GWO-LSTM could yield the best results in terms of all four evaluation indices in both the calibration and validation periods. For instance, compared with the standalone BPNN model, the proposed hybrid VMD-GWO-LSTM model could provide better forecast accuracy with decreases of 77.95% and 75.57% in terms of RMSE and MAPE and increases of 81.67% and 397.93% in terms of R and CE during the validation period, respectively. As seen in Table 3, the hybrid models, such as EMD-LSTM and VMD-LSTM, consisting of LSTM and decomposed methods outperformed the standalone LSTM model in terms of all four evaluation indices during the calibration and validation periods. For example, compared with the LSTM method, the VMD-LSTM model performed better with decreases of 72.06% and 57.51% in terms of RMSE and MAPE and increases of 52.66% and 154.96% in terms of R and CE during the validation period. In addition, Table 2 also reveals that the proposed hybrid model VMD-GWO-LSTM performed slightly better than the VMD-LSTM model in terms of the four measures both in the calibration and validation periods.

Table 2 Comparison of evaluation indexes of different models for the Xinfengjiang Reservoir
Full size table
Table 3 Peak flow estimates of different models for the Xinfengjiang Reservoir during the validation period
Full size table

To detect the performance of tracing dynamic changes in the monthly runoff, a comparison of forecasted versus observed runoff data using BPNN, SVM, LSTM, EMD-LSTM, VMD-LSTM and VMD-GWO-LSTM for the Xinfengjiang Reservoir is depicted in Fig. 5. On the whole, all models could simulate monthly runoff to some extent except for significant differences in peak flow prediction, indicating that different models have different abilities to simulate peak runoff. To comprehend the performance of the models, the scatter diagrams for the Xinfengjiang Reservoir show fewer scatters with the VMD-GWO-LSTM than the other five models and are consistent with the results in Table 2.

Fig. 5
figure 5

Comparison of the forecast results for the Xinfengjiang Reservoir during the validation period

Full size image

In addition, to assess the performance of the proposed hybrid mode in peak flow forecasting, peak flow estimates of different models over the validation period for the Xinfengjiang Reservoir can be processed by statistical analysis. As shown in Table 3, the absolute average of the relative error of the BPNN, SVM, LSTM, EMD-LSTM, VMD-LSTM and VMD-GWO-LSTM for forecasting the 21 peak flows were 38.9%, 46.0%, 43.7%, 23.2%, 10.8% and 9.4%, respectively. It can be easily concluded that in the aspect of peak flow forecasting, the VMD-GWO-LSTM model can yield much better forecast accuracy than BPNN, SVM, LSTM and EMD-LSTM models and outperform slightly better forecasts than the VMD-LSTM model.

3.5.2 Results for the Guangzhao Reservoir

The statistics of different models over the calibration and validation periods for the Guangzhao Reservoir are shown in Table 4. It can be easily seen that the hybrid methods, namely, EMD-LSTM, VMD-LSTM and VMD-GWO-LSTM, display better performance than the standalone BPNN, SVM and LSTM methods. Furthermore, Table 4 also reveals that the forecast accuracy of the LSTM model can be enhanced under the condition of optimized hyperparameters. For instance, compared to the SVM model, the VMD-LSTM model can provide better forecast accuracy with decreases of 59.06% and 65.66% in terms of RMSE and MAPE and increases of 31.73% and 80.51% in terms of R and CE during the validation period, respectively. Compared to the VMD-LSTM model, the VMD-GWO-LSTM model can provide better forecast accuracy with decreases of 36.13% and 21.39% in terms of RMSE and MAPE and increases of 2.61% and 5.34% in terms of R and CE during the validation period, respectively. Hence, this reconfirms that the proposed hybrid model is superior to the other models utilized in this study.

Table 4 Comparison of evaluation indexes of different models for the Guangzhao Reservoir
Full size table

The forecast results of different models for the Guangzhao Reservoir during the validation phase are shown in Fig. 6. It is clear from the hydrographs that the BPNN model had the worst performance in tracing dynamic changes in the monthly runoff, and the remaining models had satisfactory forecast results. It can be intuitively found that the VMD-GWO-LSTM model could offer the least forecast results among the six models and had the best performance with a trendline very near the observed data line.

Fig. 6
figure 6

Comparison of the forecast results for the Guangzhao Reservoir during the validation period

Full size image

Table 5 lists the statistics of the peak flow estimates of different models for the Guangzhao Reservoir during the validation period. From Table 5, the absolute average of the relative error of the BPNN, SVM, LSTM, EMD-LSTM, VMD-LSTM and VMD-GWO-LSTM models for forecasting the 18 peak flows were 31.4%, 33.2%, 31.7%, 15.8%, 7.6% and 6.2%, respectively. Thus, in terms of peak flow forecasting, the VMD-GWO-LSTM model can perform much better than the BPNN, SVM, LSTM and EMD-LSTM models, and slightly better than the VMD-LSTM model. As a consequence, the VMD-GWO-LSTM model is an efficient method for monthly runoff forecasting due to its superior performance over comparable models during the validation period.

Table 5 Peak flow estimates of different models for the Guangzhao Reservoir during the validation period
Full size table

3.6 Discussion

The statistics of the forecast results yielded by the models clearly indicate that the proposed model can offer the best performance among these models. In reality, once built, the proposed model can be used for one-step monthly runoff forecasting on the condition that the decomposition of the observed runoff data is executed and the forecast results of each subseries are aggregated. Generally, multistep monthly runoff forecasting can also be carried out iteratively. That is, the results of the current one-step monthly runoff forecasting are decomposed and selected as inputs to forecast the next one-step monthly runoff.

According to the forecast results provided by BPNN, SVM and LSTM, it can be directly found that there are significant differences in terms of the four evaluation indices, demonstrating the importance of model selection and model parameter calibration. For the BPNN model, the gradient-based training algorithms have some drawbacks, such as overfitting and local optima. The ordinary SVM employing the structural risk-minimization principle can obtain good generalization performance. Nonetheless, the performance of SVM usually relies on the optimization algorithm to optimize the parameters, and many studies can be found in the literature (Feng et al. 2020). As a deep learning algorithm, the LSTM can overcome the vanishing/exploding gradient problem faced by traditional RNN and can exhibit good generalization performance in hydrological time series prediction (Kratzert et al. 2018). Influenced by many factors such as human activities and climate change, runoff usually contains multifrequency components (Niu et al. 2019). Hence, it is difficult to use a standalone prediction model to completely simulate runoff precisely because only one resolution component is used and the underlying multiscale phenomena cannot be unraveled. According to the literature (Lv et al. 2020; Zuo et al. 2020), adopting decomposition methods can effectively forecast the accuracy of the LSTM model. As decomposition methods, EMD and VMD are utilized to identify the multifrequency components to decrease the modeling difficulty. Therefore, the EMD-LSTM and VMD-LSTM models performed better than the standalone LSTM. Although many successful applications of the LSTM have not involved how to optimize the hyperparameters, it is still worth considering hyperparameter optimization to enhance model performance, and swarm intelligent algorithms (i.e., GWO) can be selected as possible solutions. As revealed by Yuan et al. (2018), the hyperparameter optimization of LSTM models can enhance model performance. Consequently, the proposed VMD-GWO-LSTM model outperformed the VMD-LSTM model. Hence, the framework of the “decomposition-optimization-model” in using the LSTM, such as VMD-PSO-LSTM, was verified effectively for hydrological forecasting (Wang et al. 2021).

The probable causes of the VMD-GWO-LSTM model being superior to the comparable models can be generally attributed to the contribution of VMD and hyperparameter optimization based on the GWO in the LSTM. VMD can decompose the monthly runoff time series into several subsequences and can reveal the underlying multiscale phenomena implied in the monthly runoff time series. Each subsequence was simulated by the LSTM with hyperparameter optimization conducted by the GWO, which can identify the dynamic changes and decrease the modeling difficulty. Meanwhile, automatic optimization of hyperparameters of the LSTM conquers the drawbacks of presetting parameters, easily causing lower forecast accuracy.

Although the feasibility of the VMD-GWO-LSTM model was verified with monthly runoff data derived from two reservoirs, further research should be conducted in the future. Although the GWO has stronger robustness and searching ability than the PSO in solving optimization problems, the comparison of VMD-GWO-LSTM and VMD-PSO-LSTM models was not made in this study and can be carried out in the future. It is necessary to involve new and excellent decomposition algorithms to enhance the quality of subsequences. Of course, more machine learning techniques should be investigated and verified to improve the single model forecast accuracy. Furthermore, the standard swarm optimization algorithms, for example the GWO used in this study, should be modified to improve the quality of parametric optimization for the models.

4 Conclusion

In this study, a hybrid model, VMD-GWO-LSTM, is proposed for forecasting monthly runoff. This innovation was implemented in three steps. First the original monthly runoff data were decomposed into several subsequences. Second, each subsequence was simulated by a standalone LSTM model, of which the hyperparameters, including learning rate, epochs and hidden layer neurons, were optimized by GWO. Finally, all outputs of the standalone LSTM for each subsequence were aggregated as the final forecast results. Monthly runoff data derived from two reservoirs (Xinfengjiang and Guangzhao Reservoirs) located in China were employed to investigate the proposed hybrid model. To evaluate the model performance, four commonly used statistical evaluation indices were utilized, and five models, namely, BPNN, SVM, LSTM, EMD-LSTM and VMD-LSTM, were used for comparison. The results indicated that the proposed model outperformed the five models in terms of all four evaluation indices. The proposed method is easy to understand and implement. Hence, it is feasible and promising for improving the forecasting accuracy of monthly runoff prediction. Furthermore, it also provides a useful tool for solving other hydrological time series forecasting, such as water level forecasting.