1 Introduction

Every water distribution network (WDN) consists of various elements such as pipes, junctions, reservoirs, tanks and valves. The main aim of a WDN is to supply water at the required pressure and flow rate. As WDNs involve high construction costs, there is a high requirement for a cost-effective network design. The cost of the network increases with increasing the size of its elements. Thus, the selection of optimum pipe diameters is required for the optimal design of WDN. Even for a small pipe network, there are thousands of pipe combinations available. For example, there are 108 pipe size combinations for a small eight-pipe network with ten available pipe sizes. Therefore, it is difficult to get the optimum results using classical optimization techniques.

The use of stochastic techniques is vastly suggested in the literature for problems that have large search spaces. Savic and Walters (1997), Wu and Simpsons (2002), and Kadu et al. (2008) are only few of many researchers who used genetic algorithms (GA) in this area. An extensive literature is available on application of several other evolutionary algorithms (EAs) in WDN optimization. For instance, simulated annealing (SA) (Cunha and Sousa 1999), ant colony optimization (ACO) (Maier et al. 2003), shuffled frog leaping algorithm (SFLA) (Chung and Lansey 2009), harmony search (HS) (Geem 2006), particle swarm optimization (PSO) (Suribabu and Neelakantan 2006), differential evolution (DE) (Suribabu 2010; Dong et al. 2012), developed swarm optimizer (DSO) (Sheikholeslami and Talatahari 2016). In recent optimization studies, Fallah et al. (2019) applied improved crow search (ICS) algorithm and Pankaj et al. (2020) used self-adaptive cuckoo search (SACS) algorithm.

Most of these algorithms are evolutionary algorithms or metaphor-based algorithms inspired by the natural phenomenon. In addition to standard parameters (population size and number of generations), they require some algorithm-specific parameters. For example, mutation, crossover and selection in GA; inertia weight, cognitive and social parameter in PSO; cooling factor and elasticity of acceptance in SA; number of nests, shifting and step size control parameter in cuckoo search (CS). Tuning of these algorithm-specific parameters is crucial. Improper tuning either results in local optima or increased computational efforts. In addition, they involve a complex working process that is challenging to understand for new designers and researchers.

Addressing these problems, Rao (2020) recently introduced three algorithms, called Rao-1, Rao-2 and Rao-3. These algorithms are algorithm-specific parameter-less, metaphor-less and straightforward. In this study, Rao algorithm uses two approaches to hydraulic modelling, demand-driven analysis (DDA) and pressure-driven analysis (PDA), as DDA-Rao algorithm and PDA-Rao algorithm.

In the conventional hydraulic analysis called demand-driven analysis (DDA), it is assumed that the demands are known functions of time and are independent of pressure. DDA has produced effective solutions in many models under normal conditions. Although, it performs inadequately when abnormal conditions are considered. On the contrary, pressure-driven analysis (PDA) incorporates a relationship between demand and pressure. In PDA, if some pressure is available above the minimum required level, it is assumed that a portion of demand will be supplied at the node. Under abnormal conditions, PDA predicts better network performance as it considers both nodal requirements and pressure requirements (Babu 2021).

In the present work, a new technique has been applied in the optimization of water distribution networks. A newly developed parameter-less Rao algorithm is integrated with pressure-driven analysis as well as demand-driven analysis. The results obtained using DDA-Rao and PDA-Rao algorithms are compared to those of previously applied algorithms for validation purposes. Also, the convergence speed is shown using convergence plots for all case studies. The comparative study based on the modified performance index shows that the PDA-Rao algorithm performs exceptionally well in all performance aspects and outperforms many evolutionary algorithms.

2 Optimization Procedure

This work aims to analyze the applicability of a newly developed Rao algorithm to optimize discrete, non-linear and constrained WDN design problems. The objective function is to minimize the network cost by meeting all the constraints. The function variables are the pipe sizes and the head at each node.

2.1 Simulation Model

The hydraulic analysis is carried out using EPANET 2.2 (Rossman et al. 2020) as the simulation model. EPANET 2.2 is linked to a Python code using Water Network Tool for Resilience (WNTR). WNTR is a Python package, which contains several sub-packages. Each sub-package contains modules that include classes, methods and functions. These classes are used to generate water network models and run simulations (Klise et al. 2017). The hydraulic simulation models are used to analyze the pressure at nodes and flow velocity in pipes to satisfy the demand at each node.

2.1.1 Pressure-demand relationship

The PDA-Rao algorithm uses the pressure-demand relationship proposed by Wagner et al. (1988) as shown below:

$${\mathrm Q}_{\mathrm j,\mathrm{avl}}={\mathrm Q}_{\mathrm j,\mathrm{req}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{if}\;{\mathrm H}_{\mathrm j,\mathrm{avl}}\geq{\mathrm H}_{\mathrm j,\mathrm{req}}$$
(1)
$${\mathrm Q}_{\mathrm j,\mathrm{avl}}={\mathrm Q}_{\mathrm j,\mathrm{req}}\ast\left(\left({\mathrm H}_{\mathrm j,\mathrm{avl}}-{\mathrm H}_{\mathrm j,\min}\right)/\left({\mathrm H}_{\mathrm j,\mathrm{req}}-{\mathrm H}_{\mathrm j,\min}\right)\right)^{\left(1/2\right)}\;\;\;\;\;\mathrm{if}\;{\mathrm H}_{\mathrm j,\min}<{\mathrm H}_{\mathrm j,\mathrm{avl}}<{\mathrm H}_{\mathrm j,\mathrm{req}}$$
(2)
$${\mathrm Q}_{\mathrm j,\mathrm{avl}}=0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{if}\;{\mathrm H}_{\mathrm j,\mathrm{avl}}<{\mathrm H}_{\mathrm j,\min}$$
(3)

Qj,avl and Qj,req are available and required discharge at node j, respectively. Hj,avl, Hj,req and Hj,min are the available pressure head, required pressure head (nominal head) and minimum pressure head at node j, respectively.

2.1.2 Objective Function

The objective of this work is to minimize the network cost, which is a function of pipe diameter and pipe length, as shown below:

$$C= \textstyle\sum_{i=0}^{np}C({D}_{i})*{L}_{i}$$
(4)

C(Di) is the cost per unit length and Li is the length of pipe i; C is the cost of the network; np is the number of pipes in the network. The minimization of the objective function is carried out satisfying the following constraints:

2.1.3 Conservation of Mass

For each node, continuity of flow must be satisfied:

$$\textstyle\sum{\mathrm Q}_1-\textstyle\sum{\mathrm Q}_2={\mathrm Q}_{\mathrm j},\forall\;\mathrm j\;\epsilon\;\mathrm n\mathrm n$$
(5)

Q1 is discharge going towards a specific node; Q2 is discharge coming out from the specific node; Qj is the water demand at node j; nn is the number of nodes.

2.1.4 Conservation of Energy

The loss of head around a closed loop of pipe should be equal to zero or the conservation of the energy equation for each loop should satisfy the network design as shown in Eq. (6).

$$\textstyle\sum {\mathrm{H}}_{\mathrm{f}}=0$$
(6)

where Hf is head loss due to friction in pipe (m), which is calculated using the Hazen-Williams formula:

$${\text{H}}_\text{f}=\omega\text{L}\text{Q}^{\alpha}/{\text{C}}_{\text{hw}}{}^{\alpha}\text{D}^{\beta}$$
(7)

where L is the length (m) and D is the diameter (m) of the pipe; Q is the discharge (m3/s); α and β are the exponents; ω is the numerical conversion constant; Chw is the roughness coefficient.

2.1.5 Available Pipe Sizes

The diameter of the pipes should be selected from a set of commercially available sizes and are thus discrete:

$${\mathrm D}_{\mathrm i}\;\epsilon\;\{{\mathrm D}_1,{\mathrm D}_2\dots,{\mathrm D}_{\mathrm{ns}}\},\forall\;\mathrm i\;\epsilon\;\mathrm n\mathrm s$$
(8)

D1, D2…, Dns is the set of commercially available pipe sizes; ns is the number of candidate pipe sizes.

2.1.6 Required Pressure Head

The available pressure head at each node should be greater than the required pressure head.

$${\mathrm H}_{\mathrm j,\mathrm{avl}}\geq{\mathrm H}_{\mathrm j,\mathrm{req}},\forall\;\mathrm j\;\epsilon\;\mathrm n\mathrm n$$
(9)

2.2 Optimization Model

The optimization model is constructed using Rao algorithm in Python. Rao algorithms are recently introduced by Rao (2020). ‘The key advantage of Rao algorithms is that the algorithm-specific parameters do not need to be tuned to search for the optimal solution of design problems. Its working procedure is easy to understand and execute’ (Rao and Pawar 2020).

2.2.1 Rao Algorithm

The Rao algorithm works by moving closer to the best solution and away from the worst. With random interactions, the solution moves throughout the population. The basic procedure of Rao algorithm in optimization of WDN is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of Rao algorithm in optimization of water distribution networks

Full size image

At first, initial population of the diameters is generated using random numbers considering upper and lower bound values. These diameters are used to find the value of the objective function, C. The minimum (best) and maximum (worst) cost candidates are selected from the range of solutions. The diameters corresponding to the best and worst solutions are used to generate a new population using one of the three equations of the Rao algorithms. 'In the Rao algorithms, the Rao-1 algorithm improves the result by considering the difference between the best and worst solutions; the Rao-2 and Rao-3 algorithms improve the result by considering not only the difference between the best and worst solutions but also the random interactions of the candidate solutions. The difference between Rao-2 and Rao–3 algorithms lies in considering the absolute values of the variables in the respective equations' (Rao and Pawar 2020). Rao-2 algorithm promotes more diversity because of the random interactions. Also, absolute values of variables should be considered to find the resilient solution as the value of pipe diameter is bound to be a real number. Therefore, the Rao-2 algorithm is applied in the present work, as shown in Eq. (10).

$${\mathrm D}_{\mathrm{new}}={\mathrm D}_{\mathrm{old}}+\mathrm r1\left({\mathrm D}_{\mathrm{best}}-{\mathrm D}_{\mathrm{worst}}\right)+\mathrm r2(\left|{\mathrm D}_{\mathrm{old}}\;\mathrm{or}\;{\mathrm D}_{\mathrm{rand}}\right|-\vert{\mathrm D}_{\mathrm{rand}}\;\mathrm{or}\;{\mathrm D}_{\mathrm{old}}\vert)$$
(10)

Dnew is the diameter for new population; Dold is the diameter for old population; Dbest, Dworst and Drand are the diameters corresponding to the best, worst and random solutions, respectively; r1 and r2 are random numbers.

2.2.2 Pressure and Discharge Dependent Penalty

After calculating the cost, the feasibility of the solution is checked. The feasibility criterion is the fulfilment of the required pressure head at each node. If the solution found is infeasible, then a penalty is applied to the cost function. Using DDA, the deficiencies in pressure heads are measured assuming full supply at nodes. In contrast to actual values, this approach results in higher deficiencies. Whereas in PDA, both nodal and pressure requirements are considered to provide better performance (Abdy Sayyed et al. 2019). Thus, a pressure and discharge dependent penalty based on equivalent energy costs (Kadu et al. 2008) is used in this study, as shown below:

$$\mathrm{Penalty}=\mathrm{p}*{\mathrm{Q}}_{\mathrm{j},\mathrm{avl}}*(\mathrm{max }(0,({\mathrm{H}}_{\mathrm{j},\mathrm{req}}-{\mathrm{H}}_{\mathrm{j},\mathrm{avl}})))$$
(11)

where, p is the penalty coefficient, measured to pump a unit quantity of water into a unit head, as suggested by Kadu et al. (2008).

2.3 Modified Performance Index (MPI)

A performance index (PI) suggested by Deep and Thakur (2007) is used to measure the effectiveness of the successful run for the given objective function. A modification is made to obtain a better comparison following the parameters provided by previous researchers. The modified performance index (MPI) illustrates the algorithm's degree of reliability, efficiency and accuracy. The reliability of PDA-Rao algorithm is defined as the frequency with which it converges to the near-optimal solution, which is measured by calculating the success rate. If the optimum cost obtained in a run is within 1% accuracy of the best-known value for that problem, then a run is considered a successful run (Deep and Bansal 2009).

The relative performance of an algorithm using MPI can be calculated as:

$$MPI= \frac{1}{Np}\textstyle\sum_{i=1}^{Np}{({k}_{1}{\alpha }_{1}+{k}_{2}{\alpha }_{2}+{k}_{3}{\alpha }_{3}+{k}_{4}{\alpha }_{4}+ {k}_{5}{\alpha }_{5})}_{i}$$
(12)

where, α1 = (Sri/Tri); α2 = (LAfi/Afi); α3 = (LAti/Ati); α4 = (LMfi/Mfi); α5 = (LMti/Mti).

Sri = Number of successful runs of ith problem.

Tri = Total number of runs of ith problem.

The following terms in the calculation of the MPI are defined for the successful runs of the ith problem:

LAfi = Least of average function evaluation (AFE) numbers documented for the entire range of applied algorithms.

Afi = AFE number of the current algorithm.

LAti = Least of average computational time of an entire range of applied algorithms.

Ati = Average computational time of the current algorithm.

LMfi = Least of minimum function evaluation (MFE) numbers documented for the entire range of applied algorithms.

Mfi = MFE numbers of the current algorithm.

LMti = Least of minimum computational time of an entire range of applied algorithms.

Mti = Minimum computational time of the current algorithm.

Np = Total number of problems analyzed.

k1, k2, k3, k4 and k5 are weights such that, \({\sum }_{i=1}^{5}{k}_{i}=1\)

3 Case Studies

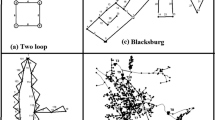
The TL, NYT and GY benchmark networks are used to evaluate the performance of PDA-Rao algorithm. Further, this algorithm is used to solve a real WDN of School of Planning and Architecture (SPA) located in Bhopal region of India. Figure 2 depicts the schematic diagrams of all of the network cases.

Fig. 2
figure 2

Schematic diagram of case study networks: a Two-loop network, b New York Tunnel network, c Goyang network, and d School of Planning and Architecture (SPA) network

Full size image

The Two-loop network is a gravity-fed network firstly used by Alperovits and Shamir (1977). Later, it has been widely used by researchers (e.g., Savic and Walters 1997; Cunha and Sousa 1999; Babu and Vijayalakshmi 2013) in the field of optimization. The New York Tunnel network was initially presented by Schaake and Lai (1969). As Suribabu (2010) reiterated, the problem aims to determine the installation of new pipes parallel to the existing network to fulfil the pressure head requirement at critical nodes (node 16—20). The Goyang network is a pumped network presented by Kim et al. (1994) in South Korea. The hydraulic data for this network are taken from Geem (2006). The School of Planning and Architecture (SPA) network is a gravity-fed network with a total pipeline length of 1890 m. Demand at each location is measured using 2 h of supply per day, taking into account acceptable requirements. The available pipe diameters and the corresponding rates for SPA network are taken following CPWD GOI (2019).

The available pipe diameters for all case study networks are given in Table 1. The Hazen–William's constants (ω = 10.667, α = 1.852 and β = 4.871) are identical for all networks and equal to the values used by EPANET 2.2. The developed module was run on an Intel (R) Core (TM) i5-8250U CPU @ 1.60 GHz with 8.00 GB RAM, using the Python programming language.

Table 1 Available pipe sizes for Two-loop, New York Tunnel, Goyang and SPA networks
Full size table

4 Results and Discussions

A simple procedure to find the minimum cost of a given water distribution network is suggested in this paper using a newly developed Rao algorithm while satisfying constraints. The solutions obtained using DDA-Rao and PDA-Rao algorithms are compared with those of other optimization algorithms based on minimum cost achieved and AFE numbers. For both techniques, the population size is fixed to 20, and the number of iterations differs based on the network size and search space.

The minimum feasible cost of the Two-loop network is stated as $419,000 by various researchers (Savic and Walters 1997; Geem 2006; Babu and Vijayalakshmi 2013). PDA-Rao algorithm converged to the minimum cost within 33 iterations in only 33 s. Thus, the MFEs for the PDA-Rao algorithm is 660 compared to 6,500 for GA (Savic and Walters 1997) and 5,000 for SA (Cunha and Sousa 1999). Comparative results of PDA-Rao algorithm are presented in Table 2, which are obtained over 30 runs. Both DDA-Rao and PDA-Rao algorithms got the best-known value of network cost in 4,000 and 840 AFE numbers, respectively. However, AFE numbers for the same network were reported as 65,000 using GA (Savic and Walters 1997), 25,000 using SA (Cunha and Sousa 1999) and 1,300 using PSO-GA (Babu and Vijayalakshmi 2013). Therefore, a 35.38% reduction in computational cost is achieved in solving the TL network problem.

Table 2 Comparison of optimal results
Full size table

In the existing design of New York Tunnel network, the pressure head value does not satisfy the requirement of pressure for multiple nodes. Thus, various algorithms are applied to extend the existing network considering new pipes parallel to the existing pipes. As reported by Geem (2006), the optimum cost is $36.66 million for this network. DDA-Rao algorithm converged to an upgraded solution ($36.33 million) in only 40 iterations. However, PDA-Rao algorithm converged to $36.03 million, which is the least-cost among the results shown in Table 2 for NYT network. It is obtained in only 64 iterations and 1,280 MFEs. As a result, the PDA-Rao algorithm outperformed all other algorithms in terms of convergence as well as cost, with a 68% reduction in computational cost and a 1.7% reduction in network cost. The pressure head values at critical nodes for the optimum solutions of DDA-Rao and PDA-Rao algorithms are shown in Table 3.

Table 3 Pressure head at critical nodes of New York Tunnel network
Full size table

According to Kim et al. (1994), the original and optimum network cost of the Goyang network is 179,428,600 Won and 179,142,700 Won, respectively. PDA-Rao algorithm converged to 177,010,359 Won as the minimum cost of this network in only 39 iterations. PDA-Rao algorithm shows 0.71% reduction in network cost with 8.9% computational cost compared to HS algorithm (Geem 2006), as shown in Table 2.

Convergence curves for DDA-Rao and PDA-Rao algorithms are plotted for the best value over 30 runs for all benchmark networks, as shown in Fig. 3. They demonstrate that the PDA-Rao algorithm converges faster than the DDA-Rao algorithm.

Fig. 3
figure 3

Convergence of Rao algorithm: a Two-loop network, b New York Tunnel network, c Goyang network, and d School of Planning and Architecture (SPA) network

Full size image

The statistical results for the TL, NYT and GY networks are shown in Table 4, which include minimum, maximum and average values of the cost obtained in 30 runs. As per the results, median of the cost is very close to the optimum cost, which shows the accuracy of PDA-Rao algorithm. The AFE number, MFE number and computation time required by PDA-Rao algorithm demonstrate the requirement of less computational efforts and good efficiency.

Table 4 Statistical results of PDA-Rao algorithm
Full size table

The MPI is used to observe the consolidated effect of success rate, function evaluation numbers and computation time on the PDA-Rao algorithm. Table 5 provides a review of studies related to the application of evolutionary algorithms in the minimum cost calculation of one or more of the three benchmark WDNs. The PI and MPI are plotted by reviewing and comparing the results of these studies to the proposed PDA-Rao algorithm. Firstly, these studies are compared to get the least of the MFE numbers, AFE numbers and computation times. Then the ratio of these least values to that of PDA-Rao algorithm are measured to calculate MPI using Eq. (12).

Table 5 Review of various studies and evolutionary algorithms used for the optimization of water distribution networks
Full size table

For a clear visualization of performance, a method is adopted as suggested by Deep and Thakur (2007). In this method, equal weights are assigned to all the terms except for one term. Hence, PI or MPI becomes a function of one variable. A geometric graph is obtained by drawing the MPI and PI on ten scaled bars, as shown in Fig. 4. The proximity of this graph to the best-performance value is an indicator of the performance of the algorithm. The graph suggests that, compared to HS (Geem 2006), the PDA-Rao algorithm consistently outperforms other optimization algorithms in solving WDN problems.

Fig. 4
figure 4

Modified performance index (MPI) and performance index (PI) plotted using various weight combinations for PDA-Rao algorithm and Harmony search algorithm

Full size image

The value of the performance index for PDA-Rao algorithm varies between 0.69 to 0.94. It demonstrates the competence of the PDA-Rao algorithm compared to conventional high-performance algorithms (genetic algorithms, particle swarm optimization algorithm, harmony search algorithm and simulated annealing algorithm) used by various researchers to optimize WDN.

After validating the approach using three benchmark networks, PDA-Rao algorithm was applied to a real WDN of School of Planning and Architecture (SPA). The hydraulic results for this network for the best of 5 test runs are given in Table 6. The population size and the maximum number of iterations are 15 and 1000, respectively. In PDA, the nominal head shall be provided at the demand nodes for the total supply. The required pressure head is taken as the nominal head, which is 13 m, and the minimum pressure head for the flow through pipes is 0 m. PDA-Rao algorithm converged to a minimum cost solution of Rs.15,40,519 for SPA network. The number of function evaluations and computation time to achieve the minimum cost solution were 7785 MFEs and 651 s, respectively.

Table 6 Hydraulic results of the School of Planning and Architecture (SPA) network using the PDA-Rao algorithm
Full size table

5 Conclusions

The present work deals with the application of a metaphor-less and algorithm-specific-parameter-less Rao algorithm in optimization of WDNs. The results obtained using GA, SA and Rao algorithms were identical and optimum for the TL network. For the GY network, best-known values were obtained and a 0.71% reduction in cost was observed using PDA-Rao compared to HS (Geem 2006). At the same time, results were significantly improved for the NYT network with a 1.7% reduction in best-known network cost. Moreover, the minimum cost solution for the real-world SPA network was found in 7785 function evaluations, which is negligible compared to the size of search space (7.17 *1056).

In conclusion, the PDA-Rao algorithm was computationally inexpensive in solving problems with large search spaces. Significantly, the methodology is straightforward to understand and execute, shows better convergence and gives more accurate results with less computational effort. It can therefore be easily applied to other extensive WDN optimization problems. From the statistical analysis, the probability of getting acceptable results using PDA-Rao algorithm is 0.77, 0.60, and 0.97 for TL, NYT and GY networks, respectively. It suggests that the probability of achieving the global best solution using PDA-Rao algorithm is extremely high. Further, this algorithmic rule can also be applied in multi-objective optimization of WDNs with slight modifications.