1 Introduction

Water resource and environmental models are widely relied upon supporting water resources management such as water allocation, reservoir operation, and flood risk assessment (Fan et al. 2016; Lindenschmidt and Rokaya 2019). These models generally use mathematical equations to represent the temporally dynamic and spatially distributed processes in water resource and environmental systems (Hipel and McLeod 1994; Li et al. 2015). However, significant uncertainties, embodied in model parameters, structures, and inputs, are associated with such descriptions (Fan et al. 2020; Tsakiris and Spiliotis 2017; Zhang et al. 2018; Wu et al. 2019). Reliable modeling practice requires an evaluation of the confidence in the model outputs, which includes quantification of the uncertainty in model results (i.e., uncertainty analysis) (Chowdhury 2019; Liu et al. 2016; Xu et al. 2001) and evaluation of how much each component (e.g. input/parameter) contributes to the output uncertainty (i.e., sensitivity analysis) (Bahremand and De Smedt 2008; Đukić and Radić 2016). Without a realistic assessment of various uncertainties, decision makers may suffer from troubles in describing water resource and environmental processes, assessing regional environmental resources situation, and making relevant decisions (Dessai and Hulme 2007; Weng et al. 2010; Maqsood et al. 2005; Tsakiris 1982). Therefore it is of great importance to quantify uncertainties in modelling water and environmental processes and further characterize the contributions of those uncertainty sources to the output results (Wu et al. 1997; Gamerith et al. 2013; Pianosi et al. 2016).

To analyze the sources of uncertainty, evaluate the contribution of each uncertainty factor, and identify the dominant uncertainty factors, various sensitivity analysis methods such as local or global methods, and qualitative or quantitative methods have been proposed in recent decades (Borgonovo and Plischke 2016; Oladyshkin et al. 2012; Pianosi et al. 2016). Local sensitivity analysis addresses sensitivity relative to point estimates of parameter values while a global sensitivity analysis examines the effects of input variations on the outputs in the entire allowable ranges of the input space (Hamby 1995; Uusitalo et al. 2015). With the ability to reflect the interactions and nonlinear relationship, global sensitivity analysis is more popular in hydrological applications (Bennett et al. 2018; Khorashadi Zadeh et al. 2017). A series of global sensitivity analysis methods including qualitative screening methods (Morris 1991) and quantitative techniques (Sobol’ 1993; Vega et al. 1998) are available. The choice of sensitivity analysis method has an important impact on model parameters sensitivities results (Pappenberger et al. 2008; Saltelli et al. 2019).

Among quantitative global sensitivity analysis methods, the analysis of variance (ANOVA) method has been widely used for identifying important uncertainty sources, quantifying individual and interactive impacts of contributors in hydrological models (Khaiter and Erechtchoukova 2019; Vitale et al. 2019). This method has been used to investigate the influence of pollutants and seasonality on the river water quality (Vega et al. 1998), the contribution of hydrological model parameters to the discharge projection uncertainty, and the impact of climate changes on flow frequency (Fan et al. 2019; Giuntoli et al. 2015). Compared with other approaches, ANOVA is handy for handling small samples and more computationally efficient in uncertainty quantification (Tang et al. 2006). However, it has been argued that the estimated variance contributions in the ANOVA method would be biased, depending on the sample size differences (Bosshard et al. 2013). To diminish the effect of the sample size, Bosshard et al. (2013) proposed a subsampling scheme to adjust the biased estimations in ANOVA (here, we refer this method as single-subsampling ANOVA). By calculating the multiplicative bias of the variance ratio in the synthetic experiment, the results indicated that the bias resulting from the variance estimator of ANOVA can be diminished effectively by the subsampling procedure. Qi et al. (2016c) used the single-subsampling ANOVA method to dynamically quantify the individual and interactive effects of algorithm parameters on hydrological model calibration. Qi et al. (2016a) also evaluated global fine-resolution precipitation products and their uncertainty quantification in ensemble discharge simulations by using the single-subsampling ANOVA method. In these investigations, single-subsampling-ANOVA has shown good performance in quantifying respective contributions of various uncertainty sources to the overall output variance. However, one single factor is merely subsampled in the above studies and there are still some issues to be addressed. Firstly, there lacks a holistic comparison for the sensitivity analysis results when different factors are subsampled in ANOVA. Secondly, the resulting parameter sensitivities may also be significantly varied if multiple factors are subsampled but no studies ever addressed this issue. Thirdly, it is also unclear how the results will change if all the factors are subsampled. Finally, the applicability of the subsampling ANOVA approach needs to be further demonstrated by comparison with some widely used benchmark methods.

Therefore, as an extension of previous studies, the objective of this study is to develop single-, multiple- and full-subsampling ANOVA approaches for enhancing applicability of ANOVA in the sensitivity analysis. Meanwhile, the influence of different subsampling schemes in the subsampling ANOVA approaches will be explored. The applicability of different subsampling ANOVA methods is illustrated through two case studies based on a three-parameter simplified model (Chen et al. 2019) and a four-parameter daily lumped rainfall-runoff model (GR4J model) (Perrin et al. 2003). The Sobol’s method is used as the benchmark method to evaluate the performance of different subsampling ANOVA approaches.

2 Methodology

2.1 ANOVA-Based Sensitivity Analysis Techniques

In order to use the same terminology to present each sensitivity technique, a generic water or environmental model is defined as:

$$ Y=F\left({X}_1,{X}_2\dots {X}_k\right) $$
(1)

Where X1, X2, …, Xk represent the independent variables (such as model parameters, or model structure) and Y represents the response (such as the model performance). Variance-based methods use a variance ratio to estimate the importance of each factor (i.e. X1, X2, …, Xk) under consideration. According to the ANOVA theory, the total sum of squares (SST) can be divided into the sum of squares due to individual factors and their interactions as follows (Saltelli et al. 2010).

$$ SST=\sum \limits_{i=1}^k{SS}_i+\sum \limits_{i=1}^k\sum \limits_{j>i}^k{SS}_{ij}+\dots +{SS}_{1,2,\dots, k} $$
(2)

where SSi represents the squares due to the individual effect of Xi and SSij to SS1,2,…,k represent the squares due to interactions among the k factors (i.e. X1, X2, …, Xk). In this model, we summarize all interaction terms into the term SSI.

$$ SSI=\sum \limits_{i=1}^k\sum \limits_{j>i}^k{SS}_{ij}+\dots +{SS}_{1,2,\dots, k}= SST-\sum \limits_{i=1}^k{SS}_i $$
(3)

Then, for each effect, the variance fractions η2 are derived as follows:

$$ {\eta}_i^2=\frac{SS_i}{ SS T} $$
(4)
$$ {\eta}_I^2=\frac{SSI}{SST} $$
(5)

where:

$$ SST=\sum \limits_{t_1=1}^{T_1}\sum \limits_{t_2=1}^{T_2}\cdots \sum \limits_{t_k=1}^{T_k}{\left({Y}^{t_1,{t}_2\cdots {t}_k}-{Y}^{0,0\cdots 0}\right)}^2 $$
(6)
$$ {SS}_i=\sum \limits_{t_1=1}^{T_1}\sum \limits_{t_2=1}^{T_2}\cdots \sum \limits_{t_k=1}^{T_k}{\left({Y}^{0,0,\cdots {t}_i\cdots 0}-{Y}^{0,0\cdots 0}\right)}^2 $$
(7)

The symbol “o” indicates the average over the particular index. The value of η2 varying between 0 and 1, indicating a contribution of an effect to the total ensemble variance (uncertainty):

$$ \sum \limits_{i=1}^k{\eta}_i^2+{\eta}_I^2=\sum \limits_{i=1}^k\frac{SS_i}{ SS T}+\frac{ SS I}{ SS T}=\frac{\sum \limits_{i=1}^k{SS}_i+ SSI}{ SS T}=1 $$
(8)

2.2 Subsampling

To diminish the effect of the sample size on the variance estimation (e.g. SST, SSi, SSI) in ANOVA, Bosshard et al. (2013) proposed a subsampling scheme as follows: Assume that there are Ti elements (or levels) for each factor Xi, represented as \( {x}_{\mathrm{i},1},{x}_{\mathrm{i},2},{x}_{\mathrm{i},3}\cdots {x}_{\mathrm{i},{\mathrm{T}}_{\mathrm{i}}} \). In each subsampling iteration, two elements are selected out of the total Ti elements which results in a total of \( {\mathrm{C}}_{{\mathrm{T}}_{\mathrm{i}}}^2 \)(specify that C is the combination symbol) possible element pairs for Xi. Therefore, for element \( {x}_{\mathrm{i},{\mathrm{t}}_{\mathrm{i}}} \), the ti is replaced by g (h, j) which is a \( 2\times {C}_{T_i}^2 \) matrix.

$$ g\left(h,j\right)=\left(\begin{array}{c}1\\ {}2\end{array}\kern1em \begin{array}{c}1\\ {}3\end{array}\kern1em \begin{array}{c}\cdots \\ {}\cdots \end{array}\kern1em \begin{array}{c}1\\ {}{\mathrm{T}}_{\mathrm{i}}\end{array}\begin{array}{c}2\\ {}3\end{array}\begin{array}{c}2\\ {}4\end{array}\kern1em \begin{array}{c}\cdots \\ {}\cdots \end{array}\kern1em \begin{array}{c}{\mathrm{T}}_{\mathrm{i}-2}\\ {}{\mathrm{T}}_{\mathrm{i}-1}\end{array}\kern1em \begin{array}{c}{\mathrm{T}}_{\mathrm{i}-2}\\ {}{\mathrm{T}}_{\mathrm{i}}\end{array}\kern1em \begin{array}{c}{\mathrm{T}}_{\mathrm{i}-1}\\ {}{\mathrm{T}}_{\mathrm{i}}\end{array}\right) $$
(9)

Here h means the row number and j means the column number. The total number of columns is defined as Ji. Therefore, h = 1 or 2 and j = 1, 2, 3,……,Ji, where \( {\mathrm{J}}_{\mathrm{i}}={C}_{T_i}^2 \) for the subsampled parameter/factor Xi. For more details of subsampling scheme, please refer to the literature (Bosshard et al. 2013).

2.3 Single-Subsampling ANOVA

Single-subsampling ANOVA means that only one parameter from the parameter vector (X1, X2, … Xk) is subsampled. Assuming that the Xn is subsampled, which mean two elements selected from vector \( {x}_{\mathrm{n},1},{x}_{\mathrm{n},2},{x}_{\mathrm{n},3}\dots \cdots {x}_{\mathrm{n},{\mathrm{T}}_{\mathrm{n}}} \)are used for Xn in each subsampling iteration. As for the rest parameters Xi, there are still Ti elements for each of them. We estimate the terms in Eqs. (2) and (3) using the subsampling procedure as follows:

$$ {SST}^j=\sum \limits_{t_1=1}^{T_1}\sum \limits_{t_2=1}^{T_2}\cdots \sum \limits_{h=1}^2\cdots \sum \limits_{t_k=1}^{T_k}{\left({Y}^{t_1,{t}_2\cdots g\left(h,j\right)\cdots tk}-{Y}^{0,0\cdots g\left(0,j\right)\cdots 0}\right)}^2 $$
(10)

For i = n:

$$ {SS}_i^j={T}_1{T}_2\cdots {T}_{n-1}{T}_{n+1}\cdots {T}_k\sum \limits_{h=1}^2{\left({Y}^{t_1,{t}_2\cdots g\left(h,j\right)\cdots {t}_k}-{Y}^{0,0\cdots g\left(0,j\right)\cdots 0}\right)}^2 $$
(11)

For i ≠ n:

$$ {SS}_i^j=2\times {T}_1{T}_2\cdots {T}_{i-1}{T}_{i+1}\cdots {T}_{n-1}{T}_{n+1}\cdots {T}_k\sum \limits_{t_i=1}^{T_i}{\left({Y}^{0,0\cdots {t}_i\cdots g\left(0,j\right)\cdots 0}-{Y}^{0,0\cdots g\left(0,j\right)\cdots 0}\right)}^2 $$
(12)

The symbol o indicates the average over the particular index and j is in 1,…, J, where \( \mathrm{J}={\mathrm{J}}_{\mathrm{n}}={C}_{T_n}^2 \)in the single-subsampling ANOVA. Then, the variance fraction η2 describing the factors’ effects is derived as follows:

$$ {\eta}_i^2=\frac{1}{J}\sum \limits_{j=1}^J\frac{SS_i^j}{{SS T}^j} $$
(13)
$$ {\eta}_I^2=1-\sum \limits_{i=1}^k{\eta}_i^2 $$
(14)

2.4 Multiple-Subsampling ANOVA

As an extension of the single-subsampling ANOVA, a multiple-subsampling ANOVA approach is introduced here. The multiple-subsampling ANOVA means that more than one parameter from the parameter vector (X1,X2,…Xk) are going to be subsampled at the same time. Assume that Xp, Xq are subsampled, tp, tq are replaced by g(hp, jp),⋯g(hq, jq) respectively. We estimate the terms in Eqs. (2) and (3) using the subsampling procedure as follows:

$$ {SST}^j=\sum \limits_{t_1=1}^{{\mathrm{T}}_1}\sum \limits_{t_2=1}^{{\mathrm{T}}_2}\cdots \sum \limits_{h_{\mathrm{p}}=1}^2\cdots \sum \limits_{h_{\mathrm{q}}=1}^2\cdots \sum \limits_{t_{\mathrm{k}}=1}^{{\mathrm{T}}_{\mathrm{k}}}{\left({Y}^{t_1,{t}_2\cdots g\left({h}_{\mathrm{p}},{j}_{\mathrm{p}}\right)\cdots g\left({h}_{\mathrm{q}},{j}_{\mathrm{q}}\right)\cdots {t}_{\mathrm{k}}}-{Y}^{o,o\cdots g\left(o,{j}_{\mathrm{p}}\right)\cdots g\left(o,{j}_{\mathrm{q}}\right)\cdots o}\right)}^2 $$
(15)

For i = p⋯q:

$$ {SS}_i^j={\mathrm{T}}_1\times {\mathrm{T}}_2\times \cdots \times {\mathrm{T}}_{\mathrm{k}}\sum \limits_{h_{\mathrm{p}}=1}^2\cdots \sum \limits_{h_{\mathrm{q}}=1}^2{\left({Y}^{t_1,{t}_2\cdots g\left({h}_{\mathrm{p}},{j}_{\mathrm{p}}\right)\cdots g\left({h}_{\mathrm{q}},{j}_{\mathrm{q}}\right)\cdots {t}_{\mathrm{k}}}-{Y}^{o,o\cdots g\left(o,{j}_{\mathrm{p}}\right)\cdots g\left(o,{j}_{\mathrm{p}}\right)\cdots o}\right)}^2 $$
(16)

For i ≠ p⋯q:

$$ {SS}_i^j=2\times \cdots \times 2\times {\mathrm{T}}_1\times {\mathrm{T}}_2\cdots {\mathrm{T}}_{\mathrm{i}-1}\times {\mathrm{T}}_{\mathrm{i}+1}\cdots {\mathrm{T}}_{\mathrm{k}}\sum \limits_{t_i=1}^{{\mathrm{T}}_i}{\left({Y}^{o,o\cdots {t}_i\cdots g\left(o,{j}_{\mathrm{p}}\right)\cdots g\left(o,{j}_{\mathrm{q}}\right)\cdots o}-{Y}^{o,o\cdots g\left(o,{j}_{\mathrm{p}}\right)\cdots g\left(o,{j}_{\mathrm{q}}\right)\cdots o}\right)}^2 $$
(17)

Where j is in 1, …, J, and \( \mathrm{J}={\mathrm{J}}_{\mathrm{p}}\times \dots \times {\mathrm{J}}_{\mathrm{q}}={C}_{T_p}^2\times \dots \times {C}_{T_q}^2 \) in the multiple-subsampling ANOVA.

Then, the variance fraction η2 for each effect is derived as follows:

$$ {\eta_i}^2=\frac{1}{J}\sum \limits_{j=1}^J\frac{SS_i^j}{{SS T}^j} $$
(18)
$$ {\eta_I}^2=1-\sum \limits_{i=1}^k{\eta_i}^2 $$
(19)

2.5 Full-Subsampling ANOVA

Moreover, a full-subsampling approach can be formulated when all parameters are going to be subsampled. In detail, the full-subsampling ANOVA means that all parameters X1,X2,…Xk are subsampled before ANOVA is calculated. Consequently, t1,t2⋯tk are replaced by g(h1,j1),g(h2,j2),⋯g(hk,jk) respectively. We estimate the terms in Eqs. (2) and (3) using the subsampling procedure as follows:

$$ {SST}^j=\sum \limits_{t_1=1}^2\sum \limits_{t_2=1}^2\cdots \sum \limits_{t_{\mathrm{k}}=1}^2{\left({Y}^{g\left({h}_1,{j}_1\right),g\left({h}_2,{j}_2\right)\cdots g\left({h}_{\mathrm{k}},{j}_{\mathrm{k}}\right)}-{Y}^{g\left(o,{j}_1\right)g\left(o,{j}_2\right)\cdots g\left(o,{j}_{\mathrm{k}}\right)}\right)}^2 $$
(20)
$$ {SS}_i^j=\sum \limits_{h_1=1}^2\sum \limits_{h_2=1}^2\cdots \sum \limits_{h_{\mathrm{k}}=1}^2{\left({Y}^{g\left({h}_1,{j}_1\right),g\left({h}_2,{j}_2\right)\cdots g\left({h}_{\mathrm{k}},{j}_{\mathrm{k}}\right)}-{Y}^{g\left(o,{j}_1\right),g\left(o,{j}_2\right),\cdots g\left(o,{j}_{\mathrm{k}}\right)}\right)}^2 $$
(21)

where j is in 1, …, J, and \( \mathrm{J}={\mathrm{J}}_1\times \dots \times {\mathrm{J}}_{\mathrm{k}}={C}_{T_1}^2\times \dots \times {C}_{T_k}^2 \) in the full-subsampling ANOVA

Then, for each effect, the variance fraction η2 is derived as follows:

$$ {\eta_i}^2=\frac{1}{J}\sum \limits_{j=1}^J\frac{SS_i^j}{{SS T}^j} $$
(22)
$$ {\eta_I}^2=1-\sum \limits_{i=1}^k{\eta_i}^2 $$
(23)

3 Case Study I: Simplified Model

3.1 Problem Statement

A simple model with three unknown parameters is employed to illustrate the proposed subsampling ANOVA approaches, which is expressed as follows:

$$ {F}_3\left({X}_1,{X}_2,{X}_3\right)={X}_1\ast {X}_3+{X}_1\ast \sin \left(\frac{\pi }{2}\ast {X}_2\right)+{X}_2\ast {e}^{\left|{X}_3\right|}+{X}_1\ast {X}_2\ast {X}_3 $$
(24)

where X1,X2 and X3 are independent variables uniformly distributed within [0, 1]. This simplified model is proposed by (Chen et al. 2019). The purpose of this model is to explore changes of parameter sensitivities for different subsampling methods in the ANOVA-based sensitivity analysis. In our study, we define ″5″ as the five levels are selected equidistantly within the initial parameter range. Then the five levels are subsampled and totally 10 (\( {\mathrm{C}}_5^2=\frac{5\ast 4}{2\ast 1}=10 \)) combinations of different level pairs are obtained for the two-level ANOVA. Similarly, ″2″ represents only two levels (maximum and minimum values) of the parameter values are selected from its range without subsampling. For example, ″522″ means that five levels of X1 are selected equidistantly from the range before subsampling, meanwhile only two levels for the X2 and X3 are selected from their corresponding ranges. In turn, we define 252, 225, 552, 525, 255, 222, 333, 444 and 555 for different subsampling ANOVA approaches. For 522, 252 and 225, only one of the three parameters is subsampled, which is used to illustrate the performance of single-subsampling ANOVA. For 552, 525 and 255, two of the three parameters are subsampled, which will demonstrate the applicability of multiple-subsampling ANOVA scheme. Similarly, 222, 333, 444, and 555 represent full-subsampling ANOVA with different parameters levels.

3.2 Results of Single- and Multiple-Subsampling ANOVA

Figure 1 presents sensitivity indices of individual and interactions of the three parameters under different subsampling ANOVA approaches. Figure 1a, b respectively shows the results for single-subsampling (i.e. one parameter subsampled) and multiple-subsampling (i.e. two parameters subsampled) ANOVA methods. Firstly, it can be observed that the parameters’ sensitivities vary significantly for different subsampling schemes. In detail, the sensitivities of X1,X2,X3 and their interactions range within 4.1–41.2%, 25.1–78.5%, 7.5–47.3%, and 7.0–15%, respectively under different subsampling schemes. In most cases, X2 is more likely to be the most sensitive parameter. Secondly, for a specific parameter, its individual sensitivity varies significantly with different subsampling schemes. For single-subsampling ANOVA, the minimum sensitivity (the red bar) of X1 is obtained in 522 where only X1 is subsampled. Similarly, the minimum sensitivities (the red bar) of X2 and X3 are obtained in 252 and 225, respectively. The results indicate that the individual sensitivity of the parameter will reduce remarkably when this parameter is subsampled in single-subsampling ANOVA. As for multiple-subsampling ANOVA in Fig. 1b, similar results can be observed with those from single-subsampling ANOVA. The maximum sensitivity for one parameter is obtained when this parameter is not subsampled. For instance, the maximum sensitivity value (blue bar) of X1 is obtained in 255 where only X1 is non-subsampled. These results suggest that, for both single- and multiple-subsampling ANOVA methods, the subsampling procedure would significantly underestimate the sensitivities for parameters to be subsampled but overestimate the sensitivities for parameters without subsampling. Thirdly, the black bars in Fig. 1 represent sensitivity indices of individual and interactions for the three parameters obtained by Sobol’s method. Compared with Sobol’s results, the subsampling process will underestimate the sensitivities of those subsampled parameters and overestimate the sensitivities of non-subsampled parameters. Finally, the subsampling process would not only change the value of parameter sensitivities but also change the order of the parameters’ sensitivities (Figs. S1–S3). For example, under the subsampling scheme of 522, the order of the parameters’ sensitivities would be X2 > X3 > interaction > X1 while under the subsampling scheme of 252, the corresponding parameter sensitivities yield a different order: X3 > X1 > X2 > interaction. These results indicate that both single- and multiple-subsampling schemes are biased and thus may lead to discrepant results.

Fig. 1
figure 1

The influence of subsampled parameter on individual and interactions sensitivity indices of parameters: (a) single-subsampling, (b) multiple-subsampling, and (c) full –subsampling. Red bar indicates that the parameter is divided into five levels first and then subsampled; blue bar represents that the parameter is only divided into two levels, without subsampling

Full size image

3.3 Results of the Full-Subsampling ANOVA

In the full-subsampling ANOVA approach, all the parameters are subsampled with different levels within their variation ranges. In this study, four scenarios would be tested with each parameter having 2, 3, 4, or 5 levels (i.e. 222, 333, 444, and 555) respectively. As presented in Fig. 1c, the individual and interactions sensitivities of three parameters change with the varying parameters levels. With parameters’ levels increasing from 222 to 555, the individual sensitivity of X1 and X3 gradually increase from 11.7% and 19.4% to 19.1% and 24.1%, respectively. At the same time, the interactive parameter sensitivity gradually decreases from 18.1% to 5.5%. The individual sensitivity of X2 keeps relatively stable, ranging from 50.9% to 52.2%. The results show that for the full–subsampling ANOVA method, the individual and interactive parameters sensitivities are affected by the subsampled parameter levels. The increased parameter levels would slightly increase the sensitivity values for low sensitive parameters and decrease the interactive sensitivity. Another thing to be noticed is that the order of parameters sensitivities would change when the parameter level increases from 2 to 3. This is because that the selection of 2 levels for all parameters would lead to a traditional ANOVA without any subsampling. While the 3 or more parameter levels are chosen, the variations of the obtained results are relatively small and the order of parameters sensitivities remain consistent with that from Sobol’s method. As a whole, the full-subsampling ANOVA approach with more than 3 levels is more robust than the single- and multiple-subsampling ANOVA methods.

4 Case Study II: Sensitivity Analysis for Hydrologic Models

4.1 Problem Statement

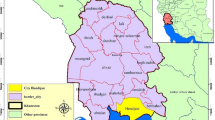
To further demonstrate the applicability of the subsampling ANOVA methods in hydrological simulation, the proposed approaches are applied for parameter sensitivity analyses of the conceptual hydrological model GR4J (Fig. 2b). The studied area is Zengjiang River which is one tributary of Dongjiang River located in the Pear River Delta, China (Fig. 2a). The meteorological data (daily evaporation and daily precipitation) are collected from Qilinzui Hydrological Station for the period of 2009–2015. The total drainage area above the Qilinzui Hydrological Station is 2866 km2, accounting for 91% of the Zengjiang River basin (3160 km2). The mean annual temperature and precipitation are 21.6 °C and 2188 mm, respectively. More details about Zengjiang River basin can be found in (Tao et al. 2011).

Fig. 2
figure 2

The location of the studied catchments (a) and diagram of the GR4J model (b)

Full size image

GR4J model is a rainfall-runoff model which is based on four free parameters from daily rainfall data. In GR4J, the production components include an interception of raw rainfall and potential evapotranspiration, a soil moisture accounting procedure to calculate effective rainfall and a water exchange term to model water losses to or gains from deep aquifers. Its routing module includes two flow components with constant volumetric split (10–90%), two unit hydrographs, and a non-linear routing store (as shown in Fig. 2). The descriptions and initial fluctuating ranges of GR4J model parameters are presented in Table S2. For more details of GR4J model, please refer to the literature (Perrin et al. 2003). However, for a specific watershed, the appropriate parameter ranges should be obtained through the calibration process that produce an acceptable model performance (Shin et al. 2013). It has been reported that the parameters sensitivities were strongly influenced by the ranges of parameter values (Shin et al. 2013). It is important to obtain an appropriate parameter range corresponding to satisfactory model performance before sensitivity analysis (SA) (Saltelli et al. 2019; Shin et al. 2013). Therefore, in this study, the model parameter ranges are calibrated based on the Metropolis-Hastings algorithm (MH) prior to SA in order to identify the input variability space. The details about MH algorithm are presented in supporting materials. Nash–Sutcliffe efficiency (NSE) is used to assess the accuracy of model results which involves standardization of the residual variance. Here, the objective functions adopted can be represented as follows (Nash and Sutcliffe 1970):

$$ NSE=1-\frac{\sum_{i=1}^n{\left({Q}_{obs,i}-{Q}_{sim,i}\right)}^2}{\sum_{i=1}^n{\left({Q}_{obs,i}-\overline{Q_{obs}}\right)}^2} $$
(25)

where Qsim is the simulated runoff, Qobs is the observed runoff, \( \overline{Q_{obs}} \) is the mean value of the observed runoff and n is the sample size.

The posterior distributions of GR4J parameters are presented in Fig. 3a. The predictive intervals of streamflows are presented in Fig. 3b. It can be observed that the parameters in GR4J are well identified after a number of iterations, and the obtained predictive intervals can generally bracket the observations, except for some overestimations in high-flow periods. Based on the posterior distributions, the proposed subsampling ANOVA methods are applied for analyzing parameters sensitivities of GR4J model in Zengjiang River basin. Similar to Sect. 3, different subsampling ANOVA approaches, including single-subsampling ANOVA (5222, 2522, 2252, and 2225), multiple-subsampling ANOVA (5522, 5252, 5225, 2552, 2525, 2255, 5552, 5525, 5255, and 2555), and full-subsampling ANOVA with different parameters level (2222, 3333, 4444, and 5555) are going to be tested.

Fig. 3
figure 3

(a) Posterior distributions of the parameters in GR4J model obtained by MH; and (b) predictive interval and real observations of stream

Full size image

4.2 Performances of Single- and Multiple-Subsampling ANOVA Approaches

With one parameter to be subsampled, the contributions of individual and interactive effects for the four parameters in GR4J model are shown in Fig. 4a. There are several findings as follows. Firstly, taking Sobol’s results as the reference results, X1 makes the largest contribution to GR4J model uncertainty in Zenjiang River, followed by the interactive effects of the four parameters. The high sensitivity of X1 indicates that runoff generation in Zengjiang basin is highly affected by the maximum capacity of the production store. The X1 increases to handle an overestimation of rainfall and decreases to handle an underestimation, thus adapts its capacity to hold and evaporate different amounts of water (Oudin et al. 2006). Secondly, the subsampling procedure would lead to a lower sensitivity value for the subsampled parameter which is similar to the results in Sect. 3.2. For example, the contributions of X1 are 0.109, 0.230, 0.275, and 0.205 for the four single-subsampling schemes of 5222, 2522, 2252, and 2225. The lowest sensitivity value for X1 is obtained in 5222, in which X1 is decomposed into five levels and then subsampled. Thirdly, the ranking of parameter sensitivity is influenced by different single-subsampling schemes (Fig. S4–S6). For instance, the sensitivity order in subsampling scheme of 5222 is Interactions >X3 > X4 > X1 > X2, while in the scheme of 2252, the sensitivity order is Interactions >X1 > X3 > X4 > X2. These results indicate that the single-subsampling ANOVA approach may generate unreliable sensitivity values, which is highly influenced by the parameter to be subsampled.

Fig. 4
figure 4

Contributions of individual and interactions for GR4J model parameters under different subsampling methods. (a) one of the four parameters are subsampled; (b) two of the four parameters are subsampled; (c) three of the four parameters are subsampled. (d) full-subsampling ANOVA methods with different subsampled parameter’s level. Red bar indicates that the parameter is divided into five levels first and then subsampled; blue bar represents that the parameter is only divided into two levels, without subsampling

Full size image

The individual and interactive effects for GR4J model parameters under different multiple-subsampling schemes are presented in Figs. 4b, c. It can be found that, for each parameter, the values of red bars, which indicate the schemes with the parameter being subsampled, are significantly lower than that of blue bars. The mean values of the red bars for X1, X2, X3, and X4 are 0.184, 0.033, 0.124, and 0.078, respectively. Meanwhile the mean values for the blue bars for X1, X2, X3, and X4 are 0.306, 0.098, 0.264, and 0.225, respectively. For each parameter, the mean value without subsampling (blue bars) is more than twice than the mean value with subsampling (red bars). These also suggest that the subsampling-procedure would significantly underestimate the individual sensitivity value for the subsampled parameters in the multiple-subsampling ANOVA approach.

4.3 Performance of Full-Subsampling ANOVA

In the full-subsampling ANOVA approach, different levels for each parameter can be chosen before the subsampling procedure. Similar with Sect. 3, four scenarios (2–5 levels) are going to be chosen for each parameter in GR4J. The contributions of individual and interactions for GR4J model parameters under different levels in full-subsampling ANOVA are presented in Fig. 4d. As the parameter level increases from 2222 to 5555, the sensitivities of X1, X2, and X4 gradually increase from 20.1%, 3.7%, and 4.7% to 31.0%, 7.6%, and 15.8%, respectively. At the same time, the contribution of X3 and interaction gradually decrease from 21.7% to 17.8% and 48.9% to 25.9%. The results indicate that the parameters levels will affect the individual and interactive sensitivities in the full-subsampling ANOVA approach. In details, the sensitivity of the most sensitive parameter and interaction would generally decrease, while the sensitivities of the other parameters increase when the parameter level increases. However, most changes would happen when the parameter level increases from 2 to 3. This is because that when 2 parameters levels are chosen, the full-subsampling ANOVA method would become the traditional ANOVA without subsampling. In comparison, the obtained results would not show noticeable variation and the order of parameters sensitivity would not change when the parameter levels are higher than three. This means that the full-subsample ANOVA approach can generate relatively robust results when the parameter level is larger than 3.

5 Discussion

In this study, the Sobol’s method (Sobol’ 1993; Wang et al. 2018) is considered as the benchmark to evaluate the performance of the developed subsampling ANOVA approaches. The deviation between subsampling ANOVA and Sobol’s approaches can be evaluated as \( \sum \limits_{i=1}^I{\left({\eta}_i^{\ast }-{\eta}_i^{sobol\hbox{'}s}\right)}^2 \), where \( {\eta}_i^{\ast } \) is the sensitivity indices calculated by the subsampling ANOVA approaches, \( {\eta}_i^{sobol\hbox{'}s} \) is the sensitivity indices calculated by Sobol’s method. Figure 5 presents deviations for parameter sensitivity values between the subsampling ANOVA and Sobol’s approaches. It can be concluded that the full-subsampling ANOVA approach is able to generate more reliable results than the single- and multiple-subsampling ANOVA approaches. Moreover, in order to get reliable parameter sensitivity results, the three or more parameter levels in the full-subsampling ANOVA approach are recommended. For instance, the deviations between results of subsampling ANOVA and Sobol’s methods vary within [0.0008, 0.114] for different subsampling schemes with different parameters levels for the three parameters model (Fig. 5a). As for the GR4J model, the corresponding deviations range from 0.024 to 0.114 for single-subsampling ANOVA and multiple-subsampling ANOVA approaches (Fig. 5b). Such noticeable deviations indicate that biased/discrepant sensitivity indices may be obtained through the single/multiple-subsampling ANOVA methods. In comparison, significantly better performances are obtained through the full-subsampling ANOVA method. The deviations are lower than 0.002 when 3 or more parameter levels are chosen in the full-subsampling ANOVA. The negligible bias show that the parameters sensitivities are very close to the “true value” when the subsampled parameter level is 3 or more in full-subsampling ANOVA method. Therefore, in order to get reliable parameter sensitivity results, the full-subsampling scheme with 3 or more parameter levels would be recommended for the application of subsampling ANOVA methods.

Fig. 5
figure 5

The deviations of parameter sensitivity between subsampling ANOVA and Sobol’s: (a) three parameters model and (b) four parameters GR4J model

Full size image

Many research works have reported that Sobol’s method is computationally expensive (Tang et al. 2008; Tian 2013). However, the subsampling ANOVA method is more computationally efficient than the Sobol’s method. To illustrate the computational efficiency of the subsampling ANOVA methods, the number of model runs and the number of calculations of variance required by subsampling ANOVA and Sobol’s methods are presented in Table 1. The details about the calculation requirements are presented in supplementary materials. For the simple three-parameter model, the Sobol’s method needs 2000 × (3 + 2) runs while it would require 3,000,000× (5 + 2) runs for the GR4J model to get stable results for parameters sensitivities, which is a very large computational requirement. However, the subsampling ANOVA methods can significantly reduce the calculation requirements to achieve a similar calculation accuracy for the GR4J model. For instance, in the full-sampling scheme of ″4444″, the only 256 runs is required to get similar sensitivity results with a negligible deviation of 0.0006. Through reducing the number of model runs, the proposed full-subsampling ANOVA methods are effective and feasible for sensitivity analysis with relatively low computational requirements.

Table 1 The number of model running and the number of calculations of variance required by subsampling ANOVA and Sobol’s
Full size table

Even though the subsampling ANOVA approaches may not produce better results than the Sobol’s method, the proposed subsampling ANOVA approaches, especially for the full-subsampling ANOVA method, have their own essential strengths. Firstly, the Sobol’s algorithm has high computational cost. The number of model evaluations required for the Sobol’s indices to converge increases rapidly with the number of parameters, making its efficiency questionable for complex water resources and environmental models (Herman et al. 2013; Khorashadi Zadeh et al. 2017). In comparison, the proposed subsampling ANOVA approaches can produce results with satisfactory accuracy levels with a much lower computational demand (Table 1). The number of model evaluations is equal to the number of combinations with all parameter levels. Meanwhile, the full-subsampling ANOVA approach can generate acceptable results with three or four levels for each parameter. Secondly, besides sensitivity analysis for parameters with continuous values (Qi et al. 2016c), the single-subsampling ANOVA algorithms has already been applied to analyze the sensitivity of discrete or non-numeric elements such as the statistical post processing scheme, precipitation products and the hydrological model (Bosshard et al. 2013; Qi et al. 2016b). Consequently, the developed multiple-/full-subsampling ANOVA approaches can also characterize sensitivities for both numeric and non-numeric variables in water resources and environmental models, which can hardly be treated by the Sobol’s approach.

6 Conclusion

In this study, three kinds of subsampling-ANOVA schemes (single-, multiple- and full-subsampling) have been proposed to characterize individual and interactive sensitivities for parameters in water resources and environmental models. The applicability of the subsampling ANOVA approaches are demonstrated through one simplified model and a rainfall-runoff conceptual model. To evaluate the performance of different subsampling ANOVA schemes, the traditional Sobol’s method is also used as the benchmark in the study. Based on the case studies, the main findings can be concluded:

  1. 1.

    The subsampling schemes can effectively diminish the bias estimation in traditional ANOVA approach. In the applications of the single- and multiple-subsampling ANOVA methods, the parameter’s individual sensitivity is related to the subsampling scheme. The subsampling process would underestimate the individual sensitivity of the parameter to be subsampled and overestimate the individual sensitivities non-subsampled parameters.

  2. 2.

    Among the proposed methods, the full-subsampling ANOVA have the most robust performance and the deviation would decrease with the increase of parameter levels. The variation of the obtained parameters sensitivities is not apparently visible and the order of parameters influences (i.e. sensitivity) would not change for three 3 or more parameter levels.

  3. 3.

    Compared with Sobol’s method, the subsampling ANOVA methods can significantly reduce the calculation requirements to achieve a similar calculation accuracy. Particularly, in order to get reliable parameter sensitivity results, the full-subsampling scheme would be adopted, and 3 or more parameter levels are recommended.

The main innovation of this research is the development of multiple- and full-subsampling ANOVA approaches to reduce bias estimation and enhance the applicability of ANOVA in sensitivity analysis. The influence of subsampling schemes in the single-, multiple- and full-subsampling ANOVA approaches are illustrated through two case studies. The proposed approaches in this study just serve as a first basis for the application of subsampling ANOVA in parameter sensitivity analysis for water resources and environmental models. The number of levels would probably be higher than three to ensure robustness for subsampling ANOVA methods for a more complex model. The subsampling ANOVA algorithms not only reduce the computing cost greatly, but also analyze the sensitivity of discrete or non-numeric elements. Further research is encouraged to examine the applicability of the subsampling ANOVA approaches in other non-numeric elements sensitivity analysis.