1 Introduction

One of primary purposes of reservoirs is to regulate fluctuating streamflow for providing stable water supplies. However, inadequate water supplies are inevitable during prolonged and severe droughts associated with low water-storage in reservoirs. A widely used measure to mitigate such water-deficit impacts is water rationing, which reduces water supplies in advance and conserves more water for future use. Hedging in reservoir operation is a compromise policy that reduces unacceptable high-water-deficits in future but at a cost of accepting a sequence of current and allowed small deficits (Maass et al. 1962). In literature, a considerable amount of studies has been devoted to investigate a variety of optimal hedging rules which includes Hashimoto et al. (1982), Bayazit and Unal (1990), Shih and ReVelle (1995), Srinivasan and Philipose (1998), Cancelliere et al. (1998), Shiau (2003), Draper and Lund (2004), You and Cai (2008), Shiau (2009, 2011), Taghian et al. (2014), Peng et al. (2015), Hu et al. (2016), Ahmadianfar et al. (2016), Ji et al. (2016); Ding et al. (2017), Ashofteh et al. (2017), and Xu et al. (2017).

Decision-making in reservoir operation often involves ambiguous and imprecise information. Fuzzy logic provides an alternative to modeling inherent vagueness characteristics and gains popularity in reservoir-operation studies over past decades. Dubrovin et al. (2002) indicated that incorporating fuzzy set theory in reservoir operation can be categorized into three categories, i.e., fuzzy optimization techniques (Kindler 1992; Tilmant et al. 2002; Akter and Simonvic 2004; Chandramouli and Nanduri 2011; Han et al. 2012; Kamodkar and Regulwar 2014; Kumari and Mujumdar 2015), fuzzy rule base systems (Russell and Campbell 1996; Panigrahi and Mujumdar 2000; Sivapragasam et al. 2008; Moeini et al. 2011), and combinations of the fuzzy approach with other techniques (Ponnambalam et al. 2003; Mousavi et al. 2007; Fu 2008; Mehta and Jain 2009; Fu et al. 2012; Teegavarapu et al. 2013; Vucetic and Simonovic 2013; Zhu et al. 2016). Among these reservoir-operation studies, however, few studies have been devoted to explore effects of fuzzy logic on hedging during droughts. Ahmadianfar et al. (2016) propose a fuzzy-rule-based approach that fuzzify rule curves to create transition zones with gradually varying rationing factors and apply to Zohre multi-reservoir system located in northern Iran to explore effects between minimum-flow and agricultural water uses during droughts.

The conventional zone-based rule-curve operation is an easily implemented rule and is classified as the discrete hedging since finite and fixed rationing factors are assigned for various zones. A drawback for such hedging is that the rationing factor would abruptly change from one zone to another. Fuzzified rule curves provide an alternative to create gradually varied rationing factors and formulate a nearly continuous hedging. In this study, impacts of conventional hedging factors (rule curves and rationing factors) and fuzzification on water-deficit characteristics are explored. The optimal hedging rules during droughts are also derived based on integrated water-shortage characteristics. The proposed approach is illustrated through an application to the Nanhua Reservoir located in southern Taiwan.

The remainder of this work is laid out as follows. Section 2 presents fuzzified rule curves, water-shortage characteristics, and multi-criteria optimization scheme. Section 3 gives parametric operation rules of the Nanhua Reservoir located in southern Taiwan. Results and discussions are given in the Section 4. Finally, in Section 5 the main conclusions of this work are summarized.

2 Methodology

2.1 Parametric Representation of Rule Curves and Rationing Factors

Fig. 1 illustrates a two (upper and lower) rule-curves operation, although the proposed approach can be extended to the reservoir operation with three or more rule curves. In this study, parametric representation of rule curves are only considered for the lower rule curve because that water-supply is the primary purpose of the Nanhua Reservoir. The lower rule curve can be represented by five segments connected with six end-points in terms of time (in unit of 10-day period) and storage. These six end-points include (1, S1), (T1, S2), (T2, S2), (T3, S3), (T4, S3), and (36, S4). Changes of S1, S2, S3, S4, T1, T2, T3, and T4 would result in different rule curve and have different impacts on water supply.

Fig. 1
figure 1

Parametric representation of the lower rule curve of the Nanhua Reservoir (southern Taiwan)

Full size image

Two rule curves partition reservoir storage into three zones which includes zone H (above upper rule curve), zone M (between upper and lower rule curves), and zone L (below lower rule curve). Water releases guided by rule curves are simply assigning a releasing coefficient or rationing factor for each zone. That is,

$$ {R}^t=\left\{\begin{array}{l}{\alpha}_H{D}^t,\mathrm{if}\ {S}^t\in H\\ {}{\alpha}_M{D}^t,\mathrm{if}\ {S}^t\in M\\ {}{\alpha}_L{D}^t,\mathrm{if}\ {S}^t\in L\end{array}\right. $$
(1)

where Rt, Dt, and St denote reservoir release, projected demand, and storage at time t, respectively; α H , α M , and α L respectively denote the rationing factor for zones H, M, and L. Value of rationing factors ranges between 0 and 1 and less-than-1 factor represents hedging. Value of α H is specified as 1 in this study since zone H represents abundant water storage.

Hedging factors involved in the conventional zone-based rule-curve operation include rule curve (S1, S2, S3, S4, T1, T2, T3, and T4) and rationing factors (α M and α L ). Changes of these factors lead to different hedging policy and result in different water-shortage characteristics. Values of these two types of hedging factors are thus determined by optimization models which minimize water-shortage characteristics.

2.2 Fuzzified Rule Curves and Rationing Factor

In contrast to conventional (crisp) rules described in Eq. (1), fuzzy rules allow storage partially and simultaneously belongs to different zones. The first step in building fuzzy rules is to determine the degree of storage belonging to each zone through the membership functions. The trapezoidal membership functions of zones H, M, and L, shown in Fig. 2, are adopted in this study and expressed as

$$ {\mu}_H=\left\{\begin{array}{l}1,\kern6.75em {S}^t> URC\\ {}\frac{S^t-{H}_L}{URC-{H}_L},\kern0.5em {H}_L<{S}^t\le URC\\ {}0,\kern6.75em {S}^t\le {H}_L\end{array}\right. $$
(2a)
$$ {\mu}_M=\left\{\begin{array}{l}0,\kern7.75em {S}^t\le {M}_L\\ {}\frac{S^t-{M}_L}{LRC-{M}_L},\kern1.25em {M}_L<{S}^t\le LRC\\ {}1,\kern5em LRC<{S}^t\le URC\\ {}\frac{M_U-{S}^t}{M_U- URC},\kern0.5em URC<{S}^t\le {M}_U\\ {}0,\kern7.75em {S}^t>{M}_U\end{array}\right. $$
(2b)
$$ {\mu}_L=\left\{\begin{array}{l}1,\kern7.25em {S}^t\le LRC\\ {}\frac{L_U-{S}^t}{L_U- LRC},\kern0.5em LRC<{S}^t\le {L}_U\\ {}0,\kern7.25em {S}^t>{L}_U\end{array}\right. $$
(2c)

where URC and LRC denote upper and lower rule curves, respectively; L U is the upper boundary of zone L; M L and M U are the lower and upper boundaries of zone M, respectively; H L is the lower boundary of zone H.

Fig. 2
figure 2

Trapezoidal membership function for fuzzified rule curves (LRC: lower rule curve, URC: upper rule curve, LU: upper boundary of zone L; ML: lower boundary of zone M; MU: upper boundary of zone M; HL: lower boundary of zone H)

Full size image

Values of L U , M L , M U , and H U are parameterized by four dimensionless parameters (β1,β2,β3, and β4) and rewritten as

$$ {L}_U= LRC+{\beta}_1\left( URC- LRC\right) $$
(3a)
$$ {M}_L= LRC-{\beta}_2\left( URC- LRC\right) $$
(3b)
$$ {M}_U= URC+{\beta}_3\left( URC- LRC\right) $$
(3c)
$$ {H}_L= URC-{\beta}_4\left( URC- LRC\right) $$
(3d)

where β1,β2,β3, and β4 are dimensionless coefficients (0 ≤ β1, β2, β3, β4, ≤ 1) used to determine boundaries of membership functions. Fuzziness effects vanish when β1 = β2 = β3 = β4 = 0.

Since storage may simultaneously belong to different zones, the releasing coefficient or rationing factor is determined by membership-values weighted average for three zones. The amount of water release thus becomes

$$ {R}^t=\frac{\alpha_H{\mu}_H+{\alpha}_M{\mu}_M+{\alpha}_L{\mu}_L}{\mu_H+{\mu}_M+{\mu}_L}{D}^t={C}_{RC}{D}^t $$
(4)

where C RC is the fuzzified rationing factor which is a function of membership values and rationing factors of three zones. Changes of boundaries of membership functions of various zones induce different fuzzified rationing factor and hence different releases. Determination of β1,β2,β3, and β4 is also dependent on the selected shortage indices and optimization framework.

2.3 Reservoir Performance Indices

Various values of three types of hedging factors including rule curve (S1, S2, S3, S4, T1, T2, T3, and T4), rationing factors (α M and α L ), and fuzzified rule curve (β1,β2,β3, and β4) would result in different releases and lead to different impacts on reservoir performance during droughts. Six water-shortage indices are therefore employed to evaluate reservoir performance.

  1. 1.

    Maximum single-period shortage ratio (MSR) is defined as the maximum shortage ratio of a single operation period (10-day period) over the study period and expressed as:

$$ MSR=\underset{t}{\operatorname{Max}}\left\{{SR}^t\right\},\kern0.5em t=1,2,\dots, N $$
(5)

where SRt denotes water-shortage ratio at time t and defined as SRt = STt/Dt × 100%, here STt is water shortage at time t which is defined as reservoir release (Rt) insufficient to meet the project demand (Dt), i.e., STt = max {Dt − Rt, 0}; N is the total operation periods.

  1. 2.

    Maximum shortage-ratio difference between two successive periods (MDSR) is used to measure how smooth-going of the hedging rules and defined by:

$$ MDSR=\underset{t}{\operatorname{Max}}\left\{\ \left|{SR}^t-{SR}^{t-1}\right|\right\},\kern0.5em t=2,\dots, N $$
(6)
  1. 3.

    Total shortage ratio (TSR) is defined as the ratio of total water shortages to the total projected demands over the study periods and expressed as:

$$ TSR=\frac{\sum \limits_{i=1}^N{ST}^t}{\sum \limits_{i=1}^N{D}^t}\times 100\% $$
(7)
  1. 4.

    Average water-shortage per shortage period (AWS) is defined as the ratio of total water shortages to the shortage duration and expressed as:

$$ AWS=\frac{\sum \limits_{i=1}^N{ST}^t}{SD} $$
(8)

where SD denote the shortage duration and defined as the total periods with insufficient supply, i.e., \( SD=\sum \limits_{i=1}^N\left\{\begin{array}{l}1,\mathrm{if}\ {ST}^t>0\\ {}0,\mathrm{otherwise}\end{array}\right. \).

  1. 5.

    Risk (RISK) is defined as the ratio of shortage duration to the total operation periods and expressed as:

$$ RISK=\frac{SD}{N} $$
(9)
  1. 6.

    Shortage-event frequency (SEF) is defined as the mean annual number of water shortage events and defined by:

$$ SEF=\frac{TSE}{N_Y} $$
(10)

where TSE denotes the total number of water-shortage events and a water-shortage event is defined as a consecutive water-shortage period; N Y is the number of years in the study period.

These six shortage indices encompass duration, severity, and frequency characteristics of water shortages at various time scales. These indices are used as objective functions in optimization models to derive the optimal hedging rule.

2.4 Multi-Criteria Optimization Framework

Minimizing all the six shortage indices formulates a multi-objective optimization problem. That is,

$$ \operatorname{Min}\ MSR, MDSR, TSR, AWS, RISK, SEF $$
(11)

Since these indices have different units and span different ranges of values, the following scheme is employed to normalize the values of objective functions.

$$ {{\mathrm{OBJ}}_i}^{\hbox{'}}=\frac{{\mathrm{OBJ}}_i-\min \left({\mathrm{OBJ}}_i\right)}{\max \left({\mathrm{OBJ}}_i\right)-\min \left({\mathrm{OBJ}}_i\right)} $$
(12)

where OBJ i and OBJ i ′ are original and normalized values of ith index (i = 1 to 6); max(OBJ i ) and min(OBJ i ) are the maximum and minimum values of the ith index. This normalization scheme ensures each index is bounded between 0 and 1 with the most and least favorable values being 0 and 1, respectively. The objective function in Eq. (11) is thus rewritten as minimization of all normalized indices.

$$ \operatorname{Min}\ {MSR}^{\hbox{'}},{MDSR}^{\hbox{'}},{TSR}^{\hbox{'}},{AWS}^{\hbox{'}},{RISK}^{\hbox{'}},{SEF}^{\hbox{'}} $$
(13)

This multi-objective optimization problem is solved by the technique for order performance by similarity to ideal solution (TOPSIS) which is initialed by Hwang and Yoon (1981). The basic idea of this approach is that the best alternative has the shortest distance from the positive ideal solution (PIS) and has the longest distance from the negative ideal solution (NIS). The weighted total distances from the PIS and NIS, denoted by D+ and D−, are calculated by

$$ {D}^{+}={\left[\sum \limits_{i=1}^6{w}_i{\left({{\mathrm{OBJ}}_i}^{\hbox{'}}-{\mathrm{OBJ}}_i^{+}\right)}^2\right]}^{1/2} $$
(14a)
$$ {D}^{-}={\left[\sum \limits_{i=1}^6{w}_i{\left({{\mathrm{OBJ}}_i}^{\hbox{'}}-{\mathrm{OBJ}}_i^{-}\right)}^2\right]}^{1/2} $$
(14b)

where w i is the weighting for the ith index and \( {\sum}_{i=1}^6{w}_i=1 \); \( {\mathrm{OBJ}}_i^{+}=0 \) and \( {\mathrm{OBJ}}_i^{-}=1 \) denote PIS and NIS of ith index, respectively.

The optimal solution is then determined by maximizing the relative distance to NIS, which is expressed as

$$ \max {D}^{\ast }=\max \frac{D^{-}}{D^{+}+{D}^{-}} $$
(15)

Value of D∗ ranges between 0 (ideally worst solution) and 1 (ideally best solution). Higher value of D∗ represents more trade-offs among conflicting objectives. Equal weighting of 1/6 is given to these six shortage objectives in this study. The optimal solution is searched by the genetic algorithm (GA) with a population size of 1000 and typical values of 0.8 and 0.05 for the crossover and mutation rates. TOPSIS-based multi-criteria optimization scheme is incorporated into the reservoir operation model to optimally determine the hedging policy simultaneously favorable to all shortage indices.

3 Nanhua Reservoir System

3.1 An Overview

Finished in 1995, the primary purpose of the Nanhua Reservoir is to offer stable domestic supplies to two major cities (Tainan and Kaohsiung) located in southern Taiwan. The Nanhua Reservoir dams the Houku Creek, a tributary of the Tsengwen Creek, and has a drainage area of 108.3 km2 and mean annual inflow of 212 million m3 for the 1959–2009 period. However, highly fluctuating streamflow (with monthly values reported in Table 1) associated with 113.8 million m3 capacity (measured in 2004) are insufficient to meet the annual domestic demand of 192 million m3 (monthly demand shown in Table 1). An interbasin transfer facility, Chiahsien diversion weir, has been constructed in 1999 and diverts excess streamflow of the nearby Chishan Creek to increase water-supply capability of the Nanhua Reservoir.

Table 1 Monthly mean inflow, projected domestic demand, reserved downstream needs, and maximum interbasin transfer at Nanhua Reservoir and Chiahsien diversion weir
Full size table

3.2 System Operation Model

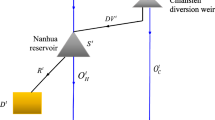
The Nanhua Reservoir associated with the interbasin Chiahsien diversion weir operation system is illustrated in Fig. 3. The amount of interbasin transfer from the Chiahsien diversion weir is determined by

$$ {DV}^t=\min \left\{\max \left\{{I}_C^t-{W}_C^t,0\right\},{DV}_{\mathrm{max}}^t,\max \left\{\frac{S_{\mathrm{max}}-{S}^t+{D}^t}{\Delta t}-\max \left\{{I}_H^t-{W}_H^t,0\right\},0\right\}\right\} $$
(16)

where \( {I}_H^t \) and \( {I}_C^t \) denote inflows at time t for the Nanhua Reservoir and Chiahsien diversion weir, respectively, streamflow series for the 1959–2009 period is used as known inputs in this study; \( {W}_H^t \) and \( {W}_C^t \) respectively denote the reserved amounts of downstream uses at the Houku Creek and Chishan Creek, which have higher priority than the domestic demands and the monthly values are summarized in Table 1; Dt is the projected domestic demands of the Nanhua Reservoir; \( {DV}_{\mathrm{max}}^t \) is the maximum interbasin transfers of the Chiahsien diversion weir and the monthly values are reported in Table 1; St is the reservoir storage of the Nanhua reservoir at the beginning of time t, which is constrained between dead storage Smin (= 0 million m3) and capacity Smax (= 113.8 million m3).

Fig. 3
figure 3

Schematic operation system of the Nanhua Reservoir and the Chiahsien diversion weir

Full size image

The reservoir storage at time t + 1 is then determined on the basis of the water-balance formula. i.e.,

$$ {S}^{t+1}={S}^t+\left({I}_H^t+{DV}^t-{R}^t-{O}_H^t\right)\Delta t-{E}^t $$
(17)

where Rt and \( {O}_H^t \) denote reservoir releases for projected demand and others, respectively; Δt denotes the operation interval and the 10-day period is used in this study; Et denotes reservoir evaporation loss which is estimated by

$$ {E}^t={e}^t\times \frac{1}{2}\left({A}^t+{A}^{t+1}\right) $$
(18)

where At and At + 1 are reservoir surface area at time t and t + 1; et is evaporation rate and the daily mean values are summarized in Table 1.

Reservoir releases for demand Dt and others are respectively determined by

$$ {R}^t=\min \left\{\frac{C_{RC}{D}^t}{\Delta t},\frac{S^t-{S}_{\mathrm{min}}-{E}^t}{\Delta t}+\max \left\{{I}_H^t-{W}_H^t,0\right\}+{DV}^t\right\} $$
(19)
$$ {O_H}^t=\min \left\{{I}_H^t,{W}_H^t\right\}+\max \left\{\max \left\{{I}_H^t-{W}_H^t,0\right\}-{R}^t+{DV}^t-\left(\frac{S_{\mathrm{max}}+{S}_{\mathrm{min}}}{\Delta t}\right),0\right\} $$
(20)

where C RC denotes the rationing factor which is determined by Eq. (1) for non-fuzzy rules and Eq. (4) for fuzzy rules.

The water-balance formula for the Chiahsien diversion weir is used to calculate the outflow of the Chiahsien diversion weir, i.e.,

$$ {O_C}^t={I_C}^t-{DV}^t $$
(21)

3.3 Current Operation and Optimization Scenarios of the Nanhua Reservoir-Chiahsien Weir System

Parametric representation of the Nanhua Reservoir-Chiahsien Weir system operation includes 14 parameters, i.e., S1, S2, S3, S4, T1, T2, T3, T4, α M , α L , β1, β2, β3, and β4. Values of these parameter for current operation are S1 = 78, S2 = 14, S3 = 88, S4 = 83 (million m3), T1 = 16, T2 = 18, T3 = 27, T4 = 34 (10-day period), α M  = 1, α L  = 0.7, and β1 = β2 = β3 = β4 = 0, which are reported in Table 2. To explore effects of the rule curve (S1, S2, S3, S4, T1, T2, T3, and T4), rationing factor (α M and α L ), and fuzziness (β1, β2, β3, and β4) on reservoir performance in terms of shortage indices, seven optimization scenarios which contain various combinations of hedging factors are applied to this system. The current operation associated with these seven optimization scenarios are categorized into two groups. The first non-fuzzy group includes scenario C (current operation), scenario R (optimizing rule curve), scenario H (optimizing rationing factors), and scenario RH (optimizing rule curve and rationing factors). The second group contains four scenarios identical to the first group with the exception of fuzzified rule curve, i.e., optimizing membership functions. The second fuzzy group thus contains scenarios CF, RF, HF, and RHF. Numbers of unknown parameters involved in scenarios C, R, H, RH, CF, RF, HF, and RHF are equaling to 0, 8, 2, 10, 4, 12, 6, and 14, respectively, and are determined by the multi-criteria optimization framework, while the other known parameters are specified to the values identical to the current operation (reported in Table 2).

Table 2 Outcomes of current and optimization scenarios for the Nanhua Reservoir-Chiahsien Weir system
Full size table

4 Results and Discussions

4.1 Performance Evaluation of Non-fuzzy Scenarios

Performance of current operation of the Nanhua Reservoir-Chiahsien Weir system is served as a basis to compare outcomes of other optimal scenarios. Values of 14 parameters of current operation are reported in Table 2 and the outcomes in terms of 6 shortage indices associated with their normalized values are summarized in Table 2. These normalized values are determined using Eq. (12) and the corresponding maximum and minimum values of each objective, which are obtained by optimizing a single objective, are also summarized in Table 2. It is clear that normalized objectives of TSR', AWS', and RISK' for scenario C are low (< 0.3), while normalized indices of MSR' and SEF' are relatively high (> 0.9).

To explore more efficient hedging for mitigating shortage impacts, three optimization scenarios (R, H, and RH) are analyzed in this section. The scenario R determines the optimal lower rule curve but keeping the current rationing factors. The derived lower rule curve, shown in Fig. 4 and reported in Table 2, is lower than the current lower rule curve and thus shrinks the rationing zone. This hedging scheme effectively reduces total shortage ratio (TSR' = 0.043), shortage duration (RISK' = 0.057), and shortage-event frequency (SEF' = 0.103) when comparing with the results of scenario C. But it increases MDSR' and AWS' to 0.606 and 0.350, respectively and maintains MSR' = 1.

Fig. 4
figure 4

Rule curves of the current operation and the derived lower rule curves for various optimization scenarios

Full size image

The scenario H searches the optimal rationing factors for fixing the current lower rule curve. The obtained optimal rationing factors α M  = 0.9 and α L  = 0.5 lead to an early hedging since rationing triggered when reservoir storage below upper rule curve. This scenario effectively reduces MSR' = 0.343, MDSR' = 0.347, and AWS' = 0.114 but at a cost of increasing TSR' = 0.437, RISK' = 0.614, and SEF' = 0.444 in comparison with outcomes of the scenario C.

It is worth to note that scenarios R and H have opposite influences on shortage indices because that the scenario R reduces the hedging zone but the scenario H increases it. The scenario RH simultaneously optimizes the rationing factors and lower rule curve and the optimal outcomes are summarized in Table 2. The optimal lower rule curve, shown in Fig. 4, roughly ranges between lower rule curves of scenarios C and R, while the rationing factor of α L  = 0.4 is the lowest among the four non-fuzzy scenarios. This hedging scheme leads to four shortage indices (MDSR, TSR, RISK, and SEF) ranged between those of other scenarios, while it also induces the lowest MSR' = 0.333 and the highest AWS' = 0.603.

Comparing to the overall index of D∗ = 0.480 for the current operation, all optimization scenarios induce a significant improvement in overall performance since obtained D∗ = 0.593, 0.607, and 0.649 for scenarios R, H, and RH, respectively. This implies that the hedging in current operation inadequately mitigates shortage impacts. Significant improvement obtained by scenario R is attributed to shrinking rationing zone, but it may cause high single-period shortage ratio since insufficient conservation for future uses. Early hedging triggered by scenario H conserves enough water to mitigate high-percentage deficits, but it also induces longer shortage duration. The scenario HR simultaneously optimizes the rule curve and rationing factors and derives more compromising results among conflicting shortage indices, which is the best alternative in the first non-fuzzy group.

4.2 Performance Evaluation of Fuzzy Scenarios

Involving fuzzified rule curve (optimizing boundaries of membership functions) into previous four non-fuzzy scenarios constructs four fuzzy scenarios of CF, RF, HF, and RHF. The optimal outcomes associated with the normalized objectives of these scenarios are all summarized in Table 2. The fuzzified current rule curve of the scenario CF creates transition zones associated with gradually varied rationing factor. The rationing factor of this scenario, comparing with the discrete two-stage rationing factor of the scenario C, is illustrated in Fig. 5. This continuous-like multiple-stage hedging reduces MDSR' = 0.428, AWS' = 0.112, and SEF' = 0.444, but at a cost of increasing RISK' = 0.428 since it induce longer shortage duration. In comparison with the overall index of D∗ = 0.480 for the current operation, the scenario CF with D∗ = 0.541 results in an improvement in overall performance.

Fig. 5
figure 5

Rationing factors of the 24th 10-day period (end of August) for various scenarios

Full size image

The scenario RF optimizes the rule curve as well as the membership function and results in a better outcome (D∗ = 0.603) than scenarios R (D∗ = 0.593) and CF (D∗ = 0.541). The obtained optimal lower rule curve (shown in Fig. 4) is close to the lower rule curve derived by the scenario R. This hedging rule effectively reduces TSR' = 0.025 and SEF' = 0.094 which are lower than those of scenarios R and CF, but it still remains MSR' = 1. The scenario HF optimizes rationing factors and fuzzified current rule curve. The obtained results (D∗ = 0.659) outperforms scenarios H (D∗ = 0.607) and CF (D∗ = 0.541). This hedging rule has α M  = 1 and α L  = 0.5 associated with fuzzified rule curve effectively reduces MSR' = 0.190 and improves MDSR' = 0.347 and SEF' = 0.41. Although the fuzzy factor involved in the optimization framework, opposite effects on shortage indices induced by scenarios RF and HF are identical to the non-fuzzy scenarios R and H.

The scenario RHF optimizes all 14 parameters and derives the best alternative (D∗ = 0.679) among four fuzzy scenarios. When comparing with outcomes of the scenario RH, identical rationing factors (α M  = 1 and α L  = 0.4) and similar rule curve (see Fig. 4) associated with fuzzifiness derived by the scenario RHF lead to a significant improvement of AWS and minor deterioration of MSR, TSR, RISK, and SEF. Shortage indices obtained by the scenario RHF are ranged between those indices of other fuzzy scenarios. Although none lowest indices derived by the scenario RHF, three hedging factors involved in the optimization framework result in the best hedging policy with trade-offs among conflicting shortage indices.

It is worth noting that the fuzzy scenarios CF, RF, HF, and RHF outperform the non-fuzzy scenarios C, R, H, and RH, respectively. A further overall improvement is obtained by involving one more fuzzy factor in the optimization models, which is attributed to greater rationing zone associated with less-than-1 rationing factor (see Fig. 5). Fuzzy scenarios thus increase shortage duration and generally induce greater RISK and smaller AWS. Besides, gradually varying hedging factor of the fuzzy scenarios induces more even shortages and reduces number of shortage events and thus leads to smaller SEF.

4.3 Discussion

Three types of hedging factors (rule curve, rationing factor, and fuzziness) involved in the current and optimization scenarios are explored to investigate effects on shortage indices. The results reveal that these hedging factors have different impacts on shortage indices. Shrinkage of rationing zone by lower rule curve effectively decrease total shortage ratio (TSR) and shortage duration (RISK), but it may conserve insufficient water during severe droughts and induces high single-period shortage (MSR and MDSR). For example, scenarios RF and R have the lowest and second lowest TSR (TSR' = 0.025 and 0.043), the second lowest and lowest RISK (RISK' = 0.072 and 0.057), the highest MSR (MSR' = 1), and the highest and second highest MDSR (MDSR' = 0.608 and 0.606) among all scenarios.

Early hedging triggered by more and smaller less-than-1 rationing factors conserves sufficient water for future use and leads to small single-period shortage (MSR and MDSR), but at a cost of inefficient uses of water, i.e., increasing total shortage ratio (TSR) and shortage duration (RISK). For instance, the scenario H has the lowest MDSR (MDSR' = 0.347), the highest TSR (TSR' = 0.437), and the highest RISK (RISK' = 0.614). The scenario HF has the lowest MSR (MSR' = 0.190), the lowest MDSR (MDSR' = 0.347), and the second highest RISK (RISK' = 0.466).

Fuzzified rule curve creates transition zone associated with gradually varied rationing factor and induces more even shortages during shortage duration. For example, the fuzzy scenarios generally have lower AWS, declined SEF, and higher RISK than the non-fuzzy scenarios. Combination of two or more hedging factors would induce trade-offs among conflicting shortage indices. Figure 6 illustrates water shortages of various scenarios for the 1980–1981 period, which is the driest period over the study periods. The non-fuzzy scenarios clearly create discrete shortage events, while the fuzzy scenarios induce early hedging and more continuous and even shortages during shortage periods.

Fig. 6
figure 6

Water shortages of various scenarios for the 1980–1981 period

Full size image

These eights scenarios can be classified into four categories according to the numbers of hedging factors to be optimized. The scenario C (current operation) contains no optimized hedging factor, one-optimized-hedging-factor scenarios include R, H, and CF, scenarios RH, RF, and HF involve two hedging factors to be optimized, and three optimized hedging factors are involved in the scenario RHF. Based on the overall index D∗, the scenario C clearly is the worst scenario due to the lowest D∗ of 0.480. Three one-optimized-hedging-factor scenarios with an improved D∗ ranged between 0.541 and 0.607 outperform the scenario C and the scenario H (D∗ = 0.607) is the best alternative among three one-factor scenarios. Two-optimized-hedging-factor scenarios have a further improved D∗ of 0.603−0.659 and are generally better than the one-factor scenarios. An exception is the scenario RH (D∗ = 0.603) slightly worse than the scenario H (D∗ = 0.607). The scenario HF with D∗ = 0.659 is the best two-factor scenario. The three-optimized-hedging-factor scenario RHF evidently ranks top among all scenarios since it contains the most parameters to be optimized and reaches the highest D∗ of 0.679. The results indicate that adjustment of rationing factors receives greater improvements of overall performance than other hedging factors. Using fuzziness in reservoir hedging enhances influences of optimized factors on shortage indices, but less improvement is obtained if fuzziness is used as a single hedging factor in reservoir operation.

5 Summaries and Conclusions

Effects of hedging factors (rule curve, rationing factor, and fuzziness) on reservoir performance in terms of six shortage objectives including maximum single-period shortage ratio (MSR), maximum shortage-ratio difference between two successive periods (MDSR), total shortage ratio (TSR), average shortage per shortage period (AWS), risk (RISK), and shortage-event frequency (SEF) are explored in this study. The proposed optimization framework searches an optimal hedging rule that has a trade-off among conflicting shortage indices and applied to the Nanhua Reservoir-Chiahsien Weir system located in southern Taiwan.

The current operation (scenario C) associated with seven optimization scenarios (R, H, RH, CF, RF, HF, and RHF) involve different numbers of hedging factors to be optimized (R, H, and F respectively representing rule curve, rationing factor, and fuzziness). The results reveal that these hedging factors have different impacts on shortage indices. Shrinkage of rationing zone by lower rule curve effectively decrease total shortage ratio (TSR) and shortage duration (RISK), but it may conserve insufficient water during severe droughts and induces high single-period shortage (MSR and MDSR). Early hedging triggered by more and smaller less-than-1 rationing factors conserves sufficient water for future use and leads to small single-period shortage (MSR and MDSR), but at a cost of increasing total shortage ratio (TSR) and shortage duration (RISK). Fuzzified rule curve creates transition zones associated with gradually varied rationing factors and induces more even shortages during shortage duration, which induces lower AWS, declined SEF, and higher RISK.

Opposite impacts on shortage indices for various hedging factors are evidently observed. More hedging factors involved in optimization framework generally result in an optimal hedging policy with trade-offs among conflicting shortage indices. According to the proposed overall index D∗ (a multi-criteria index based on normalized shortage indices), the current operation (scenario C) without optimized hedging factors clearly is the worst scenario because of the lowest D∗ of 0.480. Three one-optimized-hedging-factor scenarios outperform the scenario C and have an order of scenarios H (0.607), R (0.593), and CF (0.541). Two-optimized-hedging-factor scenarios are generally better than the one-factor scenarios and have a further improved D∗ of 0.659 (HF), 0.649 (RH), and 0.603 (RF). The three-optimized-hedging-factor scenario RHF evidently ranks top among all scenarios since it contains the most parameters to be optimized and reaches the highest D∗ of 0.679. Impacts of the optimized rationing factor on shortage indices in terms of D∗ are greater the results induced by optimized rule curve, and the fuzziness has the least impacts on shortages for the Nanhua Reservoir case under study.

Hedging is an essential component in reservoir operation to ensure sufficient water storage and supply during droughts. The results suggest that the proposed optimization models lead to a significant improvement in overall performance than the current operation. Water availability during droughts depends not only on the stored water but also the future inflow. To have effective real-time hedging during droughts, future demand and inflow as well as the drought indicators such as the standardized precipitation index (SPI) are important factors to trigger hedging. Deriving a fuzzy-rule based real-time hedging policy based on these factors remains a topic for future studies.