Two-Phase Risk Hedging Rules for Informing Conservation of Flood Resources in Reservoir Operation Considering Inflow Forecast Uncertainty

Abstract

Water shortages during dry periods can be successfully mitigated by managing reservoirs in real-time to conserve water as floods recede. The inherent uncertainty in inflow forecasts however means that it remains a challenge to balance the risks of flooding against those of water shortages. Few studies have examined how the risks of floods and water shortages can be managed using reservoir operation rules. In this study, a two-phase stochastic optimization model was built to determine the optimal conservation level for flood water by minimizing the risks from both floods and water shortages. For the optimal condition, hedging rules were analytically derived as a quasi-linear function of the storage capability and the expected water shortage. The rules indicate that the flood water conservation was achieved when the marginal upstream flood risk was equal to the marginal water shortage risk, and that the limits of three operation zones divided by the expected water availability should be used when determining the water release. The results from testing the model with data from the Xianghongdian Reservoir (China) showed that the hedging rules outperformed the capacity-constrained pre-release rules for conserving flood water without increasing the flood risk. This proposed methodology will inform the process for making decisions about how to operate reservoirs to ensure optimal real-time flood water conservation.

1 Introduction

In recent years, the conflict between the supply and demand for water resources in China has intensified drastically (Wen et al. 2018), to the extent that water resources are the main constraint on sustainable socioeconomic development in certain areas. Affected by the monsoon climate, the annual distribution of runoff to the principal rivers in the monsoon region of China (Liu and Shi 2019) varies considerably and exhibits high inter- and intra-annual variabilities. Highly variable inflows must be regulated by reservoirs (Mao et al. 2019) to maximize resource use and minimize loss during floods. Therefore, in an effort to alleviate the conflict between flood control and the water supply, it is thought that reservoirs could be operated to conserve flood water and mitigate water shortages (Shenava and Shourian 2018). Currently, the main objective of managing reservoirs during the flood season is to minimize the economic losses and social impacts caused by flood disasters (Moridi and Yazdi 2017) rather than conserve water. In this approach, the reservoir water level must be maintained below the flood limited water level (FLWL) to preserve flood storage before a flood occurs. With low levels of reservoir storage, it is thought that the spare capacity could be used to conserve flood water, reducing the waste of flood resources and using them to alleviate water shortages and improve ecological conditions. However, this conservation of flood water through reservoir operation rules is impeded by the lack of a technical method to determine a suitable conservation level, which ensures that the inherent uncertainty in the risks associated with flood control and water shortage are both acceptable and manageable (Xu et al. 2017).

Real-time reservoir operation formulates a risk decision-making problem that addresses uncertainty. A variety of optimization models, including explicit and implicit stochastic optimizations, have been developed to inform reservoir operation under uncertainty (Labadie 2004). Explicit stochastic optimization directly models uncertainty as stochastic processes and derives specific release and storage strategies (Yeh 1985; Yang et al. 2018). These models provide decision-making solutions but, because of their complexity, fail to explain the mechanism by which conflicting objectives interact and reach an optimum. This is widely recognized as a mathematical barrier that blocks the practical application of numerical optimization models. Implicit stochastic optimization, which obtains operating rules through data mining or analytical derivations based on optimal conditions (Lund and Guzman 1999), provides an alternative way to interpret the optimal conditions. In flood water conservation, Li et al. (2010) employed a capacity-constrained pre-release rule to determine that the upper limit of conservation could be as much as the pre-release capacity within an effective forecast lead-time. However, this rule fails to explicitly model the risks associated with forecast uncertainty, which could diminish the reliability of a strategy or give sub-optimal results.

Minimizing the total risks (Zhu et al. 2020) through reservoir operation by reallocating the temporal distribution of inflow involves formulating a risk hedging model (Bayazit and Unal 1990; Hashimoto et al. 1982). Analytical HRs, because of their ability to simplify the reservoir modelling operation into a two-phase (current and future phases) decision-making problem (Zhang et al. 2019), are considered advantageous for describing the optimization mechanism on the basis of the optimality principle. Various authors (Draper and Lund 2004; You and Cai 2008) used hydro-economic analysis to show that the optimal release followed the identical marginal utility regime (Zhao et al. 2011). At present, HRs have been widely used to investigate water supply (You and Cai 2008; Draper and Lund 2004; Shiau 2011), flood control (Zhao et al. 2014), reservoir refills (Wan et al. 2016; Ding et al. 2015), hydropower generation (Xu et al. 2017, 2019), and reservoir pre-release (Hui et al. 2016) operations.

Although various HRs for reservoir operation have been developed in previous studies, there is still a knowledge gap whereby the interactions between the risks of floods and water shortages are described by analytical formulae. Current HRs often address flood risks as the dominant index and determine the flood water conservation level without exceeding an acceptable level of flood risk. Using this approach, there could be over-conservation when the acceptable level of flood risk is high and the expected water shortages are low. Moreover, current HRs often assume a perfect foresight of inflow during the current phase, which potentially underestimate the occurrence probability of risks. The aim of this study therefore is to acknowledge and deal with the above knowledge gaps. The specific objectives of this study were (1) to develop a two-phase risk optimization model for conserving flood water during reservoir operation that explicitly represents flood risk and water shortage risk under uncertainties, (2) to derive analytical HRs that could characterize the optimal conservation decision based on the forecast inflow and forecast precision, and (3) to analyse the interactions between the risks of floods and water shortages under generic operating conditions.

2 Nomenclature

2.1 Abbreviations

FLWL:

Flood limited water level

CRs:

Capacity-constrained pre-release rule

HRs:

Hedging rules

FRs:

Designed flood control rules

2.2 Indices

i :

index of phase (i = 1, pre-refill phase; i = 2, pre-release phase).

2.3 Parameters

T _i :

the total number of time periods during phase i

Δt :

the time interval in each time period (s)

Vu :

the upper limit of storage for flood water conservation (m³)

r _max :

the safety threshold of reservoir outflow (m³/s)

τ :

the effective lead-time of the forecasts based on hydrological forecasts (s)

${R}_i^u$ :

the maximum water release without causing downstream flood inundation during phase i (m³)

Vs :

the beginning storage (m³)

γ _a :

the upper limit of the acceptable probability level of downstream flood risk.

ε _i :

inflow forecast error during phase i, which is assumed unbiased and considered to obey a normal distribution, such that ${\varepsilon}_i\sim N\left(0,{\sigma}_{\varepsilon_i}^2\right)$ (m³)

ε :

total uncertainty of inflow forecast errors (m³)

${\sigma}_{\varepsilon_i}^2$ :

variance of the forecast error ε_i (m³)

2.4 Functions

ω_u[⋅], ω_d[⋅], ω_s[⋅]:

damage functions of upstream flood risk, downstream flood risk and water shortage risk events.

Prob(⋅), Prob⁻¹(⋅):

probability function and inverse function of a uncertain event.

p(⋅):

is the probability density function for a normal distribution.

2.5 Variables

$\overline{q_i}$ :

the forecast average inflow discharge(m³/s)

$\overline{d}$, $\overline{D_i}$:

demand discharge (m³/s) and water (m³) during phase i

V_i,$\overline{V_i}$:

the actual and forecast (expected) ending storage (m³) at phase i

I_i,$\overline{I_i}$:

the actual and forecast inflow during phase i (m³) _i min, R_imax the lower and upper limits, respectively, of the actual or expected water release during phase i (m³)

R ₁ :

deterministic water release decision during phase one (m³)

R ₂ :

stochastic water release decision during phase one (m³)

$\overline{S_2}$ :

expected water shortage of pre-release phase (m³)

SWA, EWA:

hedging trigger range of expected water availability (m³)

MWA :

maximum expected water availability within feasible range (m³)

${R}_i^c$ :

the maximum water release capacity from all releasing facilities of the reservoir during phase i(m³)

λ₁, λ₂:

the KKT multipliers of the storage lower and upper bound constraints.

V₁min, V₁max:

the lower and upper limits of $\overline{V_1}$ (m³).

3 Methodology

The flowchart showing the framework of the coupling models that inform flood water conservation for deriving the analytical hedging rules is shown in Fig. 1. The general framework of the flood water conservation and the capacity-constrained pre-release rule (a benchmark rule) are introduced in Section 2.1. The concept and formulation of the hedging rules are introduced in Section 2.2. The two-phase optimal operation model is established, and the analytical derivation of the HRs based on the first-order optimality condition is presented, in Sections 2.3 and 2.4. Finally, the performance of the rules is examined under conditions with variable parameters and using real-time data from the Xianghongdian Reservoir, China.

Fig. 1

Flow chart of the process for deriving the hedging rules

3.1 Capacity-Constrained Pre-release Rules for Flood Water Conservation

As shown in Fig. 2, when a flood event is traced from its hydrograph, the regulation of the flood in a reservoir can be divided into three phases, namely pre-release, flood control, and pre-refill, depending on the inflow level. When flood water is conserved as a reservoir operation, water that is surplus to the water demand is stored during the pre-refill phase, and then is released to water users during the pre-release phase before the next flood occurs (Li et al. 2010). During the pre-refill phase, the average inflow discharge is predicted at $\overline{q_1}$ (m³/s) above the demand discharge $\overline{d}$ (m³/s) ($\overline{q_1}\ge \overline{d}$); this means that, when there is a water surplus, flood water would be conserved. In the pre-release phase, wherein the inflow discharge during dry periods is forecasted at the $\overline{q_2}$ (m³/s) level below the demand discharge $\overline{d}$ (m³/s) ($\overline{q_2}\le \overline{d}$), the conserved flood water becomes a resource and can be delivered to mitigate water shortages.

Fig. 2

Schematic of flood control and flood water conservation within a flood event

Real-time flood water conservation decision-making depends on the forecast inflow during the pre-refill and pre-release phases. The upper bound of the flood conservation level should be determined jointly based on the water surplus (${V}_0+\overline{I_1}-\overline{D_1}$), storage limit (Vu), water shortage ($\overline{D_2}-\overline{I_2}$), and the maximum volume of water that can be released safely to the downstream river channel during the pre-release phase (${R}_2^u$) (Chou and Wu 2013). This is characterized by the capacity-constrained pre-release method (Zhou et al. 2014; Li et al. 2010):

(1)

$$ \overline{I_i}=\overline{q_i}\cdot {T}_i\cdot \varDelta t,\overline{D_i}=\overline{d}\cdot {T}_i\cdot \varDelta t,{R}_i^u={r}_{\mathrm{max}}\cdot {T}_i\cdot \varDelta t,i=1,2 $$

(2)

The equations state that the final storage at the pre-release phase is controlled to the level of storage of the lower bound of the FLWL (V₂ = 0), such that flood water conservation does not lower the design standard of the reservoir in relation to flood control. To facilitate analysis, all storage variables refer to the relative storage level minus the storage below the FLWL.

Equation (1) indicates that the maximum conservation should neither exceed the water conservation capacity during the pre-refill phase nor surpass the water release capacity during the pre-release phase. Specifically, if $\min \left\{{V}_0+\overline{I_1}-\overline{D_1}, Vu,{R}_2^u-\overline{I_2}\right\}\ge \overline{D_2}-\overline{I_2}$, then $\overline{V_1}=\overline{D_2}-\overline{I_2}$, demonstrating that a reasonable conservation equals as much as the expected water shortage ($\overline{D_2}-\overline{I_2}$ or $\overline{S_2}$) of the pre-release phase, which is given as:

$$ \overline{S_2}=\overline{D_2}-\overline{I_2} $$

(3)

This method unfortunately fails to explicitly incorporate the influence of the inflow forecast error, thereby possibly increasing the risk and lowering the safety and reliability of the flood water conservation when operating reservoirs in real-time.

3.2 Hedging Rules

When the influence of the forecast uncertainty is addressed, flood water conservation through reservoir operation turns into a risky decision-making problem where the conflict between the risks of floods and water shortages need to be resolved, by determining the optimal conservation level and decisions about release. Uncertainty in the inflow forecasts in the pre-refill phase and in the pre-release phase could result in the risks of floods and water shortages, respectively, with contradictions and transfers of massive balances between these two types of risks. To address this, reservoir release R₁ is introduced as a function (operation rule) of the expected available water A i.e., initial storage V₀ plus the forecast inflow $\overline{I_1}$.

Among the different types of operation rules, HRs are typically useful for identifying trade-offs between releases and risks. HRs were first applied to rationalize inadequate water resources allocation between present and future stages, where the present water deliveries were curtailed and water was retained in storage for future use (Draper and Lund 2004). The hedging mechanism is used to reduce the risk of large shortages by allowing small shortages more frequently. By extending the hedging concept to model the flood water conservation rule, the conflict between the risks can be resolved. The HRs for flood water conservation through reservoir operation are shown in Fig. 3.

Fig. 3

Schematic of hedging rules on current release, where SWA and EWA denote the intersections of the hedging rule curve with the lower and upper bounds of water release, respectively

Within the feasible area of the chart, the blue upper bound of release corresponds to the minimal flood risk by releasing the maximum amount of water in phase one until ${R}_1^u$; at the red lower bound of release, the water shortage risk is minimized by storing as much water as possible until it spills over. The HRs that intersect the two bounds separate the control of the release within the feasible area into three segments, as approximated by:

$$ {R}_1=\Big\{{\displaystyle \begin{array}{c}\overline{D_1},\overline{D_1}\le A\le SWA,\left( Zone\ I\right)\\ {}{R}_1^{\ast }, SWA\le A\le EWA,\left( Zone\ II\right)\ \\ {}{R}_1^u, EWA\le A\le MWA,\left( Zone\ II I\right)\end{array}} $$

(4)

The HRs that guide release and conservation decisions are as follows:

• 1. If A is within the range of ($\left[\overline{D_1}, SWA\right]$) such that the flood risk is low and the water shortage risk is high, the release to $\overline{D_1}$ is limited and conservation is maximized to lower the water shortage risk;

• 2. If A is between the trigger range of hedging ([SWA, EWA]) such that the flood risk balances the water shortage risk, the release to ${R}_1^{\ast }$ is restricted and water is conserved at a medium level to achieve the best compromise;

• 3. Otherwise, A is in the range of ([EWA, MWA]) such that the flood risk is high and the water shortage risk is low, and water is released to ${R}_1^u$ to minimize the flood risk.

Clearly, HRs provide a solution for resolving the conflict between the risks by minimizing the total risk. Once the range threshold parameters of [SWA, EWA, MWA] and release ${R}_1^{\ast }$ are determined, the reservoir can be operated according to the rules by checking when and how hedging should be implemented.

3.3 Two-Phase Optimal Flood Water Conservation Model for Reservoir Operation

A two-phase optimal model that explicitly addresses the relationship between minimization of risks with flood water conservation was established in this study for deriving the HRs.

3.3.1 Defining the Risk

Inflow forecast uncertainty has been often identified as one of the primary sources of risk for real-time reservoir operation. It is characterized as the difference between the forecast inflow $\overline{I_i}$ and the actual inflow I_i during phase i:

$$ {I}_i=\overline{I_i}+{\varepsilon}_i,i=1,2 $$

(5)

Generally, the forecast error ε_i is assumed unbiased and considered to obey a normal distribution (Zhao et al. 2014) such that ${\varepsilon}_i\sim N\left({\mu}_i,{\sigma}_{\varepsilon_i}^2\right)$ and μ_i = 0. This assumption is acceptable because systematic forecast errors can frequently be corrected by subtracting the mean biases within real-time forecasts. The variance of the forecast error ${\sigma}_{\varepsilon_i}^2$ can be calibrated using the historical forecast and actual inflow samples.

• 1. Flood risk

The model determines a deterministic release decision in the current phase to guide the operation of power release and non-power release facilities. After making a deterministic release decision (R₁) during the current phase, the end storage adapts the forecast error in the inflow during this phase (ε₁), which could result in over-conservation of flood water (i.e., exceedance of the upper limit of conservation storage). This could result in damage within the drainage area of a reservoir or threaten the safety of a dam. Accordingly, the upstream flood risk is defined as the expected damage (L_u), which is the product of the probability (P_u) and the damage (${\omega}_u\left[\overline{I_1},\overline{I_2}\right]$):

$$ {L}_u={P}_u\cdot {\omega}_u= Prob\left({V}_1\ge Vu\right)\cdot {\omega}_u $$

(6)

Where Prob(⋅) is the probability function that evaluates the probability of a given uncertain event, and V₁ is the actual end storage at the pre-refill phase that becomes a random variable when adapting ε₁.

Note that ω_u[⋅] is the damage function of the forecast inflow, which approximates to the estimation of the loss according to the return period of floods. The expression is later simplified by ω_u .

As the final storage at the pre-release phase is controlled to the storage of the lower bound of the FLWL (V₂ = 0), water release during the pre-release phase adapts the influence of both ε₁ and ε₂. When meteorological forecasts fail to predict storm events that would occur during the pre-release phase, the amount of storm water to be released could be underestimated, meaning that it could exceed the maximum allowable water release to the downstream and cause downstream flood risk. The risk is defined as the expected flood inundation damage (L_d) to the downstream protection area and is calculated as follows:

$$ {L}_d= Prob\left({R}_2\ge {R}_2^u\right)\cdot {\omega}_d $$

(7)

• 2. Water shortage risk

When there is uncertainty in the inflow forecast, the amount of water released during the pre-release phase may be insufficient to meet demand, such that water shortages occur, and the corresponding risk (L_s) is defined as the expected loss because of the shortage:

$$ {L}_s= Prob\left({R}_2\le \overline{D_2}\right)\cdot {\omega}_s $$

(8)

3.3.2 Model Formulation

To limit catastrophic damage in the downstream protected area from uncertainty and over-conservation, the downstream risk is formulated as a chance constraint by keeping the risk probability within an acceptable level. The other two risk indices are summed to establish the minimal total risk (Nayak et al. 2018):

(1) Objective function

$$ \min \kern0.5em L={\omega}_u\cdot {P}_u+{\omega}_s\cdot {P}_s $$

(9)

(2) Constraints.

1) Water balance constraints:

$$ {V}_1={V}_0+{I}_1-{R}_1;{V}_2={V}_1+{I}_2-{R}_2 $$

(10)

2) Chance constraint on the downstream flood risk probability:

$$ Prob\left({R}_2\ge {R}_2^u\right)\le {\gamma}_a $$

(11)

3) Water release limits:

$$ {R}_1\min \le {R}_1\le {R}_1\max $$

(12)

$$ {R}_2\min \le \overline{R_2}\le {R}_2\max $$

(13)

4) Initial and boundary storage conditions:

$$ {V}_0= Vs;{V}_2=0 $$

(14)

The specific values of the boundary limits given by Eqs. (12) and (13) can be determined from the physical limitations of the reservoir system as follows:

$$ {R}_1\min =\overline{D_1};{R}_1\max =\min \left\{{R}_1^u,{R}_1^c\right\}; $$

(15)

$$ {R}_2\min =0;{R}_2\max ={R}_2^u- Pro{b}_{R_2}^{-1}\left({\gamma}_a\right); $$

(16)

With given information on $\overline{I_i},{\sigma}_{\varepsilon_i}^2,\overline{D_i}, Vu, Vs,{R}_i^u, and\;{R}_i^c$ optimal decisions about R₁ can be derived analytically by solving the two-phase optimization model, yielding the HRs.

3.4 Analytical Solutions

The risk involved in flood water conservation stems from adaptation in relation to the forecast error during the two phases through reservoir storage and water release. The propagation of uncertainty can be verified through the following equations based on Eqs. (5), (10), and (14):

(17)

(18)

Where V₁ adapts the variation of ε₁ and R₂ adapts the total uncertainty of ε from both phases. Accordingly, both V₁ and R₂ are normally distributed such that ${V}_1\sim N\left(\overline{V_1},{\sigma}_{\varepsilon_1}^2\right)$ and ${R}_2\sim N\left(\overline{R_2},{\sigma}_{\varepsilon}^2\right)$. Assuming ε₁ and ε₂ are independent, we have $\varepsilon \sim N\left(0,{\sigma}_{\varepsilon}^2\right)$ and ${\sigma}_{\varepsilon}^2={\sigma}_{\varepsilon_1}^2+{\sigma}_{\varepsilon_2}^2$.

3.4.1 Model Transformation

Using Eqs. (17) and (18), P_u and P_s can be expressed as functions of $\overline{V_1}$ as follows:

$$ {\displaystyle \begin{array}{l}{P}_u= Prob\left({V}_1\ge Vu\right)\\ {}\kern1.25em ={\int}_{Vu-\overline{V_1}}^{+\infty }p\left({\varepsilon}_1\right)d{\varepsilon}_1\end{array}} $$

(19)

$$ {\displaystyle \begin{array}{l}{P}_s= Prob\left({R}_2\le \overline{D_2}\right)\\ {}\kern1em ={\int}_{-\infty}^{\overline{D_2}-\overline{V_1}-\overline{I_2}}p\left(\varepsilon \right) d\varepsilon \\ {}\kern1em \end{array}} $$

(20)

Accordingly, the objective function of the total risk L can be characterized as:

$$ \min \kern0.5em L={\omega}_u\cdot {\int}_{Vu-\overline{V_1}}^{+\infty }p\left({\varepsilon}_1\right)d{\varepsilon}_1+{\omega}_s\cdot {\int}_{-\infty}^{\overline{D_2}-\overline{V_1}-\overline{I_2}}p\left(\varepsilon \right) d\varepsilon $$

(21)

The constraints on $\overline{V_1}$ can be specified as follows:

$$ S.T.\kern3em {V}_1\min \le \overline{V_1}\le {V}_1\max $$

(22)

where V₁min and V₁max are the lower and upper limits of $\overline{V_1}$, respectively, which can be determined using the following equations based on Eqs. (10) and (15)–(16):

$$ {V}_1\min =\max \left\{{V}_0+\overline{I_1}-{R}_1\max, {R}_2\min -\overline{I_2}\right\} $$

(23)

$$ {V}_1\max =\min \left\{{V}_0+\overline{I_1}-{R}_1\min, {R}_2\max -\overline{I_2}\right\} $$

(24)

Therefore, the two-phase model is converted to a single-variable optimization model characterized by Eqs. (21) and (22), which can be solved using the first-order optimality condition, i.e., the Karush–Kuhn–Tucker (KKT) condition.

3.4.2 Optimal Condition

The KKT condition can be used to derive the optimal solution ${\overline{V_1}}^{\ast }$ of the constrained optimization model, satisfying the following equations under feasible conditions:

$$ {\left.\frac{dL}{d\overline{V_1}}\right|}_{\overline{V_1}={\overline{V_1}}^{\ast }}-{\lambda}_1\cdot \frac{d\left(\overline{V_1}-{V}_1\min \right)}{d\overline{V_1}}{\left|{}_{\overline{V_1}={\overline{V_1}}^{\ast }}-{\lambda}_2\cdot \frac{d\left({V}_1\max -\overline{V_1}\right)}{d\overline{V_1}}\right|}_{\overline{V_1}={\overline{V_1}}^{\ast }}=0 $$

(25)

$$ {\lambda}_1\cdot \left({\overline{V_1}}^{\ast }-{V}_1\min \right)=0,{\lambda}_2\cdot \left({V}_1\max -{\overline{V_1}}^{*}\right)=0,{\lambda}_1,{\lambda}_2\ge 0 $$

(26)

Substituting P_u and P_s from Eqs. (19) and (20), respectively, into Eq. (25) gives the following:

$$ {\omega}_u\cdot \frac{\partial {\int}_{Vu-\overline{V_1}}^{+\infty }p\left({\varepsilon}_1\right)d{\varepsilon}_1}{\partial \overline{V_1}}{\left|{}_{\overline{V_1}={\overline{V_1}}^{\ast }}+{\omega}_s\cdot \frac{\partial {\int}_{-\infty}^{\overline{D_2}-\overline{V_1}-\overline{I_2}}p\left(\varepsilon \right) d\varepsilon}{\partial \overline{V_1}}\right|}_{\overline{V_1}={\overline{V_1}}^{\ast }}-{\lambda}_1+{\lambda}_2=0 $$

(27)

In this equation, the terms of ${\omega}_u\cdot \frac{\partial {P}_u}{\partial \overline{V_1}}$ and ${\omega}_s\cdot \frac{\partial {P}_s}{\partial \overline{V_1}}$ are the marginal upstream flood risk and marginal water shortage risk due to flood water conservation, respectively. ${\omega}_u\cdot \frac{\partial {P}_u}{\partial \overline{V_1}}$ is non-negative, indicating the increased upstream flood risk of per unit conservation; ${\omega}_s\cdot \frac{\partial {P}_s}{\partial \overline{V_1}}$ is non-positive, denoting the decreased water shortage risk of per unit conservation. Clearly, the optimal conservation plan depends on the balance of the two terms.

Expanding Eq. (27) gives the following:

$$ {\omega}_u\cdot \frac{1}{\sqrt{2\pi}\cdot {\sigma}_{\varepsilon_1}}{e}^{-\frac{{\left( Vu-{\overline{V_1}}^{*}\right)}^2}{2{\sigma}_{\varepsilon_1}^2}}-{\omega}_s\cdot \frac{1}{\sqrt{2\pi}\cdot {\sigma}_{\varepsilon }}{e}^{-\frac{{\left(\overline{D_2}-{\overline{V_1}}^{\ast }-\overline{I_2}\right)}^2}{2{\sigma}_{\varepsilon}^2}}={\lambda}_1-{\lambda}_2 $$

(28)

Based on the KKT condition, the solution of ${\overline{V_1}}^{\ast }$ can be classified into the following three situations:

• 1. λ₁ = 0, λ₂ > 0. An increase in $\overline{V_1}$ reduces the total risk. Therefore, ${\overline{V_1}}^{\ast }={V}_1\max$ and the operation falls within zone I.

• 2. λ₁ = λ₂ = 0. ${\overline{V_1}}^{\ast }$ is achieved by balancing the marginal risks. Therefore, ${\overline{V_1}}^{*}\in \left[{V}_1\min, {V}_1\max \right]$ and the operation falls within zone II.

• 3. λ₁ > 0, λ₂ = 0. An increase in ${\overline{V_1}}^{\ast }$ results in increasing of total risk. Therefore, ${\overline{V_1}}^{\ast }={V}_1\min$ and operation falls within zone III.

The solution of ${\overline{V_1}}^{\ast }$ in situation 2) can be derived analytically. Moreover, when ${\overline{V_1}}^{\ast }$ is kept below Vu for ${\overline{V_1}}^{*}\le Vu$, such that the upstream flood risk is reasonable, the analytical solution of ${\overline{V_1}}^{\ast }$ is characterized as follows:

$$ {\displaystyle \begin{array}{l}{\overline{V_1}}^{\ast }=\frac{1}{2{\sigma}_{\varepsilon_2}^2}\Big[-2{\sigma}_{\varepsilon_1}^2\cdot \overline{S_2}+2{\sigma}_{\varepsilon}^2\cdot Vu\\ {}-\sqrt{{\left[2{\sigma}_{\varepsilon_1}^2\cdot \overline{S_2}-2{\sigma}_{\varepsilon}^2\cdot Vu\right]}^2-4{\sigma}_{\varepsilon_2}^2\cdot \left[-{\sigma}_{\varepsilon_1}^2\cdot {\overline{S_2}}^2+{\sigma}_{\varepsilon}^2\cdot V{u}^2-2{\sigma}_{\varepsilon_1}^2{\sigma}_{\varepsilon}^2\cdot \ln \left(\frac{\omega_u}{\omega_s}\cdot \frac{\sigma_{\varepsilon }}{\sigma_{\varepsilon_1}}\right)\right]}\Big]\end{array}} $$

(29)

Equation (29) implies that ${\overline{V_1}}^{\ast }$ is a quasi-linear function of Vu and $\overline{S_2}$. Moreover, ${\overline{V_1}}^{\ast }$ is correlated negatively with $\frac{\omega_u}{\omega_s}$, demonstrating that the expected conservation level decreases if the relative ratio of flood damage divided by water shortage damage increases.

After obtaining ${\overline{V_1}}^{\ast }$ from the analytical solution, the optimal solution for R₁ can be determined by replacing ${\overline{V_1}}^{\ast }$ back to the water balance equation. Thereafter, the HRs characterized in Eq. (4) can be derived.

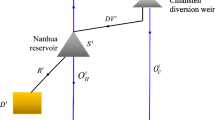
4 Overview of the Xianghongdian Reservoir System

The Pi River Irrigation District is located on one of the tributaries of the Huai River. It is part of China’s second largest irrigation district—the Pishihang Irrigation District—and has a total irrigation area of 73.33 × 10⁴ hm². The primary irrigation water is delivered from a multi-reservoir system that includes the Xianghongdian, Bailianya, Mozitan, and Foziling Reservoirs, which are all on the upstream reaches of the Pi River (Fig. 4). Irrigation water is mainly delivered from May to October, between which the rice growing season and the flood season occur in the reservoir system. The demand for irrigation water peaks during dry inflow periods in July and August after the monsoon rains. The design reliability of irrigation water supply is 80%; however, the actual reliability is 73% and the water resource use efficiency is only 50%. On the other hand, the annual water shortage is estimated at 1.45 × 10⁸ m³.

Fig. 4

Sketch map showing the location of the multi-reservoir system in the Pi River basin

The Xianghongdian Reservoir, with a storage capacity of 26.32 × 10⁸ m³, is the largest of the reservoirs in the Huai River Basin. By reserving a flood control storage of 4.76 × 10⁸ m³, it ensures the safety of the downstream protected area of Lu’an and other metropolitan regions along the Huai River during times of flood. Supported by rainfall and flood information monitoring and forecasting systems with real-time responses, the reservoir system can forecast the receding inflow with a 5-day lead-time. The technical parameters of the Xianghongdian Reservoir are provided in Table 1.

Table 1 Parameters of flood control and water supply operation for the Xianghongdian reservoir

A matrix for calculating $\frac{\omega_u}{\omega_s}$ with $\overline{I_1}$ and $\overline{I_2}$ is adopted to evaluate the risk of damage. The relevant data were provided by the operation management centre of the Xianghongdian Reservoir (Hua et al. 2020).

5 Results

5.1 Flood Water Conservation Results from Different Rules

The operation of the Xianghongdian Reservoir during the flood season is guided by phase-wise flood control rules (FRs) that determine the volume of water release relative to the current storage level and the current inflow condition. The FRs consider only flood control that protects areas upstream and downstream of the reservoir, and do not allow for flood water conservation above the FLWL after a flood recedes. The CRs consider a certain level of flood water conservation based on forecast information, but they fail to incorporate bias information and do not explicitly account for risk. Both sets of rules are selected as benchmarks for highlighting the differences in the results obtained using HRs.

The inflows forecast for the pre-refill and pre-release phases of three flood events were selected from historical records. Numerical simulations based on the derived rules were conducted within the MATLAB2018b platform. Statistics of the results achieved under the three sets of rules are compared in Table 2.

Table 2 Statistics of the results achieved under different operating rules for three typical flood events

The results indicate the following.

• 1. Of all the rules tested, the HRs result in the smallest total risk by conserving the optimal level of flood water. Relative to the feasible range of $\overline{V_1}$, HRs conserve the maximum level of flood water in case I, wherein P_s dominates P_u, an intermediate level in case II to reach the optimal equilibrium, and a minimum level in case III so that P_u is lowered.

• 2. Both the FRs and the CRs result in insufficient flood water use for addressing the dominating impact of flood control and flood risk. The conservation level associated with the two sets of rules is bound at the lower limit for case II and case III.

The results of the risks and the weighted marginal risks from the HRs under case I are plotted in Fig. 5.

Fig. 5

Risks and marginal risks for (a) case I, (b) case II and (c) case III

Figure 5 clearly shows that the effect of water shortage risk gradually weakens as $\overline{V_1}$ increases and eventually becomes dominated by the flood risk. For the cases, the intersection point between ${\omega}_s\cdot \mid \frac{\partial {P}_s}{\partial \overline{V_1}}\mid$ and ${\omega}_u\cdot \frac{\partial {P}_u}{\partial \overline{V_1}}$ is 0.72 × 10⁸ m³ and it decreases with $\frac{\omega_u}{\omega_s}$. Moreover, ${\overline{V_1}}^{*}\ge \overline{S_2}$ and the HRs outperform the CRs in terms of flood water conservation.

5.2 Results of Real-Time Operation within a Rolling Horizon

The performances of the three operating rules (i.e., FRs, CRs, and HRs) were investigated when applied to guide real-time operations within a rolling horizon during the flood season of 2015 and 2016. Model simulations were conducted with current statistical levels of forecast precision, using a 1-h time interval to reflect the hydrological variability. The executed water release for the current hour was determined as a proportion of the total water release during the pre-refill phase, and the proportion can be determined by the ratio of the forecast inflow during the current hour divided by the total forecast inflow during the pre-refill phase.

Forecast real-time inflow sequences were obtained from the forecast systems established at the operation centre of the reservoir. Eight indices (Shiau 2011) for assessing real-time reservoir operation performance during periods of flood and drought were considered: total water delivery (TWD), water supply reliability (WSR), maximum 10-day shortage ratio (MSR), total water spillage (TWS), chance of water spillage (CWS), maximum storage (MS), maximum outflow (MO), and end storage (ES). Statistics of these indices are listed in Table 3.

Table 3 Simulated statistics of indices from real-time operation strategies under different operating rules

The results verify the following observations:

• 1. HRs conserve a higher level of flood water and ensure better water delivery than both the FRs and the CRs. For the HRs, the TWD were 0.5 × 10⁸ m³ (6.3%) and 0.26 × 10⁸ m³ (3.6%) higher, the WSR were 7.1% and 5.8% higher, and the MSR was 4.5% and 1.2% lower than the results of the CRs in 2015 and 2016, respectively. This is because the HRs determine the optimal conservation level for the expected water shortage and also use information about the probability and damage to rationalize operation.

• 2. Informed decisions on flood water conservation guided by the HRs do not necessarily increase the flood risk. The MS for the HRs (0.91 × 10⁸ m³) was higher than that for the FRs in 2015, but the storage level was much less than the upper boundary of flood storage; this ensured adequate safety for controlling floods. In 2016, the MS for the HRs was 0.13 × 10⁸ m³ lower than that for the FRs, and the upstream flood risk was lower. The MO results from both the HRs and the FRs were the same, which indicates that real-time operation of HRs did not increase the downstream flood risk. This is because the HRs explicitly addressed the flood control risk as an objective and as a constraint for limiting the likelihood of flood occurrences, thereby preventing the severity of the risk when conserving flood water.

6 Discussion

Parameters that reflect the forecast precision (${\sigma}_{\varepsilon_1}$ and ${\sigma}_{\varepsilon_2}$) could affect the HRs because of the influence on objectives and feasible ranges. The influence of each parameter is examined by comparing the results of experiments under three levels.

• 1. Standard deviation of the inflow forecast error during the refill phase (${\sigma}_{\varepsilon_1}$)

Different values of ${\sigma}_{\varepsilon_1}$ were used to explore how the precision of the forecast changed. Three levels of ${\sigma}_{\varepsilon_1}$ were selected and evaluated from the historical inflow forecast and observation samples according to best, medium, and worst forecast performance. The corresponding 3D-HR curves are shown in Fig. 6, with R₁ plotted as a function of A and $\overline{I_2}$, and where the X–Y surface projection presents a traditional 2D depiction of HRs with scenarios of $\overline{I_2}$.

Fig. 6

HRs release (R₁) with expected water availability (A) and forecast inflows during the pre-release phase ($\overline{I_2}$) for ${\sigma}_{\varepsilon_1}$ of (a) 0.276 × 10⁸ m³, (b) 0.385 × 10⁸ m³, and (c) 0.474 × 10⁸ m³

The results verify the following.

• 1. The range of the flood water conservation zones decreased and narrowed as ${\sigma}_{\varepsilon_1}$ increased for the HRs. The values of SWA and EWA reached 0.88 × 10⁸ m³ and 1.07 × 10⁸ m³, respectively, at the highest precision level $\left({\sigma}_{\varepsilon_1}=0.276\times {10}^8{m}^3\right)$ (and they were attenuated to 0.51 × 10⁸ m³ and 0.69 × 10⁸ m³, respectively, at the lowest precision level $\left({\sigma}_{\varepsilon_1}=0.474\times {10}^8{m}^3\right)$. This reflects the change in the HRs because of increases in the current-phase water release to mitigate any increase in the upstream flood risk caused by deterioration in the precision of the forecast.

• 2. HRs adjusted the current-phase release (R₁) at various levels of $\overline{I_2}$ and ${\sigma}_{\varepsilon_1}$ with non-monotonic trends. In cases (a) and (b), for the HRs, R₁ increased with $\overline{I_2}$ and the flood water was maintained at a relatively low level because of the reduced water shortage risk during the pre-release phase. In case (c), the release was lower (higher conservation) on $\overline{I_2}=0.14\times {10}^8{m}^3$ than on $\overline{I_2}=0.34\times {10}^8{m}^3$. This is because the variation in ${\sigma}_{\varepsilon_1}$ changed with the marginal upstream flood risk and altered the marginal water shortage risk. As ${\sigma}_{\varepsilon_1}$ increased, the upstream flood risk distribution and the water shortage risk distribution were flattened; the optimal release or conservation is therefore determined by the result of a non-monotonic balance influenced by the variation of the magnitude of the marginal risks.

• 3. The flood control zone enlarges as ${\sigma}_{\varepsilon_1}$ increases. With the increase in ${\sigma}_{\varepsilon_1}$, both the EWA and the feasible range of flood water conservation shrink because the upstream and downstream flood risks are enhanced, indicating that the precision of the inflow forecast serves is important for conserving flood water.

• 4. Standard deviation of the inflow forecast error during the pre-release phase $\left({\sigma}_{\varepsilon_2}\right)$.

Under varied inflow forecast conditions during the pre-release phase, the value of ${\sigma}_{\varepsilon_2}$ affects the HRs. Similarly, three levels of ${\sigma}_{\varepsilon_2}$ were selected and evaluated from the historical samples, and the corresponding HRs graphs are plotted in Fig. 7.

Fig. 7

HRs release (R₁) with expected water availability (A) and forecast inflows during the pre-release phase ($\overline{I_2}$) for ${\sigma}_{\varepsilon_2}$ of (a) 0.45 × 10⁸ m³, (b) 0.6 × 10⁸ m³, and (c) 0.66 × 10⁸ m³

The following can be concluded from the figures above.

• 1. For the HRs, the range of zones I and II were slightly enhanced and broadened as ${\sigma}_{\varepsilon_2}$ increased. The values of SWA and EWA reached 0.66 × 10⁸ m³ and 0.852 × 10⁸ m³, respectively, at the highest precision level $\left({\sigma}_{\varepsilon_2}=0.45\times {10}^8{m}^3\right)$ and increased to 0.68 × 10⁸ m³ and 0.855 × 10⁸ m³, respectively, at the lowest precision level. With the reduced precision of the inflow forecast within the pre-release phase, the reservoir potentially faces an intensified risk of water shortages, meaning that the increased chance of flood water conservation should be explored.

• 2. The current-phase release (R₁) determined by the HRs has an approximate monotonic variation with $\overline{I_2}$ and ${\sigma}_{\varepsilon_2}$. In each figure, it is clear that R₁ is increasingly enhanced as $\overline{I_2}$ increases, demonstrating a monotonic trend in the reduction of flood water conservation as $\overline{I_2}$ increases. Moreover, the HRs curves in Fig. 7a–c show that, as ${\sigma}_{\varepsilon_2}$increases, there was a monotonic reduction in R₁ . This was also attributed to the intensified influence of the reduced precision in the inflow forecast on the water shortage risk during the pre-release phase.

7 Conclusions

In this study, a two-phase optimal flood water conservation model for determining the HRs of reservoir operation during the pre-refill and pre-release phases was established. With the forecast error addressed as the major source of uncertainty within the model framework, optimal HRs for determining the best balance between upstream flood risk, downstream flood risk, and water shortage risk through flood water conservation were derived analytically, based on the first-order optimality condition. The Xianghongdian Reservoir was used as an example to explore the performance and sensitivity of the rules. The main findings from the study are as follows:

• 1. Optimal flood water conservation derived by the HRs determined the optimal balance between the upstream flood risk and water shortage risk to achieve the minimum total risk.

• 2. The HRs exhibit better flood water conservation performance in real-time operations for the HRs than the RFs and CRs without increasing the flood risk.

• 3. HRs for flood water conservation are strongly affected by the precision of forecasts. Generally, the conservation level increases when the precision of the forecast improves during the pre-refill phase, and decreases when the forecast precision improves during the pre-release phase.

Analytical two-phase HRs for flood water conservation through reservoir operation provide insights that allow the optimal conservation mechanism to be described through mathematical analysis. By satisfying the assumptions of two-phase model formulation, the proposed methodologies suit systems in which the flood risk is mainly determined by forecast errors in the inflow quantity rather than in the inflow processes, particularly to regulate inflow variability in large reservoirs with high storage capacities. The study will be extended in the future to accommodate multi-phase feature analysis via stochastic optimization techniques, which will facilitate practical applications for a broad range of cases.