1 Introduction

Planning for remediation of contaminated aquifers is a challenging task. Since the remediation process is very expensive, it is desirable that proper planning be done to optimize the cost and effectiveness of the remediation. This calls for accurate tracking and assessment of the extent of the groundwater contamination. A very crucial aspect in the remediation process is to identify the location and release magnitude of the unknown contamination sources. Only then an effective remedial measure can be designed and also help to fix the responsibilities. However, the only information available from the field is, usually the spatio-temporal measurements of the contaminant concentrations and a set of suspected or possible sources.

Contaminant transport through groundwater is governed by the advection-dispersion-reaction (ADR) equation (Bear 1979). Identifying the sources of contamination from the spatial and temporal measurements of the contaminant concentrations in the aquifer is an inverse problem which requires solving the ADR equation backwards in time.

Several approaches have been proposed in the last three decades to solve the ADR equation backward in time to identify the contaminant sources in the groundwater. Atmadja and Bagtzoglou (2001) provided a comprehensive review of the available methodologies and classified them into four major groups viz., (i) Optimization approaches, (ii) Probabilistic and geo-statistical simulation approaches, (iii) Analytical solution and regression approaches and (iv) Direct approaches. Gorelick et al. (1983) first formulated the contaminant source identification problem as a simulation-optimization (SO) problem. In this approach, forward simulations are run with different plausible sets of solute sources and then the solutions are compared with the measured solute concentration data. The solute sources are found by minimizing the difference between the simulated and observed solute concentrations. They used linear programming and multiple regressions for the optimization (minimization). Wagner (1992) proposed another optimization method for simultaneous model parameter estimation and source characterization, using non-linear maximum likelihood estimation, to determine the optimal estimates of the unknown model parameters and sources. Mahar and Datta (1997, 2000) proposed a concept of optimal identification of pollutant sources with optimal design of groundwater quality monitoring networks and a nonlinear optimization to estimate the magnitude, location and release duration of groundwater pollution sources under transient conditions.

In recent years, several heuristic and soft computing techniques have been used in optimization approaches for source identification problems. Mahinthakumar and Sayeed (2005), Aral et al. (2001), Singh and Datta (2006) etc. have applied genetic algorithm in groundwater source identification. Artificial neural network based approaches have been explored by Singh et al. (2004), Singh and Datta (2007), Srivastava and Singh (2014, 2015) etc. Ayvaz (2010) and Jiang et al. (2012) have applied harmony search algorithm while Zhao et al. (2016) used surrogate based models in the source identification problems. Yeh et al. (2007) proposed a hybrid heuristic approach which combines simulated annealing and tabu search with groundwater flow and transport model for contaminant source identification. Datta et al. (2009) coupled a dynamic pollutant monitoring network to an optimization based source identification model. This method relied on sequential exchange of information between the monitoring network and source identification model for efficient determination of the sources. Datta and Prakash (2013) used concentration measurements from a heuristically designed optimal monitoring network to improve the accuracy of groundwater pollution source identification. They combined genetic programming and linked simulation-optimization model to reconstruct the solute flux history. Jha and Datta (2014) used dynamic time warping distance in the linked simulation-optimization model to design a monitoring network for efficient estimation of source characteristics. Both the source location and time of start of the pollutant release are treated as unknowns in their study.

Several other non-optimization approaches for the groundwater source identification have also been proposed such as Particle methods (Bagtzoglou et al. 1992), quasi-reversibility (Skagg and Kabala 1995), Minimum Relative Entropy inversion (Woodbury and Ulrych 1996), geostatistical techniques (Snodgrass and Kitanidis 1997), correlation coefficient optimization approach (Sidauruk et al. 1998), adjoint method (Neupauer and Wilson 1999), marching-jury backward beam equation (Bagtzoglou and Atmadja 2003), robust maximum likelihood approach (Sun 2007) etc. Each of the proposed methods has serious limitations and is applicable to only a few specific cases. The aim of present study is to develop a method for groundwater source identification which is applicable to real-world field problems.

This study proposes a simulation-optimization approach for identification of contaminant sources called RPCM-PSO-SO model. The groundwater flow and transport simulation is carried out by meshfree radial point collocation (RPCM) method (Guneshwor et al. 2016) and optimization is performed by particle swarm optimization (PSO). PSO offers advantages such as easy implementation and integration with the simulation model.

2 Methodology

2.1 Groundwater Flow and Transport Simulation

The governing equation for groundwater flow in a confined aquifer in two dimensions is given by (Bear 1979):

$$ \frac{\partial }{\partial {x}_i}\left({T}_{ij}\frac{\partial H}{\partial {x}_j}\right)=S\frac{\partial H}{\partial t}+W;\kern0.5em i,j=1,2 $$
(1)

where, T ij is the transmissivity tensor (m2/d); S is the storativity, H is the hydraulic head (m),W is the volume flux per unit area (source/sink) (m/d), x i , x j are the Cartesian coordinates.

The two dimensional advection-dispersion and reaction equation which governs contaminant transport through a saturated porous media is (Freeze and Cherry 1979):

$$ \frac{\partial }{\partial {x}_i}\left({D}_{ij}\frac{\partial C}{\partial {x}_j}\right)-\frac{\partial }{\partial {x}_i}\left({CV}_i\right)-\lambda C-\frac{c^{\prime }W}{nb}=R\frac{\partial C}{\partial t};\kern0.5em i,j=1,2 $$
(2)

where, x i , x j are the Cartesian coordinates, C is the concentration of the dissolved species (mg/l), D ij is the dispersion tensor (m2/d), V i is the seepage velocity in the direction of x i , λ is the reaction rate constant (sec−1), W is the elemental recharge rate (m/d) with solute concentration c′ (mg/l), n is the porosity, b is the aquifer thickness (m), R is the Retardation factor calculated as R = 1 + ρ b K d /n, in which ρ b is the media bulk density, K d is the sorption coefficient.

The seepage velocities V i are evaluated from the flow equations by using Darcy’s law as follows:

$$ {V}_i=-\frac{K_i}{n}\frac{\partial h}{\partial {x}_i};\kern0.5em i=1,2 $$
(3)

where K i is the hydraulic conductivity along the x i Cartesian coordinate.The elements of the dispersion coefficient tensor are evaluated from the longitudinal dispersivity (αL) and transverse dispersivity (αT) from the following relations (Bear 1979):

$$ {D}_{xx}=\frac{\alpha_L{V}_x^2+{\alpha}_T{V}_y^2}{V^2};{D}_{yy}=\frac{\alpha_L{V}_y^2+{\alpha}_T{V}_x^2}{V^2};{D}_{xy}={D}_{yx}=\frac{\left({\alpha}_L-{\alpha}_T\right){V}_x{V}_y}{V^2} $$
(4)

where, \( {V}^2={V}_x^2+{V}_y^2 \).

Equations (1) and (2) can be solved analytically or numerically (Bear 1979; Freeze and Cherry 1979; Moutsopoulos and Tsihrintzis 2009; Meenal and Eldho 2011; Guneshwor et al. 2016 etc.). Equations (3) and (4) together provide the linkage or coupling between the groundwater flow and solute transport equations. The velocities computed from the flow equation are used as input to the transport equation.

2.1.1 Meshfree RPCM Model of Groundwater Flow and Transport

In this study, the groundwater flow and transport modeling is carried out by using a recently developed meshfree method known as Radial Point Collocation Method (RPCM) (Guneshwor et al. 2016; Meenal and Eldho 2011). Meshfree methods offer advantages over the grid based methods such as finite difference (FDM), finite element (FEM) etc. in that it does not require the construction of a grid or mesh which can be computationally very costly.

In the RPCM method, the state variables are spatially interpolated by using a class of functions known as the radial basis functions (RBFs). Commonly used RBF functions are the Multi-quadrics and Gaussian or exponential RBF functions. Radial basis functions are used for scattered data interpolation and are found to have exponential convergence (Hardy 1971). The interpolation will lead to the state variable, for example the groundwater head h(x) and solute concentration C(x), being approximated as (Liu and Gu 2005),

$$ h\left(\boldsymbol{x}\right)={\boldsymbol{\Phi}}^{\boldsymbol{T}}\left(\boldsymbol{x}\right){\boldsymbol{h}}_{\boldsymbol{s}}(t) $$
(5)
$$ C(x)={\boldsymbol{\Phi}}^{\boldsymbol{T}}\left(\boldsymbol{x}\right){\boldsymbol{C}}_{\boldsymbol{s}}(t) $$
(6)

where the vector ϕT(x) is known as the shape function. The vectors h s and C s are the nodal values of the groundwater head and the solute concentration within a domain known as the local support domain (Liu and Gu 2005) of the interpolation point.

The discretization of the governing equations, such as the groundwater flow and transport equation is achieved through point collocation at the nodes (Guneshwor et al. 2016). After the discretization using meshfree RPCM, the groundwater flow and transport equations (modified forms of Eqs. 1 & 2) reduces to:

$$ \left[{S}_r{\phi}^{\boldsymbol{T}}-\theta \Delta {tT}_r\left(\frac{\partial^2{\phi}^{\boldsymbol{T}}}{\partial {x}^2}+\frac{\partial^2{\phi}^{\boldsymbol{T}}}{\partial {y}^2}\right)\right]{\boldsymbol{h}}_s^{t+\Delta t}={S}_r{h}_r^t+\Delta t\left(1-\theta \right)\left[\frac{\partial^2{\phi}^{\boldsymbol{T}}}{\partial {x}^2}+\frac{\partial^2{\phi}^{\boldsymbol{T}}}{\partial {y}^2}\right]{\boldsymbol{h}}_s^t-{Q}_w\delta \left({\boldsymbol{x}}_r-{\boldsymbol{x}}_i\right)+{q}_r $$
(7)
$$ {\displaystyle \begin{array}{l}\left[R{\boldsymbol{\Phi}}^T-\theta \varDelta t\left({D}_{xx_r}\frac{\partial^2{\boldsymbol{\Phi}}^T}{\partial {x}^2}+{D}_{yy_r}\frac{\partial^2{\boldsymbol{\Phi}}^T}{\partial {y}^2}-{V}_{x_r}\frac{\partial {\boldsymbol{\Phi}}^T}{\partial x}-{V}_{y_r}\frac{\partial {\boldsymbol{\Phi}}^T}{\partial y}\right)\right]{\boldsymbol{C}}_s^{t+\varDelta t}\\ {}\kern4.079998em ={RC}_r^t+\left(1-\theta \right)\varDelta t\left[{D}_{xx_r}\frac{\partial^2{\boldsymbol{\Phi}}^T}{\partial {x}^2}+{D}_{yy_r}\frac{\partial^2{\boldsymbol{\Phi}}^T}{\partial {y}^2}-{V}_{x_r}\frac{\partial {\boldsymbol{\Phi}}^T}{\partial x}-{V}_{y_r}\frac{\partial {\boldsymbol{\Phi}}^T}{\partial y}\right]{\boldsymbol{C}}_s^t\end{array}} $$
(8)

In the above, the reaction and elemental recharge terms have been ignored for the sake of simplicity. Equations (7) & (8) are established for all the internal nodes and appropriate boundary conditions are applied to the boundary nodes. The resulting system of linear equations is solved to obtain the nodal solutions. A coupled meshfree RPCM flow and transport model has been developed based on the above formulation. The model accuracy and effectiveness has been tested for various problems as reported in Guneshwor et al. (2016). This meshfree RPCM model has been used as the simulator in the present study.

2.2 Particle Swarm Optimization (PSO)

The Particle Swarm Optimization (PSO) is a nature-inspired swarm intelligence algorithm proposed by Kennedy and Eberhart in 1995 (Kennedy and Eberhart 1995). A swarm is a collection of multiple units known as particles that interact with each other leading to a complex behavior. PSO relies on the interactions of these particles to find the optimum value of a function.

In essence, the algorithm consists of the following three main steps which are repeated until the stopping criterion is met:

  • Evaluate the fitness of each particle in the swarm

  • Update the individual and global best fitnesses and positions

  • Update the velocity and position of each particle in the swarm

The ability of the PSO algorithm to optimize a given objective function comes from the velocity and position update steps of the algorithm. For each particle in the swarm, the velocity is updated using the following equation (Kennedy and Eberhart 1995):

$$ {v}_i\left(t+1\right)={wv}_i(t)+{c}_1{r}_1\left[{x}_b^i(t)-{x}_i(t)\right]+{c}_2{r}_2\left[{x}_g(t)-{x}_i(t)\right] $$
(9)

The position is then updated as,

$$ {x}_i\left(t+1\right)={x}_i(t)+{v}_i\left(t+1\right) $$
(10)

Here i is the index of the particle. Thus, v i (t) and x i (t) are the velocity and position respectively of the ithparticle at time (iteration) t. The parameters w,c1 and c2 are coefficients to be-specified by the user and their ranges are: 0 ≤ w ≤ 1.2, 0 ≤ c1 ≤ 2 and 0 ≤ c2 ≤ 2. The values r1 and r2(0 ≤ r1 ≤ 1 and 0 ≤ r2 ≤ 1) are random values generated for each velocity update. \( {x}_b^i(t) \) is the individual best candidate solution for the ith particle at time t, while x g (t) refers to the swarm’s global best candidate solution at time t. The velocity update equation was further improved by Clerc and Kennedy (2002) to keep the velocities within acceptable limits and also to ensure convergence to a stable point.

There are many attributes and parameters of the PSO optimizer that affects its performance. The optimal values of the PSO parameters are problem dependent. These parameters control the convergence of the algorithm. The acceleration coefficients control the tradeoff between exploitation and extrapolation aspects of the algorithm and proper selection of these parameter values is essential. The swarm population size also has a profound impact on the performance of the algorithm. Clerc and Kennedy (2002) discussed the impact of the PSO parameters and provided the recommended or typical values of the PSO parameters. The swarm population size is problem dependent and has been obtained after conducting sensitivity analysis. Aside from setting the parameter values, the convergence criterion of the algorithm needs to be properly defined. Normally the convergence criteria are either to set a tolerance value for the fitness function or to set a maximum number of iterations. Another aspect of PSO which has a major influence on the behavior of the algorithm is the neighborhood topology (Clerc and Kennedy 2002). The global best topology has a faster convergence rate. In the local best or ring topology, parts of the population can converge at different optima. It is slower to converge but less likely to converge at local sub-optima. Since groundwater source identification problem suffers from non-uniqueness (Atmadja and Bagtzoglou 2001), the local best topology has been implemented in this study since it is desirable that more exploration of the solution space be made to avoid being trapped in local sub-optima.

2.3 Source Identification Using Simulation-Optimization Models

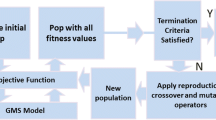
In Simulation-Optimization (SO) models, the groundwater contaminant source identification problem is formulated as forward-time simulation in conjunction with an optimization model. In this approach, several forward-time simulations of the groundwater solute transport equation are run with different sets or combinations of the potential sources and their strengths. The solutions of these forward runs are compared to the measured spatial and temporal solute concentration data. The objective of the optimization model is to select that set of potential sources which results in simulated concentrations representing the closest match with the measured solute concentration data. This approach avoids the mathematical complexities associated with direct inversion of the groundwater flow and solute transport equation. Fig. 1 shows the flow chart of the simulation-optimization approach for groundwater contaminant source identification.

Fig. 1
figure 1

Flow chart for simulation-optimization approach to groundwater source identification

Full size image

In this study, the SO approach is being followed using the PSO as the optimizer. Since the forward-time simulation of the solute transport needs to be iterated many times to search for the optimal solution, it may take very large computational time. To overcome this, a concentration response matrix described in section 2.3.3 is developed (Gorelick et al. 1983) for evaluation of the concentrations of the contaminant at the observation wells from the forward simulations.

2.3.1 Mathematical Formulation of Simulation-Optimization Models

The basic goal of a contaminant source identification model is to quantify the source characteristics e.g. location, disposal duration, and solute mass flux or volume disposal rates etc. Source identification models using optimization approach search for a feasible set of source characteristics which minimizes some weighted (objective) function of the differences or residual between the simulated and observed values of solute concentrations, usually at a few selected observation or surveillance bore wells within the model domain. Appropriate constraint conditions can be imposed on the parameters of the model.

In general, an optimization model for identification of pollution sources can be formulated as:

$$ \mathit{\operatorname{Minimize}}\kern0.75em \left(\sum \limits_{i,j}{W}_{i,j}F\Big({C}_{i,j}^{predicted}-{C}_{i,j}^{observed}\right) $$
(11)

subject to the constraints,

$$ {\boldsymbol{C}}^L\le \boldsymbol{C}\le {\boldsymbol{C}}^U $$
(12)
$$ {\boldsymbol{q}}^L\le \boldsymbol{q}\le {\boldsymbol{q}}^U $$
(13)

Here, \( {C}_{i,j}^{Predicted}= \) Predicted concentration at ith observation point at jth time step, \( {C}_{i,j}^{Observed}= \) Observed or measured concentration at ith observation point at jth time step, Wi, j= weighting function, q= source strength. \( {C}_{i,j}^{Predicted} \) is obtained from the groundwater flow and transport simulation model. The weighting function is to be specified by the modeler considering the field data quality and their reliability.

The function F(x) is usually either squared or absolute values of the differences between the predicted and observed solute concentrations but it can be any other function as well, for example. Gorelick et al. (1983) has used normalized squared deviation as the objective function. The constraints (12) and (13) ensure that practically acceptable ranges of values are considered by confining the parameters between an upper and lower limit and essentially reduce the feasible search space.

2.3.2 Defining the Objective Function for Optimization and Error Metrics

As depicted in the flow chart (Fig. 1), the simulation-optimization (SO) model seeks to match the concentrations predicted by the model to the measured (observed) concentrations. This matching is done by minimizing the sum of some function of the differences between the simulated and measured concentrations. In this study, the objective function used for minimization is the sum of squared differences between predicted and observed concentrations i.e.

$$ S=\sum \limits_{i=1}^{NO}\sum \limits_{j=1}^{NT}{\left({C}_{i,j}^{Pred}-{C}_{i,j}^{Obs}\right)}^2 $$
(14)

where,

NO :

no. of observation bore wells

NT :

no. of time steps

\( {C}_{i,j}^{Pred} \) :

Predicted concentration at the ith observation point at the jth time step

\( {C}_{i,j}^{Obs} \) :

Measured concentration at the ith observation point at the jth time step.

Further, the following two error metrics are defined for measuring the accuracy of the predictions from the source identification model:

$$ \mathrm{Root}\ \mathrm{mean}\ \mathrm{square}\ \mathrm{error}\ \mathrm{in}\ \mathrm{concentration}\ \mathrm{predictions}:\kern0.5em RMS\_ Concn=\sqrt{\frac{\sum_{i=1}^{NO}{\sum}_{j=1}^{NT}{\left({C}_{i,j}^{Pred}-{C}_{i,j}^{Obs}\right)}^2}{N}} $$
(15)
$$ \mathrm{Root}\ \mathrm{mean}\ \mathrm{square}\ \mathrm{error}\ \mathrm{in}\ \mathrm{source}\ \mathrm{strength}\ \mathrm{predictions}:\kern0.5em RMS\_ source=\sqrt{\frac{\sum_{i=1}^{NS}{\sum}_{t=1}^{NR}{\left({S}_{i,t}^{Pred}-{S}_{i,t}^{Actual}\right)}^2}{N}} $$
(16)

where, NS= no. of sources or injection wells, NR= no. of release years, \( {S}_{i,t}^{Pred}= \) Predicted strength of the ith source in the tth release year, \( {S}_{i,t}^{Actual}= \) Actual source strength of the ith source in the tth release year. The first of the error metric RMS_Concn is a measure of the effectiveness of the PSO optimization algorithm while the second error metric RMS_source is a measure of performance of the source identification model as a whole. It may be noted that the primary objective of the optimization algorithm is to minimize the difference between the measured and predicted concentrations only. It does not directly minimize the differences between the predicted and the actual source strengths. Therefore both the metrics have been defined to gauge the performance of the model.

2.3.3 Concentration Response Matrix

To construct the concentration response matrix, each of the potential source locations is considered in isolation with unit source strengths. The solute concentrations resulting at the observation points (wells) from each simulation are the concentrations (response) in the aquifer if a leak was to have occurred in only at that location. The concentration at any location when there are simultaneous multiple leaks (sources) is a linear function of these unit leaks (Gorelick et al. 1983).

For the case studies considered here, each column of this matrix stores the breakthrough curves at the observation bore wells resulting from unit release from each of the sources in a particular release year. For example, the first column stores the solute concentrations at each time step for the observation bore wells due to a unit release from the first source in the first year of solute release. The second column corresponds to the unit release from the 2nd source in the first year of release; the third column corresponds to unit release from the 3rd source and so on. When the columns (block) for all the sources in the first year of release are completed, the columns (block) for the second of year of release are populated. This is followed by the blocks for the remaining years of the releases.

Use of concentration response matrix offers a big saving on computational time when using optimization programs like PSO. In PSO, the objective function is evaluated for each particle at every iteration and the number of iterations tends to be several thousands. Without using the concentration response matrix, the groundwater transport model needs to be executed each time the objective function is evaluated which can be several thousand evaluations. Consequently the computational time will tend to be very high depending on the convergence rate.

3 Case Studies for Model Demonstration

In the following sections, the meshfree RPCM-PSO-SO model for identification of groundwater contaminant sources is demonstrated through two different case studies.

3.1 Contaminant Releases from Disposal Sites in a Hypothetical Aquifer

Consider the hypothetical confined aquifer as shown in Fig. 2 with five sources of contamination assumed to be disposal sites. The boundary conditions for flow are as depicted in the Fig. 2. This problem was studied by Gorelick et al. (1983) and is being adapted in this study to compare the performance of the meshfree RPCM-PSO-SO source identification model to the optimization models proposed by Gorelick et al. (1983). Five possible disposal sites S1, S2, S3, S4 and S5 are shown in the Fig. 2. Three observation wells W1, W2 and W3, shown in the figure, records the contaminant concentrations over a 15 year period. The thickness of the aquifer is 30.5 m while the hydraulic conductivity is 0.01 cm/s. The aquifer is assumed to be isotropic. Effective porosity is taken to be 0.3. Longitudinal and transverse dispersivities are 7.6 and 2.3 m respectively. The recharge rate of the pond has been taken as 0.0067 m/day and contributes roughly around 21% of the total flow through the system. The waste disposal rate has been kept at a low value of 1 l/s so that it does not significantly affect the groundwater hydraulic head distribution. The disposal flux, which is the product of the liquid volume disposal rate and the solute concentration of the waste, from the disposal sites has been kept at same values as in Gorelick et al. (1983) to have a comparative study. Table 1 shows the schedule of the contaminant disposals from the sites and the magnitude (disposal fluxes) of these disposals. The disposals are assumed to happen during a four year period and stopped thereafter.

Fig. 2
figure 2

Hypothetical aquifer with 5 contaminant disposal sites and 3 observation wells with the meshfree nodal distribution

Full size image
Table 1 Contamination release schedule from the sources – case study 1
Full size table

A groundwater flow and transport model using meshfree RPCM was constructed to generate the breakthrough curves at the observation wells. The nodal distribution used in the meshfree RPCM flow and transport simulation is shown in Fig. 2. A total of 177 nodal points are used in the simulation. The nodal spacing is 91.4 m in both the x- and y- directions. A circular support domain (Guneshwor et al. 2016) was employed with a radius equal to three times the nodal separation. The simulation was carried out for 15 years period with a time step size of 40 days. Additionally the time steps included all the multiples of 365 days i.e. the end of each year of the 15 years simulation period. The breakthrough curves at the three designated observation borewells obtained from the simulation are shown in Fig. 3. These breakthrough curve data will be treated as the observed concentration data for the source identification model.

Fig. 3
figure 3

Breakthrough curves at the observation wells – case study 1

Full size image

To construct the concentration response matrix, the simulation model was run to generate the breakthrough curves corresponding to unit releases from each of the five disposal sites for each year of release. A total of twenty 1-year disposal events are there in this case study (Table 1) and the simulation model was run for each of these disposal events. The breakthrough curves from these simulations are then used to construct the concentration response matrix as described in section 2.3.3. Each column of this matrix stores the breakthrough curves at the observation wells resulting from simulation of the unit release disposal events.

The observed concentration data and the concentration response matrix are then fed to the meshfree RPCM-PSO-SO source identification model for reconstructing the release histories or disposal events from the sources. The PSO optimizer tries to find the set of disposal fluxes that minimize the objective function defined in Eq. (14).

3.1.1 Results and Discussion

The number of objective function evaluations (iterations) required to achieve convergence is a measure of the efficiency of the optimizer. More iterations, in general, produce better results but at the cost of more computational time. A convergence study with respect to the number of iterations has been conducted for this case study. Table 2 shows the results of this convergence analysis. It is observed that the RMS_Concn values are very low even with only 103 iterations while the RMS_Source has much slower rate of convergence. This implies that the optimizer is very effective in minimizing the fitness function. The slower convergence rate in identifying the disposal fluxes, despite very close matching of the predicted and observed contaminant concentrations as inferred from the low values of RMS_Concn, is due to the non-uniqueness of the source identification problem (Atmadja and Bagtzoglou 2001). Several sets of source strengths (disposal fluxes) may lead to nearly the same spatial and temporal concentration distributions.

Table 2 Convergence with respect to iterations – case study 1
Full size table

Table 3 shows the comparison of the source predictions of the meshfree RPCM-PSO-SO source identification model with 105 iterations to those predicted by linear programming and stepwise regression used by Gorelick et al. (1983). It can be seen that the RPCM-PSO-SO model yields better results in comparison to the model predictions of Gorelick et al. (1983) which uses linear programming and stepwise regression as the optimizer. This may be readily inferred from the smaller value of RMS_Source of the meshfree RPCM-PSO-SO model. As can be seen from Tables 2 and 3, the PSO based model yields better results than the linear programming model of Gorelick et al. (1983) when the number of iterations touches 5 × 104. Most of the disposal fluxes were correctly identified to within 10% of their true values except for one disposal event where the error was around 30%. It may also be observed that a few erroneous or spurious sources are also predicted by the model. However their magnitudes are very small and can be safely ignored as noises. This case study showed the applicability and effectiveness of RPCM-PSO-SO model.

Table 3 Comparison of RPCM-PSO-SO model predictions with conventional optimization approaches – case study 1
Full size table

3.2 Source Identification for a Field Problem

In this case study, we investigate the migration of contaminants through a confined aquifer due to leaching from storage sites or tanks which has been occurring intermittently over a period of time. The aquifer considered, shown in Fig. 4, has been described in Guneshwor et al. (2016) and is an industrial site in Gujarat, western India. The area to be modeled is approximately 4.5 km2. It is bounded by a lake on the north, north-east, west and south-west boundaries. There are no water bodies on the rest of the boundary. The water level in the lake is used as the constant head value at the boundaries adjacent to the lake. The flux boundary value is estimated and adjusted during calibration of the model (Guneshwor et al. 2016). Six hypothetical sources located at S1, S2, S3, S4, S5and S6 (Fig. 4) are releasing TDS (Total Dissolved Solids) as a contaminant through leaching over a period of four years with concentration data as given in Table 4. It is assumed that after the 4 years of release, the sites stop releasing any contaminants. Four observation wells viz. OB-1, OB-2, OB-3 and OB-4 records the contaminant (solute) concentrations due to the releases from the sources over a period of 10 years (simulation period).

Fig. 4
figure 4

Model domain with the contaminant sources and observation bore wells shown against the groundwater head distribution in the aquifer (in m) – case study 2

Full size image
Table 4 Strength of the sources during the leaching period – case study 2
Full size table

3.2.1 Results and Discussion

The model domain was divided into a regular grid of 1008 nodal points corresponding to grid spacing along x and y directions of ∆x = 49.6 m and ∆y = 42.8 m respectively (Guneshwor et al. 2016). The flow and transport modeling was carried out using meshfree RPCM as described in the above mentioned reference. Being a meshfree method, only the nodal coordinates are required for the simulation. No information on the interconnection between the nodes is required.

Figure 5 shows the contour (in m) of hydraulic head distribution in the study area. There is a recharge zone in the area and the groundwater flow directions radiate out from this zone in all the directions (Guneshwor et al. 2016). The main flow direction is in the south-east directions.

Fig. 5
figure 5

Breakthrough curves at the observation borewells – case study 2

Full size image

The transport model tracks the migration of the contaminants for a period of 10 years (3650 days) including the 4 years during which the releases took place. The time step size used in the transport model is ∆t = 10 days and the time-stepping scheme used is the Crank-Nicholson method. The contaminant concentration values at the observation bore wells are recorded for every 30 days (monthly) to construct the breakthrough curves at the wells. Figure 5 shows the breakthrough curves of the four observation bore wells. The breakthrough curves at the four observation bore wells serve as the measured contaminant concentration data and used as input data in the source identification model. The goal of the source identification model is to reconstruct the release history of the sources (Table 4) from this given contaminant concentrations data. The use of breakthrough curves is justified, since generally in any field scenario concentrations are measured through water sample collection only at a few surveillance (observation) bore wells at a set time interval of sample collection e.g. weekly, monthly, bi-monthly etc. over a period of time, normally few years.

A concentration response matrix is constructed as described in section 2.3.3. Each column of this matrix stores the breakthrough curves at the four observation bore wells resulting from unit release magnitude from each of the sources in a particular release year.

The results of the convergence study of the source identification model are presented in Table 5 and Fig. 6 where the variation of error metrics viz., RMS_Source and RMS_Concn with the number of iterations is shown. It may be observed that acceptable values of RMS_Source are obtained when the number of iterations crosses 30 × 103. As observed in the previous case study, the RMS_Concn values are much smaller even with just 103 iterations. This implies that the optimization algorithm is very effective in matching the observed and model predicted contaminant concentrations (minimizing the objective function) but due to non-uniqueness of source identification problem, the source strength predictions are not accurate when the number of iteration are low.

Table 5 Convergence with respect to number of iterations – case study 2
Full size table
Fig. 6
figure 6

Convergence of source predictions with iterations – case study 2

Full size image

Table 6 presents the comparison of the actual source strengths with those predicted by the RPCM-PSO-SO model. The source strength predictions are presented for 3 × 103 and 5 × 103 iterations of the particle swarm optimizer. With 3 × 103 iterations, though the source predictions are accurate to within 15% of the actual values, many erroneous sources are also predicted. When the number of iterations touches 5 × 103, the magnitude of these spurious source predictions has been reduced to levels which can be safely ignored as noises.

Table 6 Source strength predictions from the PSO based source identification model – case study 2
Full size table

It is observed from Table 6 that the source identification model could construct the release histories of the sources with high accuracy i.e. within 3% error. The very low value of the RMS_Concn suggest that the PSO algorithm was very effective in minimizing the difference between simulated and measured concentration values.

3.2.2 Analysis with Limited Data

The previous case study considers that the concentration data is available for an extended period of time and assumes no missing data over the entire period. This may be divergent from the actual field situation where regular monitoring may start only after detecting solute concentrations that exceed a particular regulatory limit and may continue only for a limited period or number of years. In such cases, the concentration data will be limited. Figure 7 shows how a typical concentration data for such cases might look like. Monitoring starts when the solute concentration in the surveillance borewells crosses 200 ppm or more. These monitoring period have been chosen arbitrarily to represent a typical field condition.

Fig. 7
figure 7

Break through curves for a limited period of time

Full size image

Except for borewell OB-4, whose monitoring period is two and half years, the rest of the borewells has a monitoring period between 3 and 5 years. Due to the reduction in the input data, more number of iterations might be required to achieve convergence. Alternatively if more information from the field is available, it can be incorporated into the model to fasten the convergence. One such commonly available information in industrial waste disposal facilities is the information on the level of contamination of the waste being handled by the facility. Such information can then be incorporated as constraints in the model. For example, if the maximum concentration (level) of the contaminant that a waste disposal facility handles is available, it may be used as a global constraint on all the potential sources within the waste disposal facility. It is common in industrial practice, such as in nuclear industry, to classify wastes according to the concentration level of the contaminant being handled. Further in certain cases, within a disposal facility there may be many disposal sites and each disposal site is designated to handle a specified (or pre-classified) level of waste. In such cases, individual constraints (local constraints) can be imposed on each disposal sites (sources) in the optimization model.

Both the above cases of source strength constraints have been illustrated in the present study and compared to the case where no constraints are placed on the sources. In the first case, a maximum source strength of 2000 ppm (global constraint) is imposed on all the disposal sites. Referring to Table 4, it is approximately 30% more than the maximum release from all the sources during the 4 year release period and has been chosen arbitrarily for illustration. It will demonstrate that only a rough estimate of constraint on the concentration may be needed for the source identification model. For the case where individual constraints are to be imposed on each disposal site, the upper limit on the concentration for each site may be obtained from the maximum release concentration of each site during the 4 year release period (by referring to Table 4). Table 7 shows the individual caps on the concentration level of the contaminants handled by each disposal site as used in the source identification model.

Table 7 Concentration level of waste (contaminant) handled by individual disposal sites
Full size table

It may be observed, as in the first case, that these values are set to a value higher than the maximum release concentration of each site during the 4 years release period (see Table 4) to demonstrate that only a rough estimate may suffice. These limits are set arbitrarily for the sake of demonstration.

The source identification model is run with and without the constraints as discussed above. Table 8 shows the results of convergence study with respect to the number of iterations of the particle swarm optimizer for different scenarios discussed above. In Table 9, the actual source predictions by the SO model after 5 × 104 iterations are shown for the different scenarios. It is observed that (i) when there is no constraint on the possible releases from the disposal sites, most of the disposal events have been identified to within 20% of the actual value except for two disposal events where the errors were relatively larger at 39 and 54%. Also a few erroneous sources were predicted but their magnitudes were very small and may be ignored; (ii) the source predictions are improved when constraints are placed on the maximum concentration level of the contaminant. The best prediction was observed when individual upper limits (local constraints) are placed on the concentration of the releases for each disposal sites followed by the case where a facility wide upper limit (global constraint) was placed on the concentration of the releases from the disposal sites. In the former case, most of the disposal events were predicted within 5% of the true value except for two disposal events where the errors were 13 and 36%. The magnitude of the spurious sources predicted by the model has also reduced drastically.

Table 8 Convergence with respect to iterations for different scenarios
Full size table
Table 9 Source strength predictions from the RPCM-PSO-SO model for limited data
Full size table

It may be observed (Table 8) that the RPCM-SO model has slower convergence when no constraint is placed on the magnitude of the releases. This is inferred from the relatively high values of the RMS_Source. However, the predictions are improved by placing constraints on the source releases. This is because the solution search space has been drastically reduced by using constraints. When local constraints are placed on individual sites, the search space is minimal. Consequently the impact of non-uniqueness issue associated with source identification will be mitigated to a large extent as a result of the reduced search space. Imposing the constraints demands more information from the field. But such information’s are generally available. In case this information is not directly available, at least a rough estimate can be made from the type of waste being disposed.

Other information from the field, if available, can be incorporated into the SO model to improve the convergence and also accuracy of the predictions. The only way to mitigate the effect of non-uniqueness of groundwater source identification problem is to provide more information to the source identification model. Incorporating more field information can drastically reduce the solution search space and hence improve convergence. Field information can also be used to rule out any significant erroneous or spurious sources predicted by the model. Increasing the length of the borewell monitoring period will also improve the model predictions as the case studies presented have shown.

In this study, it is implicitly assumed that the potential sources of leak are known a priori and also that the aquifer parameters are known exactly. The first assumption is not very restrictive since in any real groundwater contamination situation, the suspected sources or facilities are always known. For example, if a chloride contamination is found in the groundwater, then all the facilities and underground pipes which handle chloride are the potential sources. The second assumption of no uncertainty in aquifer parameters does not represent the actual field conditions since aquifer parameters are known to have significant measurement errors. However, if calibrated aquifer parameters are available then they can be readily used in the model presented in this study.

4 Conclusions

Inverse modeling using simulation-optimization approach can effectively be used for groundwater source identification problem. The present study has explored the applicability of PSO based optimization algorithm as a tool for identifying the unknown sources of groundwater pollution. The PSO model has been coupled with a meshfree RPCM flow and transport model to set up the RPCM-PSO-SO model. The application of the developed RPCM-PSO-SO model has been demonstrated through two case studies of groundwater pollution. The first case is a hypothetical case study which simulates contaminant releases from several disposal sites during four years of contaminant release. The source identification model was required to construct the release histories of the disposal sites. The breakthrough curves recorded at a few observation bore wells serves as the input to the source identification model. It was found that the PSO based model was able to identify as well as quantify the leak magnitudes with sufficient accuracy and had better performance in comparison to linear programming and regression based models available in literature. The second case study considered is a field case where waste disposal (storage) at several locations in the aquifer lead to leaching and seepage of contamination to the groundwater. The waste disposal facilities are assumed to follow a specific schedule of discharging (storage) the contaminant over a four year period. It is assumed that the releases stopped after this period and the contaminants migrated throughout the aquifer. Concentration measurements are recorded at a few surveillance bore wells for a certain period of time. Using this historical concentration data, the RPCM-PSO-SO model attempted to reconstruct the release history from the sources (storage sites). It was observed that the source identification model could reconstruct the release histories from the waste disposal sites with acceptable accuracy. The present meshfree RPCM-PSO model offers advantages in terms of simplicity in implementation. PSO has few parameters to deal with and can be easily integrated into any simulation model. This study has demonstrated that the RPCM-PSO-SO model can be effectively used for real world groundwater source identification problems.