1 Introduction

Land and water are the lifeline of agriculture and proper utilization of these resources is essential. Irrigation plays an important role in agriculture as it ultimately decides the fate of the crops under cultivation where enough water is not available. There is an increasing demand to raise agricultural production to feed the growing population of the world, which can be achieved by either increasing cultivation area or by using improved mechanism & tools for cultivation. Matanga and Mariño (1979) developed an area allocation model which maximizes gross margin from yields of crops under consideration subject to total water supply. The author also considered the maximum amount of water that can be delivered for irrigation purpose and labour constraint. Mayya and Prasad (1989) presented tank irrigation system to optimize the grain yield of rice in the semiarid region of India. Dudley (1988) presented an integral consideration of the up-farm and on-farm aspects for a river valley irrigation system controlled by a single decision maker. Bras and Cordova (1981) considered the intraseasonal stochastic variation of the crop water requirements and the dynamics of the soil moisture depletion with optimal temporal allocation of irrigated water. Singh et al. (2001) formulated a linear programming model to maximize net return and optimal crop patterns under different level of water availability, farmers’ socio-economic conditions and crop preference. Kipkorir et al. (2001) developed an optimization model to aid in decision making in real time for deficit irrigation taking water demand and supply for multiple crop irrigation. Sethi et al. (2002) developed two models: (i) Ground water balance model and optimum cropping and (ii) Ground water management model to determine optimum cropping pattern and ground water allocation from private and government tubewells according to different soil type, type of agriculture and seasons. Benli and Kodal (2003) developed a non linear model with objective function as crop water benefit functions, to determine the optimum cropping pattern, farm income and water allocation under limited and inadequate water supply conditions. Sahoo et al. (2006) presented a fuzzy multi-objective and linear programming based management models for optimal land-water crop system planning for the Mahanadi-Kathajodi delta in eastern India. Tsakiris and Spiliotis (2006) presented cropping pattern planning under water supply from multiple sources aiming at maximizing the revenue from irrigation activities. Sarker and Ray (2009) presented three different approach for solving multi-objective crop planning model and analyzed the solution to give better insight from the point of view of a decision maker. Mishra et al. (2009) developed a multi-objective optimization model to determine the optimal crop pattern and optimal size of auxiliary storage reservoir. Also, Fasakhodi et al. (2010) used a multi-objective fractional goal programming approach method to determine the optimal cropping pattern and sustain water availability in a rural farming system. Along with surface water, ground water also act as a vital source for irrigation. Karamouz et al. (2010) developed a model to determine net benefits of agricultural products using genetic algorithm considering water allocation priorities and surface and ground water availability. Márquez et al. (2011) solved a multi-objective crop planning problem using a Pareto based Multi-objective Evolutionary Algorithms (MOEAs). Noory et al. (2011) presented a linear and a mixed-integer linear model to maximize net benefit with multi-crop planning and irrigation water allocation using Particle Swarm Optimization (PSO) algorithm. Regulwar and Gurav (2011) presented a multi-objective fuzzy linear programming irrigation planning model for deriving the optimal cropping pattern for Jayakwadi project in the Godavari river in Maharashtra, India. Wang et al. (2011) presented a GIS frame work for changing cropping pattern under different climate conditions and irrigation available scenarios. Sahoo and Panda (2012) presented a simulation modeling for sizing lined on-farm pond for various crop substitution ratios in rainfed uplands of Eastern India. Sahoo and Panda (2014) presented rainwater harvesting option for rice-maize cropping system in rainfed upland through root zone water balance simulation. Dogra et al. (2014) presented a compromise programming based model to maximize food production with minimum allocation of available water at watershed scale after meeting human, livestock and environment needs under different scenarios. Zhang et al. (2014) presented a virtual water assessment methodology to assess strategies of saving water by identifying products which would be better as imports rather than producing them. Kaviani et al. (2015) presented a constraint-state equation optimization model and beta function considering the stochastic variable in nonnormal state and uncertainties for both irrigation depth and soil moisture. This model uses the soil moisture budget equation for the specific plant on a weekly basis. Karandish et al. (2015) presented an application of virtual water trade to evaluate cropping pattern in arid region by considering three indices including VW, unit blue water value, and the ratio of required blue water to the total water allocation for the agriculture. Srivastava and Singh (2015) presented a multi-objective optimization problem taking crop area, soil properties, use of fertilizer, and local socio-economic conditions as constraints which is solved using fuzzy programming approach with linear, exponential and hyperbolic membership functions. Singh (2016) presented a model incorporating the ground water component to maximize the net farm revenue of an irrigated area located in northwest India by optimally allocating the available water and land resources.

Fuzzy stochastic programming is concerned with optimization problems in which some or all parameters are treated as fuzzy random variables in order to capture randomness and fuzziness under one roof. Mohan and Nguyen (1997) developed the idea of fuzzifying approach to multi-objective stochastic programming problem. Dubois and Prade (1987) proposed the linear programming with constraints having fuzzy interval co-efficient. Luhandjula (1996) generalized robust programming with interval co-efficient to the fuzzy constraints into fuzzy inclusion constraints. Recent developments in fuzzy stochastic problem can be found in: (Acharya and Biswal 2011; Sakawa et al. 2011; Wang and Watada 2012; Mousavi et al. 2013; Sakawa and Matsui 2013; Aiche et al. 2013; Acharya et al. 2014; Li et al. 2014). Montes and Montes (2015) studied the properties of fuzzy ranking and generalized their definition as compared with fuzzy random variables by means of stochastic orders. Due to the complexities of agricultural systems, the mathematical models are generally manipulated by imposing selective constraints which reduces the impact and effects of the model. To capture such ambiguity and uncertainties fuzzy stochastic model proves beneficial. Lu et al. (2008) presented an inexact two stage fuzzy stochastic programming method for water resources management under uncertainty with fuzzy punishment policies under different water availability condition. Zhang et al. (2009) proposed a robust chance constrained fuzzy possibilistic programming model for water quality management within an agricultural system, where solutions for farming area, manures/fertilizers application amount, and livestock husbandry size under different scenarios are obtained and interpreted. Guo et al. (2010) presented a fuzzy stochastic two stage programming approach for water resources management under multiple uncertainty within an agricultural system. Li et al. (2014) presented a hybrid fuzzy stochastic programming method for water trading under uncertainties of randomness and fuzziness. The method developed is applied to a water trading program within an agricultural system.

Genetic Algorithms (GA) are based on the concept of the biological process of natural selection, developed by Holland (1975). Development of this field is mainly due to John Holland and his students. GA provides a set of efficient domain independent search heuristics which are a significant improvement over other traditional methods. The model most commonly investigated is a GA with a binary alphabet, multiple bit mutation, one point crossover and proportional fitness selection. Liu and Iwamura (2001) formulated a fuzzy simulation based genetic algorithm for solving chance constrained programming models with fuzzy decision. Deb (2001) formulated a nonlinear goal programming using multi-objective genetic algorithm. (Jana and Biswal 2004; 2006) used GA in a stochastic simulation in order to solve stochastic programming problem. More detail on genetic algorithms can be found in (Liang and Leung 2011; Loghmanian et al. 2012; Ruiz et al. 2015; Lu et al. 2013; Mitchell et al. 2014; Miseviċius 2015). Particularly, in agriculture sector GA can play a vital role in providing a better alternate solutions which will help the decision maker in taking proper decision. Kuo et al. (2000) presented a model based on on-farm irrigation scheduling and simple GA method for decision support in irrigation project planning. The proposed model is applied for optimizing economic profits, simulating the water demand, crop yields and estimating the related crop area percentages with specified water supply and planted area constraints. Nagesh Kumar et al. (2006) presented a genetic algorithm (GA) model for obtaining an optimal operating policy and optimal crop water allocation from an irrigation reservoirs. The objective is to maximize the sum of the relative yields from all crops in the irrigated area. Ines et al. (2006) proposed an innovative approach to explore water management options in irrigated agriculture considering the constraints of water availability and heterogeneity of irrigation system properties. Fallah-Mehdipour et al. (2012) compared total net benefit of the water resources system and multi cropping patterns rules by three evolutionary algorithm genetic algorithm, particle swarm optimization and shuffled frog leaping algorithm.

This research paper proposes a multi-objective fuzzy stochastic model for proper allocation of agricultural land and the optimum use of water from surface runoff, with water balance for turn in period (turn-in indicates a time period that extends from harvesting of the first crop to sowing of the second crop. During this period the farmer prepares his land and makes it ready for sowing of the second crop.) or increasing the area of the farm using genetic algorithm. The paper highlights the use of a fuzzy random variable along with a fuzzy random numbers to represent the water requirement and yields of the different crops to deal with uncertain and imprecise data occurring in real world as compared with other researchers where uncertainty and impreciseness are handled separately. This paper also highlights the concept of turn in period which was not used before. The study is carried out in the region where sufficient rainfall occurs to fulfill the needs of the irrigation water which is different from other researchers work, i.e. other works are related to reservoir or where sufficient water for irrigation are not available. The water requirement of the crops is satisfied from the rainfall and surface runoff, which greatly reduces the investment cost, comparing with the other researchers works where additional cost is incurred as water pumping cost and use of ground water to fulfill the demand of irrigation water. Cropping and irrigation water are mainly characterized by uncertainty due to randomness of hydrological variables such as rainfall, evapotranspiration, soil moisture. The uncertainty in crop response lead us to take the water requirement as a fuzzy uniform distribution and yield as a fuzzy numbers. The problem was then solved using a genetic algorithm to find the Pareto solution and to analyze the minute change in cultivated area or to use the balance water for the land preparation in the next crop season. The combining affect of using fuzzy stochastic model with genetic algorithm clearly gives a better picture and also interpret the result in a better way.

The paper is organized as follows: Following this introduction, the Study Area is described in Section 2. The mathematical model formulation is provided in Section 3. Methodology is described in Section 4. Data Implementation is presented in Section 5. Results are provided in Section 6. Finally, the conclusions are provided in Section 7.

2 Study Area

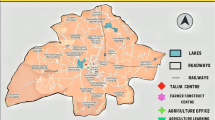
The study area chosen for the case study is the Balasore district located in the northeast coastal plain of Odisha, India, which lies between 21∘3′ to 21∘59′ N latitude to 86∘16′ to 87∘2′ E longitude. It is surrounded by Medinipur district of West Bengal in its northern side, Bay of Bengal in its east, Bhadrak district in its south and Mayurbhanj and Kendujhar district lies on its western side. The climate is characterized by high temperatures and humidity, with mean summer temperature of 30.4∘C and mean winter temperature of 21∘C. The average annual rainfall is 1700 mm which is received normally in two parts, June to September (South-West Monsoon) and October to December (North-East Monsoon). Two important rivers, Budhabalanga and Subarnarckha pass through this district from west to east before flowing into the Bay of Bengal. The district has three main types of soil, (i) Laterite Soils (uplands), (ii) Alluvial Soils (medium-lands), (iii) Coastal Alluvial Soil (lowlands). The major crops of this region are rice, wheat, maize, cereals, pulses, oilseeds, fibres, vegetables, spices, sugarcane and others (Figs. 1 and 2).

Fig. 1
figure 1

Map of Balasore

Full size image
Fig. 2
figure 2

Types of Soil in Balasore

Full size image

3 Mathematical Model Formulation

A multi-objective fuzzy stochastic programming model has been developed for optimum production under different crop patterns and water balance (water remaining after the first growing season) in a farm considering the following terminology:

  • Area under cultivation for different types of crops

  • Rainfall in growing season for each allocated area

  • Runoff from catchment area

  • Crop yields

3.1 Model Description

A multi-objective fuzzy stochastic programming model has been formulated for obtaining optimal production under different crop patterns with water remaining after the first growing season.

Parameters

  • (i)   Cultivated Area: x i ,i=1,2,⋯ ,n: is the area under cultivation of different crops, measured in hectare.

  • (ii)   Yield: Y i ,i=1,2,⋯ ,n: is the yield of different crop under cultivation, measured in kg/hectare.

  • (iii)   Water Requirement: w i ,i=1,2,⋯ ,n: is the water requirement of different crops, measured in millimeter (mm).

  • (iv)   Rain Water: w a i ,i=1,2,⋯ ,n: is the water available from rainfall to different cultivated area, measured in millimeter (mm).

  • (v)   Water from Catchment Area: W: is the total water available from catchment area, measured in millimeter(mm).

  • (vi)   Water Balance: W b j ,j=1,2,⋯ ,m: is the water remaining under different crop pattern after the growing season, measured in millimeter(mm).

  • (vii)   Decision variables: x i ,i=1,2,⋯ ,n: is the amount of area under cultivation for different crop.

3.2 Formulation of Objective Functions

The Production functions of different crops can be formulated using the cultivated area and their yields. As yields of various crops differ from year to year, so we took yield as fuzzy triangular number. If P is the production function then, P can be given by:P = Yield X Cultivated Area.Mathematically, the above expression can be expressed as: \(\large {{\sum }_{i=1}^{n} \tilde {Y_{i}} x_{i}}\).This objective is known as the maximization of crop production.

3.3 Formulation of Constraints

  • (i)   Better crop yields depends on many factors, including, timing of rainfall and/or irrigation, fertilizers, pesticides, good variety seeds, etc,. As water plays a vital role in farming, the water requirement of the crops can be incorporated as constraints, is divided into two parts, (a) water received from the rainfall and, (b) water received by means of irrigation.

    (ii)   Rainfall is a hydrological phenomenon, so, how long it will rain, with what intensity, and by how much is uncertain. The information regarding water absorbed by the soil, evapotranspiration, seepage loss, etc, can be imprecise. This lead us to consideration of water availability to the soil as a fuzzy variable. The condition of the soil in a day period do not change abruptly, so the water requirement by the crop is taken uniform over a small area. Under this concept, water available to crops by rainfall can be assumed to follow a fuzzy uniform distribution. So, the requirement of water by different crops can be given by:

    (iii)   Water requirement = Cultivated Area X (Water Requirement of the crops - Water Available (rainfall)).

    The above constraints for different crops can be mathematically expressed as:

    $$\large{\sum\nolimits_{i=1}^{n}x_{i} (\tilde{w_{i}}-w_{ai})}. $$

    The fulfillment of water requirement depends upon the total water available. Mathematically, the constraint can be expressed as:

    $$\large{\sum\nolimits_{i=1}^{n}x_{i}(\tilde{w_{i}}-w_{ai})\leq W} $$

  • The water balance after the crop season under different crops can be given by:

    Water Balance = (Total Water Available - Total Water needed by different crops under different allocated area).

    Mathematically, the above expression can be expressed as:

    $$Wb_{j}= W - \sum\nolimits_{i=1}^{n}x_{i}(\tilde{w_{i}}-w_{ai}), j = 1, 2, \cdots, m $$

  • Affinity Constraints: Depending on the regions or states, there is the tendency of farmers to grow paddy or wheat in the Kharif season (The cropping season in India during which crops are grown amidst monsoonal rains is called as kharif season in local parlance. In other words, this is also called as the rainy season in the country. This season continues for four months, starts from mid-June and continues up to mid-September of the year.) and pulse or mustard in the Rabi seasons (This season continues for six months, starts from October till end of March) for the basic food security. So, water for turn in period plays a vital role as it can save investment on water supply. The affinity constraints puts upper limits on the cultivated area for food supply.To summarize the objective function and constraints derived above, the problem can be modeled as a multi-objective fuzzy stochastic programming problem which is given below:

    $$ \max :(Z_{j})= \sum\limits_{i=1}^{n} \tilde{Y_{i}}x_{i}, j= 1,2,\cdots,m $$
    (3.1)

    Subject to

    $$ \tilde{P}(\sum\limits_{i=1}^{n}x_{i} (\tilde{w_{i}}-w_{ai})\preceq W)\succeq\tilde{\beta_{i}} $$
    (3.2)
    $$\begin{array}{@{}rcl@{}} Wb_{j}&=& W - {\sum}_{i=1}^{n}x_{i}(\tilde{w_{i}}-w_{ai}), j = 1,2, \cdots, m \end{array} $$
    (3.3)
    $$\begin{array}{@{}rcl@{}} x_{i}&\geq& 0, i = 1,2, \cdots, n \end{array} $$
    (3.4)

    where \(0\leq \tilde {\beta _{i}} \leq 1\) , \(\tilde {w_{i}}, i = 1,2, \cdots , n\) follows fuzzy uniform distribution. In order to solve the above problem, we formulated an equivalent mathematical multi-objective fuzzy stochastic programming model, which is described in the next section.

4 Methodology

A Multi-objective probabilistic programming (MOPP) problem is of the form:

$$ \max :(Z_{j})=\sum\limits_{i=1}^{n}Y_{i}x_{i}, j = 1, 2,\cdots, m $$
(4.1)

Subject to

$$\begin{array}{@{}rcl@{}} P(\sum\limits_{i=1}^{n} x_{i} (w_{i}-w_{ai}) &\leq& W)\geq{\beta_{i}} \end{array} $$
(4.2)
$$\begin{array}{@{}rcl@{}} x_{i} &\geq& L_{i}>1, i = 1, 2,\cdots,n \end{array} $$
(4.3)

where 0≤β i ≤1 and w i ,Y i ,i=1,2,⋯ ,n are random variables.

A multi-objective fuzzy probabilistic programming (MOFPP) problem is an MOPP problem of the above form where at least one of the weighted objectives w i ,Y i is a fuzzy random variable (FRV) and β i is a positive fuzzy number.In a MOFPP problem, fuzziness may be present in constraints or in the objective function or in both. Therefore, at least one of the following situation is possible.

  • At least one of the constraints has a fuzzy inequality

  • Objective function has a certain type of fuzziness

  • Co-efficient present in the constraint, in an objective function, or in both are fuzzy random variables. A multi-objective fuzzy stochastic programming problem where fuzziness and randomness are considered in the objective function as well as in the constraints can be expressed as:

    $$ \max:(Z_{j})=\sum\limits_{i=1}^{n}\tilde{Y_{i}} x_{i} , j = 1, 2,\cdots,m $$
    (4.4)

    Subject to

    $$\begin{array}{@{}rcl@{}} \tilde{P}(\sum\limits_{i=1}^{n}x_{i} (\tilde{w_{i}}-w_{ai}) \preceq {W}) \succeq\tilde{\beta_{i}} \end{array} $$
    (4.5)
    $$\begin{array}{@{}rcl@{}} x_{i}\geq L_{i}\geq 1, i=1,2,\cdots,n \end{array} $$
    (4.6)

    where \(\tilde {w_{i}}\) are fuzzy random variables, and \(\tilde {Y_{i}}\) are fuzzy random number, L i is the constant, ∀ i.

To handle the fuzziness, let \(\tilde {w_{i}},i=1,2,\cdots , n \) are independent FRVs distributed uniformly with \(\widetilde {FU}\)(\(\tilde {\mu } ,\tilde {\sigma }^{2}\)) where \(\tilde {\mu }\) and \(\tilde {\sigma }^{2}\) are mean and variance of \(\tilde {w_{i}}\), i=1,2,⋯ ,n

The α-cut of the probabilistic constraints can be expressed as:

$$\begin{array}{@{}rcl@{}} \tilde{P} (\sum\limits_{i=1}^{n}x_{i} (\tilde{w_{i}}-w_{ai}) &\leq& {W})[\alpha] \end{array} $$
(4.7)
$$\begin{array}{@{}rcl@{}} = \tilde{P}(\tilde{A_{i}}&\leq& {W})[\alpha] \end{array} $$
(4.8)
$$\begin{array}{@{}rcl@{}} \text{where}~\tilde{A_{i}}&=& \sum\limits_{i=1}^{n}x_{i} (\tilde{w_{i}}-w_{ai})\\ &=&{P(W\geq A_{i})|A_{i}\in \tilde {A_{i}}[\alpha]} \end{array} $$
(4.9)

Using fuzzy inequality, the α-cut of the fuzzy constraint (4.5) is expressed as:

$$\begin{array}{@{}rcl@{}} \tilde {P}(\sum\limits_{i=1}^{n}x_{i} (\tilde{w_{i}}-w_{ai}) &\leq& {W})[\alpha]\succeq \tilde{\beta_{i}}[\alpha] \end{array} $$
(4.10)
$$\begin{array}{@{}rcl@{}} &=& 1- \tilde{P}(W < x_{i} (\tilde{w_{i}}-w_{ai})) \end{array} $$
(4.11)
$$\begin{array}{@{}rcl@{}} &=& 1- P(W < A_{i*})\geq {\beta_{i}}^{*} \end{array} $$
(4.12)

where \([w_{i*}[\alpha ],w_{i}^{*}[\alpha ]]\in \tilde {w_{i}}[\alpha ]\) and \([\beta _{i*}[\alpha ],\beta _{i}^{*}[\alpha ]]\in \tilde {\beta _{i}}[\alpha ]\).

4.1 Fuzzy Stochastic Simulation Based GA

The fuzzy simulation based GA is designed to solve the fuzzy probabilistic programming problems. The steps of the algorithm is described as follows:

figure a

The Flow Diagram of Fuzzy Stochastic GA is shown in Fig. 3.

Fig. 3
figure 3

Flow Diagram of Fuzzy Stochastic GA

Full size image

Representation and Initialization

A population of potential solutions is generated and initialized. If x 1,x 2,.....x n be n decision variables, then each chromosome can be represented as X p =(x 1,x 2,.....x n ) p , where p=1,2,......p_s i z e, while p_size is the size of the population. To search the domain space, the p_size plays an important role which can be chosen by the user. The value of x i (i=1,2,......n) is typically chosen between 0 and the upper bound of the decision variables.

Constraints Checking by the Fuzzy Simulation

The constraints of the model are represented as fuzzy probabilistic constraints. Consider the fuzzy probabilistic constraints

$$ \tilde {P}({\sum}_{i=1}^{n}x_{i} (\tilde{w_{i}}-w_{ai})\leq {W})\succeq \tilde{\beta_{i}^{*}}. $$
(4.13)

The constraint of Eq. 4.13 are defuzzyfied using the α-cut and inequality conditions, so that the constraint reduces to

$$ 1- {P}(W < A_{i*})\geq \beta_{i}^{*}, $$
(4.14)

i=1,2,......,n as discussed before.The above inequality can be represented by

$$\begin{array}{@{}rcl@{}} {P}(W- A_{i*}< 0)\leq (1- \beta_{i}^{*}) \end{array} $$
(4.15)
$$\begin{array}{@{}rcl@{}} = {P}(t_{i}(x,s)< 0)\leq (1-\beta_{i}^{*}) \end{array} $$
(4.16)

where s=(w 1,w 2,.......,w n ,W∗) is a (n+1) dimensional continuous probability distribution, x=(x 1,x 2,x 3,.......,x n ) is the decision variable. We generate N independent random vectors as \(s^{r} = ({w_{1}^{r}}, {w_{2}^{r}}, ...... {w_{n}^{r}})\), r = 1,2,....N, i = 1,2,....,n.Let N i (≤N),i=1,2,.....,n be the number of times the following relation satisfies: t i (x,s r)<0,i=1,2,.....,nThen by the definition of probability, (4.16) will hold if \(Ni/N< (1-\beta _{i}^{*}), i=1,2,\cdots ,n\).

Fitness

The fitness value are the values of objective function which satisfies the given constraints.

Selection

Binary Tournament Selection is a robust selection mechanism which is based on fitness value from a pool of chromosomes. We randomly pick k individuals and compare their fitness, replacing the lower with higher fittest individuals. The winners are chosen for mating. The process is repeated until the desired number of individuals are achieved. Here, k is called the tournament size, which controls the selection pressure. If k = 2, then the tournament selection is called binary tournament selection. The obtained individuals by this process is treated as new population with same p_size as initial population.

Crossover

This is a genetic operator which used in varying the individuals from one generation to next generation. When it is done at a particular point, it is known as single point crossover. A random number ‘r’ is generated within (0,1) for each pair of chromosomes, which act as the crossover point. We assign the probability of crossover as pc, if r ≤ pc, the given pair is selected for crossover.

Mutation

To maintain the diversity of population from one generation to another, mutation operator is used. Mutation is a process of modifying the genetic material of a chromosome from its initial state. When the variation is done bitwise in a sequence, it is called bitwise mutation. It creates a random small diversion and stay near to the area of parents. A random number ‘r’ is generated from the interval [0,1] for every bit in the population. If r ≤ pm then the parents are selected for mutation operation, where pm is the probability of mutation of the genetic system.

Termination

The process is stopped as the desired accuracy is attained or the maximum generation fixed is completed.

5 Data Implementation

Maximizing agricultural production has become an important aspect for farmers, states or the Nation. The government provides necessary facilities required for the better production such as good varieties of seed, better irrigation, fertilizers, etc,. On the other hand, if uncultivated land can be brought under cultivation then it can add to production. In order to achieve this, a better planning and detailed study of the area is required. In this case study, we studied the effect of cropping pattern and water balance for turn in period simultaneously, keeping in view the production factor as well as farmers tendency to grow basic food crops of that region. The upper limit of area under paddy or maize cultivation were kept as 73 % of total irrigated area. This study should help to determine how much the command area can be increased where less irrigation facilities are provided. To study the cropping pattern and water balance, a command area of 0.8 hectares and a catchment area of 0.7 hectares (grassland) are assumed. Annual rainfall data was collected for 30 years and the yield of various crops data were collected for ten years. From the collected information, the pattern of rainfall data was studied and found to follow a log-normal distribution with different percentage of significance level. As the significance level was low, so we did not followed this distribution. A particular year was chosen with a sufficient amount of rainfall to study the case. Runoff and Antecedent soil moisture are calculated by the Curve number formula is given below.

$$Q=\left\{\begin{array}{ll} 0, \qquad \text{ for }P \leq I_{a}\\ \frac{(P-I_{a})^{2}}{P-I_{a} + S} \qquad \text{ for }P \leq I_{a} \end{array}\right. $$

where Q is runoff, P is rainfall, S is the potential maximum soil retention after runoff begins, I a is the initial abstraction. The runoff curve number is calculated using the formula

$$S = 254(\frac{100}{CN}-1) $$

where, CN is the curve number.

For our study purpose, we took I a = 0.3 S. As this value has been recommended for most of the watersheds in India especially which are not in black soil region and under A M C I I&I I I conditions (Bhattacharya et al. 2003).

The water requirement and yields of different crops are provided in Tables 1 and 2 respectively.

Table 1 Water Requirement of Crops
Full size table
Table 2 Yields of Crops
Full size table

To study the effect of cropping patterns and water remaining for the land preparation in the next growing season, a multi-objective fuzzy stochastic programming problem was considered. We chose five different crops: rice, maize, cotton, gram, and groundnut. Water requirement of different crops was assumed to follow a fuzzy uniform distribution as water requirement do not vary in a small farm area for a day with a hydrological conditions. The agricultural yield per season of different crops are taken as fuzzy number as it depends on many factors such temperature, climates, soil condition, etc,.

The mathematical model of the case study can be expressed as follows:

$$\begin{array}{@{}rcl@{}} \max: Z_{1}(x)&=&\tilde{Y_{1}}x_{1}+\tilde{Y_{3}}{x_{3}}+\tilde{Y_{4}}{x_{4}} \end{array} $$
(5.1)
$$\begin{array}{@{}rcl@{}} \max: Z_{2}(x)&=&\tilde{Y_{2}}x_{2}+\tilde{Y_{3}}{x_{3}}+\tilde{Y_{4}}{x_{4}} \end{array} $$
(5.2)
$$\begin{array}{@{}rcl@{}}\ \max: Z_{3}(x)&=&\tilde{Y_{1}}x_{1}+\tilde{Y_{3}}{x_{3}}+\tilde{Y_{5}}x_{5} \end{array} $$
(5.3)
$$\begin{array}{@{}rcl@{}}\ \max: Z_{4}(x)&=&\tilde{Y_{2}}x_{2}+\tilde{Y_{3}}{x_{3}}+\tilde{Y_{5}}x_{5} \end{array} $$
(5.4)
$$\begin{array}{@{}rcl@{}}\ \max: Z_{5}(x)&=&\tilde{Y_{1}}x_{1}+\tilde{Y_{4}}{x_{4}}+\tilde{Y_{5}}x_{5} \end{array} $$
(5.5)
$$\begin{array}{@{}rcl@{}}\ \max: Z_{6}(x)&=&\tilde{Y_{2}}x_{2}+\tilde{Y_{4}}{x_{4}}+\tilde{Y_{5}}x_{5} \end{array} $$
(5.6)
$$\begin{array}{@{}rcl@{}}\ \max: Z_{7}(x)&=&\tilde{Y_{1}}x_{1}+\tilde{Y_{2}}x_{2} \end{array} $$
(5.7)

Subject to

$$\begin{array}{@{}rcl@{}} \tilde{P}(x_{1}(\tilde{w_{1}}-w_{a1})+x_{3}(w_{3}-w_{a3})+x_{4}(w_{4}-w_{a4})\preceq W)\succeq \tilde{0.70} \end{array} $$
(5.8)
$$\begin{array}{@{}rcl@{}}\ \tilde{P}(x_{2}(\tilde{w_{2}}-w_{a2})+x_{3}(w_{3}-w_{a3})+x_{4}(w_{4}-w_{a4})\preceq W)\succeq \tilde{0.70} \end{array} $$
(5.9)
$$\begin{array}{@{}rcl@{}}\ \tilde{P}(x_{1}(\tilde{w_{1}}-w_{a1})+x_{3}(w_{3}-w_{a3})+x_{5}(\tilde{w_{5}}-w_{a5})\preceq W)\succeq \tilde{0.75} \end{array} $$
(5.10)
$$\begin{array}{@{}rcl@{}}\ \tilde{P}(x_{2}(\tilde{w_{2}}-w_{a2})+x_{3}(w_{3}-w_{a3})+x_{5}(\tilde{w_{5}}-w_{a5})\preceq W)\succeq \tilde{0.80} \end{array} $$
(5.11)
$$\begin{array}{@{}rcl@{}}\ \tilde{P}(x_{1}(\tilde{w_{1}}-w_{a1})+x_{4}(w_{4}-w_{a4})+x_{5}(\tilde{w_{5}}-w_{a5})\preceq W)\succeq \tilde{0.80} \end{array} $$
(5.12)
$$\begin{array}{@{}rcl@{}}\ \tilde{P}(x_{2}(\tilde{w_{2}}-w_{a2})+x_{4}(w_{4}-w_{a4})+x_{5}(\tilde{w_{5}}-w_{a5})\preceq W)\succeq \tilde{0.85} \end{array} $$
(5.13)
$$\begin{array}{@{}rcl@{}}\ \tilde{P}(x_{1}(\tilde{w_{1}}-w_{a1})+x_{2}(\tilde{w_{2}}-w_{a2})\preceq W)\succeq \tilde{0.90} \end{array} $$
(5.14)
$$\begin{array}{@{}rcl@{}} x_{i}\geq 0, w_{i}\geq 0, w_{ia}\geq 0, Y_{i}\geq 0, i=1,2,\cdots,5 \end{array} $$
(5.15)

where, \( \tilde {w_{1}},\tilde {w_{2}}, \tilde {w_{5}}\) follows fuzzy uniform distribution with \(\widetilde {FU}(\tilde {{a}},\tilde {b})\) = \(\widetilde {FU}(\tilde {1100},\tilde {1300})\), \(\widetilde {FU}(\tilde {{a}},\tilde {b})\) = \(\widetilde {FU}(\tilde {800},\tilde {1000})\), and \(\widetilde {FU}(\tilde {{a}},\tilde {b})\) = \(\widetilde {FU}(\tilde {1000},\tilde {1200})\) \(\tilde {Y_{1}}=<0.23/0.32/0.41>\), \(\tilde {Y_{2}}=<0.20/0.29/0.38>\), \(\tilde {Y_{3}}=<0.032/0.041/0.050>\), \(\tilde {Y_{4}}=<0.040/0.049/0.058>\), \(\tilde {Y_{5}}=<0.1/0.1045/0.1090>\) W = runoff water generated from grassland; x i = Area under different crops, i=1,2,⋯ ,5; w i = Water requirement for different crops(total growing season), i=1,2,⋯ ,5; w a i = Effective rainfall water in different crops, i=1,2,⋯ ,5; Y i = Yield of different crops, i=1,2,⋯ ,5;

6 Result Analysis

The proposed fuzzy stochastic simulation based GA is coded in C++ in VB2010 Professional. The population size is taken as 100. When the population size is increased, it does not yield better results as compared with the population size 100 and the computational time is also increased. When we decrease the population size it affects the result and the accuracy too, although, the computational time is less than compared with the population size 100. As we increased the number of generation then also computational time is increased with no improvement in the results. The population size is normally taken as twice the number of decision variables in the problem. In this study, we have five decision variables each with 10 bits. So, the size of the population is taken 100. Computational time is one of the factor which needs to be taken care while solving a problem so that we can handle large and complex problems. It is seen from the table that as we increase the value of α the objective value keeps on increasing. Optimum solution (Tables 3, 4, 5, 6, 7, 8, 9, 10 and 11) obtained for different values of probability of crossover(pc), mutation(pm) and α over 300 generation are given in Appendix.

It is clearly seen from the Fig. 4, that the availability of water in (W 2,W 4,W 6) are more as compared to the availability of water in (W 1,W 3,W 5,W 7). Therefore, the patterns of the crop can be easily chosen for better planning so that more farm area can be included to obtain maximum return in that region.

Fig. 4
figure 4

Water Balance for Different Crops Pattern

Full size image

From the Fig. 5, we find that the production is more in (Z 1,Z 3,Z 5,Z 7) than in (Z 2,Z 4,Z 6) under the given set of constraints. From Table 2, we see that the combination of rice, cotton and groundnut and the combination of rice, gram and groundnut are almost same as the yield of cotton and gram are same. Similarly, the case of maize, cotton and groundnut and the combination of maize, gram and groundnut. The water requirement and the yield of rice crop is more than of maize crop. So, the production is more and water availability is less in Z 1 as compared to Z 2. As water requirement of cotton and gram are slightly different with same yield, so any one crop can be chosen with rice crop. But, when we compare groundnut with cotton or gram then we find that the water requirement of groundnut is less and yield is more than cotton and gram. In (Z 2,Z 4,Z 6), the yield of the maize crop plays an important role in the production value. Since, the yield of maize crop is less than of rice crop, so, the production value is less in (Z 2,Z 4,Z 6) than in (Z 1,Z 3,Z 5,Z 7).

Fig. 5
figure 5

Production for Different Crops Pattern

Full size image

The graphical representation of the Pareto Solution Space of the case study is shown below for α = 0.5 (Fig. 6).

Fig. 6
figure 6

The Pareto Solution Space

Full size image

7 Conclusion and Discussion

In this paper, a multi-objective fuzzy stochastic model was developed to study the crop patterns and the optimal use of available water resources in a small farm. The methodology presented incorporates maximization of crop production under different combination of crops. In the objective functions where fuzziness has been incorporated as a fuzzy numbers to obtain the production of the crops under different crop patterns subjected to the availability of the irrigated water. The yield of the crops in the objective function is treated as a fuzzy numbers and imprecise data are taken from Table 2. The irrigated water provided to the soil for the growing season are from rainfall and surface runoff generated from it. The water requirement by the crops follow a fuzzy uniform distribution. The data from Table 1 is used for generating a fuzzy uniform distribution for different crops. The multi-objective fuzzy stochastic programming problem is then handle with Fuzzy Stochastic GA based approach. This study help us to know that by how much the area of the farm can be increased under the condition of availability of water and the patterns of the crop. As different crops have different water requirement, so under which pattern, how much irrigated area can be increased, or the remaining water can be used in preparing the land for the next crop season can be known from the study above. From the result section, we find that the crops pattern in (Z 1,Z 3,Z 5,Z 7) shows better production than (Z 2,Z 4,Z 6). In terms of water balance, we see that (W 2,W 4,W 6) leaves a significant amount of water for turn in period than (W 1,W 3,W 5,W 7). So, a small amount of cultivated area can be increased for (Z 1,Z 3,Z 5,Z 7) and a good amount of area can be increased for (Z 2,Z 4,Z 6) in terms of water balance.

From the above crop patterns, appropriate decisions can be made by taking into consideration the price of grains, i.e, which crop area should be increased and by how much, so that it will fetch more profit with less investment. The advantage of using GA is that the Pareto solution helps in analyzing the effect of small change in terms of cultivation area which will help the decision makers in taking appropriate decision. The present model can be extended to study the reservoir area model including different objective functions with more constraints such as labour constraints, cost related issues, under different crop season, etc. The model can also be extended to tank irrigation optimization model, ground water resources model.