1 Introduction

Evolutionary algorithms (EAs) are known as the flexible and powerful optimization tools for solving nonlinear, nonconvex, multi-modal and discrete problems. The flexibility of EAs for solving multi-criteria problems and their capabilities for links with simulation models have led to develop and expand various types of multiobjective evolutionary algorithms (MOEAs) and widely used applications in water resources and environmental engineering (Nicklow et al. 2010). Similarly, a significant increase in development and application of MOEAs for multi-objective design of water distribution systems (WDSs) has also seen over the past decade because of the high computational burden and complexity of water distribution network (WDN) design problems with a large number of pipes or decision variables. In this direction, although a few heuristic approaches have occasionally been introduced (e.g. see Shirzad et al. 2015), application of optimization tools is predominated. Keedwell and Khu (2004) highlighted the ability of MOEAs for network design purposes. This approach makes it possible to obtain a Pareto front of optimal solutions in the compromise among different criteria. Montalvoa et al. (2010) for example considered costs and the nodal pressure deficits as the main criteria minimizing by a multi-objective particle swarm optimization (PSO) algorithm. ‘Costs’ and ‘reliability’ are the main criteria which are used frequently in MOEAs for WDN design. Kanakoudis et al. (2011) introduced new performance indices and methodology for the assessment of water distribution systems. Zheng et al. (2014a) used the surplus head as the reliability index. However, this indicator does not consider the reliable looped networks in unexpected conditions such as pipe breaks. Todini (2000) introduced a “resilience” index to consider the reliability associated to the looped systems under the pipe burst conditions. The index was then improved by Prasad and Park (2004) considering the redundancy in the looped systems. They used Non-dominated Sorting Genetic Algorithm (NSGA2) for WDN design with the goal of minimizing network cost and maximizing the network resilience. Farmani et al. (2005a) carried out a comparison between the performance of NSGA2 algorithm and modified version of the Strength Pareto Evolutionary Algorithm (SPEA2) and reported that SPEA2 performed slightly better than NSGA2 for WDN design. They also investigated the application of MOEAs for obtaining the Pareto optimal curves considering total cost, surplus head, and resiliency of a WDS (Farmani et al. 2005b). Perelman et al. (2008) developed a new MOEA based on cross entropy and compared its performance against NSGA2. The method was found to be robust and superior to NSGA-II algorithm. Zheng et al. (2014a) developed a method for solving multi-objective optimization problem of WDN design based on the graph-decomposition technique. In their method, NSGA-II was firstly employed to optimize the sub-networks separately, thereby producing an optimal front for each sub-network. Then, another NSGA-II implementation was used to drive the combined sub-network front (an approximate optimal front) towards the Pareto front for the original complete WDN. Another approach used in the literature for constructing more efficient search tools is hybridizing the algorithms and combining the power of different methods. Some efforts have been made employing this approach toward the least-cost design problem of WDNs (e.g. PSO–HS by Geem 2009; hybrid discrete dynamically dimensioned search, HD–DDS, by Tolson et al. 2009; GA–LP by Cisty 2010 and Haghighi et al. 2011; SA-TS by Reca et al. 2008; PSF–HS by Geem and Cho 2011; PSO by Spiliotis 2014; DE–PSO by Sedki and Ouazar 2012; and GA–PSO by Jinesh Babu and Vijayalakshmi 2013). However, there have been less hybridized works for multi-objective WDN design problems. Keedwell and Khu (2006) hybridize cellular automaton and genetic approach for multi-objective design of WDN and showed that the new method, called as CAMOGA, outperforms the NSGA2. Another hybrid method was proposed by Vrugt and Robinson (2007), called a multialgorithm genetically adaptive multiobjective (AMALGAM). AMALGAM simultaneously employs four different algorithms within a unified framework, including NSGA2, PSO, adaptive metropolis search (AMS), and DE. The computational results over some benchmark test functions showed that the hybrid method provides an improvement approaching a factor of 10 over current optimization algorithms for more complex and higher dimensional problems. Wang et al. (2014a) compared two hybrid methodologies, low-level hybrid algorithm (LLHA) and high-level hybrid algorithm (HLHA) for design of water distribution systems. Applications to four case studies of increasing complexity showed that for the small and intermediate problems, HLHA produces better Pareto fronts; but when the network complexity increases, LLHA outperforms. di pierro et al. (2009) tested two hybrid MOEAs: ParEGO and LEMMO on a medium-size, and a large-size WDN design problem and reported that hybrid algorithms are superior to the PESA2 algorithm. The authors however reported that improving the efficiency of two hybrid optimization methods against PESA2 was at the expense of degrading the quality of optimal fronts. Raad et al. (2009) applied AMALGAM, NSGA2, NSGA2-JG, and a greedy algorithm for benchmark WDN design problems and stated that AMALGAM demonstrated the best performance overall compared to three other MOEAs across three small and medium size network design problems. Wang et al. (2014b) compared the AMALGAM and NSGA-II on a set of well-known benchmark problems and showed that AMALGAM outperforms NSGA-II for the small and medium size problems, but for the large networks, the hybrid method loses its adaptive capabilities and its performance degrades. Zheng et al. (2014b) proposed a self-adaptive multi-objective differential evolution (SAMODE) algorithm that is a hybridization of differential evolution (DE) and nonlinear programming (NLP) techniques, which outperformed NSGA2 in three different case studies. Recently, Wang et al. (2014b) attempted to explore the best-known approximations of the global Pareto fronts (PFs) for a range of well-known benchmark problems. They compared five MOEAs including NSGA2, AMALGAM, Borg, ε ‐ MOEA, and ε ‐ NSGA2 with each other across different sizes of problems and reported that there is no absolute superior algorithm among the considered MOEAs. They also concluded that NSGA2 is a suitable choice, as it produced overall better results when all benchmark problems are considered.

Most MOEAs like those enumerated above treat a multiobjective optimization problem (MOP) as a whole and generally build upon nondomination concept for evaluating the solution quality during search. MOEA/D is an alternative approach for solving multi-criteria problem, which is fundamentally different from other commonly used MOEAs. Instead of non-dominance criterion, this approach is based on the decomposition of the main multiobjective problem into several single objective subproblems, which they are solved collaboratively and simultaneously. Each single objective subproblem is minimized by the information just from its neighboring subproblems. This gives the advantage of lower computational complexity at each generation than the Pareto dominance based algorithms.

Compared to the Pareto dominance based MOEAs which have difficulties for fitness assignment and keeping diversity in the population, MOEA/D framework easily handles these tasks because it solves several optimization subproblems rather than directly optimizing a multiobjective optimization as a whole (Zhang and Li 2007). Despite these advantages, it has not been widely used in multiobjective optimization problems yet and there is little effort within the environmental and water resources engineering applications. As far as the author knows, to date this method has not been used in the context of WDN design problems. The work presented here contributes towards developing a new hybrid MOEA combining harmony search (HS) and genetic algorithm (GA) within the decomposition strategies for multi-objective design of WDSs. The hybrid method applies the HS and GA operators for enhancing the local search capabilities and uses the MOEA/D framework for the global search and maintaining the diversity in the population. The efficiency and reliability of the new hybrid algorithms is compared with those of two well-known and widely used Pareto dominance algorithms: NSGA2 and SPEA2 across four different WDN design problems with the aim of seeking the superior method and investigating the credibility of the MOEA/D approach.

2 Descriptions of MOEAs Considered

The concept of non-domination is used in most of MOEAs to sort the population according to the values of objective functions. Some examples of well-known MOEAs which uses non-dominance sorting criteria for generating Pareto-optimal solutions are PAES, microGA, NPGA, MOPSO, SPEA2, and NSGA2. We selected NSGA2 and SPEA2 among this group of MOEAs to compare them with the decomposition approach for solving MOPs.

2.1 Non-Dominated Sorting Genetic Algorithm (NSGA2)

NSGA2 is probably the most popular MOEA among the evolutionary algorithms developed so far. It is a fast elicit EA based on genetic algorithm which uses the non-domination and crowding distance (Deb et al. 2000) criteria for sorting the population.

2.2 Improving the Strength Pareto Evolutionary Algorithm (SPEA2)

SPEA2, developed by Zitzler et al. (2001), is an improved version of SPEA in which non-dominated solutions are maintained in a solution archive and updated in each generation by new non-dominated solutions. In comparison with the initial version, SPEA2 defines a new fitness assignment strategy in which both nondominated and dominated solutions affect the fitness value. In addition, it uses the K Nearest Neighbourhood (KNN) technique as the second criterion of population sorting. Furthermore, instead of archive truncation, an approach based on density information is used for controlling the size of the solution archive. This algorithm is known as one of the state-of-the-art MOEA used for performance assessment of new algorithms.

2.3 Multiobjective Evolutionary Algorithm based on Decomposition (MOEA/D)

MOEA/D (developed by Zhang and Li 2007) decomposes a MOP into a number of scalar optimization subproblems and they are optimized simultaneously (Fig. 1a, b). A weighting vector is defined for each subproblem and objective functions are aggregated to a single objective function using this vector. The number of subproblems is usually assumed equal to the population size and therefore each member of the population is representative of a solution generated by an aggregation vector. Each supproblem theoretically explores only one solution of the Pareto front at the end of the search. At each generation, the population is composed of the best solutions found so far for each subproblem. The neighbourhood similarity among the subproblems is defined based on the distance between the weighting vectors of subproblems. During the search, the solution of each subproblem is generated by the collaboration of the neighbouring members as illustrated in Fig. 1c. We called this task as the co-operation phase. Furthermore, the solution of neighbour subproblem(s) is suggested to the current subproblem (Fig. 1c) with its own aggregation vector and if the neighbour’s solution is better than the subproblem solution, it is replaced by the current one. We called this task as the competition phase. Both co-operation and completion tasks are performed for all subproblems. Therefore, there is an exchange of information among the neighbours in MOEA/D and each subproblem (i.e., scalar aggregation function) is optimized by using information only from its neighboring subproblems. Zhang and Li (2007) reported that MOEA/D has lower computational complexity at each generation than NSGA-II and has better performance according to the experimental results of well-known benchmark optimization tests. Details of the MOEA/D method and the main steps are described in the following section.

Fig. 1
figure 1

a) Decomposition of a multi-objective optimization problem by the weighted sum method, b) Decomposition of a multi-objective optimization problem by the weighted p-norm method, c) The evolutionary search of the MOEA/D approach

Full size image

2.3.1 General Framework of MOEA/D

General form of a multiobjective problem can be expressed as:

$$ \begin{array}{c}\hfill Min\kern0.24em \overrightarrow{F}(x)={\left[{f}_1(x), \dots,\;{f}_n(x)\right]}^T\hfill \\ {}\hfill \mathrm{Subject}\ \mathrm{t}\mathrm{o}\ x\in D\hfill \end{array} $$
(1)

where D is the decision variable space, F : D → R n consists of n scalar objective functions and R n is called the objective space. The above optimization problem can be decomposed into m scalar optimization subproblems. The task of decomposition can be carried out by different approaches (Zhang and Li 2007). We used herein the Tchebycheff method. Let w 1, … , w m be a set of uniformly distributed weight vectors and z* be a reference vector including the ideal values of the objective functions. In Tchebycheff method, the scalar optimization problem for a weight vector w is in the form:

$$ \begin{array}{c}\hfill Min\kern0.24em {g}^{te}\left(\left.x\right|w,{z}^{*},p\right)={\left\Vert F(x)-{z}^{*}\right\Vert}_{w,p}\hfill \\ {}\hfill \mathrm{Subject}\ \mathrm{t}\mathrm{o}\ x\in D\hfill \end{array} $$
(2)

where z* = (z *1 , … , z * n )T is the ideal point, i.e., z * i  = min{f i (x)|x ∈ D} for i = 1, … , n when the goal is minimization and ‖. ‖ w,p denotes the weighted p-norm of a vector. This norm is mathematically defined as:

$$ {\left\Vert F(x)-{z}^{*}\right\Vert}_{w,p}=\sqrt[p]{{\displaystyle \sum_{i=1}^n{w}_i{\left|{f}_i(x)-{z}^{*}\right|}^p}} $$
(3)

The extreme value of the p th norm is used in this study so that its value when p → ∞ is:

$$ {\left\Vert F(x)-{z}^{*}\right\Vert}_{w,p}=\underset{1\le i\le n}{ \max}\left\{{w}_i\left|{f}_i(x)-{z}_i^{*}\right|\right\} $$
(4)

Therefore, the objective function of the j th scalar subproblem is in the form:

$$ Min\kern0.24em {g}^{te}\left(\left.x\right|{w}^j,{z}^{*}\right)=\underset{1\le i\le n}{ \max}\left\{{w}_i^j\left|{f}_i(x)-{z}_i^{*}\right|\right\} $$
(5)

where w j = (w j1 , … , w j n ). MOEA/D minimizes all these m objective functions simultaneously in a single run. It is noticeable that the optimal solution of g te(x|w i, z*) should be close to that of g te(x|w i, z*) if w i and w j close to each other. Therefore, any information about these g te s with weight vectors close to w i should be helpful for optimizing g te(x|w i, z*). This is the main feature of MOEA/D framework.

In MOEA/D, a neighbourhood of aggregation vector w i is defined as a set of its several nearest aggregation coefficient vectors in {w 1, … , w m}. The neighbourhood of i th subproblem includes all subproblems with the aggregation vectors from the neighbourhood of w i. The population consists of the best solutions found so far for each subproblem. As mentioned earlier, for optimizing a subproblem in MOEA/D only the current solutions of neighboring subproblems are exploited.

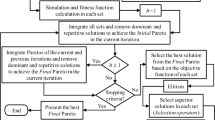
The main stages of this algorithm are shown in Fig. 2 and are summarized as follows:

Fig. 2
figure 2

The main stages of the MOEA/D approach

Full size image
  1. Stage 1

    Initialization

    1. 1.1

      Set E p  = ∅ where E p is the archive of the estimated Pareto front

    2. 1.2

      Generate uniformly the set of w 1, … , w m and after calculating Euclidian distance among them, for each i = 1, … , m, set A(i) = {i 1, … , i Q }, and define \( {w}^{i_1}, \dots,\;{w}^{i_Q} \) as the Q closest weight vectors to w i.

    3. 1.3

      Generate an initial population x 1, … , x m and evaluate their objective functions.

    4. 1.4

      Initialize the ideal vector z

  2. Stage 2

    Updating (main loop)

    For i = 1, … , m:

    1. 2.1

      Do the co-evolution task: generate a new solution vector y by cooperating the neighbour solutions in \( \left\{{x}^{i_1}, \dots,\;{x}^{i_Q}\right\} \)

    2. 2.2

      Update the ideal vector z: For each j = 1, … , n, if z(j) < f j (y), then set z j  = f j (y).

    3. 2.3

      Do the competition task and update the current solution i: for each index j ∈ A(i), if g te(y|w j, z) < g te(x j|w j, z), then set x j = y and F(x j) = y

    4. 2.4

      Update E p : Add y to E p and remove the dominated vectors

  3. Stage 3

    Check the stopping criteria

    If stopping criteria is met, then stop; otherwise go to the stage 2.

    In the co-evolutionary stage (stage 2.1), different approaches can be used to generate a new solution vector y. Here we proposed two methods, one based on the genetic algorithm operators and the other harmony search operators, which are briefly described as follows:

    1. Method a

      Genetic operators

      1. a.1

        Select randomly two vectors y 1 and y 2 among Q neighbours of the solution vector x i: {x 1, x 2 … , x i, … , x Q}

      2. a.2

        Generate a new solution vector y = (y 1, y 2, … , y n ) by crossover operator: y = Crossover(y 1, y 2)

      3. a.3

        Adjust the new solution by mutation operator if rand < P m (P m is the mutation probability):

        For j = 1 : μ, do:

        $$ {y}_{M(j)}={y}_{M(j)}+\varDelta\;.\;N\left(0,1\right) $$

        where μ is the number of variables that will be mutated, and its value depends on the mutation rate, R m . M is a vector including the indices of variables that randomly are mutated. The parameter Δ is called the step size and its value is deemed as a percentage of the variable limits of y j ; and N(0, 1) is a random number generated using a zero-mean normal distribution and having a standard deviation one.

    2. Method b

      Harmony search

      1. b.1

        Generate randomly a new solution y = (y 1, y 2, … , y n )

        For j = 1 : nVar, do:

      2. b.2

        If (rand > HMCR), replace y j by a value randomly chosen among Q neighboured solutions of the solution vector x i ˗ i.e. the set {x 1 j , x 2 j  … , x i j , … , x Q j }.

      3. b.3

        Else if (rand > PAR), adjust the value of variable y j as:

        $$ {y}_j={y}_j+Fw.\;N\left(0,1\right) $$

        where nVar is the number of decision variables, Fw is called “band width” and its value is assumed as a percentage of the variable limits of y j . HMCR and PAR are the main parameters of harmony search algorithm (Geem et al. 2001), called as ‘harmony memory consideration rate’ and ‘pitch adjustment rate’ respectively.

        In method b, step 1 does the task of exploration and step 2 works out for both exploration and exploitation based on the size of the bandwidth, Fw. The performance of step 3 depends on the size of Fw. A large value for Fw is assumed in the first iteration and then during the next iterations it is adaptively decreased by a multiplicative factor. Using this approach, step 3 helps for better exploration in early iterations and then it moves towards improvising the exploitation task as reaching to the last iterations.

3 Performance Metrics

Different comparative metrics are introduced in the literature to quantitatively compare the performance of MOEAs. To evaluate the results of MOEAs, we used two metrics: Hyper Volume (HV), and two-set coverage (CS), which are suitable measures when the global Pareto front is unknown.

3.1 Hyper Volume (HV)

This metric computes the area enveloped by the optimal solutions found with respect to a typical point and is a criterion of both convergence and diversity. The reference point can be considered as a vector of the worst objective function values. This metric is mathematically defined as (Van Veldhuizen 1999):

$$ HV= volume\left({\displaystyle {\cup}_{i=1}^n{v}_i}\right) $$
(6)

where v i is the hyper-volume constructed by the solution i and the reference point in the objective function space.

3.2 Two-Set Coverage (CS)

This metric, introduced by Zitzler et al. (2000), is used for pairwise comparison of two Pareto sets when the true Pareto front is unknown. If X′ and X″ are two Pareto sets and is considered as the non-domination solutions in X′ ∪ X″, then CS metric is defined as a mapping from the ordered pair (X′, X″) to the interval [0, 1] using the following formula:

$$ CS\left({X}^{\prime },{X}^{{\prime\prime}}\right)=\frac{\left|\left\{{a}^{{\prime\prime}}\in {X}^{{\prime\prime} };\exists {a}^{\prime}\in {X}^{\prime }:{a}^{\prime}\succeq {a}^{{\prime\prime}}\right\}\right|}{\left|X\right|} $$
(7)

If all solutions in X′ are equal to those in X″ or dominate them, then, by the above definition, CS metric is equal to one. A CS value of 0 implies the opposite. Ordinarily, both CS(X′, X″) and CS(X″, X′) need to be considered, because the set intersections are not necessarily empty.

4 Multi-Objective Design of WDNs

4.1 Mathematical Formulation

‘Network cost’ and ‘reliability’ are two major objectives that have frequently been used in the multi-objective design of water distribution systems. The same criteria are taken as the objective functions in this study, with the ‘network resilience’ indicator, proposed by Prasad and Park (2004), as the reliability measure. The first objective function involves economic considerations and the latter one provides a measure for assessing both surplus head and reliable loops in the networks with various sizes. Therefore, the objective functions can be written as:

$$ \begin{array}{l} Minimize\kern0.24em Cost={\displaystyle \sum_{i=1}^nf\left({D}_i\right).{L}_i}\\ {} Maximize\;{I}_n=\frac{{\displaystyle \sum_{j=1}^m{U}_j{Q}_j\left({H}_j-{H}_j^l\right)}}{\left[{\displaystyle \sum_{r=1}^R{Q}_r{H}_r}+{\displaystyle \sum_{i=1}^{np}\frac{P_i}{\gamma }}\right]-{\displaystyle \sum_{j=1}^m{Q}_j{H}_j^l}}\end{array} $$
(8)

where f(D i ) = the cost function for the pipe with diameter i per unit length, n and L i  = number of pipes and length of the pipe i, respectively. I n  = the network resilience, m = number of nodes, U j  = the uniformity of the node j, Qj = demand in node j, Hj = pressure head of the node j, H l j = minimum required pressure head, R = number of reservoirs, np = number of pumps and Pi = power supplied by the pump i. In the above formulation, the uniformity is defined as:

$$ {U}_j=\frac{{\displaystyle \sum_{i=1}^n{D}_i}}{n_j\times \max \left({D}_i\right)} $$
(9)

The constraints of the optimization problem include:

  1. 1)

    The continuity equation should by satisfied in each junction node:

    $$ {\displaystyle \sum {Q}_{in}}-{\displaystyle \sum {Q}_{out}={Q}_d} $$
    (10)

    where Q in and Q out are inflow and outflow of a node, respectively, and Q d is the demand of the node.

  2. 2)

    Head loss constraint that can be written for each loop as:

    $$ \begin{array}{cc}\hfill {\displaystyle \sum_{j\in Loop\;i}\varDelta {h}_j=0}\hfill & \hfill \forall i\in {n}_l\hfill \end{array} $$
    (11)

    where Δh j is the head loss in pipe j, and n l is the number of loops of the network. In each pipe, the head loss is a function of discharge, pipe diameter, and roughness coefficient of the pipe. Head loss is usually calculated using empirical equations such as the Darcy–Weisbach or the Hazen–Williams equation.

  3. 3)

    The pressure constraint between a minimum and maximum value is written as:

    $$ \begin{array}{cc}\hfill {H}_j^l\le {H}_j\le {H}_j^u\hfill & \hfill \forall j=1,2,\dots, n\hfill \end{array} $$
    (12)

    where H j is the pressure head at node j; H l j is the minimum required pressure head at node j; H u j is the maximum allowed pressure head at node j; and n is the number of demand nodes in the system.

  4. 4)

    The pipe diameter must be selected among a set of discrete commercial sizes:

    $$ \begin{array}{cc}\hfill {D}_i\in \left\{A\right\}\hfill & \hfill \forall i=1,2,\dots, k\hfill \end{array} $$
    (13)

    where D i is the diameter of pipe i, and {A} denotes the set of commercially available pipe diameters, and k the number of pipe sizes.

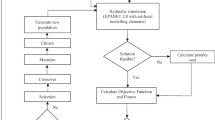
Using the penalty function method, the above constraint optimization model is easily converted to an unconstraint case. For this purpose, the pressure violations from the maximum and minimum values are added to the “cost” objective function after multiplying by a large number, assumed equal to 106 in this study. The continuity and head loss constraints are automatically satisfied using a simulator engine, (EPANET2.0 software herein).

4.2 Experimental Tests on WDNs

To justify the use of MOEA/D approach in solving WDN design problems, four relatively large size design problems were considered in this work, which are briefly described in the following.

4.2.1 Pescara Network (PES)

As shown in Fig. 3a, this network includes 99 pipes, 68 nodal demands and three reservoirs with constant head between 53.08 and 57.00 m. The pipes are made of cast iron with a Hazen-Williams coefficient of 130. The minimum head requirement is assumed as 20 m for all nodal demands and the maximum pressure heads of the nodes in this network can be found in http://www.exeter.ac.uk/benchmarks-pareto-fronts. Maximum velocity in pipes is 2 m/s. The available commercial pipe sizes with corresponding unit costs for the PES network is presented in Table 1.

Fig. 3
figure 3

Scheme of a) Pescara water distribution network (PES), b) Saemangeum irrigation network (SIN), c) Balerma irrigation network (BIN), d) West zone water distribution network (WZN)

Full size image
Table 1 Commercial diameters and corresponding unit costs of PES, SIN and BIN networks
Full size table

4.2.2 Saemangeum Network (SIN)

SIN network is an irrigation water supply system, located in the Saemangeum region, southern part of the South Korea. This network consists of 365 pipes and a reservoir with constant head in 35 m. As shown in Fig. 3b, some parts of the network, has looped configuration and some others are branched. The Hazen-Wiliams roughness coefficient is 100 for all the pipes. The total costs per length of the pipes are presented in Table 1 for different pipe diameters. The minimum and maximum pressure requirements for the nodal demands are assumed as 10 and 35 m respectively and the permissible range of flow velocity in pipes is between 0.01 and 2.5 m/s.

4.2.3 Balerma Irrigation Network (BIN)

This network is another large-size water supply system for irrigation which includes 454 PVC pipes, 443 nodal demands and four reservoirs with constant heads at the elevations 112, 117, 122 and 127 m. All pipes are assumed to have a Darcy-Weisbach coefficient of 0.0025 and the minimum pressure head in all nodal demands is 20 m. The commercial pipe sizes with their corresponding unit costs are presented in the Table 1. Figure 3c shows the scheme of the Balerma network.

4.2.4 West Zone Network (WZN)

The largest network studied in this work is a water distribution system in UK consisting of 632 pipes, 535 demand nodes and a reservoir with constant head at 146.68 m, introduced by Savic et al. (2000). Each pipe can select a diameter among 20 discrete values of commercial sizes and this leads to a large search space with 20623 pipe size combinations. The minimum pressure head requirement for all demand nodes is equal to 15 m and the costs per length of the pipes are selected the same as in Keedwell and Khu (2006). Figure 3d depicts the layout of WZN.

5 Experimental Results and Discussion

This section demonstrates the computational results obtained by executing the selected MOEAs for the four water distribution networks introduced in the previous section.

The MOEAs were coded in MATLAB and coupled with EPANET 2.0 hydraulic solver to estimate the WDS resilience and necessary hydraulic constraints during evaluating different network designs. Shown in Table 2 are the size of the search space, the number of decision variables and population size, as well as the number of function evaluations (NFE), number of iterations (NI) and pipe diameter options, for each of the four benchmark networks. The parameters of NSGA2 and SPEA2 were set based on the widely used settings in the literature, while parameter values for the MOEA/D algorithms were chosen based on both values in the literature and the results of several trial runs. The parameter values are shown in Table 3. Each MOEA was run 10 times independently to solve each problem.

Table 2 The number of function evaluation and sizes of the search space for WDN design problems
Full size table
Table 3 Parameters used in multi-objective evolutionary algorithms (MOEAs)
Full size table

The task of optimization was carried out on Intel(R) Core(TM) i7-3770 CPU @ 3.4GHz with 8GB RAM.

Firstly, we considered the minimum values of objective functions in each generation as the “ideal point” in MOEA/D, but the results showed that this strategy is not efficient. Therefore, a fixed global ideal point was considered for each of the WDN design problems considering the objective function values (zero value for the cost and resiliency index equal 1). By this approach, MOEA/D could move successfully towards an evenly distribution of solutions along the Pareto front.

The results of a typical run of each algorithm are shown in Fig. 4. As it can be visually observed, MOEA/D methods generally provided better Pareto fronts than two other well-known algorithms for all studied networks. SPEA2 outperforms NSGA2 for the PES network, i.e. the smallest network, however, for the larger problems, its performance becomes local and cannot find the tails of Pareto front like NSGA2 and two others as the complexity of the problem increases. It is obvious that MOEA/D frameworks and especially MOEA/D-HS could provide large and very even distribution of representative Pareto optimal solutions for all considered networks and NSGA2 presents the median results.

Fig. 4
figure 4

The Pareto fronts found for network problems: a) PES network, b) SIN network c) BIN network, d) WZN network

Full size image

In order to compare the algorithms quantitatively, two performance metrics described in Section 3 were used. The last column of Table 4 shows the average values of the HV metric obtained by 10 times performing the algorithms for each of the benchmark network problems. This metric shows the quality of the solutions in terms of both diversity and non-domination strength. Higher values of HV metric mean better performance. According to the contents of last column, NSGA2 gives slightly better results than SPEA2 for all network problems except the smallest one. This superiority is attributable to the ability of NSGA2 for maintaining the diversity rather than non-domination strength (Fig. 4). However, both algorithms underperform the MOEA/D methods and MOEA/D-HS outperforms the others for all network problems based on the HV values.

Table 4 Comparison of multi-objective algorithms using the HV and two-set coverage (CS) metrics
Full size table

A pairwise comparison was also carried out among the results of the algorithms based on the CS metric for all four experimental networks. The results are represented in Table 4. This metric emphasizes on the non-domination strength and by looking at the table contents, it can be realized that when the non-domination criterion is considered SPEA2 slightly outperform NSGA2 for all problems except SIN network. The pairwise comparison (diagonal values in this table) again shows that MOEA/D frameworks outperforms NSGA2 and SPEA2 for the considered WDN design problems. According to the the CS values, MOEA/D-HS slightly underperform MOEA/D-GA for the WZN problem, but it has better performance for three other networks. This confirms the general superiority of MOEA/D-HS when the non-domination criterion is considered as well, and also demonstrates the high capability of the harmony search for the local search. These results are consistent with those obtained by Yazdi et al. (2014) where NSGA2 is compared with Nondominated Sorting Harmony Search (NSHS) algorithm for the sewer pipe network application. They reported that NSHS could not find the tails of the Pareto front, as it suffered from its inability to preserve the diversity of the population during the evolutionary search steps. MOEA/D provides a platform for the local optimizer to search all parts of the search space through the aggregation vectors. This brings the advantage of generating wide Pareto fronts with extreme points and keeping the diversity in the solutions. As demonstrated in Fig. 4 and Table 4, hybridizing HS with MOEA/D in this study keeps both the quality and diversity of solutions and provides considerably better performance for solving multi-objective problems than non-dominance -based MOEAs.

At the end, to improve the performance of MOEA/D, following ideas are recommended to investigate in future research:

  • Although the aggregation weight vectors are kept fixed in this study, the results of the algorithm is sensitive to these values and thus giving adaptive values to them during the search might be more efficient.

  • MOEA/D is a very flexible framework to adapt different search operators. Other successful optimizer such as PSO and DE can be hybridized within the MOEA/D platform and their capabilities are explored for the large-scale WDN design problems.

  • The search ability of the MOEA/D algorithm depends also on the choice of a scalarizing function. The idea of using simultaneously different types of scalarizing functions can be investigated.

  • The performance of the approach can also be examined by developing strategies for allocating different computational resources to different subproblems during the search.

6 Conclusions

Multiobjective evolutionary algorithms based on decomposition were developed herein for the large-scale WDN design problems and their results were compared with those of non-dominance based MOEAs: NSGA2, and SPEA2. MOEA/D algorithms give noticeably better performance than NSGA2 and SPEA2 with regard to the both non-domination and diversity criteria. This framework divides the computational resources in all parts of the search space through the aggregation vectors and this enables MOEA/D algorithms to give better diversity and well-spread Pareto fronts with extreme point as demonstrated in Fig. 4 and Table 4. This is a major advantage of the MOEA/D compared to the Pareto dominance algorithms particularly for complicated optimization problems with large number of decision variables where they often fail to preserve the diversity and trap to partial-local Pareto fronts. MOEA/D also provides a flexible platform for employing local optimizers for the reproduction new solutions during the search. This study successfully exploited the local search capability of harmony search operators within the MOEA/D framework and as illustrated, the hybrid method outperformed the MOEA/D-GA, NSGA2 and SPEA2 algorithms.

Overall, the results of this study demonstrate that the MOEA/D framework can be successfully used for solving large-scale multiobjective design problems of WDS with greater efficiency than non-dominance based MOEAs. There are much potential to achieve more efficient and sophisticated implementations of MOEA/D. Some ideas were enumerated in this work and can be investigated in future research.