1 Introduction

In recent decades, use of optimization techniques has attracted the attention of many researchers to derive optimal reservoir operation policies. The strategies which optimize the use of water resources in the system would need to use the maximum of available resources to achieve optimum operation of the reservoir. To achieve this task, different optimization approaches such as linear programming (LP) (Ponnambalam et al. 1989; Blanchini and Ukovich 1993) dynamic programming (DP) (Yakowitz 1982; Foufoula-Georgiou and Kitanidis 1988; Mousavi et al. 2005), stochastic dynamic programming (SDP) (Stedinger et al. 1984; Alaya et al. 2003; Umamahesh and Sreenivasulu 1997; Galelli and Soncini-Sessa 2010) and evolutionary algorithms (EAs) (Cheng et al. 2008; Jian-Xia et al. 2005; Nagesh Kumar et al. 2006; Labadie et al. 2012; Afshar et al. 2015; Ahmadi et al. 2015; Bai et al. 2015; Chiang and Willems 2015; Porse et al. 2015) have been used in various studies. Yeh (1985) offered a comprehensive review of reservoir operation model, with emphasis optimization methods. Wurbs (1993), Chau and Albermani (2003), Labadie (2004), and recently, Rani and Moreira (2010) offered an extensive review in connection with various optimization methods; their research focused on optimizing the exploitation of storage system.

Although LP, DP, and SDP optimization models are useful tools in identifying optimal policies for operation of reservoir, there are some computational assumptions in these models which reduce the efficiency and flexibility of them (Momtahen and Dariane 2007). In use of LP, the main limitation is that objective function and constraint must be linear. DP and SDP models possess curse of dimensionality limits, in addition storage and inflow discretization of reservoir (Rani and Moreira 2010). Meanwhile, EAs due to the pace and accuracy in solving complex problems and high popularity owing to being independent on the type of problem are more popular.

Genetic algorithm (GA) and its different types are the most promising EAs techniques and they have wider applicability due to their flexibility and performance in optimization of complex systems (Reddy and Nagesh Kumar 2006). At first time, GA was introduced in the water resource systems by Esat and Hall (1994). Nagesh Kumar et al. (2006) used GA in optimal operation of a reservoir and declared that GA can be used to optimize use of water resources operation to reach maximum profit. Ahmed and Sarma (2005) developed a GA model to derive optimal operating policies and compared its performance with SDP. They indicated that GA benefits are more than SDP to obtain optimal operation policies. GA is well known as a beneficial method to operate reservoirs (Oliveira and Loucks 1997; Sharif and Wardlaw 2000), and its successfully application has been reported in some of issue in optimal operation of reservoir (Labadie 2004; Esat and Hall 1994).

Despite EAs advantages, the main disadvantage of these algorithms is that they cannot achieve global optimal solution and premature convergence in some cases. New EAs are being developed to overcome these problems. Imperialist competitive algorithm (ICA) is new, which was introduced by Atashpaz-Gargari and Lucas (2007). It has been used on various problems such as optimization of thermal energy transfer (Yousefi et al. 2012), classification (Mousavi Rad et al. 2012), and recognition of faces (Oskuyee 2012). Furthermore, Cuckoo Optimization Algorithm (COA) as one of the newest EAs has been recently introduced. Its application evaluated in some fields such as industrial engineering (Mellal et al. 2012) and smart electrical networks (Mokhtari Fard et al. 2012).

The reservoirs are one main resources for water supply in many regions. Optimal operation of reservoir is an effective policy that can widely help to water management. This issue is a hardness of optimization problem, which needs to use strong methods to solve it. Therefore, experts have been ever searching for appropriate optimization procedure. Use of powerful EAs being able to improve objective functions even slightly, leads to comprehensive advancement in the relevant benefits or costs. Based on “no free-lunch” theorem it is impossible for one EA to optimally solve all optimizing problems (Wolpert and Macready 1997). Hence, we assess the capability of COA and ICA in water resources management that reveals robustness of them. Owing to the results, COA and ICA are recommended for other optimization problems associated with water resources issues such as optimal cropping pattern or optimal exploitation of aquifers and etc. Therefor purpose of this paper is to assess the ability of ICA and COA to extract optimal operation policies of reservoir for the first time.

2 Materials and Methods

2.1 Genetic Algorithm

GA is a special kinds of EAs, which is based on natural selection mechanism. GA is a global method for solving different types of optimization problems, and like the majority of EAs, it works on populations of solutions called population-by-population (Goldberg and Kuo 1987). GA process form from several steps. Firstly, initial population is generated consisting of various solutions randomly. Next population is produced to improve objective function during an iterative process. At each step, chromosomes of current population are selected to create next generation. It should be considered that the selection probability of chromosomes, which showed more appropriate efficiency, is more than others. Selected chromosomes generate next population based on two genetic operator: crossover and mutation. In crossover, generating two new chromosomes is performed by changing genes between them. Mutation operator is used to change in chromosomes and their genes alteration to create diversity in population. Generating process continues in next steps to achieve appropriate result.

2.2 Imperialist Competitive Algorithm

As it mentioned, ICA was introduced by Atashpaz-Gargari and Lucas (2007). This algorithm has a population-by-population approach; similar to many other evolutionary algorithms. ICA simulates political–social evolution. At the beginning of ICA process, a population of initial solutions (countries) is generated (like as chromosome in GA). More powerful countries are considered as imperialists and others as colonies. For each optimization problem with N decision variables (these variables could be culture, language etc.) each country is defined as an array of 1 × N as follow:

$$ country=\left[{\mathrm{V}}_1,{V}_2,\dots {V}_N\right] $$
(1)
$$ \cos t=F(country) $$
(2)

Where V1, V 2, … V N are decision variables, F is objective function and cost is value of F.

In the next step, which is known as assimilation policy, the imperialists attract colonies in their empires (colonies are affected by culture and the language of imperialists). In this step, colonies with θ degree of deviation, and x units move to imperialists. This deviation causes a more comprehensive search in decision space (Fig. 1). x and θ are random numbers with uniform distribution.

Fig. 1
figure 1

Moving empire’s colonies toward the imperialist

Full size image
$$ x\sim U\left(0,\beta \times d\right) $$
(3)
$$ \theta \sim U\left(-\gamma, \gamma \right) $$
(4)

where β = a number greater than one which makes colonies close to imperialists from two sides, d is a distance between imperialists and colonies and γ is a parameter which determines the amount of deviation from the original direction.

In each generation, some countries which do not have considerable progress, encounter with revolution. Revolution operator prevents trapping algorithm in local optimum. After moving colonies toward imperialists or revolution event, it is possible that one of the colonies gets better situation than its imperialist. It could exchange colony and imperialist’s position. Imperialistic competition is the most important step in ICA, in which all the empires try to increase the number of their colonies. This process occurs by losing the weakest colony from the weakest empire’s domain and joining to stronger empires. Joining colonies to stronger empires takes place based on probability. This probability is proportional in accordance with each imperialist strength plus percentage of arbitrary from average power of colonies.

$$ T.{C}_n= Cost\left( imperiaalis{t}_n\right)+\xi\;mean\left\{ Cost\left({\mathrm{colonies}\ \mathrm{of}\ \mathrm{empire}}_{\mathrm{n}}\right)\right\} $$
(5)

where T. C n = total cost of the n th empire, and ξ = a positive number less than one, which is a user-defined parameter. Figure 2 shows the process of attracting colonies by empires with relevant probability (P). As shown in Fig. 2, empire No.1 is the weakest empire and empires No.2 to N are in competition to attract the weakest colony. With specified probability, a mechanism similar to roulette wheel has been used for selecting target empire of the weakest colony. This process continues until one of the stopping criteria would fulfill. Figure 3 shows the flowchart of ICA.

Fig. 2
figure 2

Imperialistic competition; empires competition to attract the weakest colony

Full size image
Fig. 3
figure 3

Flowchart of the ICA algorithm

Full size image

2.3 Cuckoo Optimization Algorithm

COA is a new evolutionary optimization algorithm for solving nonlinear optimization problems. This algorithm was introduced by Rajabioun (2011) inspired from lifestyle of a bird called cuckoo. In the nature, cuckoos choose nests of other birds to lay their eggs. Cuckoos lay eggs like host birds in their nests and thereby other birds survive their own generation. Nonetheless, cuckoo’s eggs may be recognized and destroyed by the host bird. In such cases cuckoos migrate to places where are more suitable for generation survival and egg-laying. Now, if living area of cuckoo is decision space, each habitat will be a solution for problem. Therefore, the algorithm begins with an initial population of cuckoos that inhabit in different places.

$$ habitat=\left[{\mathrm{V}}_1,{V}_2,\dots {V}_N\right] $$
(6)
$$ \cos t=F(habitat) $$
(7)

Where V1, V 2, … V N = decision variables, F = objective function, and cos t = value of F.

The best habitats were known by calculating their cost. Then in the next step, when eggs are growing and maturing, cuckoos migrate to the nearest current appropriate location for egg-laying. This migration is done in the nature up to a maximum certain distance. This maximum distance is called egg laying radius (ERL) that each cuckoo lays its eggs in this radius randomly. In an optimization problem for variables with upper limit (var hi ) and lower limit (var low ), ELR is calculated by the following equation:

$$ ELR=\alpha \times \frac{\mathrm{Number}\ \mathrm{of}\ \mathrm{current}\ \mathrm{cuckoo}^{\prime}\mathrm{s}\ \mathrm{eggs}}{\mathrm{Total}\ \mathrm{number}\ \mathrm{of}\ \mathrm{eggs}}\left({\operatorname{var}}_{hi}-{\operatorname{var}}_{low}\right) $$
(8)

where α = an integer number which handle maximum value of ERL. Figure 4 shows the concept of ELR.

Fig. 4
figure 4

Egg laying in ELR randomly, central star is the initial habitat of the cuckoo; other stars are the egg’s

Full size image

Because of cuckoos are found in different parts of the decision space, it is difficult to determine that which cuckoo is related to which group. K-means clustering method used for grouping cuckoos to solving this problem. Destination of other groups in the next generation will be a group which has the best relative optimality. Cuckoos do not go through all the ways toward the target in a generation during immigration. They go through only λ percent of the entire way and in this way possess deviation with φ value. λ is a number between zero and one, with a uniform distribution, and φ also has uniform distribution with interval of [−w, w]. Usually, if w is equal to π/6, it will provide necessary convergence to achieve absolute optimum. λ and φ caused a more comprehensive search in the decision space. Figure 5 shows schematic immigration of cuckoos.

Fig. 5
figure 5

Immigration cuckoo to goal habitat

Full size image
$$ \lambda =U\left(0,1\right) $$
(9)
$$ \varphi =U\left(-w,w\right) $$
(10)

There is usually a balance between populations of birds in the nature because of factors such as hunting, lack of food etc. Therefore, in COA, a number of N max controls the maximum number of cuckoos. After several iterations, all cuckoos converge to the point where the most profitable is, and the fewest number of eggs destroys. The point (habitat) would be answer of optimization problem. Figure 6 shows the COA flowchart.

Fig. 6
figure 6

Flowchart of the COA algorithm

Full size image

3 ICA and COA Application in benchmark problem

In this section, for evaluating ICA and COA in optimization issues, two mathematical test functions and a benchmark problem in water scope were considered. GA (as a criteria EAs) was used for optimizing these problems. Ackley (Ackley 1987) and Rosenbrock (Rosenbrock 1960) were regarded as mathematical functions and also operation of four reservoir system as a benchmark problem which was formulated by Chow and Cortes-Rivera (1974).

3.1 Mathematical Function

Ackley and Rosenbrock functions are well-known benchmark in evolutionary optimization issues. Related equations to these two mathematical functions are:

$$ Ackley:\kern0.5em F\left(\overrightarrow{x}\right)=-20. \exp \left(-0.2\sqrt{\frac{1}{n}{\displaystyle \sum_{i=1}^n{x}_i^2}}\right)- \exp \left(\frac{1}{n}{\displaystyle \sum_{i=0}^n \cos \left(2\pi .{x}_i\right)}\right)+20+e $$
(11)
$$ Rosenbrock:\kern1em F\left(\overrightarrow{x}\right)={\displaystyle \sum_{i=1}^{n-1}\left[100{\left({x}_{i+1}-{x_i}^2\right)}^2+{\left({x}_i-1\right)}^2\right]} $$
(12)

General information related to these two functions is shown in Table 1.

Table 1 General information for Ackley and Rosenbrock functions
Full size table

In order to optimize Ackley and Rosenbrock functions, population were considered 20 and 10, respectively. Numbers of iterations for each function were equal to 1000. The results represented that COA has a high ability to find optimal points of mentioned functions and approach to global solution with proper accuracy. ICA results represented suitable performance compared with GA. Abridgement result of running these three mentioned algorithms for Ackley and Rosenbrock functions have been shown in Table 2.

Table 2 GA, ICA, and COA running results for mathematical functions
Full size table

3.2 Four Reservoir Operation

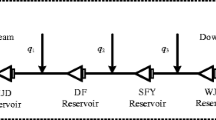
Operation of four reservoir systems is a benchmark problem for reservoir scope. This problem was introduced by Chow and Cortes-Rivera (1974). Schematic of four reservoir systems is showed in Fig. 7. The aim of this benchmark is maximization benefits which obtain from system release. Objective function for this issue is given below:

Fig. 7
figure 7

Schematic of four-reservoir system

Full size image
$$ \begin{array}{cc}\hfill Max\kern0.5em B={\displaystyle \sum_{t=1}^T{\displaystyle \sum_{n=1}^N{b}_{\left(n,t\right)}.{R}_{\left(n,t\right)}}}\hfill & \hfill n=1,2,\dots, N,\;t=1,2,\dots, T\hfill \end{array} $$
(13)

where B = objective function, b (n,t) = benefit of n th reservoir at period t, R (n,t) = release of n th reservoir at period t, T = period and N = number of reservoirs. Reservoir overflow and losses were ignored in this problem. Hence, continuity equation was expressed as follows:

$$ \begin{array}{cc}\hfill {S}_{\left(n,t+1\right)}={S}_{\left(n,t\right)}+{Q}_{\left(n,t\right)}+M.{R}_{\left(n,t\right)}\hfill & \hfill n=1,2,\dots, N,\;t=1,2,\dots, T\hfill \end{array} $$
(14)

where S (n,t + 1) = n th reservoir storage at end of period t, S (n,t) = n th reservoir storage at beginning of period t, Q (n,t) = reservoir n th inflow at period t, and M is a matrix as follows below:

$$ M=\left[\begin{array}{l}-1\kern2em 0\kern2em 0\kern2em 0\\ {}0\kern2em -1\kern2em 0\kern2em 0\\ {}0\kern2em 1\kern2em -1\kern2em 0\\ {}1\kern2em 0\kern2em 1\kern2em -1\end{array}\right] $$
(15)

Release and storage of each reservoir has a specific range. Release upper bounded to be (4, 4.5, 4.5, 8) and for all reservoirs lower bounded is equal to 0.005. In four reservoir systems, initial storage and final storage are equal and their values are (6, 6, 6, 8). In terms of inflow values, benefits which gained from release and maximum permissible storage values are as follows:

To satisfy the constraint of reservoir storage, Eqs. (16), (17), (18) were applied:

$$ \begin{array}{ccc}\hfill Penalty{1}_{\left(n,t\right)}=K{\left[{S}_{\left(n,T+1\right)}-{S}_{\left(n,t \arg et\right)}\right]}^2\hfill & \hfill for\kern1.5em n=1,\dots, N,\kern1em t=1,\dots, T\hfill & \hfill if\kern0.5em {S}_{\left(n,T+1\right)}<{S}_{\left(n,t \arg et\right)}\hfill \end{array} $$
(16)
$$ \begin{array}{ccc}\hfill Penalty{2}_{\left(n,t\right)}=K{\left[{S}_{\left(n,t+1\right)}-{S_{\max}}_{\left(n,t\right)}\right]}^2\hfill & \hfill for\kern1.5em n=1,\dots, N,\kern1em t=1,\dots, T\hfill & \hfill if\kern0.5em {S}_{\left(n,t+1\right)}<{S}_{\min \left(n,t\right)}\hfill \end{array} $$
(17)
$$ \begin{array}{ccc}\hfill Penalty{3}_{\left(n,t\right)}=K{\left[{S}_{\left(n,t+1\right)}-{S_{\max}}_{\left(n,t\right)}\right]}^2\hfill & \hfill for\kern1.5em n=1,\dots, N,\kern1em t=1,\dots, T\hfill & \hfill if\kern0.5em {S}_{\left(n,t+1\right)}>{S}_{\max \left(n,t\right)}\hfill \end{array} $$
(18)

in which Penalty1(n,t) = penalty functions which related to not being equal the storages of beginning and end of operation period, Penalty2(n,t) = penalty functions for becoming less the reservoir storage than minimum storage of reservoir; Penalty3(n,t) = penalty for becoming more reservoir storage than maximum storage of reservoir; K = constants coefficient of penalty function; S (n,target) = desirable volume of i th reservoir at the end of operation period. Meanwhile, in case of exceeds, penalty constraint was added to objective function.

Chow and Cortes-Rivera (1974) reported an optimum solution for this problem using LP with value of 308.26. Murray and Yakowitz (1979) solved this problem using Differential Dynamic Programming (DDP) method, and results showed the value of 308.23, a little less than LP. Bozorg Haddad et al. (2011) reported that optimum solution with LP solver of Lingo software was obtained 308.29. These researchers utilize Honey-Bee Mating Optimization (HBMO) algorithm in addition to LP. They also reported that average objective function for HBMO was 307.50 after 10 runs.

In this paper, ICA, COA and GA were considered with 50 population and 20,000 iterations. Objective function evaluations are approximately one million for each algorithm. ICA is close to global optimum in best condition with 306.76 value. Furthermore, average performance of ICA after 10 runs is 305.11. Also, average of objective function in different runs for COA is 306.90. In addition, COA in best condition has been converged to 307.92. Best, worst, and the average situation of GA as an objective function for explained problem are 302.42, 299.89 and 301.54, respectively. Summarized consequence of ICA and COA after 10 runs with compared to GA are written in Tables 3, 4, 5, and 6.

Table 3 Inflow values (Murray and Yakowitz 1979)
Full size table
Table 4 Values of benefit (Murray and Yakowitz 1979)
Full size table
Table 5 Maximum permissible storage value (Murray and Yakowitz 1979)
Full size table
Table 6 Results of GA, ICA, and COA for four-reservoir system
Full size table

These results showed proximity of ICA and COA to global solution with 99.50 and 99.88 %, respectively. Best convergence for GA is less than 98.09 % as shown in above. Releases and storage volumes obtained from these three algorithms are shown with their global optimum values in Figs. 8 and 9.

Fig. 8
figure 8

Monthly reservoir releases for GA, ICA, and COA

Full size image
Fig. 9
figure 9

Monthly reservoir storage for GA, ICA, and COA

Full size image

4 Case Study

Karun is one of the main rivers in Iran that emanate from Zagros Mountains. It enters to Khuzestan plain in downstream and then runs into to Persian Gulf. In recent decades, the electricity potential production of this river attracted attention of water resources operators and also extensive efforts has been done to actualize this potential. Among these actions, constructing series of Karun dams has been done for flood control and hydropower generation. Karun4 is the highest concrete dam in Iran located downstream of the confluence of Armand and Bazoft rivers and it is placed at 50°: 24ʹ and 31°: 35ʹ longitude and latitude, respectively. Annual average inflow of Karun4 dam is about 6045 million cubic meters (MCM). It aimed to hydropower utilization in Chaharmahal Va Bakhtiari province. In this paper, for operation of Karun4 dam, time series for 30 years (1971–2000) were used. Maximum permissible storage and minimum storage are 2190 and 1141, respectively and also installed power plant capacity (PPC) is 1000 megawatt (MW). The operational policy in reservoir management can be presented via a country in ICA or a habitat in COA. So if we have N (N = Number of population) operational policy, in fact, we will have N countries/habitats within the search space. Evaluation of objective functions leads us to find the best solution (countries/habitat) and presents tendency of solutions to reach near global optimum solution. According to Figs. 3 and 6, each of the proposed EAs can find out the optimal solution after particular iterations.

5 Reservoir Operation Model

Electrical energy is known as one of the friendliest type of energy which compatible with environment. In addition, electricity production by dam’s power plants is known as one of the purest type of energy. Optimal releases from reservoirs always have been important issue for managers and water resources operators. Optimal operation of water resources system is an issue with monthly time step and usually becomes more important in long terms. A policy can be effective which be optimized these resources for a long period to make profits. In this research, operation of reservoir with hydropower purpose was desired. Objective function for optimization issue is defined as follows:

$$ Min\kern0.5em F={\displaystyle \sum_{t=1}^{360}\left(1-\frac{P_t}{PPC}\right)} $$
(19)

And operating model limitations are:

$$ {S}_{\min}\le {S}_t\le {S}_{\max } $$
(20)
$$ 0\le {R}_t\le {R}_{\max } $$
(21)
$$ 0\le {P}_t\le PPC $$
(22)
$$ S{P}_t=\left\{\begin{array}{l}{S}_t+{Q}_t-{R}_t-{S}_{\max}\kern1.5em if\kern1.5em {S}_t+{Q}_t-{R}_t>{S}_{\max}\\ {}0\kern3em if\kern2em {S}_t+{Q}_t-{R}_t\le {S}_{\max}\end{array}\right. $$
(23)

The continuity equation in operation of reservoir is:

$$ {S}_{t+1}={S}_t+{Q}_t-{R}_t-S{P}_t-{L}_t $$
(24)

in which these equations, F = objective function; t = operating time step (monthly); T = duration of operation (360 months); P t = power generated during the period t (MW); PPC = power plant installed capacity (MW); S min = minimum reservoir storage (MCM); S t = reservoir storage in the beginning of period t (MCM); S max  = maximum reservoir storage (MCM); Rt = reservoir release during the period t (MCM); R max = maximum possible reservoir outflow during period t (MCM); SP t  = reservoir overflow during period t (MCM); S t+1  = reservoir storage at the end of period t (MCM); Q t  = river Inflow during the time period t (MCM); L t  = losses due to evaporation and precipitation during period t (MCM).

For calculating losses, Eq. (25) is used.

$$ \begin{array}{cc}\hfill {\mathrm{L}}_{\mathrm{t}}={\mathrm{E}}_{\mathrm{t}}\kern0.5em .\left(\frac{A_t+{A}_{t+1}}{2000}\right)\hfill & \hfill \begin{array}{cc}\hfill \mathrm{f}\mathrm{o}\mathrm{r}\hfill & \hfill \mathrm{t}=1,\dots, \mathrm{T}\hfill \end{array}\hfill \end{array} $$
(25)

In which E t = evaporation from reservoir surface during the period of t (millimeter); A t and A t+1 = reservoir areas at the beginning and end of the period t (square kilometer), respectively.

Also, for calculating power generation, the following equations were used:

$$ \begin{array}{cc}\hfill {P}_t=g.e.\frac{R{p}_t}{PF.Mu{l}_t}.\frac{\left({\overline{H}}_t-T{w}_t\right)}{1000}\hfill & \hfill for\kern1em t=1,\dots, T\hfill \end{array} $$
(26)
$$ \begin{array}{cc}\hfill Rp{s}_t={R}_t-R{p}_t\hfill & \hfill for\kern1em t=1,\dots, T\hfill \end{array} $$
(27)
$$ \begin{array}{cc}\hfill {\overline{H}}_t=\frac{H_t+{H}_{t+1}}{2}\hfill & \hfill for\kern1em t=1,\dots, T\hfill \end{array} $$
(28)

where g = acceleration of gravity (m2/sec); e = efficiency of power plant; Rp t = release from plant during period t (MCM); PF = plant functional coefficient; Mul t = 106 times of the number of seconds during period t; \( {\overline{H}}_t \) = average reservoir water level in period t (m); and Tw t = reservoir tailwater level during period t (m); Rps t = spill from plant after hydropower generation during period t (MCM); H t and H t+1 = reservoir water level in the beginning and end of the period t (m).

6 Results and discussions

GA, ICA and COA were used to find optimal operation of reservoir policies. In order to assess GA, ICA and the COA properly, it is necessary to compare their performance in best situation. The best situation is achieved when parameters are optimum. Generally, EAs parameters are opted by trial and error method. In this study, the most important parameters of GA, ICA and COA have selected to achieve applicable convergence by utilizing trial and error. In GA, this parameter is crossover fraction, in ICA, assimilation coefficient, and in COA is motion coefficient. After selecting the appropriate values, their performances were compared. For impartial comparison these algorithms, populations of each methods was considered 50.

In this research, roulette wheel was used for GA due to better performance. Uniform mutation function was also used because of its high convergence to achieve optimal solution compared to other existing functions. Crossover fraction is one of the most effective parameters in GA that suitable value was different for it. Therefore, crossover fraction was investigated to improve GA performance from 0.6 to 0.9 with a step of 0.05. This problem was run five times with each crossover fraction to determine best value for it. The average of objective function in these five runs was considered as a criterion for selecting best crossover fraction. Figure 10 shows effect of different crossover fraction value in objective function after 1000 iterations. Suitable crossover fraction for this problem is obtained 0.75.

Fig. 10
figure 10

Selection of best crossover fraction for GA

Full size image

Like as GA, ICA parameters were determined by trial and error method and sensitivity analysis of effective parameters. These parameters are summarized in Table 7. Assimilation coefficient (β) is the most sensitive parameter of ICA and in this problem β = 1.6 generated best convergence of ICA. Figure 11 shows the effect of this parameter on convergence in ICA.

Table 7 Appropriate values for ICA parameters
Full size table
Fig. 11
figure 11

Selection of best assimilation coefficient for ICA

Full size image

COA possesses various parameters. Parameters values for this algorithm are shown in Table 8 which set by trial and error method. Optimal value for these parameters depends on type of problems. Suitable value for λ is obtained from sensitivity analysis due to performance sensitivity of this algorithm to minor changes in motion coefficient (λ %). Figure 12 shows objective function values for variation in motion coefficient.

Table 8 Appropriate values for COA parameters
Full size table
Fig. 12
figure 12

Selection of best motion coefficient for COA

Full size image

After determining appropriate values for GA, ICA and COA, their performances were investigated in optimizing operation of reservoir. Since random selection of initial population in three methods makes a direct effect on final results, it should not only be satisfied with outcomes of a run, performance of methods should be assessed in a series of runs. In current study, to evaluate GA, ICA and COA, 10 runs with 2000 iterations (approximately 100,000 function evaluations) were considered. The results of these algorithms can be evaluated from several aspects:

  1. A)

    Average of objective function

    According to the results which obtained from 10 runs for each algorithm, average value of objective function for GA, ICA, and COA are 6.869, 6.461, and 5.454, respectively. Therefore, COA has an advantage over two other methods for this standpoint. Next to COA, ICA and GA are placed in second rank and third rank, respectively.

  2. B)

    Distance between average and best performance

    If distance between averages results with best performance of each method is considered as criterion for evaluation, COA again has better performance than GA and ICA. But according to this criteria GA has done better performance than ICA. Coefficient of variation for GA, ICA and COA are 0.043, 0.059 and 0.032, respectively.

  3. C)

    Best performance proximity to global optimum

    NLP solver of Lingo11 was used as an optimization tool for this problem to evaluate final answer proximity of these methods with global optimum. Objective function values attain to 5.243, after Lingo running about 90 h. With regard to this value and values obtained from objective function using ICA, GA and COA, it is clear that COA shows very high ability in achieving to global optimum. Afterwards, ICA has a good convergence to achieve global optimum. Most important advantage of COA and ICA in comparison with GA is high convergence of these methods to approach global optimum.

  4. D)

    Run-time and parameter setting time

    In terms of algorithm running time, ICA is much faster than two other methods. This merit could be a good point to choose ICA as an optimizer algorithm. ICA run times in operation of reservoir is approximately 7 times faster than COA and 5 times faster than GA. Quick and easy parameters setting is superiority of COA over other methods.

Final results which obtained from each method are shown in Table 9. According to the results, it can be say that COA and ICA are outperformed than GA, generally. Furthermore, approaching to optimum solution after 100,000 function evaluations shows ability and strength of COA algorithm in various optimization problems.

Table 9 Objective function values of GA, ICA, and COA for Karun4 dam
Full size table

7 Conclusions

This research is made of two main parts. First part, application and evaluation of GA, ICA and COA algorithm were done in test problem. Second part, contains operation of real reservoir. At first part, Ackley and Rosenbrock functions were considered as optimization functions together with benchmark problem. The results of mathematical functions showed COA, ICA and GA have higher ability to achieve optimum solution, respectively. In four reservoir systems, ranking of algorithms were same as above. In this problem, COA, ICA and GA at best convergence achieve to 99.88, 99.50, and 98.09 % of total global optimum, respectively. At second part, COA and ICA performance tested in operation of one reservoir system with hydropower aim. Karun4 dam was used as a case study for this purpose. COA, ICA, and GA were used to achieve related policies for monthly optimal reservoir operation in 30 years (1971–2000). These results indicate that COA and ICA possess better performance than GA. The average values of objective functions for COA, ICA and GA were obtained 5.454, 6.461, and 6.869, respectively.

To evaluate algorithms performance in approaching global solution, best performances of these algorithms were compared with objective function value which obtained from Lingo. According to results, COA represents highest convergence in achieving near-optimal solution and after that ICA has been more successful in approaching optimum solution. Objective function value obtained by Lingo is 5.243 and objective function for best performance of COA, ICA and GA are 5.246, 5.586 and 6.196, respectively.

In terms of algorithms run times, ICA performed better than three other algorithms. ICA run time in operation of reservoir issue is approximately seven times faster than COA and five times faster than GA. In terms of ease, COA has a general superiority of setting parameters over other algorithms. Another desirable feature of COA is high flexibility and simplicity. Due to ability and flexibility of COA and ICA in solving operation of reservoir optimization problems, these methods can be used in other water resources optimization issues. These methods not only compete with traditional optimization methods, but also traditional methods can be replaced with these methods, in solving various problems of water resource optimization.