1 Introduction

Numerical weather prediction (NWP) is a technique used to forecast weather variables by solving numerical and physical models (Ritter and Geleyn 1992). Over the last few decades, a numbers of studies have examined the development of NWP modeling and their subsequent application (Gutman and Ignatov 1998; Ishak et al. 2014; Lorenc 1986). One such model is the Mesoscale model Version 5 (MM5) (Grell et al. 1994), which was developed by the National Center for Atmospheric Research (NCAR) in the United States. After its successful application, an advanced version of the model i.e., the Weather Research Forecast (WRF) model was released to the research community (Skamarock et al. 2005). After its release, and due to the high versatility of the WRF model, a number of studies have utilized this advanced model in research related to wide range of atmospheric phenomena, producing meteorological variables, hydrological modeling, weather research, climate monitoring and change, flood forecasting and water resource management amongst others (Borge et al. 2008; Chen et al. 2011; Ishak et al. 2013; Islam et al. 2013; Price et al. 2012; Srivastava et al. 2013b, 2014a). Aside from its use as a stand-alone NWP model, the WRF model can also be used with global reanalysis datasets, such as those available from the National Centre for Environmental Prediction (NCEP) and the European Center for Medium range Weather Forecasting (ECMWF). Notably, these global datasets have coarse horizontal resolutions and need downscaling to provide information at finer resolution using models like WRF/MM5 (Caldwell et al. 2009; Heikkilä et al. 2011; Lo et al. 2008). This downscaling is required to provide high resolution meteorological datasets such as wind speed, air temperature, solar radiation, dew point and rainfall suitable for regional or local uses (Srivastava et al. 2013d, 2014b).

The hydrological processes of any basins are influenced by hydro-meteorological variables, thus changes in such variables have implications on water resources (Liolios et al. 2014; Srivastava et al. 2013c). The major weather input variables influencing the estimation of Reference Evapotranspiration (ETo) includes wind speed, air temperature, dew point and solar radiation (Allen et al. 1998). The mesoscale model downscaled weather variables could potentially be used for ETo estimation, especially in ungauged catchments (Srivastava 2013). Similarly, rainfall is also one of the fundamental variables of the Earth's hydrological cycle (Bringi et al. 2011; Islam et al. 2012b). It is an important parameter required for climate and hydrological forecasting and hence its accurate measurements are crucial for the hydrological community (Ishak et al. 2014; Islam et al. 2012a; Petropoulos et al. 2013).

Piani et al. in (2010a) showed that mesoscale model derived ETo and precipitation can be used with hydrological models after statistical bias correction to provide a more realistic datasets for hydro-meteorological applications (Piani et al. 2010b). Bias correction can be done in a number of ways, amongst which, computational intelligence techniques are the most popular among users (Islam et al. 2014). Bias correction using simple algorithms like the Generalized Linear Models (GLM) are easily applicable and least computationally demanding (Schoof and Pryor 2001; Trigo and Palutikof 2001; Weichert and Bürger 1998). Another technique is Relevance Vector Machines (RVMs), which are powerful mathematical tools used for non-linear analysis and have been applied successfully for hydro-meteorological studies (Abrahart and See 2007; Hong et al. 2004). Other potential tools which can be used for bias correction is Support Vector Machines (SVMs); however, SVMs has some drawbacks such as rapid increase of basis functions with the size of training data set and an absence of probabilistic interpretation (Srivastava et al. 2013a). To overcome these problems, a sparse Bayesian probabilistic learning framework based Relevance Vector machine (RVM) has been developed by Tipping (2001). Hence, instead of SVMs, RVM is used in this study.

In this study, the WRF model has been applied and tested over the Brue catchment, England, UK. for deriving ETo and rainfall using the global NCEP reanalysis datasets. However, before using modeled data for any application, a brief analysis of products are required for its efficiency in comparison to the observed datasets. Furthermore, before obtaining practical outputs from such models, statistical bias correction is needed. In purview of the above mentioned problems, the main aim of this research focuses on the following objectives: (1) Simulation of hydro-meteorological variables using the state of the art WRF mesoscale model and global NCEP reanalysis datasets, (2) Estimation of the seasonality pattern in the WRF estimated ETo and rainfall datasets, and (3) Assessment of the performance of GLM and RVM for bias correction using the data derived from the WRF model and the ground based station datasets.

This paper has the following structure. In Section 2, we detail the study area, data sets, WRF modeling systems, bias correction algorithms such as RVMs and GLM, equation for ETo and performance statistics. Section 3 presents the results of the performance of the approaches utilized and subsequently discusses these results. Section 4 gives final remarks and conclusions of this work.

2 Materials and Methodology

2.1 Study Area

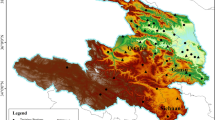
The Brue catchment is located in the south-west of England, with central coordinates of 51.11° N and 2.47° W. The geographical location of the study area is shown in Fig. 1. The meteorological datasets are provided by the British Atmospheric Data Centre (BADC), UK, including wind, net radiation, surface temperature and dew point for the period from June 2010 to November 2011. The data provided by BADC is used for evaluating the hourly downscaled meteorological data from the WRF model. The global NCEP (National Centers for Environmental Prediction) reanalysis data used in this study with WRF can be downloaded from their respective websites (http://rda.ucar.edu/). The main purposes of reanalysis data such as NCEP/NCAR are to deliver compatible, high-resolution and high quality historical global atmospheric datasets for use by the weather research community. The resolutions of these data are 1° × 1° in space and 6 h in time. Hourly datasets from the first 12 months June 2010 to May 2011 were used for training, and the remaining 6 months (June 2011-Nov2011) for validation purposes.

Fig. 1
figure 1

WRF domains employed in this study with catchment location

Full size image

2.2 Weather Research and Forecasting (WRF) Model

The model employed for this study is the WRF model (version 3.1.1). The WRF model has a rapidly growing user community and has been used for numerous hydro-meteorological and operational weather forecasting studies amongst others (Borge et al. 2008; Chen et al. 2011; Draxl et al. 2010; Heikkila et al. 2011). The WRF model is centered over the Brue catchment with three nested domains (D1, D2 and D3) of horizontal grid spacing of 81, 27 and 9 km, out of which the finest resolution innermost domain (D3) is used in this study (Fig. 1). A two-way nesting scheme is used which allows information from the child domain to be fed back to the parent domain. Imposed boundary conditions are updated every 6 h using the National Centers for Environmental Prediction (NCEP) Final Analysis (1° × 1° FNL) data set. The WRF model is used to downscale the NCEP data to produce wind, solar radiation, surface temperature, dew point temperature and rainfall. After downscaling, the ETo was estimated using the Penmen and Monteith equation discussed in section 2.5.

The main physical options included the WRF Dudhia shortwave radiation (Dudhia 1989) and Rapid Radiative Transfer Model (RRTM) long wave radiation (Mlawer et al. 1997) with Lin microphysical parameterization; the Betts-Miller-Janjic Cumulus parameterisation schemes; and the Yonsei University (YSU) planetary boundary layer (PBL) scheme (Hu et al. 2010). The Betts-Miller-Janjic Cumulus parameterization scheme was used because it is well tested for regional application and precipitation forecasting (Vaidya and Singh, 2000). Gilliland and Rowe (2007) found that it considers a sophisticated cloud mixing scheme in order to determine entrainment/detrainment which is found to be more suitable for non-tropical convection. The Arakawa C-grid was used for the horizontal grid distribution. The 3rd-order Runge–Kutta was used for time integration as it is stable without any damping (Zhong 1996), while the 6th-order centered differencing scheme was used as the spatial differencing scheme. The reason behind using this differencing scheme was its high numerical stability. The brief analysis by Chu and Fan (1997) indicated that the 6th-order scheme has error reductions by factors of 5 compared to the fourth-order difference scheme, and by factors of 50 compared to the second-order difference scheme. The Thermal diffusion scheme was used for the surface layer parameterization. The top and bottom boundary condition chosen for the study were Gravity wave absorbing (diffusion or Rayleigh damping) and Physical or free-slip respectively. The Lambert conformal conic projection was used as the model horizontal coordinates. The vertical coordinate η is defined as:

$$ \eta =\frac{\left({p}_r-{p}_t\right)}{\left({p}_{rs}-{p}_t\right)} $$
(1)

where, p r is pressure at the model surface being calculated; p rs is the pressure at the surface and p t is the pressure at the top of the model.

2.3 Relevance Vector Machine

Tipping (2001) proposed the relevance vector machine (RVM) in a Bayesian context. It is based on a probabilistic theory operated by a set of hyperparameters associated with weights iteratively estimated from the data. RVM typically utilizes fewer kernel functions and the training vectors associated with nonzero weights are called relevance vectors. The RVM model variable can be characterized for forecast y at a given x by the Eqs. (2) and (3):

$$ y=f(x)+{\varepsilon}_n\kern0.5em where\kern0.5em {\varepsilon}_n\sim N\left(0,{\sigma}_{\varepsilon_n}^2\right) $$
(2)
$$ p\left(y\left|w,{\sigma}_{\varepsilon_n}^2\right.\right)={\left(2\pi {\sigma}_{\varepsilon_n}^2\right)}^{-l/2} \exp \left\{-\frac{1}{2{\sigma}_{\varepsilon_n}^2}{\left\Vert y-{\varPhi}_w\right\Vert}^2\right\} $$
(3)

where, weights, w = (w 0, w 1,......, w l )T, \( {\sigma}_{\varepsilon_n}^2 \) is noise variance, εn are independent samples from some noise process and \( {\varPhi}_{\left({x}_i\right)}={\left[1,K\left({x}_i,{x}_1\right),K\left({x}_i,{x}_2\right),....,K\left({x}_i,{x}_l\right)\right]}^T \) in which K (xi, xl) represents kernel function.

Tipping (2001) recommended the addition of a complex penalty to the likelihood or error function to avoid the over fitting problem of w and \( {\sigma}_{\varepsilon_n}^2 \). The higher-level hyperparameters are used to constrain an explicit zero-mean Gaussian prior probability distribution over w (Ghosh and Mujumdar 2008):

$$ p\left(w\left|\alpha \right.\right)={\displaystyle \prod_{i=0}^lN\left({w}_i\left|0,{\alpha}_i^{-1}\right.\right)} $$
(4)

where α is a hyperparameter vector. The posterior overall unknowns could be computed following the Bayesian rule:

$$ p\left(w,\alpha, {\sigma}_{\varepsilon_n}^2\left|y\right.\right)=\frac{p\left(y\left|w\right.,\alpha, {\sigma}_{\varepsilon_n}^2\right)\cdot p\left(w,\alpha, {\sigma}_{\varepsilon_n}^2\right)}{{\displaystyle \int p\left(y\left|w\right.,\alpha, {\sigma}_{\varepsilon_n}^2\right)p\left(w,\alpha, {\sigma}_{\varepsilon_n}^2\right) dwd\alpha d{\sigma}_{\varepsilon_n}^2}} $$
(5)

Computation of \( p\left(w,\alpha, {\sigma}_{\varepsilon_n}^2\left|y\right.\right) \) in Eq. (5) can be decomposed as:

$$ p\left(w,\alpha, {\sigma}_{\varepsilon_n}^2\left|y\right.\right)=p\left(w\left|y\right.,\alpha, {\sigma}_{\varepsilon_n}^2\right)p\left(\alpha, {\sigma}_{\varepsilon_n}^2\left|y\right.\right) $$
(6)

While the posterior distribution of the weight can be given by

$$ p\left(w\left|y\right.,\alpha, {\sigma}_{\varepsilon_n}^2\right)=\frac{p\left(y\left|w\right.,{\sigma}_{\varepsilon_n}^2\right)\cdot p\left(w\left|\alpha \right.\right)}{p\left(y\left|\alpha \right.,{\sigma}_{\varepsilon_n}^2\right)}={\left(2\pi \right)}^{-l/2}{\left|\varSigma \right|}^{-1/2}\times \exp \left\{-\frac{1}{2}{\left(w-\mu \right)}^T{\varSigma}^{-1}\left(w-\mu \right)\right\} $$
(7)

where the posterior covariance and mean are respectively:

$$ \varSigma ={\left({\sigma}_{\varepsilon_n}^{-2}{\varPhi}^T\varPhi +A\right)}^{-1} $$
(8)
$$ \mu ={\sigma}_{\varepsilon_n}^{-2}\varSigma {\varPhi}^Ty $$
(9)

where, A = diag(α 0,....., α l ).

Therefore, the machine learning becomes a search for the hyperparameter posterior most probable, i.e., the maximization of \( p\left(\alpha, {\sigma}_{\varepsilon_n}^2\left|y\right.\right)\infty p\left(y\left|\alpha \right.,{\sigma}_{\varepsilon_n}^2\right)p\left(\alpha \right)p\left({\sigma}_{\varepsilon_n}^2\right) \) with respect to α and \( {\sigma}_{\varepsilon_n}^2 \). For uniform hyperpriors, it is required to maximize the term \( p\left(y\left|\alpha \right.,{\sigma}_{\varepsilon_n}^2\right) \), which is computable and given by:

$$ p\left(y\left|\alpha \right.,{\sigma}_{\varepsilon_n}^2\right)={\displaystyle \int \begin{array}{l}p\left(y\left|w\right.,{\sigma}_{\varepsilon_n}^2\right)p\left(w\left|\alpha \right.\right)dw={\left(2\pi \right)}^{-l/2}{\left|{\sigma}_{\varepsilon_n}^2I+\varPhi {A}^{-1}{\varPhi}^T\right|}^{1/2}\\ {}\times \exp \left\{-\frac{1}{2}{(y)}^T{\left({\sigma}_{\varepsilon_n}^2I+\varPhi {A}^{-1}{\varPhi}^T\right)}^{-1}(y)\right\}\end{array}} $$
(10)

At convergence of the hyperparameter estimation procedure, predictions can be made based on the posterior distribution over the weights, conditioned on the maximized most probable values of α and \( {\sigma}_{\varepsilon_n}^2 \), α MP and σ 2 MP respectively. The predictive distribution for a given y* can be computed using:

$$ p\left({y}_{\ast}\left|y\right.,{\alpha}_{MP},{\sigma}_{MP}^2\right)={\displaystyle \int p\left({y}_{\ast}\left|w\right.,{\sigma}_{MP}^2\right)p\left(w\left|y,{\alpha}_{MP},{\sigma}_{MP}^2\right.\right)}dw $$
(11)

Since both terms in the integrand are Gaussian, this can be readily computed, giving:

$$ p\left({y}_{\ast}\left|y\right.,{\alpha}_{MP},{\sigma}_{MP}^2\right)=N\left({y}_{\ast}\left|{t}_{\ast}\right.,{\sigma}_{\ast}^2\right) $$
(12)

where t ∗ = μ T Φ(x ∗) and σ 2∗  = σ 2 MP  + Φ(x ∗)T ΣΦ(x ∗).

The RVM predictions are probabilistic and it doesn’t make unnecessarily liberal use of basis functions like SVMs. Use of a fully probabilistic framework is a useful approach in RVMs with a priori over the model weights governed by a set of hyperparameters.

2.4 Generalized Linear Model (GLM)

Generally, in linear regression, the relationships between two variables are obtained by fitting a linear equation to observed data (Srivastava et al. 2014d). One variable is considered to be an explanatory variable (x i ), and the other is considered to be a dependent variable (y i ) (Johnson and Wichern 2002). By considering the familiar linear regression model:

$$ {y}_i={x}_ib + {e}_i, $$
(13)

where i = 1, . . ., n,; y i is a dependent variable; x i is a vector of k independent predictors; b is a vector of unknown parameters; and the e i is stochastic disturbances. The Generalized Linear Model (GLM) is a flexible generalization of ordinary linear regression that allows for response variables that have error distribution models other than a normal distribution. The GLM model is characterized by stochastic component, systematic component and link between the random and systematic components (McCullagh and Nelder 1989). The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.

2.5 ETo Estimation Using FAO56 Penman and Monteith (PM) Method

The ETo from WRF downscaled and measured meteorological variables was calculated using the Penman and Monteith (PM) method (Monteith 1965; Penman 1956). A comprehensive overview of the PM method is provided in the FAO56 report (Allen et al. 1998). The FAO Penman-Monteith method is recommended as the sole ETo method for determining reference evapotranspiration. The ETo (in mm/hr) according to the PM equation is as follows:

$$ ETo=\frac{0.408\varDelta \left({R}_n-G\right)+\gamma \frac{37}{T+273}{U}_2\left({e}_s-{e}_a\right)}{\varDelta +\gamma \left(1+\frac{r_c}{r_a}\right)} $$
(14)

where Δ = slope of the saturated vapour pressure curve (kPa/°C); R n  = net radiation at the crop surface (MJ/m2/hr); G = soil heat flux density (MJ/m2/hr); γ = psychrometric constant (kPa/°C); T = mean air temperature at 2 m height (°C); e s  = saturation vapour pressure (kPa); e a  = actual vapour pressure (kPa); e s  − e a =saturation vapour pressure deficit (kPa); U 2 = wind speed at 2 m height (m/s); r a (aerodynamic resistance) = 208/U2 s m−1; and r c (canopy resistance) = 70 s m−1.

2.6 Statistical Parameters

In this study we compared the WRF downscaled and bias corrected values of meteorological variables with the data provided by BADC. Although there are many statistics available, six of them are used in this study: root mean square error (RMSE), Index of Agreement (d) (Willmott et al. 1985), Standard Deviation (SD), MAE, %Bias and Correlation (r). Root Mean Square Error (RMSE) is represented through Eq. (15),

$$ RMSE=\sqrt{\left(\frac{1}{n}{\displaystyle \sum_{i-1}^n{\left[{y}_i-{x}_i\right]}^2}\right)} $$
(15)

Mean Absolute Error (MAE) (Eq.16),

$$ MAE=\frac{1}{n}{\displaystyle \sum_{j=1}^n\left|{y}_{(ij)}-{x}_j\right|} $$
(16)

Correlation (r) (Eq.17),

$$ r=\frac{n{\displaystyle \sum xy-\left({\displaystyle \sum x}\right)\left({\displaystyle \sum y}\right)}}{\sqrt{n\left({\displaystyle \sum {x}^2}\right)-{\left({\displaystyle \sum x}\right)}^2}\sqrt{n\left({\displaystyle \sum {y}^2}\right)-{\left({\displaystyle \sum y}\right)}^2}} $$
(17)

Percent bias (%Bias) measures the deviation of the simulated values from the observed ones. The optimal value of %Bias is 0.0, with low-magnitude values indicating satisfactory model simulation (Eq. 18).

$$ \% Bias=100*\left[{\displaystyle \sum \left({y}_i-{x}_i\right)}/{\displaystyle \sum \kern0.5em \left({x}_i\right)}\right] $$
(18)

The index of agreement (d) was proposed by (Legates and McCabe 1999; Willmott et al. 1985) to overcome the insensitivity of NSE to differences in the observed and predicted means and variances. The index of agreement represents the ratio of the mean square error and the potential error (Willmott et al. 1985) and is defined as Eq. (19):

$$ d=1-\frac{{\displaystyle \sum_{i=1}^n{\left({x}_i-{y}_i\right)}^2}}{{\displaystyle \sum_{i=1}^n{\left(\left|{y}_i-\overset{-}{x}\right|+\left|{x}_i-\overset{-}{x}\right|\right)}^2}} $$
(19)

where n is the number of observations; x i is the ground based measurements and y i is the estimated measurements; \( \overline{x} \) is the mean of ground based measurements.

3 Results and Discussion

3.1 Evaluation of Meteorological Variables Estimated from WRF

Downscaling is very important for obtaining high resolution hydro-meteorological datasets. It is a technique that provides the estimates of local weather variables at sub-grid scales from the coarser global reanalysis datasets such as NCEP to a finer resolution. In this work, the WRF downscaled estimated hydro-meteorological parameters were used for all the subsequent analysis, with domain 3 as an area of interest (Fig. 1). To evaluate the data derived from the WRF downscaled weather variables and the in-situ measurements, three statistical metrics, namely the MAE, RMSE and r were derived. The relative time series for all the variables downscaled using the WRF modelling system are presented in Fig. 2, while the performance statistics of the weather variables are provided in Table 1. The modelled surface temperature was generally greater than the measured. The downscaled temperature exhibited a good correlation with the observed and simulated temperature (r = 0.74). From the error statistics, surface temperature was found to have the third lowest error in the group and very small MAE (i.e., the model overestimates in comparison with the measured value). The MAE (3.84 °C) and RMSE (4.95 °C) showed a reasonable value for the global data. Solar radiation was the most difficult variable to downscale with significant overestimation. However, in this study, WRF downscaled solar radiation indicated a good correlation of 0.80, MAE (66.96 Watt/m2) and RMSE (133.10 Watt/m2) with the observed datasets. According to Allen et al. (1998), net solar radiation is the balance of incoming solar radiation and outgoing terrestrial radiation, which varies with seasons, which could be a possible reason for the high error. The wind speeds from the model and observation datasets revealed comparable patterns, however the downscaled wind speed values were significantly greater than the observed (MAE = 6.75 m/sec; RMSE = 8.37 m/sec) with correlation of 0.57. Errors of the same kind in overestimated wind speed were also reported by Hanna and Yang (2001). The reason for this large discrepancy is possibly due to the sensitivity of wind to local environmental conditions. Along with temperature, dew point is considered as an important weather element which affects the reference ETo of a region (Mahmood and Hubbard 2005). Dew point in the series had the highest correlation of 0.88, lowest RMSE of 2.85 °C and MAE of 2.16 °C as compared to the observed datasets.

Fig. 2
figure 2figure 2

(a-d) Time series plots of the meteorological variables under consideration

Full size image
Table 1 Performance Statistics of the data estimated using WRF downscaling in comparison to the ground observations
Full size table

3.2 Seasonal Analysis of WRF ET and Rainfall Products with Observed Datasets

This approach represents a more direct comparison between the hydro-meteorological variables with the observed station based datasets and rain gauge information. The time series obtained for ETo and rainfall are shown in Fig. 3. The pattern in ETo derived from WRF variables indicated a closer relationship with the observed station based datasets. The ETo content was higher in mid-April and August, corresponding to the dry season during the time period under study. Generally, ETo and rainfall showed marked fluctuations over the entire period with rapid and sharp responses. The comparison between ETo and rainfall exhibited a high variability with season, and followed a strong seasonal cycle. The increase in ETo can be attributed to the increasing temperature, with high evaporative demands through the April-May and August-September periods leading to a progressive drying of the soil. The rainfall pattern showed that the period between March to May was slightly drier than other months, while November-December was generally the wettest period. Generally air temperature was low over winter, and soils were near to the field capacity until mid-April, where it subsequently increased for the remaining months. Increasing air temperature after mid- April or May can lead to a substantial ETo development. Interestingly, the solar radiation values were also high during the period from April to mid- August, revealing the strong influence exerted by solar radiation conditions on both surface and subsurface response. It was observed that during the dry conditions, ETo and rainfall displayed nearly similar trends.

Fig. 3
figure 3

Seasonal variations in observed and WRF estimated ETo and rainfall

Full size image

3.3 Bias Correction Schemes and Parameterization

3.3.1 Parameterization of GLM and RVM

The GLM model used in this study was comprised of the WRF parameters as explanatory variables and the observed dataset as a dependent variable. The binomial regression family has been used with probit as a link function and binomial as a variance. The RVM technique needs to be optimised for its parameters for a satisfactory result. A preliminary analysis of parameters was performed before using it for bias correction following the method given by Srivastava et al. in (2013a). The model selection of RVM was based on subsuming hyperparameter adaptation and feature selection with respect to different model selection criteria. For the RVM model, the Gaussian radial based kernel function was used because of its popularity, high performance and general approximation ability. The sigest module supported by R language was used in this study which performs an automatic hyperparameter estimation to calculate an optimum sigma value for the Gaussian radial based function. According to Caputo et al. (2002), the “sigest” package is promising for estimating the range of values for the sigma parameter which could be used for obtaining good results. According to Caputo et al. (2002) any value between 0.1 and 0.9 quantile of \|x -x’\|^2 produce a good results. More detail about “sigest” is given over RCran web (http://cran.r-project.org/web/packages/kernlab/kernlab.pdf). The σ used for the analysis was 0.02. The RVM model produces 21 relevance vectors for best performance during the training and 9 vectors during the validation. Herein, the RVM involved very few relevant vectors for the regression to help minimise the possibility of overtraining and hence reduce the computational time. The R 2 for the rainfall during the training and validation were obtained as 0.35 and 0.30 respectively, while for the ETo, a higher training (0.77) and validation (0.72) were obtained.

3.3.2 Evaluation of the Bias Correction Schemes

The Taylor diagram (Taylor 2001) was employed herein to show the bias corrected datasets as compared to those obtained from the observed stations (Fig. 4). The perfect fit between model results and data was evaluated by using the circle mark in the x-axis, also called the reference point. In the case of a satisfactory agreement, simulated points will be closer to the reference point, indicating a better run of the model (Srivastava et al. 2014c). The result of the different runs of the simulated model was determined by the values of the correlation (r), Centered Root Mean Square Difference (RMSD) and of the Standard Deviation (SD) of the modeled data shown on the two axis of the model, whereas correlation was represented by the quarter circle. In general, when the SD of the simulated data is higher than that of the observed values, an overestimation can be predicted and vice versa. The SD analysis showed that rainfall and ETo from WRF showed a higher overestimation than the measured datasets. Furthermore, a very small r, high SD and RMSD were observed in-between the WRF and observed rainfall. On the other hand, in case of ETo, a better performance can be seen in Taylor plot. The analysis indicated a marginally higher RMSD, SD and lower r in case of GLM than RVM, imposing that probabilistic bias correction with RVM substantially improves the model's performance for both ETo and rainfall.

Fig. 4
figure 4

Taylor performance plots for the bias and non-bias corrected rainfall and ETo

Full size image
Fig. 5
figure 5

(a-b) GLM and RVM calibration and validation cumulative time series plots for the rainfall

Full size image

For a diagnostic performance evaluation of the model, four performance statistics- RMSE, %Bias, d and r, were estimated during the calibration (cal) and validation (val) to compare the observed with the WRF simulated non-bias and bias corrected datasets (Table 2). Looking at the distribution of the %Bias and (Fig. 5), the ETo was generally well simulated using the WRF model. The performance of RVM for ETo bias correction during the calibration/validation exhibited much higher r (cal = 0.76; val = 0.69) and d (cal = 0.85; val = 0.79) in comparison to the observed/WRF simulated data r (cal = 0.75; val = 0.68) and d (cal = 0.76; val = 0.72). The RMSE value for the RVM method during calibration and validation was 0.09 and 0.10 mm/hr respectively, while %Bias statistics were −1.1 and 3.9 respectively. This statistics indicate that the value of the %Bias was much higher in WRF simulated data when compared to the GLM and RVM. The RVM bias corrections of the ETo datasets showed an improved performance over GLM and WRF simulated data. Notably, the RVM bias correction of the rainfall exhibited similar values for r and d (r =0.20 and d =0.20) with lowest %Bias (2.6) and RMSE (0.44 mm/hr) during the validation. The RMSE values reported from the GLM bias correction for rainfall were 0.39 and 0.45 mm/hr during the calibration and validation respectively, while much higher values were obtained from the observed and WRF simulated rainfall. The RMSE and %Bias values compared to the Observed/WRF results indicated that the GLM did not perform very well for the bias correction in the case of rainfall. During the validation of rainfall, the GLM performance was poorer than that recorded by the RVM, indicating that RVM marginally outperformed the GLM in bias correction. Similar observations were also revealed by rainfall cumulative plots during calibration and validation (Fig. 5).

Table 2 Performance statistics for WRF, GLM, and RVM for ETo and Rainfall
Full size table

The overall analysis of GLM and RVM for Rainfall and ETo showed that the statistical bias correction of RVM was better than GLM during the both calibration and validation. This showed that the probabilistic bias correction scheme of RVM is more effective than point based bias correction of GLM. Hence, the probabilistic bias correction method could be a better choice than point-based bias correction of the data if employed with WRF downscaled hydro-meteorological variables using NCEP global reanalysis datasets.

4 Conclusions

This study provided for the first time a comprehensive model evaluation for new users who wish to apply the WRF model for hydrological modelling using the NCEP datasets. Moreover, it also provides a brief comparison of the performance of the RVM and GLM for bias correction in such models. The WRF numerical weather model was used because of its ability to downscale global reanalysis data to finer resolutions in space and time. The WRF bias correction process was found to generally improve the data quality in comparison with the original reanalysis datasets. In overall, GLM and RVM based bias correction improved the estimation of ETo and rainfall over the catchment. However, it was also observed that RVM outperformed GLM in bias correction in terms of all four statistical metrics (%Bias, RMSE, d and r).

It was found that both the GLM and RVM indicated a good applicability in bias correction and are hence accurate methods to reduce the amount of error associated with WRF downscaled data. Results from this study will potentially help in the retrieval of more accurate information from global downscaled data and will also help increase the efficiency of such data applicability in hydrological modelling. This work also provides hydrologists with valuable information on downscaled weather variables from global datasets and its applicability. However, further exploration of this potentially valuable data source by the hydro-meteorological community is recommended. The pattern obtained by precipitation with observed measurements indicates possibilities for further improvement with implication of data fusion techniques; therefore it will be attempted in future studies.