1 Introduction

Many countries are facing an acute shortage of water due to the increased population, industrialization, urbanization and higher standard of living. Industrial and agricultural activities are not only increasing the water demand but also degrading the water quality. Polluted water leads to serious health problems and threat to the ecological system. Therefore management of the water resource system is necessary both in terms of quantity as well as quality.

Several studies have been conducted on water resources planning and management (Chaturvedi 1987; Zarghami et al. 2008; Ako et al. 2010; Nikolic et al. 2012). Several researchers applied the multicriteria decision making analysis for sustainable water resources planning and management in different case studies (Duckstein et al. 1994; Raju et al. 2000; Lee and Chung 2007; Zarghami et al. 2008; Calizaya et al. 2010; Coelho et al. 2012). Sandoval-Soils et al. (2011) developed water resources sustainability index which make possible to evaluate and compare different water management policies with respect to their sustainability.

The application of the system approach gives better decision for a complex water management problem. The system approach of water resources planning is not restricted to mathematical modelling. It represents a fairly structured and ordered manner along with the important interdependencies and interactions among the various control structures and users of a water resource system for better decision making. Compared with the conventional simulation or optimisation models, the system dynamics approach is more beneficial for indicating how different changes of basic elements affect the dynamics of the system in the future. It is therefore particularly useful for representing complex systems with strong influences from social or economic elements. Several researchers applied system based approach for sustainable water resources management in different case studies (Xu et al. 2002; Tsakiris et al. 2013; Ghashghaei et al. 2013).

On the other hand, graph theory technique is a systematic and logical approach that has been applied in various disciplines to make and analyse the systems (Gandhi and Agrawal 1996). It is also widely gaining popularity as a potential tool for decision making in any type of complex problem. Many system approaches like linear programming, dynamic programming, optimization techniques and management techniques have been used by many researchers in the past to address water resources management problems. These techniques do not consider the influence and interactions between different subsystems of water resources management. Graph theory is an integrative systems approach to consider and model structural components of water resources management system along with interrelationships (interactions, dependence, flow and management decisions) between them concurrently and integratively. A few literatures are available on the application of graph theory on water resources management in water distribution network (Jacobs and Goulter 2007; Mohan Kumar et al. 2008). Some of the researchers have also applied the graph theory in different fields such as total quality management (Grover et al. 2006) as well as in manufacturing system management (Singh and Agrawal 2008).

From the above literature review, it can be said that a number of research contributions are available to manage a component of water resources system but no one has considered the structural constituents for modelling, analysing and evaluating the water resources system along with their interactions. No methodology is available for an integrated system approach for analysing the water resource system i.e. by considering the subsystems as its constituents and their interactions, interdependences and connectivity. There is a need to develop a mathematical model for analysis and indepth understanding of water resource system at the conceptual stage.

2 Methodology

2.1 Identification of Structural Constituents in Water Resources System

In order to develop the systems mathematical model, it is necessary to identify the structural constituents of water resources system. Five subsystems are identified to describe integrated water resource systems. Integrated development and management of these subsystems permits the improvement in performance, effective and efficient functioning and decision making. Figure 1 shows the tree diagram of water resources system which consists of subsystems and decomposition of the subsystems into lower level. Tree diagram of water resource development and management is designed to include all the issues needed to be addressed for effective and efficient functioning. It is flexible enough to accommodate new aspects and delete unnecessary one. Figure 2 shows the cause and effect diagram of water resources system development. This helps to identify different issues which should be addressed during development and management of water resources system. In this paper, the modelling and analysis is limited to first level decomposition only to demonstrate development of methodology. The first level subsystems are

Fig. 1
figure 1

Water resources system tree diagram

Full size image
Fig. 2
figure 2

Cause and effect diagram of water resources system development

Full size image

  • S1: Watershed management subsystem

  • S2: Groundwater development subsystem

  • S3: Surface water resources development subsystem

  • S4: Field level development subsystem

  • S5: Climate change subsystem

These five subsystems are selected to represent structurally a comprehensive water resources system and permit to address most of the issues related to the system.

2.2 Interactions in the Subsystem of the Water Resources System

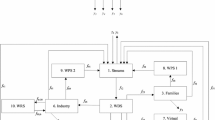
Since Figs. 1 and 2 do not show the interdependencies between the different subsystems, an interactive schematic diagram is developed in Fig 3 to show the interdependencies between the different subsystems.

Fig. 3
figure 3

Interactive block diagram of water resources system

Full size image

Precipitated water on watershed joins to surface water through runoff. Watershed subsystem has direct influence on surface water subsystem. The surface water also influences the watershed subsystem. As the pathway of river changes, it influences directly the area of the watershed. Similarly precipitated water in watershed joins to groundwater through infiltration. So watershed subsystem has direct influence on the ground water subsystem. When waterlogging takes place, groundwater subsystem influences the watershed.

Surface water joins to groundwater through infiltration and groundwater also contributes to surface water when water table will be above the bed of the stream. It indicates that both the surface water and groundwater subsystems influence each other. Climate change is significant change in measures of climate such as temperature, precipitation or wind. Climate change causes extreme precipitation and water vapour, snow and land ice melting, possible increase on evapotranspiration, change in runoff and river discharges. The ocean influences climate on regional and global scale while change in climate can fundamentally alter certain properties of ocean. Weather modification can be done artificially i.e. precipitation is possible through artificial rain. This indicates that watershed, groundwater, surface water and field level development subsystems are influenced by climate change subsystem. Since the ocean influences climate on regional and global scale, surface water, watershed, and groundwater subsystem also influence the climate change. Similarly climate change occurs due to field level development such as constructing dam, reservoirs etc. This indicates that the field level development is also influencing climate change. Pollution, deforestation etc. in a watershed can influence the climate change. Field level development has direct influence on groundwater as it decreases the infiltration of water and also influence on surface water subsystem as runoff volume increases. Artificial recharge structures are constructed to increase the level of ground water. When water logging takes place subsurface drainage is necessary. It indicates the influence of groundwater on the field level development. The interaction between the subsystems may not be always having equal weightage. So the interdependency weightage depends upon the extent of one subsystem interact with another subsystem. The interaction is coded into strong interaction, medium interaction, weak interaction and insignificant i.e. no interaction.

A few issues are identified and are associated with above five subsystems. They are a) adverse impact on fresh water caused by pollution, erosion or changes in the course of river b) water logging c) environmental degradation d) reservoir sedimentation etc. which can be improved through this model. The method provides a clear picture of all the issues in an integrative manner leading to generation of a large number of alternative solutions.

2.3 Development of Graph Theoretic Model

Graph theoretical representation is a mathematical model and is very convenient for a visual study. In order to make post processing of graph theoretical results, it is necessary to convert these graphs into algebraic models for better computer processing. A matrix is a convenient way for representation of a graph to a computer. Figures 1, 2 and 3 are the non mathematical models and are not suitable for computer processing. In Fig. 4, a diagraph is developed which represents a mathematical model. Interaction/interdependencies/interrelationships between five subsystems may be of three types under different circumstances. These may be directed, undirected or both between any two subsystems depending upon type of interactions between two subsystems. This leads to three types of representations called as directed graphs or digraphs, undirected graphs and hybrid graphs. In Fig. 4 digraph representation is selected for the development of general methodology for water resources system shown in Fig 3.

Fig 4
figure 4

Structural graph of integrative water resources system

Full size image

Let five subsystems by water resources development and management system be represented by nodes S i , i =1,2,…,5 and interactions between two subsystems i and j be represented by edges e ij and e ji . The directed edge e ij represents the influence of subsystem i on the subsystem j where directed edge e ji represents the influence of subsystem j on subsystem i. If a graph contains both types of directed and undirected edges, the graph is known as hybrid graph. If a graph contains only undirected edges, the graph is known as undirected graph. Fig 4 is a directed graph (digraph) representation of a general five subsystems of water resources development and management system. A real water resources development and management system may have edges with different weight factors depending upon the importance/effect of interactions of ith subsystem on jth subsystem.

Graph theoretic and matrix model consists of digraph representation, matrix representation and permanent representation. Diagraph representation is useful for visual analysis. Matrix model is useful for computer processing. Figure 4 shows the water resources management digraph for five factors. A digraph is used to represent the factors and their interdependencies in terms of nodes and edges. These are the directed graphs as it has directional edges. A water resources management digraph represents its subfactors (S i ) through its nodes and edges correspond to the dependence factors (e ij ). e ij represents the degree of dependence of j th factor on the i th factor and it is directed edge from node i to node j.

Matrix representation for water resources system:

There are many methods of representing the graph in the matrix form and two of them are the incidence and adjacency matrices (Deo 2000). The adjacency matrix being a square matrix is more suitable for developing algebraic results and is chosen for this purpose.

Adjacency matrix:

The adjacency matrix of the graph G with five nodes is a five order binary (0,1) square matrix, A = [a i,j ] such that:

$$ {a}_{ij}=\left\{\begin{array}{l}1, if\; subsystem\;i\; have\; an\; influence\; on\; subsystem\;j\\ {}0, if\;i\; an d\;j\; are\; not\; connected\end{array}\right\} $$

Thus the adjacency matrix A for the water resources system graph G can be written as

$$ A=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right] $$
(1)

Since a factor is not interacting with itself a ii  = 0. So the diagonal elements are represented as 0. Off diagonal elements are represented as 0 or 1 based on their interdependency / connectivity. (0,1)- matrix representation is not in a position to model a real water resources system because of its limitations.

Water resources system characteristic matrix:

The adjacency matrix A is representing the interrelationships only, while the water resources system characteristics are not represented. A water resources system characteristic matrix B is defined which characterizes the system. Water resources system characteristic matrix B is expressed as [λI-A] where I is an identity matrix of the same order as A

$$ B=\left[\begin{array}{ccccc}\hfill \lambda \hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill \\ {}\hfill -1\hfill & \hfill \lambda \hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill \\ {}\hfill -1\hfill & \hfill -1\hfill & \hfill \lambda \hfill & \hfill -1\hfill & \hfill -1\hfill \\ {}\hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill \lambda \hfill & \hfill -1\hfill \\ {}\hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill \lambda \hfill \end{array}\right] $$
(2)

where λ represents eigen values for the matrix.

As the common matrix operation allow the rows as well as columns to change positions without affecting the value of the matrix, a matrix cannot be considered as an invariant and thus not a unique representation of the interactions or the water resources system characteristics. The determinant of the water resources system characteristic matrix B leads to an invariant of this matrix and is developed as in equation given below.

$$ {\lambda}^5-6{\lambda}^3-8{\lambda}^2-3\lambda $$

This characteristic polynomial is an invariant representation of the water resources system. It forms the basis for characterising the water resources system information uniquely. As this fails to distinguish different subsystems as well as levels of interactions between them, it is not comprehensive to characterize the water resources system completely.

2.4 Water Resources System Characteristic and Interdependence Variable Matrix

Another matrix C, called as water resources subsystem characteristic and interdependence variable matrix is developed to overcome the limitation of nondiscrete representation of the subsystem of water resources system and the variable level of interactions in the subsystem in the matrix B. A five order interactive square matrix E with off diagonal elements e ij representing varying levels of interactions between the subsystem is defined as in Eq (3).

$$ E=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill {e}_{12}\hfill & \hfill {e}_{13}\hfill & \hfill {e}_{14}\hfill & \hfill {e}_{15}\hfill \\ {}\hfill {e}_{21}\hfill & \hfill 0\hfill & \hfill {e}_{23}\hfill & \hfill {e}_{24}\hfill & \hfill {e}_{25}\hfill \\ {}\hfill {e}_{31}\hfill & \hfill {e}_{32}\hfill & \hfill 0\hfill & \hfill {e}_{34}\hfill & \hfill {e}_{35}\hfill \\ {}\hfill {e}_{41}\hfill & \hfill {e}_{42}\hfill & \hfill {e}_{43}\hfill & \hfill 0\hfill & \hfill {e}_{45}\hfill \\ {}\hfill {e}_{51}\hfill & \hfill {e}_{52}\hfill & \hfill {e}_{53}\hfill & \hfill {e}_{54}\hfill & \hfill 0\hfill \end{array}\right] $$
(3)

The matrix E does not contain information related to five subsystems and needs to be updated to represent water resource development and management system conclusively.

Another subsystem matrix D, a diagonal matrix with diagonal elements representing five different subsystems is defined as in Eq (4).

$$ D=\left[\begin{array}{ccccc}\hfill {S}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {S}_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {S}_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {S}_4\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {S}_5\hfill \end{array}\right] $$
(4)

The variable characteristic matrix C is developed by substracting the matrix D from matrix E as in Eq.(5)

$$ C=\left[D-E\right] $$
(5)

The determinant of matrix C (e ij  ≠ 0) contains n! i.e.120 terms. Each of these 120 terms represents distinct combinations of five subsystems. This matrix distinctly represents characteristic features of the subsystems and their interactions. The matrix (5) does not represent the water resources system uniquely as row and columns can be interchanged. There is a weak interaction of climate change subsystem with watershed management subsystem, groundwater development, surface water development and field level development subsystem, so e 15   = e 25   = e 35  = e 45  = 0 are substituted in matrix C. The determinant of matrix C is an invariant of the water resources system and is in the multinomial form as shown in Eq. (6). The second group is generally absent in the absent of self group.

$$ \mathrm{Det}C=\begin{array}{l}\left[{S}_1{S}_2{S}_3{S}_4{S}_5\right]+\hfill \\ {}\left[-{S}_1{S}_2{S}_5{e}_{34}{e}_{43}-{S}_1{S}_4{S}_5{e}_{23}{e}_{32}-{S}_3{S}_4{S}_5{e}_{12}{e}_{21}-{S}_2{S}_4{S}_5{e}_{13}{e}_{31}-{S}_2{S}_3{S}_5{e}_{14}{e}_{41}-{S}_1{S}_3{S}_5{e}_{42}{e}_{24}\right]+\hfill \\ {}\begin{array}{l}\Big[-{S}_1{S}_5{e}_{23}{e}_{34}{e}_{42}-{S}_1{S}_5{e}_{24}{e}_{43}{e}_{32}-{S}_4{S}_5{e}_{12}{e}_{23}{e}_{31}-{S}_3{S}_5{e}_{12}{e}_{24}{e}_{41}-{S}_4{S}_5{e}_{21}{e}_{13}{e}_{32}-\\ {}{S}_2{S}_5{e}_{14}{e}_{43}{e}_{31}-{S}_2{S}_5{e}_{13}{e}_{34}{e}_{41}-{S}_3{S}_5{e}_{14}{e}_{42}{e}_{21}\Big]+\end{array}\hfill \\ {}\begin{array}{l}\Big[-{S}_5{e}_{21}{e}_{12}{e}_{34}{e}_{43}-{S}_5{e}_{13}{e}_{31}{e}_{24}{e}_{42}-{S}_5{e}_{14}{e}_{41}{e}_{23}{e}_{32}-{S}_5{e}_{12}{e}_{23}{e}_{34}{e}_{41}-{S}_5{e}_{12}{e}_{24}{e}_{43}{e}_{31}-\\ {}{S}_5{e}_{13}{e}_{34}{e}_{42}{e}_{21}-{S}_5{e}_{13}{e}_{32}{e}_{24}{e}_{41}-{S}_5{e}_{14}{e}_{43}{e}_{32}{e}_{21}-{S}_5{e}_{14}{e}_{42}{e}_{23}{e}_{31}\Big]\end{array}\hfill \end{array} $$
(6)

The loops and dyads in Eq. (6) can be represented in a simple manner as in Eq. (7). In Eq.(7) the dyad between subsystems S i and S j is represented as a loop L ij in place of e ij and e ji . A loop between subsystem S i , S j and S k i.e. e ij e jk e ki has been represented as L ijk and the reverse loop of e ji e ik e kj has been represented as L jik . Similarly the loops e ij e jk e kl e li are represented by L ijkl .

$$ \mathrm{Det}C=\begin{array}{l}\left[{S}_1{S}_2{S}_3{S}_4{S}_5\right]+\hfill \\ {}\left[-{S}_1{S}_2{S}_5{l}_{34}-{S}_1{S}_4{S}_5{l}_{23}-{S}_3{S}_4{S}_5{l}_{12}-{S}_2{S}_4{S}_5{l}_{13}-{S}_2{S}_3{S}_5{l}_{14}-{S}_1{S}_3{S}_5{l}_{24}\right]+\hfill \\ {}\left[-{S}_1{S}_5{l}_{234}-{S}_1{S}_5{l}_{432}-{S}_4{S}_5{l}_{123}-{S}_3{S}_5{l}_{124}-{S}_4{S}_5{l}_{132}-{S}_2{S}_5{l}_{431}-{S}_2{S}_5{l}_{134}-{S}_3{S}_5{l}_{421}\right]+\hfill \\ {}\left[-{S}_5{l}_{12}{l}_{34}-{S}_5{l}_{1234}-{S}_5{l}_{2431}-{S}_5{l}_{1342}-{S}_5{l}_{13}{l}_{24}-{S}_5{l}_{1324}-{S}_5{l}_{1432}-{S}_5{l}_{1423}-{S}_5{l}_{14}{l}_{23}\right]\hfill \end{array} $$
(7)

2.5 Composite Performance Index and the Permanent Function

The determinant of the matrix expressed in Eq. (5) is represented in Eq. (6). It is seen from Eq. (6) that some of its coefficients carry positive signs and some of its coefficient carries negative signs. This indicates that some information will be lost due to addition or substraction of numerical values of the terms of Eq. 6 or Eq. 7. Thus the determinant of the variable characteristic matrix does not provide complete information of the water resources management. This prompts to develop another matrix known as permanent matrix which will provide the complete information of water resources system. The permanent matrix is obtained when the negative sign from all the elements of Eq. (5) are converted into the positive ones (Minc 1966) as shown in Eq. (8). Permanent representation characterizes water resources system uniquely. It represents the effect on water resources system uniquely by a single number, which is useful for comparison, ranking and optimum selection.

$$ P=\left[\begin{array}{ccccc}\hfill {S}_1\hfill & \hfill {e}_{12}\hfill & \hfill {e}_{13}\hfill & \hfill {e}_{14}\hfill & \hfill {e}_{15}\hfill \\ {}\hfill {e}_{21}\hfill & \hfill {S}_2\hfill & \hfill {e}_{23}\hfill & \hfill {e}_{24}\hfill & \hfill {e}_{25}\hfill \\ {}\hfill {e}_{31}\hfill & \hfill {e}_{32}\hfill & \hfill {S}_3\hfill & \hfill {e}_{34}\hfill & \hfill {e}_{35}\hfill \\ {}\hfill {e}_{41}\hfill & \hfill {e}_{42}\hfill & \hfill {e}_{43}\hfill & \hfill {S}_4\hfill & \hfill {e}_{45}\hfill \\ {}\hfill {e}_{51}\hfill & \hfill {e}_{52}\hfill & \hfill {e}_{53}\hfill & \hfill {e}_{54}\hfill & \hfill {S}_5\hfill \end{array}\right] $$
(8)

The diagonal elements represent the contribution of five subsystems of water resources system and the off diagonal elements representing the interdependencies between the subsystems. In order to represent the water resources system uniquely, a permanent function of the matrix is developed. The permanent function, a standard matrix function, is similar to determinant except the sign. The permanent function carries all the terms with positive sign having a physical significance related to the system. The single numerical value is the representation of a typical water resources system in a quantitative term.

The permanent function of the matrix P in Eq. (8) is developed and represented in Eq.(9) in a general sigma form.

$$ \begin{array}{l}{\displaystyle \prod_{i=1}^5{S}_i+{\displaystyle \sum_i{\displaystyle \sum_j{\displaystyle \sum_k{\displaystyle \sum_l{\displaystyle \sum_m\left({e}_{ij}{e}_{ji}\right){S}_k{S}_l{S}_m+}}}}}}{\displaystyle \sum_i{\displaystyle \sum_j{\displaystyle \sum_k{\displaystyle \sum_l{\displaystyle \sum_m\left({e}_{ij}{e}_{jk}{e}_{ki}+{e}_{ik}{e}_{kj}{e}_{ji}\right){S}_l{S}_m+}}}}}\\ {}\left[\left({\displaystyle \sum_i{\displaystyle \sum_j{\displaystyle \sum_k{\displaystyle \sum_l{\displaystyle \sum_m\left({e}_{ij}{e}_{ji}+{e}_{kl}{e}_{lk}\right){S}_m}}}}}\right)+\left({\displaystyle \sum_i{\displaystyle \sum_j{\displaystyle \sum_k{\displaystyle \sum_l{\displaystyle \sum_m\left({e}_{ij}{e}_{jk}{e}_{kl}{e}_{li}+{e}_{il}{e}_{lk}{e}_{kj}{e}_{ji}\right){S}_m}}}}}\right)\right]\\ {}+\left[\begin{array}{l}\left({\displaystyle \sum_i{\displaystyle \sum_j{\displaystyle \sum_k{\displaystyle \sum_l{\displaystyle \sum_m\left({e}_{ij}{e}_{ji}\right)\left({e}_{kl}{e}_{lm}{e}_{mk}+{e}_{km}{e}_{ml}{e}_{lk}\right)}}}}}\right)+\\ {}\left({\displaystyle \sum_i{\displaystyle \sum_j{\displaystyle \sum_k{\displaystyle \sum_l{\displaystyle \sum_m\left({e}_{ij}{e}_{ji}\right)\left({e}_{ij}{e}_{jk}{e}_{kl}{e}_{lm}{e}_{mi}+{e}_{im}{e}_{ml}{e}_{lk}{e}_{kj}{e}_{ji}\right)}}}}}\right)\end{array}\right]\end{array} $$
(9)

The permanent function Per (P) differs with the multinomial Det (C) in Eq. (7) only in the signs of certain terms. The permanent function model is unique and complete structural representation of the water resources system with the added advantage of using numerical values of each term without any chance of losing important information in the total numerical index. The numerical index developed based on the permanent multinomial terms in Eq. (9) by giving numerical value to individual structural element is considered a composite score of the total water resources system in any performance dimension depending upon one selected for giving values to individual structural elements. This score is useful for comparison and ranking the different water resources systems. The numerical values are assigned to various subsystems and their interactions depending upon the level of effective interactions between the subsystems. For complex subsystems, the numerical value may be assigned by determining the permanent function for lower comprehensive units. i.e.

  • S1 = Per (PS1); S2 = Per (PS2); S3 = Per (PS3); S4 = Per (PS4); S5 = Per (PS5);

Where PS1, PS2, PS3, PS4, PS5 are the variable permanent matrices for all five sub systems. This shows that this methodology is applied in bottom up approach i.e. from lowest level to top water resources system level and gives the complete structural evaluation of the water resources system.

The structural elements e ij e ji , e ij e jk e ki , e ij e jk e kl e li in Eq. (9) correspond to the subsystems interacting in the form of a dyad, three-subsystem, four-subsystem loops. These terms are subsets of water resources system. The first term represents a set of five unconnected water resources management elements. Due to the nonexistent of self loops, the second group is absent. When a stream of water is taken from a reservoir to operate hydraulic turbine, flour mill etc. and returns back to the subsystem can be represented by the self loop at the vertex representing reservoir subsystem. Each term of the third group represents a set of two element loop (dyad) and three unconnected elements. Each term of the fourth group represents a set of three-element loops and two unconnected elements. The fifth group contains two subgroups. Each term of the first subgroup represents two sets of two element loop and one unconnected elements and each term of the second subgroup represents one set of four element loop and one unconnected elements. Figure 5 shows the graphical representation of different terms in different groups of the permanent multinomial.

Fig 5
figure 5

Graphical representation of permanent multinomial

Full size image

3 Structural Analysis

Every term of the multinomial is a typical combination of structural elements i.e. subsystems s i , dyads e 2 ij (a set of 2 subsystems), e ij , e jk , e ki (a closed loop of three subsystems) and other closed loops of more subsystems. Each of these structural elements provides new information based on different situations. So for m number of distinct terms corresponding to m number of situation, m distinct alternative decision about development and management of water resources system are generated leading to selection of an optimum decision.

For example, the term S 1 S 2 S 5 l 34 belongs to third group. It represents the goal of the water resources system in the direction of constructing an efficient canal networks along with proper land management. It has a set of three distinct subsystems. They are watershed subsystem, groundwater subsystem and weather modification and forecasting subsystem. The other two set of subsystems are in a loop. The element e 34 is a part of loop (e 34 e 43 ) because the efficiency of the field level development depends on the surface water subsystem as land water system is altered due to meandering of rivers. The watershed subsystem, groundwater subsystem and weather modification and forecasting are contributing to increase in efficiency in an independent manner by facilitating and controlling the subsystem.

Similarly the term S 1 S 5 L 234 belongs to fourth group. It represents the goal of the development of water resources system in a loop of groundwater, surface water and field level development. The element e 23 (e 23 e 34 e 42 ) is a part of loop because the efficiency of surface water subsystem in summer season depends on the groundwater subsystem and the field level development consists of constructing canals, dams etc. directly depends on surface water subsystem through edge e 34 . The groundwater subsystem also depends on field level development by constructing dug well for artificial recharge. The above discussions reveal that the term S 1 S 5 L 234 describes the importance of artificial recharge of groundwater. The watershed subsystem and weather modification subsystem are contributing to above cycle in an independent manner.

4 Identification and Comparison of Water Resources System Structure

Five subsystems are considered for a water resources development and management system for the development of methodology. Eq. (9) shows that for five systems, the permanent multinomial contains 5! i.e.120 terms if no e ij is zero. All 120 terms of the permanent multinomial identify all possible structural patterns contributing towards varying goals of the water resources system. It serves as 120 structural tests that may be used to analyze the total water resources system in 120 distinct ways. A systematic technique for the structural identification and comparison of the water resources system is developed. Eq. (9) contains terms arranged in n + 1 grouping. Since here n = 5, Eq. (9) is arranged in six groups.

Comparison of water resources system structure:

Since a number of alternatives are available in order to develop water resources system in a particular region, it is possible to find out the most suitable one which will be adopted for that region. All the attributes present in permanent multinomial represent the real subsystem of water resources system structure and can be used to compare different alternatives. This structure based comparison helps in the process of developing new design of water resources system development and management. Identification set of numbers for characterizing a particular water resources system is defined as

$$ \left[{J}_1/{J}_2/{J}_3/{J}_4/---/{J}_{k1}+{J}_{k2}+--{J}_{kl}/---\right] $$
(10)

Where J kl is the number of distinct terms in the lth subgroup of the kth subgroup of the permanent function (Eq. 9). This set is a powerful tool for comparison between two water resources system. Coefficient of similarity and coefficient of dissimilarity are defined using these numbers to identify structural closeness between two systems.

The coefficient of similarity and dissimilarity give a systematic method of comparison of the water resources system structure. The coefficient of similarity and dissimilarity (Singh and Agrawal 2008) is defined by two criteria shown in Eq. (11 and 12)

Criteria 1:

$$ {C}_{d-1}=\frac{1}{Y_1}{\displaystyle \sum_k{\displaystyle \sum_l{\phi}_{kl}}} $$
(11)
$$ \begin{array}{l}{Y}_1= \max \left[{\displaystyle \sum_k{\displaystyle \sum_l{J}_{kl}\; and\;{\displaystyle \sum_k{\displaystyle \sum_l{J}_{kl}^{/}}}\;}}\right]\\ {}{\phi}_{kl}=\left[{J}_{kl}-{J}_{kl}^{/}\right]\end{array} $$

Where C d-1 is Coefficient of dissimilarity and J kl and J’ kl are the numbers of distinct terms in the l th subgroup of the k th group of the permanent function of the two water resources systems.

Criteria 2:

Another criteria with more discriminating power is defined as

$$ {C}_{d-2}={\left[\frac{1}{Y_2}{\displaystyle \sum_k{\displaystyle \sum_l{\phi}_{kl}^2}}\right]}^{1/2} $$
(12)
$$ \begin{array}{l}{Y}_2= \max imum\left[{\displaystyle \sum_k{\displaystyle \sum_l{\left[{J}_{kl}\right]}^2\; and\;{{\displaystyle \sum_k{\displaystyle \sum_l\left[{J}_{kl}^{/}\right]}}}^2}}\right]\\ {}{\phi}_{kl}=\left[{J}_{kl}-{J}_{kl}^{/}\right]\end{array} $$

The value for the coefficient of dissimilarity will lie between 0 and 1. The coefficient of similarity can be calculated as

$$ \begin{array}{l}{C}_{s-1}=1-{C}_{d-1}\\ {}{C}_{s-2}=1-{C}_{d-2}\end{array} $$

Where C s-1 and C s-2 are the coefficients of similarity of two different water resources systems by criteria 1 and 2 respectively. If the value of coefficient of similarity is one, then it can be said that both the systems are completely similar. Since the different terms of permanent multinomial are contributing the different goals of the water resources system, the differences or similarities in these terms shifts the goals of the water resources system development. The total comparison is carried out based on the characteristic values of different subsystems. Since all the interactions are incorporated in permanent multinomial per(P), the numerical values assigned to these terms will result a single index of the total water resources system development.

5 Quantification of Factors and Their Interdependencies

The various subsystems affecting the water resources system is identified in Fig. 1. Similarly various factors affecting the subsystems are also identified in Figs. 1 and 2. The variable permanent function of each subsystem per(Psi) is evaluated. The evaluation of variable permanent function is to be started from bottom level. In order to avoid the complexity, a suitable value is assigned at subsystem or sub subsystem level. The value depends on weightage of that subsystem on the total system. Table 1 suggests the numerical values of factors based on their importance on the total water resources system as well as their interdependencies.

Table 1 Qualitative measure of water resources subsystems and their interdependencies
Full size table

6 Application of Methodology

In order to demonstrate the proposed methodology, the groundwater development subsystem of Patiala district located in Punjab state of India is considered. Groundwater development is a component of integrated water resource system. It is proposed to find out the system index (permanent index) for the groundwater subsystem. To determine the system index the numerical value of all sub-subsystems and their interdependencies are required.

The various factors affecting the groundwater development are a) Groundwater quantity b) groundwater quality c) groundwater recharge and d) cropping pattern. All the four factors are the sub-subsystem level and also interdependent on each other.

Figure 6 shows the diagraph of groundwater subsystem. For the diagraph shown in Fig 6, permanent multinomial is developed in terms of SS i 2 and e ij . Permanent index is developed by assigning proper numerical value to the factors depending on interaction between the sub-subsystem. The score obtained for the diagraph shown in Fig 6 will be the numerical value for groundwater development subsystem. At subsystem level the variable permanent matrix for diagraph for subsystem 2 will be considered for the score of subsystem. In this case the calculation of permanent index of only groundwater subsystem is shown. In similar way permanent indexes of all the subsystems are calculated.

Fig. 6
figure 6

Diagraph for groundwater subsystem

Full size image

Table 2 shows the Ground water resource and development potential of Patiala district, Punjab (as on 31-03-2004). The net groundwater resource of Patiala district has been estimated to be 1516.03 MCM and gross groundwater draft of the district is 2589.45 MCM having a shortfall of 1087.69 MCM. Also all the blocks come under the over exploited category. There are four artificial rainwater harvesting structures and one roof top rain water harvesting structure in a school building in this district which is recharging the ground water.

Table 2 Ground water resource and development potential of Patiala district, Punjab (as on 31-03-2004) (Source of data: Central Ground water board)
Full size table

The Groundwater quality studies around Patiala district conducted by Central Ground Water Board shows the presence of alkaline nature of water. Also their study concluded that the groundwater at some places is harmful for human consumption. But it is not harmful for irrigation purposes.

Taking consideration to above data and the interaction between sub-subsystems, suitable numerical values are used to determine the permanent matrices. Table 1 is used to assign the value to diagonal element of matrix as well as to assign the value to other than diagonal element of matrix.

$$ \begin{array}{l}{e}_1^2=2;{e}_{12}^2=4;{e}_{13}^2=4;{e}_{14}^2=4\\ {}{e}_{21}^2=2;{e}_2^2=4;{e}_{23}^2=4{e}_{24}^2=3\\ {}{e}_{31}^2=3;{e}_{32}^2=3;{e}_3^2=2;{e}_{34}^2=3\\ {}{e}_{41}^2=3;{e}_{42}^2=2;{e}_{43}^2=2;{e}_4^2=5\end{array} $$

The first sub subsystem is groundwater quantity and the value assigned to first element e1 of matrix is 2 (From Table 1 value 2 indicates for poor performance). This is because from Table 2 it is shown that there is deficiency of the quantity of groundwater available from the required. Similarly the value assigned to second element e12 is 4 because the degree of influence of groundwater quality on groundwater quantity is strong. If quality of groundwater is degraded, the water is not potable. So the quantity of potable water reduces. This indicates that there is a strong influence of groundwater quality on groundwater quantity. In similar way the other values are assigned using Table 1.

Variable permanent matrix for the groundwater subsystem can be written as

$$ per\left( PS{S}_2\right)=\left[\begin{array}{cccc}\hfill 2\hfill & \hfill 4\hfill & \hfill 4\hfill & \hfill 4\hfill \\ {}\hfill 2\hfill & \hfill 4\hfill & \hfill 4\hfill & \hfill 3\hfill \\ {}\hfill 3\hfill & \hfill 3\hfill & \hfill 2\hfill & \hfill 3\hfill \\ {}\hfill 3\hfill & \hfill 2\hfill & \hfill 2\hfill & \hfill 5\hfill \end{array}\right] $$
(13)

The value of the permanent function of the groundwater subsystem SS2 is the permanent index of the matrices represented in Eq. 13 which is equal to 2,256. Similarly the value of permanent function of other subsystems can be evaluated from the variable permanent matrices. Then for the diagraph of water resources management shown in Fig 4, permanent multinomial is developed in terms of S i 2 and e ij . Variable permanent matrix shown in Eq. 8 is to be developed. The values of the diagonal element of this matrix will be the permanent index calculated for the subsystem level and the value of the off diagonal elements will be judged from Table 1 which shows the measure of interdependencies between the subsystems. Then the permanent of Eq. 8 will be the permanent index for water resources system.

The permanent index of a system will be worst when the inheritance of all its factors and subfactors is at worst. In this example the minimum value of groundwater system index can be calculated by using the minimum value of all its factors and subfactors. Eq. 14 shows the modified variable matrix of groundwater subsystem when the inheritance of all its factors and subfactors is at worst.

$$ per\left( PS{S}_2\right)=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 4\hfill & \hfill 4\hfill & \hfill 4\hfill \\ {}\hfill 2\hfill & \hfill 1\hfill & \hfill 4\hfill & \hfill 3\hfill \\ {}\hfill 3\hfill & \hfill 3\hfill & \hfill 1\hfill & \hfill 3\hfill \\ {}\hfill 3\hfill & \hfill 2\hfill & \hfill 2\hfill & \hfill 1\hfill \end{array}\right] $$
(14)

The value of the permanent function of the groundwater subsystem SS2 is the permanent of the matrices represented in Eq. 14 which is equal to 1,159 which is the minimum value of the groundwater subsystem. Similarly the maximum value of groundwater subsystem index will be 5,544. In the current situation, the groundwater subsystem index is 2,256. The maximum and minimum value of groundwater subsystem index indicates the range with in which it will vary.

7 SWOT Analysis

SWOT analysis is proposed to identify the internal strengths and weakness of a system under consideration. This analysis helps to identify the area where it needs improvement. Let us consider the same groundwater subsystem of Patiala district located in Punjab state of India.

Strength

At some places, artificial recharge of groundwater improves the groundwater quantity.

Weakness

Quality of water at some places is not fit for domestic as well as for irrigation purpose.

Opportunities

Improvement of socio economic condition of that region, short term and long term strategic planning and development

Threat

Industrial waste water is discharge directly on land which degrades the quality of groundwater.

SWOT analysis gives a clear picture of weakness and future threat in that area. In order to reduce those effects it is necessary to consider alternate model where the weakness and threat are minimum. So the alternate model should consider which will help to improve the both quantity and quality of the ground water.

8 Concluding Remarks

The method proposed in this paper is based on graph theory and matrix algebra which is capable of addressing a variety of issues related to water resources development and management system. The present work demonstrates the ability of structural modelling of water resources components along with interactions between them in an integrated manner to find out the overall performance of the system. This will help decision makers to take decisions on different aspects concurrently and integratively. The decision on different aspect will be communicated to policy makers of local, national and international levels so that they can implement the policy which will satisfy to the society as well as stakeholders. Further an illustrative example demonstrates the application of proposed systems approach to real water resources development problem. SWOT analysis is incorporated in decision making process to help decision maker in taking most appropriate decision. The methodology is a flexible and comprehensive powerful decision making tool not only at the conceptual stage of design and development of water resources system but also at operational stage to take right decision at right time to the satisfaction of all the stakeholders.