1 Introduction

Water scarcity is a worldwide issue. To solve this problem, improving water use efficiency is a critical way. Optimization of water allocation can stimulate efficient utilization of water. Over the past 50 years, many optimization techniques including linear programming, dynamics programming, nonlinear programming, network flow programming, stochastic programming, genetic algorithms, simulated annealing, and ant colony optimization have been widely adopted for water allocation (Rani and Moreira 2010). Although optimization models can automatically search for an “optimal” solution that meets all system constraints, they are hard to adapt to the complexity of water resources system because they require mathematical expressions of all aspects that can influence the decision-making process (Sechi and Sulis 2009). Thus decision-makers often make some finite water allocation options by means of simulation, and select or rank the options according to decision objectives (Geng and Wardlaw 2013). In the process, the assessment of the allocation options is a key step. However, water allocation option is characterized by multi-criterion, uncertainty and group-decision factors in such a way that decision-makers are unable to easily select an option. They often need some methods, such as fuzzy set analysis (Wang et al. 2011; Jafarzadegan et al. 2013), maximum entropy model (Kim and Singh 2014), Grey correlation analysis (Tao et al. 2011) and TOPSIS (Afshar et al. 2011; Islam et al. 2013) amongst others, to help them in selecting and ranking the options. Amongst the methods, the fuzzy set analysis appears to be the most commonly applied method and is, especially, suitable for handling uncertainty inherent in water allocation problems (Hajkowicz and Collins 2007).

Fuzzy set analysis usually consists of three steps. Firstly, a criterion value is transformed into a criterion relative membership degree (RMD). Secondly, a criterion weighting is determined and, finally, overall RMD of the option is calculated. In computing criterion RMD, the criteria need to be categorized qualitatively and quantitatively. The quantitative criteria usually contain the beneficial criteria, the harmful criteria and the intermediate criteria. Based on the type of criteria, the corresponding formula is adopted (Chen and Hou 2004). The methods available for evaluating the RMD in the qualitative criteria include pairwise comparisons (Toosi and Samani 2012) and triangular membership function (Christodoulou and Deligianni 2010). Since the RMD formula of quantitative criteria differs from the qualitative criteria, a unified RMD formula has been developed by Chen (2001) based on pairwise comparisons.

Criterion weighting is one of the hot topics on water resources options assessment and reflects the preferences of decision-makers. The result of selecting the optimal option is different when criteria weighting is different. Hence, the key for determining criteria weighting is to express the preferences of decision-makers as much as possible. There are many methods for identifying criteria weighting; these are classified into subjective methods, objective methods and subjective-objective methods (Cheng and Chau 2001; Mutikanga et al. 2011). In fact, an objective method is a kind of recessive subjective method because it needs to choose options expressing the preferences of decision-makers to identify criteria weighting.

In many cases, the maximum principle of membership degree has been adopted in many fuzzy optimization models to select the desired option such as theory of fuzzy optimum selection for multi-stage and multi-objective decision-making system (Chen 1994) and fuzzy optimizing dynamic programming for flood control system (Cheng 1999). However, this principle is not suitable for option rating assessment because it has a mathematical logic reasoning error in the condition of the fuzzy concept rating. Thus Chen (1997) presented the rating of fuzzy optimal selection model, which used the rank feature value to select the optimal option. After this, Chen and Guo (2006) created the theory of variable fuzzy sets (VFS) according to the dynamic variability of fuzzy sets, which was developed into variable sets (VS) (Chen et al. 2013a). Since this theory is physically clean and simple, it has been successfully applied in the field of water resources (Chen et al. 2013a, b).

However, there are two drawbacks in the applications of VS. First, this theory has only been used on single-layer multi-objective fuzzy optimization. Its application is rare in water resources with multi-region, multi-principle and multi-criteria influences. Secondly, the rank feature value may overcome the drawback that the maximum principle of membership degree cannot be utilized to evaluate the option rating, but it leads to homogenization of option rating. In other words, the membership degrees against every rating may be different between two options but their rank feature values may be equivalent.

To solve the above two problems and match the structure of water resources option with multi-region, multi-principle and multi-criteria factors, this paper developed the hierarchy variable sets optimization model for water allocation options based on single-layer variable sets optimization model (Chen et al. 2013b). The concept of fuzzy rating interval (FRI) (Xu et al. 1999), which has been applied in the assessment of safety grade, is adopted to evaluate the rating and its probability of option. Finally, the case study shows that the proposed model is feasible and effective, and the evaluation results are reasonable.

2 Principle of Variable Sets

Chen et al. (2013a) developed the theory of VS from fuzzy systems to general systems, which comprises fuzzy systems and crisp systems. This theory provides the opposite axiom and the mathematical theorem of VS.

2.1 Opposite Axiom of VS

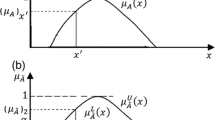
Let us suppose that there is an opposite fuzzy concept (object or phenomenon) in the universe U,  expresses characteristic of attractability and  c states repellency. Hence, for any element u(u ∈ U), \( {\mu}_{\widehat{A}}(u) \) and \( {\mu}_{{\widehat{A}}^c}(u) \) are RMDs of attractability and repellency, respectively, in the continuous interval [0,1] (for Â) and [1,0] (for  c). Mapping is defined as RMD function of u to  and  c in Eq. 1.

$$ \begin{array}{l}{\mu}_{\widehat{A}}(u),{\mu}_{{\widehat{A}}^c}(u):U\to \left[0,1\right]\hfill \\ {}\left.u\right|\to {\mu}_{\widehat{A}}(u),{\mu}_{{\widehat{A}}^c}(u)\in \left[0,1\right]\hfill \end{array} $$
(1)

Figure 1 shows the dynamic change of RMD function in the universe. Any element in their opposite features is given as:

Fig. 1
figure 1

Dynamic change of RMD function in the universe

Full size image
$$ \begin{array}{ccc}\hfill {\mu}_{\widehat{A}}(u)+{\mu_{\widehat{A}}}_c(u)=1,\hfill & \hfill 0\le {\mu}_{\widehat{A}}(u)\le 1,\hfill & \hfill 0\le {\mu_{\widehat{A}}}_c(u)\hfill \end{array}\le 1 $$
(2)

Eqs. 1 and 2 and the continuous universe constitute the basic axiom of VS, i.e. the opposite axiom of VS.

2.2 Variable Sets

2.2.1 Definition of Opposite Difference Function

Let

$$ \widehat{D}(u)={\mu}_{\hat{A}}(u)-{\mu}_{{\hat{A}}^c}(u) $$
(3)

where \( \widehat{D}(u) \) is opposite difference degree of u to  and  c. Its mapping is defined as the opposite difference function of u to  and  c in Eq. 4.

$$ \begin{array}{l}\widehat{D}:U\to \left[-1,1\right]\hfill \\ {}\left.u\right|\to \widehat{D}(u)\in \left[-1,1\right]\hfill \end{array} $$
(4)

The dynamic change in the universe is shown as in Fig. 2.

Fig. 2
figure 2

Dynamic change of opposite difference function

Full size image

2.2.2 Definition of VS

Let

$$ \begin{array}{l}\widehat{V}=\left\{\left.\left(u,U\right)\right|u\in U,\widehat{D}(u)={\mu}_{\widehat{A}}(u)-{\mu}_{{\widehat{A}}^c}(u),\widehat{D}\in \left[-1,1\right]\right\}\hfill \\ {}{\widehat{A}}_{+}=\left\{\left.u\right|u\in U,0<\widehat{D}(u)<1\right\}\hfill \\ {}{\widehat{A}}_{-}=\left\{\left.u\right|u\in U,-1<\widehat{D}(u)<0\right\}\hfill \\ {}{\widehat{A}}_0=\left\{\left.u\right|u\in U,\widehat{D}(u)=0\right\}\hfill \\ {}{\widehat{A}}_{\pm 1}=\left\{\left.u\right|u\in U,\widehat{D}(u)=\pm 1\right\}\hfill \end{array} $$
(5)

Here \( \widehat{V} \) is defined as VS of U;  +,  −,  0 and  ±1 are defined as the attracting (as priority) domain, repelling (as priority) domain, gradual qualitative change boundary and sudden qualitative change boundary, respectively.

Assume that C is a variable factor set of \( \widehat{V} \) and is given as:

$$ C=\left\{{C}_1,{C}_2,{C}_3\cdots \right\} $$
(6)

where C 1 is the variable factor 1 (time), C 2 is the variable factor 2 (space) and C 3 is the variable factor 3 (condition). Let

$$ {\widehat{A}}^{-}=C\left({\widehat{A}}_{+}\right)=\left\{\left.u\right|u\in U,0<\widehat{D}(u)<1,-1<\widehat{D}\left(C(u)\right)<0\right\} $$
(7)
$$ {\widehat{A}}^{+}=C\left({\widehat{A}}_{-}\right)=\left\{\left.u\right|u\in U,-1<\widehat{D}(u)<0,0<\widehat{D}\left(C(u)\right)<1\right\} $$
(8)

The two subsets are defined as gradual qualitative change domains of \( \widehat{V} \) about C, and \( \widehat{D}\left(C(u)\right) \) is the opposite difference function after transformation from u to \( C(u) \). Let

$$ {\widehat{A}}^{\left(+\right)}=C\left({\widehat{A}}_{\left(+\right)}\right)=\left\{\left.u\right|u\in U,0<\widehat{D}(u)<1,0<\widehat{D}\left(C(u)\right)<1\right\} $$
(9)
$$ {\widehat{A}}^{\left(-\right)}=C\left({\widehat{A}}_{\left(-\right)}\right)=\left\{\left.u\right|u\in U,-1<\widehat{D}(u)<0,-1<\widehat{D}\left(C(u)\right)<0\right\} $$
(10)

Generally, these two subsets are defined as quantitative change domains of \( \widehat{V} \) about C.

2.3 Unity of Opposite Theorem Based on VS

To any element u in the universe U, if the transformation C after the opposite RMD functions of u to  are \( {\mu}_{\widehat{A}}\left(C(u)\right) \) and \( {\mu}_{{\widehat{A}}^c}\left(C(u)\right) \), respectively. Then

$$ {\mu}_{\widehat{A}}(u)+{\mu}_{{\widehat{A}}^c}(u)\equiv {\mu}_{\widehat{A}}\left(C(u)\right)+{\mu}_{{\widehat{A}}^c}\left(C(u)\right)\equiv 1 $$
(11)

where \( 0\le {\mu}_{\widehat{A}}(u)\le 1,0\le {\mu_{\widehat{A}}}_c(u)\le 1,0\le {\mu}_{\widehat{A}}\left(C(u)\right)\le 1,0\le {\mu_{\widehat{A}}}_c\left(C(u)\right)\le 1 \).

3 Hierarchy VS Method

3.1 Hierarchy Structure of Water Allocation Option

There are usually many criteria to assess water allocation options, which form a hierarchy assessment criteria system. This system is often divided into three levels; namely objective level, principle level and criterion level as shown in Fig. 3. These are very necessary in building a hierarchy assessment model for assessing water allocation options.

Fig. 3
figure 3

Hierarchy criteria system

Full size image

3.2 RMD of Criterion

For a water resources system, there are n water allocation options u j (j = 1,2, ⋯,n) for which the ratings are categorized into c. M indicates the criteria set for assessing the rating of each option. According to the properties of criteria, l assessment principles were setup and the criteria set M divided into l criteria subsets M i , which meet:

$$ \begin{array}{ccc}\hfill M={\displaystyle \underset{i=1}{\overset{l}{\cup }}{M}_i},\hfill & \hfill {M}_i{\displaystyle \cap {M}_k=\mathrm{\O}},\hfill & \hfill i\ne k\hfill \end{array} $$
(12)

where ⋃ and ⋂ represent union and intersection of sets, respectively, and Ø states empty set; i = 1,2, ⋯, l; k = 1,2, ⋯, l.

Assuming the standard value of each criterion in criteria subset M k is known to each rating, the standard values matrix of the criteria can be obtained by:

$$ {\boldsymbol{Y}}^k=\left[\begin{array}{cccc}\hfill {y}_{11}^k\hfill & \hfill {y}_{12}^k\hfill & \hfill \cdots \hfill & \hfill {y}_{1c}^k\hfill \\ {}\hfill {y}_{21}^k\hfill & \hfill {y}_{22}^k\hfill & \hfill \cdots \hfill & \hfill {y}_{2c}^k\hfill \\ {}\hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ {}\hfill {y}_{m_k1}^k\hfill & \hfill {y}_{m_k2}^k\hfill & \hfill \cdots \hfill & \hfill {y}_{m_kc}^k\hfill \end{array}\right]={\left({y}_{ih}^k\right)}_{m_k\times c} $$
(13)

where y k ih is the standard value of i criterion belonging to h rating, m k is the number of criteria in criteria subset M k , c is the number of option ratings, i = 1,2, ⋯, m k , h = 1,2, ⋯, c, and k = 1,2, ⋯, l.

If the value of i criterion is equal to the standard value belonging to h rating, its RMD belonging to h rating is equal to 1. If the adjacent two ratings are regarded as opposite features, then according to the unity of opposite theorem, there is

$$ {\mu}_h(u)+{\mu}_{\left(h+1\right)}(u)=1 $$
(14)

Now under the k principle, the rating of each option is assessed. The k principle contains m k criteria, and the criteria values matrix of all options is given as:

$$ {\boldsymbol{X}}^k=\left[\begin{array}{cccc}\hfill {x}_{11}^k\hfill & \hfill {x}_{12}^k\hfill & \hfill \cdots \hfill & \hfill {x}_{1n}^k\hfill \\ {}\hfill {x}_{21}^k\hfill & \hfill {x}_{22}^k\hfill & \hfill \cdots \hfill & \hfill {x}_{2n}^k\hfill \\ {}\hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ {}\hfill {x}_{m_k1}^k\hfill & \hfill {x}_{m_k2}^k\hfill & \hfill \cdots \hfill & \hfill {x}_{m_kn}^k\hfill \end{array}\right]={\left({x}_{ih}^k\right)}_{m_k\times n} $$
(15)

where x k ij is the value of i criterion of j option with i = 1,2, ⋯, m k , j = 1,2, ⋯, n, and k = 1,2, ⋯, l.

Suppose that the value x k ij of i criterion of j option is between h rating and h + 1 rating, then the RMD μ h (u k ij ) of x k ij belonging to the h rating is:

$$ {\mu}_h\left({u}_{ij}^k\right)=\frac{y_{i\left(h+1\right)}^k-{x}_{ij}^k}{y_{i\left(h+1\right)}^k-{y}_{ih}^k} $$
(16)

where y k ih and y k i(h + 1) are the standard values of i criterion belonging to h rating and h + 1 rating, respectively with h = 1,2, ⋯, c.

According to Eq. 14, the RMD μ (h + 1) u k ij of x k ij belonging to h + 1 rating can be obtained, and the RMD belonging to the other rating (<h or > h + 1) is 0.

Then the RMD μ(u k j ) of j option with m k criteria under k principle belonging to each rating can be obtained by:

$$ \boldsymbol{\mu} \left({u}_j^k\right)=\left[\begin{array}{cccc}\hfill {\mu}_1\left({u}_{1j}^k\right)\hfill & \hfill {\mu}_2\left({u}_{1j}^k\right)\hfill & \hfill \cdots \hfill & \hfill {\mu}_c\left({u}_{1j}^k\right)\hfill \\ {}\hfill {\mu}_1\left({u}_{2j}^k\right)\hfill & \hfill {\mu}_2\left({u}_{2j}^k\right)\hfill & \hfill \cdots \hfill & \hfill {\mu}_c\left({u}_{2j}^k\right)\hfill \\ {}\hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ {}\hfill {\mu}_1\left({u}_{m_kj}^k\right)\hfill & \hfill {\mu}_2\left({u}_{m_kj}^k\right)\hfill & \hfill \cdots \hfill & \hfill {\mu}_c\left({u}_{m_kj}^k\right)\hfill \end{array}\right]={\left[{\mu}_h\left({u}_{ij}^k\right)\right]}_{m_k\times c} $$
(17)

3.3 Overall RMD Vector

According to the importance of each criterion, assuming the weighting vector of criteria set M k under k principle is

$$ \begin{array}{cc}\hfill {\boldsymbol{W}}^k=\left({w}_1^k,{w}_2^k,\cdots, {w}_{m_k}^k\right)=\left({w}_i^k\right),\hfill & \hfill {\displaystyle \sum_{i=1}^{m_k}{w}_i^k}=1\hfill \end{array} $$
(18)

Then the overall RMD μ h (u k j ) of j option belonging to h rating under k principle is:

$$ {\mu}_h\left({u}_j^k\right)=\frac{1}{1+{\left[\frac{d_{hj}^k}{d_{\left(h+1\right)j}^k}\right]}^{\alpha }}=\frac{1}{1+{\left[\frac{{\displaystyle \sum_{i=1}^{m_k}{\left[{w}_i^k\left(1-{\mu}_h\left({u}_{ij}^k\right)\right)\right]}^p}}{{\displaystyle \sum_{i=1}^{m_k}{\left[{w}_i^k{\mu}_h\left({u}_{ij}^k\right)\right]}^p}}\right]}^{\alpha /p}} $$
(19)

where d k hj is the weighting distance between the jth option and the hth rating, d k(h + 1)j is the weighting distance between the jth option and the (h + 1)th rating, and p is the parameter of weighting distance. If p = 1, it is called as Hamming distance. If p = 2, we call p Euclidean distance. α is the parameter of optimization principle. If α = 1, it is least absolute. If α = 2, we call it least squarest.

Using Eq. 19, the overall RMDs of j option for k principle in each criterion can be obtained, which consists of the overall RMD vector after normalizing them to \( \overrightarrow{\mu}\left({u}_j^k\right)=\left({\mu}_1\left({u}_j^k\right),{\mu}_2\left({u}_j^k\right),\cdots, {\mu}_c\left({u}_j^k\right)\right) \), h = 1,2, ⋯, c. In a similar way, Eqs. 13 to 19 can be used to get the overall RMD vector of j option with other principles, which formed the overall RMD matrix:

$$ \boldsymbol{\mu} \left({u}_j\right)=\left[\begin{array}{cccc}\hfill {\mu}_1\left({u}_j^1\right)\hfill & \hfill {\mu}_2\left({u}_j^1\right)\hfill & \hfill \cdots \hfill & \hfill {\mu}_c\left({u}_j^1\right)\hfill \\ {}\hfill {\mu}_1\left({u}_j^2\right)\hfill & \hfill {\mu}_2\left({u}_j^2\right)\hfill & \hfill \cdots \hfill & \hfill {\mu}_c\left({u}_j^2\right)\hfill \\ {}\hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ {}\hfill {\mu}_1\left({u}_j^l\right)\hfill & \hfill {\mu}_2\left({u}_j^l\right)\hfill & \hfill \cdots \hfill & \hfill {\mu}_c\left({u}_j^l\right)\hfill \end{array}\right]={\left[{\mu}_h\left({u}_j^k\right)\right]}_{l\times c} $$
(20)

According to μ(u j ) and the importance of each principle to the objective, Eq. 19 is used to evaluate the overall RMD of j option on the objective belonging to h rating, μ h (u j ). The difference now is that the weighting vector of Eq. 19 is about the principle and the RMD vector is the overall RMD vector of j option with each principle.

Then the overall RMD of j option \( \overrightarrow{\mu}\left({u}_j\right)=\left({\mu}_1\left({u}_j\right),{\mu}_2\left({u}_j\right),\cdots, {\mu}_c\left({u}_j\right)\right) \) was obtained after normalized, and \( {\displaystyle \sum_{h=1}^c{\mu}_h\left({u}_j\right)=1} \).

4 Fuzzy Rating Interval

According to the overall RMD vector of an option, the fuzzy rating interval (FRI) of an option and its median value are calculated. Using the median values, the options can be ranked. Fuzzy rating interval (FRI) was presented by Xu et al. (1999) and was applied to evaluate the safety rating. They indicate that fuzzy rating interval is not a crisp value but a fuzzy subset on the rating universe. The method of fuzzy rating interval and rating probability is further illustrated in the following section.

4.1 Fuzzy Rating Interval

Suppose that there is rating universe V = {v 1,v 2,⋯, v c}, and h increases with v h (h = 1,2,⋯,c) increases, then the option rating declines. If w h  < w h+1, then w h is smaller and the option rating is higher. Corresponding to the universe V, the value universe Ω is:

$$ \Omega =\left\{{\Omega}_{12},{\Omega}_{23},\cdots, {\Omega}_{c,c+1}\right\}=\left\{{w}_1\sim {w}_2,{w}_2\sim {w}_3,\cdots, {w}_c\sim {w}_{c+1}\right\} $$
(21)

To get Ω and fuzzy sets, the symmetrical closed triangular fuzzy number is constructed:

$$ {\mu}_{F{A}_h}(w)=\left\{\begin{array}{ll}0\hfill & \mathrm{for}\kern-0.5em w<{w}_h\hfill \\ {}\frac{2\left(w-{w}_h\right)}{w_{h+1}-{w}_h}\hfill & \mathrm{for}\kern0.5em {w}_h\le w<\frac{w_h+{w}_{h+1}}{2}\hfill \\ {}\frac{2\left(w-{w}_{h+1}\right)}{w_h-{w}_{h+1}}\hfill & \mathrm{for}\kern0.5em \frac{w_h+{w}_{h+1}}{2}\le w\le {w}_{h+1}\hfill \\ {}0\hfill & \mathrm{for}\kern0.5em w>{w}_{h+1}\hfill \end{array}\right. $$
(22)

The fuzzy set determining the rating of an option in the universe Ω is defined as fuzzy rating interval. If μ h is known, the symmetrical closed triangular fuzzy number is used to express the fuzzy rating interval as:

$$ \begin{array}{c}\hfill {H}_{\mu_h}=\left[{H}_{\mu_h}^{-},{H}_{\mu_h}^{+}\right]\hfill \\ {}\hfill =\left[{\displaystyle \sum_{h=1}^c{\mu}_h\left({w}_h+{\mu}_h\frac{w_{h+1}-{w}_h}{2}\right)},\kern0.5em {\displaystyle \sum_{h=1}^c{\mu}_h\left({w}_{h+1}+{\mu}_h\frac{w_{h+1}-{w}_h}{2}\right)}\right]\hfill \end{array} $$
(23)

Then the probability that the rating is in this interval is 100 %. The median value of the fuzzy rating interval is

$$ {H}_{M{\mu}_h}={\displaystyle \sum_{h=1}^c{\mu}_h}\frac{w_h+{w}_{h+1}}{2} $$
(24)

4.2 Probability of Rating

If \( \left[{H}_{\mu_h}^{-},{H}_{\mu_h}^{+}\right]\subseteq \left[{w}_h,{w}_{h+1}\right] \), then the probability that the rating is equal to h is 100 %. If \( \left[{H}_{\mu_h}^{-},{H}_{\mu_h}^{+}\right]\subseteq \left[{w}_h,{w}_{h+2}\right] \), then the probability that the rating is equal to h is

$$ {\pi}_h=\frac{{\displaystyle {\int}_{H_{\mu_h}^{-}}^{w_{h+1}}{\mu}_{F{A}_h}(w) dw}}{{\displaystyle {\int}_{H_{\mu_h}^{-}}^{w_{h+1}}{\mu}_{F{A}_h}(w) dw}+{\displaystyle {\int}_{w_{h+1}}^{H_{{}_{\mu_h}}^{+}}{\mu}_{F{A}_{h+1}}(w) dw}} $$
(25)

and the probability that the rating is equal to h + 1 is

$$ {\pi}_{h+1}=\frac{{\displaystyle {\int}_{w_{h+1}}^{H_{{}_{\mu_h}}^{+}}{\mu}_{F{A}_{h+1}}(w) dw}}{{\displaystyle {\int}_{H_{\mu_h}^{-}}^{w_{h+1}}{\mu}_{F{A}_h}(w) dw}+{\displaystyle {\int}_{w_{h+1}}^{H_{{}_{\mu_h}}^{+}}{\mu}_{F{A}_{h+1}}(w) dw}} $$
(26)

where \( {\mu}_{F{A}_h}(w) \) is the membership function for evaluating the fuzzy rating interval as shown in Eq. 22.

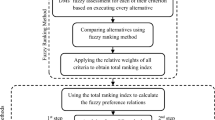
According to Section 3 and 4, the FRI computation steps of the water allocation option are shown in Fig. 4.

Fig. 4
figure 4

FRI computation process of water allocation option

Full size image

5 Case Study

As a way of comparison, the water allocation method of this study was applied for water allocation in the Jining City in Shandong Province, China, which has been studied previously with the maximum entropy principle by Zhong et al. (2010). According to the water resources distribution of the area, the Jining City is divided into three zones; namely east zone of lake, west zone of lake and yellow river zone. Thirteen assessment criteria are employed, which were categorized into the social-economic rationality, the ecological environment rationality, the water resource combination rationality and the development and utilization efficiency rationality. The option rating is divided into four grades. The value of the universe is given as:

$$ \Omega =\left\{0.5\sim 1.5,\kern0.5em 1.5\sim 2.5,\kern0.5em 2.5\sim 3.5,\kern0.5em 3.5\sim 4.5\right\} $$
(27)

The rating standard values of all the criteria are shown in Table 1. Rating I is the highest grade, which reflects that the performance of water allocation option is optimal.

Table 1 Assessment criteria and rating standard values
Full size table

Using the actual situation of Jining City, Zhong et al. (2010) made eight water allocation options for the target year 2015 from the perspectives of water supply, water demand and environmental. The criterion values of all options are listed in Table 2. Obviously, these options have the hierarchy structure of multi-region, multi-principle and multi-criteria. Hence, the above presented hierarchy assessment model based on variable sets is used for selecting the optimal option.

Table 2 Criterion values of water allocation option for target year 2020 in Jining City
Full size table

The options were assessed in turn according to each principle and each criterion. Finally, the fuzzy rating interval (FRI) of each option was obtained. According to the median values of the FRIs, all options were ranked. If the median value for FRI of an option is minimal, the option is optimal for its rating and is the closest to the highest grade rating I. Referring to the standard values of all the ratings, the relative membership degree (RMD) of each criterion for each rating is calculated by Eqs. 14 and 16. The results are shown in Table 3. Here, only a list of the RMDs for the criteria of option 1 on the east zone of lake is provided. As shown in Table 3, the sum of the RMD for each rating is 1. For example, in option 1, the industrial output values per cubic meter water for the east zone of the lake is 461.83 Yuan/m3. According to the standard values of all the ratings in Table 1, the criterion value is between I rating and II rating. Thus, the RMD of this criterion belonging to I rating is 0.7455 while the one belonging to II rating is 0.2545. Therefore, this criterion belongs more to I rating.

Table 3 RMD of each criterion of option 1 belongs to each rating in the east zone of the lake
Full size table

Based on the relative membership degree (RMD) of each criterion for each rating, Eqs. 19, 23 and 24 were used to evaluate the overall RMD of each principle to each rating, the fuzzy rating interval and its median value. The results are listed in Table 4. Here, only the results of option 1 are shown. According to Table 4, the performances of the same option under the different principles in the same zone can be compared. For example, in the west zone of the lake, the median values of the fuzzy rating interval (FRI) for all the principles are 3.082, 1.2246, 1.4453 and 1.8264, respectively. Thus in all aspects of option 1, the ecological environment rationality is best for the west zone of lake. Its FRI is [1.1539, 1.2953]. Since it is included in [0.5, 1.5], its probability belonging to rating I is 100 %. In contrast, the social-economic rationality for the water shortage rate in agriculture of option 1 is highest in the west zone of the lake and is up to 61.76 %.

Table 4 Overall RMD of option 1 to each rating in each zone under each principle
Full size table

Similarly, the performances of the same option in the different zones under the same principle can be compared. For example, under the social-economic rationality principle, the median values of fuzzy rating interval (FRI) for option 1 in all zones are 3.0282, 2.6242 and 3.4011. All the ratings are low. In all zones, the industrial output value per cubic meter water at the east zone of the lake is lowest and the water shortage rates in industrial and agriculture are minimal. However, the water shortage rates in industrial and agriculture are more important than the other criteria and its performance in this zone is highest. Additionally, the performances of the different options in the same zone under the same principle can also be compared.

Using the overall relative membership degree (RMD) to each rating under each principle and the overall RMD to each rating under all principles, the fuzzy rating interval (FRI) and the median value of FRI were obtained from a combination of Eqs. 19, 23 and 24. The results are shown in Table 5. According to the results, options in the same zone can be ranked. For example, in the west zone of the lake, the median value of FRI of option 7 is 1.0213 and is minimal in all eight options, which illustrates that the performance of the option is best. In contrast, the performance of option 8 is worst for the water resource combination of this option and is not rational. Its groundwater rate for water supply is high. Especially, there is some proportion of deep groundwater. In addition, the performances of the same option in different zones are compared. For example, the performance of option 1 is better in the east zone of the lake than that in the two others.

Table 5 Overall RMD of each option to each rating in each zone under all principles
Full size table

Based on the overall relative membership degree (RMD) of each option to each rating under all the principles, Eqs. 19, 23 and 24 can be used to evaluate the overall RMD of each option to each rating in all zones, the fuzzy rating interval (FRI) and the median value of FRI. The differences are that the importance of principle w k needs to be replaced with the importance of zone w s , and that the overall RMD of each principle u kj needs to be replaced with the overall RMD in each zone v sj . Here k is the principle number, s is the zone number and j is the option number. The results are shown in Table 6.

Table 6 Overall RMD of each option to each rating in all zones
Full size table

As shown in Table 6, the median value of fuzzy rating interval (FRI) of option 7 is minimal in all eight options while option 7 is optimal. This result is the same as that of Zhong et al. (2010), but the ranking of eight options is different. For example, in this paper the worst option is the option 8 but, in contrast, the worst option is the option 1 in Zhong et al. (2010). The two options can be emphatically analyzed using the criteria values listed in Table 2.

According to Table 5, in the west zone of the lake, the median values of FRI of option 1 and option 8 are 2.1488 and 3.1892, respectively. The ones in the east zone of the lake are 1.6505 and 1.9037, respectively. The ones in the yellow river zone are 2.6237 and 2.6035, respectively. Obviously, the main difference between the two options is from the west and the east zones of the lake, especially the west zone of the lake but the difference in the yellow river zone is small. Thus, it enabled analyses of the difference between the two options in the west and east zones of the lake. Table 7 lists the overall RMD of each principle, the FRI and the median value of FRI of option 1 and option 8 in the west zone and the east zone of the lake.

Table 7 Comparison of option 1 and option 8 in the west zone of lake and the east zone of lake
Full size table

As shown in Table 7, in the west and east zones of the lake, there is a remarkable difference in water resources combination between the option 1 and option 8 but there is not much difference in other principles. In the option 8, the deep groundwater needs to be explored since its proportion is high. This proportion is 14.7 % in the west zone of the lake and 6.1 % in the east zone of the lake. These circumstances are not propitious for groundwater resources protection. Since the water resources combination is more important, the option 8 is worse than the option 1 overall. This reflects that the ranking of options in this paper is more rational than indicated in Zhong et al. (2010).

In addition, Table 6 indicates that the median values of FRI for several options are very similar. The ratings of the options tend to be the same in such a way that the differences among the options are not obvious. For example, the median values of FRI of option 1 and option 4 are respectively 1.3894 and 1.3912, very close, both between rating I and rating II, and closer to rating I. However, the probability that option 1 belongs to rating I is 98.3 % and larger than the option 4 belonging to rating I. Hence, to a certain degree, the probability of the rating can reflect the difference between the two similar options.

However, through the case study, some limitations of the approach that needs to be pointed out as follows: 1) if the system is divided into more than three levels, both the complexity of water allocation assessment and the computation burden will be markedly increased; 2) before the assessment of water allocation options, the criterion should be independent, otherwise the interrelations between them may distort the real effect of the primary ones; and 3) on application, it is better to develop the software in advance according to the method presented in this paper for convenient use by a decision-maker.

6 Conclusions

In this paper, the optimal selection model based on variable sets has been improved from single layer to multiple layers and adapted to the structure of water resources option with multi-region, multi-principle and multi-criteria influences. The FRI has been utilized to describe option rating to overcome the disadvantage that the ratings are very close among several options. The procedure for the option assessment used in this paper is clear and simple, and provides a rational assessment of the results.

The results from the case study employed indicate that the hierarchy optimal selection model based on variable sets cannot only be used for the overall option assessment, but also for single assessment such as single zone and single principle. Therefore, this model can help decision-makers rank water resources options overall or partially to meet the demands of different interests. Additionally, by comparison with the maximum entropy model, this hierarchy optimal selection model is deemed more reliable because it overcomes the inherent weakness of the principle of maximal membership for ranking the options.

According to the assessment result, the major conclusions regarding policy implications for water allocation for the Jining City are as follows: 1) reducing the water shortage in agriculture and improving the industrial output value per cubic meter water are two crucial ways for promoting the socioeconomic rationality of the city; and 2) it is very necessary for improving water resources composition rationality of the city to reduce the exploitation of groundwater, especially deep groundwater.