1 Introduction

Many recorded annual flood peaks series are too short to allow for a reliable estimation of extreme floods, or even there is not a flow-gauging facility close to the site of interest. Because overestimation of design floods causes too high structural costs, while their underestimation results in excessive flood damage costs and even loss of lives, prediction of future floods of high return periods must be reasonably accurate. Hydrological events such as annual maximum flow (also called annual flood peak, herein) or annual maximum precipitation are random variables. The regional flood frequency analysis involves (1) identification of a homogeneous region, (2) selection of the probability distribution suitable for this homogeneous region, and (3) estimation of flood peak quantiles at (un-gauged) sites of interest; and, the first two steps are carried out using the recorded data from all gauged sites of acceptable record lengths in the region. In this study, a regional flood frequency analysis is applied to 13 selected gauging stations in The East Mediterranean River Basin in Turkey where the parameters of the candidate distributions are estimated by the method of L-moments.

If flood frequency characteristics of all stations in a geographical region are close to each other, then it is a homogeneous region from the aspect of flood frequency analysis. As verified by many relevant studies, the regional flood frequency curve of a homogeneous area is more reliable than at-site frequency curves obtained from too short recorded series in that region (e.g., Hosking and Wallis 1993; Saf 2009). For example, in a comprehensive report by the World Meteorological Organization (WMO), it is stated that: “At–site/regional methods are better than at–site methods even in the presence of a modest amount of heterogeneity.” (Cunnane 1989). Similarly, in the Abstract of their paper, which explores the suitability of various probability distributions based on L-moments diagrams using flood flow data at 61 sites across Australia, Vogel et al. (1993a) say: “Recent research indicates that regional index-flood type procedures should be more accurate and more robust than the type of at-site procedures evaluated here.”.

The probability weighted moments (PWM) and estimation of parameters of a probability distribution by the PWM method was introduced by Greenwood et al. (1979). Since then this method has been used widely in both practice and research. Hosking et al. (1986) presented the algorithm of parameter estimation by the PWM method for the Generalized Extreme Vaules (GEV) distribution and showed that the PWM method is superior to the maximum-likelihood (ML) method for the GEV distribution. Similarly, in the ‘Concluding Remarks’ chapter of the WMO report (Cunnane 1989), it is stated that: “Parameter estimation by PWM, which is relatively new, is as easy to apply as ordinary moments, is usually unbiased, and is almost as efficient as ML. Indeed in small samples PWM may be as efficient as ML. With a suitable choice of distribution PWM estimation also contributes to robustness and is attractive from that point of view. Another attraction of the PWM method is that it can be easily used in regional estimation schemes.”. Yet, it is a known fact that the magnitudes of the parameters of a distribution by the method of PWM are the same as those by the method of L-moments. Therefore, the magnitudes of any return-period flood peaks obtained by either the PWM method or the L-moments method are equal. The L-moments method applied for regional flood frequency analysis as presented by Hosking and Wallis (1997) is superior to the PWM method however, because (1) it delineates boundaries of a homogeneous region based on a heteorogenity measure, which depicts the deviation of L-variation coefficients (L-Cv’s) of individual series from the overall weighted average regional L-Cv, and (2) it determines the probability distribution most suitable to a homogeneous region by a goodness-of-fit measure, which is quantification of closeness of plots of coefficients of L-kurtosis (L-Ck) versus L-skewness (L-Cs) of both the probability distributions and of the sample series. In this study the index flood approach is used as the tool of the regional flood frequency analysis, which is in parallel with the remarks given in this WMO report: “PWM based regional index flood procedures are most efficient and least biased and are easy to apply.” (Cunnane 1989).

Regional flood frequency analysis is a necessary practice because of two reasons: (1) the need for estimation of design flood magnitudes for hydraulic structures on natural streams which have no gauged records, and (2) too short records when they exist (e.g., Acreman and Sinclair 1986; Berthet 1994; Burn 1990; Dalrymple 1960; Meigh et al. 1997; Ouarda et al. 2008; Parida et al. 1998; Rao and Hamed 1997; Saf 2009; Stedinger and Tasker 1985; Zrinji and Burn 1994, 1996). To perform a regional flood frequency analysis, the drainage basin of interest must be hydrologically a homogeneous region or it must be subdivided into homogeneous regions. The homogenity test by the index flood method was first introduced by Dalrymple (1960). Wiltshire (1986) pointed out some drawbacks of Dalrymple test and proposed a cluster analysis in light of physical basin characteristics. In 1960’s through 80’s, prior to the development of the L-moments method and ANNs techniques, distribution parameters were computed mostly by the method of moments and sometimes by the ML method, and classical regression analysis was resorted to for regionalized equations which were based on a set of covariates available at gauged sites to predict flood peak magnitudes of desired return periods at ungauged sites. Ouarda et al. (2008) give a detailed summary of the conventional methods for regional flood frequency analysis other than the L-moments and the artificial neural networks (ANNs) methods, which they categorize as hierarchical clustering, canonical correlation, and canonical krieging, applied by the commonly used probability distributions like Gumbel, 2- and 3-parameter Log-Normal, Pearson-III, Log-Pearson-III, and GEV, whose parameters are computed by the methods of ML and moments. Soon after this paper, Shu and Ouarda (2008) present the ‘adaptive neuro-fuzzy inference system’ method for regional flood frequency analysis, also. An extensive review and comparative evaluation of different regionalization methods is also given by Grehys (1996).

Hosking (1986, 1990) defined the L-moments as linear combinations of the PWMs and used L-moment ratio diagrams to choose more suitable probability distributions in a homogeneous region. Hosking and Wallis (1993, 1997) extended the use of L-moments for regional frequency analysis and developed statistics to measure possible discordancy of individual sites, homogeneity of all the sites in the region, and goodness-of-fit of candidate probability distributions. Bobee and Rasmussen (1995) state: “L-moment ratio diagrams have become popular tools for regional distribution identification, and for testing for outlier stations.”. The parameters of probability distributions estimated by the L-moments method from a recorded sample series are more robust to the possible outliers in the series, and compared with conventional moments, L-moments are less subject to bias in estimation (Vogel and Fennesy 1993; Hosking and Wallis 1997). Vogel and Fennesy (1993); Vogel et al. (1993a, b); Karim and Chowdhury (1995); Madsen et al. (1997); Mkhandi and Kachroo (1997); Rao et al. (1997); Parida et al. (1998); Sankarasubramanian and Srinivasan (1999); Kjeldsen et al. (2002); Jaiswal et al. (2003); Kumar et al. (2003); Yue and Wang (2004); Atiem and Harmancioglu (2006); Ellouze and Abida (2008), and Saf (2009) have investigated various issues involved in the regional flood frequency analysis by the L-moments approach.

The Artificial Neural Networks (ANNs), essentially a powerful black-box model, have a flexible mathematical structure that is capable of identifying complex non-linear relationships between inputs and outputs without predefined knowledge of the underlying physical processes involved in the transformation. The ANNs models are useful and efficient particularly for problems where characteristics of the cause-effect processes are difficult to describe using physical equations (French et al. 1992; Minns and Hall 1996). Jingyi and Hall (2004) applied the geographical approaches known as Ward’s Cluster Method, the Fuzzy C-means Method, and the Kohonen Neural Network method to 86 sites in the basins of Gan River and Ming River, both in southeast of China, to delineate homogeneous regions based on site characteristics and showed that lower standard errors of estimate are produced using an Artificial Neural Networks (ANNs) application.

Dawson et al. (2006) applied ANNs on data from the Centre for Ecology and Hydrology’s Flood Estimation Handbook and used the index flood method to predict T-year flood events for 850 catchments across the UK, and they concluded that ANNs were more reliable than multiple regression models.

In this study, a regional flood frequency analysis based on the index flood procedure using the L-moments method is applied to the Eeast Mediterranean River Basin, which is one of the 26 major basins in Turkey. Next, the Artificial Neural Network models of (1) the Radial Basis Neural Networks (RBNN), (2) the Generalized Regression Neural Networks (GRNN), and (3) the Multi-Layer Perceptrons (MLP) are investigated as alternatives to the L-moments method. And, the Multiple-linear and multiple-nonlinear regression models (MLR and MNLR) are also used in the analysis. A few of the gauged sites with fairly long records are treated as if they were ungauged, and the results of these six different methods are compared.

Geostatistics is a new technique in water resources engineering for regionalized quantification of probabilistic variables. This method interpolates the value of a random variable (e.g., the elevation, z, of the landscape) as a function of the geographic location of an ungauged site from observations at nearby gauged stations. The geostatistical variogram is a function describing the degree of spatial dependence of a random variable and is defined as the variance of the difference between field values at two locations across realizations of the field (Cressie 1993). Our study gets inspired from this technique and we use the spatial locations (latitude, longitude, and altitude) in modeling regional flood frequency analysis. The spatial distribution of logarithms of annual flood peaks (Ln(Q)) observed from the gauging stations are estimated by means of five independent variables, which are: drainage area (DA), elevation above sea level (EASL) (altitude), longitude (LO), and latitude (LA) of the gauging site, and return period (T), which is computed by frequency analysis applied on the annual flood peaks series observed at that gauging site. Because initial regression trials indicated a more meaningful relationship between Ln(Q) versus the independent variables, Ln(Q) was chosen as the dependent variable instead of Q.

2 L-Moments Method as Related to the Regional Flood Frequency Analysis

2.1 L-moments and L-moment Ratios

L-moments are linear combinations of probability weighted moments and are defined as (Hosking 1990; Hosking and Wallis 1997)

$$ \left. {\begin{array}{*{20}c} {{\lambda_1}={M_{100 }}} \hfill \\ {{\lambda_2}=2{M_{110 }}-{M_{100 }}} \hfill \\ {{\lambda_3}=6{M_{120 }}-6{M_{110 }}+{M_{100 }}} \hfill \\ {{\lambda_4}=20{M_{130 }}-30{M_{120 }}+12{M_{110 }}-{M_{100 }}} \hfill \\ \end{array}} \right\} $$
(1a)

where, M100 is the zeroth, M110 is the first, M120 is the second, and M130 is the third probability weighted moments. The L-mean, λ1, is a measure of central tendency which is the same as the conventional mean and the L-standart deviation, λ2, is a measure of dispersion, as λ3 and λ4 are third and fourth L-moments. M110 is the expected value of the random variable, x, weighted by its probability of non-exceedance, P nex . M120 and M130 are the expected values of x weighted by (P nex )2 and (P nex )3, respectively. The j’th probability-weighted moment is defined as

$$ \begin{array}{*{20}c} {u.b.} \\ {{{\mathrm{M}}_{{1\mathrm{j}0}}}=\smallint {{{\left( {{P_{nex }}} \right)}}^j}xf(x)dx} \\ {l.b.} \\ \end{array} $$
(1b)

where, l.b. and u.b. are the lower and upper bound values of the random variable, x, which are the end values of its range, f(x) is its probability density function, and P nex is its non-exceedence probability defined as: P nex = Prob(l.b. < x ≤ X), X being a numerical magnitude of x in: (l.b. < X ≤ u.b.) whenever it occurs randomly.

The dimensionless L-moment ratios are (Hosking 1990; Hosking and Wallis 1997):

$$ \left. {\begin{array}{*{20}c} {{\tau_2}={{{{\lambda_2}}} \left/ {{{\lambda_1}}} \right.}\left( {\mathrm{L}\text{-}\mathrm{coefficient}\,\mathrm{of}\,\mathrm{variation},\,\mathrm{L}\text{-}\mathrm{Cv}} \right)} \hfill \\ {{\tau_3}={{{{\lambda_3}}} \left/ {{{\lambda_2}}} \right.}\left( {\mathrm{L}\text{-}\mathrm{coefficient}\,\mathrm{of}\,\mathrm{skewness},\,\mathrm{L}\text{-}\mathrm{Cs}} \right)} \hfill \\ {{\tau_4}={{{{\lambda_4}}} \left/ {{{\lambda_2}}} \right.}\left( {\mathrm{L}\text{-}\mathrm{coefficient}\,\mathrm{of}\,\mathrm{kurtosis},\,\mathrm{L}\text{-}\mathrm{Ck}} \right)} \hfill \\ \end{array}} \right\} $$
(2)

Stedinger et al. (1993) present a good summary of the L-moments method applied to various distributions and give the relationships among the distribution parameters and the L-moments. Hosking and Wallis (1997) say: “L-moment ratios measure the shape of a distribution independently of its scale of measurement.”. For a probability distribution that takes only positive values, τ2 varies within the interval: 0 ≤ τ2 < 1, and the ranges of the other ratios are: −1 < τ3 < +1, and −1 < τ4 < +1. Actually, these properties of the L-moment ratios are claimed to be an advantage over the conventional coefficients of skewness and of kurtosis, because as the latter may assume very high magnitudes affected by possible outliers, the former always remain in the reasonable and confined interval of (−1, +1) (e.g., Hosking 1990; Hosking and Wallis 1997; Vogel and Fennesy 1993).

The arithmetic average of a sample series is the estimate of λ1. In order to compute the sample estimates of the L-coefficients of variation, skewness, and kurtosis, firstly, the 1st, 2nd, and 3rd sample probability weighted moments are computed as averages of magnitudes of n number of elements in the sample series multiplied by 1st, 2nd, and 3rd powers of their Pnex’s, respectively, which are estimated by a suitable plotting position formula.

2.2 L-moments Method for Regional Flood Frequency Analysis

The index-flood method with the L-moments approach is explained with examples in the book by Hosking and Wallis (1997), and it is rephrased concisely by most relevant papers (e.g., Abolverdi and Khalili 2010; Atiem and Harmancioglu 2006; Hussain and Pasha 2009; Kumar et al. 2003; Parida, et al. 1998; Saf 2009). Therefore, the rewording of this method will not be rewritten here in order to save space. Succintly however, the steps are summarized below.

Firstly, the boundaries of a potentially homogeneous region from the aspect of flood frequency analysis are estimated taking into consideration geographical, topographical, and meteorological conditions of the area. The second step is to search for those single gauged sites which may be discordant from the rest of the group. This is done by discordancy test, which is based on comparing the individual L-coefficients of variation, skewness, and kurtosis with the averaged group L-coefficients. The stations which are found to be discordant are discarded from the rest of the analyses. The next step is the homogeneity test by three standardized homogeneity statistics, which are based on differences of individual L-moment ratios from those averaged ones computed by weighting the lengths of the individual series by the total number of elements of all the single series in the region. The third step is determination of those probability distributions more suitable for the region by a goodness-of-fit procedure known as the Z DIST statistic, which is based on computing a standardized statistic measuring the differences of plotted points of L-Kc versus L-Sc computed out of the sample series from the theoretical values of L-Kc versus L-Sc of the candidate probability distributions, and checking whether │Z DIST│ is smaller than 1.64, the quantile of the standard normal distribution for a tail probability of 5 % corresponding to a confidence of 90 %.

The same procedure described in Chapter 4 of the book by Hosking and Wallis (1997) is applied to the East Mediterranean River Basin using the Fortran computer programs provided to the authors by Hosking himself.

3 Study Area

The annual instantaneous flood peaks, the series of the highest instantaneous flow rate in a particular water year over the period of record, were picked for 13 stream-gauging stations in the East Mediterranean River Basin (SWW 1994), whose record lengths varied between 10 and 39. Some characteristic information of the annual flood peaks series recorded in this basin is given in Table 1.

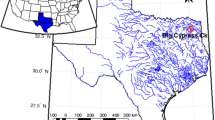
Table 1 Brief information about the 13 stream-gauging stations in the East Mediterranean River Basin
Full size table

The stream-gauging stations in Turkey are owned and operated by two governmental bureaus, which are the General Directorates of Electrical Power Resources Survey and Development Administration (known as EIE in Turkey), and of State Water Works (known as DSI in Turkey). The total drainage area at the most downstream site is 22048 km2, and the mean annual runoff of the basin is 11.07 km3/year. Hence, the mean annual yield is 15.6 l/s/km2. Fig. 1 shows the boundary of the basin area and the locations of the gauging stations of the East Mediterranean River Basin.

Fig. 1
figure 1

Map of the East Mediterranean River Basin

Full size image

Actually, in this basin there are a few small basins side by side with streams of small to moderate sizes discharging to the Mediterranean Sea, which are all bordered from north by Toros Mountains paralleling the shoreline. Because of the similarities in their geographical terrains, vegetation patterns, and climate, and because there is significant orographic precipitation at the seaward sides of the Toros Mountains, the EIE in Turkey, grouped all these small watersheds in one large basin called the East Mediterranean River Basin.

4 Regression Techniques

Before the development of the L-moments method by Hosking and Wallis (1993, 1997), classical regression analysis with multiple independent variables were common for regional flood frequency analysis (e.g., Dalrymple 1960; Ouarda et al. 2008; Wiltshire 1986). In the following two subsections, the multiple regressions used in this study are briefly summarized.

4.1 Multiple Linear Regression (MLR)

MLR is a method that can be used to model a linear relationship between a dependent variable and a few independent variables. The model is defined as follows with y as the dependent variable versus a number of independent variables: x 1 , x 2 ,...., x p :

$$ y={\beta_0}+{\beta_1}{x_1}+{\beta_2}{x_2}+\ldots +{\beta_j}{x_j}+\ldots +{\beta_p}{x_p}+\varepsilon $$
(3)

where ε, the “noise” variable, is a normally distributed random variable with a mean value of zero and a standard deviation of σ, for which an unbiased estimate can be made based on the recorded data. The values of the coefficients β 0 , β 1 , β 2 , . . ., β p are to be estimated so as to minimize the sum of squares of differences between the observed y values in the recorded series and the ones predicted by Eq. (3) (Chapra and Canale 2002).

4.2 Multiple Non-Linear Regression (MNLR)

The basic concept of nonlinear regression is similar to that of linear regression, namely to relate a dependent variable to the independent variables, with the exception of a nonlinear analytical relationship. The non-linear regression used in this study is

$$ y=dx_1^{{{C_1}}}x_2^{{{C_2}}}.....x_p^{{{C_n}}} $$
(4)

or,

$$ y=\ln (d)+{C_1}\ln \left( {{x_1}} \right)+{{\mathrm{C}}_2}\ln \left( {{x_2}} \right)+\ldots +{{\mathrm{C}}_{\mathrm{p}}}\ln \left( {{x_{\mathrm{p}}}} \right) $$
(5)

where, y is the dependent variable, C i’s are the regression coeffcients, d is the multiplicative error term, and p is the number of independent variables.

5 Artificial Neural Network Methods

5.1 The Multi-Layer Perceptrons (MLP)

A Multi-Layer Perceptrons (MLP) model distinguishes itself by the presence of one or more hidden layers, whose computation nodes are called “hidden neurons of hidden layers”. An MLP network structure is shown in Fig. 2. The function of hidden neurons is to intervene between the external input and the network output in some useful manner. By adding one or more hidden layers, the network is then enabled to extract higher order statistics. In a rather loose sense, the network acquires a global perspective despite its local connectivity due to the extra set of synaptic connections and the extra dimension of NN inter-connections. Each neuron in a specific layer is fully or partially connected to many other neurons via weighted connections. The scalar weights determine the strength of the connections between interconnected neurons. A zero weight refers to no connection between two neurons and a negative weight refers to a prohibitive relationship. The detailed theoretical information about MLP can be found at Haykin (1998) and Govindaraju and Rao (2000).

Fig. 2
figure 2

Typical ANN configuration with one hidden layer

Full size image

MLP is trained using the Levenberg–Marquardt technique because it is more powerful and faster than the conventional gradient descent algorithms (Hagan and Menhaj 1994; El-Bakyr 2003; Cigizoglu and Kisi 2005).

MLP can have more than one hidden layers; however, theoretical studies have shown that a single hidden layer is sufficient for MLP to approximate any complex nonlinear function (Cybenco 1989; Hornik et al. 1989). Therefore, in this study, a one-hidden-layer MLP was used. Throughout all the MLP simulations, the adaptive learning rates were used to speed up training. While the number of network inputs and outputs is dependent on the problem input and data, the number of hidden layer neurons must be specified by the user. Therefore, determination of the optimum number of the hidden layer neurons is very important in order to predict a parameter accurately by ANNs. Although most of the empirical approaches proposed in the literature for determining the number of hidden layer neurons depend on the numbers of input and/or output neurons (Paola 1994; Kanellopoulos and Wilkinson 1997; Gahegan et al. 1999), none of these suggestions are universally accepted (Kavzog¡lu 2001). A common strategy for finding the optimum number of hidden layer neurons starts with a few numbers of neurons and keeps increasing the number of neurons while monitoring the performance criteria, until no significant improvement is observed (Goh 1995). Accordingly, here, the number of hidden layer neurons was found using the simple trial-and-error method in all the applications.

In this study, the performance of various network models with different hidden layer neuron amounts was examined to choose an appropriate number of hidden layer neurons. Hence, two neurons were used in the hidden layer at the beginning of the process, and then the number of neurons was increased stepwise by adding one neuron at each step until no significant improvement was noted. While the number of hidden layer neurons is found using simply the trial-and-error method in all applications, the choice of the activation functions may, however, strongly influence the complexity and performance of neural networks. Various activation functions have been described in the literature (e.g., Duch and Jankovski 1999), while the most commonly used nonlinear functional forms in spatial analysis are the sigmoid (logistic) and tangent hyperbolic functions (Dawson and Wilby 1998). Here, after having tested different activation function combinations, the sigmoid and linear functions were used for the activation functions of the hidden and output nodes, respectively. These sigmoid functions were employed to generate a degree of non-linearity between the input(s) and output(s). The function is called sigmoid because it is produced by a mathematical function having an “S” shape. Often, the sigmoid function refers to the special case of the basic formula for logistic function defined as:

$$ f\left( {{h_j}} \right)=\frac{1}{{1+{e^{{-k{h_j}}}}}} $$
(6)

where k is the coeffcient that adjusts the abruptness of the function and hj is the sum of the weighted input. This function maps any value to a new value between 0.0 and 1.0. The hyperbolic tangent function is also utilized as an alternate to the logistic funtion. In fact, both the function are in sigmoid form. Mathematically, yhe hyperbolic tangent function is given as

$$ f\left( {{h_j}} \right)=\frac{2}{{1+{e^{{-2{h_j}}}}}}-1 $$
(7)

One important thing to note the tangent sigmoid activation function is that its output range is (−1, 1) (Maier 1995). The pure linear activation function is a simply a linear function that produces the same out put as its net input.

5.2 The Radial Basis Function-Based Neural Network (RBNN)

Radial Basis Function-Based Neural Networks (RBNN) was introduced to the Artifical Neural Networks literature by Broomhead and Lowe (1988). RBNN consists of two layers whose output nodes form a linear combination of the basis functions. The basis functions in the hidden layer produce a significant non-zero response to input stimulus only when the input falls within a small localized region of the input space. Hence, this paradigm is also known as a localized receptive field network (Lee and Chang 2003). The relation between inputs and outputs is illustrated in Fig. 3. Transformation of the inputs is essential for fighting the curse of dimensionality in empirical modeling. The type of input transformation of the RBNN is the local nonlinear projection using a radial fixed shape basis function. After nonlinearly squashing the multi-dimensional inputs without considering the output space, the radial basis functions play a role as regressors. Since the output layer implements a linear regressor, the only adjustable parameters are the weights of this regressor. These parameters can therefore be determined using the linear least squares method, which gives an important advantage for convergence. The basic concept and algorithm of the RBNN model are described in Lee and Chang (2003).

Fig. 3
figure 3

The RBNN network structure

Full size image

5.3 The Generalized Regression Neural Networks (GRNN)

A schematic depiction of Generalized Regression Neural Networks (GRNN) is shown in Fig. 4. Tsoukalas and Uhrig (1997) describe the theory of GRNN, which consists of four layers: input layer, pattern layer, summation layer, and output layer. The number of input units in the first layer is equal to the total number of variables. The first layer is fully connected to the second, pattern layer, where each unit represents a training pattern and its output is a measure of the distance of the input from the stored patterns. Each pattern layer unit is connected to the two neurons in the summation layer: S−summation neuron and D−summation neuron. The S−summation neuron computes the sum of the weighted outputs of the pattern layer while the D−summation neuron calculates the non-weighted outputs of the pattern neurons. The connection weight between the i th neuron in the pattern layer and the S−summation neuron is O i ; the target output value corresponding to the i th input pattern. For D−summation neuron, the connection weight is unity. The output layer merely divides the output of each S−summation neuron by that of each D−summation neuron, yielding the predicted value to an unknown input vector μ as:

$$ {O_i}\left( \mu \right)=\frac{{\sum\nolimits_{i=1}^n {{O_i}\exp \left[ {-D\left( {\mu, {\mu_i}} \right)} \right]} }}{{\sum\nolimits_{i=1}^n {\exp \left[ {-D\left( {\mu, {\mu_i}} \right)} \right]} }} $$
(8)

where n indicates the number of training patterns and the Gaussian D function in Eq. (8) is defined as:

$$ D\left( {\mu, {\mu_i}} \right)=\sum\limits_{j=1}^p {{{{\left( {\frac{{{\mu_j}-{\mu_{ij }}}}{\zeta }} \right)}}^2}} $$
(9)

where, p indicates the number of elements of an input vector. μ j and μ ij represent the j th element of μ and μ i , respectively. ζ is generally referred to as the spread factor, whose optimal value is often determined experimentally (Kim et al. 2003). A large spread corresponds to a smooth approximation function. Too large a spread means a lot of neurons will be required to fit a fast changing function. Too small a spread means many neurons will be required to fit a smooth function, and the network may not generalize well. In this study, different spreads were tried to find the best value for the given problem. The GRNN does not require an iterative training procedure as in the back-propagation method (Specht 1991).

Fig. 4
figure 4

Schematic diagram of a GRNN model

Full size image

6 Results and Discussions

6.1 L-moments Analysis

A regional flood frequency analysis by the index flood method coupled with the L-moments method is applied to the East Mediterranean River Basin in Turkey using the recorded annual flood peaks series of 13 stream-gauging stations in it. The geographical position of the studied basin, the natural streams and the locations of the gauging sites are shown in Fig. 1. Some relevant numerical information is given in Table 1, and the L-Cv, L-Cs, and L-Ck values computed using the recorded sample series of these 13 stations are given in Table 2. Values of the site discordancy measure, D i , the heterogeneity measure, H, and the goodness-of-fit measure, Z DIST, are computed for the whole region using the Fortran computer program developed and provided by Hosking (1991). The maximum value of Discordancy, D i , is 2.71, which suggests that no site is discordant because 2.71 is less than 3.0, meaning all the 13 gauged sites will be included in the homogeneity test. The heterogeneity measures, H(1) and H(3), computed by carrying out 500 simulations using the data of 13 sites are 0.21 and 0.25, which indicate that the East Mediterranean River Basin as a whole is a homogeneous region, because both H(1) and H(3) are smaller than 1.0 (Hosking and Wallis 1997).

Table 2 LCv, LCs, LCk and Di values at various gauging stations in the East Mediterranean River Basin
Full size table

The goodness-of-fit value, Z DIST, is computed for the distributions of Generalized Logistic, Generalized Extreme Values, Generalized Normal, Pearson Type III, and Generalized Pareto, and as seen in Table 3 the Z DIST is smaller than 1.64 for two of these distributions for the East Mediterranean River Basin, which are Generalized Logistic (GLO) and Generalized Extreme Values (GEV). So, either one of the GLO and GEV distributions can be used as the probability distribution suitable for this homogeneous region. Interestingly, these two distributions seem to be the most suitable for regional frequency analysis in homogeneous regions at many parts of the world. For example, Ellouze and Abida (2008) found the GEV distribution as the best in seven and the GLO distribution as the best in three homogeneous regions in Tunisia. Also, Noto and Loggia (2009) found GEV to be the most suitable distribution for all five homogeneous regions of Sicily, Italy.

Table 3 Values of the Z DIST Statistic of various distributions for the East Mediterranean River Basin
Full size table

The magnitudes of the regional parameters for the GEV and GLO distributions as well as the 5-parameter Wakeby distribution are given in Table 4. Because of the analytical form of its distribution function, the Wakeby distribution cannot be numerically included in the Z DIST goodness-of-fit test, similar to 3-parameter distributions (Hosking and Wallis 1997). However, with its five parameters, more than most of the well-known distributions, it has a wider range of distributional shapes than the other distributions, and therefore the Wakeby distribution is recommended as a parent distribution in regional flood frequency analysis by Hosking and Wallis (1997).

Table 4 Regional parameters for various frequency distributions in the East Mediterranean River Basin
Full size table

Using the GEV, GLO, and Wakeby distributions, standardized quantiles have been computed at the selected return periods of T = 1.11111, 1.25, 2, 5, 10, 20, 100, 200, 500 and 1000 years and plotted against the respective return periods (Table 5). Next, data generated for each site are fitted to the regional distribution, and the simulated dimensionless quantile estimates for each site and the region are computed. It is then possible to obtain the flood estimates for each site by multiplying the dimensionless quantiles by the sample means of each site. For ungauged catchments however, the at-site means can not be computed because of the absence of the observed data. Hence, similar to many others, in this study a regional regression expression has been developed relating the mean annual flood peak to the catchment area, which, for the East Mediterranean River Basin has turned out to be Eq. (10) below.

$$ \begin{array}{*{20}c} {\overline{Q}=1.371{A^{0.6878 }}} \hfill & {\left( {{R^2}=0.79} \right)} \hfill \\ \end{array} $$
(10)

where, A is the drainage area in km2, and the equation is fairly meaningful with a determination coefficient of R 2 = 0.79.

Table 5 Values of dimensionless growth factors (QT/Qave) for various return periods in the East Mediterranean River Basin
Full size table

Although both GLO and GEV distributions passed the Z DIST test, GLO performed better than GEV in the East Mediterranean River Basin (0.20 << 1.56, in Table 3), and therefore the former may be preferred in the regional flood frequency analysis. Hence, the flood peak quantile having a probability of non-exceedance of F can be computed by Eq. (11) below, which is developed using the GLO distribution.

$$ \frac{Q}{\overline{Q}}=-0.314+1.238{{\left( {\frac{1-F }{F}} \right)}^{-0.189 }} $$
(11)

6.2 Regression Analysis

The spatial distribution of logarithms of annual flood peaks (Ln(Q)) observed from the gauging stations has been estimated by means of five independent variables, which are: drainage area (DA), elevation above sea level (EASL), longitude (LO) and latitude (LA) of the gauging site, and return period (T), which is computed by frequency analysis applied on the observed annual flood peaks series of that gauging site. Initial regression trials indicated a more meaningful relationship between Ln(Q) versus the independent variables instead of Q as the dependent variable. In modeling studies, the available data is generally divided into two sub-sets: a training set and an independent validation set (Maier and Dandy 2000). Before application of the MLR, MNLR and the other ANN methods, the available dataset were randomly divided into two independent parts. The training data was used for learning, and the testing data was used for comparison of the models. To overcome some extrapolation difficulties in prediction of the extreme values, the minimum and maximum magnitudes of the variables used in the modelling were set in the training data. Ten gauging stations were selected for the training phase and the rest three gauging stations for testing. The minimum and maximum values of the model variables are summarized in Table 6. Next, both MLR and MNLR techniques were applied to the training dataset, which resulted in the following expressions to offer the best statistical fit for the dataset trained, respectively:

$$ \mathrm{Ln}\left( \mathrm{Q} \right)=-10.37+0.00022\mathrm{DA}-0.00177\mathrm{EASL}-0.702\mathrm{LO}+1.061\mathrm{LA}+0.0172\mathrm{T} $$
(12)
$$ \mathrm{Ln}\left( \mathrm{Q} \right)=3.987\frac{{\mathrm{D}{{\mathrm{A}}^{0.000225 }}\mathrm{L}{{\mathrm{A}}^{0.6654 }}{{\mathrm{T}}^{0.0231 }}}}{{\mathrm{EAS}{{\mathrm{L}}^{0.0015 }}\mathrm{L}{{\mathrm{O}}^{0.6225 }}}} $$
(13)
Table 6 The minimum and maximum values of the input and output parameters
Full size table

The t values of the coefficients of Equtaions (12) and (13) were found to be 17.6, −11.0, −10.6, 5.2, 6.3 and 17.3, −11.8, −10.0, 11.7, 7.2 for DA, EASL, LO, LA and F, respectively, all of them passing the t-test having 222 degrees of freedom with a probability of non-exceedance of 0.99.

6.3 Analysis of Artificial Intelligence Methods

Three different ANN models, namely RBNN, GRNN and MLP, were developed to improve the outputs of the MLR and MNLR techniques for regional flood frequency analysis at ungauged sites. For this purpose, three different artificial neural network program codes were written in MATLAB programming language. The tangent sigmoid, logarithmic sigmoid, and pure linear transfer functions were tried as activation functions for hidden and output layer neurons to determine the best network model. The most appropriate results were obtained by the ANN model comprising 5 input, 8 hidden and 1 output layer neurons, denoted as ANN(5, 8, 1), using the logarithmic sigmoid activation functions for both hidden and output layer neurons.

For the RBNN applications, different numbers of hidden layer neurons and spread constants were examined in the study. The number of hidden layer neurons that gave the minimum root mean square errors (RMSE) was found to be 6. The spread is a constant which is selected before the RBNN simulation. The larger the spread is the smoother the function approximation will be. Too large a spread means a lot of neurons will be required to fit a fast changing function. Too small a spread means many neurons will be required to fit a smooth function, and the network may not generalize well. The spread that gave the minimum MSE was 0.48. This was found with a simple trial-error method adding some loops to the program codes. The spread parameter values providing the best testing performance of the GRNN model was equal to 0.01 with 228 hidden layer neurons.

Magnitudes of the root mean square error (RMSE), mean absolute error (MAE), mean absolute relative error (MARE), which are defined by Eqs. 14–16 below, and R2 (determination coefficient) values by the MLR, MNLR, ANNs, and L-moments methods for both training and testing phases are given in Table 7.

$$ RMSE=\sqrt{{\frac{1}{N}{{{\sum\limits_{i=1}^N {\left[ {Ln{(Q)_{{{i_{measured }}}}}-Ln{(Q)_{{{i_{predicted }}}}}} \right]}}}^2}}} $$
(14)
$$ MAE=\frac{1}{N}\sum\limits_{i=1}^N {\left| {\left. {Ln{(Q)_{{{i_{measured }}}}}-Ln{(Q)_{{{i_{predicted }}}}}} \right|} \right.} $$
(15)
$$ MARE=\frac{1}{N}\sum\limits_{i=1}^N {\left| {\left. {\frac{{Ln{(Q)_{{{i_{measured }}}}}-Ln{(Q)_{{{i_{predicted }}}}}}}{{Ln{(Q)_{{{i_{measured }}}}}}}} \right|} \right.} \times 100 $$
(16)

in which N is the number of elements in the series.

Table 7 The training and testing performances of the MLR, MNLR, GRNN, RBNN, MLP and L-Moments in regional flood estimation
Full size table

As seen from Table 7, the MLP model provided the smallest RMSE (0.173), MAE (0.146), and MARE (2.7 %) for the testing phase. The L-moments and MLP models gave similar results for the training phase. According to the test results, the MLP estimations are slightly better than those of the L-moments and these two produced more accurate results than the GRNN, RBNN, MLR, and MNLR models.

Although GRNN gave better statistical results in comparison with RBNN in the training phase, the RBNN model gave better predictions in the testing phase, because of the large number of hiden layer neurons of the GRNN algorithm. It can be seen from Table 7 that ANNSs performed better than MLR and MNLR in both training and testing phases.

A comparison between the MLR and ANN models for logs of maximum discharge values, Ln(Q), is presented in Table 8 and shown in Fig. 5 in terms of residual analysis. The determination coefficient (R2) of the predicted versus observed values (according to a linear regression equation as Predicted = a + b × Observed) and analysis of the residuals were calculated for the East Mediterranean Drainage Basin. The MLP and L-moments approaches gave more accurate results than those of the RBNN, GRNN, MLR, and MNLR models. The MLP model performed better in terms of sum of square errors (SSE), mean, and linear biases (2.75, 0.0012, and −0.003, respectively) than the L-moments (8.27, −0.271, and −0.145 for SSE, mean, and linear biases, respectively). These two methods gave more accurate results than those of the others. The regression analysis of predicted and measured Ln(Q) values obtained by MNLR and MLR had the biggest SSE, mean, and linear biases. As seen from Fig. 5, both MLR and MNLR overestimated the small values and underestimated the high values. The RBNN and GRNN models had large distribution of residuals. The L-moments had high mean and linear biases, therefore it overestimates for the most parts of the floods.

Table 8 Regression equations, coefficient of determinations, sum of square error (SSE) and linear biases between predicted and observed values of ln(Q), obtained using MLR, MNLR, GRNN, RBNN, MLP and L-Moments models
Full size table
Fig. 5
figure 5

Residual (= observed – predicted) values compared with the observed Ln(Q) for the MLR, MNLR, RBNN, GRNN, MLP, and L-moments models

Full size image

The performances of all methods analysed herein are shown in Figs. 6 and 7, which indicate that MLR and MNLR are unsatisfactory in prediction of Ln(Q) values in comparison with the artificial neural network methods of RBNN, GRNN, MLP, and with L-moments. The MLP and L-moments models seem to provide similar accuracy and both are significantly superior to the RBNN, GRNN models. Although the L-moments model has high R2 values than MLP, the L-moments estimations are over the exact fit line, whereas the MLP estimations are distributed around it.

Fig. 6
figure 6

Histogram of the estimated flood values by MLR, MNLR, RBNN, GRNN, MLP, and L-moments in testing dataset

Full size image
Fig. 7
figure 7

Scatter plot of the estimated flood values by MLR, MNLR, RBNN, GRNN, MLP, and L-moments in testing dataset

Full size image

7 Conclusions

The hydrological homogeneity of the East Mediterranean River Basin in Turkey from the standpoint of annual flood peaks frequency is analyzed and a regional equation for the T-year flood peak is developed by the method of L-moments. Next, black-box models by the Artificial Neural Networks (ANNs) methods of multi-layer perceptrons (MLP), radial basis function-based neural networks (RBNN), and generalized regression neural networks (GRNN), and by multiple linear regression, and by multiple nonlinear regression are also developed for prediction of flood peaks of various return periods at ungauged sites in this basin. The MLP model is observed to provide estimates close to the L-moments approach. The MLR and MNLR models produce less accurate results than those of the three ANNs models and L-moments. For the testing phase, the MLP model yield slightly better results with the smallest MARE and RMSE statistics (2.7 % and 0.173 m3/s, respectively) than the L-moments method (5.0 % and 0.298 m3/s, respectively). These two models perform better than the RBNN, GRNN, MLR, and MNLR models. The MLP model proposed herein yields an acceptable accuracy, with less computational effort, and a smaller amount of input data, in comparison with more detailed models such as the L-moments method. This study indicates that the MLP model can be employed successfully in estimation of flood peaks at ungauged sites in a hydrologically homogeneous region. As an outcome of this study, the natural logarithm of an annual flood peak of any return period (T) can be reasonably estimated for any ungauged site of a natural stream in the East Mediterranean River Basin as a function of the drainage area (DA), elevation above sea level (EASL), longitude (LO) and latitude (LA) of the site, and the return period (T). For a hydrologically homogeneous basin or sub-basin elsewhere in the world, it is believed that a similar model can be developed for rational prediction of annual flood peaks at both gauged and ungauged sites.