Keywords

15.1 Introduction

Assessment of extreme rainfall for a desired return period is of utmost importance for the planning and design of minor and major hydraulic structures, viz., dams, bridges, barrages, and storm water drainage systems. Such information can be applied to the planning and design of water resources projects linked to reservoir design, river bank protection works, soil and water conservation, etc., as well as to the prevention of floods and droughts (CWC 2010). In the post-commissioning stage, where it is necessary to analyze the risk of hydraulic structures failing, extreme rainfall occurrences are crucial (Baratti et al. 2012). Extreme rainfall with a desirable return duration is used, depending on the design life of the structure. Extreme value analysis (EVA), which involves fitting a probability distribution to the series of annual 1-day maximum rainfall (AMR) data, can be used to achieve this (Abida and Ellouze 2008). The robust forecasts of precipitation patterns at a significant lead time can be of great importance in managing water resources as well as mitigating the risk associated with prolonged and flash flooding (Das et al. 2020; Floods 2019; Goswami et al. 2018). Numerical weather prediction models are conventionally used to forecast these extremes by mathematically modeling the governing physical processes (Bauer et al. 2015; Dueben et al. 2021). Being inspired by the learning capability of neural networks, an advancement in machine learning from nonlinear complex data (Pisner and Schnyer 2020; Scher and Messori 2018), we have incorporated artificial neural networks (ANNs) to model and predict the monthly rainfall of all three considered stations with Bayesian regularization to overcome the issue of overfitting in the data.

15.2 Literature Review

For analyzing the rainfall data, a variety of probability distributions from the normal, gamma, and extreme value families of distributions will be provided (Arvind et al. 2017; Esberto, 2018; Sasireka et al. 2019). The distributions that are most frequently applied and employed in EVA are the two-parameter normal (N2) and log normal (LN2), Pearson type 3 (P3), log Pearson type 3 (LP3), extreme value type 1 (EV1), and generalized extreme value (GEV) distributions. From this, it is clear that the N2 and LN2 belong to the family of normal distributions, the P3 and LP3 to the family of gamma distributions, and the EV1 and GEV to the family of extreme value distributions (Bhuyan et al. 2010; Mujere 2011; Olumide et al. 2013; Haberlandt and Radtke 2014; Sharma and Sharma 2019; Singh et al. n.d.; Tank et al. 2021). The parameter estimation algorithms method of moments (MoM), maximum likelihood method (MLM), and L-moments (LMO) are used to determine the distribution’s parameters based on the planned applications and the variate under consideration (Acar et al. 2008; Malekinezhad et al. 2011; Vivekanandan 2020).

Using Gumbel (also known as EV1), LN2, and LP3, AlHassoun (2011) conducted a study on establishing an empirical formula to estimate rainfall intensity in the Riyadh region. He came to the conclusion that among the three distributions examined for the assessment of rainfall intensity, the LP3 provides greater accuracy. In order to calculate the extreme rainfall depths at several rain gauge stations in southeast United Kingdom, Esteves (2013) used the EV1 distribution. For the purpose of creating intensity-duration-frequency curves for seven divisions in Bangladesh, Rasel and Hossain (2015) used the EV1 distribution. In the Bamenda Mountain region of Cameroon, Afungang and Bateira (2016) used the EV1 distribution to estimate the maximum quantity of rainfall for various times. Eight probability distributions were used by Baghel et al. (2019) to analyze the frequency of daily maximum rainfall data in the Udaipur district. For the Anakapalli, Atchutapuram, Kasimkota, and Parvada sites, Vivekanandan and Srishailam (2020) examined the MoM and MLM estimators of the EV1, LN2, and LP3 distributions utilized in the EVA of rainfall. The question of which distribution model best fits a given collection of data comes frequently when multiple probability distributions are used in the EVA of rainfall. Both quantitative and qualitative analyses may be able to provide an answer, and the conclusions are quantifiable and trustworthy. The effectiveness of fitting the selected probability distributions is assessed quantitatively using chi-square (χ2) and Kolmogorov-Smirnov (KS), and diagnostic (viz., D-index) tests, as well as qualitatively using fitted curves for the estimated extreme rainfall. The methods used in the EVA of rainfall and the evaluation of EVA results using GoF and diagnostic tests are succinctly discussed with an example, and the outcomes of the study are reported in the paper.

There have been numerous attempts to predict rainfall using different physical, empirical, and physio-empirical models. In many parts of the world, these models have been used to predict rainfall on an annual, seasonal, monthly, and daily scale (Bauer et al. 2015; Goyal et al. 2018; Nardi et al. 2018). Physical models are created taking into account the synoptic climate and the physical processes by which various climatic variables interact to produce rainfall in a location. In order to anticipate rainfall in physical models, numerical models are created to describe ingrained physical processes (Goyal and Ojha 2010). These models require data and knowledge on numerous land-ocean-atmospheric variables and are typically quite complicated. In spite of this, physical models frequently fail to provide accurate rainfall predictions, because they frequently use crude approximations of complicated physical events (Coles 2001; Su et al. 2012). Physical models have been replaced with empirical models based on statistical techniques. These models are typically created with a specific climate variable in mind, such as rainfall prediction, based on the connection defined by statistics between that variable and its antecedent variables. Statistical models are always region-specific; thus, the model created using the statistical relationship between local rainfall and other atmospheric factors is only applicable for the region (Goyal et al. 2012; Katz 2013). These models are also referred to as empirical models for this reason. In most instances, empirical models are more accurate than physical models and are easier to construct and apply. The primary flaw of empirical models is their total reliance on the historical data utilized to construct them. As a result, they are unable to replicate rainfall in an unknown environment. For instance, empirical models cannot accurately predict the abrupt variations in rainfall that the region has experienced recently and is expected to experience in the future since the models were not constructed with such a wide range of data (Hewitson et al. 2014). In this circumstance, physical models are used as a forecasting option. The development of physical-empirical models, in which empirical models are based on the variables physically responsible for the region’s climate, has recently received attention in an effort to address the limitations of both types of modeling approaches (Vergés et al. 2016).

Regression analysis, including linear and higher-order polynomial (nonlinear) regressions, is typically used to create statistical models (Chen and Zhang 2022; Su et al. 2012). However, the relationship between rainfall and the climatic variables that cause it is frequently enigmatic and cannot be captured using commonly used statistical approaches. Complex regression analysis is frequently created using machine learning (ML) methods (Hinge et al. 2018; Sharma and Goyal 2020). Climate extremes in changing climate are getting worse, and robust prediction of these extremes is one of the most essential aspects in managing water resources and disaster management (Poonia et al. 2021a, b). As a result, the focus of meteorologists has been shifted to the development of machine learning (ML)-based physical-empirical forecasting models in recent years. ANNs are one of the numerous possibilities explored and presented in the literature for prediction. They are a flexible and rich concept that may be used to tackle difficulties with clustering, time series, and function approximation in addition to classification tasks (Rautela et al. 2022). The adaptability of ANNs encouraged researchers to look into their suitability for classification and regression problems (Vu et al. 2019). Studies reveal that ANNs and other artificial intelligence techniques are capable of outperforming conventional statistical techniques. The Bayesian assessment of an ANN for prediction indicates that the performance of the neural architecture is critical to its configuration, because it strongly influences the estimate efficacy of the framework (Burden and Winkler 2008). To avoid over fitting, however, in this study we concentrate on Bayesian regularization (BR) of the ANN employed for predicting monthly rainfall (Okut 2016). The huge amount of complex nonlinear meteorological data from various sources necessitate great care to avoid over fitting ANN algorithm (Ye et al. 2021). We have implemented BR-ANN to explore the nonlinear relationships associated with monthly rainfall at three stations and predict it for the next.

15.3 Methodology

The cumulative distribution function (CDF) and quantile estimator of six distributions (viz., N2, LN2, P3, LP3, EV1, and GEV) adopted in EVA is presented in Table 15.1. The empirical equations involved in determining the MoM, MLM, and LMO estimators of the distributions are presented in Table 15.2 (Rao and Hamed 2000).

Table 15.1 CDF with quantile estimator six probability distributions
Full size table
Table 15.2 Determination of parameters of six distributions using MoM, MLM, and LMO
Full size table

15.3.1 MoM of P3 Distribution

The MoM estimators of P3 distribution (Bobee and Askhar 1991) can be determined by solving the system of equations, which is given as below:

$$ {\mathrm{M}}_r^{\hbox{'}}=\frac{\exp \left( r\xi \right)}{{\left(1- r\alpha \right)}^{\beta }} $$
(15.1)

where in 1-rα > 0, r = 1, 2, 3

$$ \mu (x)={\mathrm{M}}_1^{\hbox{'}},\kern0.62em \sigma {(x)}^2={\mathrm{M}}_2^{\hbox{'}}-{\left({\mathrm{M}}_1^{\hbox{'}}\right)}^2\mathrm{and}\kern0.6em \gamma (x)={\mathrm{M}}_3^{\hbox{'}}-3{\mathrm{M}}_2^{\hbox{'}}{\mathrm{M}}_1^{\hbox{'}}+2{\left({\mathrm{M}}_1^{\hbox{'}}\right)}^3 $$
(15.2)

where \( {M}_r^{\hbox{'}} \) is the rth moment of x about the origin and μ(x) is the coefficient of skewness of the observed data.

15.3.2 MLM of P3 Distribution

The MLM estimators of P3 distribution (Bobee and Askhar 1991) can be determined by solving the following system of equations:

$$ \left.\begin{array}{l}\sum \limits_{i=1}^{\mathrm{N}}\left(x(i)-\xi \right)=\mathrm{N}\alpha \beta \\ {}\sum \limits_{i=1}^{\mathrm{N}}\frac{1}{\alpha}\left(x(i)-\xi \right)=\mathrm{N}\psi \left(\beta \right)\\ {}\sum \limits_{i=1}^{\mathrm{N}}\frac{1}{\left(x(i)-\xi \right)}=\frac{\mathrm{N}}{\alpha \left(\beta -1\right)}\end{array}\right\} $$
(15.3)

Here, ψ(β) is the digamma function of estimator of the scale parameter (β).

In Table 15.2, λ1, λ2, and λ3 are the first, second, and third, respectively, LMOs (Hosking 1990) that can be determined in Eq. (15.4), which is given as below:

$$ {\uplambda}_1={\mathrm{b}}_0,\kern0.5em {\uplambda}_2=2{\mathrm{b}}_1-{\mathrm{b}}_0,\kern0.5em {\uplambda}_3=6{\mathrm{b}}_2-6{\mathrm{b}}_1+{\mathrm{b}}_0\kern0.5em \mathrm{and}\kern0.75em {\uptau}_3={\uplambda}_3/{\uplambda}_2 $$
(15.4)

wherein λr + 1 is the r + 1th LMO (Hosking and Wallis 1993), which is defined by:

$$ {\lambda}_{r+1}=\sum \limits_{k=0}^r\frac{{\left(-1\right)}^{r-k}\left(r+k\right)!}{{\left(k!\right)}^2\left(r-k\right)!}\;{b}_k $$
(15.5)

wherein bk is an unbiased estimator (Saf 2009; Gubareva and Gartsman 2010) and given by:

$$ {\mathrm{b}}_k={\mathrm{N}}^{-1}\sum \limits_{i=k+1}^{\mathrm{N}}\frac{\left(i-1\right)\left(i-2\right)..\dots \left(i-k\right)}{\left(\mathrm{N}-1\right)\left(\mathrm{N}-2\right)..\dots \left(\mathrm{N}-k\right)}x(i) $$
(15.6)

where x(i) is the observed data of ith sample and N is the total number of samples.

15.3.3 Goodness-of-Fit Tests

GoF tests are essential for checking the adequacy of probability distributions to the AMR series in rainfall estimation. Out of a number GoF tests available, the widely accepted GoF tests are χ2 and KS (Zhang 2002), which are used in the study.

χ2 test statistic is defined by:

$$ {\chi}^2=\sum \limits_{j=1}^{\mathrm{NC}}\frac{{\left({\mathrm{O}}_j(x)-{\mathrm{E}}_j(x)\right)}^2}{{\mathrm{E}}_j(x)} $$
(15.7)

where Oj(x) is the observed frequency value of x for jth class, Ej(x) is the expected frequency value of x for jth class, and NC is the number of frequency classes (Charles Annis 2009). The rejection region of χ2 statistic at the desired significance level (η) is given by \( {\chi}_C^2\ge {\chi}_{1-\eta, \mathrm{NC}-\mathrm{m}-1}^2 \). Here, m denotes the number of parameters of the distribution, and \( {\chi}_C^2 \) is the computed value of χ2 statistic by the probability distribution.

KS test statistic is defined by:

$$ \mathrm{KS}=\underset{i=1}{\overset{\mathrm{N}}{\operatorname{Max}}}\left|{\mathrm{F}}_e\left(x(i)\right)-{\mathrm{F}}_c\left(x(i)\right)\right| $$
(15.8)

where x(i) is the observed data for ith sample, Fe(x(i)) = r/(N + 1) is the empirical CDF of x(i) of ith sample, “r” is the rank assigned to sample values arranged in ascending order (i.e., x(1) < x(2) < … ..x(N)), and Fc(x(i)) is the computed CDF of x(i) of ith sample.

Test criteria: If the computed values of GoF tests statistic given by the distribution are less than that of the theoretical values at the desired level of significance, then the distribution is considered to be acceptable for EVA at that level.

15.3.4 Diagnostic Test

Sometimes the GoF test results would not offer a conclusive inference, thereby posing a bottleneck for the user in selecting the suitable distribution for the application. In such cases, a diagnostic test in adoption to GoF is applied for making inference. The selection of the most suitable distribution is performed through the D-index test (United States Water Resources Council (USWRC) 1981), which is defined as:

$$ \mathrm{D}-\mathrm{index}=\left(1/\mu (x)\right)\sum \limits_{i=1}^6\left|x(i)-x{(i)}^{\ast}\right| $$
(15.9)

Here, x(i) (i = 1 to 6) and x(i)* are the six highest observed and the corresponding estimated values of ith sample. The probability distribution having the least D-index is considered as a better suited for rainfall estimation.

15.3.5 Bayesian Regularized Artificial Neural Network

BR-ANN (Burden and Winkler 2008; Okut 2016) is a more robust variant of ANNs than the standard ANN (Sasireka et al. 2019). This robustness of BR-ANN is obtained through the BR of the ANN parameters. A popular error function (ED) of ANN is as follows:

$$ {\mathrm{E}}_{\mathrm{D}}\left(\mathrm{D}|w,\mathrm{M}\right)=\sum \limits_{i=1}^n{\left({\mathrm{t}}_i-{\hat{\mathrm{t}}}_i\right)}^2 $$
(15.10)

where w denotes weight, M denotes ANN structure, n denotes size of training data, ti is the ith target output, and \( {\hat{t}}_i \)is the ith model (BR-ANN) output.

Regularizing ANN with the Bayesian technique aids in optimizing the ANN parameter by utilizing prior ANN parameter values. In order to do this, an additional term (Ew) is added to the BR-ANN’s target function as follows:

$$ {\mathrm{E}}_{\mathrm{D}}\left(\mathrm{D}|\mathrm{w},\mathrm{M}\right)=\sum \limits_{i=1}^{\mathrm{n}}{\left({\mathrm{t}}_i-{\hat{\mathrm{t}}}_i\right)}^2+{\mathrm{E}}_w $$
(15.11)

In order to improve generalization and gradual conversion, Ew is employed to compensate the unrealistic weights. The function is minimized using an optimization technique based on gradients:

$$ \mathrm{F}=\beta \kern0.5em {\mathrm{E}}_{\mathrm{D}}\left(\mathrm{D}|\mathrm{w},\mathrm{M}\right)=\sum \limits_{i=1}^{\mathrm{n}}{\left({\mathrm{t}}_i-{\hat{\mathrm{t}}}_i\right)}^2+\alpha \kern0.5em {\mathrm{E}}_{\mathrm{w}}\left(\mathrm{w}|\mathrm{M}\right) $$
(15.12)

where the hyper-parameters that need to be optimized are represented by α and β and Ew(w|M) represent sum of square of the ANN architecture. BR-ANN is an efficient predictive model, because it can uncover theoretically complex input-output relationships.

15.4 Application

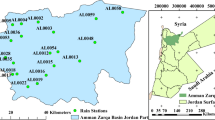
In this paper, a study on the comparison of six probability distributions (viz., N2, LN2, P3, LP3, EV1, and GEV) adopted in the EVA of rainfall is carried out. MoM, MLM, and LMO determine the distribution’s characteristics, which are also employed in the estimation of rainfall. The daily rainfall data recorded at the Afzalpur, Kalaburagi, and Aland locations from 1970 to 2018 and 1970 to 2017, respectively, are used. From the daily rainfall data, the AMR series is taken out and used for EVA CWPRS (2021) do not have data for the intermittent period, according to a review of the daily rainfall statistics. Additionally, it is highlighted that the observed rainfall at Kalaburagi, which was 1.5 mm in 1993 and 15.6 mm in 2015, is inconsistent and was not taken into account while analyzing the data. However, the data for the missing years are ignored and not taken into account in EVA because of the significance of the hydrological extremes. The AMR descriptive data are provided in Table 15.3. The index map shown in Fig. 15.1 shows the locations of the rain gauge stations taken into consideration for the investigation.

Table 15.3 Descriptive statistics of the observed AMR
Full size table
Fig. 15.1
2 illustrations. 1. A map of India and an inset. The inset illustrates a magnified satellite map of the 3 marked sites in the state of Maharashtra. 2. A map of the study site with the 3 marked locations.

Index map of the study area with locations of rain gauge stations

Full size image

From the descriptive statistics (Table 15.3), it is noted that the higher order moments (CS and CK) of the AMR series behave differently for Afzalpur when compared to the values for Aland and Kalaburagi. The CV of the AMR series of Afzalpur, Aland, and Kalaburagi varies between about 27% and 67%, as shown in Table 15.3.

15.5 Results and Discussion

By applying the procedures as described above, a computer code was developed and used in the EVA of rainfall. The code computes the (1) parameters of N2, LN2, P3, LP3, EV1, and GEV (using MoM, MLM, and LMO) distributions; (2) extreme rainfall estimates for different return periods; and (3) GoF test statistic and D-index values.

15.5.1 Estimation of Extreme Rainfall

The MoM, MLM and LMO were used to determine the characterisitcs of N2, LN2, P3,LP3, EV1 and GEV distributions adopted in EVA, wherever applicable. These parameters are used in the following study. Tables 15.4, 15.5, and 15.6 provide estimates of the 1-day maximum rainfall for Afzalpur, Aland, and Kalaburagi for various return periods. The EVA and GoF test results of P3 (LMO) and LP3 (LMO) are not shown in Tables 15.4, 15.5, 15.6, and 15.7 due to the absence of LMO in P3 and LP3 distributions. From the EVA results, it can be seen that, when compared to the values of other distributions for the return periods ranging from 20 to 1000 years, the LP3 (MLM) offered higher estimates for Afzalpur and Aland and the EV1 (MLM) for Kalaburagi.

Table 15.4 Estimated 1-day maximum rainfall for different return periods by six probability distributions for Afzalpur
Full size table
Table 15.5 Estimated 1-day maximum rainfall for different return periods by six probability distributions for Aland
Full size table
Table 15.6 Estimated 1-day maximum rainfall for different return periods by six probability distributions for Kalaburagi
Full size table
Table 15.7 Computed and values of GoF and diagnostic tests statistic by six probability distributions for Afzalpur, Aland, and Kalaburagi
Full size table

15.5.2 Analysis of Results Based on GoF Tests

Six distributions were used to compute the GoF test values for the AMR series of Afzalpur, Aland, and Kalaburagi. The results are shown in Table 15.7. In the current study, the number of frequency classes (NC) is taken into account to be six, and as a result, the degree of freedom (NC-m-1) is taken into account to be two for distributions with three parameters (m), namely, P3, LP3, and GEV, and three for distributions with two parameters (m), namely, N2, LN2, and EV1, when computing the two statistic values. According to the degree of freedom, the theoretical values at the 5% level of significance are observed to be 5.99 for P3, LP3, and GEV and 7.815 for N2, LN2, and EV1. Likewise, the theoretical values of the KS statistic at 5% level of significance with reference to the number of samples considered in EVA are observed as 0.196 for Afzalpur, 0.203 for Aland, and 0.200 for Kalaburagi. From the GoF test results, some of the observations drawn from the study were summarized and presented below:

  • χ2 test results didn’t support the use of MoM, MLM, and LMO estimators of five distributions (viz., LN2, P3, LP3, EV1, and GEV) for the EVA of rainfall for Afzalpur and Aland.

  • χ2 test results supported the use of MoM, MLM, and LMO estimators of all six distributions adopted in EVA of rainfall for Kalaburagi.

  • KS test results didn’t support the use of MoM, MLM, and LMO estimators of N2, LN2, and P3 distributions for EVA of rainfall for Afzalpur.

  • KS test results confirmed the applicability of MoM, MLM, and LMO estimators of all six distributions adopted in the EVA of rainfall for Aland and Kalaburagi.

15.5.3 Analysis of Results Based on Diagnostic Test

In addition to the GoF test, the D-index was used to determine which of the six distributions in the EVA model best fit the criteria for estimating rainfall. These values were calculated using the N2, LN2, P3, LP3, EV1, and GEV distributions and are shown in Table 15.7. Based on the results of the diagnostic tests, it can be deduced that the D-index values of P3 (MoM) for Afzalpur, EV1 (MLM) for Aland, and LP3 (MoM) for Kalaburagi are less than those of other distributions used in the EVA.

15.5.4 Selection of Probability Distribution

Based on the EVA results from the diagnostic tests and GoF quantitative assessment, it was determined that the analysis produced conflicting inferences, necessitating qualitative evaluation. As a result, the best fit for rainfall estimates was again evaluated using fitted curves of the estimated severe rainfall along with D-index values, and a decision was taken as a result.

  • According to the results of the diagnostic tests, EVA could be performed using P3 (MoM) for Afzalpur, EV1 (MLM) for Aland, and LP3 (MoM) for Kalaburagi.

  • The MoM estimators of the distributions, however, are frequently less precise than MLM and LMO, as were previously mentioned. As a result, while choosing the best fit for estimating rainfall in Afzalpur and Kalaburagi, the D-index values obtained from P3 (MoM) and LP3 (MoM) are not taken into account.

  • In light of the foregoing, it is determined that the D-index value of GEV (LMO) is the second subsequent minimum for Afzalpur and Kalaburagi after excluding the D-index values obtained from MoM of P3 and LP3 distributions from the selection.

  • The GEV (LMO) is more matched among the six distributions chosen in EVA for rainfall estimation for Afzalpur and Kalaburagi, whereas EV1 (MLM) is better suited for Aland, according to the qualitative assessment (plots of EVA results) of the outcomes. Figure 15.2 shows the plots of the estimated 1-day maximum rainfall with 95% confidence limits based on the chosen distribution and actual AMR data for the Afzalpur, Aland, and Kalaburagi sites.

Fig. 15.2
3 graphs plot 1 day maximum rainfall versus return period. They illustrate scatterplots and lines with increasing trends. The scatterplots are labeled observed. The lines are labeled upper confidence limit, G E V in graph 1 and 3, E V 1 in graph 2, and lower confidence limit.

Plots of estimated 1-day maximum rainfall by the selected distribution and observed AMR data for Afzalpur, Aland, and Kalaburagi

Full size image

15.5.5 Efficiency Analysis of BR-ANN

Since a neural network demands comparatively more data to recognize the probable pattern (correlation) associated in a time series, the monthly rainfall dataset of all three sites, Afzalpur, Aland, and Kalaburagi, have been taken for 64 years, starting from January 1951 to December 2014. We have distributed this data for all three sites in the percentage of 70:30 for training and validation (testing) purposes to avoid overfitting in the performance evaluation of the predicting capability of ANN.

The performance of the ANN model with the BR technique used in predicting the targeted output has been expressed for training, validation, and the collective monthly rainfall data of all three sites, as shown in Fig. 15.3 (Afzalpur), Fig. 15.4 (Aland), and Fig. 15.5 (Kalaburagi). The efficiency of predicting outputs and targets through fit and errors has also been presented collectively for training and testing for all three sites. The model shows a high correlation between output and targeted input monthly rainfall data while training for all three stations. Since the model was trained for the training dataset, it has a higher correlation of approximately 0.95 between model output and target, whereas it gets reduced to approximately 0.40 in the case of validation (testing).

Fig. 15.3
4 illustrations. 1, 2, and 3. The graphs with scatterplots and superimposed line graphs with increasing trends. They are titled training, test, and all. 4. A line graph with error plots. It plots model B R A N N output versus target output. It illustrates an irregular trend with multiple peaks.

Scatter plot showing correlation between the outputs of BR-ANN and input monthly data (target) of (a) training dataset; (b) testing dataset; and (c) all dataset of Afzalpur; (d) time series plot of predicted monthly rainfall using BR-ANN

Full size image
Fig. 15.4
4 illustrations. 1, 2, and 3. The graphs with scatterplots and line graphs plot output versus target. They are titled training, test, and all and have increasing trends. 4. A line graph with error plots. It plots model B R A N N output versus target output. It plots multiple peaks.

Scatter plot showing correlation between the outputs of BR-ANN and input monthly data (target) of (a) training datasets; (b) testing dataset; and (c) all the dataset of Aland; (d) time series plot of predicted monthly rainfall using BR-ANN

Full size image
Fig. 15.5
4 illustrations. 1, 2, and 3. The graphs with scatterplots and line graphs plot output versus target with increasing trends. They are titled training, test, and all. 4. A line graph with error charts plot model B R A N N output versus target output. It illustrates an irregular trend and peaks.

Scatter plot showing correlation between the outputs of BR-ANN and input monthly data (target) of (a) training datasets; (b) testing dataset; and (c) all the dataset of Kalaburagi; (d) time series plot of predicted monthly rainfall using BR-ANN

Full size image

15.5.6 Conclusions

This study compared the MoM, MLM, and LMO estimators of six probability distributions (N2, LN2, P3, LP3, EV1, and GEV) used in the EVA of rainfall for Afzalpur, Aland, and Kalaburagi with the aim of identifying the best distribution for rainfall estimation through quantitative (GoF tests using χ2 and KS, and diagnostic test using D-index) and qualitative (fitted curves of the estimated rainfall) assessments. The monthly rainfall patterns of all three stations have also been proposed to model and predict using an ANN with Bayesian regularization technique. The inferences made from the study were condensed and are given below based on the EVA data and BR-ANN predictions:

  • χ2 test results didn’t support the use of all six distributions for EVA of rainfall for Afzalpur. For Aland, the χ2 test result indicates the N2 distribution is acceptable for EVA.

  • χ2 test results supported the use of all six distributions for EVA of rainfall for Kalaburagi.

  • KS test results didn’t support the use of N2, LN2, and P3 distributions for EVA of rainfall for Afzalpur.

  • KS test results confirmed the applicability of all six distributions for EVA of rainfall for Aland and Kalaburagi.

  • The GEV (LMO) is the superior choice among the six distributions chosen in EVA for rainfall estimation for Afzalpur and Kalaburagi, while EV1 (MLM) is better suited for Aland, according to the qualitative assessment (plots of EVA findings) of the outcomes, which was weighed with D-index values.

  • The BR-ANN model has shown high correlation (approximately 0.95) in predicted output values and targeted input data at monthly scale from all three sites while training the datasets.

  • The proposed model has shown comparatively lesser correlation between output and target values in validation, which means the model can be further optimized by hyper tuning the Bayesian regularization parameters.

By considering the data length (i.e., 48 years for Afzalpur, 45 years for Aland, and 46 years for Kalaburagi) of the AMR series available for the study, the study suggested that the estimated rainfall for the return period beyond 200 years may be cautiously used due to uncertainty in the higher-order return periods while designing the hydraulic structures in the respective sites. Some other machine learning algorithms, such as support vector machine (regression), Bayesian linear regression, etc., and some deep learning models, such as recurrent neural network, long short-term memory, etc., can also be explored to model nonstationary and complex rainfall patterns in a comparative analysis.