1 Introduction

In recent decades, the scientific literature concerning the design and management of water supply systems has addressed aspects related to the concept of network reliability, i.e. the ability of a distribution system to satisfy, in both quantitative and qualitative terms, users’ water demand in various situations that may arise throughout its working life (Hashimoto et al. 1982; Wagner et al. 1988a, b; Todini 2000; Tanymboh et al. 2001; Kjeldsen and Rosbjerg 2004; Jun et al. 2008; Liberatore and Sechi 2009; Ramos et al. 2010; Kuo and Hsu 2011; Martínez-Rodríguez et al. 2011). In order to guarantee an adequate degree of reliability in situations of mechanical failure (breakage or maintenance of pipes and devices), the network design must feature isolation valves, as the closure of such devices enables the isolation of the part of the network (segment) containing the pipe or device that needs maintenance or repair, and thereby prevents service disruptions in the network or in large portions thereof (Walski 1993a, b).

The literature contains various studies into the analysis and design of isolation valve systems (Creaco et al. 2010; Giustolisi and Savic 2010; Alvisi et al. 2011; Creaco et al. 2011). In particular, the analysis of an existing system of valves enables its relative reliability and economic burden to be evaluated; reliability is generally expressed as the maximum (Giustolisi and Savic 2010) or weighted average (Creaco et al. 2010) of water demand shortfalls associated with isolation of the various network segments, while the economic burden is characterized by the means of either the total cost of the valves (Creaco et al. 2010), or the total number of valves (as a surrogate for the cost) (Giustolisi and Savic 2010). In the search for the “optimal” solution, i.e. that which guarantees a good trade-off between system reliability and economic burden, various possible valve system configurations are compared using optimization algorithms (Creaco et al. 2010; Giustolisi and Savic 2010; Alvisi et al. 2011; Creaco et al. 2011).

Hence, both the analysis and design phases require the adoption of methods that enable the effective identification of the nodes and pipes disconnected from the source after segment isolation via isolation valve closure. Various such approaches can be found in the literature (e.g. Bentley Systems 2006; Jun and Loganathan 2007; Kao and Li 2007; Creaco et al. 2010; Giustolisi and Savic 2010; Alvisi et al. 2011; Creaco et al. 2011).

Once the segments disconnected from the source points have been identified, the reliability of the valve system can be assessed by evaluating the demand shortfall associated with each. This variable is obtained by summing the demands of the users positioned along the disconnected pipes (Creaco et al. 2010; Giustolisi and Savic 2010; Alvisi et al. 2011; Creaco et al. 2011), taking into account the water demand not supplied through the isolated segment and any accidental disconnections, i.e. parts of the network that are outside the isolated segment but remain unintentionally disconnected from the source points after isolation (Jun and Loganathan 2007). However, this procedure for evaluating the water demand shortfall (hereafter referred to as the topological procedure) is fairly approximate, as it refers only to the topological aspect and does not take into account the demand shortfall related to the hydraulic aspect, i.e. the pressure-lowering effects that may occur in the active part of the network, that which remains connected to the source points after segment isolation; this represents a considerable drawback, as the occurrence of low pressures may cause supplied flow-rates to be lower than the user demands at network nodes, even when the nodes themselves remain hydraulically connected to the source points after segment isolation.

In order to address these issues, Kao and Li (2007) propose the use of pressure-driven hydraulic modelling in association with methods to identify disconnections (the resulting procedure is hereinafter referred to as the hydraulic procedure). Although this method should be more accurate than the topological procedure, thus far the two have not been directly compared with reference to the problems of analysis and design of isolation valve systems. In other words, though the topological and hydraulic procedures will undoubtedly yield different water demand shortfall estimations for each network segment, it is worth investigating the extent of these differences in terms of global evaluation of network reliability. Thus, after a brief description of the two procedures, this paper reports their application to two different case studies: 1) a looped network in which all the pipes have an equal distribution function and 2) a looped network featuring a main branched structure comprising pipes that have both distribution and transmission functions. For both case studies the analysis and re-design problems, consisting of the study of a preset system of isolation valves and the search for the optimal position of the valves, respectively, are addressed in terms of reliability and economic burden. The application sections are followed by an analysis of the results and conclusions.

2 Procedures

After identifying the segments formed as a result of the placement of a predefined set of valves (by means of one of the methods proposed by Bentley Systems 2006; Jun and Loganathan 2007; Kao and Li 2007; Creaco et al. 2010; Giustolisi and Savic 2010; Alvisi et al. 2011; Creaco et al. 2011), the topological procedure requires that the water demand shortfall be associated with the generic i th segment S i . Using the topological procedure, this demand shortfall, hereinafter indicated with the symbol \( D_i^{{top}} \), is obtained by summing the demands of the pipes disconnected after the isolation of S i (Creaco et al. 2010; Giustolisi and Savic 2010; Alvisi et al. 2011; Creaco et al. 2011). In contrast, after the network segments are identified, the hydraulic procedure requires a pressure-driven hydraulic simulation to be performed on these pipes (Giustolisi et al. 2008). This enables the water demand actually met by the connected network to be evaluated. According to the pressure-driven modelling approach, there is a link between nodal outflow and pressure. This link, usually represented by means of the Aoki (1998) formula, can be expressed by the following vector relationship (Alvisi and Franchini 2009):

$$ {\text{q}}\prime { = }{{\text{A}}_{{{22}}}} \cdot {\text{q,}} $$
(1)

where column vectors q and q′ represent nodal demands and actual outflows, respectively; matrix A 22 is diagonal and its generic element (j, j) is defined as:

$$ {\mathbf{A}}_{{{\mathbf{22}}}} {\left( {j,j} \right)} = \left\{ {\begin{array}{*{20}l} {0 \hfill} & {{h_{j} < h_{{\min ,j}} } \hfill} \\ {{{\left( {\frac{{h_{j} - h_{{\min ,j}} }} {{h_{{des,j}} - h_{{\min ,j}} }}} \right)}^{{\frac{1} {2}}} } \hfill} & {{h_{{\min ,j}} \leqslant h_{j} < h_{{des,j}} } \hfill} \\ {1 \hfill} & {{h_{j} \geqslant h_{{des,j}} } \hfill} \\ \end{array} ,} \right. $$
(2)

where the pressure heads h j , h min,j and h des,j relative to node j are the actual value, the minimum value needed to ensure outflow and the desired value, i.e. that required to fully meet water demand, respectively. The link between each nodal demand and demands distributed along network pipes (considered for the assessment of network reliability following segment isolation, as mentioned above) is based on the assumption that the demand along each pipe is distributed equally over the length of the pipe; it is therefore divided into equal parts between the end nodes of the pipe (following the top-down procedure described in Walski et al. 2003). The following relationship is used to evaluate the nodal demand, vector q, starting from vector d, comprising the demands along all of the connected pipes:

$$ {\mathbf{q}} = \frac{1}{2}\left| {{{\mathbf{A}}_{{{\mathbf{21}}}}}} \right|{\mathbf{d}}, $$
(3)

In this formula, A 21 is the transpose of matrix A 12 , where A 12 is the topological matrix that indicates the end nodes for each network pipe (see Todini and Pilati 1988). It is worth remarking that Eq. (3) is to be applied to the network configuration obtained after each segment isolation; in other words, at each application of Eq. (3) vector d comprises only elements relative to the pipes that remain connected upon segment isolation.

Summing up, application of the pressure-driven hydraulic simulation model enables evaluation of the nodal outflows in the part of the network connected to the source points, taking into account the pressure reduction that follows isolation of segment S i . The sum of these outflows yields the water flow-rate Q i actually supplied to users. The water demand shortfall \( D_i^{{hydr}} \) (where the superscript “hydr” indicates that this variable is calculated using the hydraulic procedure) associated with the i th segment is obtained by subtracting the flow-rate Q i from the whole network demand.

It is worth reiterating that, since it also takes into account the reduction in nodal outflows due to pressure drop in the network, the estimated water demand shortfall \( D_i^{{hydr}} \) obtained by means of the hydraulic procedure is always greater than or equal to the estimate \( D_i^{{top}} \) derived by considering only the topological disconnections (see methods by Creaco et al. (2011) and Giustolisi and Savic (2010)). Furthermore, it should be remarked that the assessment of water demand shortfalls via the hydraulic procedure can be performed using either snapshot or extended period simulations (Bentley Systems 2006). Adopting extended period simulations (Todini 2003) is advantageous as it takes into account the emptying processes that may occur in tanks during prolonged outages, and may increase the overall shortfall volume. However, for comparison with the topological procedure, which does not consider tank level variations, and to limit the computation times (especially in optimal design phase: see below), the snapshot version, considering only the daily average consumption, was applied hereinafter.

2.1 Assessment of Reliability and Economic Burden of the Isolation Valve System

The economic burden of an isolation valve system can be assessed by calculating the total number N valv and cost C valv of all valves installed in the network. In detail, C valv can be obtained by summing the cost C of each valve; this can be calculated as a function of the diameter of the pipe the valve is installed in, by using (power or exponential) regression equations calibrated on the basis of data provided in the manufacturers’ catalogues (Creaco et al. 2010; Alvisi et al. 2011; Creaco et al. 2011).

Once water demand shortfalls \( D_i^{{top}} \)(topological procedure) and \( D_i^{{hydr}} \) (hydraulic procedure) associated with the isolation of the i th segment have been evaluated, the reliability of the system can be assessed with reference to the values D max (Giustolisi and Savic 2010) and \( \overline D \) (Creaco et al. 2010; Alvisi et al. 2011; Creaco et al. 2011). In particular, D max is associated with the isolation of the largest segment (hydraulically speaking): the estimates of this variable according to the topological and hydraulic procedures are indicated with \( D_{{max}}^{{top}} \) and \( D_{{max}}^{{hydr}} \) respectively. \( \overline D \), on the other hand, is the weighted average of the demand shortfalls in the N s segments of the network, obtained using the following relationship (Creaco et al. 2010; Alvisi et al. 2011; Creaco et al. 2011):

$$ \overline D = \sum\limits_{{i = 1}}^{{{N_s}}} {{W_i}\,D_i} $$
(4)

In particular, in order to obtain the estimates \( {\overline D^{{top}}} \) and \( {\overline D^{{hydr}}} \) of this variable according to the topological and hydraulic procedures, demand shortfall values \( D_i^{{top}} \) and \( D_i^{{hydr}} \), respectively, have to be used in Eq. (4). The weight W i associated with the i th segment can be calculated as the ratio of the expected number of breakages in the segment to the total expected number of breakages in the whole system over a fixed time interval; when sufficient breakage data is not available for the calibration of models able to predict the expected number of breakages in the network (see Le Gat and Eisenbeis (2000), Kleiner and Rajani (2001, 2002)), it is possible to estimate each weight W i as the ratio of the total length of the pipes in the i th segment to the whole length of the network (Creaco et al. 2010; Walski et al. 2006).

Once again, the values \( D_{{max}}^{{hydr}} \) and \( {\overline D^{{hydr}}} \) (hydraulic procedure) are always greater than or equal to the corresponding values \( D_{{max}}^{{top}} \) and \( {\overline D^{{top}}} \) (topological procedure) due to the pressure-driven simulation model taking into account the reduction in supply as a result of low pressures at network nodes.

3 Application

3.1 Case Studies

The above approaches were applied to two case studies. Case Study 1 considered a simplified schematic of the water distribution system of the city of Ferrara (Italy) (Fig. 1); this system is made up of 49 nodes (two of which, 1 and 49, are reservoir nodes with heads set at 30 m), 76 pipes and 29 loops; the ratio of the number of loops to the number of nodes yields a figure close to 0.60. The whole (average daily) network demand is equal to 367 L/s. Data regarding network pipes, in terms of end nodes and relative elevations z, length L, diameter, Manning roughness coefficient n and water demand d, are reported in Table 1. For the Ferrara network the coefficients h min,j and h des,j of Eq. (2) are set at 5 m and 28 m respectively, on the basis of indications provided by the operator. The total length of the network is about 25.2 Km. In this network, all the pipes have both distribution and transmission functions. It is worth remarking that this skeleton network was taken as an example of large, highly-connected networks and was not used to derive information on the reliability of the real original network, as this also contains small pipes which carry a sizeable portion of the load when the main lines are isolated.

Fig. 1
figure 1

Case Study 1—layout of the schematic distribution network serving the city of Ferrara (Italy): pipe numbers are in brackets []. Pipes 1 and 2 are “pure” transmission mains (no customers linked to them) that link the two reservoirs to the distribution system

Full size image
Table 1 Case Study 1—data relative to the pipes of the schematic distribution network of Ferrara
Full size table

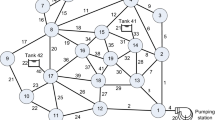
Case Study 2 considered the entire distribution network of the town of Goro (Italy) (Fig. 2), a network made up of 71 nodes (including reservoir node 1 with head set at 27 m), 95 pipes and 25 loops; the ratio of the number of loops to the number of nodes yields 0.35. Though looped, this network presents a branched main structure, in which pipes have a transmission function in addition to their distribution function (see grey line in Fig. 2). The whole (average daily) water demand of the network is equal to 14.94 L/s. The total length of the network is about 13.9 Km. Data relative to network pipes are reported in Table 2. It is worth underlining that in the Goro network there is a lumped demand at node 71, equal to 2.58 L/s, which supplies the Gorino district, although this is not considered in detail in Case Study 2 (incidentally, however, the presence of the Gorino district demand explains the transmission function of the pipes highlighted in Fig. 2). For the Goro network, the coefficients h min,j and h des,j of Eq. (2) were set at 5 m and 25 m respectively. Data concerning network pipes are reported in Table 2.

Fig. 2
figure 2

Case Study 2—layout of the entire distribution network serving the town of Goro (Italy): pipe numbers are in brackets []. Pipes 1 and 2 constitute the “pure” transmission mains (with no linked customers) that link the reservoir to the distribution system. The grey lines represent the pipes that have mainly transmission function

Full size image
Table 2 Case Study 2—data relative to the pipes of the Goro network
Full size table

In the subsequent sections, the cost of each isolation valve installed in the network was calculated using the following exponential equation (derived from Creaco et al. (2010)), which links the cost itself C [€] to the nominal diameter DN[m] of the pipe in which the valve is installed:

$$ C\left( {\text{DN}} \right) = 71.6{e^{{8.7{\text{DN}}}}} $$
(5)

As regards the reliability of the valve system, and in particular the evaluation of the weighted average water demand shortfall (\( {\overline{D}^{{top}}} \) and \( {\overline{D}^{{hydr}}} \)), the weights W i of Eq. (4) are evaluated on the basis of the lengths of the various network segments (as explained in section 2.1).

3.2 Analysis of the Isolation Valve System

The first applications concerned the evaluation of the economic burden and reliability for both case studies. Preset systems of isolation valves were thus considered for explicative purposes, in order to highlight the differences in the reliability indicators D max and \( \overline{D} \) evaluated by the two procedures (topological and hydraulic procedures).

As regards the identification of the disconnections associated with the isolation of the segments, obtained given the number and location of isolation valves placed in the network, this operation was carried out using the procedure proposed by Alvisi et al. (2011). After applying this algorithm, \( D_i^{{top}} \) was evaluated for each segment identified. As regards the pressure-driven hydraulic simulation, the model proposed by Alvisi and Franchini (2009) was used; the hydraulic simulations enabled the evaluation of \( D_i^{{hydr}} \) for each segment identified. Finally \( D_{{max}}^{{hydr}} \) and \( {\overline D^{{hydr}}} \)(relative to the hydraulic procedure) and \( D_{{max}}^{{top}} \) and \( {\overline D^{{top}}} \) (relative to the topological procedure) were evaluated as explained in Section 2.1.

For the first case study (a schematic representation of a real distribution network), a system of valves was randomly generated, within certain constraints (Fig. 3); in particular, in the random generation a probability value equal to 0.25 was assumed for each of the following types of valve installation in every pipe of the network: a) no valve is present, b) one valve is present in proximity to the first/upstream end node (taking into account the topological direction of the pipe—see definition of the topological matrix, for instance, in Todini and Pilati 1988), c) one valve is present in proximity to the second/downstream end node, d) valves are present in proximity to the nodes at both ends of the pipe (two valves per pipe); furthermore, two further assumptions were made: 1—the absence of valves in the transmission mains that link the source point(s) to the network; 2—the installation of at least one valve in the pipes directly connected to the transmission mains, in proximity to the node common to the mains themselves. For the second case study, the system of valves actually present in the network was considered (Fig. 4).

Fig. 3
figure 3

Case Study 1: schematic distribution network of the city of Ferrara—randomly generated valve system (valves represented as pipe disconnections); the topological and hydraulic procedures identify the same group of pipes and nodes as the largest segment from the hydraulic perspective (in the Figure the pipes belonging to this segment are plotted with a thick line)

Full size image
Fig. 4
figure 4

Case Study 2: Goro town network—system of valves actually installed (valves represented as pipe disconnections); the topological and hydraulic procedures associate D max (maximum demand shortfall) with two different groups of pipes (in the Figure the two groups of pipes are plotted with a thick line). For segments S1 and S2 see Fig. 5

Full size image

The results are shown in Table 3 in terms of total number N valv and cost C valv of the valves installed in the network, number N s of segments and values of \( D_{{max}}^{{hydr}} \), \( {\overline{D}^{{hydr}}} \) and \( D_{{max}}^{{top}} \), \( {\overline{D}^{{top}}} \). As is evident, in the case of the network in Fig. 1 (Case Study 1), \( D_{{max}}^{{hydr}} \) is close to \( D_{{max}}^{{top}} \) and \( {\overline{D}^{{hydr}}} \) is close to \( {\overline{D}^{{top}}} \). Furthermore, within this network, the largest segment, i.e. that which presents the highest value of the demand shortfall (D max ), is identified in the same way by both procedures (see Fig. 3). In general it is possible to state that in both cases of D max and \( \overline D \) the equal quantification of the reliability is due to the fact that the network has many loops and all the pipes have equal distribution and transmission functions. As a result of this, the pressure-lowering effects after isolation of the various network segments are moderate (although isolation of a segment leads water to search for other paths, these new paths do not increase head losses in the network); for each segment i, the demand shortfall rate associated with the pressure lowering is negligible, and \( D_i^{{top}}\, \cong \,D_i^{{hydr}} \), as shown in graph (a) in Fig. 5. Overall, we can argue that in highly connected networks (with pipes having both distribution and transmission function as in the schematic version of the Ferrara network) there is good agreement between the results yielded by the topological procedure and those produced by the hydraulic procedure as regards the quantification of segment shortfalls and global reliability indicators.

Table 3 Results of the analysis of the valve systems considered in the two case studies
Full size table
Fig. 5
figure 5

Comparison of \( D_i^{{top}} \) and \( D_i^{{hydr}} \) for the various segments of the networks of Ferrara a and Goro b. Dots S1 and S2 pertain to the segment that present the largest differences between \( D_i^{{hydr}} \) and \( D_i^{{top}} \) in the Goro network (see Fig. 4)

Full size image

In the case of the Goro network, \( D_{{max}}^{{hydr}}\, > D_{{max}}^{{top}} \) and \( {\overline{D}^{{hydr}}} > {\overline{D}^{{top}}} \) (see Table 3); the different behaviour of this network with respect to the previous can be ascribed to the fact that in this case it is possible to detect a branched main structure which has a mainly transmission function. Hence, isolation of a segment that includes a part of this structure moves water towards other paths along which head losses are significantly larger, due to the inadequacy of pipe diameters outside the main structure.

It is also worth noting that in this case, due to the abovementioned effects of isolation of a part of the main structure in a network similar to Case Study 2, the two procedures (topological and hydraulic) identify the largest network segment (to which D max corresponds) in different ways (see Fig. 4). Indeed, the use of the topological procedure identifies the largest segment as the pipe/segment with the highest water demand (see Table 2), whereas the use of the hydraulic procedure identifies it as that made up of pipes belonging to the branched main structure. As expected, the differences in the values of \( D_i^{{top}} \) and \( D_i^{{hydr}} \) for the generic i th segment of the network result in different values for D max and \( \bar{D} \) for the two procedures, as illustrated in graph (b) in Fig. 5; in particular, this graph shows that the largest differences are observed for segments S1 and S2, which include pipes belonging to the main structure of the network (see Fig. 4 to identify the positions of such segments). Overall, it appears that in networks featuring a branched main structure with transmission function, the topological procedure may underestimate the reliability of the valve system.

Table 4 gives the computation times necessary for the hydraulic (\( D_i^{{hydr}} \)) and topological (\( D_i^{{top}} \)) evaluation of the demand shortfalls associated with all the network segments each case study. Comparison of these values clearly shows that the hydraulic procedure requires significantly larger computation times than the topological procedure (particularly when the pressure-driven mechanism is fully activated in the algorithm for network resolution).

Table 4 Computation times (s) relative to the application of the hydraulic and topological procedures for the evaluation of water demand shortfalls to the analysis of the preset systems of isolation valves
Full size table

3.3 Isolation Valve System Design

The topological and hydraulic procedures were coupled with the multi-objective optimization algorithm described in Creaco et al. (2010) for the design of the isolation valve systems in Case Studies 1 and 2. This algorithm is a modified version of NSGAII (Deb et al. 2002), and enables the use of either the total number N valv or the total cost C valv of the valves as the first objective function concerning the economic burden of the system, and the maximum D max or weighted average \( \overline D \) demand shortfall as the second objective function regarding reliability (whose quantification can be obtained by either the topological or the hydraulic procedure).

In the algorithm, the individuals in the population represent different configurations of valves in the network and the individuals’ genes represent four possible installations of valves in each pipe; in particular they can take on values of 0, 1, 2 and 3, which, in relation to each pipe, respectively indicate conditions under which no valve is present, one valve is present in proximity to the first or second end node (respecting the topological direction), and valves are present in proximity to the nodes at both ends of the pipe (two valves per pipe). Furthermore, in the algorithm (see Creaco et al. 2010) a constraint is used in order to enable isolation of the transmission mains that link the source points to the network and, at the same time, facilitate the formation of network segments. This constraint is encoded in all the individuals and generations of the genetic algorithm, and consists of positioning valves in the network pipes linked to each of the transmission mains, in proximity to the node common to the mains themselves; in particular, in Case Studies 1 (Fig. 1) and 2 (Fig. 2), it involves the installation of 6 valves (in pipes 3, 8, 9, 12, 14, 73) and 2 valves (pipes 3 and 10), respectively. For the Goro network (Case Study 2), a further constraint is used in order to isolate the supply to the Gorino district; according to this constraint, a valve is installed in pipe 95, close to node 70.

The initial population of the genetic algorithm is set at 100 individuals for its application to both case studies; in the initial individuals, 98 were generated randomly and 2 were predefined in order to facilitate the convergence of the genetic algorithm towards solutions with small or large number of valves, respectively. In detail, the first individual was encoded in order to contain only the valves relative to the constraints described above, i.e. 6 valves for the Ferrara network (Case Study 1, Fig. 1) and 3 valves for the Goro network (Case Study 2, Fig. 2); the second individual, instead, was encoded following the N-valve rule (Walski et al. 2006); this rule consists of installing valves in all the pipes that converge at each network node. This implies the installation of 148 and 185 valves, for Case Studies 1 and 2, respectively. The characteristics of the preset individuals, in terms of total number N valv and cost C valv of the valves installed, number N s of segments, and values D max and \( \overline D \) obtained by applying the topological and hydraulic procedures, are shown in Table 5.

Table 5 Characteristics of the preset individuals (see text) in the initial population in case studies 1 and 2. Individuals 1 and 2 represent the initial configurations with the lowest and highest number of valves, respectively
Full size table

For each of the case studies, optimization was carried out considering two different pairs of objective functions. In particular, “type I optimization” was performed with the pairs of objective functions N valv —D max (as proposed by Giustolisi and Savic 2010); “type II optimization”, instead, was performed with the pairs of objective functions C valv —\( \overline D \) (as suggested by Creaco et al. 2010). Furthermore, for both types of optimizations, the demand shortfall was evaluated using either the topological or the hydraulic procedure, thereby yielding a total number of 4 optimizations for each case study.

The Pareto fronts for each combination are shown in Fig. 6 (Case study 1) and Fig. 7 (Case study 2). In both Figures, each graph contains a third curve (indicated as topological procedure re-evaluated), plotted by re-evaluating a posteriori, by means of the hydraulic procedure, the dots/solutions of the Pareto front relative to the topological procedure. In other words, in relation to the configuration of valves corresponding to the generic dot of the Pareto front obtained using the topological procedure, a series of pressure-driven hydraulic simulations was carried out to enable calculation of the values D max (type-I optimization) and \( \overline{D} \) (type-II optimization). In Fig. 8, the relationship between N val and C val for the solutions of the Pareto fronts C val —\( \overline{D} \), obtained using type-II optimization, is reported for both case studies.

Fig. 6
figure 6

Case Study 1: schematic distribution network of the city of Ferrara—Pareto fronts obtained using the topological and hydraulic procedures for the evaluation of demand shortfalls, considering the objective functions D max and N val (a: type-I optimization), and \( \overline D \) and C val (b: type-II optimization) in the optimization process; the solutions of the Pareto front associated with the topological procedure have been re-evaluated a posteriori in terms of D max and \( \overline D \), making use of the hydraulic procedure. The dots A (hydraulic procedure) and A’ (topological procedure) represent the solution encoding only 6 valves installed in correspondence to the pipes linked to the transmission mains connected to the reservoir; the dots B (hydraulic procedure) and B’ (topological procedure) pertain to the solution encoded with N valves (see text). Dots D represent the real configuration analysed in Section 3.2 and shown in Fig. 3, evaluated using the hydraulic procedure

Full size image
Fig. 7
figure 7

Case Study 2: Goro town distribution network—Pareto fronts obtained using the topological and hydraulic procedures for the evaluation of demand shortfalls considering the objective functions D max and N val (a: type-I optimization) and \( \overline D \) and C val (b: type-II optimization) in the optimization process; the solutions of the Pareto front associated with the topological procedure have been re-evaluated a posteriori in terms of D max and \( \overline D \), making use of the hydraulic procedure. The dots A (hydraulic procedure) and A’ (topological procedure) represent the solution encoding only 6 valves installed in correspondence to the pipes linked to the transmission mains connected to the reservoir; the dots B (hydraulic procedure) and B’ (topological procedure) pertain to the solution encoded with N valves (see text). Concerning dot C, see text and legend to Fig. 9. Dots D represent the current valve configuration analysed in Section 3.2 and shown in Fig. 4, evaluated through the hydraulic procedure

Full size image
Fig. 8
figure 8

Relationship between C val and N val with reference to the optimizations performed using the hydraulic and topological procedures and considering \( \overline D \) and C val as objective functions (type-II optimization) both for Ferrara a and Goro b networks

Full size image

By analysing Figs. 6 and 7, it is possible to note that the first preset individual, encoded in the initial population in order to contain 6 and 3 valves for the networks in Fig. 1 (Case Study 1) and Fig. 2 (Case Study 2), respectively, is present as the initial dot of the various Pareto fronts (see dot A for the topological procedure and dot A’ for the hydraulic procedure). This individual corresponds to the optimal valve configuration that determines the formation of a single network segment. Being dominated, the second preset individual, encoded in the initial population following the N rule (Walski et al. 2006), does not belong to the fronts (see dot B for the topological procedure and dot B’ for the hydraulic procedure). As a matter of fact, even if the N-valve configuration always makes it possible to achieve the highest reliability levels (lowest values of D max and \( \overline D \)), the optimal solutions placed at the right end of the Pareto fronts feature the same reliability levels even with fewer valves; as an example, in type-II optimization of the Goro network, the solution at the right end of the Pareto front features \( {\overline D^{{hydr}}} = 0.{675 }{{L} \left/ {\text{s}} \right.} \) (like the N valve configuration—see Table 5) with a lower number of valves (122 vs. 185).

With reference to Fig. 6 (relative to Case Study 1), the Pareto fronts and the curve obtained by the a posteriori re-evaluation coincide in both type I and II optimizations. This means that, for the design of the isolation valve system for the Case Study 1 network, the accurate evaluation of the demand shortfall (hydraulic procedure) does not determine significant variations in the results with respect to the approximate evaluation (topological procedure). This is due to the characteristics of the network in Case Study 1, which is made up of a large number of loops, making the pressure-lowering effects occurring after segment isolation negligible. In this case, the demand shortfall estimate based on the hydraulic procedure almost coincides with that obtained by means of the topological procedure, although we can argue that the latter is preferable as it necessitates much shorter computation times (see Table 6).

Table 6 Computation times (h) necessary for the application of the hydraulic and topological procedures to the isolation valve system design
Full size table

With reference to Fig. 7 (Case Study 2—Goro network) the Pareto fronts yielded by the two demand shortfall evaluation procedures in type-I optimization are very different, while comparable fronts are obtained once more in type-II optimization. In particular, the Pareto front obtained by type I optimization of the hydraulic procedure is very short; in fact, the solution corresponding to the right end of the Pareto front (see dot C in Fig. 7a—type-I optimization) is characterised by only 11 valves, and its \( D_{{max}}^{{hydr}} = { 1}0.{4 }{{\text{L}} \left/ {\text{s}} \right.} \). This is to be ascribed to the placement of the valves corresponding to this individual (Fig. 9). As a result of this placement, the segment that presents \( D_{{max}}^{{hydr}} \) (largest segment in terms of demand shortfall) is made up of only pipe 5, and cannot be split into smaller segments in order to obtain solutions with higher N valv and lower D max . Moreover, with reference to this pipe/segment, with low associated water demand supplied to the users (see Table 2), the value \( D_{{max}}^{{hydr}} = { 1}0.{4 }{{\text{L}} \left/ {\text{s}} \right.} \) can be almost entirely ascribed to the pressure-lowering effects occurring after isolation of the segment itself. Indeed, isolation of pipe 5 (which is one of the pipes with the largest diameter in the network, i.e. 200 mm) causes a significant reduction in the pressure values at the downstream nodes; although they remain connected to the source point, these nodes are no longer able to fully meet the users’ demand. This is due to the topological structure of the network, which is characterized, as highlighted above, by a branched main structure featuring both transmission and distribution functions; furthermore, the loops connected to the main structure are made up of pipes with small diameter having only the distribution function: diverting the main flow into secondary loops determines significant head losses, as stated in previous sections.

Fig. 9
figure 9

Case Study 2: Goro network—type-I optimization by means of hydraulic procedure for the evaluation of demand shortfall (valves represented as pipe disconnections); the largest segment from the hydraulic point of view is plotted with a thick line. The system of valves shown herein (11 valves) corresponds to dot C of the Pareto front in Fig. 7a

Full size image

With reference to type-I optimization, the Pareto front relative to the topological procedure is far lower than that obtained by the hydraulic procedure. This is due to the fact that the estimate \( D_i^{{top}} \) is far lower than that obtainable by the hydraulic procedure (\( D_i^{{hydr}} \)) for some network segments (comprising pipes that belong to the branched main structure); in other words, the demand shortfall evaluation based only on the topological analysis yields an incorrect quantification of the demand not supplied to network users. Furthermore, the valve placement obtained by the topological procedure is dominated by the placement provided by the hydraulic procedure, as proven by the position of the curve showing the re-evaluation of the topological curve. This analysis also applies to the type-II optimization, though the respective distances between the three curves are now smaller. We can therefore argue that, in the case of networks similar to that considered in Case Study 2, optimization carried out using only the topological procedure is not reliable when it involves the pair of objective functions N valv —D max ; on the other hand, the inaccuracy reaches acceptable limits when the variables used in the optimization are C valv and \( \overline{D} \).

In summary, with reference to both Case Studies 1 and 2, we can recommend that, for practical purposes, optimization be carried out using the pair C valv —\( \overline{D} \) in association with the topological procedure for the evaluation of demand shortfalls. Indeed, if the pair C valv —\( \overline{D} \) is used, the errors connected with the adoption of the topological procedure are small, in terms of Pareto fronts, even in cases similar to the Goro network (looped network with branched main structure); moreover, the computation times are far lower than those required by the hydraulic procedure (which would require hydraulic simulation of each segment generated in the optimization phase), as is evident in Table 6.

Furthermore, analysis of the Pareto fronts in Figs. 6 and 7 shows that the optimal configurations dominate the preset systems of valves considered for explicative purposes in Section 3.2. As regards the real system of valves of the Goro network, in Fig. 7(a) we can see that the current system features a value of D max close to the solution corresponding to the right end of the Pareto front N val —D max obtained by means of the hydraulic procedure (see dot C in Fig. 7a—type-I optimization) with a much greater number of valves; however, as D max only refers to the largest network segment, analysing a system of valves only in terms of D max is incomplete and misleading; in Fig. 7b we can see that the real system of valves is close to the Pareto front C val —\( \overline D \) produced by the hydraulic procedure. However, this Pareto front features a solution where C val  = 15223 € (close to C val of the real system), N val  = 88, N s  = 63, \( D_{{max}}^{{hydr}} = { 1}0.{45 }{{\text{L}} \left/ {\text{s}} \right.} \) and \( {\overline D^{{hydr}}} = 0.{72 }{{\text{L}} \left/ {\text{s}} \right.} \). The advantage of this latter solution with respect to the actual configuration of valves in the real system is that it features a higher number of segments, despite being made up of a smaller number of valves. The fact that the optimization procedures here presented produce solutions with fewer valves than those observed in the corresponding real case can be ascribed to several reasons: first and foremost, the current valve dislocation is a consequence of the expansion of the network over many years, without referring to a global design, and, secondly, valves may have been installed due to specific local necessities, and these are not considered in the optimization procedure. This however suggests that a global design of valve location should be based on several considerations, among which the Pareto front can play an important role.

As an extra criterion for assessing valve configurations, an analysis concerning the number of valves that have to be closed in order to enable the isolation of a generic segment can also be carried out either on real systems of valves or on optimal valve configurations obtained at the end of an optimization process. Starting from this analysis, we can derive the distribution of the number of segments that require 1, 2, 3, etc. valves to be closed in order to achieve a shutdown. In this context, it is worth highlighting that configurations where most segments can be isolated by using a small number of valves are more advantageous because the higher the number of valves for segment shutdown the higher the probability that a valve fails and the outage must extend to the next segment. We then applied this latter analysis criterion to make a further comparison between the real valve configuration of the Goro network and the optimal one provided by the optimizer for C val  = 15223 €; the results of this comparison are reported in Table 7 and show that the optimal configuration is more advantageous, not presenting segments which need more than 5 valves to be isolated. The analysis of the results also points out that both valve configurations present one segment (made up of the pipe which feeds Gorino district) which can be disconnected by using a single valve; it is worth reminding that this valve was present in the real system of valves and was considered as a constraint in the optimization process.

Table 7 Case study 2: distribution of the number of segments that require the closure of 1, 2, …, 7 valves to be isolated
Full size table

4 Conclusions

In this paper, two estimates of the water demand shortfall occurring after isolation of network segments were compared. In particular, the first estimate is yielded by a procedure based on simple topological analysis, while the second results from a procedure combining topological analysis and hydraulic simulation under pressure-driven conditions. The comparison was made with reference to two different case studies, with computation times also being taken into account.

The first case study concerned a highly looped network in which all pipes possess transmission and distribution functions, whereas the second case study involved a looped network featuring a branched main structure possessing mainly a transmission function. In both cases, the analysis and re-design issues were addressed by studying a preset (or current) system of isolation valves and aiming to determine the optimal position of the valves, respectively. In the latter problem the objective functions considered were the economic burden (expressed in terms of number N val or cost C val of installed valves) and the reliability of the system (expressed in terms of maximum D max and weighted average \( \overline D \) water demand shortfall). Results highlighted that, although the two procedures for evaluating demand shortfall were comparable in the first case study, they yielded discrepant results in the second. The magnitude of these discrepancies was dependent on which of the global variables (D max or \( \overline D \)) was chosen to characterize the demand shortfalls in the network segments. Overall, the coupled use of the topological procedure and global variable \( \overline D \) is recommended in the design phase, since it ensures short computation times and produces system reliability estimates similar to those produced by the superior but unwieldy hydraulic procedure.