Memory-Efficient and High-Speed VLSI Implementation of Two-Dimensional Discrete Wavelet Transform Using Decomposed Lifting Scheme

Abstract

Novel decomposed lifting scheme (DLS) is presented to perform one-dimensional (1D) discrete wavelet transform (DWT) with consistent data flow in both row and column dimension. Based on the proposed DLS, intermediate data can be transferred seamlessly between the column processor and the row processor in the hardware implementation of two-dimensional (2D) DWT, resulting in the reduction of on-chip memory, output latency and control complexity. Moreover, the implementation of 2D DWT can be easily extended to achieve higher processing speed with controlled increase of hardware cost. Memory-efficient and high-speed architectures are proposed to implement 2D DWT for JPEG2000, which are called fast architecture (FA) and high-speed architecture (HA). FA and HA can perform 2D DWT in N ²/2 and N ²/4 clock cycles for an N×N image, respectively, but the required internal memory is only 4N for 9/7 DWT and 2N for 5/3 DWT. Compared with the works reported in previous literature, the proposed designs provide excellent performance in hardware cost, control complexity, output latency and computing time. The proposed designs were implemented to process 2D 9/7 DWT in SMIC 0.18 μm CMOS logic fabrication with 4 KB internal memory for the image size 512 × 512. The areas are only 999137 um ² and 1333054 um ² for FA and HA, respectively, but the operation frequency can be up to 150 MHz.

1 Introduction

Discrete Wavelet Transform (DWT) has been widely applied in the area of signal processing and multimedia compression as an effective analysis tool of multi-resolution due to its excellent local characters in time-frequency. Recent image coding standards, such as JPEG2000 still image coding [1] and MPEG-4 still texture coding, have adopted two-dimensional (2D) DWT as their transform coder. Because of complex data flow and intensive arithmetic computation, high processing speed and low hardware cost has become the main challenge in VLSI implementation of 2D DWT.

In recent years, many hardware implementations of 2D DWT have been proposed to meet the requirements of real time processing. Among the various architectures, there have been several line-based architectures proposed for the convolution-based hardware implementation of 2D DWT. Andra et al. [2] proposed four-processor architecture for 2D DWT by classifying the wavelet filters into two cases: two-matrix(2M) lifting factorization and four-matrix(4M) lifting factorization. In [3], efficient architecture for 2D DWT was proposed with the polyphase decomposition technique and the coefficient folding technique. Hardware parallel structures were developed in [4] to speed up the processing speed of 2D DWT and control the increase of hardware cost at the same time. Recent research on DWT architecture has been concentrated on the methodology of lifting scheme [5] and a complete survey for lifting-based DWT architecture can be found in [6]. By factorizing the conventional filter banks into several lifting steps, the lifting-based DWT provides excellent performance in memory requirement and arithmetic complexity. Efficient implementation for 9/7 DWT was presented in [7] based on lifting scheme where symmetric extension was utilized to reduce the internal memory requirement without additional computations and clock cycles. Seo et al. [8] organized a new architecture of line-based lifting processor with optimized unit cells to execute lifting calculations. Lan et al. [9] proposed a 2D architecture to process two rows simultaneously with two pixels in each clock cycle. Embedded decimation technique was exploited in [10] to optimize the architecture for 1D DWT, and two 2D DWT architectures, called fast architecture (FA) and high-speed architecture (HA), were proposed with parallel and pipeline technique. In [11], a novel lifting-based reconfigurable DWT architecture was proposed which featured dynamically reconfigurable capability with processing element array and address generator. Although the lifting-based DWT involves many advantages over the convolution-based one, the longer and irregular data path are the major limitations for the efficiency of hardware implementation. To solve this problem, Huang et al. proposed a flipping structure for lifting scheme [12] by inversing the multiplier coefficients, which aims at shortening the critical path of the lifting-based 1D DWT architecture with little hardware overhead of pipeline registers. Another modified lifting scheme [13] merged the computation of the lifting step and implemented 1D DWT with less arithmetic resource and shorter critical path.

For the implementation of 2D DWT architectures, the memory issue is the dominant factor of the hardware cost and complexity. According to the analysis of [14], line-based method [15] is en efficient alternative in tradeoff between the speed and area by use of an on-chip line buffer and has become one of the most commonly-used methods of hardware implementation. The on-chip line buffer needed in line-based DWT can be decomposed into two categories, temporary buffer and data buffer [16]. Temporary buffer is mapped from the registers used in the 1D DWT architecture and used to store temporary data in the computation of lifting steps, which is dependent on the adopted DWT filters. Data buffer is used to store and transpose the intermediate decomposition coefficients due to the insistent data flow between row and column processor, which is independent of DWT filters and only related to the data flow of the DWT architecture. The rate of data flow also affects the processing speed of 2D DWT. By increasing the throughput of the architecture, computing time can be decreased by times, but more hardware cost is required accordingly.

In this paper, we focus on the issues of internal memory requirement and processing speed of 2D DWT architecture. To solve the inconsistency between the data flow of two 1D DWT processors, a novel decomposed lifting scheme (DLS) is proposed by rearranging the data path of the lifting step. Based on DLS, image data can be processed in raster scan manner in both the column processor and the row processor. Thus the size of the on-chip line buffer is reduced greatly by eliminating the implementation of data buffer. Moreover, the DLS-based 2D DWT architecture can be designed to achieve high processing speed, but the hardware cost is controlled in a certain range.

The rest of this paper is organized as follows. In Section 2, the traditional lifting scheme is reviewed briefly and then the proposed DLS is presented in detail. The precision issue in terms of overflow problem and the round-off noise is analyzed in Section 3. Section 4 proposes novel 1D DWT structures for column processor and row processor based on DLS. Memory-efficient and high-speed 2D architectures are presented in Section 5 to implement 9/7 and 5/3 DWT for JPEG2000. Section 6 presents the comparison and analysis, and followed by the implementation results. Finally, a brief conclusion is stated in Section 7.

2 Proposed Decomposed Lifting Scheme for JPEG2000

The principle of the lifting scheme [5] is to factorize the wavelet filters into a sequence of lifting steps. In JPEG2000 standard, the biorthogonal 5/3 and 9/7 DWT are adopted as the default transform coders for lossless and lossy image compression. The 9/7 DWT includes two lifting steps while the 5/3 DWT can be regarded as a special case with one lifting step. Thus 9/7 DWT is taken as an example to review the traditional lifting scheme and propose a modified lifting scheme later.

The detailed lifting scheme of the 9/7 DWT is mathematically described in (1). First, the input data sequence x _i is split into even part $s_i^0$ and odd part $d_i^0$. Then the two parts are predicted and updated to produce the high-pass lifting results $d_i^m$ and low-pass one $s_i^m$, where m denotes the stage of lifting steps. Finally the low-pass and high-pass wavelet coefficients denoted as s _i and d _i are obtained through scaling factors k. The detailed value of lifting coefficients, α, β, γ, δ and k, can be found in [1].

$$ s_i^0 = {x_{2i}} $$

(1a)

$$ d_i^0 = {x_{2i + 1}} $$

(1b)

$$ d_i^1 = d_i^0 + \alpha \times \left( {s_i^0 + s_{i + 1}^0} \right) $$

(1c)

$$ s_i^1 = s_i^0 + \beta \times \left( {d_{i - 1}^1 + d_i^1} \right) $$

(1d)

$$ d_i^2 = d_i^1 + \gamma \times \left( {s_i^1 + s_{i + 1}^1} \right) $$

(1e)

$$ s_i^2 = s_i^1 + \delta \times \left( {d_{i - 1}^2 + d_i^2} \right) $$

(1f)

$$ {s_i} = k \times s_i^2 $$

(1g)

$$ {d_i} = {1 \mathord{\left/{\vphantom {1 k}} \right.} k} \times d_i^2 $$

(1h)

It can be seen from (1) that at least three image samples are required to be available together to carry out the computation of predictor and updater step in lifting scheme. When the image data is inputted in raster scan manner, it is consistent with the processing order of row DWT. However, in the implementation of 2D DWT, image data has to be reordered into column wise sequence to perform column DWT. This intrinsic property also lies in previous modified lifting schemes such as flipping structure [12] and merged lifting scheme [13]. With line-based method [15], rows of image data are buffered and transposed to prepare enough samples for column DWT, which induces the implementation of data buffer and suffers from additional memory cost, transform latency and control logic. Some other architectures reduced the data buffer into several registers by use of special data scan method such as Z-scan [17] and dual-scan [18] at the cost of complex control logic and additional power consumption during image data access.

To solve the inconsistency problem between the processing order in row DWT and column DWT, we propose a decomposed lifting scheme (DLS) to perform both row and column DWT in the same data flow. The data path of the lifting step is rearranged by further decomposing the computation in lifting steps so that lifting steps can be partially performed with every inputted image sample. Thus the implementation of data buffer can be eliminated, resulting in the decrease of on-chip memory cost, output latency and complexity of control logic. Moreover, this modified lifting scheme can also be used to implement row DWT to increase the throughput. In the following, the formulas of DLS are derived in detail.

It is obvious that the predictor stage in the first lifting step (1c) can be decomposed into three parts, as shown in (2a)–(2c), where $d_i^{\prime 1}$ and $d_i^{\prime \prime 1}$ are denoted as the intermediate results of the predictor stage.

$$ d_i^{\prime 1} = \alpha \times s_i^0 $$

(2a)

$$ d_i^{\prime \prime 1} = d_i^{\prime 1} + d_i^0 $$

(2b)

$$ d_i^1 = d_i^{\prime \prime 1} + \alpha \times s_{i + 1}^0 $$

(2c)

The updater stage (1d) is expressed similarly in (2d)–(2f) with a factor 1/β derived to use the predicator result $d_i^1$ directly, where ${1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime 1}$ and ${1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime \prime 1}$ stand for the intermediate results of the updater stage. In (2e) the even sample $s_i^0$ is substituted by the intermediate result of the predictor stage $d_i^{\prime 1}$ to remove the dependence on the even sample.

$$ {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime 1} = d_{i - 1}^1 $$

(2d)

$$ {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime \prime 1} = {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime 1} + {1 \mathord{\left/{\vphantom {1 {\beta \times }}} \right.} {\beta \times }}s_i^0 = {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime 1} + {1 \mathord{\left/{\vphantom {1 {\alpha \beta \times }}} \right.} {\alpha \beta \times }}d_i^{\prime 1} $$

(2e)

$$ {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^1 = {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime \prime 1} + d_i^1 $$

(2f)

Assume image data is received one by one. When the even data is accepted, the operations in equation (2a), (2c), (2d) and (2f) are executed and the intermediate results are stored as $d_i^{\prime 1}$ and ${1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime 1}$; when the odd data is accepted, the operations of equation (2b) and (2e) are executed and the intermediate results are stored as $d_i^{\prime \prime 1}$ and ${1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^{\prime \prime 1}$. Similar modification can also be applied to the second lifting step as shown in (2g)–(2l) by taking $d_i^1$ and ${1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^1$ as the even and odd input samples, respectively.

$$ d_i^{\prime 2} = \beta \gamma \times {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^1 $$

(2g)

$$ d_i^{\prime \prime 2} = d_i^{\prime 2} + d_i^1 $$

(2h)

$$ d_i^2 = d_i^{\prime \prime 2} + \beta \gamma \times {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_{i + 1}^1 $$

(2i)

$$ {1 \mathord{\left/{\vphantom {1 \delta }} \right.} \delta } \times s_i^{\prime 2} = d_{i - 1}^2 $$

(2j)

$$ {1 \mathord{\left/{\vphantom {1 {\delta \times }}} \right.} {\delta \times }}s_i^{\prime \prime 2} = {1 \mathord{\left/{\vphantom {1 {\delta \times }}} \right.} {\delta \times }}s_i^{\prime 2} + {1 \mathord{\left/{\vphantom {1 {\delta \times }}} \right.} {\delta \times }}s_i^1 = {1 \mathord{\left/{\vphantom {1 {\delta \times }}} \right.} {\delta \times }}s_i^{\prime 2} + {1 \mathord{\left/{\vphantom {1 {\gamma \delta \times }}} \right.} {\gamma \delta \times }}d_i^{\prime 2} $$

(2k)

$$ {1 \mathord{\left/{\vphantom {1 {\delta \times }}} \right.} {\delta \times }}s_i^2 = {1 \mathord{\left/{\vphantom {1 {\delta \times }}} \right.} {\delta \times }}s_i^{\prime \prime 2} + d_i^2 $$

(2l)

Equation (2) can be rewritten into Eq. (3), which is suitable for the implementation of row DWT. More details are given in Section 3.

$$ d_i^1 = \alpha \times s_i^0 + d_i^0 + \alpha \times s_{i + 1}^0 $$

(3a)

$$ {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^1 = d_{i - 1}^1 + {1 \mathord{\left/{\vphantom {1 {\alpha \beta }}} \right.} {\alpha \beta }} \times \alpha \times s_i^0 + d_i^1 $$

(3b)

$$ d_i^2 = \beta \gamma \times {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^1 + d_i^1 + \beta \gamma \times {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_{i + 1}^1 $$

(3c)

$$ {1 \mathord{\left/{\vphantom {1 \delta }} \right.} \delta }s_i^2 = d_{i - 1}^2 + {1 \mathord{\left/{\vphantom {1 {\gamma \delta }}} \right.} {\gamma \delta }} \times \beta \gamma \times {1 \mathord{\left/{\vphantom {1 \beta }} \right.} \beta }s_i^1 + d_i^2 $$

(3d)

$$ {s_i} = k\delta \times {1 \mathord{\left/{\vphantom {1 \delta }} \right.} \delta }s_i^2 $$

(3e)

$$ {d_i} = {1 \mathord{\left/{\vphantom {1 k}} \right.} k} \times d_i^2 $$

(3f)

It should be noted that, besides the odd symmetric DWT filters such as 9/7 and 5/3 DWT, the proposed lifting scheme can also adapt to other biorthogonal DWT filters. For the lifting-based wavelet filters, DLS can be employed by rearranging the data path of the lifting steps so that row DWT and column can be performed with consistent data flow. To show the efficiency of the p lifting scheme, the even linear 6/10 filter has been studied as well, which is mathematically described as followers.

$$ s_i^0 = {x_{2i}} $$

(4a)

$$ d_i^0 = {x_{2i + 1}} $$

(4b)

$$ d_i^1 = d_i^0 + a \times s_i^0 $$

(4c)

$$ s_i^1 = s_i^0 + b \times d_i^1 + c \times d_{i - 1}^0 $$

(4d)

$$ d_i^2 = d_i^1 + d \times s_{i + 1}^1 + e \times s_i^1 $$

(4e)

$$ s_i^2 = s_i^1 - f \times d_i^2 + g \times d_{i - 1}^2 + f \times d_{i - 2}^2 $$

(4f)

$$ {s_i} = {K_2} \times s_i^2 $$

(4g)

$$ {d_i} = {K_1} \times d_i^2 $$

(4h)

where a, b, c, d, e, f, g, K ₁ and K ₂ are the corresponding lifting coefficients and scale factors, respectively and the real values can be referred to [12].

By applying DLS, the computation of the first lifting step can be decomposed as Eq. (5), where $d_i^{\prime 1}$ and ${{s_i^{\prime 1}} \mathord{\left/{\vphantom {{s_i^{\prime 1}} b}} \right.} b}$ are denoted as the intermediate results of the predictor and updater stage, respectively.

$$ d_i^{\prime 1} = a \times s_i^0 $$

(5a)

$$ {{cd_i^1} \mathord{\left/{\vphantom {{cd_i^1} b}} \right.} b} = {c \mathord{\left/{\vphantom {c b}} \right.} b} \times \left( {d_i^0 + d_i^{\prime 1}} \right) $$

(5b)

$$ {{s_i^{\prime 1}} \mathord{\left/{\vphantom {{s_i^{\prime 1}} b}} \right.} b} = {{cd_{i - 1}^1} \mathord{\left/{\vphantom {{cd_{i - 1}^1} b}} \right.} b} + {1 \mathord{\left/{\vphantom {1 b}} \right.} b} \times s_i^0 $$

(5c)

$$ {{s_i^1} \mathord{\left/{\vphantom {{s_i^1} b}} \right.} b} = s_i^{\prime 1} + \left( {d_i^{\prime 0} + d_i^0} \right) $$

(5d)

Assuming image data is received one by one, the commutation of the first lifting step is performed as follows. When the even data is accepted, the operations in Eqs. (5a) and (5c) are executed and the intermediate results are stored as $d_i^{\prime 1}$ and ${{s_i^{\prime 1}} \mathord{\left/{\vphantom {{s_i^{\prime 1}} b}} \right.} b}$; when the odd data is accepted, the operations of Eqs. (5b) and (5d) are executed while the updater and predictor lifting results are obtained as ${{cd_i^1} \mathord{\left/{\vphantom {{cd_i^1} b}} \right.} b}$ and ${{s_i^1} \mathord{\left/{\vphantom {{s_i^1} b}} \right.} b}$, respectively.

Similarly, the computation of the second lifting step can be decomposed as Eq. (6) by using the lifting results of the first lifting step, ${{cd_i^1} \mathord{\left/{\vphantom {{cd_i^1} b}} \right.} b}$ and ${{s_i^1} \mathord{\left/{\vphantom {{s_i^1} b}} \right.} b}$, as input data directly, where ${c \mathord{\left/{\vphantom {c b}} \right.} b} \cdot d_i^{\prime 2}/{c \mathord{\left/{\vphantom {c b}} \right.} b} \cdot d_i^{\prime \prime 2}$ and ${c \mathord{\left/{\vphantom {c {bf \cdot }}} \right.} {bf \cdot }}s_i^{\prime 2}/{c \mathord{\left/{\vphantom {c {bf \cdot }}} \right.} {bf \cdot }}s_i^{\prime \prime 2}$ are denoted as the intermediate results of the predictor and updater stage, respectively.

$$ {c \mathord{\left/{\vphantom {c b}} \right.} b} \cdot d_i^{\prime 2} = cd \times {{s_i^1} \mathord{\left/{\vphantom {{s_i^1} b}} \right.} b} $$

(6a)

$$ {c \mathord{\left/{\vphantom {c b}} \right.} b} \cdot d_i^{\prime \prime 2} = {e \mathord{\left/{\vphantom {e d}} \right.} d} \times d_i^{\prime 2} + {{cd_i^1} \mathord{\left/{\vphantom {{cd_i^1} b}} \right.} b} $$

(6b)

$$ {{cg} \mathord{\left/{\vphantom {{cg} {bf \cdot }}} \right.} {bf \cdot }}d_i^2 = {g \mathord{\left/{\vphantom {g f}} \right.} f} \times \left( {d_i^{\prime \prime 2} + d_{i + 1}^{\prime 2}} \right) $$

(6c)

$$ {c \mathord{\left/{\vphantom {c {bf \cdot }}} \right.} {bf \cdot }}s_i^{\prime 2} = {1 \mathord{\left/{\vphantom {1 {df}}} \right.} {df}} \times d_i^{\prime 2} + {{cg} \mathord{\left/{\vphantom {{cg} {bf \cdot }}} \right.} {bf \cdot }}d_{i - 1}^2 $$

(6d)

$$ {c \mathord{\left/{\vphantom {c {bf \cdot }}} \right.} {bf \cdot }}s_i^{\prime \prime 2} = d_i^{\prime \prime 2} + d_{i + 1}^{\prime 2} $$

(6e)

$$ {c \mathord{\left/{\vphantom {c {bf \cdot }}} \right.} {bf \cdot }}s_i^2 = s_i^{\prime 2} - s_i^{\prime \prime 2} + s_{i - 2}^{\prime \prime 2} $$

(6f)

Thus the computation of the second lifting step is performed with image data received one by one. When the even data is accepted, the operations in Eqs. (6a), (6c), (6e) and (6f) are executed and the intermediate results are stored as ${c \mathord{\left/{\vphantom {c b}} \right.} b} \cdot d_i^{\prime 2}$ and ${c \mathord{\left/{\vphantom {c {bf \cdot }}} \right.} {bf \cdot }}s_i^{\prime \prime 2}$ while the updater and predictor lifting results are obtained as ${{cg} \mathord{\left/{\vphantom {{cg} {bf \cdot }}} \right.} {bf \cdot }}d_i^2$ and ${{cs_i^2} \mathord{\left/{\vphantom {{cs_i^2} {bf}}} \right.} {bf}}$, respectively; when the odd data is accepted, the operations of Eqs. (6b) and (6d) are executed and the intermediate results are stored as ${c \mathord{\left/{\vphantom {c b}} \right.} b} \cdot d_i^{\prime \prime 2}$ and ${c \mathord{\left/{\vphantom {c {bf \cdot }}} \right.} {bf \cdot }}s_i^{\prime 2}$.

In this way, the 6/10 filter can be rewritten as Eq. (7) by employing DLS.

$$ d_i^1 = d_i^0 + a \times s_i^0 $$

(7a)

$$ {{s_i^1} \mathord{\left/{\vphantom {{s_i^1} b}} \right.} b} = {c \mathord{\left/{\vphantom {c b}} \right.} b} \times d_{i - 1}^1 + {1 \mathord{\left/{\vphantom {1 b}} \right.} b} \times s_i^0 + d_i^1 $$

(7b)

$$ {{cd_i^2} \mathord{\left/{\vphantom {{cd_i^2} b}} \right.} b} = {e \mathord{\left/{\vphantom {e d}} \right.} d} \times {{cds_i^1} \mathord{\left/{\vphantom {{cds_i^1} b}} \right.} b}{{ + cd_i^1} \mathord{\left/{\vphantom {{ + cd_i^1} b}} \right.} b} + cd \times {{s_{i + 1}^1} \mathord{\left/{\vphantom {{s_{i + 1}^1} b}} \right.} b} $$

(7c)

$$ {{cs_i^2} \mathord{\left/{\vphantom {{cs_i^2} {bf}}} \right.} {bf}} = {{cd_{i - 2}^2} \mathord{\left/{\vphantom {{cd_{i - 2}^2} b}} \right.} b} + {g \mathord{\left/{\vphantom {g f}} \right.} f} \times {{cd_{i - 1}^2} \mathord{\left/{\vphantom {{cd_{i - 1}^2} b}} \right.} b} + {1 \mathord{\left/{\vphantom {1 {df}}} \right.} {df}} \times {{cds_i^1} \mathord{\left/{\vphantom {{cds_i^1} b}} \right.} b} - {{cd_i^2} \mathord{\left/{\vphantom {{cd_i^2} b}} \right.} b} $$

(7d)

$$ {s_i} = {{{K_2}bf} \mathord{\left/{\vphantom {{{K_2}bf} c}} \right.} c} \times {c \mathord{\left/{\vphantom {c {bf}}} \right.} {bf}} \cdot s_i^2 $$

(7e)

$$ {d_i} = {{{K_1}bf} \mathord{\left/{\vphantom {{{K_1}bf} {cg}}} \right.} {cg}} \times {{cg} \mathord{\left/{\vphantom {{cg} {bf}}} \right.} {bf}} \cdot d_i^2 $$

(7f)

3 Precision Analysis

In the hardware implementation of DWT, the fixed-point representation is used for internal data and multiplier coefficients instead of the floating-point one to reduce the computation complexity and arithmetic resource. To analyze the precision of the finite word length, it is important to discuss the overflow issue and the round-off error.

The overflow problem can be solved with enough guard bits in the representation of internal data. If the maximum of input signals is given as M, the maximal values of the four lifting results for 9/7 DWT in DLS can be calculated as 4.172 M, 27.220 M, 2.110 M, 3.829 M according to Eq. (3). Thus the maximum of internal data is 27.220 M and 5 guard bits are needed to avoid the instance of overflow. In order to reduce the required guard bits, the computations of each lifting steps are scaled as Eq. (8), where the maximum of internal data is down to 1.460 M. Therefore the number of guar bit is decreased to one so that more bits can be used for the representation of fractional value, which would increase the precision of fixed-point computation of DWT significantly.

$$ {{d_i^1} \mathord{\left/{\vphantom {{d_i^1} 4}} \right.} 4} = {\alpha \mathord{\left/{\vphantom {\alpha 4}} \right.} 4} \times s_i^0 + \frac{{d_i^0}}{4} + {\alpha \mathord{\left/{\vphantom {\alpha 4}} \right.} 4} \times s_{i + 1}^0 $$

(8a)

$$ {1 \mathord{\left/{\vphantom {1 {32\beta }}} \right.} {32\beta }}s_i^1 = \frac{{{{d_{i - 1}^1} \mathord{\left/{\vphantom {{d_{i - 1}^1} 4}} \right.} 4}}}{8} + {1 \mathord{\left/{\vphantom {1 {8\alpha \beta }}} \right.} {8\alpha \beta }} \times {\alpha \mathord{\left/{\vphantom {\alpha 4}} \right.} 4} \times s_i^0 + \frac{{{{d_i^1} \mathord{\left/{\vphantom {{d_i^1} 4}} \right.} 4}}}{8} $$

(8b)

$$ {{d_i^2} \mathord{\left/{\vphantom {{d_i^2} 2}} \right.} 2} = 16\beta \gamma \times {1 \mathord{\left/{\vphantom {1 {32\beta }}} \right.} {32\beta }}s_i^1 + 2 \times {{d_i^1} \mathord{\left/{\vphantom {{d_i^1} 4}} \right.} 4} + 16\beta \gamma \times {1 \mathord{\left/{\vphantom {1 {32\beta }}} \right.} {32\beta }}s_{i + 1}^1 $$

(8c)

$$ {1 \mathord{\left/{\vphantom {1 {4\delta }}} \right.} {4\delta }}s_i^2 = \frac{{{{d_{i - 1}^2} \mathord{\left/{\vphantom {{d_{i - 1}^2} 2}} \right.} 2}}}{2} + {1 \mathord{\left/{\vphantom {1 {2\gamma \delta }}} \right.} {2\gamma \delta }} \times 16\beta \gamma \times {1 \mathord{\left/{\vphantom {1 {32\beta }}} \right.} {32\beta }}s_i^1 + \frac{{{{d_i^2} \mathord{\left/{\vphantom {{d_i^2} 2}} \right.} 2}}}{2} $$

(8d)

$$ {s_i} = 4k\delta \times {1 \mathord{\left/{\vphantom {1 {4\delta }}} \right.} {4\delta }}s_i^2 $$

(8e)

$$ {d_i} = {2 \mathord{\left/{\vphantom {2 k}} \right.} k} \times {{d_i^2} \mathord{\left/{\vphantom {{d_i^2} 2}} \right.} 2} $$

(8f)

To illustrate the overall effect of the round-off error, several test images, comprising airplane, baboon, boat, clock, lena, peppers and truck are simulated by performing one-level 2D DWT under different precision. As shown in Fig. 1, the reconstructed image quality is denoted in terms of PSNR and grows linearly with the increase of the number of bits used for internal data, where one guard bit are used to avoid overflow, 8 decimal bits are occupied for raw data, and others represent fractional bits.

Figure 1

Finite precision performance with different bits of internal data.

Beside the internal data, the fixed-point multiplier coefficients also impact the image precision. To evaluate the real effect of round-off noise in DLS and the traditional lifting scheme, the test images are simulated by performing 1D DWT with 16-bit finite precision for internal data. As presented in Fig. 2, the x axis specifies the number of fractional bits of multiplier coefficients whereas y axis denotes the image quality in terms of average PSNR. From Fig. 2, it can be concluded that the image quality of DLS outperforms the traditional lifting scheme. For the word-length of the multiplier coefficients, it is reasonable to use 12 fractional bits to reach ideal quality of reconstructed image.

Figure 2

Finite precision comparison with different bits of multiplier coefficients and 16-bit internal data.

4 Proposed 1D DWT module

4.1 Proposed Column Processor with Single-Input and Single-Output

Based on DLS, a novel column processor (CP) is proposed for 9/7 filter to perform 1D DWT in column dimension with single-input and single-output (SISO) per clock cycle. Though the lifting steps are carried out along each column, input image samples and output wavelet coefficients are sequenced in raster scan manner as shown in Fig. 3(a).

Figure 3

a Input and output data sequence in CP; b DFG of CPE; c proposed structure of CPE.

Note that the detailed formulas for the first lifting step of 9/7 filter (shown in (2a)–(2f)) have the same form as that for the second one (shown in (2g)–(2l)). Thus the two lifting steps can be implemented in the same structure defined as a column processing element (CPE), and the whole CP can be implemented with two cascaded CPEs. The data flow graph (DFG) of CPE for the first lifting step is plotted in Fig. 3(b), where only multiplier coefficients α and 1/αβ are replaced by βγ and 1/γδ for the second lifting step. The computation along the jth column is illustrated in Fig. 3(b) and polygonal lines are inserted to separate the computations in different rows. CPE reads one image sample per clock cycle. When the even-row data $s_{(i,j)}^0$ is accepted, the computations in Eqs. (2a), (2c), (2d) and (2f) are carried out and two intermediate results, $d_i^{\prime \prime 1}$ and $s_i^{\prime \prime 1}$, are updated by $d_i^{\prime 1}$ and $s_i^{\prime 1}$ for the following computations; when the odd-row data $d_{(i,j)}^0$ is accepted, the computations in Eqs. (2b) and (2e) are carried out and two intermediate results, $d_i^{\prime 1}$ and $s_i^{\prime 1}$, are updated by $d_i^{\prime \prime 1}$ and $s_i^{\prime \prime 1}$ for the following computations. It can be seen from the DFG that the output latency in CPE is 2N+2 clock cycles for an N×N image. The timing diagram of the DFG indicates that only one multiplier and two adders are used at each clock cycle, and the critical path is no longer than one multiplier delay.

The detailed structure of CPE is derived from the DFG and depicted in Fig. 3(c), which consists of one multiplier, two adders, two temporary buffer, five pipeline registers, as well as a set of multiplexers. By employing folding technique, the predictor stage and the updater stage are designed to share one multiplier and two adders. Five pipeline registers are inserted in the data path to limit the critical path delay into one multiplier delay. The intermediate results, $d_i^{\prime 1}\left( {d_i^{\prime \prime 1}} \right)$ and $s_i^{\prime 1}\left( {s_i^{\prime \prime 1}} \right)$, are respectively stored in two temporary buffers, denoted as D_H and D_L, with the size of the row length. The multiplexers are controlled by signal sel and sel_d to choose the correct data path to carry out the computations in DLS. The value of signal sel is set to 0 and 1 when the even-row and odd-row data is accepted respectively, and signal sel_d is one clock cycle delay of signal sel.

4.2 Proposed Row Processor with Dual-Input and Dual-Output

The proposed DLS-based row processor (RP) performs 1D 9/7 DWT in row dimension with dual-input and dual-output (DIDO) per clock cycle. Image samples and wavelet coefficients are received and generated in raster scan manner, as shown in Fig. 4(a). Those samples included in the same dashed block are inputted or outputted at the same clock cycle.

Figure 4

a Input and output data sequence in RP with DIDO; b DFG of RPE with DIDO; c proposed structure of RPE with DIDO.

Note that the detailed formulas for the first lifting step of 9/7 filter (shown in (3a)–(3b)) have the same form as that for the second one (shown in (3c)–(3d)). Thus the two lifting steps can be implemented in the same structure defined as a row processing element (RPE) and the whole RP can be implemented with two cascaded RPEs. The DFG of RPE with DIDO for the first lifting step is illustrated in Fig. 4(b), where only multiplier coefficients α and 1/β are replaced by βγ and β/δ for the second lifting step. Two image samples, namely a pair of even sample and odd sample, are received at the same clock cycle. The predictor stage is carried out with three original image samples as Eq. (3a) while the updater stage is carried out with two predictor results and one even sample as Eq. (3b). The DFG shows that the wavelet coefficients are generated in 3 clock cycles delay with the low-pass and high-pass wavelet coefficients available together at each clock cycle, which is the same as the input sequence and ensures that two RPEs can be cascaded directly. For an N×N image, it spends N ²/2 clock cycles to perform 1D DWT in row dimension. The timing diagram of the DFG indicates that two multipliers and four adders are needed at each clock cycle, and the critical path is no longer than one multiplier delay.

The detailed structure of RPE with DIDO is derived from the DFG and depicted in Fig. 4(c), which is composed of two multipliers, four adders, two delay registers and five pipeline registers.

4.3 Proposed Row Processor with Quad-Input and Quad-Output

To increase the processing speed, the throughput of the RP can be extended to four image samples per clock cycle based on DLS with controlled increase of hardware cost. The row processor (RP) of 9/7 filter is proposed with quad-input and quad-output (QIQO), where image samples and wavelet coefficients are received and generated in raster scan manner, as shown in Fig. 5(a). Those samples included in the same dashed block are input or output at the same clock cycle.

Figure 5

a Input and output data sequence in RP with QIQO; b DFG of RPE with QIQO; c proposed structure of RPE with QIQO.

Similar as the RP with DIDO, the two lifting steps in the RP with QIQO can be implemented in the same structure defined as a row processing element (RPE) and the whole RP can be implemented with two cascaded RPEs. The DFG of RPE with QIQO for the first lifting step is illustrated in Fig. 5(b), where four image samples, namely two even samples and two odd samples, are received at the same clock cycle. The predictor stage is carried out twice in parallel with five successive image samples as Eq. (3a) while the updater stage is carried out twice in parallel with three predictor results and two even samples as Eq. (3b). The DFG shows that the wavelet coefficients are generated in 3 clock cycles delay with two low-pass and two high-pass wavelet coefficients available together at each clock cycle, which is the same as the input sequence and ensures that two RPEs can be cascaded directly. For an N×N image, it spends N ²/4 clock cycles to perform 1D DWT in row dimension. The timing diagram of the DFG indicates that four multipliers and eight adders are needed at each clock cycle, and the critical path is no longer than one multiplier delay.

The detailed structure of RPE with QIQO is derived from the DFG and shown in Fig. 5(c), which is composed of four multipliers, eight adders, two delay registers and twelve pipeline registers.

5 Proposed 2D DWT Architecture

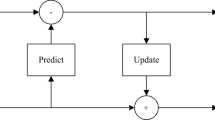
Figure 6 shows a generic scheme for DLS-based 2D DWT with L-input and L-output, which is mainly composed of a column processor (CP), a row processor (RP) and a scale unit (SU). The 2D DWT is performed in column-row fashion to be compatible with JPEG2000 standard. The CP and RP perform lifting steps in column and row dimensions, respectively, and the SU combines the scaling steps in column DWT and row DWT to reduce the number of required multipliers. These components are cascaded and executed in parallel and pipeline with image data received in raster scan manner.

Figure 6

Generic DLS-based 2D DWT with L-input and L-output.

5.1 Proposed Fast Architecture for 2D DWT

Using the proposed CPE with SISO and RPE with DIDO in the subsections 4.1 and 4.2, we can get our proposed fast architecture (FA) for 2D 9/7 DWT, as shown in Fig. 7(a). Image samples are received with the throughput of two samples per each clock cycle in raster scan manner as in Fig. 4(a). The CP is composed of four CPEs, which are cascaded in pairs to process the two samples received at each clock cycle in parallel, namely one even-column and one odd-column sample. For an N×N image, the sizes of the temporary buffers, D_L and D_H, in each CPE are both N/2, and thus the total buffer size of the CP is 4N. The 1D wavelet coefficients from the CP are transmitted to the RP directly, which is composed of two cascaded RPEs with DIDO. The SU is designed with two multipliers and two multiplexers, as shown in Fig. 7(b). From Eq. (3), it can be obtained that the scaling coefficients for the subband LL, LH/HL, HH are k ² δ ², and 1/δ ², respectively. When the two samples received by SU are belong to the even row, the multiplexers select 0 to generate two 2D DWT coefficients in subband LL and HL; when the two samples received by SU are belong to the odd row, the multiplexers select 1 to generate the 2D DWT coefficients in subband LH and HH. Note that the proposed FA can be easily applied for the implementation of 2D 5/3 DWT. Because only one lifting step is required to be carried out in 5/3 DWT, the FA for 2D 5/3 DWT consists of two CPEs, one RPE and one SU.

Figure 7

a DLS-based fast architecture for 2D 9/7 DWT; b structure of SU in fast architecture.

5.2 Proposed High-Speed Architecture for 2D DWT

Higher processing speed can be achieved with increased throughput in the implementation of 2D DWT. With more CPEs working in parallel and the proposed RPE with QIQO in the subsection 4.3, we can get our proposed high-speed architecture (HA) for 2D 9/7 DWT, as shown in Fig. 8(a). Image samples are received with the throughput of four samples per each clock cycle in raster scan manner as in as in Fig. 5(a). The CP is composed of eight CPEs, which are cascaded in pairs to process the four samples received at each clock cycle in parallel, namely two even-column and two odd-column samples. For an N×N image, the sizes of the temporary buffers, D_L and D_H, in each CPE are both N/4, and thus the total buffer size of the CP is still 4N, the same as that in FA. The 1D wavelet coefficients from the CP are transmitted to the RP directly, which is composed of two cascaded RPEs with QIQO. The SU is designed as shown in Fig. 8(b) with four multipliers and two multiplexers. From Eq. (3), it can be obtained that the scaling coefficients for the subband LL, LH/HL, HH are k ² δ ², δ and 1/δ ², respectively. When the four output samples received by SU are belong to the even row, the multiplexers select 0 to generate two 2D DWT coefficients in subband LL and two in subband HL; when the four output samples received by SU are belong to the odd row, the multiplexers select 1 to generate two 2D DWT coefficients in subband LH and two in subband HH. Similar as the FA, the proposed HA can be easily applied for the implementation of 2D 5/3 DWT. Note that the proposed HA can be easily applied for the implementation of 2D 5/3 DWT. Because only one lifting step is required to be carried out in 5/3 DWT, the HA for 2D 5/3 DWT consists of four CPEs, one RPE with QIQO and one SU.

Figure 8

a DLS-based high-speed architecture for 2D 9/7 DWT; b structure of SU in high-speed architecture.

6 Performance Comparison and Experiment Result

Table 1 summarizes the detailed hardware specifications of each component and the overall 2D architectures for 9/7 and 5/3 DWT, where N and L are the width of the image and the number of the samples received at each clock cycle, respectively. The proposed designs have simple structures with regular processing elements for the computation of lifting steps, and can be easily extended to support higher throughput with controlled increase of hardware cost. By exploiting pipeline technique in each component, time delay of the critical path in the proposed designs is reduced to one multiplier delay, resulting in high working frequency. Based on the proposed DLS, the CP and RP are designed to work in raster scan manner with consistent data flow so as to eliminate the implementation of data buffer, which reduces efficiently the on-chip memory size, the output latency and the control complexity. Thus the required internal memory only includes the temporary buffers used in CP, which is totally 4N and 2N for 9/7 and 5/3 DWT. For an N×N image, the computing time of proposed FA and HA is N ²/2 and N ²/4 clock cycles, respectively. Though the number of multipliers and adders increase twice in HA, the total internal memory size remains the same as that in FA. Consider that the memory issues dominate the hardware cost and complexity of 2D DWT architecture, the proposed design provides high-speed solutions with controlled increase of hardware cost.

Table 1 Hardware specification of each module and the overall proposed 2D DWT architectures for an N×N image with L-input and L-output.

The proposed 2D DWT architectures are compared with those reported in [2–4, 7–10, 13] in the aspect of hardware complexity, critical path, output latency and computing time. Tables 2 and 3 show the comparison results for 9/7 and 5/3 DWT respectively. It can be seen that the on-chip memory size of our designs is the smallest in all related 2D architectures but the arithmetic cost is less than most others, which is mainly because of the employment of the proposed DLS. Moreover, the proposed design HA achieves the highest processing speed in all related 2D DWT architectures, which can perform 2D DWT in N ²/4 clock cycles for an N×N image. Although the number of multipliers is a little more than some others with the same computing time, the additional cost is far less than the area reduction of the on-chip memory, and affects the total hardware cost little.

Table 2 Comparisons of various 2D DWT architectures for an N×N image with 9/7 DWT. Tm and Ta is the time delay of multiplier and adder, respectively.

Table 3 Comparisons of various 2D DWT architectures for an N×N image with 5/3 DWT. Tm and Ta is the time delay of multiplier and adder, respectively.

To show the efficiency of the proposed DLS-based 2D DWT architectures, they were described with Verilog HDL language to implement 9/7 DWT, where internal data was represented in 16 bits with 7 bits for fractional data and the multiplier coefficients were represented with 12 fractional bits in canonic sign digital (CSD) expression to reduce production terms. The designs were implemented in SMIC 0.18 μm CMOS logic fabrication, and the operation frequency can be up to 150 MHz. The floorplans of FA and HA are given in Fig. 9(a) and (b), respectively, which can accommodate up to 512 × 512 image size with 4 KB internal memory. Due to the regular read and write operation in each temporary buffer, these buffers can be realized as a whole with Artisan 0.18 μm standard library register file generator to decrease the occupied area. The temporary buffer in Fig. 9(a) was implemented with a dual-port register file which contained 256 128-bit words, whereas that in Fig. 9(b) was implemented with two dual-port register files each of which contained 128 128-bit words because the maximum word length of register file is limited to 128 bits by the Artisan register file generator. The detailed specification of the floorplans is shown in Table 4.

Figure 9

a Floorplan of FA; b floorplan of HA.

Table 4 Specification of the floorplans of the proposed 2D DWT architectures.

7 Conclusion

In the hardware implementation of 2D DWT, data buffer is required due to the data flow inconsistency in the row processor and column processor. Using the proposed DLS, image data can be processed in raster scan manner without the implementation of data buffer, resulting in the reduction of on-chip memory, output latency and control complexity. Furthermore, the 2D DWT architecture can be easily extended to achieve higher processing speed with controlled increase of hardware cost. Memory-efficient and high-speed architectures are proposed to implement 2D DWT for JPEG2000, which are called FA and HA. The computing time of FA and HA is N ²/2 and N ²/4 clock cycles for an N×N image, respectively, but the required internal memory is only 4N for 9/7 DWT and 2N for 5/3 DWT. Compared with the works reported in previous literature, the proposed designs provide excellent performance in hardware cost, control complexity, output latency and computing time. The designs were implemented in SMIC 0.18 μm CMOS logic fabrication with 4 KB internal memory for the image size 512 × 512. The areas are only 999137 um ² and 1333054 um ² for FA and HA, respectively, but the operation frequency can be up to 150 MHz.