Introduction

Distance-based methods are widely used in ecology, and have proven their worth for many purposes, most notably as employed in ordination or cluster analysis for arranging sites according to similarity in species composition (Legendre and Legendre 1998). These applications calculate the dissimilarity metric across a number of descriptors of the same type and measured on the same scale (commonly species presence or abundance data) and use it to either group sites or arrange them in a lower-dimension ordination space. Other distance-based methods treat a group of conceptually related indicators as one entity. For example, several measures of soil properties may be used to calculate a compound dissimilarity metric that describes overall soil properties. The Mantel test assesses the significance of the relationship between two or more distance matrices (Mantel 1967; McCune and Grace 2002). Distance-based methods are particularly valuable in ecology because they allow explicit incorporation of geographic distances into analyses. Dissimilarity metrics exist for both quantitative and qualitative data types, allowing the analysis of many types of information. Significance testing for dissimilarity methods is usually done with permutation tests, so these methods make no assumptions about underlying distributions.

There are three major explicitly distance-based methods (Table 1). The simple Mantel test tests the association between two simple or compound distance matrices, while the partial Mantel test controls for one or more additional dissimilarities, analogous to a partial correlation. Multiple regression on distance matrices (MRM) incorporates each individual data vector as a separate individual distance matrix. Although MRM is sometimes described as being comparable to partial Mantel tests, the similarity is only superficial, due to the inclusion of more than two distance matrices, and the hypotheses tested are quite different. Instead, simple Mantel tests and MRM are analogous. For the former, all the dependent variables are included in one compound distance matrix, while in the latter, each is converted to a distance matrix separately. In all the three cases, the user must be careful to state hypotheses and conclusions in terms of distances rather than raw data.

Table 1 Hypotheses of three common statistical tests on distance matrices
Full size table

Two major questions have been raised about the explicitly distance-based approach. The first question concerns the relationship between correlations (or other analyses) on raw data and those on dissimilarities. The Mantel r M statistic, a correlation on dissimilarity matrices, is frequently much lower than a correlation coefficient on raw data, and is often significant even at values <0.10 (Dutilleul et al. 2000; Legendre 2000). This poses problems of interpretation, since ecologists naturally assume that r M scales from 0 to 1 identically to a correlation coefficient calculated from raw data. The second question concerns the difference between including all the related variables in one dissimilarity matrix, as is done in ordination, clustering, and some Mantel testing, or using each variable to construct a separate dissimilarity matrix, as is done in MRM and some Mantel testing (Legendre et al. 1994; Urban et al. 2002; Goslee and Urban 2007; Lichstein 2007). There is very little guidance available on when to combine several explanatory variables into a compound distance matrix or when to leave them as separate variables.

The frequent and successful use of ordination methods and cluster analysis demonstrates that distance matrices do retain considerable information about their component variables. Here, the simulated data are used to explore the relationship between correlation on dissimilarity matrices and correlation on raw data, and to examine the effects of combining variables into a compound dissimilarity matrix (simple Mantel test) or using them separately (MRM).

Methods

Although a large number of dissimilarity metrics have been described (reviewed in Legendre and Legendre (1998) and elsewhere), analyses here will focus on the commonly used Euclidean distance. Euclidean distance is the most conceptually and computationally straightforward, since it is analogous to simple geographic distance between two points on a map (Eq. 1).

$$ ED_{\rm pq} = \sqrt{\sum _{\rm i=1}^n (p_{\rm i}- q_{\rm i})^2} $$
(1)

where p i and q i are the ith elements of the data vectors p and q. The Euclidean distance is metric, part of a subset of the group of dissimilarity coefficients that satisfy the triangle inequality and thus can be represented exactly in n-dimensional space (Legendre and Legendre 1998). The Bray–Curtis dissimilarity coefficient is commonly used by ecologists, but is non-metric (and thus a dissimilarity rather than a distance; Eq. 2).

$$ BC_{\rm pq} = {\frac{\sum _{\rm i=1}^n |p_{\rm i} - q_{\rm i}|}{\sum _{\rm i=1}^n (p_{\rm i} + q_{\rm i})}} $$
(2)

The analyses here are primarily concerned with correlations between raw data vectors (r raw) and between dissimilarity matrices (Mantel statistic r M), calculated using the Pearson correlation coefficient r (Eq. 3).

$$ r_{\rm pq} = {\frac{\sum _{\rm i=1}^n (p_{\rm i} - \bar{p}) (q_{\rm i} - \bar{q})}{(n-1) s_{\rm p} s_{\rm q}}} $$
(3)

where p i and q i are the ith elements of the data vector p with mean \(\bar{p}\) and standard deviation s p and the data vector q with mean \(\bar{q}\) and standard deviation s q. For clarity, the correlation coefficient calculated on raw data will be denoted r raw, and on dissimilarities r dist (= Mantel statistic r M).

When two or more variables are combined into a compound dissimilarity matrix, the relative magnitudes of the individual variables can have a large effect on the values of the dissimilarities (Legendre and Legendre 1998). Prior to calculating Euclidean distances, standardization to z-scores with mean = 0 and standard deviation = 1 is recommended. The correlation of compound dissimilarities is affected by choice of scaling, but the correlation of the raw data is not. Bray–Curtis dissimilarity cannot be calculated for z-scores because it assumes that all data values are non-negative. If used with negative data, the Bray–Curtis dissimilarity calculation can give negative values, and negative distances are not readily interpretable. Instead, data should be relativized to have a constant maximum, either using the maximum observed value or the maximum theoretical value (e.g., percentages).

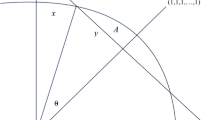
The simplest case for distance-based analysis, both conceptually and mathematically, involves two sets of data, the dependent variables y, and the independent (explanatory) variables x. If the x variables are orthogonal, as for example geographic coordinates, then the system has a geometric analog with the x variables forming the coordinate system (Fig. 1). The length of the y j vector represents its total correlation with x, and the correlation of each y variable with each x variable is the projection of y j on x i. Each y j vector must fall on the unit circle, or within it if r xy < 1.

Fig. 1
figure 1

Two dependent y variables plotted against two orthogonal x variables, providing a geometric analog of correlation analysis on the raw data. The vector y 1 represents the magnitude and direction of the correlation of y 1 with all x variables. The projection of y 1 on the x 1 axis represents the correlation r x_1 y 1 between x 1 and y 1

Full size image

Simulation methods

All the analyses were done using the statistical software R (version 2.7.1, R Development Core Team (2008)). Source code and functions are available from the author.

For comparing correlations for raw data and distances, corgen() from the ecodist package (Goslee and Urban 2007) was used to simulate two vectors of length 1,000 with a random correlation between −1 and 1. Each vector was converted to Euclidean distances, and the correlation calculated. The simulation was repeated with artificial data drawn from normal, uniform, Poisson, and gamma distributions.

A similar procedure was used to generate multivariate normal data for use in comparing compound and individual distances. For non-orthogonal sets of variables x or y, rcorrmatrix() from the clusterGeneration package (Qiu and Joe 2007) was used to generate a positive definite correlation matrix, and the mvrnrom() function from the MASS package (Venables and Ripley 2002) was used to simulate multivariate normal random data with that correlation structure. Simulations were conducted for all the combinations of 1–5 for the number of x and y variables, and for both orthogonal and correlated x variables. Correlation structure within the y variables and between x and y variables was always random. Variable length was 1,000, and 500 repetitions of each simulation were used unless otherwise specified.

Results

Correlations on raw data and distances

For pairs of individual normal variables, the correlation between Euclidean distances on scaled data is linearly related to the squared correlation on raw data (r 2raw = r dist, Fig. 2). Dutilleul et al. (2000) discuss this relationship for data drawn from a normal distribution. The relationship is approximately true for other distributions (r = 0.999 for normal; r = 0.997 for uniform; r = 0.999 for Poisson; r = 0.997 for gamma; 1,000 simulations for each). Although only applicable to distance vectors calculated from a single variable, this relationship provides a way to consider correlations between multivariate dissimilarities as well.

Fig. 2
figure 2

Correlation coefficients on raw data (r raw and r 2raw ) and on scaled Euclidean distances (r dist) for 1,000 pairs of randomly generated vectors of length 1,000 with correlation coefficients from −1 to 1

Full size image

Orthogonal axes

The particular case where one of the raw data matrices consists of m orthogonal variables (the x variables, for example, geographic coordinates) is geometrically interesting, as described above, and shows some intriguing statistical properties. The second data matrix contains n variables of interest (y variables, such as species abundances) that may or may not be correlated. Given the m by n matrix of all the individual pairwise distances (equivalent to squared correlations on the raw data), the total relationship of each individual y j variables together with all the geographic variables x can be calculated as

$$ Y_{\rm j} = \sqrt{\sum_{\rm i=1}^m (r_{{\rm x_i}{y_{\rm j}}})^2} $$
(4)

The predicted correlation between distance matrices is then

$$ r_{\rm dist} {\text{pred}} = \sqrt{\frac{(\sum_{\rm j=1}^n Y_{\rm j})^2}{mn}} $$
(5)

In other words, the correlation between two compound distance matrices can be calculated from the correlations among the two sets of individual single-variable distance matrices. The Mantel r M statistic relating a compound Euclidean distance matrix calculated from a set of scaled orthogonal x variables and the compound distance matrix calculated from a set of scaled y variables is a function of the individual correlations of the separate Euclidean distance matrices calculated for each x i and y j. Each individual variable makes a predictable contribution to the overall distance matrix.

Even if each of the y variables has a correlation of 1 with the x variables, the maximum r M may be less than 1. The total possible sum of Y j = the minimum of m and n (when each y variable is perfectly correlated with one of the x variables), and the maximum correlation of distances is

$$ r_{\rm dist} max = \sqrt{\frac{n}{m}} $$
(6)

if n < m. If n > m, then the model is overdetermined and the maximum r M = 1. This upper bound complicates the interpretation of the Mantel r M statistic, and contributes to the generally low values of r M noted earlier. Referring to Fig. 1 helps to clarify the importance of the orthogonal and non-orthogonal systems. The length of each Y j vector in m-space (the correlation of y j with all X) is determined by the correlation of y j with all the individual x i variables because the x variables describe the axes of a Euclidean space. The total compound correlation is a function of all the individual correlations. Moving from raw data to distances, the maximum correlation is no longer 1, but a function of the number of x and y variables involved, and n and m additionally require a square-root transformation.

Three simple examples will demonstrate the concepts and calculations involved. Both examples use m = 2 and n = 3, that is, two orthogonal x variables and three possibly correlated y variables. In the first example, the y variables are each perfectly correlated with one of the x variables (2). The total relationship of each Y j variable with all x is the square root of the sum of squares of the values in that column of the table, and the predicted Mantel r M is calculated as in Eq. 5, from the sum of the Y j variables squared. The maximum Mantel r M is \(\sqrt{2/3}\) for 2a. Note that even with a “perfect” correlation among the x and y variables, the maximum Mantel r M is less than 1. The second example (Table 2) is worked similarly. This example has a more complex correlation structure, and a lower total Mantel r M, although the predicted Mantel r M is the same because n and m have not changed.

Table 2 Worked examples with m = 2 (orthogonal x variable) and n = 3 (dependent y variables). Actual Mantel r M is from simulated data of length 1,000 with the given correlation structure
Full size table

Simulated data with n and m both varying from 1 to 5 were used to empirically assess the relationship between the actual and predicted r dist values. Each of the x and y data vectors were of length 1,000 and had a randomly generated joint correlation structure. The simulation was repeated 500 times for each combination of m and n. The overall relationship between actual and predicted for all sets of m, n is shown in Table 3. The actual Mantel r M may be somewhat different from the calculated r M due to the numerical properties of the mvrnorm() algorithm and the imprecision and rounding error inherent in computer simulations.

Table 3 Correlations between actual and predicted values of r dist for varying levels of m (number of orthogonal x variables) and n (number of dependent y variables) on 500 simulated data vectors of length 1,000 and random correlation structure for y
Full size table

Multiple regression methods on dissimilarity matrices have been suggested as alternatives to the Mantel test approach, with the advantage that they do not require groups of variables to be combined into a compound dissimilarity matrix (Legendre et al. 1994; Lichstein 2007). MRM can provide any of the multiple regression coefficients, but only one, the coefficient of multiple correlation R, is examined here. For the particular class of data analyzed here, r 2dist (squared simple Mantel coefficient) and R from MRM are closely related (Table 4; linear regression for all simulations: adjusted r 2 = 0.759, P < 0.001).

Table 4 Correlation between R 2 from multiple regression on distance matrices and the Mantel r 2dist for varying levels of m (number of orthogonal x variables) and n (number of dependent y variables) on 500 simulated data vectors of length 1,000 and random correlation structure for y
Full size table

Ecologists frequently use dissimilarities other than Euclidean distance. For the simulated data used here, Bray–Curtis dissimilarity on relativized data gives very similar results to Euclidean distance for simple Mantel tests (linear regression with intercept = 0 for all simulations: adjusted r 2 = 0.996, P < 0.001), and for MRM (linear regression with intercept = 0 for all simulations: adjusted r 2 = 0.994, P < 0.001). Using individual component dissimilarities to predict correlations with a compound dissimilarity was also moderately successful (linear regression for all the simulations: adjusted r 2 = 0.751, P < 0.001).

Correlated axes

The relationships derived above are only mathematically correct for orthogonal x variables, but are approximately correct for moderate degrees of collinearity among x. Ecologists rarely deal with orthogonal variables. The more highly correlated the x variables, the greater the maximum value of r dist (Fig. 3). When the independent x variables are correlated, the calculation of maximum r dist becomes progressively less accurate, as does the relationship between a compound distance matrix and its component individual distance matrices. Referring back to Fig. 1, if x 1 and x 2 are not orthogonal, y 1 is no longer constrained to fall within the unit circle, and so the actual correlation can exceed the predicted correlation. While geographic coordinates are by definition uncorrelated, ecologists often wish to compare two sets of variables in which the members are collinear to some extent, such as soil data and plant species composition. In these cases, the greatest interpretability is obtained by dropping one member of each highly correlated pair (r raw > 0.70) as appropriate. If it is important to understand the contribution of each x variable, ordination methods could be used to create a system of orthogonal \(\acute{x}\) variables from the original set.

Fig. 3
figure 3

Response of r dist between y and x 12 to varying degrees of correlation between x 1 and x 2 simulated for 1,000 randomly generated y vectors of length 1,000. The horizontal line indicates the maximum r dist value for uncorrelated x data with m = 2 and \(n=1 (\sqrt{n/m})\)

Full size image

In practice, when correlations among the x variables are allowed to vary randomly, the accuracy of prediction of compound r dist from its component distances is still very high (r =  0.923 for m and n from 1 to 5), and the relationship between Mantel and MRM results is correspondingly good (r = 0.913 for m and n from 1 to 5). These mathematical relationships are inaccurate when strong correlations exist among the x variables (Fig. 3), making it impossible to predict maximum r dist or relate individual and compound distance matrices, so removing highly correlated variables is recommended.

As for the uncorrelated data, when using x data with random correlation structure, the Bray–Curtis dissimilarity on relativized data gives very similar results to Euclidean distance for simple Mantel tests (linear regression with intercept = 0 for all simulations: adjusted r 2 = 0.977, P < 0.001), and for MRM (linear regression with intercept = 0 for all simulations: adjusted r 2 = 0.919, P < 0.001). Using individual component dissimilarities to predict correlations with a compound dissimilarity was also successful (linear regression for all simulations: adjusted r 2 = 0.882, P < 0.001).

Discussion

For Mantel tests, when one set of variables is orthogonal (or only weakly correlated), the correlation with a second set of variables follows a mathematically predictable relationship that can be derived from the correlations of the individual distance matrices between the two sets. Moreover, for scaled data, there is a direct relationship between the correlation of raw data vectors and the correlation of distance matrices. These relationships demonstrate that the Mantel test approach can provide interpretable results when used with multivariate distance matrices, and that the low values often seen in Mantel testing is in fact due to the statistical method itself.

These results demonstrate that multiple regression on individual distance matrices is mathematically similar to Mantel testing with compound distance matrices, at least for a particular combination of particular distance and data scaling. The choice of Mantel or MRM testing should thus be driven by ecological hypotheses rather than by concerns about the mathematical suitability of a particular test. If the overall relationship of dissimilarities is of interest, then Mantel testing is appropriate, while if the contributions of distances within individual variables are of interest, then MRM should be used. In either case, the hypotheses must be framed in terms of distances rather than raw data.

The relationships described here are strictly true only for a very limited category of data. Orthogonality is perhaps the strictest limit, but variable selection or ordination procedures provide a way to reduce or eliminate collinearity in one set of variables. Euclidean distance is the most mathematically tractable because of its metric nature and close relationship to the correlation coefficient. Preliminary results suggest that the Bray–Curtis dissimilarity coefficient often used in vegetation studies follows the same relationship between univariate and multivariate dissimilarities. The simulated data used in this study do not contain frequent zero values, and thus do not necessarily resemble the kinds of data for which ecologists use Bray–Curtis dissimilarities.

Scaling the data is very important for all the dissimilarity-based methods because it provides a consistent frame of reference for the coefficients. While correlation on raw data is unchanged by any linear scaling method, if the variables that make up a multivariate dissimilarity coefficient are on different scales, then the resulting multivariate coefficient can vary widely. Scaling or other standardization should be employed for all the analyses unless an a priori justification exists for using the raw data.

For certain cases (Euclidean distances on scaled data), the many-to-one relationship from a set of variables to a compound dissimilarity matrix is both straightforward and mathematically tractable. Information obtained from this special case can provide insight into other types of dissimilarity-based analyses as well. An understanding of the relationship between correlations on raw data and correlations on dissimilarity matrices also explains the distribution of the Mantel r M values and how to determine the maximum obtainable r M for a particular set of data. This maximum value aids in interpretation of the low but significant Mantel r M values often seen in the literature.