In Australia, the enrolment figures in mathematics education in upper secondary school are on the decline. The National Mathematics Curriculum: Framing paper (2009) attributes the decline to the middle school students’ disengagement in mathematics education. Clearly, reform in middle school mathematics education is urgently needed to improve students’ mathematics performance. Among various potential actions to reverse the downward trend, improvement in pedagogical approaches so as to enhance learning effectiveness would be helpful. Nevertheless, there are certain topics in the mathematics curriculum that are intrinsically difficult to learn. A typical example is solving problems that involve percentage changes. A problem asking students to find the price of an item when it is increased by 5 % and then decreased by 5 % is an intrinsically difficult algebra problem (Parker and Leinhardt 1995). To teach students in 8th grade to solve this problem, the Australian Curriculum v3.0 Mathematics (ACARA 2012) does not specify a particular approach. Most Australian mathematics textbooks (Kalra and Stamell 2005) tend to use a short-cut version of the unitary method to teach this topic. Although other possible approaches may work better for most students, no research to date has scrutinized the effectiveness of the commonly used approaches. In the present study, we attempted to delineate the cognitive load involved in three approaches (unitary, pictorial, and equation) for learning how to solve percentage change problems. We hope to provide evidence for an improved instructional design for teaching the topic of percentage change problems.

Importance of percentage change problems

The study of percentage change problems represents an integral part of the early junior secondary mathematics curriculum. Students learn to calculate a pay rise, a discount or a markup price, Government sale tax (GST), sales commission, a rise in rent, petrol price and so on. Essentially, the mastery of percentages should enable students to judge, which is a better offer when there is a discount of 10 % or two successive discounts of 5 % each, to interpret “What does it mean to have 0.5 % increase in unemployment?”. This knowledge will hopefully help students make wise decisions in everyday contexts.

Why is it difficult to teach percentages?

The learning of percentages and changes in percentages is unfortunately a major challenge to many students. Parker and Leinhardt (1995) have provided a comprehensive review of such challenges. For example, students tend to write ½ and ½ % interchangeably as if they could disregard the % symbol. Conversion between percentages and decimal fractions is also problematic for many students, and particularly so with percentages greater than 100 %. A typical example is that students often express 120 % as 0.12. It also seems difficult for some students to grasp the conversion of common fractions and percentages (e.g., one and a half = 150 %). Some students are also confused when both a decimal number and the percentage symbol appear together (e.g., 0.5 %). Parker and Leinhardt’s findings demonstrate that the teaching and learning of percentages is challenging because students need to process information in different forms at the same time (e.g., converting fractions, decimals and percentages that share a common numerical value but presented in different forms). The relational nature of percentages poses yet another challenge to students (Parker and Leinhardt 1995). Students tend to rely on their intuitions using addition and subtraction to solve both of these: (a) Find the price when it is increased by $5 and decreased by $5; (b) Find the price when it is increased by 5 % and then decreased by 5 %. Most students are unaware of the multiplicative relation required to solve the percentage change problems.

Cognitive load in percentage change problems

Central to cognitive load theory (Sweller et al. 1998; Merriënboer and Sweller 2005) is a human cognitive structure that comprises working memory and long-term memory. Working memory is limited in capacity (Miller 1956) when processing unfamiliar information. Long-term memory has unlimited capacity to store organized information structures in the form of schemas with varying degrees of automation. In mathematics, a schema implies abstract knowledge for a category of problems together with their associated solution steps. An expert who possesses an automated schema is able to solve problems by-passing working memory limitations, because the information and solution steps can be processed as a single unit, which can be easily handled cognitively. In the absence of a schema, an instructional tool may provide a guideline to generate the missing schema in long-term memory. Ideally, the presentation of instructional materials would guide the process of knowledge elaboration (Kalyuga 2009) through which the knowledge structures in the long-term memory will be integrated with the new knowledge structure to form a relevant schema. Hence the aim of any mathematics instruction is to assist learners to acquire a schema and then with further practice, to automate the acquired schema (Cooper and Sweller 1987). In this study, we examined the effectiveness of three approaches to assisting learners to acquire a schema for solving percentage change problems from a cognitive load perspective. The approaches are: (1) the unitary approach which first reduces percentages to 1 % and uses this as a basis for calculating the changed amount, (2) the pictorial approach which uses a diagram to depict both the concept of percentage change and the procedure for calculating it, and (3) the equation approach which guides the learners to formulate and solve an algebraic equation. In the following, we first describe the various kinds of cognitive load and then illustrate how cognitive load is associated with each of the three problem solving approaches.

Cognitive load research has described three types of cognitive load that may influence the effects of instructional materials: (1) intrinsic cognitive load, (2) extraneous cognitive load, and (3) germane cognitive load. Each of these plays an important role in influencing the learners’ acquisition of schema. These are discussed with regard to solving percentage change problems, which is the focus of this study.

Intrinsic cognitive load

Intrinsic cognitive load arises from the interaction between elements within a task (see Sweller 1994, 2010; Sweller and Chandler 1994). Learning material has low element interactivity and thus low intrinsic cognitive load if each element can be processed and learned in isolation. In contrast, learning material constitutes high intrinsic cognitive load when learning depends on an understanding of the interaction between multiple elements, which is likely to overload working memory.

For a percentage change problem such as, “A discount of 10 % was given for a digital camera with a marked price of $350. Find the price paid after the discount.”, the learner needs to identify relevant information in different units (10 %, $350), specify key words such as ‘price paid’, and construct a relation between values and variable (price paid) in an equation: price paid = $350–$350 × 10 %. Although there are only three elements (price paid, $350, 10 %), the interaction between these elements must be considered simultaneously to allow understanding to occur. This mental process involving high element interactivity may overwhelm working memory.

Nevertheless, whether element interactivity would constitute learning difficulty depends on the learner’s expertise in the domain (Kalyuga et al. 2001). An expert can process several interrelated elements as a single unit (e.g., $350 × 10 %) and thus would expect to experience less intrinsic cognitive load associated with the problem. However, for most students learning percentage change problems as a novice, the interacting elements that require simultaneous processing inevitably generate an unduly high cognitive load. To enable a novice to accomplish a task with high element interactivity, instruction can be introduced as separate but sequential units (Gerjets et al. 2004), which are later integrated as a whole (Pollock et al. 2002). The premise is to build hierarchical levels of concepts to build the schema. This idea was adopted in designing the equation approach, which will be discussed later.

Extraneous cognitive load

Extraneous cognitive load occurs when inappropriate instruction compels the learners to engage in cognitive activities that are unrelated to schema acquisition (e.g., searching for a solution path). Earlier cognitive load theory research focuses on designing worked examples to reduce extraneous cognitive load (Cooper and Sweller 1987; Paas and Merriënboer 1993, 1994; Sweller and Cooper 1985; Merriënboer and Sweller 2005). A worked example integrating text with a diagram was found to reduce extraneous cognitive load by minimizing the split-attention effect arising from processing information from disparate sources (Sweller et al. 1990). As will be discussed later, the unitary approach imposes extraneous cognitive load due to the need to search and match percentage and quantity from disparate sources of information. For the pictorial approach which uses a diagram to help learners visualize the relations between elements, the extraneous cognitive load arises from searching and matching percentage and quantity in the diagram.

Germane cognitive load

Germane cognitive load occurs when the learner exerts mental effort to understand relevant aspects of a schema. As will be discussed later, the use of mental effort to process relevant information in the diagram of the pictorial and equation approaches constitutes germane cognitive load. Furthermore, when students are asked to practise solving a variety of problems to reinforce their schema acquisition, the process inevitably generates germane cognitive load. Because the variability of the worked examples during the practice process helps to foster schema acquisition, germane cognitive load is “healthy” as it facilitates the learners to comprehend identical structural features across different contexts (Paas and Merriënboer 1994; Quilici and Mayer 1996). Therefore, in our study, we incorporated multiple example-problem pairs similar to variability of worked examples that introduce germane cognitive load to facilitate the mastery of major concepts and problem solving capabilities.

Recent development in cognitive load theory (Beckmann 2010; Sweller 2010, 2011, 2012) has included element interactivity to define extraneous cognitive load as well as germane cognitive load. Sweller (2010) argued that only an instructional designer is able to distinguish the variation between the three aspects (intrinsic, extraneous, germane) of the cognitive load but not a learner. Presented with a task, a learner needs to invest cognitive load to process the interacting elements; and the more interacting elements the learner needs to process, the higher the cognitive load. An instructional designer would regard those interacting elements as extraneous cognitive load if they inhibit learning; otherwise, they would constitute germane cognitive load. In line with the recent formulation of cognitive load theory, we adopted element interactivity as the point of reference in distinguishing the design features of the unitary, pictorial and equation approaches discussed below.

Instructional approaches

Unitary approach

The unitary approach calculates 1 % of a given quantity and then a multiple of this amount to arrive at the answer. This approach involves interaction between multiple elements that imposes a high level of cognitive load. Consider this problem: ‘If your father wants to increase your weekly allowance of $20 by 5 %, what will be your new weekly allowance?’ A typical unitary approach solution procedure is shown in Table 1 below.

Table 1 Unitary approach, pictorial approach and equation approach for solving a percentage increase task
Full size table

Step 1 has two elements, 5, 100 %, and the learner needs to handle two sets of concepts: (1) that 5 % is an addition on top of 100 %, and (2) that 105 % denotes an increase above the original amount. These elements and concepts need to be processed together.

Step 2 has two elements, $20 and $100, and involves three sets of concepts: (1) $20 as the original quantity, (2) 100 as the concept of percentage (100 out of 100 in this case), and (3) the sub-goal is 1 % of the original quantity although no % sign is used anywhere. The mental processing involves an interaction among three elements: money value ($20), the equivalence of 100 % to $20, and 1 % of the money value.

Step 3 has two elements and three concepts like step 2. However, it is further complicated by the concept of $105 %, which exceeds the limit of 100 % in the concept of percentage, which is often a source of difficulty for many learners (Parker and Leinhardt 1995).

Further to the interactivity of the elements in each step that would introduce intrinsic cognitive load, the interaction between the three steps introduces further intrinsic cognitive load. This is because each step cannot be considered in isolation. For example, the learner needs to refer to 105 % in step 1 in order to understand the role of 105 % in step 3. Therefore, the consideration of the elements in each step and across different steps simultaneously is likely to overwhelm working memory capacity.

Apart from dealing with the high intrinsic load as a result of the high element interactivity within and across solution steps, the lack of clarity between the three solution steps would impose extraneous cognitive load. In step 1, the interpretation of percentage change will be difficult without a point of reference such as $20 means 100 %. To overcome this, the learners need to search and make inferences between $20 and 100 %. This is possible by integrating information from two separate sources (i.e., percentage in step 1 and quantity in step 2), and this involves a split attention between two discrete sources (Chandler and Sweller 1992; Yeung et al. 1998). In short, the combined consequences of high element interactivity within and across the solution steps, coupled with extraneous load to search for relevant information may overwhelm limited working memory capacity especially for the novices, leaving inadequate cognitive resources to learn the percentage increase problem.

It should be noted that instead of three steps, the authors of some mathematics textbooks (Kalra and Stamell 2005) condense them to two steps without providing a clear rationale for the step skipping: 100 % + 5 % = 105 % (step 1); and 105 % × $20 = $21 (step 2). The absence of unit percentage (skipped step) will further increase extraneous cognitive load because the learners need to search for too many missing elements.

Pictorial approach

White and Mitchelmore (2005) designed a diagram depicting 100 % as ten equal chunks with each chunk represented 10 %. This is similar to a percentage bar diagram used in previous research to facilitate learning of percentage problems (Heuvel-Panhuizen 2003). The main idea is to calculate 10 % of a quantity, and then to derive all other percentage quantities based on multiples of 10. The concept of 10 % is frequently used in the context of percentage problems because it is an easy number to conceptualize during mental calculation and estimation. The pictorial approach in the study performed by White and Mitchelmore (2005) was therefore found to enhance primary students’ grasp of percentage quantity (e.g., 54 × 20 %), though their learning outcomes fell short of what the authors had expected.

Because of the apparently strong effect of the visual stimulus, previous researchers (Edens and Potter 2008; Hegarty and Kozhevnikov 1999; Zahner and Corter 2010) advocated the use of diagrams to scaffold the underlying problem structure in the problem texts. We adapted the work of White and Mitchelmore (2005) to construct the pictorial approach (Table 1) to highlight the underlying problem structure. The diagram in the pictorial approach comprising 10 equal blocks scaffolds the relative position of 10, 20, 30 % and up to 100 % which corresponds to the original amount ($20). Therefore, the diagram depicts the structural feature of the original amount ($20) in the problem text and the implicit 100 % that corresponds to the original amount. Accordingly, the calculation of a subgoal such as 10 % is derived from the point of reference where $20 means 100 %. In other words, the diagram uncovers the proportion concept relating to a multiple of 10 % required to solve the percentage change problem. The cognitive load involved in the pictorial approach is detailed in Table 1.

For the same percentage increase problem as in the unitary approach above, the pictorial approach requires students to learn solution steps in conjunction with the diagram (Table 1). Step 1 has two elements, 10 % and $20. The learner needs to handle two sets of concepts: (1) one out of 10 blocks (i.e., each block in the diagram) represents 10 %, and (2) that 100 % represents $20. The learner needs to process these elements and concepts simultaneously. Since the diagram aligns the original amount ($20) and its corresponding 100 % so as to act as a point of reference, it reduces extraneous cognitive load by avoiding a split-attention effect between $20 and 100 %. In addition, the germane cognitive load is increased to elicit the proportion concept in a multiple of 10 % to enable the learners to deduce 10 % of $20.

Step 2 has two elements, 5 % and $20. However, it involves three sets of concepts: (1) $20 is the original quantity, (2) 5 % is an addition on top of 100 %, (3) an increase of 5 % is only half of 10 % (i.e., half of a block in the diagram). Hence the mental processing here involves an interaction between these elements and therefore a high intrinsic cognitive load. Furthermore, half a block representing 5 % is not explicitly illustrated in the diagram so the learner is required to infer the relation between percentage and money value. This involves extraneous cognitive load. Step 3 has two elements, $20 and $1; and it involves three sets of concepts. (1) $20 is the original amount, (2) $1 is the increased amount, (3) the sum of the original ($20) and the increased amount ($1) gives the new allowance ($21). For this step, intrinsic cognitive load is not particularly high because the two elements have the same unit ($), and can easily be added up.

Therefore, for this particular problem, only step 2 in the diagram seems to involve high cognitive load. For a problem involving percentage other than a multiple of 10 % (e.g., an increase of 12 %), the diagram using each block to represent 10 % does not help at all because the learner needs to generate an extra step (such as a unit percentage) to solve the problem.

In sum, on one hand, the alignment of the original amount ($20) and 100 % in the diagram eliminates a split-attention effect and highlights the structural feature of the problem situation, which facilitates learning. On the other hand, the diagram imposes extraneous cognitive load when the learners need to search relevant information that is not explicitly depicted in the diagram (e.g., half a block represents 5 %). Furthermore, the diagram is unable to provide a consistent procedure for percentage change problems in a variety of contexts (e.g., increase 12 %). Therefore, the pictorial approach may not offer instructional advantage any better than the unitary approach.

Equation approach

Prior research has supported the use of proportional thinking expressed in the form of an equation for teaching and learning percentage problems (Dole 2000; Jitendra et al. 2011; Shield and Dole 2008). For example, Dole (2000) put the known and unknown variables on a single-line to facilitate the translation of proportional thinking into an equation such as 25/100 = ?/60 in order to solve 25 % of 60. However, it is necessary for the learner to have prior knowledge of proportion; otherwise, he or she may fail to see the link between various concepts within a hierarchy of concepts (Low and Over 1992; Zhu and Simon 1987).

To ascertain that learners had adequate prerequisites so as to form a schema for factorization, Zhu and Simon (1987) required students to review the concepts of (1) the product of two numbers (e.g., 2 × 4), and (2) the sum of these two numbers (i.e., 2 + 4), which formed part of the factorization (e.g., x 2 + 6x + 8). Reviewing these concepts in isolation may have alleviated the intrinsic cognitive load associated with factorization where multiple concepts are broken down into separate manageable steps.

The equation approach presented here used the same rationale. In essence, this approach divided the learning process into two parts (Table 1). Part 1 started with a revision of prior knowledge such as percentage quantity that students had previously learned. The review process of prior knowledge is expected to involve low cognitive load. This is because first, students had learned these before; and second, this process with each step building on the preceding step engages students in deductive reasoning (Stacey and Vincent 2009) in which the connection between fraction and percentage, which constitutes a major concern in learning percentage problems (Parker and Leinhardt 1995), is analytically handled. This assists the learners to capitalize on their prior knowledge of the relation between fraction and quantity so as to master the relation between percentage and quantity.

Part 2 followed by translating the problem situation and integrating the multiple components. This was done through adapting Zhu and Simon’s (1987) approach of building links between the components and Dole’s (2000) approach of putting these components together within an equation. Hence, the focus of Part 2 is on problem translation and integration (Table 1). Again, similar to previous research (Edens and Potter 2008; Hegarty and Kozhevnikov 1999; Zahner and Corter 2010), the horizontal line in the diagram serves to represent the underlying problem structure. Therefore, germane cognitive load is increased to process the horizontal line depicting the underlying problem structure that comprises the original amount and increased amount. The horizontal line not only assists the learners to activate the schema of percentage quantity (increased amount) established in Part 1, but it also helps the learners express the problem structure in an equation for generating subsequent solution steps. It should be stressed that the activation of schema such as percentage quantity allows the learners to process the problem using fewer elements in working memory (also see Jitendra et al. 2007; Nathan et al. 1992; Ngu et al. 2009; Weaver and Kintsch 1992).

Apart from processing the diagram in Part 2, the learners need to process the solution procedure in Part 2. The mental processes associated with the solution steps will be: Step 1 translates the problem structure into an equation. As the diagram clearly illustrates the relation between the original and increased amount, translating such a relation into an equation that adds up these two amounts will involve little cognitive load. Step 2 comprises two elements—the original amount ($20) and the increase (5 %), but also two concepts: (1) the multiplicative relation between $20 and 5 % to form $20 × 5 %, and (2) the sum of $20 and $20 × 5 %. The element interactivity would normally constitute high cognitive load. Nevertheless, given the schema reinforcement procedure in Part 1 above, which has presumably built a link between the $ and  % components (Zhu and Simon 1987), the cognitive load involved in assimilating these elements together within an equation would have been lowered.

In essence, by reviewing percentage quantity in Part 1, students are expected to reinforce their schema for $20 × 5 % and treat this as a single unit, hence reducing the burden on working memory. Accordingly, manipulating the interaction between the two elements in Part 2 ($20 and $20 × 5 %) through knowledge elaboration described by Kalyuga (2009) to generate a schema expressed in a single equation would constitute relatively low intrinsic cognitive load. For step 3, the values in the same unit ($) can be added up easily and, as described in the pictorial approach above, is unlikely to impose a high cognitive load.

The current study

Based upon prior studies (Dole 2000; Jitendra et al. 2011; Shield and Dole 2008; White and Mitchelmore 2005; Zhu and Simon 1987), we evaluated the relative merits of the unitary, equation and pictorial approaches from a cognitive load perspective. Both the unitary and pictorial approaches not only involve high element interactivity but also impose extraneous cognitive load due to the need to search for critical information. In contrast, the cognitive load invested to process two elements in the equation approach is expected to be lower. Therefore, we hypothesized that test scores subsequent to these respective approaches would favor the equation approach.

Method

Participants

Participants were 60 eighth grade Australian students (31 girls, 29 boys, mean age = 14 years) studying in a private secondary college in a rural community of Australia who consented to participate in the study. According to the head teacher, all students had learned percentage quantity as illustrated in Appendix A. Some students were taught how to solve percentage change problems via a short-cut version of unitary method (see Unitary approach) commonly found in mathematics textbooks (Kalra and Stamell 2005). As our purpose was to test the effects of intervention on new learning, these students were excluded from the analysis. In short, all students had gone through the same mathematics curriculum and there was no evidence of any difference in prior knowledge of the contents covered in the experiment.

Materials

Materials were designed for a pre-test, an instruction sheet, acquisition problems, and a post-test. Both the instruction sheet and acquisition problems were used to facilitate learning. The pre-test and post-test were used to establish the instructional effects upon learning.

Instruction sheet

The first page of the instruction sheet was common across the three groups. It had the definition and meaning of percentage as well as the revision for percentage quantity, which they had learned earlier (Appendix A). For each approach, two worked examples were given-one percentage increase problem and one percentage decrease problem.

Acquisition problems

We constructed booklets including six pairs of acquisition problems structured respectively in terms of each approach. In other words, the three approaches have identical material but the presentation of the material differs. For each of these pairs, a worked example was paired with an equivalent practice problem sharing a similar problem structure. Three of the six pairs were percentage increase problems, and the other three pairs were percentage decrease problems. The acquisition problems were designed to capitalize on the variability of the problems with varying surface features to foster schema acquisition by generating a “healthy” germane cognitive load (Paas and Merriënboer 1994; Quilici and Mayer 1996). At the top of the first page of acquisition problems, there was a written instruction informing the students to study each worked example carefully to ensure that they understood it so as to use the same way to solve the following problems. Students were required to show their work in the space provided in the booklet.

Both the instruction sheet and acquisition problems constituted the learning phase whereby students were exposed to 14 percentage change problems (two worked examples in the instruction sheet, plus six pairs of acquisition problems). Though both the instruction sheet and acquisition problems were expected to contribute toward schema acquisition, the acquisition of schema would predominately occur when students studied a worked example alternated with solving a practice problem across the six pairs of acquisition problems. In fact, the worked examples providing full solution steps served as direct instruction. The extent to which students had acquired schema would be assessed on the basis of their ability to solve test items. If students could show correct solution steps (even if they made computational errors), this will mean that they had acquired schema.

Pre-test and post-test

The pre-test had identical content to the post-test. Two types of tasks were included (Table 2)—the simple tasks (the first 10 items) and the complex tasks (the last two items). The differentiation between simple and complex tasks was based on their structural and surface features (Fuchs et al. 2004; Holyoak and Koh 1987; Reed 1987; Reed et al. 1994; Richland and McDonough 2010). In our case, the simple tasks were isomorphic to the acquisition problems because both shared the same solution (problem structure) but had different story contexts (Reed 1987). The complex tasks included features (e.g., 120 % in the first complex test item) that did not appear in the acquisition problems (Reed et al. 1994).

Table 2 Correct solutions for simple and complex tasks (in %) across the unitary, pictorial, and equation approaches
Full size table

Procedure

The data collection was scheduled to align with the sequence of the mathematics topics to be covered in actual classroom. Data collection occurred after the students had learned percentage quantity. Students in 8th grade were invited to participate in the study. The aims of the study and students’ involvement were explained in the invitation letter to their parents. Sixty students from whom consent were obtained were randomly assigned to three conditions: 20 in the unitary approach, 20 students in the pictorial approach, and 20 students in the equation approach, respectively.

The three conditions were conducted concurrently on the same day in three separate classrooms. Each of these conditions was conducted in a single 40 min lesson by a researcher and a class teacher. Students in each condition were told to work individually to complete a pre-test, an acquisition phase (an instruction sheet + acquisition problems) and a post-test. The pre-test took 10 min. Next, students were given 5 min to study their respective instruction sheets (Appendix A) in which the first page was common across the groups. They were encouraged to seek help if they could not understand the materials in the instruction sheet. Then, the class teacher gave each student a booklet to work on six pairs of acquisition problems. For each of these pairs, students were instructed to follow the respective solution procedure (unitary, pictorial, equation) depicted in the worked example and adapt this to solve a practice problem sharing a similar problem structure. Students were allowed to have access to the instruction sheet while working on the acquisition problems. They completed as many acquisition problems as they could in the 15 min allocated. Because they were randomly assigned to groups, differential completion of practice problems would be inferred as a function of the approaches rather than students’ prior knowledge. We expected differential completion of practice problems, which would also impact upon the performance outcomes. The students took 20 min to complete the acquisition phase (instruction sheet + acquisition problems). Finally, all students undertook a post-test (10 min), which had identical content to the pre-test.

In sum, the consistency between the three conditions was maintained where students across the three groups were matched in terms of time and content materials. All handouts (test papers, instruction sheet, acquisition problems) were collected after each phase.

Results

Coding and analysis

Of the 60 participants, four students scored 8 or above in the pre-test indicating their prior knowledge of percentage change problems, and one student did not hand in the practice problems. Thus the scores of these five students from different treatment groups were excluded from the analysis. Because our focus was on conceptual rather than computation accuracy, computational errors were ignored. Therefore, one mark was awarded for demonstrating correct solution steps. If a student demonstrated accurate solution steps but made a computational error, the solution was scored correct.

Each task was allocated one mark, except for one item in the complex task, which had two parts, and thus two marks were allocated for this task. We also recorded the frequency of non-attempted problems and errors made. Any problem unsolved was regarded as a non-attempted problem. The errors made included conceptual and other errors. For example, a conceptual error included inability to calculate the subgoal of 1 % in the unitary approach (i.e., $95/55 instead of $95/100 for test item 1, Table 2). Other errors included incomplete or obscure solutions. The sum of these errors was recorded as errors made.

The dependent variable for group comparisons of pre-test scores was correct solutions. For each of the six pairs of acquisition problems, the first was a worked example, and the second was a practice problem. We analyzed the six practice problems only. For both practice problems and post-test, the dependent variables for group comparisons were correct solutions, non-attempted problems, and errors made. However, the post-test items could be further differentiated into simple or complex tasks, which were analyzed separately.

In the pre-test, the Cronbach’s alpha was 0.87 (10 items) for the simple tasks. The Cronbach’s alphas was not computed for complex tasks because only one student from the equation approach attempted the complex tasks. In the post-test, the respective Cronbach’s alpha for the simple and complex tasks was 0.96 and 0.90. One of the researchers scored all test items and a mathematics teacher scored 20 % of the test items. The inter-scorer correlation computed on the 20 % test items was above 0.95. In cases where the scorers differed, they discussed and decided on a mutually agreed score. The same procedure was used for establishing the reliability of the correct solutions, non-attempted items and errors.

To establish equivalence of sample across groups, we used a one-way analysis of variance (ANOVA) on the pre-test scores (simple and complex tests separately). To detect any differential gains between pre-test and post-test scores among the three conditions, we performed a 3 group (unitary, pictorial, equation) x 2 test (pre-test, post-test) ANOVA, with group as a between-group factor and test as a repeated measure. We also examined the correlations between practice problems and post-test scores to determine whether superior post-test performance can be attributed to the success in solving practice problems. Finally, we also analyzed the solution strategies adopted by students in the post-test as explicated on the answer sheets. The purpose was to ascertain that the post-test results were a direct consequence of the instructional approach.

Pre-test

Table 3 presents the proportion of correct solutions for the pre-test. The analysis was conducted separately for the simple and complex tasks.

Table 3 Means and (SD) of scores in practice problems, pre-test, and post-test, and frequency of non-attempt problems and errors made
Full size table

Simple test

One-way ANOVA on pre-test simple tasks indicated non-significant difference across the three groups, F(2, 52) = 1.02, MSE = 0.04, p = 0.37. Thus there was no differential performance on pre-test between the three groups prior to the intervention.

Complex test

Nonsignificant difference was also found among the three groups on pre-test, F(2, 52) = 1.12, MSE = 0.00, p = 0.33. Once again, the three groups did not show differential performance prior to the intervention.

Practice problems

Table 3 shows the means and standard deviations of correct solutions, non-attempted problems and errors made in the practice problems. One-way ANOVA performed on these variables for the three groups indicated significant differences on correct solutions, F (2, 52) = 8.30, MSE = 42.41, p < 0.01, non-attempted problems, F (2, 52) = 3.19, MSE = 12.85, p = 0.05, and errors made, F (2, 52) = 5.51, MSE = 14.85, p = 0.01.

In regard to correct solutions, post hoc Tukey test showed significant mean differences between the equation and pictorial approaches, Ms = 4.53 and 1.66 respectively, SE = 0.75, p < 0.01; unitary and pictorial approaches, Ms = 3.95 and 1.66 respectively, SE = 0.73, p = 0.01. For the non-attempted problems, significant mean difference was found between unitary and pictorial approaches, Ms = 0.84 and 2.47 respectively, SE = 0.65, p = 0.04. In relation to the errors made, significant difference was found between the equation and pictorial approaches, Ms = 0.00 and 1.82 respectively, SE = 0.55, p = 0.01. In short, the equation group solved significantly more practice problems than the unitary group, which solved more than the pictorial group. The pictorial group tended to have more non-attempted problems and made more errors.

Post-test

Table 2 shows correct solutions (in percentages) generated for individual post-test items across the three groups. For the simple test that resembled acquisition problems, the unitary approach ranged from 45 % (items 8 and 9) to 70 % (items 3, 5 and 6), the pictorial approach ranged from 21.1 % (item 9) to 50 % (item 1); and the equation approach ranged from 70.6 % (item 9) to 88.2 % (items 2, 4 and 6). A similar pattern emerged for the complex test. The equation group performed considerably better than either the unitary or pictorial group. The respective percentage score for items 11, 12(a) and 12(b) across the three groups was: 67.8, 64.7, 47.1 % (equation approach), 22.5, 20, 15 % (unitary approach), and 10.5, 5.3, 5.3 % (pictorial approach).

Simple test

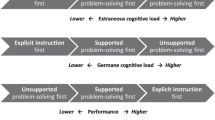
Table 3 presents proportion correct solutions for the post-test, non-attempted problems and errors. A 3 (group) x 2 (test) ANOVA with group as a between-group factor and test as a within-subjects repeated measure showed a significant group effect, F(2, 52) = 8.43, MSE = 0.11, p < 0.01, η 2 = 0.25, a significant test effect, F(1, 52) = 101.37, MSE = 0.06, p < 0.01, η 2 = 0.66, and a significant group x test interaction effect, F(2, 52) = 8.60, MSE = 0.06, p < 0.01, η 2 = 0.25. These results indicated that there were significant differences on the performance from pre-test to post-test across the three groups after the intervention. As shown in Fig. 1a, all three groups improved from pre-test to post-test, but the pictorial group experienced the least improvement.

Fig. 1
figure 1

Pre-test and post-test for the unitary, pictorial and equation approaches for a simple test, and b complex test

Full size image

As the equivalence across groups was established at the pre-test, it was possible to compare post-test group means directly. One-way ANOVA was conducted on correct solutions, non-attempted problems and errors made in the post-test. Significant difference was found between the groups on correct solutions, F (2, 52) = 10.88, MSE = 1.4, p < 0.01. Post-hoc Tukey test indicated significant differences between the unitary and pictorial approaches, Ms = 0.57 and 0.29 respectively, SE = 0.12, p = 0.04; and also between the equation and pictorial approaches, Ms = 0.85 and 0.29 respectively, SE = 0.12, p < 0.01; but the difference between the unitary and equation approaches was not statistically significant (p > 0.05).

For the non-attempted problems, significant difference was found across the three groups, F (2, 52) = 6.20, MSE = 0.57, p < 0.01. Post-hoc Tukey test showed significant difference between the equation and pictorial approaches, Ms = 0.07 and 0.43 respectively, SE = 0.10, p < 0.01. There was no significant difference between the three groups on errors made, F (2, 52) = 1.60, MSE = 0.14, p = 0.21.

The results so far partially support the hypothesis. The mean correct solutions were higher for the equation group than for the other groups, but the superiority of the equation group was statistically significant only over the pictorial group, not the unitary group. Hence the equation group experienced only marginal advantage over the unitary group in simple tasks.

Complex test

The same analytical procedure for simple tasks was followed. The 3 (group) x 2 (test) ANOVA found significant test effect, F(1, 52) = 36.31, MSE = 0.06, p < 0.01, η 2 = 0.41, significant group effect, F(2, 52) = 9.10, MSE = 0.07, p < 0.01, η 2 = 0.26, and significant group x test interaction effect, F(2, 52) = 8.29, MSE = 0.06, p < 0.01, η 2 = 0.24. As shown in Fig. 1b, the equation group experienced greater improvement from pre-test to post-test than either the unitary or pictorial group. Similar to the simple test, the pictorial group experienced the least improvement from pre-test to post-test.

Directly comparing the post-test scores, we conducted one-way ANOVAs. Significant difference was found between the groups on post-test solutions, F (2, 52) = 8.83, MSE = 1.12, p < 0.01. Post-hoc Tukey test showed that significant differences were between the equation and unitary approaches, Ms = 0.58 and 0.19 respectively, SE = 0.12, p = 0.01; and between the equation and pictorial approaches, Ms = 0.58 and 0.11, SE = 0.12, p < 0.01. This implies clear superiority of the equation approach over the other two approaches.

Significant difference was found between the three groups on non-attempted problems, F (2, 52) = 14.29, MSE = 1.93, p < 0.01. Post-hoc Tukey test showed that the differences were between the equation and unitary approaches, Ms = 0.24 and 0.74 respectively, SE = 0.12, p < 0.01; and between the equation and pictorial approaches, Ms = 0.24 and 0.86 respectively, SE = 0.12, p < 0.01. There was significant difference across three groups on errors made, F (2, 52) = 3.16, MSE = 0.11, p = 0.05. Post-hoc Tukey test indicated significant difference between the equation and pictorial approaches, Ms = 0.19 and 0.04 respectively, SE = 0.06, p = 0.05.

The results further support the hypothesis. The equation group significantly outperformed not only the pictorial group but also the unitary group. The unitary group did not outperform the pictorial group. Between the unitary and pictorial groups, although the unitary group seemed to do better, the advantage of the unitary approach was not particularly great.

Evidence of acquisition effects

Taking the practice problems as reflecting the learning process and the posttest as reflecting the outcome of learning, we would be able to examine the relation between learning and outcome in respective approaches. Specifically, the correlation between practice problems and post-test scores would indicate whether the post-test outcome could be attributed to the instructional approach.

Simple test

Strong positive correlation coefficients were found between practice problems and simple test scores for all three groups: unitary, r = 0.81, p < 0.01; pictorial, r = 0.77, p < 0.01; and equation, r = 0.73, p < 0.01. It appears that the ability to solve practice problems was translated into success in solving post-test problems of a similar nature, irrespective of approach.

Complex test

A strong positive correlation was found between the practice problems and the complex test scores for the equation group, r = 0.70, p < 0.01 indicating that students in the equation group were able to translate their learning to solve complex tasks that were different from the practice problems in terms of problem structure. Relatively weaker correlations were found between practice problems and complex test scores for the unitary group, r = 0.40, p = 0.09 and for the pictorial group, r = 0.53, p = 0.02. However, these correlations did provide support for the effects of the practice exercise leading to the post-test scores. Hence the critical difference between the three approaches lies with the success of the acquisition process.

Solution strategies

We inspected the solution strategies adopted by students across the three groups. These were the students’ scribble in the space provided on the post-test paper where the students worked out their solutions. The solution strategy adopted by a student each in the unitary, pictorial and equation approaches respectively is presented in Fig. 2. The student in the unitary group attempted to find the value of 1 % and used it for calculating the changed value. The student in the pictorial group attempted to use 10 % for a similar purpose. The student in the equation group attempted to use an equation that included all values on a single line. Interestingly, almost no student was able to use the pictorial approach to solve complex tasks. As can be seen in Fig. 2, the solution strategy in the unitary approach for the complex task involved far more steps than the equation approach. This provided evidence for the high cognitive load involved in the problem solving process.

Fig. 2
figure 2

Solution strategies adopted by a student each in unitary, pictorial and equation groups

Full size image

Further to this evidence, an analysis of all students’ solution strategies revealed that the percentage of students who used their respective solution strategies to successfully solve simple tasks were 42, 10 and 82 % for the unitary, pictorial and equation approaches respectively. For complex tasks, the respective percentages were 16, 0 and 59 %. Evidently, the equation approach was much easier to follow. It was therefore not surprising for the students using the equation approach to outperform those who used the other two approaches.

Discussion

Findings

Irrespective of simple or complex tasks, the equation approach yielded significantly more correct solutions, fewer non-attempted problems and errors. The positive instructional effect of the equation approach over the unitary or pictorial approach was more marked for the conceptually more difficult complex tasks rather than the simple tasks. Superior performance of the equation group can be attributed to the success in solving the practice problems, which contributed to their success in the post-test. The equation approach was easier to follow, evidenced in the high percentage of students’ actual application of the approach in the post-test. Its instructional effectiveness was evidenced in the high success rate during practice (M = 4.53, SD = 2.10) with many students completing all six practice items with zero-error performance. In sum, the two-part process in the equation approach allowed the students to learn with less difficulty and perform with more precision for complex percentage change tasks.

An analysis of individual test items (Table 2) revealed that the gain in learning for the equation group exceeded those in the unitary or pictorial group for most items, and particularly for the complex tasks. Evidently, about half of the students in the equation group were capable of relying on a combination of multiplicative and subtraction (or addition) relations (see items 11 and 12 in Table 2) to successfully solve the complex tasks. Interestingly, one or two students in the unitary or pictorial group were able to generate a modified 2-step equation approach, like the performance of the students in the equation group, despite not gaining access to the instruction on the equation approach. This reflects major limitations of the unitary and pictorial approaches in providing useful and manageable directions for learners to follow in order to obtain a solution for complex tasks.

Why does the unitary approach need improvement?

The beneficial effect of the unitary approach was found in the simple tasks but not the complex tasks. The unitary approach does not effectively address the intrinsic cognitive load related to unit percentage so as to lower the extent of interaction among the multiple elements. Furthermore, searching for the relation between the quantity involved and its corresponding percentage imposes extraneous cognitive load. Because such a relation was not explicated in the solution steps, students who were unable to comprehend the relation of elements expressed in different units would not be able to acquire a schema to handle the sophistication of complex tasks.

To improve the design of the unitary approach, one may need to incorporate a diagram depicting the relation between percentage and quantity to avoid the need to search and integrate these two elements. A revision of the proportion concept may also help to ensure that students understand how to calculate unit percentage. With these instructional cues in place, the unitary approach can be modified to incur less cognitive load.

Alternatively, one may design a unitary approach comprising solution steps such as: (1) calculate 1 % of the allowance ($0.2), (2) calculate 5 % of the allowance ($1), and (3) add the change amount ($1) to the original allowance ($20) to get the new allowance. However, the merit of this alternative unitary approach will require additional research.

Why does the pictorial approach need improvement?

The pictorial approach exhibited the worst performance among the three approaches. The pictorial approach requires an integration of multiple elements within and between the solution steps. The diagram does not provide instructional support to explicate the logic of the solution steps (e.g., half a block represents 5 %). It is therefore not surprising that it would impose a high cognitive load. The pictorial approach could even have generated cognitive conflict in the form of heavy extraneous load when the test problems involved percentages other than a multiple 10 %, which is the only multiple the diagram illustrates. Consequently, the use of the cognitive resources to search for an appropriate solution strategy may further exacerbate the cognitive load incurred leading to the formation of a fragmented schema.

The development of the pictorial approach seems to be in its infancy. One could probably improve its design by modifying the diagram. An improved pictorial approach will need to subdivide each block in the rectangle into 10 equal units so that each unit represents 1 %. With this additional feature, the solution steps of an improved pictorial approach will consist of: (1) calculate 10 %, (2) calculate 1 %, and (3) calculate a multiple of 1 % to obtain an answer. In other words, with the alignment of original allowance ($20) and 100 % as a point of reference, the relative positions of 100 %, 10 %, 1 % in the diagram will facilitate the grasp of their corresponding quantities, which should lead to the calculation of a quantity to match a multiple of 1 % (e.g., 12 %). Therefore, this improved pictorial approach may provide a means to solve percentage change problems irrespective of whether these problems fall into a category having a multiple of 10 %. Such explicit guidance is expected to reduce cognitive load required to process the pictorial approach.

Alternatively, one can design a pictorial approach to align original allowance ($20) with 100 %, and new allowance (x) with (105 %), where 105 % represents the percentage after an increase of 5 %. Then, one can form an equation such as, 20/100 = x/105, solve forx. The use ofx to represent the new allowance represents algebra method in problem solving. The cognitive load involved in this format of pictorial approach will be affected by the learners’ prior knowledge of algebra.

Why does the equation approach work?

The superiority of the equation approach may have stemmed from the application of instructional design principles associated with cognitive load theory. The incorporation of review in relation to percentage quantity (which the students had learned earlier) has allowed the students to build a hierarchy of percentage concepts. The two-part process has been crucial in alleviating the intrinsic cognitive load associated with the element interactivity involved in handling percentage change problems.

With the aid of a horizontal line, the germane cognitive load is increased to deduce the underlying problem structure comprising the original amount plus the changed amount (i.e., percentage quantity). With the help of review on percentage quantity, the changed amount would be established in the learners’ schema and can therefore be treated as a single element. As a result, processing the original and changed amount would constitute two elements only, and this would greatly reduce the cognitive load that would have been unmanageable for a novice when all various elements had to be handled simultaneously. This coupled with the germane cognitive load by studying numerous pairs of worked examples and solving equivalent problems seems to have helped students solve percentage change problems effectively. Presumably, the acquisition of an automated schema in a single equation (e.g., $20 + $20 ×5 %) resulted in freeing up cognitive resources to comprehend structural features, especially in the complex tasks in which the interaction between such features are different from the simple tasks (Cooper and Sweller 1987). The evidence shows that about half of the students in the equation group were able to use the multiplicative and subtraction (or addition) relation concepts to solve complex tasks.

The equation approach is essentially an algebra approach in problem solving when students use a variable, x, to interpret the new allowance. Whereas the equation approach is found to be an effective instructional method, its usefulness depends on students’ prior knowledge and skills. Unless the students have a strong foundation of a range of algebraic skills, it is unlikely that they would benefit from this approach for higher order complex percentage change problems as discussed later. Hence there is room to further improve the effectiveness of this approach by identifying ways to firmly establish the link between prior knowledge and the application of this approach, and this will require further research.

Limitations and future directions

The study was conducted in a single school with a particular sample of students; it is possible that differential students’ abilities had influenced the learning outcomes. In line with the recent studies related to expertise reversal effect (Kalyuga et al. 2003; Kalyuga 2007; Kalyuga and Renkl 2010) in which novices would require greater instructional support than those experts who have greater knowledge in the domain, future research needs to include individual differences as a variable when testing the learning effects among the three approaches.

To assess the instructional effects of different approaches on facilitating schema development resulting in automation of information processing, further research may include the measure of speed in addition to accuracy of performance. It would also be worthwhile to further examine the retention of the schema to scrutinize long-terms effects of instruction. By including these additional features in future investigations, we would be able to draw stronger conclusions regarding the role of cognitive load across different instructional approaches in facilitating short-term and long-term outcomes.

Not all existing cognitive load research includes a measure of relative instructional efficiency. In our study, the use of cognitive load theory to predict the relative instructional efficiency of unitary, pictorial and equation approaches was supported. Indirectly, this provides a degree of theoretical validation. Nonetheless, we recognize that a direct measure of relative instructional efficiency will strengthen the theoretical rationale. Therefore, future research should include a Likert scale to record the mental effort invested in the learning phase (Paas and Merriënboer 1993) to more directly link performance scores to cognitive load.

So far, prior cognitive load theory researchers (Gerjets et al. 2004; Pollock et al. 2002) have managed to design part-task processes to reduce the intrinsic cognitive load that arises from the complexity of the task itself. Our study differs from previous research in that we designed three approaches with varying degrees of element interactivity and tested their relative strength in fostering schema acquisition for percentage change problems. To verify the impact of the varying degrees of element interactivity upon learning outcomes, additional research could include a rapid online method (Kalyuga 2008) for diagnosing the level of the learners’ knowledge base after exposure to the three approaches. Students in three respective groups would be expected to generate different solution formats (unitary, pictorial, equation) for the same test items. Therefore, we anticipate accurate rapid diagnosis of solution steps would favor the equation approach followed by the unitary approach and lastly the pictorial approach in line with the hypothesized degree of element interactivity associated with the respective approaches.

We did not assess at which point of time the activation of prior knowledge occurred for the learners. The horizontal line in the diagram is divided into two components reflecting the problem structure that consists of the original amount plus increased amount. It is possible that exposure to this schematic diagram during the treatment activates prior knowledge of percentage quantity (increased amount, $20 × 5 %). Future research could incorporate a think-aloud protocol (Hong and O’Neil 1992) to find out at which point of time the activation of prior knowledge occurred.

Among the three approaches, the equation approach seems to be a promising instructional format for enhancing students’ problem solving skills in percentage change tasks especially the complex tasks. The unitary approach has limitation in solving complex tasks. Parker and Leinhardt (1995) suggest that higher order complex percentage change tasks are particularly difficult for students to learn. Students tend to use their additive intuitions to solve a markup task such as: ‘After a 12 % markup, the shoes now cost $34. How much did they originally cost?’ (p. 448). Students tend to find 12 % of $34 and subtract this amount from $34 to arrive at the original cost. It appears that students draw on their prior knowledge of percentage quantity (e.g., calculate $34 × 12 %), which is incorrect in this context. Also, they rely on their intuitions to subtract $34 (cost after 12 % markup) from $34 × 12 %, as they perceive that the original cost should be less than $34. Clearly, there is a difficulty in decoding what is required. Nevertheless, students’ errors can be a source of excellent learning experience if sufficient scaffolding is provided by the teacher through diagrams, models and concrete aids. The unitary method, however, is unlikely to provide such kind of learning experience. However, the incorporation of a diagram in the unitary method may improve its design. The diagram aligning the relative position of amount ($) and  % not only enables the learners to distinguish the relation between the original amount, changed amount, and marked up price, but also it eliminates a split-attention effect. Hence future research needs to include a diagram in the unitary method.

Nevertheless, a limitation of the study is the use of a diagram for both the equation and pictorial approaches. In particular, incorporating a diagram in the equation approach weakens the evidence of efficacy for the equation approach because it is unclear whether the effects found in the equation approach was due to the generation of an equation or due to the inclusion of a diagram, or both. Future research will benefit from separating the effect of the diagram from the generation of an equation. However, it is important to note that at least some students may not be able to make sense of the instruction for the equation approach unless the “change” concept is triggered (see Appendix A). Consider the example presented in Appendix B. Unless “increased amount” is defined, the equation approach would not make sense to some learners. In order to define this concept of “change”, we could use a few sentences but the text is likely to increase cognitive load which counters our purpose of reducing it. Hence instead of using text, a better way which we chose to use was the inclusion of a simple diagram to bring out the concept of change but did not give specific information as did the diagram in the pictorial approach which also guided the learners to follow problem solving procedures. In essence, the diagram forms a necessary part of the equation approach which depicts the relation between the unknown variable and values in the problem text so as to activate students’ prior knowledge of percentage quantity (increased amount in this case), which mediates the construction of an equation for generating a solution (Jitendra et al. 2007; Xin et al. 2005).

Even though the higher post-test scores in the equation approach suggest that the diagram is unlikely to be the contributing factor to success in solving the problem, future research should consider alternative ways to clearly tease out the effects of the three approaches. One possibility is to design another method of presentation in the instruction for the equation approach to avoid the confounding diagram. Another possibility is to separately scrutinize the equation approach by testing it with and without a diagram, or also with and without a defining text. A third possibility is to use a diagram for all three approaches, probably with the unitary and equation approaches sharing a simpler diagram just depicting the concept without giving the specific problem-solving procedures delivered in the pictorial approach. However, the question regarding the effects of the diagram may still remain. In any case, future research should attempt to delineate the contribution of the diagram from the effective problem-solving approach.

Although the diagram in the pictorial approach did not seem to benefit problem solving, the diagram in the equation approach seems to work better. The beneficial effect of a horizontal line in the equation approach may extend to the higher order complex percentage change tasks. Hence, for the above marked up task, the use of a horizontal line to depict the underlying problem structure comprising the original cost, changed amount, marked up price may help learners to grasp the relationship between these structural features. Then, the learners can usex, a variable, to represent the original cost and set up an equation such as $34 = x + x × 12 % to solve the task. Nonetheless, as noted previously, the interaction between intrinsic cognitive load and a learner’s expertise (Kalyuga et al. 2003; Kalyuga 2007; Kalyuga and Renkl 2010) necessitates the selection of appropriate prior knowledge (e.g., algebraic skills, factorization, equation with fractions) for revision prior to learning how to solve this higher order complex percentage change task. Hence, additional research needs to test the merit of equation approach for higher order complex percentage change tasks and elucidate how it may reduce cognitive load.

Conclusion

To conclude, the design of the equation approach supported by the cognitive load framework yielded better results than the other two approaches. The presence of a horizontal line and the incorporation of prior knowledge reinforcement may help to decrease intrinsic load and the two-part process would involve minimal strain on working memory. The pictorial approach, and to a lesser extent, the unitary approach, incurred extraneous load as the learners needed to search for critical information to solve percentage change problems. In addition, both approaches lacked a mechanism to address high element interactivity. One can hardly expect reform in middle school mathematics education to have a positive impact unless mathematics educators are willinging to incorporate school-based research evidence in structuring middle school mathematics curriculum. It is hoped that evidence generated from this study will enable researchers and educators to identify areas that need improvement. By identifying weaknesses and strategically improving instruction, hopefully more middle school students will enjoy mathematics and more will pursue mathematics education in upper secondary school.