1 Introduction

Hydrodynamic lubrication theory shows that there is no pressure generation in perfectly parallel contacts between mating and sliding surfaces. This is because no wedge action exists in the contact area. However, there are many machine elements with a flat–flat contact area such as thrust bearings, mechanical face seals, piston-skirt systems, and slide guide ways in which hydrodynamic lubrication action is anticipated. If some surface irregularity exists, a local wedge action may produce hydrodynamic pressure to support a load. Although this concept was first suggested to investigate the hydrodynamic pressure mechanism in parallel sliding contacts, it has recently been investigated and used to enhance the tribological performance by using macro-features one or two orders of size smaller than the contact area. However, the hydrodynamic lubrication mechanism produced by a textured surface is still poorly understood and is thus being investigated.

In the current paper, the authors propose a new mechanism in which the incorporation of a textured pattern could promote a hydrodynamic lubrication action. This mechanism considers the equilibrium of the moment applied to a pad, which has been ignored in past studies. The variation in the shape of the pressure distribution by the incorporation of a textured feature increases the convergence ratio of the surfaces, at which the equilibrium of the moment is achieved. The increased convergence ratio results in greater pressure generation by the wedge action over the contact area. The current paper derives the analytical equations for the pressure, shear stress, load, friction, and moment in the case where a single dimple is created on the pad. A parametric investigation of the dimple size and location is also conducted.

2 Background

During the last two decades, a great deal of work on enhancing lubrication characteristics using textured surfaces has been conduced in accordance with the recent significant developments in texturing techniques [1]. However, the basic principle for textured surfaces was suggested in past years and is still the accepted mechanism.

The first basic principle is based on micro-hydrodynamic lubrication bearings, in which an unsymmetrical pressure distribution appears, including the occurrence of cavitation at the diverging zone of the textured feature. The produced pressure is not more negative than the vapour pressure of the lubricant in the diverging zone of the film, whereas the growth of the positive pressure is not limited to the converging zone of the film. As a result, an unsymmetrical pressure distribution is produced, giving a normal net force to support the load. Salama [2] pioneered surface texturing. Although his motivation was different, he was the first to experimentally and theoretically investigate the influence of surface texturing, giving attention to the hydrodynamic lubrication mechanism for flat–flat contacts as mechanical face seals. Salama [2] created transverse grooves over a stationary ring pressed against a rotating flat disc to measure the frictional torque. His theoretical model considered cavitation to use the Reynolds boundary condition. The results for the friction coefficients predicted by the theory were in good agreement with the experimental results for thick films, whereas they were smaller than those for thin films. Hamilton et al. [3] created photoetched micro-asperities on the stators of mechanical face seals and showed that the load capacity increased depending on the specifications of these asperities. By directly observing the seal area between a glass rotor and a stator, they showed that local pressurisation occurs at each micro-asperity, while cavitation appears at the divergence zone of the asperity. Following this work [3], Anno et al. [4] proposed that small tilts at the top of asperities might contribute to the load capacity. However, in a later work [5], they showed that pores could also improve the load capacity up to the same order as asperities and offered a greater leakage advantage than the asperities.

Cavitation problems such as those involving the threshold pressure and boundary condition have remained a principal area of concern in relation to the mechanism of micro-textured hydrodynamic lubrication bearings. Olver et al. [6] suggested a new mechanism, in which a cavitation pressure lower than atmospheric pressure in a textured pocket located at the inlet side produces an additional Poiseuille flow to support the load as ‘inlet suction’. It was found that a lower cavitation pressure is expected to cause inlet suction. Their group extended this concept to fixed pad bearings and found that an inlet suction could contribute to load support up to a convergence ratio of around 0.01 [7, 8]. Ausas et al. [9] compared the pressure distributions between the Reynolds boundary condition and p–θ model proposed by Elrod and Adams [10], considering the mass conservation of the flow. They showed that the load support with the Reynolds boundary condition was overestimated for micro-textured bearings. Qiu and Khonsari [11] also compared three boundary conditions—the half-Sommerfeld, Reynolds, and Floberg-Jakobsson-Olsson (JFO)—for cavitation in dimpled surfaces for mechanical seal-like contacts. They found that the JFO theory predicted the smallest pressure generation, whereas the greatest pressure was produced under the Reynolds boundary condition. This implies that the use of the half-Sommerfeld condition or Reynolds condition overestimates the load capacity. Qiu and Khonsari [12] conducted a series of parametric simulations based on the JFO model. They showed that cavitation does not always have a positive effect on the load capacity, depending on the operating conditions, and that its pressure is crucial to the performance.

Direct observation of cavitation in textured patterns has been conducted in recent studies. Negative results as well as positive results have been reported, which may arise from cavitation. Qiu and Khonsari [13] showed that the dimple-textured specimen caused cavitation in dimples to provide lower friction coefficient than the flat specimen for steel rings, while wear of the textured specimen increased. Tokunaga et al. [14] showed ‘cavitation rings’ in mechanical face seals, on which dimple-patterned lines were created in the circumferential direction, with lower friction compared to flat specimen. Zhang et al. [15] showed that the observed cavitation patterns were in good agreement with those estimated by the JFO theory. Wahl et al. [16] created crossed micro-channels on pins to observe cavitation in the channels. Their experimental results showed that the friction coefficient increased when cavitation was observed in the micro-channels. Yang et al. [17] showed a negative impact of groove pattern on lubrication characteristics in fixed block pad contacts on a moving transparent disc.

The second basic principle produced by textured surfaces was proposed by Tønder [18, 19]. Tønder suggested that the partial incorporation of roughness on a stationary surface in the inlet region causes pressure generation in a way similar to Rayleigh step bearings [20], resulting in no cavitation due to texturing. When the film thickness in the land zone is comparable to or greater than the roughness height, this type of bearing is less effective than fixed pad bearings. When the film thickness is smaller than the roughness height, the load capacity and leakage advantages appear.

In the 1990s, a great deal of work was conducted on the enhancement of lubrication characteristics by textured surfaces, as represented by Etsion’s work [1]. Etsion and Burstein [21] conducted numerical analyses for mechanical face seals, in which numerous pores were incorporated into the stator. In their model, a controlled region with a single pore hemisphere is extracted for calculation by assuming negligible interaction between the pores. They assumed that the boundary condition for the cavitation of the lubricant was based on the half-Sommerfeld condition. Their results showed that the optimum pore to contact area ratio is 0.2. The optimum pore size decreased with a decrease in viscosity and an increase in sealed pressure. Etsion et al. [22] showed experimentally that substantial increases occurred in the film thickness and seizure load of mechanical face seals with micro-pores textured by a laser over the stationary ring. They [23, 24] improved the numerical model to change the depth of the dimple and boundary condition for the cavitation occurring at the diverging zone of each dimple and found that the depth to diameter ratio of the dimple is a significant parameter. They also applied laser surface texturing to other types of contact such as thrust bearings [25, 26], conformal pin-on-disc contact [27], reciprocating motion [28, 29], and gas lubrication [30], producing beneficial tribological performances.

One of the most noteworthy findings in Etsion’s work is that the partial incorporation of a textured pattern in the contact area improves the tribological performance. In the case of mechanical face seals, creating pores at the outer side of the ring was found to increase the hydrostatic pressure [24]. In contacts with sliding motion such as thrust bearings [25, 26] and piston rings [28, 29], partial texturing at the inlet side is expected to generate a hydrodynamic pressure in a way similar to the Rayleigh step principle, which was suggested by Tønder [18, 19]. A drastic increase in film thickness (of approximately three times) was experimentally found to be achieved in the case of partial-textured bearings compared to the case of un-textured bearings over an entire load range [26]. This increase in film thickness represented a reduction in friction of more than 50 % compared with the un-textured bearing. However, partial texturing at both sides of the inlet and outlet [26, 29] and central local texturing [28] were also observed to substantially reduce the friction.

Most of the works on textured surfaces have attempted to improve the tribological performance of lubricated areas such as mechanical face seals, piston rings, thrust bearings, and flat–flat contacts, which have low or zero converging film shapes. For such contacts, the rigidity of the supporting systems for the mating surfaces seems to be important because the wedge film action appears to play a significant role in pressure generation, with even a slight increase in the convergence ratio between the mating surfaces compared to that in the parallel position. In the current study, the authors focus attention on the movement of mating surfaces, which have been ignored, as an important action to be explored to determine the lubrication characteristics of textured surfaces.

3 Theory

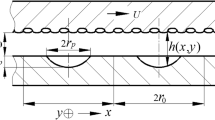
Figure 1 shows a schematic of a centrally pivoted pad bearing. The upper surface is a stationary pad with width l, which is supported by a pivot located at the centre of the pad that allows it to be freely rotated. The lower surface slides from left to right with a constant speed u. A lubricant with viscosity η enters the contact area by the drag of the sliding surface. In this type of bearing, no hydrodynamic lubrication pressure p is generated in a parallel film [31, 32]. The origin of the coordinates is located at the left side of the contact area on the lower surface. Thus, the position of the pivot is l pv = 0.5 l. A single dimple with depth h d is located at the inlet side of the contact area. The step points at the left side and right side areas are l 2 and l 3. Both surfaces are flat, with no elastic deformation, except for the dimple feature.

Fig. 1
figure 1

Schematic of pad bearing

Full size image

For the flow of a lubricant film with thickness h, the following incompressible one-dimensional Reynolds equation can be used:

$$ \frac{d}{{{\text{d}}x}}\left( {h^{3} \frac{{{\text{d}}p}}{{{\text{d}}x}}} \right) = 6u\eta \frac{{{\text{d}}h}}{{{\text{d}}x}} $$
(1)

A dimensionless form of the above equation is

$$ \frac{d}{{{\text{d}}X}}\left( {H^{3} \frac{{{\text{d}}P}}{{{\text{d}}X}}} \right) = \frac{{{\text{d}}H}}{{{\text{d}}X}} $$
(2)

where

$$ H = \frac{h}{{h_{0} }}, \quad P = \frac{{h_{0}^{2} p}}{6\eta lu}, \quad X = \frac{x}{l} $$

The film thickness h can be described as follows:

$$ h = h_{0} + k\left( {l - x} \right)\quad 0 \le x \le l_{2} \,{\text{and}}\,l_{3} \le x \le l $$
(3)
$$ h = h_{0} + h_{\text{d}} + k\left( {l - x} \right)\quad l_{2} \le x \le l_{3} $$
(4)
$$ k = \frac{{\left( {h_{1} - h_{0} } \right)}}{l} $$
(5)

where h 0 is the film thickness at the outlet (x = l), h 1 is the film thickness at the inlet (x = 0), and k is the gradient of the film thickness. The dimensionless forms of these equations are as follows:

$$ H = 1 + K\left( {1 - X} \right) \quad 0 \le X \le L_{2} \,{\text{and}}\,L_{3} \le X \le 1 $$
(6)
$$ H = 1 + H_{d} + K\left( {1 - X} \right)\quad L_{2} \le X \le L_{3} $$
(7)
$$ K = \frac{{\left( {h_{1} - h_{0} } \right)}}{{h_{0} }} = H_{1} - 1, \quad H_{1} = \frac{{h_{1} }}{{h_{0} }}, \quad H_{\text{d}} = \frac{{h_{\text{d}} }}{{h_{0} }}, \quad L_{2} = \frac{{l_{2} }}{l}, \quad L_{3} = \frac{{l_{3} }}{l} $$

where K is the convergence ratio.

The shear stress s applied to the moving surface, and the dimensionless value S is calculated as follows:

$$ s = - \frac{\eta u}{h} - \frac{h}{2}\frac{{{\text{d}}p}}{{{\text{d}}x}} $$
(8)
$$ S = - \frac{{h_{0} s}}{\eta u} = \frac{1}{H} + 3H\frac{{{\text{d}}P}}{{{\text{d}}X}} = S_{\text{c}} + S_{\text{p}} $$
(9)
$$ S_{\text{c}} = \frac{1}{H}, \quad S_{\text{p}} = 3H\frac{{{\text{d}}P}}{{{\text{d}}X}} $$

where the first term of the equations, S c, is the contribution of the Couette flow, and the second term, S p, is that of the Poiseuille flow.

The load w can be calculated by integrating the pressure distribution over the contact area. The friction f is the integrated value of the shear stress over the contact area. The following equations can be used for load w, dimensionless load W, friction f, and dimensionless friction F:

$$ w = \int\limits_{0}^{1} {p{\text{d}}x} = w_{0} $$
(10)
$$ W = \frac{{h_{0}^{2} w}}{{6\eta l^{2} u}} = \int\limits_{0}^{1} {P{\text{d}}X} $$
(11)
$$ f = \int\limits_{0}^{1} {s{\text{d}}x} = \int\limits_{0}^{1} { - \frac{\eta u}{h} - \frac{h}{2}\frac{{{\text{d}}p}}{{{\text{d}}x}}{\text{d}}x} $$
(12)
$$ F = - \frac{{fh_{0} }}{\eta lu} = \int\limits_{0}^{1} {\frac{1}{H} + 3H\frac{{{\text{d}}P}}{{{\text{d}}X}}{\text{d}}X} $$
(13)

where the negative sign in Eq. (12) implies that the friction is applied in the opposite direction to the sliding motion. Dimensional and dimensionless equations for the flow rate can be written as follows:

$$ q = q_{\text{c}} + q_{\text{p}} $$
(14)
$$ q_{\text{c}} = u\frac{h}{2}, \quad q_{\text{p}} = - \frac{{h^{3} }}{12\eta }\frac{{{\text{d}}p}}{{{\text{d}}x}} $$
$$ Q = \frac{q}{{h_{0} u}} = Q_{\text{c}} + Q_{\text{p}} $$
(15)
$$ Q_{\text{c}} = \frac{{q_{\text{c}} }}{{h_{0} u}} = \frac{H}{2}, \quad Q_{\text{p}} = \frac{{q_{\text{p}} }}{{h_{0} u}} = - \frac{{H^{3} }}{2}\frac{{{\text{d}}P}}{{{\text{d}}X}} $$

where q is the total flow rate, q c is the Couette flow rate, q p is the Poiseuille flow rate, Q = q/(h 0 u), Q c = q c/(h 0 u), and Q p = q p/(h 0 u).

The equilibrium equations for the moment m and dimensionless moment M around the pivot point can be written as follows:

$$ m = \int\limits_{0}^{1} {p\left( {x - l_{\text{pv}} } \right){\text{d}}x = 0} $$
(16)
$$ M = \frac{{h_{0}^{2} m}}{{6\eta l^{3} u}} = \int\limits_{0}^{1} {P\left( {X - L_{\text{pv}} } \right){\text{d}}X} = 0 $$
(17)
$$ L_{\text{pv}} = \frac{{l_{\text{pv}} }}{l} $$

In order to obtain a solution of H 1 that satisfies the equations of motion, the Newton–Raphson method is used as follows.

$$ M_{n} + \left. {\frac{\partial M}{{\partial H_{1} }}} \right|_{{H_{1,n} }} \Updelta H_{1} = 0 $$
(18)
$$ H_{1,n + 1} = H_{1,n} + \Updelta H_{1} $$
(19)

where n is the iteration number of the calculation. Equation (18) is solved to obtain ΔH 1. After solving Eq. (14), the approximate value of H 1 is revised in Eq. (19).

The dimensionless pressure P can be found analytically by considering the continuity of the flow in the left land zone, step zone, and right land zone. The analytical solution of dimensionless pressure P is found as follows:

$$ P = \frac{1}{K}\left( {\frac{1}{H} - \frac{1}{{H_{1} }} - \left( {\frac{1}{{H^{2} }} - \frac{1}{{H_{1}^{2} }}} \right)Q} \right)\quad0 \le X \le L_{2} $$
(20)
$$ P = \frac{1}{K}\left( {\frac{1}{H} - \frac{1}{{H_{{2{\text{d}}}} }} - \left( {\frac{1}{{H^{2} }} - \frac{1}{{H_{{2{\text{d}}}}^{2} }}} \right)Q} \right) + P_{2} \quad L_{2} \le X \le L_{3} $$
(21)
$$ P = \frac{1}{K}\left( {\frac{1}{H} - 1 - \left( {\frac{1}{{H^{2} }} - 1} \right)Q} \right)\quad L_{3} \le X \le 1 $$
(22)

where dimensionless pressure P 2 at X = L 2 and dimensionless flow rate Q are expressed as follows.

$$ P_{2} = \frac{1}{K}\left( {\frac{1}{{H_{2} }} - \frac{1}{{H_{1} }} - \left( {\frac{1}{{H_{2}^{2} }} - \frac{1}{{H_{1}^{2} }}} \right)Q} \right) $$
(23)
$$ Q = \frac{{\left( {\frac{1}{{H_{2} }} - \frac{1}{{H_{1} }}} \right) + \left( {\frac{1}{{H_{{3{\text{d}}}} }} - \frac{1}{{H_{{2{\text{d}}}} }}} \right) + \left( {\frac{1}{{H_{3} }} - 1} \right)}}{{\left[ {\left( {\frac{1}{{H_{2}^{2} }} - \frac{1}{{H_{1}^{2} }}} \right) + \left( {\frac{1}{{H_{{3{\text{d}}}}^{2} }} - \frac{1}{{H_{{2{\text{d}}}}^{2} }}} \right) + \left( {\frac{1}{{H_{3}^{2} }} - 1} \right)} \right]}} $$
(24)
$$ H_{2} = 1 + K\left( {1 - L_{2} } \right) $$
(25)
$$ H_{{2{\text{d}}}} = 1 + H_{\text{d}} + K\left( {1 - L_{2} } \right) $$
(26)
$$ H_{{3{\text{d}}}} = 1 + H_{\text{d}} + K\left( {1 - L_{3} } \right) $$
(27)
$$ H_{3} = 1 + K\left( {1 - L_{3} } \right) $$
(28)

The dimensionless shear stress on the moving surface is as follows.

$$ S_{\text{c}} = \frac{1}{H}\quad 0 \le X \le 1 $$
(29)
$$ S_{\text{p}} = 3\left( {\frac{1}{H} - \frac{2Q}{{H^{2} }}} \right)\quad 0 \le X \le 1 $$
(30)
$$ S = S_{\text{c}} + S_{\text{p}} $$
(31)

The dimensionless Couette and Poiseuille flow rates—Q c and Q p, respectively—are calculated as follows:

$$ Q_{c} = \frac{H}{2}\quad 0 \le X \le 1 $$
(32)
$$ Q_{\text{P}} = - \frac{{H^{3} }}{2}\left( {\frac{1}{{H^{2} }} - \frac{2Q}{{H^{3} }}} \right)\quad 0 \le X \le 1 $$
(33)
$$ Q = Q_{\text{c}} + Q_{\text{P}} $$
(34)

The dimensionless load W, dimensionless friction F, and dimensionless moment M are found as follows.

$$ \begin{aligned} W & = \frac{1}{{K^{2} }}\left( { - \ln \left( {\frac{{H_{2} }}{{H_{1} }}} \right) - K\left( {\frac{{L_{2} }}{{H_{1} }}} \right)} \right) - \frac{Q}{{K^{2} }}\left( { - K\left( {\frac{{L_{2} }}{{H_{1}^{2} }}} \right) + \left( {\frac{1}{{H_{2} }} - \frac{1}{{H_{1} }}} \right)} \right) \\ & \quad + \frac{1}{{K^{2} }}\left( { - \ln \left( {\frac{{H_{{3{\text{d}}}} }}{{H_{{2{\text{d}}}} }}} \right) - K\left( {\frac{{L_{3} - L_{2} }}{{H_{{2{\text{d}}}} }}} \right)} \right) - \frac{Q}{{K^{2} }}\left( { - K\left( {\frac{{L_{3} - L_{2} }}{{H_{{2{\text{d}}}}^{2} }}} \right) + \left( {\frac{1}{{H_{{3{\text{d}}}} }} - \frac{1}{{H_{{2{\text{d}}}} }}} \right)} \right) + P_{2} \left( {L_{3} - L_{2} } \right) \\ & \quad + \frac{1}{{K^{2} }}\left( { - \ln \left( {\frac{1}{{H{}_{3}}}} \right) - K\left( {1 - L_{3} } \right)} \right) - \frac{Q}{{K^{2} }}\left( { - K\left( {1 - L_{3} } \right) + \left( {1 - \frac{1}{{H_{3} }}} \right)} \right) \\ \end{aligned} $$
(35)
$$ \begin{aligned} F & = 4\frac{1}{K}\ln \left( {\frac{{H_{2} }}{{H_{1} }}} \right) + 6\frac{Q}{K}\left( {\frac{1}{{H_{2} }} - \frac{1}{{H_{1} }}} \right) \\ & \quad + 4\frac{1}{K}\ln \left( {\frac{{H_{{3{\text{d}}}} }}{{H_{{2{\text{d}}}} }}} \right) + 6\frac{Q}{K}\left( {\frac{1}{{H_{{3{\text{d}}}} }} - \frac{1}{{H_{{2{\text{d}}}} }}} \right) \\ & \quad + 4\frac{1}{K}\ln \left( {\frac{1}{{H{}_{3}}}} \right) + 6\frac{Q}{K}\left( {1 - \frac{1}{{H_{3} }}} \right) \\ \end{aligned} $$
(36)
$$ \begin{aligned} M & = - \frac{1}{{K^{2} }}\left( {\left( {1 + \frac{1}{K}} \right)\ln \left( {\frac{{H_{2} }}{{H_{1} }}} \right) + L_{2} + \frac{{KL_{2}^{2} }}{{2H_{1} }}} \right) \\ & \quad + \frac{Q}{{K^{2} }}\left( { - \left( {\frac{1}{{H_{2} }} - \frac{1}{{H_{1} }}} \right) - \frac{1}{K}\ln \left( {\frac{{H_{2} }}{{H_{1} }}} \right) - \frac{1}{K}\left( {\frac{1}{{H_{2} }} - \frac{1}{{H_{1} }}} \right) + \frac{{KL_{2}^{2} }}{{2H_{1}^{2} }}} \right) \\ & \quad - \frac{1}{{K^{2} }}\left( {\left( {1 + \frac{{(1 + H_{\text{d}} )}}{K}} \right)\ln \left( {\frac{{H_{{3{\text{d}}}} }}{{H_{{2{\text{d}}}} }}} \right) + (L_{3} - L_{2} ) + \frac{{K(L_{3}^{2} - L_{2}^{2} )}}{{2H_{2d} }}} \right) \\ & \quad + \frac{Q}{{K^{2} }}\left( { - \left( {\frac{1}{{H_{{3{\text{d}}}} }} - \frac{1}{{H_{{2{\text{d}}}} }}} \right) - \frac{1}{K}\ln \left( {\frac{{H_{{3{\text{d}}}} }}{{H_{{2{\text{d}}}} }}} \right) - \frac{{(1 + H_{\text{d}} )}}{K}\left( {\frac{1}{{H_{{3{\text{d}}}} }} - \frac{1}{{H_{{2{\text{d}}}} }}} \right) + \frac{{K(L_{3}^{2} - L_{2}^{2} )}}{{2H_{{2{\text{d}}}}^{2} }}} \right) + \frac{1}{2}P_{2} \left( {L_{3}^{2} - L_{2}^{2} } \right) \\ & \quad - \frac{1}{{K^{2} }}\left( {\left( {1 + \frac{1}{K}} \right)\ln \left( {\frac{1}{{H_{3} }}} \right) + (1 - L_{3} ) + \frac{{K(1 - L_{3}^{2} )}}{2}} \right) \\ & \quad + \frac{Q}{{K^{2} }}\left( { - \left( {1 - \frac{1}{{H_{3} }}} \right) - \frac{1}{K}\ln \left( {\frac{1}{{H_{3} }}} \right) - \frac{1}{K}\left( {1 - \frac{1}{{H_{3} }}} \right) + \frac{{K(1 - L_{3}^{2} )}}{2}} \right) \\ & \quad - WL_{\text{pv}} = 0 \\ \end{aligned} $$
(37)

For the above equations of pressure, load, friction, and moment, the numerical errors increase as the convergence ratio decreases to 0. Additionally, the equations cannot be calculated at K = 0, because K is included in the denominators. However, substituting the equations for the film thickness and Maclaurin expansion for the log terms into the equations can eliminate K in the denominators. The derivation of these equations is described in the Appendix. The equations for the pressure, load, friction, and moment are arranged as follows.

$$ P = \frac{X}{{H_{1} H}}\left( {1 - \left( {\frac{1}{{H_{1} }} + \frac{1}{H}} \right)Q} \right)\quad 0 \le X \le L_{2} $$
(38)
$$ P = \frac{{(X - L_{2} )}}{{H_{{2{\text{d}}}} H}}\left( {1 - \left( {\frac{1}{{H_{{2{\text{d}}}} }} + \frac{1}{H}} \right)Q} \right) + P_{2} \quad L_{2} \le X \le L_{3} $$
(39)
$$ P = \frac{(1 - X)}{H}\left( {1 - \left( {\frac{1}{H} + 1} \right)Q} \right)\quad L_{3} \le X \le 1 $$
(40)

where P 2 and Q are expressed as follows.

$$ P_{2} = \frac{{L_{2} }}{{H_{1} H_{2} }}\left( {1 - \left( {\frac{1}{{H_{1} }} + \frac{1}{{H_{2} }}} \right)Q} \right) $$
(41)
$$ Q = \frac{{\left( {\frac{{L_{2} }}{{H_{1} H_{2} }} + \frac{{(L_{3} - L_{2} )}}{{H_{{2{\text{d}}}} H_{{3{\text{d}}}} }} + \frac{{(1 - L_{3} )}}{{H_{3} }}} \right)}}{{\left( {\frac{{L_{2} (H_{1} + H_{2} )}}{{H_{1}^{2} H_{2}^{2} }} + \frac{{(L_{3} - L_{2} )(H_{{2{\text{d}}}} + H_{{3{\text{d}}}} )}}{{H_{{2{\text{d}}}}^{2} H_{{3{\text{d}}}}^{2} }} + \frac{{(1 - L_{3} )(1 + H_{3} )}}{{H_{3}^{2} }}} \right)}} $$
(42)
$$ \begin{aligned} W & = \frac{{L_{2}^{2} }}{{2H_{1}^{2} }} - Q\frac{{L_{2}^{2} }}{{H_{1}^{2} H_{2} }} + \sum\limits_{n = 3}^{\infty } {\frac{{L_{2}^{n} }}{{nH_{1}^{n} }}} K^{n - 2} \\ & \quad + \frac{{(L_{3} - L_{2} )^{2} }}{{2H_{{2{\text{d}}}}^{2} }} - Q\frac{{(L_{3} - L_{2} )^{2} }}{{H_{{2{\text{d}}}}^{2} H_{{3{\text{d}}}} }} + P_{2} (L_{3} - L_{2} ) + \sum\limits_{n = 3}^{\infty } {\frac{{(L_{3} - L_{2} )^{n} }}{{nH_{{2{\text{d}}}}^{n} }}} K^{n - 2} \\ & \quad + \frac{{(1 - L_{3} )^{2} }}{{2H_{3}^{2} }} + Q\frac{{(1 - L_{3} )^{2} }}{{H_{3} }} - \frac{{(1 - L_{3} )^{2} }}{{H_{3} }} + \sum\limits_{n = 3}^{\infty } {\frac{{(1 - L_{3} )^{n} }}{{nH_{3}^{n} }}} K^{n - 2} \\ & \quad - 1 < \frac{{KL_{2} }}{{H_{1} }} < 1, - 1 < \frac{{K(L_{3} - L_{2} )}}{{H_{{2{\text{d}}}} }} < 1, - 1 < \frac{{K(1 - L_{3} )}}{{H_{3} }} < 1 \\ \end{aligned} $$
(43)
$$ \begin{aligned} F & = - 4\left( {\frac{{L_{2} }}{{H_{1} }} + \frac{{(L_{3} - L_{2} )}}{{H_{{2{\text{d}}}} }} + \frac{{(1 - L_{3} )}}{{H_{3} }}} \right) + 6Q\left( {\frac{{L_{2} }}{{H_{1} H_{2} }} + \frac{{(L_{3} - L_{2} )}}{{H_{{2{\text{d}}}} H_{{3{\text{d}}}} }} + \frac{{(1 - L_{3} )}}{{H_{3} }}} \right) \\ & \quad - 4\sum\limits_{n = 2}^{\infty } {\left( {\left( {\frac{{L_{2} }}{{H_{1} }}} \right)^{n} + \left( {\frac{{(L_{3} - L_{2} )}}{{H_{{2{\text{d}}}} }}} \right)^{n} + \left( {\frac{{(1 - L_{3} )}}{{H_{3} }}} \right)^{n} } \right)} \frac{{K^{n - 1} }}{n} \\ & \quad - 1 < \frac{{KL_{2} }}{{H_{1} }} < 1, - 1 < \frac{{K(L_{3} - L_{2} )}}{{H_{{2{\text{d}}}} }} < 1, - 1 < \frac{{K(1 - L_{3} )}}{{H_{3} }} < 1 \\ \end{aligned} $$
(44)
$$ \begin{aligned} M & = \frac{{L_{2}^{3} }}{{3H_{1}^{3} }} - Q\frac{{L_{2}^{3} }}{{H_{1}^{2} H_{2} }} + Q\frac{{L_{2}^{3} }}{{3H_{1}^{3} }} + \sum\limits_{n = 3}^{\infty } {\frac{{L_{2}^{n} }}{{nH_{1}^{n} }}} K^{n - 2} + (1 + Q)\sum\limits_{n = 4}^{\infty } {\frac{{L_{2}^{n} }}{{nH_{1}^{n} }}} K^{n - 3} \\ & \quad + \frac{{(L_{3} - L_{2} )^{2} L_{2} }}{{2H_{{2{\text{d}}}}^{2} }} + (1 + H_{\text{d}} )\frac{{(L_{3} - L_{2} )^{3} }}{{3H_{{2{\text{d}}}}^{3} }} - Q\frac{{(L_{3} - L_{2} )^{2} L_{3} }}{{H_{{2{\text{d}}}}^{2} H_{{3{\text{d}}}} }} + Q\frac{{(L_{3} - L_{2} )^{3} }}{{3H_{{2{\text{d}}}}^{3} }} \\ & \quad + \sum\limits_{n = 3}^{\infty } {\frac{{(L_{3} - L_{2} )^{n} }}{{nH_{{2{\text{d}}}}^{n} }}} K^{n - 2} + (1 + H_{\text{d}} + Q)\sum\limits_{n = 4}^{\infty } {\frac{{(L_{3} - L_{2} )^{n} }}{{nH_{{2{\text{d}}}}^{n} }}} K^{n - 3} + \frac{{P_{2} }}{2}(L_{3}^{2} - L_{2}^{2} ) \\ & \quad + \frac{{(H_{3} - 1)(1 - L_{3} )^{3} }}{{2H_{3}^{2} }} - \frac{{(1 - L_{3} )^{2} }}{{2H_{3}^{2} }} + \frac{{(1 - L_{3} )^{3} }}{{3H_{3}^{3} }} - Q\left( {\frac{{(H_{3} + 1)(1 - L_{3} )^{3} }}{{2H_{3}^{2} }} - \frac{{(1 - L_{3} )^{2} }}{{H_{3} }} - \frac{{(1 - L_{3} )^{3} }}{{3H_{3}^{3} }}} \right) \\ & \quad + \sum\limits_{n = 3}^{\infty } {\frac{{(1 - L_{3} )^{n} }}{{nH_{3}^{n} }}} K^{n - 2} + (1 + Q)\sum\limits_{n = 4}^{\infty } {\frac{{(1 - L_{3} )^{n} }}{{nH_{3}^{n} }}} K^{n - 3} \\ & \quad - WL_{pv} = 0 \\ & \quad - 1 < \frac{{KL_{2} }}{{H_{1} }} < 1, - 1 < \frac{{K(L_{3} - L_{2} )}}{{H_{2d} }} < 1, - 1 < \frac{{K(1 - L_{3} )}}{{H_{3} }} < 1 \\ \end{aligned} $$
(45)

These equations can be used in a low convergence ratio region, including the parallel contact case (K = 0), because K is eliminated in the denominators. In the parallel contact case (K = 0), the dimensionless pressure P, flow rate Q, load W, friction F, and moment M become.

$$ P = X\left( {1 - 2Q} \right)\quad 0 \le X \le L_{2} $$
(46)
$$ P = \frac{{(X - L_{2} )}}{{\left( {1 + H_{\text{d}} } \right)^{3} }}\left( {1 - \frac{2}{{\left( {1 + H_{\text{d}} } \right)}}Q} \right) + P_{2} \quad L_{2} \le X \le L_{3} $$
(47)
$$ P = (1 - X)\left( {1 - 2Q} \right)\quad L_{3} \le X \le 1 $$
(48)
$$ Q = \frac{{\left( {L_{2} + \frac{{(L_{3} - L_{2} )}}{{(1 + H_{\text{d}} )^{2} }} + (1 - L_{3} )} \right)}}{{2\left( {L_{2} + \frac{{(L_{3} - L_{2} )}}{{(1 + H_{\text{d}} )^{3} }} + (1 - L_{3} )} \right)}} $$
(49)
$$ P_{2} = L_{2} \left( {1 - 2Q} \right) $$
(50)
$$ W = \frac{{L_{2}^{2} }}{2} - QL_{2}^{2} + \frac{{(L_{3} - L_{2} )^{2} }}{{2(1 + H_{\text{d}} )^{2} }} - Q\frac{{(L_{3} - L_{2} )^{2} }}{{(1 + H_{\text{d}} )^{3} }} + P_{2} (L_{3} - L_{2} ) - \frac{{(1 - L_{3} )^{2} }}{2} + Q(1 - L_{3} )^{2} $$
(51)
$$ F = - 4\left( {L_{2} + \frac{{(L_{3} - L_{2} )}}{{(1 + H_{\text{d}} )}} + (1 - L_{3} )} \right) + 6Q\left( {L_{2} + \frac{{(L_{3} - L_{2} )}}{{(1 + H_{\text{d}} )^{2} }} + (1 - L_{3} )} \right) $$
(52)
$$ \begin{aligned} M & = \frac{{L_{2}^{3} }}{3} - Q\frac{{2L_{2}^{3} }}{3} \\ & \quad + \frac{{(L_{3} - L_{2} )^{2} L_{2} }}{{2(1 + H_{\text{d}} )^{2} }} + \frac{{(L_{3} - L_{2} )^{3} }}{{3(1 + H_{\text{d}} )^{2} }} - Q\frac{{(L_{3} - L_{2} )^{2} L_{3} }}{{(1 + H_{\text{d}} )^{3} }} + Q\frac{{(L_{3} - L_{2} )^{3} }}{{3(1 + H_{\text{d}} )^{3} }} \\ & \quad + \frac{{P_{2} }}{2}(L_{3}^{2} - L_{2}^{2} ) - \frac{{(1 - L_{3} )^{2} }}{2} + \frac{{(1 - L_{3} )^{3} }}{3} - \frac{{2Q(1 - L_{3} )^{3} }}{3} + Q(1 - L_{3} )^{2} \\ & \quad - WL_{\text{pv}} = 0 \\ \end{aligned} $$
(53)

Figure 2 shows comparisons for dimensionless load W and moment M between the exact form and explicit form with the maximum number n max = 20 of the power series terms. It can be seen that the numerical errors of the exact forms for the load and moment increase with decreasing convergence ratio K. For the solution of moment M, the numerical error appears at higher convergence ratios of about 10−4 compared to that for the solution of the load. The solution calculated by the explicit form asymptotically approaches the value at K = 0 with a decreasing convergence ratio for both the load and moment. In the current simulation, the explicit forms were used at convergence ratios K < 0.01. Above this value, the solutions were obtained by calculating the exact forms.

Fig. 2
figure 2

Comparisons of dimensionless load W and moment M between exact form and explicit form at L 2 = 0.1, L 3 = 0.2, and H d = 1.0. a Dimensionless load W, b dimensionless moment M

Full size image

4 Results

Figure 3 shows the variation in the dimensionless load W for various dimensionless dimple depths H d with L 2 = 0.1 and L 3 = 0.2. This graph has a logarithmic axis for the dimensionless dimple depth H d to show the variation over a wide range. It can be seen that there is an optimum value for the dimensionless dimple depth for the dimensionless load. At H d = 0.001, the load has already been produced. As H d increases, the load increases to reach a maximum value of 0.0145 at H d = 0.5. Beyond the maximum point, the load drops significantly and is 1.51 × 10−3 at H d = 10.0, which is similar to the value at H d = 0.001.

Fig. 3
figure 3

Dimensionless load W for various dimensionless dimple depths H d at L 2 = 0.1 and L 3 = 0.2

Full size image

Figure 4 shows the variation in the convergence ratio K for various dimensionless dimple depths H d, with the same dimple specifications as shown in Fig. 3. The curve for the variation in the convergence ratio K has a shape similar to that of the variation in the dimensionless load, W, in Fig. 3. The maximum value of the convergence ratio is obtained at H d = 0.5, which is the same as the maximum point for the dimensionless load. By comparing the results for dimensionless load W and convergence ratio K, it is found that the dimensionless load increases in accordance with the increase in the convergence ratio.

Fig. 4
figure 4

Convergence ratio for various dimensionless dimple depths at L 2 = 0.1 and L 3 = 0.2

Full size image

Figure 5 shows the variation in the dimensionless friction, F, for various dimensionless dimple depths H d. The curve for the dimensionless friction, F, has a different shape than those for the dimensionless load W and convergence ratio K. The friction decreases gradually with increasing dimensionless dimple depth from 0.001. At H d = 0.5, the friction has a minimum value of 0.9238 and then begins to immediately increase with a further increase in H d. The friction reaches a maximum value of 0.9355 at H d = 3.0 and then starts to drop beyond the maximum point.

Fig. 5
figure 5

Dimensionless friction for various dimensionless dimple depths at L 2 = 0.1 and L 3 = 0.2

Full size image

Figure 6 shows the variation in the dimensionless flow rate Q with the dimensionless dimple depth H d. It can be seen that the flow rate is higher than the Couette flow rate in the case of parallel contact for all dimple depths. It is found that the flow rate has a high value when the convergence ratio is high. Thus, the incorporation of a single dimple on the pad opens the inlet of the contact area more widely to promote the drag of lubricant into the contact area.

Fig. 6
figure 6

Dimensionless flow rate Q for various dimensionless dimple depths at L 2 = 0.1 and L 3 = 0.2

Full size image

Figures 7, 8, 9, 10, and 11 show a series of dimensionless results for film thickness H, pressure P, shear stress S, and flow rate Q for various dimensionless dimple depths H d.

Fig. 7
figure 7

Profiles of dimensionless film thickness, pressure, shear stress, and flow rate at L 2 = 0.1 and L 3 = 0.2 and H d = 0.1. a Film thickness and pressure, b shear stress, c flow rate

Full size image
Fig. 8
figure 8

Profiles of dimensionless film thickness, pressure, shear stress, and flow rate at L 2 = 0.1 and L 3 = 0.2 and H d = 0.5. a Film thickness and pressure, b shear stress, c flow rate

Full size image
Fig. 9
figure 9

Profiles of dimensionless film thickness, pressure, shear stress, and flow rate at L 2 = 0.1 and L 3 = 0.2 and H d = 1.0. a Film thickness and pressure, b shear stress, c flow rate

Full size image
Fig. 10
figure 10

Profiles of dimensionless film thickness, pressure, shear stress, and flow rate at L 2 = 0.1 and L 3 = 0.2 and H d = 5.0. a Film thickness and pressure, b shear stress, c flow rate

Full size image
Fig. 11
figure 11

Profiles of dimensionless film thickness, pressure, shear stress, and flow rate at L 2 = 0.1 and L 3 = 0.2 and H d = 10.0. a Film thickness and pressure, b shear stress, c flow rate

Full size image

The variation in the film profile shows that the inlet of the contact area is gradually opened from H d = 0.1–0.5. Then, the inlet is gradually closed from H d = 1.0–10.0, in which the bottom of the dimple is out of the range of the graphs, in accordance with the variation in the convergence ratio shown in Fig. 3. At H d = 10.0, the contact area becomes nearly parallel.

Hydrodynamic pressure is generated over the contact area as a result of the wedge film action, as shown in Figs. 7, 8, 9, 10, and 11. The pressure increases linearly in the left land zone and within the dimple, whereas in the right land zone, it shows a parabolic curve, which dominates most of the contact area. The pressure distribution has a lower gradient in the left land zone and a higher gradient in the dimple than elsewhere. The pressure distribution maintains the same shape with a lower gradient in the left land zone and a higher gradient in the dimple, although the magnitude of the pressure has a maximum peak at H d = 0.5, as shown in Fig. 8.

One of the most important findings in the shear stress distributions is that the shear stress in the dimple is higher than elsewhere in the cases of shallower dimple depths of H d = 0.1, 0.5, and 1.0. This is because the shear stress produced by the Poiseuille flow S p is high, even though the shear stress produced by the Couette flow S c decreases as a result of the greater thickness of the dimple. In the right land zone, the shear stress decreases along the sliding direction because the pressure gradient decreases and has negative values beyond the maximum pressure point. This action caused by the Poiseuille flow reduces the friction from H d = 0.001–0.5. At more than H d = 0.5, the Poiseuille flow decreases in accordance with the decrease in the convergence ratio. Thus, the friction begins to increases until H d = 5.0. However, at deeper dimple depths, the shear stress is significantly reduced because both the Couette and Poiseuille flows decrease significantly. The reduction in the shear stress in the dimple contributes to the second decrease in friction.

It is found that the magnitude of the Poiseuille flow rate increases in the dimple with increasing dimple depth, although the pressure drops at a high H d. This is because the thick film in the dimple results in a significant decrease in the resistance to flow. Therefore, even a small pressure generation is sufficient to compensate for the great variations in the Couette flow at deep dimple depths.

Figure 12 shows the influence of the dimple position on the load for various dimple depths with a dimple width of 0.1. L 2 = 0 implies that the dimple is opened to the outside, which corresponds to the step of the Rayleigh step bearing. It is found that the film shape of the Rayleigh step bearing (L 2 = 0) is the greatest for a dimensionless load. The dimensionless load W decreases as the position of the dimple moves closer to the centre of the contact area. At around L 2 = 0.15, the load decreases considerably and thus no equilibrium solution can be found.

Fig. 12
figure 12

Influence of dimple position on load for various dimensionless dimple depths

Full size image

Figure 13 shows the influence of the dimple width on the load for various dimple positions, with dimple depth H d = 0.5. It is found that at L 2 = 0, which corresponds to the Rayleigh step bearing, the dimensionless load W is the greatest and can be obtained in the widest range of dimple widths. A Rayleigh step bearing with a wide width of 0.52 has the greatest dimensionless load W of 2.88 × 10−2. At greater dimensionless widths of more than 0.58, no equilibrium solution can be found. As the position of the dimple moves closer to the centre, the dimensionless load decreases. The dimple width range in which an equilibrium solution can be obtained also decreases as the dimple position approaches the centre.

Fig. 13
figure 13

Influence of dimple width on load for various dimensionless dimple positions

Full size image

5 Discussion

The above theoretical analysis shows that the incorporation of a micro-feature on a stationary surface could produce pressure over a parallel contact area, which was modelled as a centrally pivoted pad bearing with flat surfaces and thus could generate no pressure according to the hydrodynamic lubrication theory. The mechanism suggested in the current study considers variations in the convergence ratio by the incorporation of a micro-feature, at which the equilibrium of the moment applied to the pad is achieved, and thus is totally different from those suggested and investigated in past studies [2–19]. A representative mechanism for the textured surface is based on the micro-hydrodynamic lubrication bearing concept, having an unsymmetrical pressure distribution with a cavitation zone [2–5]. However, the current results show no negative pressure generation in the dimple. Variations in the convergence ratio, which increase in most cases, promote the wedge action of the film to generate hydrodynamic pressure over the contact area, as well as at the dimple.

When the convergence ratio is small, with the surfaces close to parallel, a negative pressure can be produced in the dimple [6–8]. The negative pressure in the dimple causes suction of the lubricant into the contact area to produce a higher load capacity [6–8]. Cavitation around textured patterns has experimentally been observed in parallel pad bearings [16, 17], mechanical face seals [14], and seal-like rings [3, 4, 13, 15]. Figure 14 shows the pressure distributions at various convergence ratios in the case where a single dimple is created at the leading side of the contact area. It can be seen that the pressure decreases linearly from the inlet when the convergence ratio K is small. In addition, the total pressure decreases, which results in a decrease in the load capacity, with a decreasing convergence ratio. Figure 15 shows the variations in dimensionless load W and minimum pressure P min for various convergence ratios. It can more clearly be seen that the load capacity at higher convergence ratios is higher than that at lower convergence ratios, in which the inlet suction appears. The dimensionless load increases and then begins to decrease with increasing K. For convergence ratios below 0.03, the minimum pressure is negative, resulting in the appearance of inlet suction. For convergence ratios higher than 0.03, the balancing wedge action is effective, as shown in Figs. 14 and 15. In a comparison of the load capacities between low convergence ratios and high convergence ratios, the dimensionless load is found to be smaller at low convergence ratios compared with that at higher convergence ratios. Yang et al. [17] showed higher load-carrying capacity of inclined pad bearings compared to that of parallel pad bearings when grooves were textured on the pad. They described that incorporating of grooves generated cavitation to less contribute to enhancement of load-carrying capacity.

Fig. 14
figure 14

Dimensionless pressure distributions for various convergence ratios at L 2 = 0.1 and L 3 = 0.2 and H d = 0.5

Full size image
Fig. 15
figure 15

Variations in dimensionless load W and minimum pressure P min with convergence ratio at L 2 = 0.1 and L 3 = 0.2 and H d = 0.5. a Dimensionless load W, b Dimensionless minimum pressure P min

Full size image

As shown in Figs. 14 and 15, the inlet suction appears at low convergence ratios of less than 0.03. However, such a small convergence ratio appears to be impossible for actual machine elements because the equilibrium of the moment should be considered. For example, in a case where the convergence ratio K is 0.168, at which the maximum load capacity can be obtained as shown in Figs. 3 and 4, the film thickness difference between the sides is about 168 nm at h 0 = 1 μm. In actual machine elements, the surfaces are supported by parts with some rigidity. There are also many machine elements such as mechanical face seals, piston-skirt systems, and vanes in rotary compressors, in which the surfaces are not rigidly supported or can be moved. Incorporation of textured patterns onto the surface of non-rigidly supported lubricated areas is expected to change the moment balance, developing a wedged film shape. Therefore, the suggested mechanism may act in general cases, as well as in the case of pivoted pad bearings.

The ‘balancing wedge action’ mechanism reduces the friction and generates pressure, as shown in Figs. 7, 8, 9, 10, and 11. In the mechanism of a micro-hydrodynamic lubrication bearing, the shear stress can be ignored in the dimples because of cavitation. It has been believed that reducing the shear stress in dimples is an important contribution to reduce friction. However, in the case of shallower dimples, in which the maximum dimensionless load is obtained, the shear stress is greater in the dimple than elsewhere because of the greater positive pressure gradient, as shown in Figs. 7, 8, and 9, which produces a shear stress in the same direction as that produced by the Couette flow. The main contribution to the reduction in friction is the decrease in the shear stress in the right land zone, which does not seem to be focused. Actually, the load capacity is also enhanced, which leads to an increase in film thickness by the incorporation of the dimple.

The trends for the load in relation to the dimple’s width, depth, and location have complex behaviours. One of the important findings is that the left land zone reduces the effectiveness of the wedge action promotion, as shown in Fig. 12, although the land zone plays a significant role in inlet suction [6–8]. The film shape of the Rayleigh step bearing has the highest load capacity, with a wide range of dimple sizes, and the possible size of the dimple decreases when the dimple is not opened to the outside. Yang et al. [17] also showed higher load-carrying capacity of the Rayleigh step bearing shape compared to those of groove-textured pad bearings. Pressure generation in a Rayleigh step bearing can also be obtained by the partial incorporation of multiple micro-features at the inlet side [18, 19, 25]. Therefore, a multiple dimple pattern may improve the load capacity in a Rayleigh step bearing.

In summary, the suggested mechanism, called ‘balancing wedge action’, was found to play a significant role in the enhancement of tribological performance such as in the generation of load capacity and the reduction in friction. The current study is the first step for ‘balancing wedge action’ because the current model is simple, consisting of a one-dimensional centrally pivoted pad bearing. Further investigation of this mechanism appears to be required to obtain a better understanding of the capacity of textured surfaces.

6 Conclusions

This paper suggested and investigated a new mechanism called ‘balancing wedge action’, which is produced by textured surface. The authors focused attention on the equilibrium of the moment applied to the mating surfaces. Incorporation of a textured feature on one of the mating surfaces increases the convergence ratio between the surfaces, resulting in the promotion of the whole wedge action in the contact area. The current study analysed a centrally pivoted bearing model, which is initially parallel in the flat case and thus produces no hydrodynamic pressure. The obtained conclusions are as follows.

  1. 1.

    As a single dimple is created at the inlet side on the stationary pad, the pad is inclined to form a converging film shape. This converging film generates hydrodynamic pressure distributed over the contact area.

  2. 2.

    The pressure distribution has three specific shapes: a lower gradient in the left land zone, a higher gradient in the dimple, and a parabolic curve in the right land zone.

  3. 3.

    The dimensionless load is the highest at dimensionless dimple depth H d = 0.5. This value for the dimensionless dimple depth agrees with that for the maximum convergence ratio.

  4. 4.

    The friction in the textured case is smaller than that in the parallel case. This reduction in friction is not attributed to the thicker film in the dimple, in which the shear stress is higher than elsewhere. The decrease in shear stress in the right land zone contributes to the reduction in friction at around the optimum value of H d.

  5. 5.

    When the dimple is opened to the outside, the dimple feature changes the Rayleigh step bearing, which generates the highest load capacity. As the location of the dimple approaches the centre of the contact area, the load capacity decreases considerably. When the dimensionless position of the left step point L 2 is more than about 0.15, there is no equilibrium solution for the moment.

  6. 6.

    The load capacity increases with increasing dimple width. However, there is a maximum width at which an equilibrium solution can be obtained. As the location of the dimple approaches the centre, the width range decreases.