1 Introduction

With the advent of the increased interest by both engineers and orthopaedic surgeons into biomechanics of degenerative joint disease, different modes of lubrication in movable joints are studied as they exhibit low friction and almost negligible wear properties. Also, articular cartilage serves as bearing and shock absorbing material of synovial joint, but, for various reasons, a long-term process of cartilage degeneration (osteoarthritis) often arises. This degenerative process leads to deterioration of normal joint function of the joint, and this natural joint must be replaced by artificial one. The knee is the most loaded and the most complex human body joint from the point of view of biomechanics.

The performance of human articular joints is strictly connected with the viscoelastic properties of synovial fluid (SF), which determine load transmission, lubrication, wear inhibition and protection of the articular cartilage and soft tissue surfaces from mechanical stresses during joint function.

Friction occurs in all types of joints, both in natural and artificial. The heat generation and dissipation is a process that takes place every time the joint is used. Another factor important for frictional heat generation is the lubrication in natural joints; it is accomplished by means of the synovial fluid, probably liquid crystalline biological substances [1]. In normal human hip joints, the temperature elevation measured is of the order +2.5 °C during walking and probably more during running.

The viscous dissipation under strain is generally related to the friction arising from three different interactions:

  1. (1)

    A friction caused by the interactions of single Hyaluronic acid (HA) molecules with the medium (solvent and other solutes) and by the hydrodynamic interactions amongst the flow fields of chain segments of single HA molecules. This behaviour is typical of dilute polymeric solutions [2].

  2. (2)

    A friction arising amongst intermolecular contacts during chain slipping.

  3. (3)

    A friction connected with the formation of entanglements when, in concentrated solutions, the polymer molecular weight exceeds the critical value [3].

Since the joints have no blood capillaries, the process of imbibition and exudation provides nutritional pathways to the cells of the cartilage and lubrication to the articulating surfaces at the joint. In addition, the intra-articular heat generated within the joint cavity during motion is transferred to cartilage by the interstitial fluid exchange and thereafter diffuses through bones. The wear at the joints is directly proportional to friction and the heat generated. This results in disorganization of the joint and functional impairment. It has been observed experimentally that there is hardly any increase in the temperature in the normal joints, but, in a diseased state, the increase in the temperature has been noted [4]. This is due to autoimmunity.

The factors possibly influencing the amount of heat produced in the knee implants are the performed activity, the body weight and the coefficient of friction in the joint which depends on the materials [5] and the lubricating property of the synovial fluid [6, 7]. The final temperatures in the prosthesis and surrounding bone and soft tissues depend on the activity duration, the volume of the synovial fluid [8, 9]. The influence of elevated temperatures on biological tissues depends on the cell type (bone, soft tissue), the temperature and exposure time [10]. After a long run, the surfaces of the wrung-out cartilage become more congruent, stiffer, less permeable, and the filtration becomes lower compared with the recovered (swollen) cartilage [11].

Heat shock proteins may enable cells to withstand increased temperatures. The volume of the synovial fluid can drastically influence the heat transfer to the surrounding structures [6, 12] and varies much between individuals [9].

Recently Sawyer et al. [13] presented a thermal analysis for the UHMWPE tibial component of the total knee replacements and discussed the sensitivity of the frictional heating to activity frequency, thermal conductivity of the femoral component and heat transfer coefficient of the synovial fluid. Bergmann et al. [14, 15] studied to determine the implant temperature in vivo in varying loading conditions. Fialho et al. [16] developed a computational simulator for the hip to compute the wear, heat generation on artificial joints, and show that frictional produced on artificial hip joints originates wear rates that can lead to failure of the implant, and furthermore, heating can increase the wear.

Until now there is very small analytical attempt that has been done in this direction [4, 17, 18]. Bali and Shukla [19] considered the equation of energy in terms of the transport properties in which the effect of fluid velocity in energy transfer is very small and also considered that at line of symmetry the temperature is zero. In this article, an attempt has been made to present more realistic analysis by considering that the temperature in the fluid film region is distributed symmetrical and at the bony end the temperature is constant. We have developed in this article a mathematical model for the temperature regulation is squeezing flow of synovial fluid in between the approaching poroelastic cartilaginous surfaces and flow of suspending medium of the lubricant within the intra-articular gap. The synovial fluid has been represented by viscoelastic fluid. The solution to the model is obtained by perturbation method, and results have been discussed with the available experimental observations.

2 Formulation of the Problem

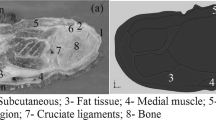
Figure 1a and b represents a normal knee joint, and its simplified geometrical counterpart for the model proposed in this article

Fig. 1
figure 1

(a) Normal knee joint and (b) simplified geometrical counterpart

Full size image

In order to formulate a mathematical tractable problem, we introduce the following admissible assumptions:

  1. (1)

    Articular cartilage behaves strictly as elastic.

  2. (2)

    Body forces and diffusional couples do not exist.

  3. (3)

    The solid and fluid phases are isotropic, homogeneous and incompressible.

  4. (4)

    The ratio of solidity to fluidity (v) is constant.

  5. (5)

    The effect of viscosity of interstitial fluid is negligible except where it implicitly contributes to the diffusional drag.

  6. (6)

    Owing to small transients during articulation, inertial forces are negligible.

  7. (7)

    Under these assumptions, the governing differential equations of continuity, momentum and constitutive relations of each phase of the cartilage matrix and the fluid film region are given separately below.

2.1 For the Porous Cartilage Matrix: \( - \left( {h^{\prime } + H^{\prime } } \right) \le y^{\prime} \le - h^{\prime} \; {\text{and}}\; h^{\prime} \le y^{\prime } \le (h^{\prime } + H^{\prime } ) \)

In order to obtain the effects of small local variations in the permeability of the cartilage, we introduce this relative velocity in the continuity equation of the fluid and derive the governing equation for the pressure distribution within the cartilage.

$$ \nabla \cdot \left( {k^{\prime } \nabla \bar{p}^{\prime } } \right) = 0 $$

The permeability of the porous matrix, due to the normal body weight during prolonged standing or jumping, decreases with y-coordinate \( k = k_{0} \left( {1 - \beta y^{\prime } } \right) \) in the region \( h^{\prime } \le y^{\prime } \le \left( {h^{\prime } + H^{\prime } } \right) \).

The pressure distribution within the porous matrix \( \bar{p}\left( {x^{\prime } ,y^{\prime } } \right) \) is given by the equation

$$ {\frac{{\partial^{2} \bar{p}^{\prime } }}{{\partial x^{\prime 2} }}} + {\frac{\partial }{{\partial y^{\prime } }}}\left[ {k_{0} \left( {1 - \beta y^{\prime } } \right){\frac{{\partial \bar{p}^{\prime } }}{{\partial y^{\prime } }}}} \right] = 0 $$
(1)

3 Fluid Film Region: \( - h^{\prime } \le y^{\prime } \le h^{\prime } \)

Oldroyd’s elastico-viscous fluid is the simplest and most accurate for describing the linear viscoelastic properties and predicting most of the other observed non-linear rheological behaviours of synovial fluid.

Using the assumptions of the lubrication theory, the governing equation for momentum and continuity can be written as:

$$ - {\frac{{\partial p^{\prime } }}{{\partial x^{\prime } }}} + \mu {\frac{\partial }{{\partial y^{\prime } }}}\left\{ {{\frac{{\partial u^{\prime } }}{{\partial y^{\prime } }}} - \varepsilon_{0} \left( {{\frac{{\partial u^{\prime } }}{{\partial y^{\prime } }}}} \right)^{3} } \right\} = 0 $$
(2)
$$ - {\frac{{\partial p^{\prime } }}{{\partial y^{\prime } }}} = 0 $$

3.1 Equation of Continuity

$$ {\frac{{\partial u^{\prime } }}{{\partial x^{\prime } }}} + {\frac{{\partial v^{\prime } }}{{\partial y^{\prime } }}} = 0 $$
(3)

where \( u^{\prime } ,\;v^{\prime } \) are the horizontal and normal components of velocity, p′ is the pressure, μ is the coefficient of viscosity and \( \varepsilon_{0} \) is the viscoelastic parameter of the fluid representing synovial fluid.

In ultra-filtration regime, within the intra-articular gap a linear normal velocity is assumed as

$$ v^{\prime } = a + by^{\prime } $$
(4)

satisfying the boundary conditions;

$$ v^{\prime } (0) = 0,\quad v^{\prime } (h) = v_{\text{n}}^{\prime } - {\frac{{{\text{d}}h^{\prime } }}{{{\text{d}}t^{\prime } }}} $$
(5)

where \( v_{\text{n}} \) is the normal velocity of the fluid at the interface. The normal component of the velocity is given by

$$ v^{\prime}_{\text{n}} = - k_{0} \left( {1 - {\frac{{\bar{D}}}{E}}} \right){\frac{{\partial \bar{p}^{\prime } }}{{\partial y^{\prime } }}}\quad {\text{at}}\;y^{\prime } = h^{\prime } $$
(6)

where E is the bulk modulus, k 0 is the constant permeability and \( \bar{D} \) is the diffusion coefficient.

These governing equations through (1)–(3) are subjected to following boundary conditions:

$$ \begin{array}{*{20}c} {{\frac{\partial u^{\prime }}{\partial y^{\prime }}} = 0} \hfill & {{\text{at}}\;y^{\prime } = 0} \hfill \\ {u^{\prime} + {\frac{{k_{0} }}{\mu }}{\frac{{\partial \bar{p}^{\prime} }}{{\partial x^{\prime} }}} = - \sigma^{\prime} {\frac{{\partial u^{\prime} }}{{\partial y^{\prime} }}}} \hfill & {{\text{at}}\;y^{\prime} = h^{\prime} } \hfill \\ {p^{\prime} \;{\text{and}}\;\bar{p}^{\prime} = 0} \hfill & {{\text{at}}\;x^{\prime} = \pm l^{\prime} } \hfill \\ {{\frac{{\partial p^{\prime} }}{{\partial x^{\prime} }}} = 0,\;{\frac{{\partial \bar{p}^{\prime} }}{{\partial x^{\prime} }}} = 0} \hfill & {{\text{at}}\;x^{\prime} = 0} \hfill \\ {p^{\prime} = \bar{p}^{\prime} } \hfill & {{\text{at}}\,y^{\prime} = h^{\prime} } \hfill \\ {{\frac{{\partial \bar{p}^{\prime} }}{{\partial y^{\prime} }}} = 0} \hfill & {{\text{at}}\;y^{\prime} = h^{\prime} + H^{\prime} } \hfill \\ \end{array} $$
(7)

where \( \sigma ^{\prime } \) is the parameter associated with slip velocity, \( H^{\prime } \) is the thickness of articular cartilage.

4 Intra-Articular Heat Exchange

We introduced the following assumptions

  1. (1)

    It is assumed that no internal heat transfer phenomena from inside or outside or vice versa, i.e. \( \dot{Q} = 0 \), where \( \dot{Q} \) is the rate of heat transfer.

  2. (2)

    Energy flux (q) and viscous stress (τ) are taken in terms of temperature gradient and velocity gradient, respectively.

  3. (3)

    The temperature is time-independent in both the regions.

The equation of energy in terms of the fluid temperature T for the biomechanical system [20]

$$ \rho c_{v} {\frac{{{\text{d}}T}}{{{\text{d}}t}}} = - \left( {\nabla \cdot q} \right) - T\left( {{\frac{\partial p}{\partial T}}} \right)_{\text{V}} \left( {\nabla \cdot v} \right) - (\tau{:}\,\nabla v) $$
(8a)
$$ \left( {\tau{:}\,\nabla v} \right) = - \mu_{0} \varphi_{\text{v}} $$
(8b)

The above equation states that the temperature of a moving synovial fluid element changes because of (a) heat conduction, (b) expansion effect, and (c) viscous heating. The quantity \( \varphi_{\text{v}} \) is known as the dissipation function. In this model we have considered that the model is free from the expansion effect.

The governing energy equation may be written for the two regions separately as given below

$$ \rho c_{v} u{\frac{{\partial T^{\prime} }}{{\partial x^{\prime} }}} = K\left( {{\frac{{\partial^{2} T^{\prime} }}{{\partial x^{\prime 2} }}} + {\frac{{\partial^{2} T^{\prime} }}{{\partial y^{\prime 2} }}}} \right) + 2\mu_{0} \left( {{\frac{{\partial u^{\prime} }}{{\partial x^{\prime} }}}} \right)^{2} + \mu_{0} \left( {{\frac{{\partial u^{\prime} }}{{\partial x^{\prime} }}}} \right)^{2} $$
(9a)
$$ \rho c_{v} \left( {\bar{u}^{\prime} {\frac{{\partial \bar{T}^{\prime} }}{{\partial x^{\prime} }}} + \bar{v}^{\prime} {\frac{{\partial \bar{T}^{\prime} }}{{\partial y^{\prime} }}}} \right) = K\left( {{\frac{{\partial^{2} \bar{T}^{\prime} }}{{\partial x^{\prime 2} }}} + {\frac{{\partial^{2} \bar{T}^{\prime} }}{{\partial y^{\prime 2} }}}} \right) + 2\mu_{0} \left[ {\left( {{\frac{{\partial \bar{u^{\prime} }}}{\partial x^{\prime}}}} \right)^{2} + {\frac{1}{{\left( {h_{1} } \right)^{2} }}}\left( {{\frac{{\partial \bar{v^{\prime}}}}{\partial y^{\prime}}}^{2} } \right)} \right] + \mu_{0} \left\{ {\left( {{\frac{{\partial \bar{u^{\prime}}}}{\partial y^{\prime}}}} \right) + \left( {{\frac{{\partial \bar{v^{\prime}}}}{\partial x^{\prime}}}} \right)} \right\}^{2} $$
(9b)

The terms contained in the braces { } are associated with viscous dissipation and small velocity gradients. Where \( T^{\prime} \) and \( \bar{T}^{\prime} \) are the temperatures in fluid film and cartilage matrix, respectively, K is the thermal conductivity, ρ is the density, c v is the specific heat at constant volume and \( \mu_{0} \) is the constant value of the parameter referring to corresponding physical quantities for the suspending medium without hyaluronic acid molecules.

Conditions for the above equations

$$ T^{\prime }\left( {0,y} \right) = \bar{T}^{\prime} \left( {l,y} \right),\quad \bar{T}^{\prime} \left( {0,y} \right) = \bar{T}^{\prime} \left( {l,y} \right) $$
(10)
$$ {\frac{\partial T^{\prime }}{\partial y^{\prime }}} = 0 \quad {\text{at}}\;y^{\prime} = 0 $$
(11)
$$ \bar{T}\left( {x,y} \right) = T_{0} \quad {\text{at}}\;y^{\prime } = h^{\prime } + H^{\prime } $$
(12)

Continuity of the heat flux at the cartilage interface is given by

$$ D_{1} {\frac{{\partial T^{\prime}}}{{\partial y^{\prime}}}} = \alpha^{\prime} \, {\frac{{\partial \bar{T}^{\prime} }}{{\partial y^{\prime} }}}\quad {\text{at}}\;y^{\prime} = h^{\prime} $$
(13)

In addition to the condition (10)–(13) a condition is required at lubricant–cartilage interface. This is introduced by extrapolating the temperature distribution in the bulk of the porous medium. This is known as temperature-slip boundary condition:

$$ {\frac{\partial T^{\prime }}{\partial y^{\prime }}} = - {\frac{\alpha ^{\prime }}{v}}\left( {T^{\prime } - \bar{T}^{\prime} } \right)\quad {\text{at}}\;y^{\prime } = h^{\prime } $$
(14)

where \( \alpha ^{\prime } \) is the slip temperature parameter and ν is the pore length scale parameter.

4.1 Non-Dimensional Scheme

$$ \begin{gathered} x = {\frac{{x^{\prime} }}{\ell }},\;y = {\frac{{y^{\prime} }}{{h_{0} }}},\;p = {\frac{{p^{\prime} }}{{\rho v_{0}^{2} }}},\;\bar{p} = {\frac{{\bar{p}^{\prime} }}{{\rho v_{0}^{2} }}} \hfill \\ h = {\frac{{h^{\prime} }}{{h_{0} }}} ,\; Re = {\frac{{\rho_{0} v_{0} h_{0} }}{\mu }},\; D = {\frac{{D^{\prime} }}{{D_{0} }}}, \hfill \\ u = {\frac{{u^{\prime} }}{{v_{0} }}},\;v = {\frac{{v^{\prime} }}{{v_{0} }}},\;T = {\frac{{T^{\prime} }}{{T_{0} }}},\;\bar{T} = {\frac{{\bar{T}^{\prime} }}{{\bar{T}_{0} }}} \hfill \\ \end{gathered} $$
(15)

and non-dimensional parameters are

$$ \varepsilon = \varepsilon_{0} {\frac{{v^{{\prime 2}} }}{{h_{0}^{2} }}},\quad \sigma = {\frac{{\sigma^{\prime}}}{{h_{0} }}},\quad Re = {\frac{{\rho v_{0} h_{0} }}{\mu }} $$
(16)

\( v_{0 } \) is the characteristic velocity, \( \rho \) is the mass density of the fluid, Re is the Reynolds number and Pe is the Peclet number.

The non-dimensional form of the governing equations of motion, equation of continuity and boundary conditions are given below:

Governing equations for flow in both the regions:

$$ {\frac{\partial p}{\partial x}} + {\frac{1}{{Re\,h_{0} }}} {\frac{\partial }{\partial y}} \left( {{\frac{\partial u}{\partial y}} - \varepsilon \left( {{\frac{\partial u}{\partial y}}} \right)^{3} } \right) = 0 $$
(17)
$$ {\frac{\partial p}{\partial y}} = 0 $$
(18)
$$ h^{\prime}_{0} {\frac{{\partial^{2} p}}{{\partial x^{2} }}} + {\frac{\partial }{\partial y}} \left\{ {\left( {1 - \beta^{\prime}y} \right){\frac{\partial p}{\partial y}}} \right\} = 0 $$
(19)

Boundary and matching conditions in non-dimensional form can be written as:

$$ \begin{array}{*{20}c} {{\frac{\partial y}{\partial x}} = 0} \hfill & {{\text{at}}\;y = 0} \hfill \\ {u = - {\frac{{k_{0} Re}}{\ell }} {\frac{\partial p}{\partial x}} - \sigma_{1} {\frac{\partial u}{\partial y}}} \hfill & {{\text{at}}\;y = h} \hfill \\ {{\frac{\partial p}{\partial x}}\;{\text{and}}\,{\frac{{\partial \bar{p}}}{\partial x}} = 0} \hfill & {{\text{at}}\;x = 0} \hfill \\ {p\;{\text{and}}\;\bar{p} = 0} \hfill & {{\text{at}}\;x = \pm 1} \hfill \\ {p = \bar{p}} \hfill & {{\text{at}}\;y = h} \hfill \\ {{\frac{{\partial \bar{p}}}{\partial y}} = 0} \hfill & {{\text{at}}\;y = h + H} \hfill \\ \end{array} $$

Equations for temperature distribution:

$$ Re\,Pr\,u{\frac{\partial T}{\partial x}} = \left( {{\frac{{\partial^{2} T}}{{\partial x^{2} }}} + {\frac{1}{{h_{{1 }}^{2} }}} {\frac{{\partial^{2} T}}{{\partial y^{2} }}}} \right) + 2\mu \,Br\left( {{\frac{\partial u}{\partial x}}} \right)^{2} + {\frac{1}{{h_{{1 }}^{2} }}} Br\left( {{\frac{\partial u}{\partial y}}} \right)^{2} $$
(20)
$$ Re\,Pr\left( {\bar{u}{\frac{{\partial \bar{T}}}{\partial x}} + {\frac{{\bar{v}}}{{h_{1} }}}\,{\frac{{\partial \bar{T}}}{\partial y}}} \right) = \left( {{\frac{{\partial^{2} \bar{T}}}{{\partial x^{2} }}} + {\frac{1}{{h_{{1 }}^{2} }}}\,{\frac{{\partial^{2} \bar{T}}}{{\partial y^{2} }}}} \right) + 2\mu \,Br\left[ {\left( {{\frac{{\partial \bar{u}}}{\partial x}}} \right)^{2} + {\frac{1}{{h_{{1 }}^{2} }}}\,\left( {{\frac{{\partial \bar{v}}}{\partial y}}} \right)^{2} } \right] + \mu \,Br\left\{ {\left( {{\frac{{\partial \bar{u}}}{\partial y}}} \right) + \left( {{\frac{{\partial \bar{v}}}{\partial x}}} \right)} \right\}^{2} $$
(21)

The boundary and matching conditions in non-dimensional form

$$ \begin{gathered} T\left( {0,y} \right) = T\left( {1,y} \right) \hfill \\ \bar{T}\left( {0,y} \right) = \bar{T}\left( {1,y} \right) \hfill \\ {\frac{\partial T}{\partial y}} = 0 \quad {\text{at}}\; y = 0 \hfill \\ \bar{T}\left( {x,y} \right) = 1\quad {\text{at}}\;y = h + H \hfill \\ \end{gathered} $$
(22)

where \( Pr = {\frac{{\mu c_{p} }}{K}} \) Prandtal number, \( Br = {\frac{{\mu v_{0}^{2} }}{{K\left( {T - T_{0} } \right)}}} \) Brinkman number and K is the thermal diffusivity.

5 Solution of the Problem

The problem reduces to the solution of a two-region mixed boundary value problem of flow and thermal diffusion. The velocity field is determined by the Eqs. 1–7. These solutions are introduced into the thermal diffusion equation.

Solution for pressure distribution in porous matrix given by Eq. 1 with suitable matching and boundary condition is obtained as:

$$ \bar{p} = \sum\limits_{n = 0}^{\infty } {C_{n} \,{ \cos }\,\lambda_{n} x\left\{ {\psi \left( {h,H} \right)I_{0} \left( {{\frac{{2\lambda_{n} h^{\prime}_{0} \sqrt {1 - \beta^{\prime}y} }}{{\beta^{\prime}}}}} \right) + K_{0} \left( {{\frac{{2\lambda_{n} h^{\prime}_{0} \sqrt {1 - \beta^{\prime}y} }}{{\beta^{\prime}}}}} \right)} \right\}} $$
(23)

where

$$ \begin{aligned} \psi \left( {h,H} \right) = & - {\frac{{K_{0}^{\prime} \left( {2\lambda_{n} h_{0}^{\prime} \sqrt {1 - \beta^{\prime} h - \beta^{\prime} H} /\beta^{\prime} } \right)}}{{I_{0}^{\prime} \left( {2\lambda h_{0}^{\prime} \sqrt {1 - \beta^{\prime} h - \beta^{\prime} H} /\beta^{\prime} } \right)}}} \\ C_{n} = & {\frac{{4v_{0} \left( { - 1} \right)^{n} }}{{Re\,h_{0}^{\prime} h\sigma_{1} \lambda_{n}^{3} \left\{ {\left\{ {{\frac{{ - k_{0} Re}}{l}}\phi_{1} \left( h \right) + {\frac{{v_{0} }}{{hh_{0} \lambda_{n}^{2} }}}F_{1} \left( h \right)} \right\}{\frac{1}{{\text{Re} h_{0}^{\prime} h\sigma_{1} }}} - \phi_{1} \left( h \right)} \right\}}}} \\ \phi_{1} \left( h \right) = & - K_{0}^{\prime} \left( {{\frac{{2\lambda_{n} h_{0}^{\prime} \sqrt {1 - \beta^{\prime} h - \beta^{\prime} H} }}{{2\lambda h_{0}^{\prime} \sqrt {1 - \left( {\beta^{\prime} h - \beta^{\prime} H} \right)} /\beta^{\prime} }}}} \right) I_{0} \left( {{\frac{{2\lambda_{n} h_{0}^{\prime} \sqrt {1 - \beta^{\prime} h} }}{{\beta^{\prime} }}}} \right) + K_{0} \left( {{\frac{{2\lambda_{n} h_{0}^{\prime} \sqrt {1 - \beta^{\prime} h} }}{{\beta^{\prime} }}}} \right) \\ \lambda_{n} = & \left( {2n + 1} \right){\frac{\pi }{2}} \\ \end{aligned} $$
(24)

where \( I_{0} \)(x) and \( K_{0\,} \left( x \right) \) are the modified Bessel’s functions

Velocity in porous region can be obtained by using Darcy’s law

$$ \bar{u} = - {\frac{{k_{0} }}{\mu }}\,{\frac{{\partial \bar{p}}}{\partial x}},\quad \bar{v} = {\frac{{k_{0} \left( {1 - \beta y^{\prime}} \right)}}{\mu }}\,{\frac{{\partial \bar{p}}}{\partial y}} $$
(25)

Taking approximations for small values of x

$$ \begin{gathered} I_{0} \left( {ax} \right) = 1, \quad K_{0} \left( {ax} \right) = - { \log }\left( {ax} \right) \hfill \\ \alpha I_{0}^{\prime} \left( {\alpha x} \right) = {\frac{{\alpha^{2} }}{2}}x,\quad I_{0}^{\prime} \left( {\alpha x} \right) = {\frac{\alpha x}{2}},\quad K_{0}^{\prime} \left( {\alpha x} \right) = - \frac{1}{ax} \hfill \\ \psi \left( {h,H} \right) = a_{1} \hfill \\ \end{gathered} $$
(26)

where

$$ a_{1} = {\frac{{\beta^{\prime 2} }}{{4\lambda_{n}^{2} h_{0}^{\prime 2} \left( {1 - \beta^{\prime} \left( {h,H} \right)} \right)}}} $$

Approximated horizontal and vertical component of velocity in porous region can be written as:

$$ \bar{u} = a_{2} x + a_{3} xy,\quad \bar{v} = \left( {a_{4} + a_{5} x^{2} } \right)\left( {a_{6} - a_{7} y} \right) $$
(27)

where

$$ \begin{gathered} a_{2} = {\frac{{k_{0} }}{\mu }}\left( {\mathop \sum \nolimits ( - C_{n} )\lambda_{n}^{2} a_{1} + \mathop \sum \nolimits C_{n} \lambda_{n}^{2} \,{\text{In}}\left( {{\frac{{2\lambda_{n} h^{\prime}_{0} }}{{\beta^{\prime}}}}} \right)} \right) \hfill \\ a_{3} = {\frac{{k_{0} }}{\mu }}\mathop \sum \nolimits - C_{n} \lambda_{n}^{2} \beta^{\prime} \hfill \\ a_{4} = - \mathop \sum \nolimits C_{n} {\frac{{k_{0} }}{\mu }},\quad a_{5} = \mathop \sum \nolimits C_{n} {\frac{{k_{0} \lambda_{n}^{2} }}{2\mu }} \hfill \\ a_{6} = a_{n} \lambda_{n} h_{0}^{\prime 2} + {\frac{{\beta^{\prime} }}{2}}, \quad a_{7} = - a_{1} \lambda_{n} h_{0}^{\prime 2} y. \hfill \\ \end{gathered} $$

Approximated horizontal and vertical component of velocity in fluid region can be written as:

$$ u = z_{1} y^{2} x + z_{2} x,\quad v = z_{2} y $$
(28)

where

$$ z_{1} = {\frac{{Reh^{\prime}_{0} }}{2}}\left( {b_{1} - h^{2} - 2\sigma_{1} h} \right),\quad z_{2} = - {\frac{{b_{3} Reh^{\prime}_{0} }}{2}} $$

Boundary conditions suggest the following dimensionless form of the temperature distribution for fluid film region

$$ T = T_{0} + g\left( y \right) + x^{2} q\left( y \right) $$
(29)

For small cross flow Reynolds number Re, we consider a power series solution for g and q in the following form

$$ g\left( y \right) = g_{0} \left( y \right) + Re\,g_{1} \left( y \right) $$
(30)
$$ q\left( y \right) = q_{0} \left( y \right) + Re\,q_{1} (y) $$
(31)

Finally we have

$$ T = T_{0} + g_{0} \left( y \right) + Re\,g_{1} \left( y \right) + x^{2} q_{0} \left( y \right) + Re\,x^{2} q_{1} (y) $$
(32)

and in cartilage region the temperature

$$ \bar{T} = T_{0} + \overline{{g_{0} \left( y \right)}} + Re\overline{{g_{1} \left( y \right)}} + x^{2} \overline{{q_{0} \left( y \right)}} + Re\,x^{2} \overline{{q_{1} \left( y \right)}} $$

6 Results and Discussion

A simplified mathematical model has been developed for analysing the combined effect of permeability of cartilage, slip velocity, viscoelastic fluid and intra-articular gap on temperature distribution in a synovial joint. The physical properties of the articular surface and properties of synovial fluid may be affected by the heating due to friction. Heat generated by friction is a thermo-mechanical coupled effect in nature, i.e. the temperature rise, develops additional deformation especially in contacting area. This change in configuration, in turn, affects the contact condition between contacting articular surface. If the friction coefficient is smaller by a few orders of magnitude and joints are able to function for much longer time, under conditions of variable speed and reciprocating motion, with almost no wear and no significant increase of temperature.

Results of our model are same as we have predicted. The temperature at the surface of the articular cartilage is extreme and decreases towards the bone cartilage interface. This is due to the fact due to friction temperature rises at the surface of cartilage. Therefore, temperature of the fluid also increases. This heated fluid imbibes into the cartilage due to the process of imbibition. As this fluid goes towards the bone cartilage interface this heated fluid cools down; therefore, temperature of the fluid decreases towards the bony ends; therefore, there is hardly any change in the temperature. It is observed from Fig. 2 that the temperature decreases with depth within the cartilage. These results agree with the experimental observations made by the orthopaedic surgeons [4].

Fig. 2
figure 2

Temperature distribution in articular cartilage \( \bar{T} \) for different values of the permeability parameter (β)

Full size image

Figure 3 describes the variation of the temperature for different articulate gap. Synovial fluid had direct contact with the articular cartilage; therefore, its peak temperature was nearly the same as in cartilage surface. Higher knee contact forces results in a greater amount of heat generation as obvious from the figure that as “h” decreases, i.e. as surface come closer temperature increases at the surface of cartilage. If we consider that heavier patient produces high knee contact during a particular activity, then logically a heavier patient should generate more heat, resulting in higher temperatures in and around the knee joint. The same results we are observing from the results of our model.

Fig. 3
figure 3

Temperature distribution in articular cartilage \( \bar{T} \) for different intra-articular gaps (h)

Full size image

Figure 4 plotted for temperature distribution in cartilage (\( \bar{T} \)) for different values of the viscoelastic parameter. This is due to the fact that the friction coefficient decreases as the viscoelastic parameter increases. The normal friction coefficient between the cartilage surfaces of the synovial joints is reported to the range 0.001 to 0.1. The lubrication mechanism primarily depends on the synovial fluid, where hyaluronic acid is considered to be the primarily effective constituent. In osteoarthritis conditions, hyaluronic acid molecules die out and lose their characteristics. A time, when viscosity decreases, external medicines are added to change the overall viscosity of the synovial fluid.

Fig. 4
figure 4

Temperature distribution in articular cartilage \( \bar{T} \) for different values of the viscoelastic parameter (ε)

Full size image

Figure 5 shows the variation of temperature cartilage for different values of the slip parameter. The variation in the slip parameter identifies the properties of the cartilage, i.e. decrease in pore size prevents the fluid exchange process, and therefore, heat may be generated at the articular surface and temperature may increase in the gap; therefore, friction may also increase as observed by [4] for diseased joints.

Fig. 5
figure 5

Temperature distribution in articular cartilage \( \bar{T} \) for different values of the slip parameter α′

Full size image

7 Conclusions

This article presents a more realistic model for discussing temperature distribution in human and may be used for predicting temperature variation in artificial joint. Temperature rises, resulting even if they are not significant, make the synovial fluid less viscous. As described above, overall temperature rise estimated was not more than 1.5 °C, and there would exist some locally enhanced temperature gradients. We may prepare model for artificial joints also, where temperature enhancement is a major problem.