1 Introduction

Mixed convection inside enclosure is still one of the researcher’s interested vehicles because it is a useful tool of heat transfer augmentation. It provides efficient cooling (or heating) for many engineering applications like building ventilation, cooling of electronic devices, cooling of chemical reactors and emergency cooling system of nuclear reactors. Several studies have confirmed different issues of mixed convection according to the geometry of the flow channel. For ventilation requirements and optimal performance, the flow channel can be designed in various different shapes. Mezrhab et al. (2010) have considered a vented T-shaped cavity. Biserni et al. (2007) optimized the geometry of H-shaped cavity. Pardeshi (2013) investigated the L-shaped cooling passage for the trailing edge of gas turbine blade with a combination of ribs and pin fins.

A growing interest of reinforcing the natural convection in square or rectangular enclosures has led to extensive studies and innovations; one of these is providing the enclosed cavities by vents, i.e., switching the forced convection, which its interaction with the natural convection can augment the heat transfer process. Angirasa (2000) has discussed the complex interaction between the natural and forced convection in square vented cavity, where the inlet and vent ports were situated at the left edges of the bottom and top walls, respectively. He declared to an augmented heat transfer when Reynolds number increased. Boulard et al. (2002) have reviewed and simulated the turbulent convection in the ventilated greenhouse, which are provided by heating pipes. They discussed the improvement of the greenhouse climate through better plant protection and enhancements of the design and control aspects of the greenhouse. Raji et al. (2008) have discussed the mixed convection in a rectangular cavity supplied by air jet from an inlet at the left vertical wall, and the flow exits from a vent at the opposing wall. They constructed relations for heat transfer by forced convection and confirmed the interaction between natural and forced convective modes. There are special applications like cables of electric transmission, fire research, and brake housing of an aircraft (Desai and Vafai 1992) which can be modeled as an open-ended cavities. Studies interested in this practical topic are carried out experimentally (Chen et al. 1985; Showole and Tarasuk 1993; Elsayed and Chakroun 1999) and analytically (Vafai and Ettefagh 1990a, b; Mhiri et al. 1998; Besbes et al. 2001; Khanafer and Vafai 2000, 2002; Khanafer et al. 2002). Two distinct conclusions can be drawn from these studies. The first is that the heat transfer coefficient has no clear relation with the tilting angle and the configuration of the cavity, and the second is that when the flow is normal to the open-ended side this will act as an insulator between the cavity and the surrounding medium (Khanafer and Vafai 2002). Anil Lal and Reji (2009) have employed the restricted domain approach to study the natural convection in an open-edge cavity with vented sidewalls. They reviewed various numerical techniques implemented in simulation of natural convection in open cavity. Xu et al. (2014) conducted a numerical study regarding the double-diffusive mixed convection in a square vented enclosure containing a circular cylinder of high temperature and concentration fixed at the middle of the cavity. They predicted complicated interactions between the mixed convection parameter (Richardson number) and the double-diffusive parameters (Lewis number and buoyancy ratio). Kuznetsov and Sheremet (2010) have analyzed numerically conjugate mixed convection in a ventilated cavity with a local heater. They obtained the diagram of the heat convection modes depending on the Grashof and Reynolds numbers. Ghalambaz et al. (2017) have studied triple-diffusive mixed convective heat and mass transfer of a mixture in an enclosure filled with a Darcy porous medium. The results indicated that the presence of one pollutant phase could significantly affect the pollutant distribution of the other phase.

However, when the heat transfer augmentation is a challenging issue, the mixed convection can be supported by improving the properties of the working fluid. Over the past decade, nanofluid was demonstrated as a powerful interesting field in heat transfer enhancement. It is the dispersing of nanosized solid particles of superior thermal conductivity into the working base fluid (Choi and Eastman 1995). The resulting mixture experiences an improved thermal conductivity and increased heat capacity. Nanofluid is familiar strategy in enclosures (Tiwari and Das 2007); nevertheless, they are also used in vented cavities; Mahmoudi et al. (2010), Shahi et al. (2010), Nasrin et al. (2013), Bahlaoui et al. (2016) and Sheremet et al. (2015). It is worth mentioning that in practice, these vented cavities are parts of enclosed loop system because the nanofluid is toxic and expensive; thus, it is not acceptable to discharge it to environment. The common feature among these studies (except in some situations) is that the heat transfer increases with increasing the volume fraction of the nanoparticles.

Porous media are encountered in many industrial and environmental situations surrounding us such as solar collectors and food applications. Plenty variety of studies regarding the convection in saturated porous enclosures along with their respective applications are described in very interested books of Nield and Bejan (2017), Ingham and Pop (2005), Vafai (2015) and Shenoy et al. (2016). A first published study debating the effect of ventilating enclosures saturated with porous media may be referred to Mahmud and Pop (2006). They adopted the geometry of Angirasa (2000), but for porous medium with relatively low modified Rayleigh number (\({ Ra} \le 1000\)), i.e., they assumed the Darcy model. They coded the problem using finite volume method and based the geometry representation on the finite element approach. They found that the flow and heat transfer are significantly sensitive to the width of the inlet and vent ports. Behzadi et al. (2015) investigated the mixed convection in a square enclosure filled with porous media provided with inlet, at the lower of the left wall, and vent at the upper of the right wall. They used Darcy–Brinkman model to simulate the fluid flow within the porous medium. They showed that when the Darcy number and the diameter of the particles forming the porous matrix increase, the mean heat transfer decreases.

In practice, there are many applications requiring coupling the momentum exchange between two adjacent layers: porous layer and homogeneous fluid layer. Filtration processes, draying process, material solidification, pollution of ground water and many other biological applications are some of the practical issues of such geometry. Different configurations of superimposed adjacent two layers, confined in enclosures have been extensively studied by Beavers and Joseph (1967), Kim et al. (1987), Chen and Chen (1992), Kim and Choi (1996), Zhao and Chen (2001), Lopez and Tapia (2001), Hirata et al. (2009), Bagchi and Kulacki (2012), Sheremet and Trifonova (2013), Sheremet and Trifonova (2013), Beckermann et al. (1987), Gobin et al. (2005), Chamkha and Ismael (2014), Ismael and Chamkha (2015) and Arpino et al. (2015). The common finding of these studies is that the existence of the porous layer in a specified thickness and porosity can significantly affect the behavior of the flow and heat.

However, the literature review above led us to be certain and to the best of the authors’ knowledge that the problem of mixed convection in a vented square cavity with a triangular porous layer has not been examined yet. Hence, the numerical solution and investigation will be the objective of the current study. It is believed that this study will reveal the contributions of enhancing the thermal performance in porous cavities, which has industrial applications significance particularly in solar collectors with a porous absorber, grain storage/drying and modeling with an interested inclined interface.

2 Problem Definition

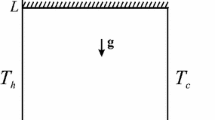
The present study concerns with mixed convection in a composite square cavity with side length of L as shown in Fig. 1. The cavity is composed of two layers such as a triangular porous layer confined with a fluid (water or air). The porous layer is saturated with the same fluid. An input and output ports are localized at the lower and upper ends of the left and right walls, respectively, with an opening value of say L/10. The left and right walls of the cavity are thermally insulated. A hot element is localized at the bottom wall with \(T = T_\mathrm{h}\) and size of \(H = L/4\). The top wall is kept isothermal at cold temperature \(T_\mathrm{c}\). Cavity walls are impermeable except the inclined interface between the porous layer and the fluid. The Brinkman–extended Darcy model is invoked for the momentum exchange within the porous layer.

Fig. 1
figure 1

Schematic of the present problem

Full size image

The Navier–Stokes equations based on the previous assumptions in Cartesian coordinates for (porous and fluid layers) can be written as follows:

For the porous layer:

Continuity equation:

$$\begin{aligned} \frac{\partial u_\mathrm{p} }{\partial x}+\frac{\partial v_\mathrm{p}}{\partial y}=0 \end{aligned}$$
(1)

x-direction momentum equation:

$$\begin{aligned} \rho _\mathrm{f} \left( {u_\mathrm{p} \frac{\partial u_\mathrm{p} }{\partial x}+v_\mathrm{p} \frac{\partial u_\mathrm{p} }{\partial y}} \right) =-\varepsilon ^{2}\frac{\partial p}{\partial x}+\varepsilon \mu _\mathrm{f} \left( {\frac{\partial ^{2}u_\mathrm{p} }{\partial x^{2}}+\frac{\partial ^{2}u_\mathrm{p} }{\partial y^{2}}} \right) -\varepsilon ^{2}\frac{\mu _\mathrm{f} }{K}u_\mathrm{p} \end{aligned}$$
(2)

y-direction momentum equation:

$$\begin{aligned} \rho _\mathrm{f} \left( {u_\mathrm{p} \frac{\partial v_\mathrm{p} }{\partial x}+v_\mathrm{p} \frac{\partial v_\mathrm{p} }{\partial y}} \right)= & {} -\varepsilon ^{2}\frac{\partial p}{\partial y}+\varepsilon \mu _\mathrm{f} \left( {\frac{\partial ^{2}v_\mathrm{p} }{\partial x^{2}}+\frac{\partial ^{2}v_\mathrm{p} }{\partial y^{2}}} \right) \nonumber \\&-\varepsilon ^{2}\frac{\mu _\mathrm{f} }{K}v_\mathrm{p} +\varepsilon ^{2}\rho _\mathrm{f} \beta _\mathrm{f} g\left( {T_\mathrm{p}-T_\mathrm{c} } \right) \end{aligned}$$
(3)

Energy equation:

$$\begin{aligned} u_\mathrm{p} \frac{\partial T_\mathrm{p} }{\partial x}+v_\mathrm{p} \frac{\partial T_\mathrm{p} }{\partial y}=\alpha _\mathrm{eff} \left( {\frac{\partial ^{2}T_\mathrm{p} }{\partial x^{2}}+\frac{\partial ^{2}T_\mathrm{p} }{\partial y^{2}}} \right) \end{aligned}$$
(4)

For the fluid layer:

Continuity equation:

$$\begin{aligned} \frac{\partial u_\mathrm{f} }{\partial x}+\frac{\partial v_\mathrm{f} }{\partial y}=0 \end{aligned}$$
(5)

x-direction momentum equation:

$$\begin{aligned} \rho _\mathrm{f} \left( {u_\mathrm{f} \frac{\partial u_\mathrm{f} }{\partial x}+v_\mathrm{f} \frac{\partial u_\mathrm{f} }{\partial y}} \right) =-\frac{\partial p}{\partial x}+\mu _\mathrm{f} \left( {\frac{\partial ^{2}u_\mathrm{f} }{\partial x^{2}}+\frac{\partial ^{2}u_\mathrm{f} }{\partial y^{2}}} \right) \end{aligned}$$
(6)

y-direction momentum equation:

$$\begin{aligned} \rho _\mathrm{f} \left( {u_\mathrm{f} \frac{\partial v_\mathrm{f} }{\partial x}+v_\mathrm{f} \frac{\partial v_\mathrm{f} }{\partial y}} \right) =-\frac{\partial p}{\partial y}+\mu _\mathrm{f} \left( {\frac{\partial ^{2}v_\mathrm{f} }{\partial x^{2}}+\frac{\partial ^{2}v_\mathrm{f} }{\partial y^{2}}} \right) +\rho _\mathrm{f} \beta _\mathrm{f} g\left( {T_\mathrm{f} -T_\mathrm{c} } \right) \end{aligned}$$
(7)

Energy equation:

$$\begin{aligned} u_\mathrm{f} \frac{\partial T_\mathrm{f} }{\partial x}+v_\mathrm{f} \frac{\partial T_\mathrm{f} }{\partial y}=\alpha _\mathrm{f} \left( {\frac{\partial ^{2}T_\mathrm{f} }{\partial x^{2}}+\frac{\partial ^{2}T_\mathrm{f} }{\partial y^{2}}} \right) \end{aligned}$$
(8)

For the given problem, the appropriate boundary conditions at the system boundaries are:

  • 1. at \(y = 0\) (bottom wall) and \(\frac{L-H}{2}\le x\le \frac{L+H}{2}\) we have \(T = T_{h}\), otherwise, \(\frac{\partial T}{\partial y}=0\)

  • 2. at \(y = H\) (top wall) \(T = T_{c}\)

  • 3. at \(x = 0\) (left wall) and \(x = L\) (right wall) \(\frac{\partial T}{\partial x}=0\)

  • 4. in the input vent: \(u = u_\mathrm{in}\), \(v = 0\), and in the outlet vent, \(p = 0\) and \(v = 0\)

  • 5. along the interface line S:

Continuity of horizontal and vertical velocity components, \(u_{p} = u_{f}\), \(v_{p} = v_{f}\)

Shear stress, Neale and Nader (1974), \(\mu _\mathrm{eff} ({\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}})_\mathrm{p} =\mu _\mathrm{f} ({\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}})_\mathrm{f}\)

Continuity of pressure, \(p_{p} = p_{f}\)

Temperature and heat flux, \(T_\mathrm{p} =T_\mathrm{f}\), \(-k_\mathrm{eff} \frac{\partial T_\mathrm{p}}{\partial n}=-k_\mathrm{f} \frac{\partial T_\mathrm{f} }{\partial n}\).

The formulation is based on the stream function, \(u=\frac{\partial \psi }{\partial y}\), \(v=-\frac{\partial \psi }{\partial x}\) and the vorticity, \(\omega =\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\), and on the following non-dimensional parameters:

$$\begin{aligned} X= & {} \frac{x}{L}, \, Y=\frac{y}{L}, \, U=\frac{u}{u_\mathrm{in} }, \, V=\frac{v}{u_\mathrm{in} }, \, P=\frac{\left( {p+\rho _\mathrm{f} gy} \right) }{\rho _\mathrm{f} u_\mathrm{in}^2 }, \\ \varPsi= & {} \frac{\psi }{u_\mathrm{in} L}, \, \varOmega =\frac{\omega L}{u_\mathrm{in} }, \, \theta =\frac{T-T_\mathrm{c} }{T_\mathrm{h} -T_\mathrm{c} } \end{aligned}$$

Following the usual manipulation of eliminating pressure gradient terms from momentum equations, the dimensionless governing equations become:

For porous layer:

$$\begin{aligned}&\frac{\partial ^{2}\varPsi _\mathrm{p} }{\partial X^{2}}+\frac{\partial ^{2}\varPsi _\mathrm{p} }{\partial Y^{2}}=-\varOmega _\mathrm{p} \end{aligned}$$
(9)
$$\begin{aligned}&\frac{\partial \varPsi _\mathrm{p} }{\partial Y}\frac{\partial \varOmega _\mathrm{p} }{\partial X}-\frac{\partial \varPsi _\mathrm{p} }{\partial X}\frac{\partial \varOmega _\mathrm{p} }{\partial Y}=\frac{\varepsilon }{Re}\left( {\frac{\partial ^{2}\varOmega _\mathrm{p} }{\partial X^{2}}+\frac{\partial ^{2}\varOmega _\mathrm{p} }{\partial Y^{2}}-\frac{\varepsilon }{Da}\varOmega _\mathrm{p} } \right) +\varepsilon ^{2}Ri\frac{\partial \theta _\mathrm{p} }{\partial X} \end{aligned}$$
(10)
$$\begin{aligned}&\frac{\partial \varPsi _\mathrm{p} }{\partial Y}\frac{\partial \theta _\mathrm{p} }{\partial X}-\frac{\partial \varPsi _\mathrm{p} }{\partial X}\frac{\partial \theta _\mathrm{p} }{\partial Y}=\frac{{\alpha _\mathrm{eff} }/{\alpha _\mathrm{f} }}{Re\cdot { Pr} }\left( {\frac{\partial ^{2}\theta _\mathrm{p} }{\partial X^{2}}+\frac{\partial ^{2}\theta _\mathrm{p} }{\partial Y^{2}}} \right) \end{aligned}$$
(11)

and for clear fluid:

$$\begin{aligned}&\frac{\partial ^{2}\varPsi _\mathrm{f} }{\partial X^{2}}+\frac{\partial ^{2}\varPsi _\mathrm{f} }{\partial Y^{2}}=-\varOmega _\mathrm{f} \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial \varPsi _\mathrm{f} }{\partial Y}\frac{\partial \varOmega _\mathrm{f} }{\partial X}-\frac{\partial \varPsi _\mathrm{f} }{\partial X}\frac{\partial \varOmega _\mathrm{f} }{\partial Y}=\frac{1}{Re}\left( {\frac{\partial ^{2}\varOmega _\mathrm{f} }{\partial X^{2}}+\frac{\partial ^{2}\varOmega _\mathrm{f} }{\partial Y^{2}}} \right) +Ri\frac{\partial \theta _\mathrm{f} }{\partial X} \end{aligned}$$
(13)
$$\begin{aligned}&\frac{\partial \varPsi _\mathrm{f} }{\partial Y}\frac{\partial \theta _\mathrm{f} }{\partial X}-\frac{\partial \varPsi _\mathrm{f} }{\partial X}\frac{\partial \theta _\mathrm{f} }{\partial Y}=\frac{1}{{ Re} \cdot { Pr}}\left( {\frac{\partial ^{2}\theta _\mathrm{f} }{\partial X^{2}}+\frac{\partial ^{2}\theta _\mathrm{f} }{\partial Y^{2}}} \right) \end{aligned}$$
(14)

The appropriate dimensionless boundary conditions can be written in following form:

  • 1. at \(Y = 0 ({\varOmega =-\frac{\partial ^{2}\varPsi }{\partial Y^{2}}, \varPsi =0})\) and \(\frac{1-H/L}{2}\le X\le \frac{1+H/L}{2}\), \(\theta = 1\), otherwise, \(\frac{\partial \theta }{\partial Y}=0\).

  • 2. at \(Y = 1 ({\varOmega =-\frac{\partial ^{2}\varPsi }{\partial Y^{2}}, \varPsi =0})\) and \(\theta = 0\).

  • 3. at \(X = 0\) (left wall) and \(X = 1\) (right wall) \(\frac{\partial \theta }{\partial X}=0\), \(\varOmega = -\frac{\partial ^{2}\varPsi }{\partial X^{2}}\), \(\varPsi =0\)

  • 4. in the input port \(\varOmega =0\), \(\frac{\partial \varPsi }{\partial Y}=1\), and in the output port \(\frac{\partial \theta }{\partial X}=\frac{\partial \varPsi }{\partial X}=\frac{\partial \varOmega }{\partial X}=0\)

  • 5. The interface boundary conditions are derived from equating (continuity) of tangential and normal velocities, temperature and the heat flux across the interface. Hence, the interface conditions can be written as follows:

    $$\begin{aligned} \theta _\mathrm{p}= & {} \theta _\mathrm{f} , \, \frac{\partial \theta _\mathrm{f} }{\partial n}=\frac{k_\mathrm{eff} }{k_\mathrm{f} }\frac{\partial \theta _\mathrm{p} }{\partial n}\end{aligned}$$
    (15a)
    $$\begin{aligned} \varPsi _\mathrm{p}= & {} \varPsi _\mathrm{f} , \, \frac{\partial \varPsi _\mathrm{f} }{\partial n}=\frac{\partial \varPsi _\mathrm{p} }{\partial n} \end{aligned}$$
    (15b)
    $$\begin{aligned} \varOmega _\mathrm{p}= & {} \varOmega _\mathrm{f} , \, \frac{\partial \varOmega _\mathrm{f} }{\partial n}=\frac{\partial \varOmega _\mathrm{p} }{\partial n} \end{aligned}$$
    (15c)

Here Eqs. (15b) and (15c) were derived from the continuity of horizontal and vertical velocity components.

The following relation can calculate the effective thermal conductivity of porous medium

$$\begin{aligned} k_\mathrm{eff} =\left( {1-\varepsilon } \right) k_\mathrm{s} +\varepsilon k_\mathrm{f} \end{aligned}$$
(16)

The dynamic viscosity in both layers is assumed equal (\(\mu _\mathrm{eff} = \mu _{f}\)). The agreement of this assumption was proved experimentally by Neale and Nader (1974) and adopted by Sheremet and Trifonova (2013) and Sheremet and Trifonova (2014).

The local Nusselt number along the heater is \(Nu=-\frac{\partial \theta }{\partial Y}\).

The average Nusselt number at the heater is defined as follows:

$$\begin{aligned} Nu_\mathrm{avg} =\frac{L}{H}\int \limits _{0.5\left( {1-H/L} \right) }^{0.5\left( {1+H/L} \right) } {Nu \, \mathrm{d}X} \end{aligned}$$
(17)

3 Numerical Method

The partial differential equations (9)–(14) with the corresponding boundary conditions have been solved by the finite difference method. Detailed description of the used numerical technique has been presented earlier in Kuznetsov and Sheremet (2010), Sheremet et al. (2015), Shenoy et al. (2016), Sheremet and Trifonova (2013) and Sheremet and Trifonova (2014).

The present model, in the form of an in-house computational fluid dynamics code, has been validated successfully against the works of Lauriat and Prasad (1989) and Bhardwaj et al. (2015) for natural convection in a non-Darcian porous cavity. The results presented in Table 1 show a good comparison for the average Nusselt number at the hot wall between the obtained data and the numerical data of other authors.

Table 1 Comparison of the average Nusselt number at the hot wall
Full size table

In the case of natural convection in a composite cavity, the benchmark solution has been obtained by using the results of Singh and Thorpe (1995). The laminar natural convection in a cavity containing a fluid layer overlying a porous layer saturated with the same fluid is analyzed. The enclosure is heated on one vertical wall and cooled on the opposite wall, while the top and bottom walls are adiabatic. Figures 2 and 3 show a good agreement between the obtained streamlines and isotherms at different Rayleigh numbers and the results by Singh and Thorpe (1995) for the case when the height of the porous layer is equal to the height of the fluid layer. Results on the basis of the Brinkman–extended Darcy model is (—–) and on the basis of the Darcy model is (- - - -).

Fig. 2
figure 2

Comparison of streamlines \(\Psi \) and isotherms \(\Theta \) at \({ Da} = 10^{-5}\), \({ Ra} = 10^{5}\): numerical results of Singh and Thorpe (1995) (a), present study b

Full size image
Fig. 3
figure 3

Comparison of streamlines \(\Psi \) and isotherms \(\Theta \) at \({ Da} = 10^{-5}\), \({ Ra} = 10^{6}\): numerical results of Singh and Thorpe (1995) (a), present study (b)

Full size image

We have conducted also the grid independent test, analyzing natural convection in the considered cavity presented in Fig. 1 for \({ Ri} = 1\), \({ Da} = 10^{-3}\), \({ Pr} = 6.26\), \({ Re} = 100\), \(\varepsilon = 0.398\), \(\varLambda = A = 1.2042\), \(\delta = H/L=0.3\), \(S_{1} = S_{2} = 0.75 L\). Five cases of the uniform grid are tested: a grid of \(60 \times 60\) points, a grid of \(100 \times 100\) points, a grid of \(200 \times 200\) points, a grid of \(300 \times 300\) points and a grid of \(400 \times 400\) points. Table 2 shows the effect of the mesh parameters on the average Nusselt number of the heater.

Taking into account the conducted verifications, the uniform grid of \(200 \times 200\) points has been selected for the further investigation.

4 Results and Discussion

The considered problem has been analyzed at the following values of the governing parameters: Richardson number (\({ Ri} = 0.01 -10\)), Darcy number (\({ Da} = 10^{-7} - 10^{-1}\)), Prandtl number (\({ Pr} = 6.26\)), Reynolds number (\({ Re} = 100\)), thermal conductivity ratio \(({\varLambda ={k_{{ eff}}}/{k_\mathrm{f}}=1.2042})\), thermal diffusivity ratio \(({A={\alpha _\mathrm{eff} }/{\alpha _\mathrm{f}}=1.2042})\), porosity (\(\varepsilon = 0.398\)), heat source length \(({\delta =H/L=0.2-0.4})\) and the following geometry of the triangular porous layer: (I) \(S_{1} = S_{2} = 0.75 L\), (II) \(S_{1} = L\), \(S_{2} = 0.5 L\) and (III) \(S_{1} = 0.5 L\), \(S_{2} = L\). Particular efforts have been focused on the effects of these parameters on the fluid flow and heat transfer inside the cavity. Streamlines and isotherms as well as the average Nusselt number for different values of key parameters mentioned above are illustrated in Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19.

Figure 4 presents distributions of the streamlines and isotherms for case (I) at \({ Da} = 10^{-3}\), \(\delta = 0.3\) and different values of the Richardson number. The line in the streamlines and isotherms reflects a location of a porous layer as presented in Fig. 1. Low Richardson numbers (\({ Ri} \le 1.0\)) for the case (I) characterize a formation of a flow from the inlet to the outlet without significant circulations. Only one minor recirculation appears near the inlet due to the effect of the porous layer. At the same time, one can find a formation of a small vortex in the right bottom corner. This vortex vanishes with a growth of the Richardson number. High values of Ri illustrate an appearance of additional recirculation in the upper part of the cavity. It should be noted that a rise of the Richardson number is due to a growth of the Grashof number. The Grashof number in the present problem reflects the temperature differences between the bottom heater and the top cooler. Therefore, high values of Gr characterize an essential vertical temperature difference that leads to a formation of a convective cell inside the cavity while the main flow is distorted close to the bottom and right walls. The temperature field supplements the whole thermohydrodynamic behavior. The thermal plume formed over the heater develops along the right adiabatic wall because the incoming fluid is cold which deforms this thermal plume. Also, one can find that an increase in the Richardson number leads to a reduction of the thermal boundary layer thickness along the right vertical wall due to the effect of the incoming cold flow.

Table 2 Variations of the average Nusselt number of the heater with the uniform grids
Full size table
Fig. 4
figure 4

Streamlines \(\uppsi \) and isotherms \(\uptheta \) for case (I) at \({ Da} = 10^{-3}\), \(\delta = 0.3\): \({ Ri} = 0.01\) (a), Ri = 0.1 (b), \({ Ri} = 1.0\) (c), \({ Ri} = 10.0\) (d)

Full size image

Figure 5 shows profiles of the horizontal velocity and temperature at the middle cross section \(x = 0.5\). As has been mentioned above, an increase in Ri leads to an augmentation of the velocity along the bottom wall while in the upper part, the horizontal velocity decreases and for \({ Ri} = 10.0\) one can find a formation of reverse flow. It is worth noting that a border of the porous layer in the velocity profiles is inconspicuous due to the high value of the Darcy number. The temperature profiles at \(x = 0.5\) also illustrate a significant decrease in temperature along a small distance. One can observe that the dimensionless temperature reduces from 1.0 at the heater to 0.0 at 30% of the cavity height and this magnitude decreases with Ri.

Fig. 5
figure 5

Profiles of horizontal velocity u (a) and temperature \(\uptheta \) (b) at middle cross section \(x = 0.5\) for case (I) at \({ Da} = 10^{-3}\), \(\delta = 0.3\) and different Richardson numbers

Full size image

In the case of the vertical velocity and temperature profiles along the horizontal cross section \(y = 0.5\) (Fig. 6), it is possible to note an essential flow acceleration near the right adiabatic wall with an increase in the Richardson number, while the fluid flow in the left part of the cavity is attenuated. A growth of Ri leads to the temperature reduction close to the right vertical wall.

Figure 7 presents profiles of the local Nusselt number along the heater for different values of the Richardson number. An increase in Ri leads to a growth of Nu along the heater. At the same time, the Nusselt number decreases from the left side of the heater till \(x \sim 0.61\) and increases for \(x > 0.62\). The physical reason for such behavior is a formation of ascending thermal boundary layer over the heater, and the maximum value of the Nusselt number occurs at the beginning of the layer. A local increase in Nu near the right border of the heater is due to a stopping of the heater effect.

Fig. 6
figure 6

Profiles of vertical velocity v (a) and temperature \(\uptheta \) (b) at middle cross section \(y = 0.5\) for case (I) at \({ Da} = 10^{-3}\), \(\delta = 0.3\) and different Richardson numbers

Full size image
Fig. 7
figure 7

Profiles of local Nusselt number along the heater for case (I) at \({ Da} = 10^{-3}\), \(\delta = 0.3\) and different Richardson numbers

Full size image

The effect of the Darcy number on the fluid flow and heat transfer is presented in Fig. 8. Low values of Da (\({ Da} \le 10^{-4}\)) illustrate low intensive flow where the fluid occupies the whole porous layer without recirculations inside the cavity. An increase in the Darcy number (\({ Da} = 10^{-1}\)) leads to a formation of the convective cell over the porous layer due to more essential effect of the buoyancy force when the permeability of the medium is significant and close to the clear fluid. The temperature field also reflects a formation of the thermal plume near the right vertical adiabatic wall.

Fig. 8
figure 8

Streamlines \(\uppsi \) and isotherms \(\uptheta \) for case (I) at \({ Ri} = 1.0\), \(\delta = 0.3\): \({ Da} = 10^{-7}\) (a), \({ Da} = 10^{-4}\) (b), \({ Da} = 10^{-1}\) (c)

Full size image

More detailed description of the velocity components and the temperature profiles is presented in Figs. 9 and 10 for the middle cross sections \(x = 0.5\) and \(y = 0.5\) for the case of horizontal and vertical velocity components. The temperature profiles with Da are similar to the effect of the Richardson number (Figs. 5, 6). As for the velocity components, it should be noted that the typical velocity behavior close to the solid walls inside the porous layer for low Darcy numbers (\({ Da} \le 10^{-5}\)) is with essential velocity gradient (Sheremet and Trifonova 2013, 2014). An increase in the permeability of the medium leads to an essential growth of the velocity in the bottom part and a formation of a reverse flow near the upper part.

Fig. 9
figure 9

Profiles of horizontal velocity u (a) and temperature \(\uptheta \) (b) at middle cross section \(x = 0.5\) for case (I) at \({ Ri} = 1.0\), \(\delta = 0.3\) and different Darcy numbers

Full size image
Fig. 10
figure 10

Profiles of vertical velocity v (a) and temperature \(\uptheta \) (b) at middle cross section \(y = 0.5\) for case (I) at \({ Ri} = 1.0\), \(\delta = 0.3\) and different Darcy numbers

Full size image
Fig. 11
figure 11

Variations of average Nusselt number at the heater for case (I) for \(\delta = 0.3\) and different values of Richardson and Darcy numbers

Full size image
Fig. 12
figure 12

Streamlines \(\uppsi \) and isotherms \(\uptheta \) for case (I) at \({ Ri} = 1.0\), \({ Da} = 10^{-3}\): \(\delta = 0.2\) (a), \(\delta = 0.4\) (b)

Full size image
Fig. 13
figure 13

Profiles of horizontal velocity u (a) and temperature \(\uptheta \) (b) at middle cross section \(x = 0.5\) for case (I) at \({ Ri} = 1.0\), \({ Da} = 10^{-3}\) and different values of heater length

Full size image
Fig. 14
figure 14

Profiles of vertical velocity v (a) and temperature \(\uptheta \) (b) at middle cross section \(y = 0.5\) for case (I) at \({ Ri} = 1.0\), \({ Da} = 10^{-3}\) and different values of heater length

Full size image

Variations of the average Nusselt number at the heater with Da and Ri are presented in Fig. 11. As has been mentioned above, an increase in Ri leads to a heat transfer enhancement. The maximum Nusselt number is recorded at the lower value of Darcy number (\({ Da} = 10^{-7}\)), and this can be attributed to the large drag exerted by the lower permeable porous medium which in turn reduce the penetration of water entering the cavity. As such, the diffusion phenomenon is less significant compared with the convective heat transfer. A growth of the Darcy number until a critical value of \(10^{-3}\) illustrates a reduction in heat transfer rate. This is because the reduction in the drag force stimulates the conductive heat transfer, while for \({ Da} > 10^{-3}\) one can find a rise of the average Nusselt number due to a more significant influence of the buoyancy force for the medium with a high permeability. At the same time, it should be noted that it is a partially porous cavity and we have to take into account the momentum and energy interactions between porous layer and clear fluid at interface, while the heater is located near this boundary. An increase in porous layer thickness can lead to a formation of classical behavior when a growth of Darcy number leads to the heat transfer enhancement. Therefore, the main reason for such behavior is a proximity to the porous–fluid interface combined with above mentioned physical features. It is worth noting that a high rate of the average Nusselt number growth is at high values of the Richardson number.

Figures 12, 13 and 14 show the effect of the heater length on the streamlines, isotherms and the profiles of the temperature and velocity components. As expected, an increase in \(\delta \) leads to more essential heating of the cavity bottom part, and as a result, the average temperature inside the cavity increases. A growth of the horizontal velocity in the bottom part due to a continuing effect of the buoyancy force is presented in Fig. 13a. At the same time, a reduction of u in the upper part (Fig. 13a) and v in the left part (Fig. 14a) can be explained by an interaction between the buoyancy force and the inertia force. A growth of temperature with the heater length is presented in Figs. 13b and 14b. It is worth noting that at the right vertical wall (\(y = 0.5\)), an increase in the heater length from 0.2 till 0.4 leads to a growth of the temperature from 0.29 till 0.40 and the dimensionless vertical velocity component rises from 0.20 till 0.23.

Figure 15 presents the variations of the average Nusselt number at the heater with the heater length and the Darcy number. An increase in the heater length leads to a reduction in the heat transfer rate, and a more essential decrease in \({\overline{Nu}}\) occurs for a rise of the heater length from 0.2 till 0.3.

Fig. 15
figure 15

Variations of average Nusselt number at the heater for case (I) at \({ Ri} = 1.0\) and different values of heater length and Darcy number

Full size image
Fig. 16
figure 16

Streamlines \(\uppsi \) and isotherms \(\uptheta \) at \({ Ri} = 1.0\), \({ Da} = 10^{-3}\), \(\delta = 0.3\): case (I) (a), case (II) (b), case (III) (c)

Full size image
Fig. 17
figure 17

Profiles of horizontal velocity u (a) and temperature \(\uptheta \) (b) at middle cross section \(x = 0.5\) for \({ Ri} = 1.0\), \({ Da} = 10^{-3}\), \(\delta = 0.3\) and different cases

Full size image
Fig. 18
figure 18

Profiles of vertical velocity v (a) and temperature \(\uptheta \) (b) at middle cross section \(y = 0.5\) for \({ Ri} = 1.0\), \({ Da} = 10^{-3}\), \(\delta = 0.3\) and different cases

Full size image
Fig. 19
figure 19

Variations of average Nusselt number at the heater for \({ Ri} = 1.0\), \(\delta = 0.3\), different cases and Darcy numbers

Full size image

The effect of different porous layer positions on the streamlines, isotherms and the profiles of velocity and temperature is presented in Figs. 16, 17 and 18. The main feature is that an increase in the distance between the top wall and the porous layer leads to a formation of a convective cell inside the cavity (Fig. 15b), while the other parameters concerning the fluid flow and heat transfer patterns are the same. The abovementioned feature illustrates an increase in the horizontal velocity at the bottom part (Fig. 17a) due to a small deformation of the main incoming flow, and as a result, one can find a weak velocity reduction in the upper part. Such intensification of the fluid flow illustrates an increase in the temperature in the central part of the cavity.

Figure 19 demonstrates the heat transfer enhancement for the case (III) when the heater is half-covered by the porous layer. As a result, a lack of the solid matrix of the porous medium leads to an essential intensification of the heat transfer.

5 Conclusion

A numerical analysis of the mixed convection in an open cavity partially filled with a porous medium in the presence of a local heater has been carried out in a wide range of the Richardson and Darcy numbers, as well as the heater length and location of the porous layer. The governing equations formulated in the dimensionless stream function, vorticity and temperature have been solved by the finite difference method using the Brinkmann–extended Darcy model for the porous layer. The obtained results presented for the distributions of streamlines, isotherms and the profiles of velocity and temperature as well as the local and average Nusselt number profiles reveal the following:

  1. 1.

    An increase in the Richardson number leads to an intensification of the fluid flow and heat transfer. High values of Ri illustrate a formation of additional recirculation inside the cavity. At the same time, the dimensionless temperature decreases in the right part of the cavity.

  2. 2.

    A growth of the Darcy number reflects a reduction in the heat transfer rate for \({ Da} < 10^{-3}\), while the following increase for \({ Da} > 10^{-3}\) characterizes a heat transfer enhancement. It should be noted that high values of the Darcy number lead to a formation of a convective cell inside the cavity due to more essential effect of the buoyancy force.

  3. 3.

    A rise of the heater length illustrates the diminution of the heat transfer rate with an intensification of the flow and increase in the average temperature for a long heater.

  4. 4.

    An increase in the distance between the top wall and the porous layer leads to a formation of a convective cell inside the cavity, while the heat transfer enhancement occurs for the case (III) when the heater is half-covered by the porous layer.