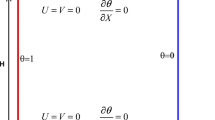Introduction

The basic idea of using a wavy cold wall is to enhance heat transfer by convection, as the wavy wall has a greater length than a straight wall between a fixed distance. Applications of porous cavities in geothermal, biological, and engineering fields are reported by Cheong et al. [1, 2]. Also, it has broad applications in fields like solar energy, building design, and the electronics industry. This phenomenon is also relevant in challenges involving industrial boilers or ovens containing porous materials, as reported by Sheremet et al. [3].

The study of natural convection has gained significant attention among researchers. Among them, Prasad [4], Nield and Bejan [5] presented an extensive discussion about convection in porous media. Kumar et al. [6] studied free convection in a porous cavity having a wavy bottom wall and uniform heating from the bottom, and they reported that the sinusoidal bottom wall is not helpful for convection. Also, the effect of non-Darcian porous media in natural convection in a wavy cavity is investigated by Kumar and Shalini [7], they concluded that in the presence of surface disturbances, the non-Darcian effect introduced by Forchheimer terms causes the Nusselt number to increase. While the Prandtl number is set to unity, the effects of the Rayleigh number, the number of wavy surface undulations, and the amplitude of the wavy surface on the flow structure and heat transfer characteristics are explored by Khanafer et al. [8] in detail from their study of free convection heat transfer inside a wavy cavity packed by porous media. The effect of the volumetric heat source during natural convection in a wavy porous cavity is studied by Oztop et al. [9], and they reported that the heat transfer rate is proportional to the amplitude of the wavy wall. Buonomo et al. [10] numerically studied time-dependent mixed convection in a channel with an open cavity filled with porous media. Sompong and Witayangkurn [11] eported that larger Rayleigh and Darcy numbers resulted in increased flow strength and temperature dispersion from their numerical investigation of free convection in a trapezoidal cavity having a top wavy wall.

Abu-Nada and Chamkha [12] modeled and reproduced constant laminar mixed convection flow in a lid-driven enclosure with a wavy wall filled with nanofluid. They reported that the introduction of nanoparticles provides significant heat transfer enhancement for all Richardson numbers and lower wall geometry ratios. Sheremet et al. [13, 14] numerically studied free convection heat transfer in an open porous cavity filled with nanofluids. They employed Buongiorno’s nanofluid model and Tiwari and Das’ nanofluid model for their discussion, and they discussed the effect of wall waviness controlled by amplitude and number of undulations. Also, Sheremet et al. [3] investigated the effect of a magnetic field on the natural convection of nanofluid in an open wavy cavity heated from the corner and reported that the Rayleigh number enhances heat transfer, and the Hartmann number reduces heat transfer. In contrast, the magnetic field inclination angle causes non-monotonic changes in the heat transfer rate.

Cheong et al. [1, 2] investigated free convection heat transfer in a wavy porous cavity. They studied the effect of sinusoidal heating, internal heat generation, and the effect of aspect ratio. The studies explain the effect of wall waviness on natural convection and other governing parameters. The effect of magnetic field and sinusoidal heating on natural convection in a wavy cavity is studied numerically by Ahmed et al. [15]. \(Cu{-}water\) nanofluid is taken for their investigation, and it is reported that as the undulation parameter increases from 1 to 5, the flow strength is decreased by \(31.8\%\). The effect of local thermal non-equilibrium on natural convection in a porous cavity is investigated by Alsabery et al. [16, 17]. Their studies explored the effects of non-Darcian parameters in a wavy porous cavity and also the effects of wavy porous layers. In an open trapezoidal cavity, a numerical investigation of power law fluid–structure interaction is carried out by Yaseen and Ismael [18]. Also, local thermal non-equilibrium free convection in a porous annulus is carried out by Tayebi and Chamkha [19] and Tayebi et al. [20]. The studies are focused on non-Darcian effects and conjugate heat transfer between purely nanofluid and porous layers.

Rao and Barman [21] and Barman and Rao [22] investigated free convection heat transfer in wavy cavities under a different mode of heating and the effects of different types of nanofluids. They have considered geometry similar to that of Cheong et al. [1]. The obtained results explain the effect of wall waviness during natural convection through Darcian porous media. Tayebi [23] investigated entropy generation in a non-Darcian porous cavity with consideration of the local thermal non-equilibrium model. They found that local Nusselt numbers diminish with a rise in porosity due to the diminished effective thermal conductivity. Zidan et al. [24] investigated free convection in a porous, trapezium-shaped cavity with nanofluid, influenced by various parameters like Rayleigh, Hartmann, and Darcy numbers. They reported that adjusting these parameters can enhance cooling efficiency and the economic feasibility of using nanomaterials. Prince at al. [25] investigated the effects of magnetic field inclination and Reynolds numbers on heat and mass transfer in a trapezoidal enclosure with rotating cylinders using various nanofluids. They also developed an ANN model that predicts results with high accuracy, achieving over 96% accuracy in simulating heat and mass transfer outcomes.

From the above literature survey and the best of authors’ knowledge, the proposed model of numerical study of convective heat transfer in an open porous cavity with a partial heat source will be discussed for the first time.

Governing Equations

A cavity, having wavy vertical wall on the right side, is placed parallel to the horizon. The left vertical wall is considered the \(y-axis\), and the bottom wall is the \(x-axis\). The cavity has an opening on the top wall, and a heat source of length \(\epsilon H\) is placed on the left vertical wall, H being the height and width of the square cavity. The cavity is packed by porous media and pure fluids, both are in thermal equilibrium, Fig. 1 represents the domain of computation. The porous media is homogeneous, and the fluid flow is steady and laminar, so Darcy law is valid for the investigation. The fluid is incompressible and Newtonian, considering Boussinesq approximation for the body force (gravity (g)), governing equations in the dimensional coordinate are obtained following Cheong et al. [1] as:

$$\begin{aligned} u_x+v_y&=0 \end{aligned}$$
(1)
$$\begin{aligned} \left( u,v\right)&=K\mu ^{-1}\left( -P_x,-P_y+g\rho \beta (T-T_c)\right) \end{aligned}$$
(2)
$$\begin{aligned} \rho C_p\left( uT_x+vT_y\right)&=k\left( T_{xx}+T_{yy}\right) \end{aligned}$$
(3)

With boundary conditions:

$$\begin{aligned} \begin{aligned}&\text{ On } (0 \le x \le H, y=0): \psi =0,T_y=0 \\&\text{ On } (x=H-aH(1-\cos (2N\pi y/H)), 0 \le y \le H): \psi =0,T=0 \\&\text{ On, } (0 \le x \le 1, y=0): \psi _y=0,~\theta _y=0 \\&\text{ Left } \text{ wall, } (x=0): {\left\{ \begin{array}{ll} ( \frac{1-\epsilon }{2} \le y \le \frac{1+\epsilon }{2}): \psi =0,T_x=q^{''}/k \\ \text{ Otherwise: } \psi =0,\frac{\partial \theta }{\partial X}=0 \end{array}\right. }\\ \end{aligned} \end{aligned}$$
(4)

Here, \(u_x=\frac{\partial u}{\partial x}\), \(u_y=\frac{\partial u}{\partial y}\), etc. are partial derivatives with respected to spacial coordinates. The following parameters are applied to produce non-dimensional governing equations, \((X,Y)=\frac{(x,y)}{H}\), \((U,V)=\frac{(u,v)H}{\alpha }\), \(\theta =\frac{k(T-T_c)}{q^{''}H}\) and \(Ra=\frac{Kg\beta q^{''}H^2}{k\alpha \nu }\). Here (x, y), (u, v) and T represents dimensional coordinate system, velocity components and temperature respectively; (X, Y), (U, V) and \(\theta \) represents non-dimensional coordinate system, velocity components and temperature respectively.

The following non-dimensional governing equations in two dimension are obtained from:

$$\begin{aligned} \frac{\partial ^2 \psi }{\partial X^2}+\frac{\partial ^2 \psi }{\partial Y^2}= & -Ra\frac{\partial \theta }{\partial X} \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial ^2 \theta }{\partial X^2}+\frac{\partial ^2 \theta }{\partial Y^2}= & U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y} \end{aligned}$$
(6)

Subjected to the boundary conditions:

$$\begin{aligned} \begin{aligned}&\text{ Bottom } \text{ wall, } (0 \le X \le 1, Y=0): \psi =0,\frac{\partial \theta }{\partial Y}=0 \\&\text{ Right } \text{ wall, } (X=1-a(1-\cos (2N\pi Y)), 0 \le Y \le 1): \psi =0,\theta =0 \\&\text{ Top } \text{ wall, } (0 \le X \le 1, Y=0): \frac{\partial \psi }{\partial Y}=0,\frac{\partial \theta }{\partial Y}=0 \\&\text{ Left } \text{ wall, } (X=0): {\left\{ \begin{array}{ll} ( \frac{1-\epsilon }{2} \le Y \le \frac{1+\epsilon }{2}): \psi =0,\frac{\partial \theta }{\partial X}=-1 \\ \text{ Otherwise: } \psi =0,\frac{\partial \theta }{\partial X}=0 \end{array}\right. }\\ \end{aligned} \end{aligned}$$
(7)

Here the boundary condition for the opening is obtained from Sheremet et al. [3, 14].

The non-dimensional stream function is denoted by \(\psi \) and defined by \(((-\frac{\partial \psi }{\partial X},\frac{\partial \psi }{\partial Y})=(V,U))\). Also, \(q^{''},~\alpha ,~\beta ,~K,~k\) and \(\nu \) represent rate of heat flux, thermal diffusivity, thermal expansion coefficient, permeability of the porous medium, thermal conductivity and kinematic viscosity respectively.

Fig. 1
figure 1

A diagram representing the computation region

Full size image

The non-dimensional parameters Nusselt number \((Nu)=\frac{hH}{k}\) is calculated along the thermally active wall. Substituting \(h=\frac{q^{''}}{T-T_c}\) and incorporating non-dimensional parameters, the local Nusselt number is calculated. Further integrating over the heat generating wall, the average Nusselt number \((\overline{Nu})\) is calculated. After simplification, the Nu and \(\overline{Nu}\) are calculated as followed:

$$\begin{aligned} Nu(Y)&= \frac{1}{\theta }{\Big \vert }_{X=0}, \vert 2Y-1 \vert \le \epsilon \nonumber \\ \overline{Nu}&= \frac{1}{\epsilon }\int _0^\epsilon Nu(Y) dY \end{aligned}$$
(8)

Using an algebraic transformation, \(\xi =\frac{X}{1-a(1-cos(2N\pi Y))}\), \(\eta =Y\) the domain of computation is transformed into a square domain computation having \(0\le \xi , \eta \le 1\), and the Laplace operator \((\nabla \equiv \frac{\partial ^2}{\partial X^2}+\frac{\partial ^2}{\partial Y^2})\) is transformed into \(\nabla _{new}\equiv (\xi _X^2+\xi _Y^2)\frac{\partial ^2}{\partial \xi ^2}+2\xi _Y\frac{\partial ^2}{\partial \xi \partial \eta }+\frac{\partial ^2}{\partial \eta ^2}+\xi _{YY}\frac{\partial }{\partial \xi }\). So, the governing Eqs. (5) and (6) can be represented as:

$$\begin{aligned} \nabla _{new} \psi= & -Ra.\xi _X\frac{\partial \theta }{\partial \xi } \end{aligned}$$
(9)
$$\begin{aligned} \nabla _{new} \theta= & \xi _X {\Big (} \frac{\partial \psi }{\partial \eta }\frac{\partial \theta }{\partial \xi } - \frac{\partial \psi }{\partial \xi }\frac{\partial \theta }{\partial \eta } {\Big )} \end{aligned}$$
(10)

And corresponding boundary conditions,

$$\begin{aligned} \begin{aligned}&\text{ Bottom } \text{ wall, } (0\le \xi \le 1, \eta =0): \psi =0, \xi _Y\frac{\partial \theta }{\partial \xi }+\eta _Y\frac{\partial \theta }{\partial \xi }=0 \\&\text{ Right } \text{ wall, } (\xi =1,0\le \xi \le 1): \psi =0, \theta =0 \\&\text{ Top } \text{ wall, } (0\le \xi \le 1, \eta =1): \xi _Y\frac{\partial \psi }{\partial \xi }+\eta _Y\frac{\partial \psi }{\partial \xi }=0, \xi _Y\frac{\partial \theta }{\partial \xi }+\eta _Y\frac{\partial \theta }{\partial \xi }=0 \\&\text{ Left } \text{ wall, } (\xi =0): \psi =0, \xi _X\frac{\partial \theta }{\partial \xi }+\eta _X\frac{\partial \theta }{\partial \xi }= {\left\{ \begin{array}{ll} -1, \vert 2\eta -1 \vert \le \epsilon \\ 0, \text{ Otherwise } \end{array}\right. } \end{aligned} \end{aligned}$$
(11)

Using a reverse transformation, contour plots for streamline and isotherms are presented in the \(X-Y\) plane.

Validation of Numerical Method

An approximated result of the proposed model is calculated by in-house CFD code written in C-programming language. The transformed domain of computation is subdivided by a collocated grid (\(\psi \) and \(\theta \) are calculated at the same point) by taking uniform spacing in either direction. The derivatives are approximated by second-order accurate finite difference approximation, and the obtained system of equations is solved iteratively till \(max {\Big (}\frac{\sum \vert \theta ^{previous}-\theta ^{new}\vert }{\sum \vert \theta ^{new}\vert }\), \(\frac{\sum \vert \psi ^{previous}-\psi ^{new}\vert }{\sum \vert \psi ^{new}\vert }{\Big )}<\frac{1}{10^6}\) is achieved. A comprehensive details about the finite difference method for convection heat transfer in a wavy cavity is given in [21, 22].

The CFD code is verified and tested for grid independence, the code is tested for the convection in a square porous cavity by comparing the Nusselt number with previously published papers, presented in Table 1. Then the code is tested for convection in a open wavy porous cavity by comparing flow pattern and isotherms, which are presented in Fig. 2. Also, the Table 2 shows the effect of grid on average Nusselt number, the test is conducted for \(Ra=10^3\), \(N=5\), \(a=0.25\), and \(\epsilon =0.5\). The above comparisons and variation of average Nusselt number indicates that the in house code may be suitable for the investigation.

Table 1 Comparison of \(\overline{Nu}\) with previously published articles
Full size table
Fig. 2
figure 2

Streamlines and isotherms are compared with previously published results

Full size image
Table 2 Effect of mesh grid on \(\overline{Nu}\) at \(Ra=10^3\), \(N=5\), \(a=0.25\) and \(\epsilon =0.5\)
Full size table
Fig. 3
figure 3

Isotherms and Streamlines (solid lines) at \(Ra=10\) and \(\epsilon =0.25\)

Full size image
Fig. 4
figure 4

Isotherms and Streamlines (solid lines) at \(Ra=10\) and \(\epsilon =0.5\)

Full size image
Fig. 5
figure 5

Isotherms and Streamlines (solid lines) at \(Ra=10\) and \(\epsilon =1.0\)

Full size image
Fig. 6
figure 6

Isotherms and Streamlines (solid lines) at \(Ra=10^2\) and \(\epsilon =0.25\)

Full size image
Fig. 7
figure 7

Isotherms and Streamlines (solid lines) at \(Ra=10^2\) and \(\epsilon =0.5\)

Full size image
Fig. 8
figure 8

Isotherms and Streamlines (solid lines) at \(Ra=10^2\) and \(\epsilon =1.0\)

Full size image
Fig. 9
figure 9

Isotherms and Streamlines (solid lines) at \(Ra=10^3\) and \(\epsilon =0.25\)

Full size image
Fig. 10
figure 10

Isotherms and Streamlines (solid lines) at \(Ra=10^3\) and \(\epsilon =0.5\)

Full size image
Fig. 11
figure 11

Isotherms and Streamlines (solid lines) at \(Ra=10^3\) and \(\epsilon =1.0\)

Full size image

Results and Discussion

In this numerical investigation the obtained results for the governing parameters, such as Ra Ra, \(\epsilon \), N and a are presented. The fluid flow and heat transfer in a top-open wavy cavity are driven by buoyancy forces resulting from the temperature difference between the heat source and the cold wavy wall.

The isotherms and streamlines for a range of governing parameter values are presented in the Figs. 3, 4, 5, 6, 7, 8, 9, 10 and 11, where streamlines are presented as solid lines and the colour gradients represent isotherms. In this process of free convection, the fluid near the heat source becomes less dense and exits the cavity through the left side of the open wall. Simultaneously, cold fluid enters the cavity along the wavy wall, moving toward the left wall, resulting in a flow within the wavy porous cavity. The temperature variation between the right wavy wall and the heat source is observed, with isotherms (represented as color gradients) spread between the adiabatic walls and the thermally active wall.

In the Figs. 3, 4 and 5 streamlines and isotherm for the case \(Ra=10\) are presented. At \(Ra=10\), the length of heat source and wall waviness impact the flow pattern, manifestation of a circulation zone at the majority of free space inside cavity and small eddies covering undulations are obvious. The pattern of circulation inside the cavity depends on wall waviness. The increment in wall waviness (growth in a and N) shrinks effective free space inside wavy cavity. For \(Ra=10\), buoyancy force is not so strong that fluid the cavity leaves, resulting a circulation at the most of free spaces of the porous cavity. Although, for \(N=1\) with \(0.05\le a\le 0.25\) and \(a=0.05\) with \(1\le N\le 5\), all streamlines are semi circular. The circulation inside the wavy cavity is not manifested when \(\epsilon =1\), as a larger part of thermally active wall generates sufficient amount buoyancy force that fluid penetrates the cavity leaves totally. The flow strength \((max(\vert \Psi \vert ))\) of at \(Ra=10\) increases with the augmentation of \(\epsilon \) from 0.25 to 1. The values are observed to be \(max(\vert \Psi \vert )_{\epsilon =0.25}=0.237<\) \(max(\vert \Psi \vert )_{\epsilon =0.50}=0.451<\) \(max(\vert \Psi \vert )_{\epsilon =1.0}=0.78\).

The isotherms are semi circular covering close to heat source for \(\epsilon <1\), and the lines are parallel to thermally active wall for \(\epsilon =1\). The results show that propagation of heat is prominent close to the top wall than the bottom wall. In this case, the maximum of dimensionless temperature \((max(\vert \Theta \vert ))\) inside the wavy cavity is produced at heat source. Also, it is observed that the a lager heat source results significantly higher amount of \((max(\vert \Theta \vert ))\) and the numerical values of \(max(\vert \Theta \vert )\) at \(Ra=10\) is as follows \(max(\vert \Theta \vert )_{\epsilon =0.25}=0.319<\) \(max(\vert \Theta \vert )_{\epsilon =0.50}=0.5006<\) \(max(\vert \Theta \vert )_{\epsilon =1.0}=0.744\).

For Ra at \(10^2\), the isotherms and streamlines, presented in Figs. 6, 7, and 8, has a similar patterns to the results presented for \(Ra=10\). With a higher Ra gives raise to the buoyancy force inside the cavity, resulting an augmentation of flow strength and maximum temperature. Interestingly, a circulation at the center of free space of the cavity is observed only when \(a=0.25\). The strong flow makes isotherms tilted towards top right corner of the wavy cavity.

As the Ra is increased from 10 to \(10^2\), the flow strength is augmented nearly \(77.4\%\) having flow strength of \(max(\vert \Psi \vert )_{Ra=10^2}=3.452\). Similarly, the increased convection process assists lowering the maximum temperature of the heat flux. A reduction in \(max(\vert \Theta \vert )\) is reported for \(Ra=10^2\) than \(Ra=10\), and the reduction is nearly \(90.8\%\) having \(max(\vert \Theta \vert )_{Ra=10^2}=0.390\).

Further, observing the streamlines and isotherms from Figs. 9, 10, 11 for \(Ra=10^3\) it is found that the flow strength is increased due to significantly higher buoyancy force. The fluid circulations are not manifested inside the most of the free spaces of the open cavity. Energy taping eddies are observed in between undulated areas only. With \(Ra=10^3\) the maximum flow strength (\(max(\vert \Psi \vert )=10.083\)) is observed for \(\epsilon =1\). In this case the outgoing fluid transfers most of the heat towards top left corner of the cavity, so isotherms are mostly clustered close to the heat flux and upper half of the cavity. Further reduction in maximum temperature is reported with the incremental Ra. The value of \(max(\vert \Theta \vert )=0.17201\) is observed for this case having \(\epsilon =1\).

For a fixed \(\epsilon \) and Ra, the wall waviness resists fluid flow inside the open wavy cavity, and \(max(\vert \Psi \vert )\) gets reduced as wall waviness increases. But, for a fixed \(\epsilon \) and \(Ra<10^3\), \((max(\vert \Theta \vert ))\) get reduced as wall waviness increases, although it gets increased with increasing wall waviness at \(Ra=10^3\).

The non-dimensional heat transfer parameter Nu is inverse to the dimensionless temperature along the heat source, so higher Nu denotes less temperature along with the heat source. Figures 12, 13 and 14 illustrates the Nu values along heat source for \(Ra=10,10^2\) and \(10^3\) respectively. The impact of wall waviness on Nu is attentive at \(Ra=10\), and it reduces as Ra increases to \(10^3\). The Nu along the heat source is maximum at the corners of heat source for \(Ra=10\) and \(\epsilon <1\). At \(Ra=10\) (Fig. 12), it is observed that increasing a the local heat transfer increases significantly; the increment of N also enhances the heat transfer. With a higher Ra, the circulations are not manifested as the wall waviness increases. So, the change in local heat transfer due to wall waviness is in the opposite direction for \(Ra=10^3\); in this case, the local Nusselt number decreases as wall waviness increases.

Fig. 12
figure 12

Convection along heat source at \(Ra=10\)

Full size image
Fig. 13
figure 13

Convection along heat source at \(Ra=10^2\)

Full size image
Fig. 14
figure 14

Convection along heat source at \(Ra=10^3\)

Full size image

The average Nusselt number \((\overline{Nu})\) for all the cases taken in consideration are presented in the Table 3. From the table, it is clear that waviness of wall enhances overall heat transfer inside the cavity at \(Ra<10^3\). At \(Ra=10\) or \(10^3\) for a fixed \(\epsilon \) the increment a and N enhances convection process inside the cavity, for example for \(Ra=10^3\), \(\epsilon =0.5\) the \(\overline{Nu}\) value admits \(\overline{Nu}=4.227\) at \(a=0.25, N=5\) and \(\overline{Nu}=4.403\) at \(a=0.05, N=1\). But at \(Ra=10^3\) the \(\overline{Nu}\) decreases due to wall waviness.

Table 3 Value of \(\overline{Nu}\) in different cases
Full size table

Conclusions

The investigation of natural convection in an open porous enclosure having a wavy wall leads to the conclusions as follows:

  • The flow strength is proportional to Ra or \(\epsilon \) keeping other parameters fixed in an open wavy porous cavity.

  • The maximum temperature of heat source is reduced with increasing wall waviness for \(Ra<10^3\) at a fixed \(\epsilon \), and get increased as wall waviness increases at \(Ra=10^3\).

  • The average Nusselt number suggests that for a fixed \(\epsilon \), the wall waviness increases convection in the wavy cavity at \(Ra<10^3\), and at \(Ra=10^3\) the convection process is reduced with increasing a and N in an open porous cavity.

  • An increasing length of heat flux reduces the average Nusselt number. For an open wavy porous cavity, the \(\overline{Nu}\) is decreased about \(36.8\%\) for changing \(\epsilon =0.25\) to 1 with \(Ra=10^3,~N=3,~a=0.15\).