1 Introduction

There is an extensive and growing literature on transport phenomena found in disordered media, from amorphous semiconductors, to aquifers, to living cells. The nature and type of disorder in these systems varies considerably, but if it is sufficiently extensive, there are global features—the so-called “anomalous” transport behavior—that are described by the equation we solve in this paper. The dynamic stochastic processes in these media are often centered on random walk models, which are characterized by the probability of the walker steps or rates or transitions. It is the distribution of these transitions \(\psi (t)\) that is our focus and leads to the aforementioned global features.

One system that is of key importance in environmental research pertains to groundwater aquifers, which are disordered due to the porous structure, enormous permeability variation, presence of fractures, and chemical heterogeneity. In aquifers, we need to know how contaminant plumes advance: In particular, early time arrivals are related to pollution of water resources, while late time arrivals are related to remediation activities. Most past modeling efforts (Berkowitz et al. 2006; Eggleston and Rojstaczer 1998) have used the advection–dispersion equation (ADE) in efforts to quantify ubiquitous non-Fickian (or anomalous) transport. We have shown that a \(\psi (t)\)-based random walk is necessary to explain anomalous behavior, in the framework of a continuous time random walk (CTRW). We outline our method, but first, we add an historical note.

It is already 110 years ago that Albert Einstein published his now famous paper on Brownian motion (Einstein 1905). His analysis involved a recursion relation, which described a simple random walk at a uniform step rate. An expansion led to the diffusion equation, and a solution showed for the first time that the displacement (rms) \(\sigma \) of the Brownian particle is proportional to \(\sqrt{t}\) and not equal to vt as was being assumed in those years. By using the t-dependence, the experimentalists were puzzled by the need to invoke a time-dependent velocity v that increased as \(t\rightarrow 0\) (i.e., \(\sigma =c\sqrt{t}\), so forcing vt to achieve the same \(\sigma \) required \(v=c/\sqrt{t}\), with v increasing as \(t\rightarrow 0)\). Einstein investigated systems with one effective rate of transitions. The different time dependence of the particle displacement (\(\sqrt{t})\), as now commonly understood, is due to the nature of diffusive motion. Seventy years later, observations of the transit time \(\tau _{r}\) of electrons in disordered semiconductors presented a similar puzzle. The electron mobility (velocity per unit electric field), considered to be an intrinsic property of the material, was found to depend on sample length, electric field etc. (any variable that changes the duration of the experiment). Again the problem was traced to using the wrong relationship for the mean displacement, l, of the electron packet. Instead of \(l=vt\), it was discovered that \(l\;\alpha \;t^{\beta } \quad (0<\beta <1)\) (Scher and Montroll 1975). What is the origin of this anomalous behavior? In contrast to previous work for this case, the difference is ascribed to a wide distribution of rates due to the disorder of the system.

This result amounts to a generalization of what Einstein used, wherein the time between steps is a random variable described by a PDF, \(\psi ( s_{i} , t )\), which couples the spatial displacement \(s_{i}\) and time t of the site transfer. This PDF is key; it is the core of the equation for the probability \(R( s_{i} , t )\) to just arrive at the site location \(s_{i}\) at time t:

$$\begin{aligned} R( s_{i} ,t )-\sum _{s_{i} ^{\prime }} {\int \limits _{0}^{t} {\psi ( s_{i} -s_{i}^{\prime },t-{t}' )} } R( s_{i}^{\prime },{t}' )d{t}'=\delta _{{{s}_{i}} ,0} \delta ( t-0^{+} ) \end{aligned}$$
(1)

where tensor notation is used, i.e., a lowercase index denoted component, a “,” followed by a lowercase index is the covariant derivative and a repeated lowercase index implies summation.

The sum over the space, time transitions of all the paths leading to \(s_{i}\), t now contains an integral over time (with the form of a time convolution). Equation (1) defines the CTRW. The usefulness for our class of problems is determined by a related function—the probability \(P( s_{i}, t )\) to be found at the site location \(s_{i}\) at time t:

$$\begin{aligned} P( s_{i} ,t )= & {} \int \limits _{0}^{t} {\varPsi ( t-t' )} R( s_{i} ,t' )d{t}',\, \nonumber \\ \varPsi (t)= & {} 1-\int \limits _{0}^{t} \psi ( {t}' )d{t}',\;\psi ( t )\equiv \sum _{{s}_{i} } {\psi ( s_{i} ,t )} \end{aligned}$$
(2)

where \(\varPsi ( t )\) is the probability for a walker to remain on a site until time t. We outline the development of the CTRW from (1) to a partial differential equation (PDE) transport equation continuous in space and time; further details can be found in, e.g., Berkowitz et al. (2006).

We transform (1) into a generalized master equation (GME), which is completely equivalent to (1)

$$\begin{aligned} \frac{\partial P\left( {s_i ,t} \right) }{\partial t}= & {} -\sum _{s_i ^{\prime }} {\int \limits _0^t {\phi \left( {s_i -s_i ^{\prime },t-{t}'} \right) P} \left( {s_i ,{t}'} \right) d{t}'}\nonumber \\&+\sum _{s_i ^{\prime }} {\int \limits _0^t {\phi \left( {s_i -s_i ^{\prime },t-{t}'} \right) P} \left( {s_i ^{\prime },{t}'} \right) d{t}'} \end{aligned}$$
(3)

and \(\tilde{\phi }( s_{i} ,u )={u\tilde{\psi }( s_{i} ,u )}/{( {1-\tilde{\psi }( u )} )}\) is the Laplace Transform (LT) of \(\phi ( s_{i} ,t )\).

It is expedient at this point to introduce \(\psi ( s_{i} ,t )=p( s_{i} )\psi ( t )\), which is an excellent approximation for compact \(p( s_{i} )\) (Berkowitz et al. 2006). We assume the limit of a continuum instead of a discrete space [i.e., the sums in (3) are replaced by integrals], and change the notation \(s_{i}\) to \(x_{i}\) to conform to the continuum in what follows. We develop a Taylor expansion of the function \(P( s_{i}', t' )\), (3), about the point \(s_{i}\), which causes a separation between the advective and dispersive terms. The \(P( s_{i} , t )\) is the normalized concentration, and we switch notation, replacing \(P( s_{i}, t )\) by \(C( x_{i}, t)\), to be in conformity with Sect. 2, to arrive at

$$\begin{aligned} \frac{\partial C\left( {x_i ,t} \right) }{\partial t}= & {} -\int \limits _0^t {M\left( {t-\tau } \right) \left\{ {v_i C_{,i} \left( {x_i ,\tau } \right) -\left[ {D_{ij} C_{,j} \left( {x_i ,\tau } \right) } \right] _{,i} } \right\} } d\tau \end{aligned}$$
(4)
$$\begin{aligned} u\tilde{C}\left( {x_i ,u} \right) -C_0 \left( {x_i } \right)= & {} -\tilde{M}\left( u \right) \left\{ {v_i \tilde{C}_{,i} \left( {x_i ,u} \right) -\left[ {D_{ij} \tilde{C}_{,j} \left( {x_i ,u} \right) } \right] _{,i} } \right\} \end{aligned}$$
(5)

where

$$\begin{aligned} v_i =\frac{1}{\bar{{t}}}\int \limits _V {p(x_i )x_i {d}V} , D_{ij} =\frac{1}{\bar{{t}}}\int \limits _V {\frac{1}{2}p(x_i )x_i x_j {d}V} , \end{aligned}$$
(6)

and

$$\begin{aligned} \tilde{M}\left( u \right) \equiv \bar{{t}}u\frac{\tilde{\psi }(u)}{1-\tilde{\psi }(u)} \end{aligned}$$
(7)

is a “memory function,” which plays a key role in our finite element method (FEM) solution of (4), \(\bar{t}\) is a characteristic time, V is the domain volume and (5) is the LT of (4), which appears in Sect. 2.

The CTRW model is a broad one. A number of models in use to describe anomalous transport, e.g., multiple rate mass transfer (MRMT, e.g., Haggerty and Gorelick 1995; Carrera et al. 1998) and some fractional PDEs (e.g., Metzler and Klafter 2000), are subsets of CTRW (e.g., Berkowitz et al. 2006 and references therein; Metzler and Klafter 2000; Silva et al. 2009). In many formulations of MRMT, a different definition of a “memory function,” expressed as a sum of exponentials, is applied in a particular form of governing equation; this function is distinct from the M(t) appearing in the convolution Eq. (4). The key purpose of this paper is to develop an accurate representation of M(t) that enables efficient numerical solution of (4) and avoids dealing repeatedly with the entire time history at each iteration of the FEM method.

The \(\tilde{C}( x_{i}, u )\) can now be expressed in terms of \(\tilde{C}_{1} ( x_{i}, u )\), which is the solution of (5) for \(\tilde{M}( u )=1\) (the ADE) and the same boundary conditions as \(\tilde{C}( x_{i}, u )\). In Dentz et al. (2004), the solution is listed for \(\kappa =1,2,3\) (where \(\kappa \) is the dimension). For our implementation of CTRW, it suffices to show the 1D solution:

$$\begin{aligned} \tilde{C}\left( {x_i ,u} \right) =\frac{1}{\tilde{M}\left( u \right) }\tilde{C}_1 \left( {x_i ,\frac{u}{\tilde{M}\left( u \right) }} \right) \end{aligned}$$
(8)

Specifically,

$$\begin{aligned} \tilde{C}\left( {x_1 ,u} \right) =\frac{\exp \left[ {-\frac{v}{2D}\left\{ {\sqrt{x_1^2 +4x_1^2 \frac{uD}{\tilde{M}\left( u \right) v^{2}}}-x_1 } \right\} } \right] }{\tilde{M}\left( u \right) v\sqrt{1+4\frac{uD}{\tilde{M}\left( u \right) v^{2}}}} \end{aligned}$$
(9)

The next step is an essential one, namely—the choice of \(\psi ( t )\) . To enable consideration of both non-Fickian and Fickian transport behaviors, we employ a truncated power law (TPL):

$$\begin{aligned} \psi \left( t \right) =N\frac{\exp \left( {-t/{t_2 }} \right) }{\left( {1+t/{t_1 }} \right) ^{1+\beta }} \end{aligned}$$
(10)

with the normalization constant

$$\begin{aligned} N=\left\{ {t_1 \tau _2^{-\beta } \exp \left( {\tau _2^{-1} } \right) \varGamma \left( {-\beta ,\tau _2^{-1} } \right) } \right\} ^{-1} \end{aligned}$$
(11)

where \(\tau _{2} \equiv t_{2} /t_{1}\) and \(\varGamma ( a, x )\) is the incomplete gamma function (Abramowitz and Stegun 1970). The power law factor in (10) with \(0<\beta <2\) characterizes the disorder of the system and gives rise to non-Fickian transport (it is the same \(\beta \) as in \(l\;\alpha \;t^{\beta })\). The exponential factor marks the time \(( t_{2} )\) for the transition to Fickian transport. One can now see that a choice for \(\bar{t}\) above is \(t_{1}\) in (10), which is the time for the onset of power law behavior.

The LT of the truncated power law (10) is given by

$$\begin{aligned} \tilde{\psi }\left( u \right) =\left( {1+\tau _2 ut_1 } \right) ^{\beta }\exp \left( {t_1 u} \right) \frac{\varGamma \left( {-\beta ,\tau _2^{-1} +t_1 u} \right) }{\varGamma \left( {-\beta ,\tau _2^{-1} } \right) } \end{aligned}$$
(12)

and is the building block of (7), the memory function. The basis of the calculations of the breakthrough curves (BTCs) is (9), (12) and (7). They are contained in a CTRW Toolbox (Cortis and Berkowitz 2005), along with a numerical inverse LT, for free use.

The solutions using the CTRW Toolbox have proven highly effective in comparison with experiments (Berkowitz et al. 2006; Cortis and Berkowitz 2005) on chemical transport in geological porous media, which have focused mostly on laboratory column tests constructed to simulate natural heterogeneity. A validation of the Toolbox solution is the excellent agreement with the method of particle tracking (PT) (Dentz et al. 2004). The PT uses the TPL \(\psi (t)\) (10) to advance large groups of particles to obtain numerical stability directly in the time domain. This body of work has clearly established the connection between disorder and its representation by a power law in \(\psi (t)\) and the occurrence of non-Fickian behavior. One limitation that has arisen in the Toolbox solution, however, is the occasional instabilities in executing the inverse LT of (9) for certain parameter ranges. In principle, the FEM solution of (4) can avoid use of the inverse LT of (9). We will expand on this point in our concluding remarks. Our present method uses the Toolbox to obtain the optimal parameters of M(t), v, and D. The essential element in obtaining a numerical solution of (4) is to limit the recursion steps of the discretization of time. One has to work with special forms of M(t) to achieve this limitation. This is accomplished with a sum of exponentials.

Sum-of-exponentials approximations have been applied to increase the speed of evaluation of convolution integrals in many applications. In fact, they have been used to accelerate the evaluation of heat potentials (Greengard and Lin 2000; Greengard and Strain 1990; Jiang et al. 2015) and the evaluation of exact, non-reflecting boundary conditions for the wave, Schrodinger and heat equations (Alpert et al. 2000; Jiang and Greengard 2004, 2008). A recent paper also discussed its application to the evaluation of fractional integrals (Li 2010). Viscoelasticity is another field in which such models are used, e.g., Ben-Zvi (1990) and references therein.

In Sect. 2, aspects of (4) in the time domain and (5) in the Laplace domain are discussed along with the boundary conditions, which are more flexible in the FEM solution. In Sect. 3, we detail the spatial discretization of the FEM, which is straightforward, and in Sect. 4, the more exacting time discretization is detailed. The boundary conditions are presented in Sect. 6. Some numerical issues are briefly mentioned in Sect. 7. Validation of the solution is then demonstrated (Sect. 8), and the convergence characteristics of the scheme are assessed in Sect. 9. We conclude with a number of notes and recommendations. Overall, numerical solution of the transport equation (4) with its potential to incorporate further algorithms to represent M(t) is an important addition to the framework of modeling phenomena in disordered systems.

2 The CTRW Transport Equation

The general, time-dependent, equation for the concentration distribution in three dimensions in an anisotropic medium may be expressed in the Laplace domain as

$$\begin{aligned} u\tilde{C}\left( {x_i ,u} \right) -C_0 \left( {x_i } \right) +\tilde{j}_{i,i} \left( {x_i ,u} \right) =\tilde{S}\left( {x_i ,u} \right) \end{aligned}$$
(13)

where tensor notation is used, C is the concentration, u is the Laplace variable, \(x_{i}\) is the i-th coordinate, \(j_{i}\) is the flux vector, S is source, \(``\sim \)” denotes transformed to the u domain, subscript 0 denotes initial conditions (IC) and “, ” indicates covariant derivative. The flux vector is defined by

$$\begin{aligned} \tilde{j}_i \left( {x_i ,u} \right) \,=\,\tilde{M}(u)\left[ {\tilde{q}_i^c (x_i ,u)+\tilde{q}_i^d (x_i ,u)} \right] \end{aligned}$$
(14)

where \(q^{c}\) and \(q^{d}\) are the advection and the dispersion terms, respectively, defined by

$$\begin{aligned} \tilde{q}_i^c (x_i ,u)\doteq & {} \tilde{v}_i (x_i ,u)\tilde{C}(x_i ,u), \end{aligned}$$
(15)
$$\begin{aligned} \tilde{q}_i^d (x_i ,u)\doteq & {} -\tilde{D}_{ij} (x_i ,u)\tilde{C}_{,j} (x_i ,u), \end{aligned}$$
(16)

\(v_{i}\) is the velocity vector, \(D_{ij}\) is the dispersion tensor [both defined in (6)] and M is the memory function [(defined in (7)]. In the following, we also use the mass flux \(\tilde{q}_i \left( {x_i ,u} \right) \,\dot{=}\,\tilde{{q}}_{i}^{c} {(x}_{i} {, u)}+\tilde{{q}}_{i}^{d}{(x}_{i} {, u)}\) for short.

In the time domain, the \((u\tilde{C}-C_{0} )\) term becomes \(\dot{C}(t)\), and multiplication of two u-functions, say \(\tilde{f}(u)\tilde{g}(u)\), becomes a time convolution:

$$\begin{aligned} \int \limits _0^t {f(t-\tau )g(\tau )d\tau }\, \dot{=}\,f(t)\otimes g(t) \end{aligned}$$
(17)

Therefore, (13) may be written in the time domain as

$$\begin{aligned} \dot{C}\left( {x_i ,t} \right) +j_{i,i} \left( {x_i ,t} \right) =S\left( {x_i ,t} \right) \end{aligned}$$
(18)

and (14) becomes

$$\begin{aligned} j_i \left( {x_i ,t} \right) =M(t)\otimes \left[ {q_i^c \left( {x_i ,t} \right) +q_i^d \left( {x_i ,t} \right) } \right] \end{aligned}$$
(19)

where t is time and “\(\cdot \)” denotes time derivative.

The following types of boundary conditions (BCs) are accounted for:

  • Prescribed boundary concentration (Dirichlet):

    $$\begin{aligned} C(x_i ,t)=\bar{{C}}(t)\quad on \,\varGamma ^{D} \end{aligned}$$
    (20)

  • Prescribed boundary derivative term, \(q^{d}\) (Neumann):

    $$\begin{aligned} n_i q_i^{(d)} (x_i ,t)=\bar{{q}}(t)\quad on\, \varGamma ^{N} \end{aligned}$$
    (21)

  • Prescribed boundary flux (Robin):

    $$\begin{aligned} n_i j_i (x_i ,t)=\bar{{j}}(t)\quad on \,\varGamma ^{R} \end{aligned}$$
    (22)

where overbar denotes “prescribed,” the domain boundary \(\varGamma \) is entirely covered by the non-overlapping parts \(\varGamma ^{D}\), \(\varGamma ^{N}\) and \(\varGamma ^{R}\) and \(n_{i}\) is its outwards unit normal. In the Laplace domain, similar expressions prevail with u replacing t.

Note: The advection–dispersion equation (ADE) is recovered when \(\tilde{M}(u)=1\), leading to \(M(t) = \delta (t)\) and therefore, for the ADE:

$$\begin{aligned} j_i (x_i ,t)=q_i^c (x_i ,t)+q_i^d (x_i ,t) \end{aligned}$$
(23)

3 Spatial Discretization by the Finite Element Method (FEM)

We begin with spatial semi-discretization of (13) by the finite element method (FEM). The domain, V, is discretized by a grid consisting of non-overlapping (non-uniform in general) elements.

The basic FEM assumption is that the concentration \(C( x_{i}, t )\) within an element is related to its nodal values \(C_{J} ( t )\)—referred to as degrees of freedom (DOFs)—by assumed functions, \(N_{J} ( x )\), called shape functions, which are local and continuous across elements faces:

$$\begin{aligned} C(x_i ,t)=N_J (x_i )\,C_J (t), \hbox {or equivalently, } \tilde{C}(x_i ,u)=N_J (x_i )\,\tilde{C}_J (u) \end{aligned}$$
(24)

where capital indices refer to nodal indices (lowercase indices denote spatial dimension as before) and repeated index indicates summation on all the nodes belonging to the element. In what follows, the “\(\sim \),” the \(x_{i}\) and the t (or u) dependence will be omitted for brevity.

Applying (24) for the flux \(j_{i}\) defined in (14) yields

$$\begin{aligned} j_{i} =M( v_{i} N_{J} -D_{ij} N_{J,j} )C_{J} \end{aligned}$$
(25)

and the initial condition (IC), \(C_{0}\), within an element is related to the DOFs IC through

$$\begin{aligned} C_0 =N_{J} \, C_{0J} \end{aligned}$$
(26)

We further assume that the source term distribution within an element is also of the same form

$$\begin{aligned} S=N_{J} \,S_{J} \end{aligned}$$
(27)

The FEM derivation details are quite standard, and are given in Appendix 1. The spatial semi-discretization results appear in (76)–(85).

4 Temporal Discretization

We now apply a time discretization, where (starting from the initial conditions) we advance the solution from time \(t^{n}\) to \(t^{n+1}=t^{n}+\varDelta t\) (superscripts are the number of the time step).

4.1 Numerical Convolution Treatment

The convolution term in (83) (see “Appendix 1”) requires special care to avoid storing all of the time steps results. Rather, we will approximate it such that only the former time step results are needed. The discrete form of (82) (see “Appendix 1”) is

$$\begin{aligned} I_{J}^{n} =\int \limits _{0}^{{t}^{n}} M(t^{n}-\tau ) C_{J} ( \tau )d\tau \end{aligned}$$
(28)

Therefore,

$$\begin{aligned} I_{J}^{n+1} =\int \limits _{0}^{{t}^{n+1}} M(t^{n+1}-\tau ) C_{J} ( \tau )d\tau =\int \limits _{0}^{{t}^{n}} M(t^{n+1}-\tau ) C_{J} ( \tau )d\tau +\int \limits _{{t}^{n}}^{{t}^{n+1}} M(t^{n+1}-\tau ) C_{J} ( \tau )d\tau \end{aligned}$$
(29)

A specific choice for M(t) is now made: M(t) is approximated by the P-terms series

$$\begin{aligned} M(t)\cong a_{0} \delta ( t )+\sum _{p=1}^{P} a_{p} e^{{-b_{p} t}} \,\dot{=}\,a_{0} \delta ( t )+\sum _{p=1}^{P} M_{p} (t) \end{aligned}$$
(30)

This model (also known as a “Prony series” or “sum-of-poles” in the literature; see Appendix 2 for further details) is referred to as the EXP model in the remainder of this study.

The last term in (29), termed \(K_{J}^{n+1}\), is approximated by assuming that \(C_{J} (t)\) is linear in \(\tau \) within each time step. This may be written in parametric form as

$$\begin{aligned} \tau= & {} \omega t^{n+1}+\left( {1-\omega } \right) t^{n}, \end{aligned}$$
(31)
$$\begin{aligned} C_J \left( \tau \right)\cong & {} \omega C_J^{n+1} +\left( {1-\omega } \right) C_J^n \end{aligned}$$
(32)

where \(\omega \) is a time step interval parameter between 0 and 1.

Therefore,

$$\begin{aligned} K_J^{n+1}\doteq & {} \int \limits _{t^{n}}^{t^{n+1}} {M(t^{n+1}-\tau )} C_J \left( \tau \right) d\tau \nonumber \\&\quad \cong a_0 C_J^{n+1} +\sum _{p=1}^P {\int \limits _{\omega =0}^{\omega =1} {a_p e^{-b_p \varDelta t\left( {1-\omega } \right) }\left[ {\omega C_J^{n+1} +\left( {1-\omega } \right) C_J^n } \right] \varDelta td\omega } } \end{aligned}$$
(33)

The integral may be calculated analytically, and after rearrangement, we finally obtain

$$\begin{aligned} K_J^{n+1} \cong a_0 C_J^n +\sum _{p=1}^P {\left( {\gamma _p^n C_J^n +\gamma _p^{n+1} C_J^{n+1} } \right) } \end{aligned}$$
(34)

where

$$\begin{aligned} \gamma _{p}^{n}= & {} \gamma \left[ {a_{p} -\left( {b_{p} \varDelta t+1} \right) M_p \left( {\varDelta t} \right) } \right] \end{aligned}$$
(35)
$$\begin{aligned} \gamma _{p}^{n+1}= & {} \gamma \left[ {a_{p} \left( {b_{p} \varDelta t-1} \right) +M_p \left( {\varDelta t} \right) } \right] \end{aligned}$$
(36)
$$\begin{aligned} \gamma= & {} \frac{1}{b_{p}^{2} \varDelta t} \end{aligned}$$
(37)

Note that, in the first attempt, \(K_{J}^{n+1}\) was approximated by the trapezoidal rule quadrature:

$$\begin{aligned} K_{J}^{n+1} \cong \frac{\varDelta t}{2}\left[ {M(\varDelta t)C_{J}^{n} +M(0)C_{J}^{n+1} } \right] \end{aligned}$$
(38)

This approximation is of lower order in \(\varDelta t\), and the error accumulation limited the time step to about 100 times smaller than in the above approximation.

Using (30) in (28)

$$\begin{aligned} I_{J}^{n}= & {} \int \limits _{0}^{{t}^{n}} {\left[ {a_{0} \delta \left( {{t}^{n}-\tau } \right) +\sum _{p=1}^{P} {M_{p} } (t^{n}-\tau )} \right] C_{J} (\tau )d\tau }\nonumber \\= & {} a_{0} C_{J}^{n} +\sum _{p=1}^{P} {\int \limits _{0}^{{t}^{n}} {a_{p} } e^{{-b}_{p} (t^{n}-\tau )}C_{J} (\tau )d\tau } \,\dot{=}\,a_{0} C_{J}^{n} +\sum _{p=1}^{P} {I_{Jp}^{n} } \end{aligned}$$
(39)

Substituting (30) to (29) and using (34) and (39), the recursion expression becomes

$$\begin{aligned} I_{J}^{n+1}\cong & {} \int \limits _{0}^{{t}^{n}} {a_{0} \delta \left( {{t}^{n+1}-\tau } \right) } C_{J} \left( \tau \right) d\tau \nonumber \\&+\sum _{p=1}^{P} {e^{{-b}_{p} \varDelta t}\int \limits _{0}^{{t}^{n}} {a_{p} e^{{-b}_{p} t^{n}}C_{J} \left( \tau \right) d\tau } } +K_{J}^{n+1} \nonumber \\= & {} \sum _{p=1}^{P} {e^{{-b}_{p} \varDelta t}I_{Jp}^{n} } +K_{J}^{n+1} \end{aligned}$$
(40)

Therefore, to calculate \(C_{J}^{n+1}\), we require only \(C_{J}^{n}\)and \(I_{Jp}^{n}\) from the former step (and, of course, the Prony parameters, the geometry, the velocity and the dispersion, the initial conditions and the grid).

4.2 Implicit Scheme

The implicit time discretization is again quite standard, and details are given in “Appendix 1,” (86)–(93).

5 One-Dimensional Linear Element

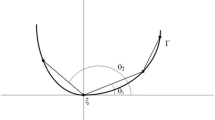
In 1D, there are single components of \(v_{i}\), \(D_{ij}\), \(n_{i}\), \(q_{i}\) and \(j_{i}\), hereafter denoted v, D, n, q and j for brevity. In the present implementation, we use a linear element that has two nodes, with coordinates \(x_{1}\) and \(x_{2}\) . We employ a normalized coordinate \(\xi \)

$$\begin{aligned} \xi =\frac{2}{h}\left( {x-x_2 } \right) +1 \end{aligned}$$
(41)

where

$$\begin{aligned} h=x_2 -x_1 \end{aligned}$$
(42)

such that \(\xi =-1\) at \(x_{1}\) and \(\xi =+1\) at \(x_{2}\) .

The shape functions of this element are

$$\begin{aligned} N_1 (\xi )= & {} (1-\xi )/2, \end{aligned}$$
(43)
$$\begin{aligned} N_2 (\xi )= & {} (1+\xi )/2, \end{aligned}$$
(44)

such that at \(x_{1}\), \(N_{1} (\xi =-1)=1\), \(N_{2} (\xi =-1)=0\) and at \(x_{2}\), \(N_{1} (\xi =+1)=0\), \(N_{2} (\xi =+1)=1\) .

The volume element, dV, is

$$\begin{aligned} {d}V=s\;{{d}}x=s\;h\;{{d}}\xi /2 \end{aligned}$$
(45)

where s is the element cross-sectional area (normal to x).

Using (41)–(45) in the general definitions (77)–(81) (“Appendix 1”) results in

$$\begin{aligned} A_{ IJ}= & {} s\frac{h}{6}\left[ {{\begin{array}{ll} 2&{} \quad 1 \\ 1&{} \quad 2 \\ \end{array} }} \right] \end{aligned}$$
(46)
$$\begin{aligned} L_{ IJ}= & {} s\frac{v}{2}\left[ {{\begin{array}{ll} - 1&{} \quad - 1 \\ + 1&{} \quad + 1 \\ \end{array} }} \right] \end{aligned}$$
(47)
$$\begin{aligned} P_{ IJ}= & {} s\frac{D}{h}\left[ {{\begin{array}{ll} +1&{} \quad -1 \\ -1&{} \quad +1 \\ \end{array} }} \right] \end{aligned}$$
(48)

Notes

  • The consistent mass matrix \(A_{ IJ}\) in (46) may optionally be replaced by a diagonal mass matrix

    $$\begin{aligned} A{ }_{ IJ}^{(d)} =s\frac{h}{2}\left[ {{\begin{array}{ll} 1&{} \quad 0 \\ 0&{} \quad 1 \\ \end{array} }} \right] \end{aligned}$$
    (49)

  • The advection matrix \(L_{ IJ}\) in (47) causes oscillations or instability when advection is pure or dominant, i.e., when the element Peclet number, \({Pe}_{h} ={hv}/{D}\), absolute value exceeds 2. In this implementation, a hybrid scheme is used to rectify this limitation as an option by replacing this matrix by a linear combination of the original matrix and an upwind matrix

    $$\begin{aligned} L_{ IJ}^*=\phi L_{ IJ}^{(up)} +\left( {1-\phi } \right) L_{ IJ} \end{aligned}$$
    (50)

where \(\phi \) is the upwind parameter, and the upwind matrix is given by

$$\begin{aligned} L_{ IJ}^{(up)} =s\frac{v}{2}\left\{ {{\begin{array}{ll} {\left[ {{\begin{array}{ll} -2&{}\quad 0 \\ +2&{}\quad 0 \\ \end{array} }} \right] \quad if\quad v>0} \\ {\left[ {{\begin{array}{ll} 0&{} \quad -2 \\ 0&{} \quad +2 \\ \end{array} }} \right] \quad if\quad v<0} \\ \end{array} }} \right. \end{aligned}$$
(51)

  • Only a uniform grid (\(h=\)cons, \(s=\)cons for all elements) is currently implemented.

  • Only uniform properties (\(v=\)cons, \(D=\)cons for all elements) are currently implemented.

The nodal flux for this element is now developed from (14) to (16) (transformed to the time domain), the discretization (24), definitions (41), (42) and the shape functions for this element (43), (44). We will calculate the element nodal flux j and its advective and dispersive ingredients, \(q^{c}\) and \(q^{d}\), i.e., at \(\xi =-1\), \(+1\), and then add the contributions from neighbor elements.

The shape function \(N_{I}\) is by definition 1 at node I and 0 at the other node of the element. Its x derivative is calculated by the chain rule as

$$\begin{aligned} \frac{\partial N_I }{\partial x}=\frac{\partial x}{\partial \xi }\frac{\partial N_I }{\partial \xi }=\frac{2}{h}\frac{\partial N_I }{\partial \xi } \end{aligned}$$
(52)

so that

$$\begin{aligned} \frac{\partial N_1 }{\partial x}= & {} -\frac{1}{h}, \end{aligned}$$
(53)
$$\begin{aligned} \frac{\partial N_2 }{\partial x}= & {} +\frac{1}{h} \end{aligned}$$
(54)

and these are constant throughout the element.

The advective term, \(q^{c}\), is

$$\begin{aligned} q^{c} \left( \xi \right) =vN_J C_J \end{aligned}$$
(55)

At the nodes, it is

$$\begin{aligned} q^{c} \left( {\xi =-1} \right)= & {} vC_1 , \end{aligned}$$
(56)
$$\begin{aligned} q^{c} \left( {\xi =+1} \right)= & {} vC_2 \end{aligned}$$
(57)

or

$$\begin{aligned} q_{I}^{c} =Q_{ IJ}^c C_J \end{aligned}$$
(58)

where

$$\begin{aligned} Q_{ IJ}^{c} =v\left[ {{\begin{array}{ll} 1&{} \quad 0 \\ 0&{} \quad 1 \\ \end{array} }} \right] \end{aligned}$$
(59)

The dispersive term, \(q^{d}\), is

$$\begin{aligned} q^{d} \left( \xi \right) =-DN_{J,x} C_J \end{aligned}$$
(60)

(constant over the element, i.e., independent of \(\xi )\), so at the nodes

$$\begin{aligned} q^{d} \left( {\xi =-1} \right)= & {} -D\left( {-\frac{1}{h}C_1 +\frac{1}{h}C_2 } \right) , \end{aligned}$$
(61)
$$\begin{aligned} q^{d} \left( {\xi =+1} \right)= & {} -D\left( {-\frac{1}{h}C_1 +\frac{1}{h}C_2 } \right) \end{aligned}$$
(62)

or

$$\begin{aligned} q_{I}^{d} =Q_{ IJ}^d C_J \end{aligned}$$
(63)

where

$$\begin{aligned} Q_{ IJ}^{d} =\frac{-D}{h}\left[ {{\begin{array}{ll} {-1}&{} \quad {+1} \\ {-1}&{} \quad {+1} \\ \end{array} }} \right] \end{aligned}$$
(64)

The nodal flux is therefore

$$\begin{aligned} j_I =F_{ IJ} C_J \otimes M=F_{ IJ} I_J \end{aligned}$$
(65)

where (82) was used and

$$\begin{aligned} F_{ IJ} =Q_{ IJ}^c +Q_{ IJ}^d \end{aligned}$$
(66)

While \(q^{c}\) is continuous between elements (because \(N_{I}\) is), \(q^{d}\) is not (because \(N_{I,x}\) is not, being constant at each element), and therefore j is also discontinuous. In other words, \(N_{I}\) is \(C^{0}\) continuous. The nodal value of \(q^{d}\) and j will be the average of the contributions from the neighboring elements. On boundaries, there will be a contribution from a single element.

6 Discrete BCs

6.1 Robin-Type BC

This is the simplest type of BC. Given the boundary node, its normal and the flux value as a function of time, its contribution to \(Q_{I}\) is given by the last term of (81) (see “Appendix 1”). For the linear 1D element, the boundary node contribution is \(s\bar{{j}}_{I} ( t )\) on \(\varGamma ^{R}\) .

6.2 Dirichlet-Type BC

If the concentration at a boundary node is given, it is possible to partition the solved equation system (87) (see “Appendix 1”) and reduce the size of the problem. This will now be schematically illustrated.

Suppose the unknown DOFs are \(C_{a}\), the prescribed DOFs are \(\bar{{C}}_{b}\) and the equations are reordered to form the block-matrix equation

$$\begin{aligned} \left[ {{\begin{array}{ll} {\alpha _{aa} }&{} {\alpha _{ab} } \\ {\alpha _{ba} }&{} {\alpha _{bb} } \\ \end{array} }} \right] \left\{ {{\begin{array}{ll} {C{ }_a} \\ {\bar{{C}}_b } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ll} {R{ }_a} \\ {R_b } \\ \end{array} }} \right\} \end{aligned}$$
(67)

where \(C_{a}\), \(\bar{{C}}_{b}\), \(R_{a}\) and \(R_{b}\) are vectors and \(\alpha _{aa}\), \(\alpha _{ab} , \alpha _{ba} , \alpha _{bb}\) are matrices.

The \(C_{a}\) partition can be readily calculated from the first block

$$\begin{aligned} C_a =\alpha _{aa}^{-1} \left( {R{ }_a-\alpha _{ab} \bar{{C}}_b } \right) \end{aligned}$$
(68)

because the right-hand side is known. If desired, \(R_{b}\) may then be calculated from

$$\begin{aligned} R_b =\alpha _{ba} C_a +\alpha _{bb} \bar{{C}}_b . \end{aligned}$$
(69)

This straightforward method is exact, but it is a bit more complex to program than the approximate alternative below [suggested by Zienkiewicz and Taylor (2000)].

In the solved equation, we may add a large term \(Y>>max|a_{ IJ} |\) to \(a_{II}\) for the node(s) I where Dirichlet BCs \(C=\bar{{C}}_{I}\) are prescribed and replace \(R_{I}^{n+1}\) with \(Y\bar{{C}}_{I}\). This will result in (approximately) satisfying these BCs without need to change the dimensions of the matrices and reorder them. This method is implemented in the present 1D FEM solver.

6.3 Neumann-Type BC

Hereafter, we will limit our treatment to linear 1D elements.

6.3.1 Prony Model

The Neumann BC contribution to \(Q_{I}\) consists of the first three terms of (81). The first term includes \(I_{J} ( t )\) multiplied by a surface integral. The surface integral is easily calculated using the shape functions (43), (44). At a boundary along \(\xi =-1\), it is \(\left( {snv\;\left[ {{\begin{array}{ll} 1&{} 0 \\ 0&{} 0 \\ \end{array} }} \right] } \right) \), and along \(\xi =+1\), it is \(\left( {snv\;\left[ {{\begin{array}{ll} 0&{} 0 \\ 0&{} 1 \\ \end{array} }} \right] } \right) \). Therefore, \(Q_{I}\) will only have a contribution at the boundary node I, which is \(snvI_{I} (t)\).

The second term pre-integral factor is similarly \([ C_{J} (t)-I_{J} (t) ]\) and the surface integral is similarly calculated. In this case, there is a contribution also from the neighbor node of the element, denoted here by the subscript K. The contribution of this term to \(Q_{I}\) is only at node I again and it is \(sD\{ {[ {C_{I} (t)-I_{I} (t)} ]-[ {C_{K} (t)-I_{K} (t)} ]} \}/{| h |}\).

The third term contribution is simply \(s\bar{{q}}_{I} (t)\).

Table 1 Calibrated TPL and numerical parameters for Scheidegger (1959) and Jardine et al. (1993) cases
Full size table
Table 2 M(t) parameters for Scheidegger (1959) and Jardine et al. (1993) cases
Full size table
Fig. 1
figure 1

FEM solution for the Scheidegger (1959) case: \(q( x,t )(-)\) versus \(x(\hbox {m})\) at various \(t(\hbox {min})\)

Full size image

Collecting all terms for step \(n+1\)

$$\begin{aligned} Q_I^{n+1} =s\left\{ {nvI_I^{n+1} +{D\left[ {\left( {C_I^{n+1} -I_I^{n+1} } \right) -\left( {C_K^{n+1} -I_K^{n+1} } \right) } \right] }/{\left| h \right| }+\bar{{q}}_I^{n+1} } \right\} \quad on \, \varGamma ^{N} \end{aligned}$$
(70)

6.3.2 ADE Model

With \(M( t )=\delta ( t )\), following similar (and much simpler) route, we have

$$\begin{aligned} Q_I^{n+1} =s\left\{ {nvC_I^{n+1} +\bar{{q}}_I^{n+1} } \right\} \quad on \, \varGamma ^{N} \end{aligned}$$
(71)

Note that the BC term, \(Q_{I}\), of both models depends on the solution [(terms of step \(n+1\) in (70) and (71)]. In a fully implicit scheme, these terms should be included in the solution of the equations system by changing the matrix or by an iterative solution. This is not done in the present implementation, so \(Q_{I}\) lags one step behind the solution, \(C_{I}\) .

7 Numerical Issues

When the number of linear equation (87) (see “Appendix 1”) is relatively small, it may be solved directly using LU decomposition. For a large system, the time and the storage required to the solution may become impractically large. In addition, the results may become inaccurate due to round-off errors. Therefore, the stabilized bi-conjugate gradient iterative solver, biCGstab

figure a

, by Sleijpen and Van der Vorst (1995), Sleijpen and Van der Vorst (1996), based on the PhD thesis of Fokkema (1996) and implemented by Botchev (http://www.staff.science.uu.nl/~vorst102/bcg2.f) is used here, which is capable of solving large non-symmetric equation systems.

Fig. 2
figure 2

Comparison of the solutions for the BTC of Scheidegger (1959) case: normalized \(q( L=1,t )(-)\) versus \(t(\hbox {min})\)

Full size image
Fig. 3
figure 3

Comparison of the solutions for the BTC of Jardine et al. (1993) case: normalized \(q( L=1,t )(-)\) versus \(t(\hbox {min})\)

Full size image

Throughout, 64-bit arithmetics were applied to all real variables.

8 Validation

Two verification cases are presented here, based on previous study (Cortis and Berkowitz 2004) that analyzes experiments of Scheidegger (1959) and of Jardine et al. (1993). In both cases, a Robin-step BC was applied at the inlet, \(x=0\), of a soil column of length L and a Neumann homogeneous BC was applied at the outlet; the IC was homogeneous and the breakthrough curves (BTC), \(q(L,t)\,\dot{=}\,q_{i}^{c} (L,t)+q_{i}^{d} (,t)\), were measured. The length was normalized, 500 uniform elements (\(h=2\times 10^{-3}\hbox {m})\) and a time step of \(\varDelta t=0.1\) min were used. An implicit temporal scheme, central spatial scheme and a diagonal mass matrix were used. The BTC was normalized by

$$\begin{aligned} q(L,\infty )=v\tilde{M}\left( {u=0} \right) \end{aligned}$$
(72)

The parameters used were obtained as follows: The CTRW Toolbox (Cortis and Berkowitz 2005) was first applied to find the five parameters (\(v,D, \beta , t_{1}\) and \(t_{2} )\) of the TPL model to best fit the BTC. The resulting memory function in the Laplace variable, \(\tilde{M}(u)\), was fitted to the exponential form (30) from its distribution along the imaginary u axis using a previously published method (Jiang 2001; Jiang and Greengard 2004; Xu and Jiang 2013). These parameters, together with the same v and D, were then used as input to the FEM solver.

Fig. 4
figure 4

Comparison of the solutions for the BTC of Scheidegger (1959) case: normalized \(q(L=1,t)(-)\) versus \(t(\hbox {min})\)—convergence with the time step

Full size image

The first case refers to experimental results of Scheidegger (1959). The calibrated TPL parameters for this case are shown in Table 1 and the fitted M(t) Prony series appear in Table 2. The FEM solver was run with these data until \(t=340\) min. The axial q distributions at various times are depicted in Fig. 1. The BTC at \(x=1\hbox { m}\) is compared in Fig. 2 to the experimental and the Toolbox results using both the TPL and EXP models. It is seen that the agreement is satisfactory. When the trapezoidal quadrature (38) was used for calculation of \(K_{J}^{n+1}\), it was found necessary to use time steps much smaller than the advective and the diffusive stability limits. As mentioned above, using the linear assumption for the calculation of \(K_{J}^{n+1}\) (34) enables a time step, \(\varDelta t\), that is about 100 times larger (see Table 1). Because the cell Peclet number, vh / D, in this case was small (1.15), the central scheme was preferred to the upwind scheme with its numerical dispersion (also known as false diffusion, Patankar 1980). Roughly 15 iterations were required by the biCGstab

figure b

to reduce the residuals to less than \(10^{-9}\) .

The second case presents a comparison with experimental results of Jardine et al. (1993). The parameters for this case are shown in Table 1 and Table 2. The BTC at \(x=1\hbox { m}\) for \(t\le 300\) min is compared in Fig. 3 to the experimental and the Toolbox results using both the TPL and EXP models. The agreement is again seen to be satisfactory. In this case, more iterations were required (about 300–500) to reach the same convergence criterion as in the former case. This may be attributed to the much larger \(D \varDelta t/h^{2}\) in the present case.

9 Convergence

The first validation case serves to assess the developed scheme convergence, in both time and space.

To check solution dependence on the time step, a fixed uniform grid of 500 elements was used, while changing the time step. Up to \(\varDelta t=0.25\) the solution was stable. Results for \(\varDelta t=0.1\), 0.25 are compared in Fig. 4 to the experiment and the Toolbox solution using the TPL model. The difference between these time steps results is negligible. With higher \(\varDelta t\), the solution becomes unstable when the concentration at \(x=L\) starts rising, although an implicit time scheme is used here. This may be because the BCs lag one step beyond the inner domain solution, because the solved equation is not ADE, and therefore, there is no guarantee that such a scheme is unconditionally stable, or for some other reason. This should be studied further in the future. However, for the problem at hand, it seems unlikely that good accuracy can be achieved with larger steps for a process that mainly proceeds in about \(100\hbox { min }( {140<t<240})\) .

Fig. 5
figure 5

Comparison of the solutions for the BTC of Scheidegger (1959) case: normalized \(q(L=1,t)(-)\) versus \(t(\hbox {min})\)—convergence with the grid size

Full size image

Next, we fixed the time step at \(\varDelta t=0.1\) and modified the number of (uniform) elements as depicted in Fig. 5. For finer grids (500, 200 and 100 elements with \(Pe_{h} =1.15\), 2.9, and 5.8, respectively), the central advection matrix was used with no instabilities. Using a central scheme with 50 elements (\(Pe_{h} =11.5)\), the solution showed wiggles (overshoots), which became larger for 20 elements (\(Pe_{h} =29)\). Switching to upwind advection is seen to overcome this issue, but the numerical dispersion of this scheme reduces the accuracy as the grid is coarser. Error estimation from Fig. 5 shows that the error for the upwind runs (Ne = 20, 50) is indeed O(h), as expected (see Patankar 1980), due to a numerical dispersion coefficient of vh/2, added to the true value, D.

10 Conclusions and Recommendations

A FEM formulation for a class of integro-differential transport equations was presented and specialized for 1D and a kernel M(t) has been used to model non-Fickian contaminant flow in porous media. Using a Prony series form of the memory function yielded an efficient solution, in which only the former time step results should be stored. The proposed formulation was successfully validated and its convergence characteristics were demonstrated.

The following extensions may be implemented in the future (the list order does not reflect item importance nor implementation difficulty and is rather arbitrary):

  • Implement non-uniform grid.

  • Improve the time-stepping efficiency, so that fewer steps are required while maintaining high accuracy.

  • Implement a higher-order element (e.g., quadratic shape functions rather than linear).

  • Allow for 2D (planar or axisymmetric) and 3D problems, implying also

    • Anisotropy.

    • Non-orthogonal elements.

    • Various elements shapes (2D: Quadrilateral and triangular, 3D: hexagonal, tetrahedral).

    • Generalized upwind or other scheme for advection-dominated flow. Use of the Petrov–Galerkin method (Zienkiewicz and Taylor 2000) is currently studied.

  • Allow for element-wise properties, including the velocity and the dispersion, or—even more generally—both being functions of \(x_{i}\) and t.

  • Generalize the BCs to allow for space and time dependence.

  • Add a Navier–Stokes solver, so the velocity field is calculated prior to the concentration solver rather than being prescribed.

  • Implement the source term and inhomogeneous IC.

  • Combine the BCs and the solution to fully adhere to the scheme implicitness.

  • Extend the equation and its BCs to include additional physical and chemical phenomena.

  • Optimize the fitting routine without using the Toolbox (thus avoiding the numerical inverse Laplace transform).