1 Introduction

Recently the present authors have been sorting out the important interactions between the effects of various agencies that remove the symmetry (about the mid-plane) in the onset of convection in a horizontal layer occupied by a porous medium with symmetric boundary conditions. These agencies include vertical heterogeneity and vertical throughflow. The situation is complicated when there is local thermal non-equilibrium (LTNE, see Patil and Rees 2013) because then heterogeneity of the interphase heat transfer is involved, throughflow occurs only in the fluid phase, and the heterogeneity of each of fluid conductivity and solid conductivity are pertinent. A further complication occurs in the double-diffusive situation because convection of a solute can occur only in the fluid phase. The effects of heterogeneity (with a layered medium) and LTNE diffusion (but not throughflow) were studied by Nield and Kuznetsov (2013) for the double-diffusive case. In each case, the medium was heated from below.

In the present paper, the study in Nield and Kuznetsov (2014) is repeated, but now for the case of internal heating rather than bottom heating. With internal heating, the basic vertical temperature gradient changes sign, from positive in the lower part of the domain to negative in the upper part, and as a result most of the convection, when it occurs, takes place in the upper part. Thus vertical heterogeneity now plays a greater role. The present paper is an extension, to the case of double diffusion, of the work by Kuznetsov and Nield (2014). Besides having a uniform volumetric heat source, we now have a uniform volumetric solute source. As far as we are aware, this combination has not been studied previously, even in the case of a homogeneous medium with LTE. A new internal solutal Rayleigh number is introduced.

Possible applications include a situation where the fluid and/or the solid is radioactive, and one in which there is solute deposition.

The authors have written a companion paper for the case of bottom heating (Nield et al. 2015). For completeness we cite two more of our papers on closely connected topics. In these only single diffusion is involved and bottom heating rather than internal heating is discussed, but other extensions are made. In Kuznetsov and Nield (2015) and Nield and Kuznetsov (2014), the effect of vertical throughflow is included. In the latter, the effect of heterogeneity is added to the mix.

The following analysis is closely similar to that in our previous papers, and so, the presentation has been shortened where that is possible.

2 Analysis

2.1 General Equations

Asterisks are used to denote dimensional variables. The \(z^{*}\)-axis is taken in the upward vertical direction, and the porous medium is unbounded in the \(x^{*}\) and \(y^{*}\) directions. Subscripts 1 and 2 are used to denote the two layers, of depths \({\delta }H\) and \((1-\delta )H\), where \(\delta \) is less than unity. The first occupies the region \(0\le z^{*}<\delta H\), and the second occupies the region \(\delta H\le z^{*}\le H\). A uniform temperature \(T_{0}\) and a uniform concentration \(C_{0}\) are imposed at each of the upper and lower boundaries.

The Oberbeck–Boussinesq approximation is invoked. The equations representing the conservation of mass, Darcy’s law, and the conservation of thermal energy for each phase, and the conservation of solute, take the form

$$\begin{aligned}&\displaystyle \nabla ^{*}\cdot \mathbf{u}^{*}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle 0=-\nabla ^{*} P^{*}-\frac{\mu }{K}\mathbf{u}^{*}-\rho _0 \left[ {\beta (T^{*}_\mathrm{f} -T_0)+\beta _\mathrm{C} (C^{*}_\mathrm{f} -C_0)} \right] \mathbf{g}, \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle \phi (\rho c)_\mathrm{f} \left[ {\frac{\partial T_\mathrm{f}^{*}}{\partial t^{*}}+\mathbf{u}^{*}\cdot \nabla ^{*} T_\mathrm{f}^{*}} \right] =\phi k_\mathrm{f} \nabla ^{*2}T_\mathrm{f}^{*}+h(T_\mathrm{s}^{*}-T_\mathrm{f}^{*})+\phi Q_\mathrm{f} , \end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle (1-\phi )(\rho c)_\mathrm{s} \frac{\partial T_\mathrm{s}^{*}}{\partial t^{*}}=(1-\phi )k_\mathrm{s} \nabla ^{2}T_\mathrm{s}^{*}+h(T_\mathrm{f}^{*}-T_\mathrm{s}^{*})+(1-\phi )Q_\mathrm{s} , \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \phi \frac{\partial C^{*}}{\partial t^{*}}+\mathbf{u}^{*}\cdot \nabla ^{*} C^{*}=\phi D_\mathrm{C} \nabla ^{*2}C^{*}+\phi Q_\mathrm{C}, \end{aligned}$$
(5)

where

$$\begin{aligned}&\phi =\phi _1 , K=K_1 , k_\mathrm{f} =k_\mathrm{f1} , k_\mathrm{s} =k_\mathrm{s1} , h=h_1 , \nonumber \\&Q_\mathrm{f} =Q_\mathrm{f1} ,Q_\mathrm{s} =Q_\mathrm{s1} , Q_\mathrm{C} =Q_\mathrm{C1} \hbox { in }0\le z^{*}<\delta H, \nonumber \\&\phi =\phi _2 , K=K_2 , k_\mathrm{f} =k_\mathrm{f2} , k_\mathrm{s} =k_\mathrm{s2} , h=h_2 , \nonumber \\&Q_\mathrm{f} =Q_\mathrm{f2} ,Q_\mathrm{s} =Q_\mathrm{s2} ,Q_\mathrm{C} =Q_\mathrm{C2} \hbox { in }\delta H<z^{*}\le H. \end{aligned}$$
(6)

Here the Darcy velocity is denoted by \(\mathbf{u}^{*}=(u^{*},v^{*},w^{*})\), where \(t^{*}\) is the time, \(P^{*}\) is the pressure (excess over hydrostatic), \(T^{*}\) is the temperature and \(C^{*}\) is the solute concentration, while K is the permeability, \(\phi \) is the porosity, \(k_\mathrm{f}\) and \(k_\mathrm{s}\) are the thermal conductivities in the fluid and solid phases, respectively, \((\rho c)_\mathrm{f}\) and \((\rho c)_\mathrm{s}\) are the heat capacities of the fluid and the solid, respectively, \(D_\mathrm{C}\) is the diffusivity of the solute, \(\mu \) is the fluid viscosity, \(\rho _{0}\) is the fluid density at temperature \(T_{0}\), \(\beta \) is the thermal expansion coefficient of the fluid, \(\beta _\mathrm{C}\) is the corresponding solutal coefficient, and g is the gravitational acceleration vector. The standard formulation of Darcy’s law, in which time derivatives are assumed to be negligible, has been adopted in Eq. (2). Since we consider a situation in which the thermal conductivity in each phase is piecewise constant, spatial derivatives of \(k_\mathrm{f}\) and \(k_\mathrm{s}\) do not appear in Eqs. (3) and (4), where the interface heat transfer coefficient (incorporating the specific surface area) between the fluid and solid particles is denoted by h. The flow is assumed to be slow so that an advective term and a Forchheimer quadratic drag term do not appear in the momentum equation. It has been assumed that there are uniform volumetric heat sources (with averages taken over representative elementary volumes) \(Q_{1}\) and \(Q_{2}\) in the respective layers, and uniform volumetric solute sources (resulting, for example, from the process of dissolution) of \(Q_\mathrm{C1}\) and \(Q_\mathrm{C2}\) (assumed to be in the fluid phase in the subsequent analysis) in the respective layers.

We suppose that the upper and lower boundaries are both impermeable. At the interface between the two regions, the normal velocity and the pressure are continuous. Thus the hydrodynamic boundary conditions are

$$\begin{aligned}&w_1^{*}=0\hbox { at }z^{*}=0, w_2^{*}=0\hbox { at }z^{*}=H, \end{aligned}$$
(7a,b)
$$\begin{aligned}&w_1^{*}=w_2^{*}\hbox { and }\frac{1}{K_1 }\frac{\partial w_1 ^{*}}{\partial z^{*}}=\frac{1}{K_2 }\frac{\partial w_2 ^{*}}{\partial z^{*}}\hbox { at }z^{*}=\delta H. \end{aligned}$$
(8a,b)

Equation (8b) expresses the continuity of pressure at the interface, and the momentum equation has been used to get this form.

We also suppose that the upper and lower boundaries are both perfectly conducting, and hence, one has local thermal equilibrium there, and also that the concentration is held constant there. At the interface between the two regions, we assume that the temperature and heat flux in each phase are continuous (see Nield 2012), and likewise the concentration and solute flux are continuous. Thus for the thermal boundary conditions we take

$$\begin{aligned}&T_\mathrm{f}^{*}=T_\mathrm{s}^{*}=T_0 , C^{*}=C_0 \hbox { at }z^{*}=0\hbox { and at }z^{*}=H, \end{aligned}$$
(9a,b,c,d,e,f)
$$\begin{aligned}&T_\mathrm{f1}^{*}=T_\mathrm{f2}^{*}, T_\mathrm{s1}^{*}=T_\mathrm{s2}^{*}, C_1^{*} =C_2^{*}, \nonumber \\&k_\mathrm{f1} \frac{\partial T_\mathrm{f1}^{*}}{\partial z}= k_\mathrm{f2} \frac{\partial T_\mathrm{f2}^{*}}{\partial z^{*}} , k_\mathrm{s1} \frac{\partial T_\mathrm{s1}^{*}}{\partial z^{*}}= k_\mathrm{s2} \frac{\partial T_\mathrm{s2}^{*}}{\partial z^{*}}, \phi _{1} \frac{\partial C_1^{*}}{\partial z^{*}}= \phi _{2} \frac{\partial C_2^{*}}{\partial z^{*}}\hbox { at }z^{*}=\delta H.\nonumber \\ \end{aligned}$$
(10a,b,c,d,e,f)

The heat flux solid–fluid interface conditions given by Eq. (10d,e) are not the only ones that one could impose. Two conditions need to be specified, and the heat flux could be divided between the two phases in various ways. Alternatives are discussed by Nield (2012). In the absence of any further information, we believe that the choice which makes the best physical sense is the one made here.

We introduce dimensionless variables as follows. For simplicity, we chose to scale in terms of quantities pertaining to region 1. If any adjustments for weighted algebraic mean quantities are desirable, then these can be made later.

We define

$$\begin{aligned}&(x,y,z)=\frac{1}{H}(x^{*},y^{*},z^{*}), t=\frac{k_\mathrm{f1} }{(\rho c)_\mathrm{f} H^{2}}t^{*}, \nonumber \\&(u,v,w)=\frac{(\rho c)_\mathrm{f} H}{k_\mathrm{f1} }(u^{*},v^{*},w^{*}) ,P=\frac{(\rho c)_\mathrm{f} K_1 }{\mu k_\mathrm{f1} }P^{*}, \end{aligned}$$
(11)
$$\begin{aligned}&T_\mathrm{f1} =\frac{(\rho c)_\mathrm{f} \rho _0 g\beta K_1 H}{\mu k_\mathrm{f1} }(T_\mathrm{f1}^{*}-T_0), T_\mathrm{s1} =\frac{(\rho c)_\mathrm{f} \rho _0 g\beta K_1 H}{\mu k_\mathrm{f1}}(T_\mathrm{s1}^{*}-T_0), \nonumber \\&T_\mathrm{f2} =\frac{(\rho c)_\mathrm{f} \rho _0 g\beta K_1 H}{\mu k_\mathrm{f1} }(T_\mathrm{f2} ^{*}-T_0), T_\mathrm{s2} =\frac{(\rho c)_\mathrm{f} \rho _0 g\beta K_1 H}{\mu k_\mathrm{f1} }(T_\mathrm{s2}^{*}-T_0), \nonumber \\&C_1 =\frac{(\rho c)_\mathrm{f} \rho _0 g\beta _\mathrm{C} K_1 H}{\mu k_\mathrm{f1} }(C_1 ^{*}-C_0), C_2 =\frac{(\rho c)_\mathrm{f} \rho _0 g\beta _\mathrm{C} K_1 H}{\mu k_\mathrm{f1} }(C_2^{*}-C_0). \end{aligned}$$
(12)

Equations (1–5), now written explicitly for the case of two regions, take the form:

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf{u}=0, \end{aligned}$$
(13)
$$\begin{aligned}&\displaystyle 0=-\nabla p-\frac{1}{\hat{{K}}}\mathbf{u}+(T_\mathrm{f} +C){\hat{\mathbf{e}}}_z , \end{aligned}$$
(14)
$$\begin{aligned}&\displaystyle \frac{\partial T_\mathrm{f} }{\partial t}+\mathbf{u}\cdot \nabla T_\mathrm{f} =\hat{{k}}_\mathrm{f} \nabla ^{2}T_\mathrm{f} +\frac{\hat{{h}}}{\hat{{\phi }}}N(T_\mathrm{s} -T_\mathrm{f} )+2\hat{{Q}}_\mathrm{f} {Ra}, \end{aligned}$$
(15)
$$\begin{aligned}&\displaystyle \hat{{\varepsilon }}\alpha \frac{\partial T_\mathrm{s} }{\partial t}=\hat{{k}}_\mathrm{s} \nabla ^{2}T_\mathrm{s} +\hat{{\delta }}\hat{{h}}\gamma N(T_\mathrm{f} -T_\mathrm{s})+2\hat{{Q}}_\mathrm{s} {Ra}, \end{aligned}$$
(16)
$$\begin{aligned}&\displaystyle \hbox {Le}\frac{\partial C}{\partial t}+\frac{{Le}}{\hat{{\phi }}}\mathbf{u}\cdot \nabla C=\nabla ^{2}C+2\hat{{Q}}_\mathrm{C} {Ra}_\mathrm{C} , \end{aligned}$$
(17)

where, for \(0\le z<\delta \),

$$\begin{aligned} \hat{{K}}=1, \hat{{k}}_\mathrm{f} =1, \hat{{k}}_\mathrm{s} =1, \hat{{\phi }}=1, \hat{{h}}=1, \hat{{\delta }}=1, \hat{{\varepsilon }}=1, \hat{{Q}}_\mathrm{f} =1, \hat{{Q}}_\mathrm{s} =1,\hat{{Q}}_\mathrm{C} =1, \end{aligned}$$
(18a)

and, for \(\delta <z\le 1\),

$$\begin{aligned}&\hat{{K}}=K_\mathrm{r}, \hat{{k}}_\mathrm{f} =k_\mathrm{fr} , \hat{{k}}_\mathrm{s} =k_\mathrm{sr} , \hat{{\phi }}=\phi _\mathrm{r}, \hat{{h}}=h_\mathrm{r},\nonumber \\&\hat{{\delta }}=\delta _\mathrm{r}, \hat{{\varepsilon }}=\varepsilon _\mathrm{r},\hat{{Q}}_\mathrm{f} =Q_\mathrm{fr} , \hat{{Q}}_\mathrm{s} =Q_\mathrm{sr} ,\hat{{Q}}_\mathrm{C} =Q_\mathrm{Cr} , \end{aligned}$$
(18b)

where

$$\begin{aligned}&K_\mathrm{r} =\frac{K_2 }{K_1 }, k_\mathrm{fr} =\frac{k_\mathrm{f2} }{k_\mathrm{f1} }, k_\mathrm{sr} =\frac{k_\mathrm{s2} }{k_\mathrm{s1} }, \phi _\mathrm{r} =\frac{\phi _2 }{\phi _1 }, h_\mathrm{r} =\frac{h_2 }{h_1 }, \nonumber \\&\delta _\mathrm{r} =\frac{1-\phi _1 }{1-\phi _2 }, \varepsilon _\mathrm{r}=\frac{(\rho c)_\mathrm{s2} }{(\rho c)_\mathrm{s1} } , Q_\mathrm{fr} =\frac{Q_\mathrm{f2} }{Q_\mathrm{f1} }, Q_\mathrm{sr} =\frac{Q_\mathrm{s2} }{Q_\mathrm{s1} }, Q_\mathrm{Cr} =\frac{Q_\mathrm{C2} }{Q_\mathrm{C1} }. \end{aligned}$$
(19)

We have also defined

$$\begin{aligned} {Ra}=\frac{(\rho c)_\mathrm{f} \rho _0 g\beta K_1 H^{3}Q_\mathrm{f1} }{2\mu k_\mathrm{f1}^{2}},Ra_\mathrm{C} =\frac{(\rho c)_\mathrm{f} \rho _0 g\beta _\mathrm{C} K_1 H^{3}Q_\mathrm{C1} }{2\mu k_\mathrm{f1} D_\mathrm{C} }, \end{aligned}$$
(20a,b)
$$\begin{aligned} \alpha =\frac{(\rho c)_\mathrm{s1} }{(\rho c)_\mathrm{f1} }\frac{k_\mathrm{f1} }{k_\mathrm{s1} }, N=\frac{h_1 H^{2}}{\phi _1 k_\mathrm{f1} }, \gamma =\frac{\phi _1 k_\mathrm{f1} }{(1-\phi _1)k_\mathrm{s1} }, {Le}=\frac{k_\mathrm{f1} }{(\rho \hbox {c})_\mathrm{f} D_\mathrm{C}}. \end{aligned}$$
(21a,b,c,d)

Here N is an interface heat transfer parameter. Vadász (2006) called this type of parameter the Nield number, citing Nield (1998). The parameters \(\alpha \) and \(\gamma \) are modified thermal diffusivity and thermal conductivity ratios, respectively, and Le is a Lewis number.

The boundary and matching conditions become

$$\begin{aligned}&w_1 =0, T_\mathrm{f1} =0, T_\mathrm{s1} =0, C_1 =0\hbox { at }z=0 , \end{aligned}$$
(22a,b,c)
$$\begin{aligned}&w_2 =0, T_\mathrm{f2} =0, T_\mathrm{s2} =0, C_2 =\hbox {0 at }z=1, \end{aligned}$$
(23a,b,c)
$$\begin{aligned}&W_1 =W_2 , \frac{\partial W_1 }{\partial z}=\frac{1}{K_\mathrm{r} }\frac{\partial W_2 }{\partial z}, T_\mathrm{f1} =T_\mathrm{f2} , T_\mathrm{s1} =T_\mathrm{s2} , C_1 =C_2 , \nonumber \\&\frac{\partial T_\mathrm{f1} }{\partial z}= k_\mathrm{fr} \frac{\partial T_\mathrm{f2} }{\partial z} , \frac{\partial T_\mathrm{s1} }{\partial z}= k_\mathrm{sr} \frac{\partial T_\mathrm{s2} }{\partial z}, \frac{\partial C_1 }{\partial z}= \phi _\mathrm{r} \frac{\partial C_2 }{\partial z}\hbox { at }z=\delta .\nonumber \\ \end{aligned}$$
(24a,b,c,d,e,f,g,h)

2.2 Basic Solution

We seek a time-independent quiescent solution of Eqs. (13–17) with temperatures and concentration varying in the z-direction only, that is a solution of the form

$$\begin{aligned} \mathbf{u}=0, P=P_\mathrm{B} (z), T_\mathrm{f} =T_\mathrm{fB} (z), T_\mathrm{s} =T_\mathrm{sB} (z), C=C_\mathrm{B} (z), \end{aligned}$$
(25)

subject to the boundary and initial conditions (22–24). Equations (14–17) reduce to

$$\begin{aligned}&\displaystyle 0=-\frac{dP_\mathrm{B} }{dz}+T_\mathrm{fB} +C_\mathrm{B} , \end{aligned}$$
(26)
$$\begin{aligned}&\displaystyle \hat{{k}}_\mathrm{f} \frac{d^{2}T_\mathrm{fB} }{dz^{2}}+\frac{\hat{{h}}}{\hat{{\phi }}}N(T_\mathrm{sB} -T_\mathrm{fB} )+2\hat{{Q}}_\mathrm{f} {Ra}=0, \end{aligned}$$
(27)
$$\begin{aligned}&\displaystyle \hat{{k}}_\mathrm{s} \frac{d^{2}T_\mathrm{sB} }{dz^{2}}+\hat{{\delta }}\hat{{h}}\gamma N(T_\mathrm{fB} -T_\mathrm{sB} )+2\hat{{Q}}_\mathrm{s} {Ra}=0, \end{aligned}$$
(28)
$$\begin{aligned}&\displaystyle \frac{d^{2}C}{dz^{2}}+2\hat{{Q}}_\mathrm{C} {R}a_{\mathrm{C}} =0. \end{aligned}$$
(29)

We now write these equations explicitly for the two regions.

Equations (27–29) in explicit form are

$$\begin{aligned}&\frac{d^{2}T_{\mathrm{fB}1} }{dz^{2}}+N(T_\mathrm{sB1} -T_\mathrm{fB1})+2{Ra}=0, \end{aligned}$$
(30a)
$$\begin{aligned}&\frac{d^{2}T_\mathrm{sB1} }{dz^{2}}+\gamma N(T_\mathrm{fB1} -T_\mathrm{sB1} )+2{Ra}=0, \end{aligned}$$
(30b)
$$\begin{aligned}&\frac{d^{2}C_1 }{dz^{2}}+2\hbox {R}a_\mathrm{C} =0, \end{aligned}$$
(30c)
$$\begin{aligned}&k_\mathrm{fr} \frac{d^{2}T_\mathrm{fB2} }{dz^{2}}+\frac{h_\mathrm{r}}{\phi _\mathrm{r}}N(T_\mathrm{sB2} -T_\mathrm{fB2})+2Q_\mathrm{fr} {Ra}=0, \end{aligned}$$
(30d)
$$\begin{aligned}&k_\mathrm{sr} \frac{d^{2}T_\mathrm{sB2} }{dz^{2}}+\delta _\mathrm{r} h_\mathrm{r} \gamma N(T_\mathrm{fB2} -T_\mathrm{sB2})+2Q_\mathrm{sr} {Ra}=0, \end{aligned}$$
(30e)
$$\begin{aligned}&\frac{d^{2}C_2 }{dz^{2}}+2Q_\mathrm{Cr} {R}a_\mathrm{C} =0. \end{aligned}$$
(30f)

These equations must be solved subject to the boundary and interface conditions

$$\begin{aligned} T_\mathrm{fB1} (0)=0, T_\mathrm{sB1} (0)=0, C_\mathrm{B1} (0)=0, \end{aligned}$$
(31a,b,c)
$$\begin{aligned} T_\mathrm{fB2} (1)=0, T_\mathrm{sB2} (1)=0 , C_\mathrm{B2} (1)=0, \end{aligned}$$
(31d,e,f)
$$\begin{aligned} T_\mathrm{fB1} (\delta )=T_\mathrm{fB2} (\delta ), T_\mathrm{sB1} (\delta )=T_\mathrm{sB2} \left( \delta \right) , C_\mathrm{B1} (\delta )=C_\mathrm{B2} (\delta ), \end{aligned}$$
(31g,h,i)
$$\begin{aligned} \frac{dT_\mathrm{fB1} }{dz}(\delta )= k_\mathrm{fr} \frac{dT_\mathrm{fB2} }{dz}(\delta ) , \frac{dT_\mathrm{sB1} }{dz}(\delta )= k_\mathrm{sr} \frac{dT_\mathrm{sB2} }{dz}(\delta ),\frac{dC_\mathrm{B1} }{dz}(\delta )= \phi _\mathrm{r} \frac{dC_\mathrm{B2} }{dz}(\delta ).\nonumber \\ \end{aligned}$$
(31j,k,l)

The solutal equations are decoupled from the thermal equations and have the solution

$$\begin{aligned}&C_\mathrm{B1} ={Ra}_\mathrm{C} \left\{ {\left[ {\frac{\phi _\mathrm{r} Q_\mathrm{Cr} \left[ {1+(2\phi _\mathrm{r} -1)\delta ^{2}} \right] -\phi _\mathrm{r}\delta ^{2}}{1+(\phi _r -1)\delta }+2\delta (1-\phi _\mathrm{r} Q_\mathrm{Cr})} \right] z-z^{2}} \right\} ,\qquad \end{aligned}$$
(32a)
$$\begin{aligned}&C_\mathrm{B2} ={Ra}_\mathrm{C} \left\{ {\left[ {\frac{Q_\mathrm{Cr} \left[ {1+(2\phi _\mathrm{r} -1)\delta ^{2}} \right] -\delta ^{2}}{1+(\phi _\mathrm{r}-1)\delta }} \right] (z-1)+Q_\mathrm{Cr} \left( {1-z^{2}} \right) } \right\} . \end{aligned}$$
(32b)

The solution to the differential thermal equation system in the general case is too complicated to present here. This system has been studied by Nield and Kuznetsov (2014), who showed that weak LTNE did not change the basic solution significantly from the LTE solution,

$$\begin{aligned}&T_\mathrm{fB1} ={Ra}\left\{ {\left[ {\frac{Q_\mathrm{fr} \left[ {1+(2k_\mathrm{fr} -1)\delta ^{2}} \right] -k_\mathrm{fr} \delta ^{2}}{1+(k_\mathrm{fr} -1)\delta }+2\delta (1-Q_\mathrm{fr})} \right] z-z^{2}} \right\} , \end{aligned}$$
(33a)
$$\begin{aligned}&T_\mathrm{sB1} ={Ra}\left\{ {\left[ {\frac{Q_\mathrm{sr} \left[ {1+(2k_\mathrm{sr} -1)\delta ^{2}} \right] -k_\mathrm{sr} \delta ^{2}}{1+(k_\mathrm{sr} -1)\delta }+2\delta (1-Q_\mathrm{sr})} \right] z-z^{2}} \right\} , \end{aligned}$$
(33b)
$$\begin{aligned}&T_\mathrm{fB2} ={Ra}\left\{ {\left[ {\frac{Q_\mathrm{fr} \left[ {1+(2k_\mathrm{fr} -1)\delta ^{2}} \right] -k_\mathrm{fr} \delta ^{2}}{k_\mathrm{fr} \left[ {1+(k_\mathrm{fr} -1)\delta } \right] }} \right] (z-1)+\frac{Q_\mathrm{fr} }{k_\mathrm{fr} }\left( {1-z^{2}} \right) } \right\} , \end{aligned}$$
(33c)
$$\begin{aligned}&T_\mathrm{sB2} ={Ra}\left\{ {\left[ {\frac{Q_\mathrm{sr} \left[ {1+(2k_\mathrm{sr} -1)\delta ^{2}} \right] -k_\mathrm{sr} \delta ^{2}}{k_\mathrm{sr} \left[ {1+(k_\mathrm{sr} -1)\delta } \right] }} \right] (z-1)+\frac{Q_\mathrm{sr} }{k_\mathrm{sr} }\left( {1-z^{2}} \right) } \right\} . \end{aligned}$$
(33d)

Of particular interest for the stability problem is the distribution of the negative basic temperature gradient in the fluid phase, which we denote by F(z) and which is given by the linear expression \({Ra}(2z - 1)\) in a homogeneous medium with uniform heating. From Eqs. (33a,c) we have

$$\begin{aligned}&F_1 (z)\equiv {Ra}f_1 (z) ={Ra}\left\{ {2z-\frac{Q_\mathrm{fr} \left[ {1+(2k_\mathrm{fr} -1)\delta ^{2}} \right] -k_\mathrm{fr} \delta ^{2}}{1+(k_\mathrm{fr} -1)\delta }-2\delta (1-Q_\mathrm{fr})} \right\} ,\qquad \end{aligned}$$
(34a)
$$\begin{aligned}&F_2 (z)\equiv {Ra}f_2 (z) ={Ra}\left\{ {\frac{2Q_\mathrm{fr} }{k_\mathrm{fr} }z-\frac{Q_\mathrm{fr} \left[ {1+(2k_\mathrm{fr} -1)\delta ^{2}} \right] -k_\mathrm{fr} \delta ^{2}}{k_\mathrm{fr} \left[ {1+(k_\mathrm{fr} -1)\delta } \right] }} \right\} . \end{aligned}$$
(34b)

Likewise the negative basic solutal gradient is G(z) where

$$\begin{aligned}&G_1 (z)\equiv {Ra}_\mathrm{C} g_1 (z)={Ra}_\mathrm{C} \left\{ {2z-\frac{\phi _\mathrm{r} Q_\mathrm{Cr} \left[ {1+(2\phi _\mathrm{r} -1)\delta ^{2}} \right] -\phi _\mathrm{r} \delta ^{2}}{1+(\phi _\mathrm{r} -1)\delta }-2\delta (1-\phi _\mathrm{r} Q_\mathrm{Cr})} \right\} , \end{aligned}$$
(35a)
$$\begin{aligned}&G_2 (z)\equiv {Ra}_\mathrm{C} g_2 (z)= {Ra}_\mathrm{C} \left\{ {2Q_\mathrm{Cr} z-\frac{Q_\mathrm{Cr} \left[ {1+(2\phi _\mathrm{r} -1)\delta ^{2}} \right] -\delta ^{2}}{1+(\phi _\mathrm{r}-1)\delta }} \right\} . \end{aligned}$$
(35b)

2.3 Perturbation Equations

We now superimpose perturbations on the basic solution. We write

$$\begin{aligned} \mathbf{u}=\mathbf{{u}'},p=p_\mathrm{B} +{p}', T_\mathrm{f} = T_\mathrm{fB} +{T}'_\mathrm{f} , T_\mathrm{s} = T_\mathrm{sB} +{T}'_\mathrm{s} , C=C_\mathrm{B} +{C}', \end{aligned}$$
(36)

substitute in Eqs. (13–17), and linearize by neglecting products of primed quantities. The following equations are obtained:

$$\begin{aligned}&{\displaystyle } \nabla \cdot \mathbf{{u}'}=0, \end{aligned}$$
(37)
$$\begin{aligned}&{\displaystyle } 0=-\nabla {p}'-\frac{1}{\hat{{K}}}\mathbf{{u}'}+({T}'_\mathrm{f} +{C}') {\hat{\mathbf{e}}}_z , \end{aligned}$$
(38)
$$\begin{aligned}&{\displaystyle } \frac{\partial {T}'_\mathrm{f} }{\partial t}+\frac{dT_\mathrm{Bf} }{dz}{w}'=\hat{{k}}_\mathrm{f} \nabla ^{2}{T}'_\mathrm{f} +\frac{\hat{{h}}}{\hat{{\phi }}}N({T}'_\mathrm{s} -{T}'_\mathrm{f}), \end{aligned}$$
(39)
$$\begin{aligned}&{\displaystyle } \hat{{\varepsilon }}\alpha \frac{\partial {T}'_\mathrm{s} }{\partial t}=\hat{{k}}_\mathrm{s} \nabla ^{2}{T}'_\mathrm{s} +\hat{{\delta }}\hat{{h}}\gamma N({T}'_\mathrm{f} -{T}'_\mathrm{s}), \end{aligned}$$
(40)
$$\begin{aligned}&{\displaystyle } {Le}\frac{\partial {C}'}{\partial t}+\frac{{Le}}{\hat{{\phi }}}\frac{dC_\mathrm{B} }{dz}{w}'=\nabla ^{2}{C}', \end{aligned}$$
(41)
$$\begin{aligned}&{\displaystyle } {w}'=0, {T}'_\mathrm{f} =0, {T}'_\mathrm{s} =0, {C}'=0\hbox { at }z=0\hbox { and at } z =1. \end{aligned}$$
(42)

The reader will note that, since there is no convection in the solid phase, the basic temperature gradient in the solid phase is not involved in the instability problem.

The seven unknowns \({u}',{v}',{w}',{p}',{T}'_\mathrm{f} ,{T}'_\mathrm{s} ,{C}'\) can be reduced to four by operating on Eq. (38) with \({\hat{\mathbf{e}}}_z \cdot curl\,curl\) and using the operator identity \(curl\,curl \equiv grad\,div-\nabla ^{2}\) and Eq. (37). The result is

$$\begin{aligned} \nabla ^{2}{w}'=\hat{{K}}\nabla _H^2 ({T}'_\mathrm{f} +{C}'). \end{aligned}$$
(43)

Here \(\nabla _H^2\) is the two-dimensional Laplacian operator on the horizontal plane.

The boundary and interface conditions are

$$\begin{aligned}&{w}'_1 =0, {T}'_\mathrm{f1} =0, {T}'_\mathrm{s1} =0, {C}'_1 =0 \hbox { at }z=0, \end{aligned}$$
(44a,b,c,d)
$$\begin{aligned}&{w}'_2 =0, {T}'_\mathrm{f2} =0, {T}'_\mathrm{s2} =0, {C}'_2 =0 \hbox { at } z =1, \end{aligned}$$
(45a,b,c,d)
$$\begin{aligned}&{W}'_1 ={W}'_2 , \frac{\partial {W}'_1 }{\partial z}=\frac{1}{K_\mathrm{r} }\frac{\partial {W}'_2 }{\partial z}, {T}'_\mathrm{f1} ={T}'_\mathrm{f2} , {T}'_\mathrm{s1} ={T}'_\mathrm{s2} , {C}'_1 ={C}'_2 , \nonumber \\&\frac{\partial {T}'_\mathrm{f1} }{\partial z}= k_\mathrm{fr} \frac{\partial {T}'_\mathrm{f2} }{\partial z} , \frac{\partial {T}'_\mathrm{s1} }{\partial z}= k_\mathrm{sr} \frac{\partial {T}'_\mathrm{s2} }{\partial z}, \frac{\partial {C}'_1 }{\partial z}= \phi _\mathrm{r} \frac{\partial {C}'_2 }{\partial z}\hbox { at }z=\delta .\nonumber \\ \end{aligned}$$
(46a,b,c,d,e,f,g,h)

The differential equations (43), (39–41) and the boundary and interface conditions (44–46) constitute a linear boundary-value problem that can be solved using the method of normal modes. We write

$$\begin{aligned} ({w}',{T}'_\mathrm{f} ,{T}'_\mathrm{s} ,{C}')=[W(z),\Theta _\mathrm{f} (z),\Theta _\mathrm{s} (z),\Gamma (z)]\exp (st+ilx+imy), \end{aligned}$$
(47)

and substitute into the differential equations to obtain

$$\begin{aligned}&{\displaystyle } (D^{2}-a^{2})W+\hat{{K}} a^{2}\Theta _\mathrm{f} +\hat{{K}} a^{2}\Gamma =0, \end{aligned}$$
(48)
$$\begin{aligned}&\displaystyle -\frac{\hbox {d}{ T}_\mathrm{fB} }{{\hbox {d}}z}W+\left( {\hat{{k}}_\mathrm{f} (D^{2}-a^{2})-s-\frac{\hat{{h}}}{\hat{{\phi }}}N} \right) \Theta _\mathrm{f} +\frac{\hat{{h}}}{\hat{{\phi }}}N\Theta _\mathrm{s} =0,\end{aligned}$$
(49)
$$\begin{aligned}&{\displaystyle } \hat{{\delta }}\hat{{h}}\gamma N\Theta _\mathrm{f} +\left[ {\hat{{k}}_\mathrm{s} (D^{2}-a^{2})-\hat{{\varepsilon }}\alpha s-\hat{{\delta }}\hat{{h}}\gamma N} \right] \Theta _\mathrm{s} =0, \end{aligned}$$
(50)
$$\begin{aligned}&\displaystyle -\frac{{\hbox {d}}C_\mathrm{B} }{{\hbox {d}}z}W+\left[ {\frac{\hat{{\phi }}}{{Le}}\left( {D^{2}-a^{2}} \right) -\hat{{\phi }}s} \right] \Gamma =0, \end{aligned}$$
(51)

where

$$\begin{aligned} D\equiv \frac{d}{{\hbox {d}}z}\hbox { and }a=(l^{2}+m^{2})^{1/2}. \end{aligned}$$
(52)

Thus a is a dimensionless horizontal wavenumber.

The boundary and interface conditions are

$$\begin{aligned}&W_1 =0, \Theta _\mathrm{f1} =0, \Theta _\mathrm{s1} =0, \Gamma _1 =0 \hbox { at }z=0, \end{aligned}$$
(53a,b,c,d)
$$\begin{aligned}&W_2 =0, \Theta _\mathrm{f2} =0, \Theta _\mathrm{s2} =0 , \Gamma _2 =0 \hbox { at } z =1, \end{aligned}$$
(54a,b,c,d)
$$\begin{aligned}&W_1 =W_2 , (1/K_1)DW_1 =(1/K_2)DW_2 , \Theta _\mathrm{f1} =\Theta _\mathrm{f2} , \Theta _\mathrm{s1} =\Theta _\mathrm{s2} , \Gamma _1 =\Gamma _2 , \nonumber \\&k_\mathrm{f1} D\Theta _\mathrm{f1} = k_\mathrm{f2} D\Theta _\mathrm{f2} , k_\mathrm{s1} D\Theta _\mathrm{s1} = k_\mathrm{s2} D\Theta _{\mathrm{s}2} , \phi _1 D\Gamma _1 = \phi _2 D\Gamma _{2} \hbox { at }z=\delta .\nonumber \\ \end{aligned}$$
(55a,b,c,d,e,f,g,h)

For neutral stability the real part of s is zero. Hence we write \(s = i\omega \), where \(\omega \) is real and is a dimensionless frequency. Our main objective is to investigate the relative importance of the various heterogeneity effects, and we would expect that these effects would be maximized for the case when the thermal and solutal buoyancy forces aid (rather than oppose) each other, that is for the non-oscillatory case. For this reason, and also because of the large number of parameters that are involved, we confine our attention to the case of non-oscillatory instability. The oscillatory case can be left for future investigation.

Accordingly, we put \(\omega = 0\). As a result of this, the parameters \(\hat{{\varepsilon }}\) and \(\alpha \) that appear in Eq. (50) now drop out of the system of differential equations.

We employed a Galerkin-type weighted residuals method to obtain an approximate solution to the system of Eqs. (48–51), (53–55). This method has been employed extensively in our previous papers (e.g. Kuznetsov and Nield 2013, 2014, 2015; Nield and Kuznetsov 2014, 2015), and so for brevity the details are omitted here. The idea is to choose trial functions that satisfy the boundary and interface conditions exactly (in our case low-order polynomials) and solve the differential equations exactly in an averaged sense, by imposing the condition that the residuals are orthogonal to the trial functions. The result is a set of homogeneous equations whose non-trivial solution leads to an eigenvalue equation with Ra as the eigenvalue. Thus Ra is found in terms of the other parameters.

3 Results and Discussion

Because of the large parameter space, we simplified the analysis. In order to have a tractable analysis, we employed a second-order Galerkin approximation. We believe that this relatively severe approximation is acceptable in this work because we are concerned just with sorting out the major effects of heterogeneity and LTNE, and hence it is relative changes to, rather than absolute values of, the critical Rayleigh number that are of interest. The eigenvalue equation then takes the form of the vanishing of a determinant of order 8. We solved this numerically to obtain values of Ra.

We recover the homogeneous results when we set the heterogeneity ratios [those quantities defined in Eq. (19)] equal to unity and take one of the limits, either \(\delta \) tends to zero or \(\delta \) tends to 1, N tends to zero, or both N and \(\gamma \) tend to infinity. Also, for our investigation of the interaction between LTNE and heterogeneity, we may take as typical values \(\delta = 0.5\), \(N= 1\), \(\gamma = 1\). We also fix \(Le = 1\). This value is taken for illustrative purposes. In practical cases the value of Le will be greater than unity.

We now confine our attention to some special cases.

3.1 Homogeneity and Local Thermal Equilibrium

In this case we have

$$\begin{aligned} T_\mathrm{B} ={Ra}(z-z^{2}), C_\mathrm{B} ={Ra}_\mathrm{C} (z-z^{2}). \end{aligned}$$
(56)

We write

$$\begin{aligned} \tilde{\Theta }=\frac{\Theta }{{Ra}}, \tilde{\Gamma }=\frac{{Le}\Gamma }{{Ra}_\mathrm{C} }. \end{aligned}$$
(57)

Then Eqs. (48–51) become

$$\begin{aligned}&\left( {D^{2}-a^{2}} \right) W+a^{2}\left( {{Ra}\tilde{\Theta }+\frac{{Ra}_\mathrm{C} }{{Le}}\tilde{\Gamma }} \right) =0, \end{aligned}$$
(58)
$$\begin{aligned}&\left( {2z-1} \right) W+\left( {D^{2}-a^{2}} \right) \tilde{\Theta }=0, \end{aligned}$$
(59)
$$\begin{aligned}&\left( {2z-1} \right) W+\frac{1}{{Le}}\left( {D^{2}-a^{2}} \right) \tilde{\Gamma }=0. \end{aligned}$$
(60)

Eliminating \(\tilde{\Theta }\hbox { and }\tilde{\Gamma }\) between these equations we get

$$\begin{aligned} \left( {D^{2}-a^{2}} \right) ^{2}W+a^{2}\left( {{Ra}+{Ra}_\mathrm{C} } \right) \left( {1-2z} \right) W=0. \end{aligned}$$
(61)

Using Eq. (58) we see that the boundary conditions on W are now

$$\begin{aligned} W=0, D^{2}W=0\hbox { at }z=0\hbox { and at }z=1. \end{aligned}$$
(62)

We observe that we have the same differential equation system as for the single-diffusive problem, but now the thermal Rayleigh number Ra is replaced by an effective combined Rayleigh number \({Ra}_\mathrm{eff}\) defined by

$$\begin{aligned} {Ra}_\mathrm{eff} ={Ra}+{Ra}_\mathrm{C} . \end{aligned}$$
(63)

The critical Rayleigh number for the thermal problem was found by Kulacki and Ramchandani (1975) to be 235.67, obtained at a critical wavenumber 4.67. Thus for the double-diffusive case, the critical combined Rayleigh number is 235.67. In other words, the non-oscillatory stability boundary is

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C} =235.67. \end{aligned}$$
(64)

In the same way, one can readily show that the oscillatory instability boundary is given by

$$\begin{aligned} \frac{{Le}}{{Le}+1}{Ra}+\frac{1}{{Le}+1}{Ra}_\mathrm{C} =235.67 \end{aligned}$$
(65)

provided that

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C} <235.67. \end{aligned}$$
(66)

These results mirror those for the bottom-heated/top-soluted problem given by Eqs. (9.20) and (9.21) of Nield and Bejan (2013).

3.2 Weak Heterogeneity and Weak Local Thermal Non-equilibrium

For the case

$$\begin{aligned}&k_\mathrm{fr} =1+\varepsilon _\mathrm{fk} , k_\mathrm{sr} =1+\varepsilon _\mathrm{sk} , K_r =1+\varepsilon _K , Q_\mathrm{fr} =1+\varepsilon _\mathrm{fQ} , Q_\mathrm{Cr} =1+\varepsilon _\mathrm{CQ} , \nonumber \\&h_\mathrm{r} =1+\varepsilon _h , \phi _\mathrm{r} =1+\varepsilon _\phi , \delta _\mathrm{r} =1+\varepsilon _\delta , \end{aligned}$$
(67)

where \(\varepsilon _\mathrm{fk} ,\varepsilon _\mathrm{sk} , \varepsilon _K , \varepsilon _\mathrm{fQ} , \varepsilon _\mathrm{CQ} ,\varepsilon _h , \varepsilon _\phi , \varepsilon _\delta \), are all small compared with unity and with a fixed at the value 4.67, we obtained the following approximate expressions for the critical combined Rayleigh number.

For \({Ra}_\mathrm{C} = 0\), \(\delta = 0.1\),

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C}= & {} 251.9+422.0\varepsilon _\mathrm{fk} +0.1\varepsilon _\mathrm{sk} -252.4\varepsilon _K -243.6\varepsilon _\mathrm{fQ} \nonumber \\&+\,5.5\varepsilon _h -5.6\varepsilon _\phi -0.1\varepsilon _\delta . \end{aligned}$$
(68a)

For \({Ra}_\mathrm{C} = 0\), \(\delta = 0.5\),

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C}= & {} 251.9+275.1\varepsilon _\mathrm{fk} +0.1\varepsilon _\mathrm{sk} -213.5\varepsilon _K -67.7\varepsilon _\mathrm{fQ} \nonumber \\&+\,5.0\varepsilon _h -5.1\varepsilon _\phi -0.1\varepsilon _\delta . \end{aligned}$$
(68b)

For \({Ra}_\mathrm{C} = 0\), \(\delta = 0.9\),

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C}= & {} 251.9+18.5\varepsilon _\mathrm{fk} +0.0\varepsilon _\mathrm{sk} -62.5\varepsilon _K +6.9\varepsilon _\mathrm{fQ}\nonumber \\&+\,0.2\varepsilon _h -0.2\varepsilon _\phi -0.0\varepsilon _\delta . \end{aligned}$$
(68c)

These results are consistent with those obtained by Kuznetsov and Nield (2014) for the single-diffusive problem.

We also obtained the following results:

For \({Ra}_\mathrm{C} = 100\), \(\delta = 0.1\),

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C}= & {} 249.6+250.0\varepsilon _\mathrm{fk} +0.1\varepsilon _\mathrm{sk} -252.4\varepsilon _K -144.7\varepsilon _\mathrm{fQ} \nonumber \\&+\,3.3\varepsilon _h +71.3\varepsilon _\phi -0.1\varepsilon _\delta -98.9\varepsilon _\mathrm{CQ} . \end{aligned}$$
(69a)

For \({Ra}_\mathrm{C} = 100\), \(\delta = 0.5\),

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C}= & {} 249.6+163.4\varepsilon _\mathrm{fk} +0.1\varepsilon _\mathrm{sk} -213.6\varepsilon _K -40.2\varepsilon _\mathrm{fQ} \nonumber \\&+\,3.0\varepsilon _h +83.0\varepsilon _\phi -0.1\varepsilon _\delta -27.3\varepsilon _\mathrm{CQ} . \end{aligned}$$
(69b)

For \({Ra}_\mathrm{C} = 100\), \(\delta = 0.9\),

$$\begin{aligned} {Ra}+{Ra}_\mathrm{C}= & {} 249.6+11.0\varepsilon _\mathrm{fk} +0.0\varepsilon _\mathrm{sk} -62.5\varepsilon _K +4.1\varepsilon _\mathrm{fQ} \nonumber \\&+\,0.1\varepsilon _h +10.5\varepsilon _\phi -0.0\varepsilon _\delta +2.8\varepsilon _\mathrm{CQ} . \end{aligned}$$
(69c)

We see immediately that weak heterogeneity of the interphase heat transfer coefficient h, the solid thermal conductivity \(k_\mathrm{s}\) and the volume fraction \(\delta \) each have little effect on stability. Accordingly we can now concentrate on the heterogeneity of the remaining quantities, namely the fluid thermal conductivity, the permeability, the source strength in the fluid phase, the porosity and the concentration source strength.

Comparison of Eqs. (69a–c) with (68a–c) shows that the constant and the permeability coefficient are little altered, as one would expect. When the solutal Rayleigh number is increased, the fluid conductivity and the fluid-phase heat-source-strength coefficients are reduced in magnitude and the porosity coefficient is increased. Also, of course, the heterogeneity of concentration source strength becomes effective.

Further, from the signs of the coefficients in Eqs. (68a–c) and (69a–c), we make the following conclusions. An increase in permeability in the upwards direction is destabilizing, while an increase in fluid thermal conductivity in the upwards direction is stabilizing. An increase in the upward direction of the heat source strength in the fluid phase is generally destabilizing. These trends, noted by Kuznetsov and Nield (2014), are in agreement with our expectation. With internal heating, the basic temperature gradient is positive in the upper portion of the domain, and so anything that aids the onset of convection in the upper portion is expected to be destabilizing. We also see that an increase in the upward direction of the concentration source strength is generally destabilizing.

A validation of the correlations expressed by Eqs. (68a–c) and (69a–c) is provided by a comparison with the results obtained by using a fully numerical solution of Eqs. (48–55). Numerical results with a high accuracy have been obtained by means of a Runge–Kutta solver coupled with the shooting method. This numerical procedure has been performed by employing the software package Mathematica 10 ( Wolfram Research, Champaign, IL). More details on this method can be found in the literature as, for example, Straughan (2008), Rees and Bassom (2000) and Barletta and Storesletten (2011). Table 1 reveals that the discrepancy is smaller than 10 %. Higher discrepancies are found when the heterogeneity parameters become higher. For this reason, the analysis for strong heterogeneity performed in the next section was carried out numerically by employing the highly accurate numerical solver. The initial guess for the shooting method was generated by the second-order weighted residuals solution described at the beginning of this section.

Table 1 Critical values of the combined Rayleigh number for \(\delta = 0.5\), \(N =10\), \(\gamma = 10\), \(K_\mathrm{r}=1\), \(k_\mathrm{fr} = 1\), \(k_\mathrm{sr} = 1\), \(h_\mathrm{r} = 1\), \(\delta _\mathrm{r} = 1\), Le \(=1\), \({Ra}_\mathrm{C} = 100\): comparison between the analytical and the numerical solution
Full size table

3.3 Strong Heterogeneity

We consider the case of layers of equal thickness \((\delta = 0.5)\), where the variation of each heterogeneity parameter is doubled or halved, and with the LTNE values set at \(N= 1\), \(\gamma =1\) and with \(\hbox {Le}=1\). Since our weak heterogeneity results have shown that variation in \(k_\mathrm{s}\), h or \(\delta \) is not important, we have set \(k_\mathrm{sr} = 1\), \(h_\mathrm{r} = 1\), \(\delta _\mathrm{r} = 1\) for our subsequent calculations. Further, since the effects of heterogeneity of K and \(k_\mathrm{f}\) are already well understood (see Kuznetsov and Nield 2014), we also set \(K_\mathrm{r}=1\), \(k_\mathrm{fr} = 1\). This leaves us with the heterogeneity of \(Q_\mathrm{f}\), \(Q_\mathrm{C}\) and \(\phi \) to be examined in more detail. We obtained the results presented in Table 2.

Table 2 Critical values of the combined Rayleigh number and the corresponding wavenumber for various ratios of the heat source strength in the fluid phase, concentration source strength and porosity. Case \(\delta = 0.5\), \(N =1\), \(\gamma = 1\), \(K_\mathrm{r}=1\), \(k_\mathrm{fr} = 1\), \(k_\mathrm{sr} = 1\), \(h_\mathrm{r} = 1\), \(\delta _\mathrm{r} = 1\), Le=1, \({Ra}_\mathrm{C} = 100\)
Full size table

These results show that, in moving from region 1 to region 2, increase in \(\phi \) is stabilizing (increasing the critical Rayleigh number), while increase in any of \(Q_\mathrm{f}\) or \(Q_\mathrm{C}\) is destabilizing (decreasing the critical Rayleigh number). The effect of heterogeneity of \(\phi \) is substantial when double diffusion comes into play. These trends are in accord with those obtained for weak heterogeneity. The source effects are in accord with our expectation. A more intense heat or concentration source in the upper region (where the vertical basic temperature gradient is negative) aids the onset of convection. The effect of porosity heterogeneity is more subtle and the trend was not anticipated. It appears to be a consequence of the fact that the convective transfer of solute concentration occurs only in the fluid phase. Thus the greater the porosity, the more the solutal buoyancy effect is weakened by being more spread out.

The critical wavenumber is affected to a lesser degree. Increase in either \(Q_\mathrm{f}\) or \(Q_\mathrm{C}\) results in an increase in that wavenumber, while increase in \(\phi \) leads to a variable change in the critical wavenumber.

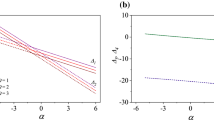
In Figs. 1 and 2 we have plotted curves showing the variation of the critical combined Rayleigh number and the corresponding critical wavenumber with the most critical parameters. These show in more accessible format the trends shown in Table 2.

Fig. 1
figure 1

Plots of the critical combined Rayleigh number \(Ra + {Ra}_\mathrm{C}\) (a) and the critical wavenumber \(a_\mathrm{c}\) (b) versus fluid heat source strength ratio \(Q_\mathrm{fr}\) for various values of the porosity ratio \(\phi _\mathrm{r}\). Case \(\delta = 0.5\), \(N =1\), \(\gamma = 1\), \(K_\mathrm{r}=1\), \(k_\mathrm{fr} = 1\), \(k_\mathrm{sr} = 1\), \(h_\mathrm{r} = 1\), \(\delta _\mathrm{r} = 1\), Le = 1, \(Q_\mathrm{Cr} = 1\), \({Ra}_\mathrm{C} = 100\)

Full size image
Fig. 2
figure 2

Plots of the critical combined Rayleigh number \(Ra + {Ra}_\mathrm{C}\) (a) and the critical wavenumber \(a_\mathrm{c}\) (b) versus concentration source strength ratio \(Q_\mathrm{Cr}\) for various values of the porosity ratio \(\phi _\mathrm{r}\). Case \(\delta = 0.5\), \(N =1\), \(\gamma = 1\), \(K_\mathrm{r}=1\), \(k_\mathrm{fr} = 1\), \(k_\mathrm{sr} = 1\), \(h_\mathrm{r} = 1\), \(\delta _\mathrm{r} = 1\), Le = 1, \(Q_\mathrm{fr} = 1\), \({Ra}_\mathrm{C} = 100\)

Full size image

4 Conclusion

We have investigated the interaction between the effects of heterogeneity and local thermal non-equilibrium on the onset of double-diffusive convection in a porous medium consisting of two horizontal layers with volumetric heat and solute sources. There is a large parameters space, and in performing our investigations we found which parameters are important; this can be crucial for further numerical investigations of this system. We found that, as in the case of single-diffusive convection, major effects result from heterogeneity of permeability, fluid thermal conductivity and heat source strength in the fluid phases. With double diffusion there are additional major effects from the heterogeneity of solutal source strength and the heterogeneity of porosity (as distinct from heterogeneity of permeability). A lesser effect results from heterogeneity of the interphase heat transfer coefficient. Heterogeneity of solid thermal conductivity and heterogeneity of heat source strength in the solid phase are relatively unimportant. Our results also show in which direction the changes in the effective combined Rayleigh number will occur and the likely magnitude of those changes.

We remark that further complications would arise if one included the effect of throughflow.