1 Introduction

The demand of water for human consumption is continuously increasing. Although the amount of water is estimated to be about \(1.38\,\hbox {billion km}^{3}\) worldwide, only 2.5 % of this amount is freshwater. Most of it is locked up in ice and in the underground leaving only about 1.2 % of all freshwater (only 2.5 % of all water) as surface water, which provides most of life needs (USGS 2014 with data from Shiklomanov 1993). The availability of good-quality freshwater resources is also decreasing dramatically because of the increase in severe pollution and irrational waste (Mathioulakis et al. 2007). Therefore, new low-cost desalination processes have been a topic of growing research interest (Spiegler and El-Sayed 2001; Anderson et al. 2010; Villar et al. 2010).

Capacitive deionization (CDI) is an electrochemical water treatment process that can be a viable alternative for treating water at low energy demand. CDI works by sequestering ions, or other charged species, in the electrical double layers of ultracapacitors. The ion removal step stores capacitive energy that can be recycled to reduce the total energy budget of the process (Anderson et al. 2010; Porada et al. 2013). The process efficiency depends on the electrode available area to store ions. Therefore, porous materials with high surface area are chosen as electrodes. Mesoporous carbon materials are suitable for CDI electrodes because of their high surface area and desirable pore size range (Zhou et al. 2008; Liu et al. 2010; Tsouris et al. 2011).

Biesheuvel and Bazant (2010) presented a model for capacitive charging and desalination by ideally polarizable porous electrodes. This model excludes effects of faradaic reactions or specific adsorption of ions. The authors discussed the theory for the case of a dilute, binary electrolyte using the Gouy–Chapman–Stern (GCS) model of the EDL. This model has been extended to include faradaic reactions and a dual-porosity (macropores and micropores) approach (Biesheuvel et al. 2011) which considers that the electrodes are composed of solid particles that are porous themselves. Biesheuvel et al. (2011) for the first time used a novel modified-Donnan (mD) approach for the micropores, valid for strongly overlapped double layers. Biesheuvel et al. (2012) also presented a porous electrode theory for ionic mixtures, including faradaic reactions. Recently, Biesheuvel and Porada (2014) improved the mD model by making the ionic attraction term dependent on total ion concentration in the carbon pores. The authors reported that the new mD model significantly improves predictions of the influence of salt concentration on CDI performance.

The goal of this paper is to use the volume averaging method (Whitaker 1999) to conduct a detailed analysis of the CDI process in the case of porous materials of homogeneous size distribution.

2 Theoretical Development

2.1 Model Description

The physical model used in this work is based on the one proposed by Biesheuvel and Bazant (2010). The porous electrode is divided into pore space filled with quasi-neutral electrolyte and a solid matrix. The solution inside the pore space exchanges ions with a charged, thin double-layer “skin” on the electrode matrix. A key assumption in this model is that the double-layer “skin,” containing the diffuse ionic charge that screens the surface charge, is thin compared to the typical pore size in the electrode (Levich 1962; Tiedemann and Newman 1975; Bazant et al. 2004; Chu and Bazant 2006; Biesheuvel et al. 2009).

The Biesheuvel and Bazant (2010) approach is based on Newman’s macroscopic porous electrode theory (Johnson and Newman 1971; Newman and Thomas-Alyea 2004), with the same assumptions made. The local salt concentration and electrostatic potential of the quasi-neutral solution within the pores are assumed to vary slowly enough to permit volume averaging to yield smooth macroscopic variables. The exchange of ions with the double layers on the pore surfaces is modeled as a slowly varying volumetric source/sink term in the macroscopic, volume-averaged transport equations. The porous electrode is thus treated as a homogeneous mixture of charged double layers and quasi-neutral solution, see original work by Biesheuvel and Bazant (2010) for more details.

We will follow a route based on the volume averaging method (VAM) developed by Prof. S. Whitaker and co-workers over a period of many years (Whitaker 1999). In the bulk of the quasi-neutral solution filling the pores, the Nernst–Planck (NP) equation is used (Pivonka et al. 2007, 2009; Scheiner et al. 2010). The ion flux of species i is given by:

$$\begin{aligned} \underline{N}_{i} = -D_{i} \{\underline{\nabla }c_{i} + (z_{i}\, F\,c_{i} / R\,T) \underline{\nabla }\phi \}, \end{aligned}$$
(1)

where \(N_{i}\) is the ion flux, \(c_{i}\) is the ion concentration, \(\underline{\nabla }\) is the nabla operator for one-dimensional variation in \(x\) the spatial position, \(z_{i}\) is the ion charge, \(D_{i}\) is the diffusion coefficient of ionic species \(i\), and \(\phi \) is the electrostatic potential in the pores. Equation (1) has been derived assuming that the isotropic mobility, \(u_{i}\), is given by the Nernst–Einstein relation (Bockris et al. 2000) for constant absolute temperature \(T \;(u_{i} = D_{i} /R\,T)\).

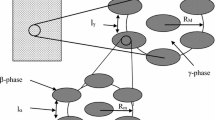
We consider a two-phase medium consisting of an \(\upalpha \) phase (liquid) and a \(\upbeta \) phase (solid) as shown in Fig. 1. The point species molar continuity equation, including the NP expression for the molar flux for the \(\upalpha \) phase, is given by:

$$\begin{aligned} \partial c_{i}/\partial t = - \underline{\nabla }\bullet \underline{N}_{i}. \end{aligned}$$
(2)

Substituting Eq. (1) into (2) yields:

$$\begin{aligned} \partial c_{i}/\partial t = \underline{\nabla }\bullet (D_{i} \{\underline{\nabla } c_{i} + z_{i} c_{i} \underline{\nabla } \phi /V_\mathrm{T}\}). \end{aligned}$$
(3)

Here, the thermal voltage \((V_\mathrm{T})\) is given by, \(V_\mathrm{T}= R\,T / F\). In the case of a monovalent ionic salt, NaCl for example, Eq. (3) leads to two differential equations for the positive and negative ions. Adding up these equations leads to a single equation in the salt concentration, \(c\), where the migration terms disappear if \(c_{-} = c_{+} = c\) and \(D = D_{-} = D_{+}\):

$$\begin{aligned} \partial c/\partial t = \underline{\nabla }\bullet (D \underline{\nabla } c). \end{aligned}$$
(4)

The corresponding boundary condition at the liquid–solid interface \((A_{\upalpha \upbeta })\) is given by:

$$\begin{aligned} - \underline{n}_{\upalpha \upbeta } \bullet (D \underline{\nabla } c) = J_\mathrm{salt}, \end{aligned}$$
(5)

where \({\underline{n}}_{\underline{{\upalpha \upbeta }}}\) is the unit outwardly directed normal vector pointing from the \(\upalpha \)-phase into the \(\upbeta \)-phase, and \(J_\mathrm{salt}\) is the salt molar flux from the pore phase into the diffuse double layers on the electrode surface.

Fig. 1
figure 1

Porous medium and representative elementary volume (REV)

Full size image

In order to calculate the electrostatic potential in the system, we follow the Johnson and Newman (1971) derivation. This formulation requires that we solve for the pore phase of the electrode the differential Ohm’s law for the current carried by the ions per unit area \((\underline{I}_{e})\) given by:

$$\begin{aligned} \underline{I}_e / F =\sum _{i=1}^N {z_i\,\underline{N}_{i}}, \end{aligned}$$
(6)

where \(F\) is the Faraday constant. We assume \(c_{+} = c_{-} = c, D = D_{-} = D_{+},\) and \(z_{+} = 1 = -z_{-}\) and substitute Eq. (1) into Eq. (6) to obtain:

$$\begin{aligned} \underline{I}_{e}/ F = = - \kappa \underline{\nabla }\phi , \end{aligned}$$
(7)

where \(\kappa \), the effective conductivity of the solution phase, is calculated using:

$$\begin{aligned} \kappa = c\,F (u_{+} + u_{-}) = 2 D\,F\,c / R\,T. \end{aligned}$$
(8)

A local charge balance in the bulk fluid for a quasi-neutral binary electrolyte leads to:

$$\begin{aligned} \underline{\nabla }\bullet (\underline{I}_{e}/F) = - \underline{\nabla }\bullet (\kappa \underline{\nabla }\phi ) = - \underline{\nabla }\bullet \left( \frac{2 D}{V_\mathrm{T}}c \underline{\nabla }\phi \right) = 0, \end{aligned}$$
(9)

with the corresponding boundary condition at the interphase \(\upalpha \)–\(\upbeta \):

$$\begin{aligned} - \underline{n}_{\upalpha \upbeta } \bullet (\kappa \underline{\nabla } \phi ) = J_\mathrm{charge}. \end{aligned}$$
(10)

Here, \(J_\mathrm{charge}\) describes the charge-transfer flux from the pore solution into the interphase.

In order to close the porous electrode model, we follow Biesheuvel and Bazant (2010) to relate the rate of charge removal from the liquid phase, \(J_\mathrm{charge}\), to the excess charge density, \(-q\), by:

$$\begin{aligned} \partial q/\partial t = J_\mathrm{charge}, \end{aligned}$$
(11)

and \(J_\mathrm{salt}\) to the excess salt adsorbed, \(w\), by:

$$\begin{aligned} \partial w/ \partial t = J_\mathrm{salt}. \end{aligned}$$
(12)

Equations (11) and (12) define source terms that will enter into the averaged equations during the averaging process. These source terms will be described in this work using a methodology similar to the one proposed by Carbonell and Whitaker (1983) in their study of nonlinear adsorption. We propose using the GCS model (Bazant et al. 2004; Chu and Bazant 2006; Zhao et al. 2010) that leads to:

$$\begin{aligned} w= & {} F(c, \phi ) = 8 \lambda _\mathrm{D} C_{\infty }\sqrt{c/C_\infty } \,\hbox {sinh}^{2}(\Delta \phi _\mathrm{D}/4/ V_\mathrm{T}), \end{aligned}$$
(13)
$$\begin{aligned} \hbox {and}\,q= & {} G(c, \phi ) = - 4 \lambda _\mathrm{D} C_{\infty } \sqrt{c/C_\infty }\,\hbox {sinh}(\Delta \phi _\mathrm{D}/2/V_\mathrm{T}), \end{aligned}$$
(14)

where \(C_{\infty }\) is the bulk concentration, \(\Delta \phi _\mathrm{D}\) is the potential difference over the diffuse layer, (\(\Delta \phi _\mathrm{D}=\phi _\mathrm{Stern}-\phi ), \phi _\mathrm{Stern}\) is the Stern potential, \(\lambda _\mathrm{D}\) is the Debye length (\(\lambda _\mathrm{D}=1/\sqrt{8 \pi \lambda _\mathrm{B} N_\mathrm{av} C_\infty }), N_\mathrm{av}\) is the Avogadro number, and \(\lambda _\mathrm{B}\) (the Bjerrum length) is \(\sim 0.72\,\hbox {nm}\) at room temperature.

Zhao et al. (2010) reported that a key property of the porous electrode is the charge efficiency of the double layer, \(\varLambda \), defined as the ratio of equilibrium salt adsorption over electrode charge, and from Eqs. (13) and (14), the charge efficiency is given by, \(\varLambda = \hbox {tanh}(\Delta \phi _\mathrm{D}/4)\). The authors also presented experimental data for \(\varLambda \) as a function of voltage and salt concentration and used this data set to characterize the double-layer structure inside of the electrode and determine the effective area for ion adsorption.

Equations (9) and (10) cannot be solved independently for the electrostatic potential in the liquid phase \((\phi )\) due to the dependence of the effective conductivity of the solution on the ionic strength \(c\). This is an important difference with the electrophoretic problem studied by Locke (1998), where the electrostatic potential can be calculated independently of the solute concentration in most situations. Therefore, the averaging procedure will yield two differential equations in the potential and salt concentration which can only be solved simultaneously.

2.2 Species Continuity Equation

We start our derivation from Eq. (4) and the boundary condition at the \(\upalpha \)–\(\upbeta \) interphase given by Eq. (5). The boundary conditions in the input–output area of the macroscopic domain are not relevant to the volume averaging method, as several authors (Ryan et al. 1980; Carbonell and Whitaker 1984; Nozad et al. 1985; Whitaker 1986; Quintard and Whitaker 1998; Locke 1998; Ulson de Souza and Whitaker 2003) have proved that the problem under study can be always expressed by a local problem that does not require knowledge of these boundary conditions. The physical system defined by Eqs. (4) and (5) is somewhat similar to the diffusion with surface adsorption problem studied by several authors (Quintard and Whitaker 1998; Ulson de Souza and Whitaker 2003). The source term enters into the volume- averaged equation through the boundary condition. The source terms in this work are highly nonlinear, describing the mass and charge- transfer fluxes into the double layers.

A variety of averages is encountered in this type of analysis (Whitaker 1999). The traditionally encountered averages are the phase average given by:

$$\begin{aligned} \langle c_{\upalpha }\rangle =\frac{{1}}{{V}}\int \limits _{V} {{c}_{\upalpha }{\hbox { d}V}} , \end{aligned}$$
(15)

and the intrinsic phase average which takes the form:

$$\begin{aligned} \langle {c}_{\upalpha } \rangle ^{\upalpha }=\frac{{1}}{{V}_\upalpha }\int \limits _{V} {{c}_{\upalpha } {\hbox { d}V}} = \varepsilon _{\upalpha } \langle {c}_{\upalpha } \rangle . \end{aligned}$$
(16)

Here, \(V\) is the volume of the REV, \({V}_\upalpha \) represents the volume of the \(\upalpha \) phase contained within the REV, and \(\varepsilon _{\upalpha }\) is the volume fraction given explicitly by \(\varepsilon _{\upalpha }={V}_\upalpha /V\). We also use the spatial averaging theorem (Gray and Lee 1977) that takes the form for a scalar variable \(\psi _{\upalpha }\):

$$\begin{aligned} \langle \underline{\nabla }{\psi }_{\upalpha } \rangle =\underline{\nabla }\langle {\psi }_{\upalpha } \rangle +\frac{{1}}{{V}}\int \limits _{{A}_{\upalpha \upbeta }} {{{\underline{{n}}}_{{\upalpha \upbeta }} {\psi }_{\upalpha }} {\hbox { d}A}}. \end{aligned}$$
(17)

After repeated use of the averaging tools described above, plus algebraic manipulations, we obtain the following volume-averaged equation:

$$\begin{aligned} \varepsilon _{\upalpha } \partial \langle {c}_\upalpha \rangle ^{\upalpha }/\partial t = \underline{\nabla } \bullet \left( {\underline{\underline{D}}}_{\mathrm{eff}} \bullet \underline{\nabla }\langle {c}_\upalpha \rangle ^{\upalpha }\right) + \underline{\nabla } \bullet (D \varepsilon _{\upalpha } \underline{u} \partial \langle {w}\rangle _{\upalpha \upbeta } /\partial t) - a_{v} \partial \langle {w}\rangle _{\upalpha \upbeta } /\partial t. \end{aligned}$$
(18)

Here, \(a_{v}\) is the effective area, and \(\langle {w}\rangle _{\upalpha \upbeta } \) is the excess salt adsorption averaged at the interphase area \(\upalpha \)–\(\upbeta \) and calculated by:

$$\begin{aligned} \partial \langle {w}\rangle _{\upalpha \upbeta } /\partial t = \langle {J}_{\mathrm{salt}} \rangle _{{\upalpha \upbeta }} =\frac{\partial }{\partial { t}}\left\{ \frac{{1}}{{A}_{\upalpha \upbeta }}\int \limits _{{A}_{{\upalpha \upbeta }}} {{ w}} \hbox { d}A\right\} . \end{aligned}$$
(19)

Here, we have used Eq. (12) and permutated the integral and derivative operations. \({\underline{\underline{D}}}_{\mathrm{eff}}\) is the effective diffusivity tensor given by:

$$\begin{aligned} {\underline{\underline{D}}}_{\mathrm{eff}} ={\varepsilon }_{\upalpha } {D} \left( {\underline{\underline{I}}} +\frac{1}{A}_{{\upalpha \upbeta }}\int \limits _{{A}_{{\upalpha \upbeta }}}{\underline{{n}}}_{{\upalpha \upbeta }} \underline{{f}}_{1} \hbox { d}A\right) . \end{aligned}$$
(20)

The vector \(\underline{u}\) is given by:

$$\begin{aligned} \underline{{u}}=\frac{{1}}{{V}_{\upalpha }}\int \limits _{{A}_{{\upalpha \upbeta }}} {{\underline{{n}}}_{{\upalpha \upbeta }} {f}_{2} {\hbox { d}A}} . \end{aligned}$$
(21)

In the derivation of the volume-averaged equations, we have used the following equations:

$$\begin{aligned} c_{\upalpha }= & {} \langle {c}_\upalpha \rangle ^{{\upalpha }}+{\tilde{c}}_{\upalpha } \end{aligned}$$
(22)
$$\begin{aligned} \hbox {and}\; {\tilde{c}}_{\upalpha }= & {} \underline{{f}}_{1} {\bullet }\underline{\nabla }\langle {c}_\upalpha \rangle ^{{\upalpha }}+ f_{2} \partial \langle {w}\rangle _{\upalpha \upbeta }/\partial t. \end{aligned}$$
(23)

Equation (22) is an application of Gray’s decomposition (Gray 1975), while Eq. (23) has been derived by introducing Eq. (22) into the boundary condition given by Eq. (5). In the derivation of Eq. (23), we considered the local closure problem to be quasi-stationary. Crapiste et al. (1986) in their study of diffusion with first-order reaction in porous media concluded that the local process in the REV is quasi-stationary when the following restriction holds:

$$\begin{aligned} t^{*} {D}/{l}_{\upalpha }^{2} >> 1, \end{aligned}$$
(24)

where \(t^{*}\) is the characteristic time for the mass transport process, \(l_{\upalpha }\) is a characteristic length of the micro-scale, and \(D\) is the diffusion coefficient. According to Biesheuvel and Bazant (2010), the characteristic time for the supercapacitor regime (\({t}_{C}^{\bullet }\)) and the characteristic time for the desalination regime (\({t}_{D}^{\bullet }\)) both satisfy the condition given by Eq. (24).

The \(\underline{f}_{1}\) vector field and the scalar \(f_{2}\) field required for calculation of the effective diffusivity tensor and the \(u\)-vector given by Eq. (21) are calculated by solving the following boundary value problems:

Problem 1

$$\begin{aligned}&\underline{\nabla }^{{2}}\underline{{f}}_{1} ={0} \end{aligned}$$
(25)
$$\begin{aligned}&- \underline{n}_{\upalpha \upbeta } \bullet \underline{\nabla }\underline{{f}}_1 = \underline{n}_{\upalpha \upbeta }, \end{aligned}$$
(26)

in the \(A_{\upalpha \upbeta }\) and for spatially periodic porous media,

$$\begin{aligned} \underline{f}_{1}(\underline{r}+\underline{l}_{i}) = \underline{f}_{1}(\underline{r}). \end{aligned}$$
(27)

Problem 2

$$\begin{aligned}&\underline{\nabla }^{{2}}{f}_{2} =-a_{v}/{({\varepsilon }_\upalpha {D)}} \end{aligned}$$
(28)
$$\begin{aligned}&- \underline{n}_{\upalpha \upbeta } \bullet \underline{\nabla }{f}_2 = 1/D, \end{aligned}$$
(29)

in the \(A_{\upalpha \upbeta }\) and also for spatially periodic porous media,

$$\begin{aligned} \underline{f}_{2}(\underline{r}+\underline{l}_{i}) = \underline{f}_{2}(\underline{r})\quad \hbox {for}\; i = 1, 2, 3. \end{aligned}$$
(30)

Here, and in Eq. (25), \(\underline{l}_{i}\) represents the three non-unique lattice vectors that are needed to describe a spatially periodic porous medium (Brenner 1980).

An order of magnitude analysis based upon Eq. (29), see “Appendix,” proves that the second term on the right-hand-side can be eliminated compared to the last. This leads to:

$$\begin{aligned} \varepsilon _{\upalpha } \partial \langle {c}_\upalpha \rangle ^{\upalpha } / \partial t = \underline{\nabla } \bullet ({\underline{\underline{D}}}_{\mathrm{eff}} \bullet \underline{\nabla } \langle {c}_\upalpha \rangle ^{\upalpha }) - a_{v} \partial \langle {w}\rangle _{\upalpha \upbeta } / \partial t. \end{aligned}$$
(31)

Equation (31) is identical to the one derived by Biesheuvel and Bazant (2010). This result is also similar to those obtained by Ryan et al. (1980) and Crapiste et al. (1986) for the case of diffusion and first-order reaction in porous media. Ryan et al. (1980) concluded that the effect of the heterogeneous reaction on the \(\underline{f}_{1}\)-field was negligible and that a geometrical surface source term, represented by \(\underline{n}_{\upalpha \upbeta }\), was the dominant characteristic of the flux boundary condition. After this simplification, problem 1 is the only relevant closure problem to be solved. This problem was presented earlier by Ryan et al. (1980) and solved numerically to produce excellent agreement between theory and experiment. Several authors have also solved successfully this closure problem or similar ones (Kim et al. 1987; Gabitto 1991; Quintard 1993; Ochoa-Tapia et al. 1993; Borges da Silva et al. 2007; Valdes-Parada and Alvarez-Ramirez 2010). The boundary value problem defined by Eqs. (25)–(27) depends only upon the geometric characteristics of the porous medium and, therefore, can be solved to evaluate the effective diffusivity tensor.

2.3 Electrical Potential

We start our derivation from Eq. (9) and the boundary condition at the \(\upalpha \)–\(\upbeta \) interphase given by Eq. (10). Again, the boundary conditions in the input–output area of the macroscopic domain are not relevant to the volume averaging method, as the problem can be expressed by a local problem. The physical system defined by Eqs. (9) and (10) is somewhat similar to the diffusion–dispersion problem with heterogeneous reaction and/or absorption studied by several authors (Carbonell and Whitaker 1983; Quintard and Whitaker 1998; Ochoa-Tapia et al. 1994; Borges da Silva et al. 2007; Ulson de Souza and Whitaker 2003; Paine et al. 1983; Buyuktas and Wallender 2004). In the dispersion studies, we have an independently calculated vector field (\(\underline{v}\)) that influences the value of the concentration scalar field. The analysis of electrophoretic transport done by Locke (1998) presented a similar situation with the electric field vector, also independently calculated, replacing the velocity vector field. In both cases, the vector field satisfies a zero divergence condition. The source term enters into the volume-averaged equation through the boundary condition. However, in this work, the concentration and potential gradient distributions cannot be calculated independently.

We proceed applying the phase average operation defined by Eq. (12) to both sides of Eq. (9). Repeated use of the tools described above leads to:

$$\begin{aligned}&\underline{\nabla } \bullet \left\{ {\underline{\underline{U}}}_{\mathrm{eff}} \bullet \langle {c}_\upalpha \rangle ^{\upalpha } \underline{\nabla }\langle \phi _\upalpha \rangle ^{{\upalpha }}\right\} +\underline{\nabla }{\bullet }\left\{ \frac{{\varepsilon }_{\upalpha } { U}{\left\langle {{c}_{\upalpha }} \right\rangle }^{\upalpha }}{{V}_{\upalpha }}\left( \int \limits _{{A}_{{\upalpha \upbeta }}} \underline{{n}}_{{\upalpha \upbeta }} {g}_{2}\hbox { d}A\right) \frac{\partial {\left\langle {q} \right\rangle }_{{\upalpha \upbeta }}}{\partial {t}} \right\} \nonumber \\&\quad + \,\underline{\nabla } \bullet \left\{ \frac{{\varepsilon }_{\upalpha } { U}}{{V}_{\upalpha }}\int \limits _{{V}_\upalpha } {{{\tilde{c}}}_\upalpha \underline{\nabla }{\tilde{\phi }}_\upalpha { \hbox { d}V}} \right\} - a_{v} \quad \frac{\partial {\left\langle {q} \right\rangle }_{{\upalpha \upbeta }}}{\partial {t}} = 0. \end{aligned}$$
(32)

Here, \(U= 2 D/V_\mathrm{T}\) and \(\partial \langle q\rangle _{\upalpha \upbeta } /\partial t\) is the time variation of the excess charge averaged at the interphase area \(\upalpha \)–\(\upbeta \) calculated by:

$$\begin{aligned} \partial \langle {q}\rangle _{\upalpha \upbeta }/\partial t = \langle {J}_{\mathrm{charge}} \rangle _{{\upalpha \upbeta }} =\frac{\partial }{\partial { t}}\left\{ \frac{{1}}{{A}_{\upalpha \upbeta }}\int \limits _{{A}_{{\upalpha \upbeta }}} {{q}}\hbox { d}A\right\} . \end{aligned}$$
(33)

We have used Eq. (11) to relate the excess adsorbed charge \(q\) to \(J_\mathrm{charge}\). The effective mobility tensor, \({\underline{\underline{U}}}_{\mathrm{eff}}\), is given by:

$$\begin{aligned} {\underline{\underline{U}}}_{\mathrm{eff}} ={\varepsilon }_{\upalpha } \frac{{2 D}}{{V}_\mathrm{T}}\left( {\underline{\underline{I}}} +\frac{{1}}{{V}_{\upalpha }}\int \limits _{{A}_{{\upalpha \upbeta }}} {\underline{{n}}}_{{\upalpha \upbeta }} \underline{{g}}_{1}\hbox { d}A\right) . \end{aligned}$$
(34)

The term \(\frac{{1}}{{V}_{\upalpha }}\int \limits _{{V}_\upalpha } {{{\tilde{c}}}_\upalpha \underline{\nabla }{\tilde{\phi }}_\upalpha {\hbox { d}V}} =\langle {{\tilde{c}}}_\upalpha \underline{\nabla }\tilde{\phi }\rangle ^{{\upalpha }}\) accounts for the “dispersion-like” interaction between the salt concentration and the electric field. It should be noted that the dispersion-like term depends upon a volume integral.

In deriving Eq. (32), we have used that

$$\begin{aligned} \phi _{\upalpha }=\langle \phi _\upalpha \rangle ^{{\upalpha }}+\tilde{\phi }_{\upalpha }, \end{aligned}$$
(35)

and

$$\begin{aligned} \tilde{\phi }_\upalpha =\underline{{g}}_{1} {\bullet }\underline{\nabla }\langle \phi _\upalpha \rangle ^{{\upalpha }}+ g_{2} \partial \langle {q}\rangle _{\upalpha \upbeta }/\partial t. \end{aligned}$$
(36)

Equation (35) is an application of Gray’s decomposition for \(\phi _{\upalpha }\). Equation (36) has been derived by introducing Eq. (35) into the boundary condition given by Eq. (10) and following the procedure presented by Carbonell and Whitaker (1983) to obtain the local closure problem. In the derivation of Eq. (36), we have also considered the local closure problem to be quasi-stationary and used order of magnitude analysis.

The vector field \(\underline{g}_{1}\) and the scalar field \(g_{2}\) that map the gradient of the averaged potential in the liquid phase and the excess charge source term onto the potential deviations can be calculated by solving the following boundary value problems:

Problem 3

$$\begin{aligned}&\underline{\nabla }^{{2}}\underline{{g}}_{1} =0 \end{aligned}$$
(37)
$$\begin{aligned}&- \underline{n}_{\upalpha \upbeta } \bullet \underline{\nabla }\underline{{g}}_1 = \underline{n}_{\upalpha \upbeta }, \end{aligned}$$
(38)

in the \(A_{\upalpha \upbeta }\) and for spatially periodic porous media,

$$\begin{aligned} \underline{{g}}_1 (\underline{r}+\underline{l}_{i})=\underline{{g}}_1 (\underline{r}). \end{aligned}$$
(39)

Problem 4

$$\begin{aligned} \underline{\nabla }^{{2}}{g}_{2}= & {} {-a}_{v} {V}_\mathrm{T}/ \left( 2 \varepsilon _\upalpha D{\left\langle {{c}_{\upalpha }} \right\rangle }^{\upalpha }\right) \end{aligned}$$
(40)
$$\begin{aligned} - \underline{n}_{\upalpha \upbeta } \bullet \underline{\nabla }{g}_{2}= & {} V_\mathrm{T}/ (2 D{\left\langle {{c}_{\upalpha }} \right\rangle }^{\upalpha }), \end{aligned}$$
(41)

in the \(A_{\upalpha \upbeta }\) and for spatially periodic porous media:

$$\begin{aligned} {g}_{2} (\underline{r}+\underline{l}_{i})={g}_{2} (\underline{r}). \end{aligned}$$
(42)

Inspection of the closure problems shows that problem 3 is identical to problem 1 and problem 4 becomes dependent on the average salt concentration. The latter result reflects the fact that salt migration depends on the interaction between the electric field \((-\underline{\nabla }\phi )\) and the salt concentration \((c_{\upalpha })\).

An order of magnitude analysis conducted on Eq. (32) shows that the third term can be neglected compared to the first and the second compared to the fourth, see “Appendix.” This conclusion leads to the following equation:

$$\begin{aligned} \underline{\nabla } \bullet \left\{ {\underline{\underline{U}}}_{\mathrm{eff}} \bullet \langle {c}_\upalpha \rangle ^{\upalpha } \underline{\nabla } \langle \phi _\upalpha \rangle ^{{\upalpha }}\right\} - a_{v} \quad \partial \langle {q}\rangle _{\upalpha \upbeta } /\partial t = 0. \end{aligned}$$
(43)

Equation (43) is identical to the one derived by Biesheuvel and Bazant (2010). This result makes it not necessary to solve problem 4, while the solution of problem 1 will allow us to calculate the value of the salt effective mobility tensor (\({\underline{\underline{U}}}_{\mathrm{eff}})\). An interesting additional result is that from Eqs. (20) and (34), we can see that the salt effective mobility tensor is related to the salt effective diffusivity tensor by the Einstein equation:

$$\begin{aligned} {\underline{\underline{U}}}_{\mathrm{eff}} = \frac{2{\underline{\underline{D}}}_{\mathrm{eff}}}{{V}_\mathrm{T} { F}}. \end{aligned}$$
(44)

2.4 Alternative Treatment of Source Terms

The source terms \(\partial \langle {w}\rangle _{\upalpha \upbeta }/\partial t\) and \(\partial \langle {q}\rangle _{\upalpha \upbeta }/\partial t\), which appear in Eqs. (31) and (43), could only be calculated numerically. In order to overcome this problem, we derived an alternative theoretical formulation based upon values of \(\langle {c}_\upalpha \rangle ^{{\upalpha }}\) and \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\). We followed Quintard and Whitaker (1998), expressing \(\langle {w}\rangle _{\upalpha \upbeta }\) as a function of \(\langle {c}_\upalpha \rangle ^{\upalpha }\) and \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\) using:

$$\begin{aligned} \langle {w}\rangle _{\upalpha \upbeta } = F\left( \langle {c}_\upalpha \rangle ^{{\upalpha }}, \langle \phi _\upalpha \rangle ^{{\upalpha }}\right) , \end{aligned}$$
(45)

and

$$\begin{aligned} \partial \langle {w}\rangle _{\upalpha \upbeta } /\partial t \!=\! \partial F/\partial \langle {c}_\upalpha \rangle ^{\upalpha }\partial \langle {c}_\upalpha \rangle ^{\upalpha }/\partial t \!+\! \partial F/\partial \langle \phi _\upalpha \rangle ^{{\upalpha }}\partial \langle \phi _\upalpha \rangle ^{{\upalpha }}/\partial t \!=\! F_{1} \partial \langle {c}_\upalpha \rangle ^{\upalpha }/\partial t \!+\! F_{2} \partial \langle \phi _\upalpha \rangle ^{{\upalpha }}/\partial t.\nonumber \\ \end{aligned}$$
(46)

In Eq. (46), \(F_{1}\) and \(F_{2}\) represent the partial derivatives of \(F\) with respect to \(\langle {c}_\upalpha \rangle ^{\upalpha }\) and \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\), respectively. Quintard and Whitaker (1998) derived the length-scale constraint associated with Eq. (45). Following their approach, we also required that variations of \(F_{1}\) and \(F_{2}\) be neglected within the averaging volume. Introducing Eq. (46) into Eq. (31), we obtained:

$$\begin{aligned} \varepsilon _{\upalpha } (1+a_{v} F_{1}/\varepsilon _{\upalpha }) \partial \langle {c}_\upalpha \rangle ^{\upalpha }/\partial t = \underline{\nabla } \bullet ({\underline{\underline{D}}}_{\mathrm{eff}} \bullet \underline{\nabla }\langle {c}_\upalpha \rangle ^{\upalpha }) - a_{v} F_{2}\partial \langle \phi _\upalpha \rangle ^{{\upalpha }}/\partial t. \end{aligned}$$
(47)

Equation (47) is similar to the one derived by Quintard and Whitaker (1998) and Ulson de Souza and Whitaker (2003) studying diffusion with nonlinear adsorption. The extra source term dependent on the potential appears because the excess salt concentration depends upon both concentration and potential.

We can also express \(\langle {q}\rangle _{\upalpha \upbeta } \) as a function of \(\langle {c}_\upalpha \rangle ^{\upalpha }\) and \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\) using:

$$\begin{aligned} \langle {q}\rangle _{\upalpha \upbeta } = G(\langle {c}_\upalpha \rangle ^{{\upalpha }}, \langle \phi _\upalpha \rangle ^{{\upalpha }}), \end{aligned}$$
(48)

and

$$\begin{aligned} \partial \langle {q}\rangle _{\upalpha \upbeta } /\partial t = \partial G/\partial \langle {c}_\upalpha \rangle ^{\upalpha }\partial \langle {c}_\upalpha \rangle ^{\upalpha }/\partial t + \partial G/\partial \langle \phi _\upalpha \rangle ^{{\upalpha }}\partial \langle \phi _\upalpha \rangle ^{{\upalpha }}/\partial t = G_{1}\, \partial \langle {c}_\upalpha \rangle ^{\upalpha }/\partial t + G_{2} \partial \langle \phi _\upalpha \rangle ^{{\upalpha }}/\partial t.\nonumber \\ \end{aligned}$$
(49)

Here, \(G_{1}\) and \(G_{2}\) represent the partial derivatives of \(G\) with respect to \(\langle {c}_\upalpha \rangle ^{\upalpha }\) and \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\), respectively. We also required that the length-scale constraints associated with Eq. (48) be valid and that variations of \(G_{1}\) and \(G_{2}\) be neglected within the averaging volume. Introducing Eq. (49) into Eq. (43) leads to:

$$\begin{aligned} a_{v} \, G_{2} \partial \langle \phi _\upalpha \rangle ^{{\upalpha }}/\partial t = \underline{\nabla } \bullet \{{\underline{\underline{U}}}_{\mathrm{eff}} \langle {c}_\upalpha \rangle ^{\upalpha } \underline{\nabla }\langle \phi _\upalpha \rangle ^{{\upalpha }}\} - a_{v} \,G_{1} \partial \langle {c}_\upalpha \rangle ^{\upalpha }/\partial t. \end{aligned}$$
(50)

Equation (50) shows that the potential field depends upon the time variation of the salt concentration field. The value of the two source terms depends upon the partial derivatives of \(q\) with respect to potential and concentration. The terms \(F_{1}, F_{2}, G_{1}\) and \(G_{2}\) can be computed using an appropriate EDL model, for example, the modification to the GCS model in the case of thin EDLs proposed by Biesheuvel and Bazant (2010). These authors set the ratio of the diffuse-layer Debye–Hückel and Stern-layer capacitances (\(\delta )\) equal to zero; therefore, \(\Delta \phi _\mathrm{D}=\phi _{1} - \phi \).

Equations (47) and (50) provide an alternative set of equations equivalent to the ones reported by Biesheuvel and Bazant (2010) and can be used to simulate the transport process.

These equations show explicitly terms depending upon the average electrical potential and salt concentration and not based on \(w\) and \(q\). The treatment of the source terms presented here has not been reported in literature before.

3 Numerical Calculations

3.1 Effective Diffusion Coefficients

The calculation of the effective diffusivity tensor defined by Eq. (20) has been done several times in the literature for homogeneous and heterogeneous porous media, as mentioned above. However, we solved it numerically for the case of 3D homogeneous porous media in order to validate our numerical scheme for the calculation of the other unit cell parameters given by Eqs. (25)–(27), (37)–(39) and (40)–(42). Our goal is to implement these calculations into the transport in porous electrodes model.

In the system depicted in Fig. 2, the particles are considered rectangular prisms of infinite height. Under this assumption, the process can be described by a simple two-dimensional unit cell of sides \(L_{a}\) and \(L_{b}\) containing particles of sides \(l_{a}\) and \(l_{b}\). We analyzed the isotropic case where \(l_{a} = l_{b}\). This system was originally solved by Ryan et al. (1980) and produced excellent agreement between theory and experiments.

Fig. 2
figure 2

Schematic of the isotropic porous medium

Full size image

The dimensionless diffusion tensor is calculated from:

$$\begin{aligned} {\underline{\underline{D}}}_{\mathrm{eff}} / D={\varepsilon }_{\upalpha } ({\underline{\underline{I}}} +\underline{\underline{\tau }}_{\mathrm{eff}}). \end{aligned}$$
(51)

Here, \({\underline{\underline{\tau }}}_{\mathrm{eff}}\) is the tortuosity tensor calculated from the following integral over the interphase area of the vector field \(\underline{f}_{1}\):

$$\begin{aligned} {\underline{\underline{\tau }}}_{\mathrm{eff}} =\frac{{1}}{{A}_{{\upalpha \upbeta }}}\int \limits _{{A}_{{\upalpha \upbeta }}} {{\underline{{n}}}_{{\upalpha \upbeta }} \underline{{f}}_{1} {\hbox { d}A}} . \end{aligned}$$
(52)

Since the system depicted by Fig. 2 is transversely isotropic, then \(\tau _{xx}=\tau _{yy}\) and \(\tau _{xy}=\tau _{yx}=0\). This means that the only independent, nonzero component of the effective diffusivity tensor \((D_{xx})\) is given by:

$$\begin{aligned} {D}_{{xx}} {/ D}={\varepsilon }_{\upalpha } ({1}+\tau _{{xx}}). \end{aligned}$$
(53)

3.2 “Dispersion-Like” Terms

The vector \(\underline{u}\) that appears in Eq. (21) and the “dispersion-like” term that appear in Eq. (32) were calculated numerically for the same periodic system used for calculation of the effective diffusivity coefficient. The vector \(\underline{u}\) depends upon the value of the coefficient \(f_{2}\) and was calculated using the area integral defined by Eq. (21). The \(f_{2}\) values were calculated by solving Eq. (28) subjected to the boundary conditions (29) and (30). The calculated numerical results supported the conclusion reached using order of magnitude estimates.

In order to numerically estimate the values of the second and third terms in Eq. (32), we solved for the scalar field \(g_{2}\). These parameters were calculated by solving Eqs. (40)–(42). However, the problem is dependent upon the \(\langle {c}_\upalpha \rangle ^{\upalpha }\) value. An iterative scheme was used with the following procedure. First, values of the average salt concentration, \(\langle {c}_\upalpha \rangle ^{\upalpha }\), potential, \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\), and the time derivatives, \(\partial \langle w\rangle _{\upalpha \upbeta }/\partial t\), and \(\partial \langle q\rangle _{\upalpha \upbeta }/\partial t\), were provided. Then, the deviations and concentration point values for the basic unit cell were calculated using Eqs. (22) and (23). The term \(\langle {{\tilde{c}}}_\upalpha \underline{\nabla }{\tilde{\phi }}_{\upalpha } \rangle ^{{\upalpha }}\) is calculated from the values of \(\underline{g}_{1}\) and the scalar field \(g_{2}\) by performing numerical volume integration in the basic unit cell. The values of \(\underline{g}_{1}\) were calculated using that the \(\underline{g}_{1}\) values are equal to the \(\underline{f}_{1}\) values. The whole procedure was implemented as a subroutine in a computer program that solves the full system of equations proposed in this work for simulating the CDI process in porous electrodes (Sharma et al. 2013). The values of average concentration and potential in the overall numerical scheme are calculated by iteration. We included the procedure presented here to evaluate the vector \(\underline{u}\) and the term \(\langle {{\tilde{c}}}_\upalpha \underline{\nabla }{\tilde{\phi }}_\upalpha \rangle ^{{\upalpha }}\) within the general iterative scheme. Finite difference schemes were used to solve the closure problems using the calculated average values of \(\langle {c}_\upalpha \rangle ^{\upalpha }, \langle \phi _\upalpha \rangle ^{{\upalpha }}, \partial \langle {w}\rangle _{\upalpha \upbeta }/\partial t\) and \(\partial \langle {q}\rangle _{\upalpha \upbeta }/\partial t\).

4 Results

The computer code described in Sect. 3 was validated in two different ways. First, we calculated values of the effective diffusivity tensor and compared them to simulation results and experimental data available in literature. Second, we compared calculated closure parameters with published literature results. In all our calculations, we used the simple square unit cell depicted in Fig. 2 to solve the closure problems. This unit cell was originally used by Ryan et al. (1980). Whitaker (1999) established that the only relevant geometrical information required by this transport problem in isotropic porous media was the void fraction \((\varepsilon _{\upalpha })\). In the case of anisotropic porous media, the matter is more complex (Ochoa-Tapia et al. 1994).

The results for the effective diffusivity calculations are shown in Fig. 3. We can see that there is very good agreement with results from Ryan et al. (1980) and experimental data. These results validate the proposed numerical procedure to calculate the unit cell parameters \(\underline{f}_{1}, f_{2}, \underline{g}_{1}\) and \(g_{2}\). We also calculated the integrals of the deviations variables and the gradients of these deviations variables. The accuracy of the calculations was checked by requiring that the integrals of the deviations variables be equal to zero. This condition was satisfied up to the precision error of the computer program.

We followed the reasoning of Ryan et al. (1980) and Kim et al. (1987) in order to calculate the profiles of the unit cell parameters. In the solution of the boundary value problems 1 through 4, the solution profiles are generated by the interphase boundary conditions; therefore, based on these boundary conditions, we can predict whether the profiles are symmetric or skew-symmetric. Kim et al. (1987) showed that determination of the symmetry conditions allows one to solve the boundary value problem in one quarter of the unit cell instead of the whole domain. In this work, we calculated both the entire unit cell profiles using periodic boundary conditions and the quarter unit cell using the symmetry boundary conditions. Very good agreement was found between both sets of results.

Fig. 3
figure 3

Comparison of calculated effective diffusivity values with experimental data from Currie (1960) on the diffusion of hydrogen in air through beds made of unconsolidated solids (after Satterfield 1970) and calculated values from Ryan et al. (1980)

Full size image

Our computed results for the isotropic effective diffusivity are represented by the following equation:

$$\begin{aligned} {D}_{{xx}} { /}{D}_{i}^{o} ={\varepsilon }_\upalpha ^{3} -{0.7548}{\varepsilon }_\upalpha ^{2} +{ 0.7452}{\varepsilon }_\upalpha . \end{aligned}$$
(54)

The only information published in the literature on closure parameters has been related to the vector \(\underline{f}_{1}\) calculated by solving problem 1 (Ryan et al. 1980; Kim et al. 1987; Gabitto 1991; Ochoa-Tapia et al. 1994; Valdes-Parada and Alvarez-Ramirez 2010; among others). In the case of isotropic porous media the tortuosity tensor defined by Eq. (52) is transversely isotropic, then, only the \(x\) component of the vector \(\underline{f}_{1}\) needs to be calculated.

Figure 4 depicts a contour plot for the \(x\) component of the vector \(\underline{f}_{1}\) calculated in this work using the isotropic unit cell depicted in Fig. 2. The dark lines depict the borders of the unit cell. The central particle is represented by the white square in the middle of the figure, armchair seat. The \(z\)-axis depicts the values of the \(f_{x}\) component. Red to yellow colors represent positive values, while light to dark blue colors represent negative values of \(f_{x}\).

Fig. 4
figure 4

Contour plot depicting the \(f_{x}\) field in the proposed periodic unit cell

Full size image

The results presented in Fig. 4 show the typical “armchair” distribution of the \(f_{x}\) field values around the central solid particle reported by several authors (Ryan et al. 1980; Kim et al. 1987; Gabitto 1991; Ochoa-Tapia et al. 1994; Valdes-Parada and Alvarez-Ramirez 2010; among others). A symmetry analysis can be conducted by dividing the unit cell domain drawing two straight lines, one parallel to the \(y\)-axis and passing through \(x = 0.5\) and the other parallel to the \(x\)-axis passing by \(y = 0.5\). The two straight lines divide the domain into four areas. Analyzing the \(f_{x}\) function in the four areas, we can conclude that the \(f_{x}\) function is symmetric around the \(y = 0.5\) line (\(f_{x}\) right = \(f_{x}\) left). We can also conclude that the \(f_{x}\) field is skew-symmetric around the \(x = 0.5\) line (\(f_{x}\) above = \(- f_{x}\) below). These symmetries have also been reported by Ryan et al. (1980) and Kim et al. (1987). It is important to state that the symmetry conditions were not imposed by the authors, but resulted from setting the appropriate boundary conditions on the boundaries of the central solid particle.

The calculated \(f_{2}\) scalar field, not shown here, was found out to be completely symmetric; therefore, the integral given by Eq. (21) should be zero and, consequently, the vector \(\underline{u}\). Whitaker (1999) reached the same conclusion using mathematical arguments. Same results were found for the scalar field \(g_{2}\). Other numerical results, not shown here, show that the “dispersion-like” term appearing in Eq. (32) is negligible compared to the other terms. These findings confirm our order of magnitude estimates.

A practical problem appears in the calculation of the time derivatives, \(\partial \langle {w}\rangle _{\upalpha \upbeta } {/}\partial {t}\) and \(\partial \langle {q}\rangle _{\upalpha \upbeta } {/}\partial {t}\). In Sect. 2.4 we assumed that \(\langle {w}\rangle _{\upalpha \upbeta }\) and \(\langle {q}\rangle _{\upalpha \upbeta } \) are explicit functions of the average functions, \(\langle {c}_\upalpha \rangle ^{\upalpha }\) and \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\). However, the average variables are function of time themselves following a complex functionality given by the solution of Eqs. (31) and (43). Therefore, originally, we computed these derivatives numerically in a computer code that simulates the CDI process (Sharma et al. 2013).

The alternative treatment presented in Sect. 2.4 allows one to calculate the source terms by evaluation of functions of the average values. However, it requires the calculation of the terms \(F_{1}, F_{2}, G_{1}\) and \(G_{2}\) using an EDL model. In this work, we used the modification of the GCS model, in the case of thin EDLs, proposed by Biesheuvel and Bazant (2010) to calculate the partial derivatives of \(\langle {q}\rangle _{\upalpha \upbeta }\) and \(\langle {w}\rangle _{\upalpha \upbeta }\) with respect to \(\langle {c}_\upalpha \rangle ^{\upalpha }\) and \(\langle \phi _\upalpha \rangle ^{{\upalpha }}\). In this modification, the ratio of the diffuse-layer Debye–Hückel and Stern-layer capacitances \((\delta )\) was assumed to be equal to zero; therefore, \(\Delta \phi _\mathrm{D}=\phi _{1}- \phi \).

Our calculated results are presented in Figs. 5, 6 and 7. Figure 5 shows the time variation of the \(F_{1}, F_{2}, G_{1}\) and \(G_{2}\) functions used to calculate the source terms using Eqs. (46) and (49). Figures 6 and 7 show a comparison between the two procedures used to calculate the source terms. These results were calculated using typical experimental values for the CDI process, electrode thickness \((L_{e})\,=\,0.001\,\hbox {m}, D_{o}\,=\,1.5\, 10^{-9}\,\hbox {m}^{2}/\hbox {s}\), pore diameter = 50 nm, void fraction = 0.5, salt concentration = 0.05 M and half-electrode potential = 0.25 V, and the characteristic time (\(\tau \)) was equal to 11.1 minutes. In all the calculations using Eqs. (46) and (49), we approximated the point values of the required variables by the corresponding average values.

Fig. 5
figure 5

Time variation of the \(F_{1}, F_{2}, G_{1}\) and \(G_{2}\) functions [Eqs. (46), (49)]

Full size image
Fig. 6
figure 6

Time variation of source terms (\(\partial \langle {w}\rangle _{\upalpha \upbeta }/\partial {t}\) and \(\partial \langle {q}\rangle _{\upalpha \upbeta }/\partial {t})\) calculated using two different procedures

Full size image
Fig. 7
figure 7

Time variation of average salt concentration in the liquid phase calculated using different procedures for source terms evaluation

Full size image

Figure 5 shows that the absolute values of the \(q\) derivatives are bigger than the corresponding values of the \(w\) derivatives. However, for positive electrode potential \((\phi _{1})\), the values for the derivative of \(w\) with respect to concentration and the derivative of \(q\) with respect to potential are negative, while the remaining derivatives are positive. The time evolution is similar for all the functions, i.e., big variation in value at short times and small variation at longer times.

The time variation of the source terms is shown in Fig. 6. We can see that the values of the source terms calculated numerically and using Eqs. (46) and (49) are practically identical. The source term for salt concentration decreases continuously as time increases until it approaches zero. The source term for charge increases continuously as time increases until it approaches zero. This behavior is produced because the excess charge density is negative for a positive electrode.

The values of the source terms calculated using both procedures influence the results of the computations. Figure 7 shows the time variation of typical average values of \(\langle {c}_\upalpha \rangle ^{\upalpha }\) in the electrode calculated using both procedures. Each value shown in Fig. 7 has been calculated by arithmetically averaging all \(\langle {c}_\upalpha \rangle ^{\upalpha }\) values inside the electrode. Therefore, \(C_\mathrm{av}\) represents an average value of the salt concentration in the porous electrode.

In Fig. 7, once again both methods predict the same values. The calculated results show an initial decrease in the average value of the concentration inside the pores. This effect is produced by the fast charging of the EDLs at short times that depletes the solution (supercapacitor regime). The source terms continuously decrease in absolute values as time increases until a minimum concentration point is reached when the diffusive flow from outside the electrode, that increases the electrode salt concentration, equates the charging process that decreases it and, from that point on, the average concentration inside the electrode increases (desalination regime).

Figures 6 and 7 confirm that both procedures predict the same results, within numerical error; therefore, both formulations can be considered equivalent.

5 Conclusions

The volume averaging method has been used to derive the average equations describing salt capture in porous electrodes by electrosorption. We have derived the complete form of the volume- averaged equations starting from the point equations and the appropriate boundary conditions. The concentration and electrostatic potential deviation fields were found to be functions of the corresponding averaged variables and the excess charge and salt values inside the double layers, \(J_\mathrm{charge}\) and \(J_\mathrm{salt}\). These terms act like source terms in the derived equations and lead to the presence of “dispersion-like” terms that represent the contributions of the source terms to the deviation fields of concentration and electrostatic potential. Calculation of the values of the source terms was accomplished by numerical calculations using a computer program that combines a transport model with a double-layer model (GCS) of the transport process by diffusion and electromigration in porous electrodes.

The effective diffusivity in an isotropic porous electrode was calculated using the procedure presented by Ryan et al. (1980). The agreement between our results, experimental data and Ryan et al. results was used to determine the accuracy of our numerical procedure. Order of magnitude analysis and computed results support neglecting the vector \(\underline{u}\) term in the mass equation and the “dispersion-like” terms in the potential equation. These simplifications led to final equations identical to the ones reported by Biesheuvel and Bazant (2010). Finally, an alternative formulation that includes source terms based upon values of the time derivatives of the average concentration and electrical potential was also derived. This alternative formulation is similar to the equations derived by Quintard and Whitaker (1998) and Ulson de Souza and Whitaker (2003) and can be used instead of the formulation originally proposed by Biesheuvel and Bazant (2010).