1 Introduction

Subsurface gas flow has received considerable attention in the past few decades because of its importance in many areas of soil physics. These areas include petroleum engineering (Al-Hussainy et al. 1966; Ikoku 1984), hydrological sciences (Scanlon et al. 2002), and environmental and chemical engineering (Massmann 1989; Morrison 1972).

Petroleum industry was the first sector which has been interested in investigating gas flow in porous media (Muskat 1946). The investigation of gaseous flow through tight porous media is of practical importance when dealing with extraction of hydrocarbon gases from unconventional gas reservoirs, such as shale gas and coal bed methane reservoirs. Gas flow models are systematically used to estimate the gas permeability and other reservoir parameters in natural gas production. Therefore, a considerable amount of studies has been performed on the theory and application of isothermal gas flow through porous media in petroleum engineering (Dake 1978; Ikoku 1984).

Transient gas flow in porous media occurs also through the backfill following a nuclear test after an underground nuclear explosion (Morrison 1972). The simulations of vapor carbon dioxide \((\hbox {CO}_{2})\) transport in \(\hbox {CO}_{2}\) sequestration projects are also performed using gas flow models (Zhang et al. 2005). It should be noted that the growth of plants and crops is also affected by the flow of water vapor in soil (Scanlon et al. 2002).

Vadose zone hydrology is another important sector of soil physics, where gas flow models are frequently used. The vadose zone is always susceptible to groundwater contaminations, which represent a serious problem in industrialized countries. These contaminations are generally caused by spilling or leaking of some contaminants (Massmann 1989; Shan et al. 1992; Wu et al. 1998; Massmann et al. 2000; Shan 2006). These contaminants include volatile organic chemicals (VOCs) such as petroleum products and organic solvents, and non-aqueous phase liquids (NAPLs). VOCs and NAPLs may act as long-term sources of groundwater contamination, and the need to remove these contaminants becomes a necessity for groundwater protection. Shan (2006) mentioned two possibilities to the removal of contaminants from contaminated sites: soil excavation and in situ remediation. For shallow and accessible contamination sources, the first one, i.e., excavation, is preferable since it is faster and cheaper. However, for deep and inaccessible contamination sources, in situ remediation techniques such as soil vapor extraction (SVE) and air injection have to be used (Wu et al. 1998; Shan 2006). These techniques have proven to be very efficient methods for the removal of VOCs and NAPLs from the vadose zone. The SVE technic can carry the contaminant vapors away from the vadose zone, while subsurface air injection can help evaporate the contaminants into the soil gas flow stream.

Contrary to liquid flow where Darcy’s law is often applied, conventional Darcy’s law has many limitations when dealing with gas flow. This is due to the nature of the porous medium and peculiarities of the flow regimes. For a gas flow through tight gas reservoirs, the mean free path of gas molecules may approach the pore dimension. Therefore, gas molecules may slip along pore surfaces. This gas slippage phenomenon causes an additional flux beside the viscous flux. This leads to an overestimation of the gas permeability being measured in comparison with the permeability to liquid. Gas permeability is then enhanced by ‘slip flow.’ Adzumi (1937) was the first who studied the gas slippage in porous media. Later on, Klinkenberg (1941) derived an expression of the gas permeability defined as a function of the liquid permeability, the gas pressure and the gas slippage factor, which called also the Klinkenberg coefficient. This phenomenon is known as the Klinkenberg effects (Wu et al. 1998; Ho and Webb 2006). Klinkenberg effects may be neglected for pressure conditions associated with gas reservoirs (Aronofsky 1954; Al-Hussainy et al. 1966). However, they may have significant impact on gas flow in low permeability media (Wu et al. 1998; Ho and Webb 2006).

Gas slippage phenomenon makes the governing equation of gas flow to be nonlinear and difficult to solve analytically. Therefore, numerical models have been developed and used extensively in the study and applications of gas flow in porous media. Among the numerical codes which are frequently used to model gas flow in porous media, we cite TOUGH2 (Pruess 1991), FEHM (Zyvoloski et al. 1996) and STOMP (White and Oostrom 1996).

Despite the existence of sophisticated numerical models to solve gas flow equations in porous media, analytical solutions are still attractive because, in one side, they allow the validation of numerical solutions, and in the other, they can be used as screening tools for quick evaluations and for field cases where numerical simulations are not feasible. For instance, Fekete (www.fekete.com) and KAPPA (www.kappaeng.com) software which are commonly used in modeling shale gas are based on semi/analytical methods. A few number of research papers has been devoted to the development of analytical solutions of gas flow in porous media. These analytical solutions include both steady state (Morrison 1972; Shan et al. 1992; Falta 1995; Wu et al. 1998) and transient gas flow (Kidder 1957; Katz 1959; Morrison 1972; Massmann 1989; Johnson et al. 1990; McWhorter 1990; Baehr and Hult 1991; Baehr and Joss 1995; Falta 1995; Wu et al. 1998; DiGiulio and Varadhan 2001; Shan 2006; Beygi and Rashidi 2011). Most of the existent solutions are semi-analytical, which are obtained by using linearization techniques. Li et al. (2011) presented a comparative study between two linearization methods. The first one is the conventional method, which assumes constant gas diffusivity, and the second is the original method introduced by Wu et al. (1998), which employs spatially averaged but time-dependent gas diffusivity. They founded that the solution proposed by Wu et al. (1998) generally provides more accurate results than the conventional solution. This later always underestimates the pressure, while the Wu solution generally underestimates the pressure near the higher-pressure boundary and overestimates the pressure near the lower-pressure boundary. As a consequence, the existing analytical solutions obtained from linearization techniques exhibit some discrepancies with respect to numerical solutions, especially for high pressure values. Therefore, finding exact solutions of the gas flow equation, if they exist, is an important and challenging problem. To our knowledge, no exact solutions for gas flow in porous media exist in the literature.

The objective of this paper was to derive some exact and simple benchmark solutions for the one-dimensional transient gas flow equation in porous media without using linearization techniques. Such solutions are more accurate than those obtained by linearization. The exact solutions take into account gravity and Klinkenberg effects, and there is no limitation about the averaged value of the gas pressure. They can be used with simple and realistic initial and boundary conditions. The proposed solutions are specially intended to be reference solutions for validating numerical ones.

2 Mathematical Model

The governing equation describing the one-dimensional transient flow of a gas in a porous medium can be obtained from the mass balance Eq. (1) and the ‘generalized’ Darcy law (2)

$$\begin{aligned} \phi \frac{\partial \rho }{\partial t}+\frac{\partial \left( {\rho u} \right) }{\partial x}=0 \end{aligned}$$
(1)

and

$$\begin{aligned} u=-\frac{k_\mathrm{g} \left( p \right) }{\mu }\left( {\frac{\partial p}{\partial x}-\rho g} \right) \end{aligned}$$
(2)

where \(x\) is the position coordinate directed downward \(\left( L \right) ,\, t\) is time \(\left( T \right) ,\, \phi \) is the porosity of the porous medium \(\left( - \right) ,\, \rho \) is the gas density \(\left( {ML^{-3}} \right) ,\, u\) is the generalized Darcy velocity of the gas-phase \(\left( {ML^{-1}} \right) ,\, \mu \) is the gas-phase viscosity \(\left( {ML^{-1}T^{-1}} \right) ,\, p\) is the gas-phase pressure \(\left( {ML^{-1}T^{-2}} \right) ,\, k_\mathrm{g} \) is the effective gas-phase permeability \(\left( {L^{2}} \right) \), which may include Klinkenberg effects, and \(g\) is the gravitational constant. Klinkenberg (1941) suggests that the effective gas permeability \(k_\mathrm{g} \) may be written as function of the gas pressure according to the following relation

$$\begin{aligned} k_\mathrm{g} \left( p \right) =k\left( {1+\frac{b}{p}} \right) \end{aligned}$$
(3)

where \(k\) is the effective permeability to liquids \(\left( {L^{2}} \right) \) and \(b\) is the Klinkenberg coefficient \(\left( {ML^{-1}T^{-2}} \right) \), which is generally a function of the porous medium, the gas properties, and the temperature.

Assuming an ideal gas, the relationship between the gas density and pressure can be written as

$$\begin{aligned} \rho =\beta p \end{aligned}$$
(4)

where \(\beta \) is the compressibility factor defined by \(\beta =M_\mathrm{g} \big /RT\) with \(M_\mathrm{g} \) being the gas-phase molecular weight, \(R\) is the gas constant, and \(T\) is the absolute temperature.

The combination of Eqs. (1)–(4) leads to the following equation where the gas pressure is the sole dependent variable

$$\begin{aligned} \frac{\mu \phi }{k}\frac{\partial p}{\partial t}-\frac{\partial }{\partial x}\left( {\left( {p+b} \right) \left( {\frac{\partial p}{\partial x}-g\beta p} \right) } \right) =0 \end{aligned}$$
(5)

We shall present an exact solution of (5) as a traveling wave.

3 Traveling Wave Solution

A traveling wave solution represents the limit profile for a continuous feed problem when the inflow pressure stabilizes to a fixed value \(P_1 \). We denote by \(P_0 \) the pressure value far away from the inflow boundary. A traveling wave solution of (5) is subject to the following boundary conditions

$$\begin{aligned} {\mathop {\lim }\limits _{x\rightarrow -\infty } p\left( {x,t} \right) =P_1},\quad {\mathop {\lim }\limits _{x\rightarrow +\infty } p\left( {x,t} \right) =P_0} ,\quad {\mathop {\lim }\limits _{x\rightarrow \pm \infty } \frac{\partial p}{\partial x}\left( {x,t} \right) =0},\quad {t>0} \end{aligned}$$
(6)

The last condition in (6) means that the gas pressure stabilizes at large distances.

Mathematically, a traveling wave solution of Eq. (5) is obtained by introducing a new variable \(\xi \) called the traveling wave coordinate for which the gas pressure can be expressed as

$$\begin{aligned} p\left( {x,t} \right) =P\left( \xi \right) ,\quad {\xi =x-Vt} \end{aligned}$$
(7)

where \(V\) is the constant speed, called also wave velocity, at which the pressure wave is assumed to be moving. The advantage of introducing the transformation (7) is that the partial differential equation (5) is transformed into an ordinary differential equation, which is easier to integrate. Substituting (7) into (5), we get after integrating once with respect to \(\xi \)

$$\begin{aligned} \frac{\mu \phi V}{k}P+\left( {P+b} \right) \left( {\frac{\hbox {d}P}{\hbox {d}\xi }-g\beta P} \right) =C \end{aligned}$$
(8)

where \(C\) is a constant of integration, which must be determined with the constant speed \(V\) from the transformed boundary conditions (9) of (6)

$$\begin{aligned} \mathop {\lim }\limits _{\xi \rightarrow -\infty } P\left( \xi \right) =P_1,\quad \mathop {\lim }\limits _{\xi \rightarrow +\infty } P\left( \xi \right) =P_0 ,\quad {\mathop {\lim }\limits _{\xi \rightarrow \pm \infty } \frac{\hbox {d}P}{\hbox {d}\xi }\left( \xi \right) =0} \end{aligned}$$
(9)

Taking into account the boundary conditions (9) into Eq. (8), we get

$$\begin{aligned} V=\frac{g\beta k\left( {P_0 +P_1 +b} \right) }{\mu \phi } \end{aligned}$$
(10)

and

$$\begin{aligned} C=g\beta P_0 P_1 \end{aligned}$$
(11)

Substituting (10) and (11) into (8), we obtain

$$\begin{aligned} \frac{\hbox {d}P}{\hbox {d}\xi }=\frac{g\beta \left( {P-P_0 } \right) \left( {P-P_1 } \right) }{P+b} \end{aligned}$$
(12)

A solution \(\xi =\xi \left( P \right) \) can be obtained from (12) as follows. Let choose an arbitrary gas pressure \(P^{*}\) between \(P_0 \) and \(P_1 \) and assuming that \(P^{*}\) is the value of \(P\) at some \(\xi =\xi ^{*}\). Therefore, after solving (12), we get

$$\begin{aligned} \xi \left( P \right) =\xi ^{*}+\frac{1}{g\beta }\log \left( {\left( {\frac{P_1 -P}{P_1 -P^{*}}} \right) ^{A}\left( {\frac{P-P_0 }{P^{*}-P_0 }} \right) ^{B}} \right) \end{aligned}$$
(13)

where \(A=\frac{P_1 +b}{P_1 -P_0 }\) and \(B=-\frac{P_0 +b}{P_1 -P_0 }\).

Equation (13) expresses explicitly \(\xi \) as function of the variable pressure \(P\). This equation represents the exact traveling wave solution. For any gas pressure value between \(P_0 \) and \(P_1 \), the traveling wave variable \(\xi \left( P \right) \) is uniquely determined from (13). Note that an explicit solution \(P\left( \xi \right) \) can be obtained from (13) for special values of \(P_0 \) and \(P_1 \). For example, for the special choice \(P_1 =2P_0 +b\), we have \(A=2\) and \(B=-1\). Substituting these values into (13), this later can be solved for \(P\), which leads to

$$\begin{aligned} P\left( \xi \right) =\frac{1}{2}\left( {2P_1 +\gamma \left( \xi \right) -\sqrt{\left( {\gamma \left( \xi \right) } \right) ^{2}+4\gamma \left( \xi \right) \left( {P_1 -P_0 } \right) }} \right) \end{aligned}$$
(14)

where

$$\begin{aligned} \gamma \left( \xi \right) =\frac{\left( {P_1 -P^{*}} \right) ^{2}}{\left( {P^{*}-P_0 } \right) }\exp \left( {g\beta \left( {\xi -\xi ^{*}} \right) } \right) . \end{aligned}$$
(15)

The exact solution in the original \(\left( {x,t} \right) \)-space can be obtained by substituting (7) into (13). We get

$$\begin{aligned} x=Vt+\xi ^{*}+\frac{1}{g\beta }\log \left( {\left( {\frac{P_1 -p}{P_1 -P^{*}}} \right) ^{A}\left( {\frac{p-P_0 }{P^{*}-P_0 }} \right) ^{B}} \right) \end{aligned}$$
(16)

Similarly, the exact expression of the pressure for the special case \(P_1 =2P_0 +b\) can be obtained from (14) as

$$\begin{aligned} p\left( {x,t} \right) =\frac{1}{2}\left( {2P_1 +\gamma \left( {x-Vt} \right) -\sqrt{\left( {\gamma \left( {x-Vt} \right) } \right) ^{2}+4\left( {P_1 -P_0 } \right) \gamma \left( {x-Vt} \right) }} \right) \end{aligned}$$
(17)

4 Discussion on the Traveling Wave Solution

4.1 Characteristics

The exact traveling wave solution defined by (13) can be analyzed from Eq. (12). Indeed, by definition, we have from (12) \(\frac{\hbox {d}P}{\hbox {d}\xi }\le 0\) since \(P\) lies between \(P_0 \) and \(P_1 \). Therefore, the traveling wave solution is a decreasing function of \(P\). This suggests that physical solutions are only those correspond to \(P_1 >P_0 \). Moreover, the traveling wave solution has a unique inflection point at \(\xi _I =\xi \left( {P_I } \right) \) where \(P_I =-b+\sqrt{b^{2}+\left( {P_0 +P_1 } \right) b+P_0 P_1 }\). Therefore, the traveling wave solution is a decreasing front solution connecting \(P_1 \) at \(-\infty \) and \(P_0 \) at \(+\infty \). From Eq. (12), we observe that gravity effects are necessary for the existence of the traveling wave solution. The shape of the traveling wave solution is independent from the permeability \(k\) of the porous medium and depends only on the Klinkenberg coefficient \(b\), the compressibility factor \(\beta \), and the boundary limits at infinity \(P_0 \) and \(P_1 \). However, the permeability controls the velocity (i.e., speed) of the traveling wave in the \(\left( {x,t} \right) \)-space as can be seen in Eq. (10). Clearly, the wave speed increases as \(k\) increases, which means that the wave front propagates faster in permeable media.

Figure 1 shows the typical shapes of the traveling wave profiles for various values of \(P_1 \). The value of \(P_0 \) is fixed to \(10^{5}\) Pa. The values of parameters \(b\) and \(\beta \) used in this example are \(b=4.75\times 10^{4}\) Pa and \(\beta =1.18\times 10^{-5}\,\hbox {kg}/\hbox {Pa\,m}^{3}\). As can be seen, the front becomes steeper as the difference \(\left| {P_1 -P_0 } \right| \) between the limiting pressures increases.

Fig. 1
figure 1

The traveling wave profiles for different values of \(P_1 \). The value of \(P_0 \) is fixed to \(10^{5}\) Pa

Full size image

From Eq. (12), we observe that, for a fixed gas pressure, the larger the value of the Klinkenberg coefficient \(b\), the smaller the value of \(\left| {\frac{\hbox {d}P}{\hbox {d}\xi }} \right| .\) This means that the front gets wider as the value of \(b\) increases. Therefore, the interval where the truncated part (i.e., the part with strong decrease of gas pressure) of the profile is defined increases as \(b\) increases. This can be clearly seen on Fig. 2, which shows the evolution of the gas pressure profile for different values of the Klinkenberg coefficient for \(P_0 =10^{5}\) Pa and \(P_1 =5\times 10^{5}\) Pa. Note that the profile is generally not symmetrical.

Fig. 2
figure 2

The traveling wave profiles for different values of the Klinkenberg coefficient

Full size image

4.2 Stability

In this section, we investigate the numerical stability of the traveling wave front solution defined by Eq. (16). The idea is to solve numerically Eq. (5) subject to various initial conditions and show how the pressure profile behaves when time increases. Equation (5) is solved numerically in a large domain of length \(2l\) much larger than the front width to avoid any effect of the lateral boundaries. Constant boundary conditions at large distances of Dirichlet types are specified, i.e., \(p\left( {-l,t} \right) =P_1 \) and \(p\left( {l,t} \right) =P_0 \). For the initial distribution of the gas pressure, we used the family of functions of the form

$$\begin{aligned} p\left( {x,0} \right) =P_1 -\frac{P_1 -P_0 }{2}\left[ {1+\hbox {tanh}\left( {\frac{x-x_0 }{w_0 }} \right) } \right] \end{aligned}$$
(18)

where \(x_0 \) is an arbitrary constant and \(w_0 \) is the front width of the initial gas pressure distribution. Clearly, Eq. (18) is characterized by a front connecting the two pressure values \(P_1 \) and \(P_0 \). The front of the initial profile (18) becomes steeper as \(w_0 \) decreases and wider as \(w_0 \) increases. In particular, when \(w_0 \) tends to zero, the initial condition (18) becomes a stepwise function centered at \(x_0 \) and connecting \(P_1 \) at \(-\infty \) and \(P_0 \) at \(+\infty \). The Matlab solver ‘pdepe’ (www.mathworks.com) is used in order to solve numerically Eq. (5) with the initial condition defined by (18). This solver can solve a system of initial boundary value problems in one space variable and time. In order to insure that the time and space discretizations produce a physically correct solution, the time step size \({\Delta }t\) must at least respect the Neumann criterion (Hindmarsh et al. 1984): \(N_{eu} =2D{\Delta }t\big /\left( {{\Delta }x} \right) ^{2}\le 1\), where \({\Delta }x\) is the mesh spacing and \(D\) is the diffusion coefficient.

Figure 3 shows the evolution with time of an initial gas pressure labeled ‘Initial Profile’ and obtained from (18) for the following set of parameter values: \(x_0 =0,\,w_0 =10^{5}\,\hbox {m},\,P_0 =10^{5}\,\hbox {Pa}\) and \(P_1 =5\times 10^{5}\,\hbox {Pa}\), and for the successive times \(t_0 =0,\,t_1 =2\times 10^{13},\,t_2 =4\times 10^{13},\,t_3 =6\times 10^{13}\) and \(t_4 =8\times 10^{13}\) s. Figure 3 shows also the exact traveling wave solutions obtained from Eq. (16) for the same times. The physical parameter values used for this comparison are: \(\phi =0.3,\,k=10^{-15}\,\hbox {m}^{2},\,b=4.75\times 10^{4}\,\hbox {Pa}, \,\beta =1.18\times 10^{-5}\,\hbox {kg}/\hbox {Pa\,m}^{3}\) and \(\mu =1.84\times 10^{-5}\) Pa s. The initial condition used for the numerical solutions can be regarded as a perturbation of the exact profile at \(t_0 =0\) with wider front width. For the early time \(t_1 \), we observe small differences between the numerical and exact profiles. This can be explained by the fact that at this time, the numerical solution is still affected by the initial profile. However, for the larger times, the numerical solution is relaxed to the exact solutions at each time, and thus confirming that the solution we have developed is stable. The stability of the traveling wave front solution is confirmed for other value of \(P_1 \). Figure 4 shows the results for \(P_1 =2\times 10^{5}\) Pa and for the same parameter values used in the previous example except that the front width is too small \((w_0 =10^{-6}\,\hbox {m})\). This case corresponds to a stepwise initial front. As can be seen on the figure and contrary to the previous example, the front width of the initial profile used for the numerical solutions is steeper than that of the exact profile. Again, we observe that the numerical solution converges to the exact solution for large times.

Fig. 3
figure 3

The exact traveling wave profiles obtained from Eq. (16) for successive times versus the numerical profiles obtained from the initial condition defined by (18) and corresponding to \(x_0 =0,\,w_0 =10^{5}\,\hbox {m},\,P_0 =10^{5}\) Pa and \(P_1 =5\times 10^{5}\) Pa

Full size image
Fig. 4
figure 4

The exact traveling wave profiles obtained from Eq. (16) for successive times versus the numerical profiles obtained from the initial condition defined by (18) and corresponding to \(x_0 =0,\,w_0 =10^{-6}\,\hbox {m}, \,P_0 =10^{5}\) Pa and \(P_1 =2\times 10^{5}\) Pa

Full size image

5 Benchmark Solutions in Semi-infinite Domain

In this section, we show how the traveling wave solution (16) can be used to define benchmark solutions defined over the semi-infinite domain \([ {0,+\infty } [\) with constant initial condition or constant boundary condition. The defined benchmark solutions are useful for verifying numerical solutions. The technique used in here is similar to that used previously in soil science (Vanderborght et al. 2005; Zlotnik et al. 2007).

The function \(\xi \left( P \right) \) as defined in Eq. (13) characterizes the transition zone of the gas pressure between the two stable pressure values \(P_0 \) and \(P_1 \). The extent of the transition zone is theoretically infinite since the gas pressures \(P_1 \) and \(P_0 \) are only reached at \(-\infty \) and \(+\infty \), respectively. However, we could define the truncated part of the gas pressure profile as the part located between two stable regions where the pressures are almost constant. In practice, we introduce two gas pressure values \(P_0^*\) and \(P_1^*\) close to \(P_0 \) and \(P_1 \), respectively, and defined as follows: \(P_0^*=P_0 +\delta _0 \) and \(P_1^*=P_1 -\delta _1 \), where \(\delta _0 \) and \(\delta _1 \) are two small positive values. Accordingly, the truncated part of the gas pressure profile is defined over the interval \(\left[ {\xi _1^*,\xi _0^*} \right] \) where \(\xi _1^*=\xi \left( {P_1^*} \right) \) and \(\xi _0^*=\xi \left( {P_0^*} \right) \). In order to make the traveling wave front solution of practical value, we shall approximate the exact traveling wave (13) by the following function

$$\begin{aligned} P\left( \xi \right) =\left\{ {{\begin{array}{ll} {P_1^*,} &{}\quad {-\infty <\xi \le \xi _1^*} \\ {\hbox {solution of}\left( {13} \right) ,} &{} \quad {\xi _1^*<\xi <\xi _0^*} \\ {P_0^*,} &{}\quad {\xi _0^*\le \xi <+\infty } \\ \end{array} }} \right. \end{aligned}$$
(19)

In the \(\left( {x,t} \right) \)-space, the exact traveling wave (16) is replaced by

$$\begin{aligned} p\left( {x,t} \right) =\left\{ {{\begin{array}{lll} {P_1^*,} &{}\quad {-\infty <x\le x_1 \left( t \right) ,} &{}\quad {t>0} \\ {\hbox {solution of}\left( {16} \right) ,} &{}\quad {x_1 \left( t \right) <x<x_0 \left( t \right) ,} &{}\quad {t>0} \\ {P_0^*,} &{}\quad {x_0 \left( t \right) \le x<+\infty ,}&{}\quad {t>0} \\ \end{array} }} \right. \end{aligned}$$
(20)

where \(x_1 \left( t \right) =\xi _1^*+Vt\) and \(x_0 \left( t \right) =\xi _0^*+Vt\).

The parameters \(\delta _0 \) and \(\delta _1 \) can be chosen as small as desired. Clearly, decreasing the values of these two parameters will increase the length \(l^{*}=\left| {\xi _1^*-\xi _0^*} \right| \) of the interval \(\left[ {\xi _1^*,\xi _0^*} \right] \) and will expand the portion of the exact profile defined by (13). In other words, the function defined by (20) converges to the exact traveling wave solutions (16) as \(\delta _0 \) and \(\delta _1 \) tend to zero. In practice, we choose \(\delta _0 \) and \(\delta _1 \) such that \(\delta _0 \sim \delta _1 \le \varepsilon P_0 \) if \(P_0 \ne 0\), where \(\varepsilon \) ranges from \(10^{-4}\) to \(10^{-1}\). If \(P_0 =0\), we take \(\delta _0 \sim \delta _1 =\varepsilon \).

5.1 Solution with Uniform Initial Condition and Non-uniform Boundary Condition

The function (20) is used now to define a benchmark solution of Eq. (5) in the \(({x,t})\)-domain with constant initial gas pressure and time-dependent boundary condition. We are interested in the part of the solution inside the semi-infinite domain \([ {0,+\infty } [\), which we call the flow domain. We assume that at \(t_0 =0\), the gas is uniformly distributed over the semi-infinite domain \([ {0,+\infty } [\) with constant pressure equal to \(P_0^*\). For \(t>t_0 \), the semi-infinite domain is fed by gas with larger pressure values than \(P_0^*\) at \(x=0\) from the outside of the flow domain (i.e., from the region \(x<0)\). This means that the value of the pressure at \(t_0 =0\) calculated from the truncated part of Eq. (20) (i.e., the part defined by (16)) is equal to \(P_0^*\) at \(x=0\), and it increases with time. This situation corresponds to \(\xi ^{*}=0\) and \(P^{*}= P_0^*\) in Eq. (16). Figure 5 shows how the benchmark solution is constructed. As can be seen, the truncated part of the initial profile is completely located outside the semi-infinite domain \([ {0,+\infty } [\). As time increases, the gas enters the inlet boundary with time-dependent pressure until reaching \(P_1^*\) at some time \(t^{*}\). The time \(t^{*}\) is the time required to the truncated part fully crosses the inlet boundary. After this time, the pressure becomes constant at the inlet boundary and equal to \(P_1^*\).

Fig. 5
figure 5

Construction of the benchmark solution with uniform initial condition and non-uniform boundary condition. The truncated part of the initial profile at \(t_0 =0\) is completely located outside the flow domain \([ {0,+\infty } [\), and the part with constant pressure \(P_0^*\) is inside the flow domain. After this time, the gas pressure increases with time at the inlet boundary \(x=0\) until reaching the constant gas pressure \(P_1^*\) at \(t^{*}\)

Full size image

The benchmark solution in the semi-infinite domain \([ {0,+\infty } [\) is then defined by

$$\begin{aligned} p\left( {x,t} \right) =\left\{ {{\begin{array}{lll} {P_0^*,} &{}\quad {x=0,} &{}\quad {t=0} \\ {\hbox {solution of:}x=Vt+\frac{1}{g\beta }\log \left( {\left( {\frac{P_1 -p}{P_1 -P_0 -\delta _0 }} \right) ^{A}\left( {\frac{p-P_0 }{\delta _0 }} \right) ^{B}} \right) ,} &{}\quad {x>0,} &{}\quad {t>0} \\ \end{array} }} \right. \end{aligned}$$
(21)

The solution (21) can be used to verify numerical solutions of Eq. (5). This solution has uniform initial condition defined by

$$\begin{aligned} p\left( {x,0} \right) =P_0^*, \quad {x>0} \end{aligned}$$
(22)

and time-dependent boundary condition \(p_0 \left( t \right) \). The boundary condition is defined as follows

$$\begin{aligned} p_0 \left( t \right) =\left\{ {{\begin{array}{ll} {P_0^*,} &{} \quad {t=0} \\ {\hbox {solution of:}Vt+\frac{1}{g\beta }\log \left( {\left( {\frac{P_1 -p_0 \left( t \right) }{P_1 -P_0 -\delta _0 }} \right) ^{A}\left( {\frac{p_0 \left( t \right) -P_0 }{\delta _0 }} \right) ^{B}} \right) =0,} &{} \quad {0<t\le t^{*}} \\ {P_1^*,} &{} \quad {t\ge t^{*}} \\ \end{array} }} \right. \end{aligned}$$
(23)

The time \(t^{*}\) can be calculated analytically from the second row of Eq. (23) by substituting \(t=t^{*}\) and \(p_0 \left( {t^{*}} \right) =P_1^*\). We obtain

$$\begin{aligned} t^{*}=-\frac{1}{g\beta V}\log \left( {\left( {\frac{\delta _1 }{P_1 -P_0 -\delta _0 }} \right) ^{A}\left( {\frac{P_1 -P_0 -\delta _1 }{\delta _0 }} \right) ^{B}} \right) \end{aligned}$$
(24)

Note that in the special case \(P_1 =2P_0 +b\), Eqs. (21) and (23) can be written in explicit forms as

$$\begin{aligned}&\!\!\!\!p\left( {x,t} \right) \nonumber \\&\!\!\!\!\quad =\left\{ {{\begin{array}{lll} {P_0^*,} &{}\, {x=0,} &{}\, {t=0} \\ {\frac{1}{2}\left( {2P_1 +\gamma \left( {x-Vt} \right) -\sqrt{\left( {\gamma \left( {x-Vt} \right) } \right) ^{2}+4\left( {P_1 -P_0 } \right) \gamma \left( {x-Vt} \right) }} \right) ,} &{} \,{x>0,} &{}\, {t>0} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(25)

and

$$\begin{aligned} p_0 \left( t \right) =\left\{ {{\begin{array}{ll} {P_0^*,} &{} \quad {t=0} \\ {\frac{1}{2}\left( {2P_1 +\gamma \left( {-Vt} \right) -\sqrt{\left( {\gamma \left( {-Vt} \right) } \right) ^{2}+4\left( {P_1 -P_0 } \right) \gamma \left( {-Vt} \right) }} \right) ,} &{} \quad {0<t\le t^{*}}\\ {P_1^*,} &{} \quad {t\ge t^{*}} \\ \end{array} }} \right. \end{aligned}$$
(26)

where \(\gamma \left( \xi \right) =\frac{\left( {P_1 -P_0 -\delta _0 } \right) ^{2}}{\delta _0 }e^{g\beta \xi }\). In this case, the time \(t^{*}\) is simplified to \(t^{*}=-\frac{1}{g\beta V}\log \left( {\frac{\delta _0 \delta _1^2 }{\left( {P_1 -P_0 -\delta _1 } \right) \left( {P_1 -P_0 -\delta _0 } \right) }} \right) \).

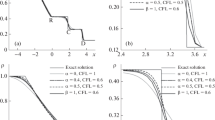
Figure 6 shows a comparison between the numerical solution and the benchmark solution (21) for the following set of parameters: \(\phi =0.3,\,k=10^{-12}\,\hbox {m}^{2},\,b=3.95\times 10^{3}\,\hbox {Pa}, \,\beta =1.18\times 10^{-5}\,\hbox {kg}/\hbox {Pa\,m}^{3},\,\mu =1.84\times 10^{-5}\,\hbox {Pa}\,\hbox {s},\,P_0 =10^{5}\,\hbox {Pa},\,P_1 =2P_0 +b,\,\delta _0 =10^{-3}\) and \(\delta _1 =10^{-1}\). The numerical solutions are obtained from the same solver mentioned in the previous section. The solutions are presented for the following successive times \(t_1 =2.4\times 10^{10}\,\hbox {s}, \,t_2 =2.9\times 10^{10}\,\hbox {s}\) and time \(t_3 =4\times 10^{10}\) s. As can be seen, excellent agreements are obtained between the numerical and exact solutions for all times.

Fig. 6
figure 6

Comparison between the numerical solution and the exact benchmark solution with uniform initial condition for successive times (\(t_1 <t_2 <t^{*}\) and \(t_3 >t^{*}\))

Full size image

5.2 Solution with Non-uniform Initial Condition and Uniform Boundary Condition

The solution with non-uniform initial condition and uniform boundary condition corresponds to the case where the truncated part of the profile is initially fully in the flow domain. This is for example the case of the profile corresponding to \(t=t_3 > t^{*}\) in Fig. 5. We assume that at \(t=t_0 =0\), the truncated part is completely present in the region \(x>0\). Therefore, the pressure value at the inlet boundary would be constant and equal to \(P_1^*\). This situation corresponds to \(\xi ^{*}=0\) and \(P^{*}= P_1^*\) in Eq. (16). The benchmark solution in the semi-infinite domain \([ {0,+\infty } [\) is then defined by

$$\begin{aligned} p\left( {x,t} \right) =\left\{ {{\begin{array}{lll} {P_1^*,} &{} \quad {x=0,} &{} \quad {t=0} \\ {\hbox {solution of:}x=Vt+\frac{1}{g\beta }\log \left( {\left( {\frac{P_1 -p}{\delta _1 }} \right) ^{A}\left( {\frac{p-P_0 }{P_1 -P_0 -\delta _1 }} \right) ^{B}} \right) ,} &{} \quad {x>0,} &{} \quad {t>0} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(27)

The solution (27) is the benchmark solution with uniform boundary condition and non-uniform initial condition. This solution can be used to verify numerical solutions of Eq. (5) with constant gas pressure at the inlet boundary defined by

$$\begin{aligned} p\left( {0,t} \right) =P_1^*,\quad {t\ge 0} \end{aligned}$$
(28)

The initial condition \(p_i \left( x \right) \) is determined from the second equation of (27) by substituting \(t=0\) and \(p=p_i \left( x \right) \). We get

$$\begin{aligned} x=\frac{1}{g\beta }\log \left( {\left( {\frac{P_1 -p_i \left( x \right) }{\delta _1 }} \right) ^{A}\left( {\frac{p_i \left( x \right) -P_0 }{P_1 -P_0 -\delta _1 }} \right) ^{B}} \right) \end{aligned}$$
(29)

For the special case \(P_1 =2P_0 +b\), Eqs. (27) and (29) can be written in explicit forms as follows

$$\begin{aligned}&\!\!\!\!p\left( {x,t} \right) \nonumber \\&\!\!\!\!\quad =\left\{ {{\begin{array}{lll} {P_1^*,} &{}\, {x=0,} &{} \,{t=0} \\ {\frac{1}{2}\left( {2P_1 +\gamma \left( {x-Vt} \right) -\sqrt{\left( {\gamma \left( {x-Vt} \right) } \right) ^{2}+4\left( {P_1 -P_0 } \right) \gamma \left( {x-Vt} \right) }} \right) ,} &{} \,{x>0,} &{}\,{t>0} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(30)

and

$$\begin{aligned} p_i \left( x \right) =\frac{1}{2}\left( {2P_1 +\gamma \left( x \right) -\sqrt{\left( {\gamma \left( x \right) } \right) ^{2}+4\left( {P_1 -P_0 } \right) \gamma \left( x \right) }} \right) \end{aligned}$$
(31)

where \(\gamma \left( x \right) =\frac{\delta _1^2 }{P_1 -P_0 -\delta _1 }e^{g\beta x}\).

In Fig. 7, we show a comparison between the benchmark solution (27) and the numerical solution of Eq. (5) with uniform boundary condition (28) and non-uniform initial condition (29) for successive times \(t_1 =10^{10},\,t_2 =2\times 10^{10}\) and \(t_3 =3\times 10^{10}\) s. The same parameters values of the previous case are used. Since the entire truncated part of the solution is initially inside the semi-infinite domain \([ {0,+\infty } [\), the solution at each time is a translation of the initial profile traveling with constant velocity defined by (10). Figure 7 shows excellent agreement between the benchmark solution and the numerical solution for each time.

Fig. 7
figure 7

Comparison between the numerical solution and the exact benchmark solution with constant boundary condition for successive times

Full size image

Note that in the benchmark solutions defined by (21) and (27), there is no restriction about the values of the pressures \(P_0 \) and \(P_1 \) (or \(P_0^*\) and \(P_1^*\)). Contrary to the analytical solutions obtained from linearization techniques where accurate solutions are only obtained for low gas pressure values, the above solutions can be used for any value of the gas pressures \(P_0^*\) and \(P_1^*\). For example, solution (27) is of interest in problems related to gas flow in the backfill following an underground nuclear explosion. For such problems, the entry pressure \(P_1^*\) is generally much higher than \(P_0^*\). We would like to mention that the same technique can be applied for a flux boundary condition at \(x=0\). The flux at this boundary can be derived directly from the calculated pressure by applying the definition of the flux and the exact solution (16).

6 Conclusion

We presented an exact traveling wave solution for the one-dimensional transient gas flow equation in porous media. The model takes into account gravity and Klinkenberg effects. The traveling wave solution is defined on the whole infinite domain. It is obtained by introducing a traveling wave variable, which transforms the partial differential equation to an ordinary differential equation admitting an exact solution. This method avoids any linearization. In a first step, we presented the characteristics of the traveling wave solution and we investigated numerically the stability of the front solutions. Then, two benchmark solutions defined on the semi-infinite domain are presented. One with uniform initial gas pressure and non-uniform boundary condition, and the other with uniform boundary condition and non-uniform initial condition. These benchmark solutions are useful for validating numerical solutions with uniform initial and boundary conditions. They can be used for problems where Klinkenberg effects are important, and there is no restriction about the averaging pressure value. The benchmark solutions are simple and easy to use. We presented some numerical experiments to compare the benchmark solutions with numerical solutions, and the results have shown good agreements between them.