1 Introduction

Recent interest in double-diffusive convection in porous media has been motivated by its wide range of applications, from the solidification of binary mixtures to the heat transfer in geothermal reservoirs. Double-diffusive convection has implications for many geological processes, such as crustal heat and solute transport, metamorphism, the diagenetic evolution of sedimentary basins and ore genesis. Besides its importance in the hydrogeological context, double diffusive convection in porous media has wide variety of geotechnical applications, among them contaminant transport in saturated soil, underground disposal of nuclear wastes, liquid re-injection, the migration of moisture in fibrous insulation, and electro-chemical and drying processes. The problem of double-diffusive convection in porous medium has been extensively investigated and the growing volume of work devoted to this area is well documented by Nield and Bejan (2006); Ingham and Pop (1998), (2005); Vafai (2000); Vafai (2005) and Vadas (2008).

The study of double diffusive convection in a rotating porous media is motivated both theoretically and by its practical applications in engineering. To mention only a few engineering applications let us consider the food process industry, chemical process industry and rotating machinery. More specifically, packed bed mechanically agitated vessels are used in food processing and chemical engineering industries in batch process. The packed bed consists of solid particles of fibers of material which form the solid matrix while fluid flows through the pores. As the solid matrix rotates, due the mechanical agitation, a rotating frame of reference is a necessity when investigating these flows. The role of the flow of fluid through these beds can vary from drying processes to extraction of soluble components from the solid particles. Another important application of rotating flows in porous media is in the design of a multi-pore distributor in a gas–solid-fluidized bed. A commonly used solution to avoid maldistribution of gas and bed instability is cyclic interchange fluidization, where the distributors are rotating at constant angular velocities. Modeling of flow and heat transfer in porous media is also applied for the design of heat pipes using porous wicks and includes effects of boiling in unsaturated porous medium, surface tension driven flow with heat transfer and condensation in unsaturated porous media. When the heat pipe is used for cooling devices which are subject to rotation the corresponding centrifugal and Coriolis effects become relevant as well.

There are only few studies available on double-diffusive convection in a porous medium in the presence of rotation. Chakrabarti and Gupta (1981) have analyzed the nonlinear thermohaline convection in a rotating porous medium. The effect of rotation on linear and nonlinear double-diffusive convection in a sparsely packed porous medium was studied by Rudraiah et al. (1986). The Lyapunov direct method is applied to study the nonlinear conditional stability problem of a rotating doubly diffusive convection in a sparsely packed porous layer by Guo and Kaloni (1995). The nonlinear stability of the conduction–diffusion solution of a fluid mixture heated and salted from below and saturating a porous medium in the presence of rotation is studied by Lombardo and Mulone (2002) using Lyapunov direct method.

Thermal convection is considered to be an important and in many practical cases a major mechanism for the transport and deposition of salts and other chemicals in sedimentary basins. A variety of chemical reactions can occur as fluid, carrying various dissolved species, moves through a permeable matrix. The nature of the resulting dissolution or precipitation depends on the reaction kinetics and the influence of temperature, pressure, and other factors on them has been studied by Phillips (2009). The effect of chemical reactions on convective motion is not fully known and has received relatively little attention. The first study on the effect of chemical reaction on the onset of convection in a porous medium was due to Steinberg and Brand (1983, 1984). Their analysis is restricted to the regime where the chemical reaction was sufficiently fast that the solutal diffusion could be neglected. Gatica et al. (1989) and Viljoen et al. (1990) investigated the effect of exothermic-reaction on the stability of the porous system. Their study is limited to the case where the thermal and solutal diffusivities are equal so that overdamped oscillations are not possible. Malashetty and Gaikwad (2003) performed linear stability analysis for chemically driven instabilities in binary liquid mixtures with fast chemical reaction. They found analytical expressions for the onset of stationary and oscillatory instabilities. Recently, Pritchard and Richardson (2007) made an exhaustive study of the effect of temperature dependent solubility on the onset of thermosolutal convection in an isotropic porous medium. A linear stability analysis was used to investigate how the dissolution or precipitation of concentration affects the onset of convection and selection of an unstable wavenumber. The analysis was further extended using a Galerkin method to predict the structure of the initial bifurcation, and they compared analytical results with numerical integration of the full nonlinear equations. More recently, Malashetty and Biradar (2011) have investigated the onset of double-diffusive reaction–convection in an anisotropic porous layer.

Due to the structure of a porous material there can be a pronounced anisotropy in properties such as permeability or thermal diffusivity. Anisotropy is generally a consequence of preferential orientation or asymmetric geometry of porous matrix or fibers encountered in numerous systems in industry and nature. In geological processes such as sedimentation, compaction, frost action, and the reorientation of the solid matrix are responsible for the creation of an anisotropic porous medium. Anisotropy is particularly important in a geological context, since sedimentary rocks generally have a layered structure; the permeability in the vertical direction is often much less than in the horizontal direction. Anisotropy can also be a characteristic of artificial porous materials like pelletting used in chemical engineering process and fiber material used in insulating purpose. The review of research on convective flow through anisotropic porous media has been well documented by McKibbin (1985) and Storesletten (1998); Storesletten (2004). The effect of anisotropy in mechanical and thermal properties on thermohaline convection in a porous layer has been analyzed by Tyvand (1980). The onset of double-diffusive convection in an anisotropic porous medium with additional constraints like rotation and cross diffusion effects including weak nonlinear theory has been studied by Malashetty and co-workers (2008, 2010, 2011). The study on convection in anisotropic porous media saturated with binary fluid is very sparse.

It is demonstrated that the dynamics occurring in the mushy layer are critical to the quality of the final product and suppression of convection is an important factor. The rotation is being used as a means to suppress convection. The earlier studies have modeled the mushy layer as isotropic porous medium. Realistically, the permeability and thermal diffusivity are anisotropic. In view of these, it is of interest to gain a general understanding of the manner in which rotation affects the hydrodynamic stability of a double diffusive anisotropic porous layer. Therefore, in the present paper, we study the effect of rotation on the onset of double diffusive reaction–convection in an anisotropic porous medium. The main aim of this study is to analyze the linear and weak non-linear stability of a rotating reactive binary mixture in a horizontal porous layer with anisotropic permeability and thermal diffusivity. The porous medium is assumed to be isotropic in the horizontal plane. Our objective is to study how the onset criterion for stationary, oscillatory, and steady finite-amplitude convection is affected by the Taylor number, chemical reaction parameter, and anisotropy parameters.

2 Mathematical Formulation

Consider a reactive, anisotropic porous layer, saturated with Boussinesq fluid of infinite horizontal extent confined between the planes \(z\) = 0 and \(z=d\), with the vertically downward gravity force \(\mathbf{g}\) acting on it. A uniform adverse temperature difference \(\Delta T=(T_\mathrm{l} -T_\mathrm{u} )\) and a stabilizing concentration difference \(\Delta S=(S_\mathrm{l} -S_\mathrm{u} )\) where \(T_\mathrm{l} >T_\mathrm{u} \) and \(S_\mathrm{l} >S_\mathrm{u}\) are maintained between the lower and upper boundaries. A Cartesian frame of reference is chosen with the origin in the lower boundary and the \(z\) axis vertically upwards. The porous layer rotates uniformly about the \(z\) axis with a constant angular velocity \(\varvec{\Omega } = ({0,0,\Omega })\). The Darcy model that includes the Coriolis term is employed for the momentum equation. The transport of heat and solute is described by the advection–diffusion equations Phillips (2009). The Boussinesq approximation, which states that the variation in density is negligible everywhere in the conservations except in the buoyancy term, is assumed to hold. With these assumptions the governing equations are

$$\begin{aligned}&\nabla \cdot \mathbf{q}=0,\end{aligned}$$
(2.1)
$$\begin{aligned}&\nabla p+2 \varvec{\Omega }\times \mathbf{q}+\mu \mathbf{K}\cdot \mathbf{q}-\rho \mathbf{g}=0,\end{aligned}$$
(2.2)
$$\begin{aligned}&({\rho c})_\mathrm{m} \frac{\partial T}{\partial t}+({\rho c})_\mathrm{f} ({\mathbf{q}\cdot \nabla }) T =({\rho c})_{m} \nabla \cdot ( \varvec{\kappa }_\mathbf{T} \cdot \nabla T),\end{aligned}$$
(2.3)
$$\begin{aligned}&\varepsilon \frac{\partial S}{\partial t}+({\mathbf{q}\cdot \nabla })S=\varepsilon \kappa _\mathrm{S} \nabla ^{2}S+k ({S_\mathrm{eq}(T)-S}), \end{aligned}$$
(2.4)
$$\begin{aligned}&\rho =\rho _{0} [{1-\beta _\mathrm{T}} ({T-T_0}) + {\beta _\mathrm{S}} ({S-S_0}) ], \end{aligned}$$
(2.5)

where \(\mathbf{q}=(u,v,w)\) is the velocity, \(p\) the pressure, \(T\) the temperature, \(S\) the concentration, \(\varepsilon \) represents the porosity, \(\varvec{\Omega } = ({0,0,\Omega })\) angular velocity of rotation, \(\mathbf{K}=K_x^{-1} \mathbf{ii}+K_y^{-1} \mathbf{jj}+K_z^{-1} \mathbf{kk}\) is the inverse of the anisotropic permeability tensor and \(\varvec{\kappa }_\mathbf{T} =\kappa _{\mathrm{T}x} \mathbf{ii}+\kappa _{\mathrm{T}y} \mathbf{jj}+\kappa _{\mathrm{T}z} \mathbf{kk}\) is the anisotropic thermal diffusion tensor. We restrict consideration to horizontal isotropy in mechanical and thermal properties of the porous medium, i.e., \(K_x =K_y \) and \(\kappa _{\mathrm{T}x} =\kappa _{\mathrm{T}y} \). The permeability and thermal diffusivity tensors of the porous medium are assumed to have principal axes aligned with the coordinate system. Further, \(\kappa _\mathrm{S} \)is the solute diffusivity and \(k\) is a lumped effective reaction rate, and \(S_\mathrm{eq} (T)\) is the equilibrium concentration of the solute at a given temperature. The quantities \(\beta _\mathrm{T}\) and \(\beta _\mathrm{S}\) are the thermal volume expansion coefficient and density coefficient for salinity, respectively, and both are positive. The volumetric heat capacity of the fluid is denoted by \(({\rho c})_\mathrm{f}\) and that of the saturated medium as a whole by \(({\rho c})_{m} = \left( {1-\varepsilon } \right)\left( {\rho c} \right)_\mathrm{s} +\varepsilon \left( {\rho c} \right)_\mathrm{f}\), where the subscripts f, s, and m denote the properties of the fluid, solid, and porous matrix, respectively. Following Pritchard and Richardson (2007), and Jupp and Woods (2003), it is assumed that the equilibrium solute concentration is a linear function of temperature so that \(S_\mathrm{eq} (T)= S_0 +\phi ({T-T_0 })\). Further, if chemical equilibrium at the boundaries is assumed, then \(\phi = \frac{S_\mathrm{l} -S_\mathrm{u}}{T_\mathrm{l} -T_\mathrm{u}} = \frac{\Delta S}{\Delta T}\). The coefficient \(\phi \) in general may be positive or negative. Obviously, if \(\phi >\) 0, the solubility increases with temperature, while if \(\phi <\) 0, the solubility decreases with temperature. It should be noted that, only the case \(\phi >0\) is considered in the present paper.

The boundary conditions are that at the upper boundary, \(T=T_\mathrm{u}, S=S_\mathrm{u}\) and at the lower boundary \(T=T_\mathrm{l}, S=S_\mathrm{l}\), and the vertical component of velocity vanishes at both the boundaries. The basic state of the fluid is assumed to be quiescent. We then find the temperature and solute distribution in the basic state as

$$\begin{aligned} T_\mathrm{b} (z)= -\frac{\Delta T}{d}z +T_\mathrm{l} \text{ and} S_\mathrm{b} (z)= -\frac{\Delta S}{d}z +S_\mathrm{l} \end{aligned}$$
(2.6)

The initial distribution of solute is \(S_\mathrm{b} =S_\mathrm{eq} ({T_\mathrm{b}})\) and since \(S_\mathrm{eq}\) is linear in \(T\), we allow the existence of a steady basic state in which the solute is everywhere in chemical equilibrium with the solid matrix and therefore the vertical flux of solute is constant in space. We study the stability of this basic state using the method of small perturbations. Now, we superpose infinitesimal perturbations on this basic state in the form

$$\begin{aligned} \mathbf{q}=\mathbf{q}_\mathrm{b} +\mathbf{q}^{\prime }, T=T_\mathrm{b} (z)+T^{\prime }, S=S_\mathrm{b} (z)+S^{\prime }, p=p_\mathrm{b} (z)+p^{{\prime }}, \rho =\rho _\mathrm{b} (z)+\rho ^{{\prime }} \end{aligned}$$
(2.7)

where the prime indicates perturbations. Substituting Eq. (2.7) into Eqs. (2.1–2.5), and using the basic state solutions, we get the linearized equations governing the perturbations in the form

$$\begin{aligned}&\nabla .\mathbf{{q}^{\prime }}=0,\end{aligned}$$
(2.8)
$$\begin{aligned}&\nabla {p}^{\prime }+2 \varvec{\Omega }\times \mathbf{q}^{\prime }+\mu \mathbf{K}\cdot \mathbf{q}^{\prime }+\rho _0 \left( {\beta _\mathrm{T} {T}^{\prime }-\beta _\mathrm{S} {S}^{\prime }} \right) \mathbf{g}=0,\end{aligned}$$
(2.9)
$$\begin{aligned}&({\rho c})_{m} \frac{\partial {T}^{\prime }}{\partial t}+ ({\rho c})_\mathrm{f} \left(\left({\mathbf{{q}^{\prime }}\cdot \nabla }\right){T}^{\prime }-{w}^{\prime }\frac{\Delta T}{d}\right) =({\rho c})_{m} \nabla \cdot ( \varvec{\kappa }_\mathbf{T} \cdot \nabla {T}^{\prime }),\end{aligned}$$
(2.10)
$$\begin{aligned}&\varepsilon \frac{\partial {S}^{\prime }}{\partial t}+\left( {\mathbf{q}^{\prime }\cdot \nabla } \right){S}^{\prime }-\left( {w^{\prime }\frac{\Delta S}{d}} \right)=\varepsilon \kappa _\mathrm{S} \nabla ^{2}{S}^{\prime }+k\left( {S_\mathrm{eq} (T^{\prime })-S^{\prime }} \right). \end{aligned}$$
(2.11)

By operating curl twice on Eq. (2.9), we eliminate \({p}^{\prime }\) from it and then render the resulting equation and the Eqs. (2.8–2.11) dimensionless by setting

$$\begin{aligned}&\left( {{x}^{\prime },{y}^{\prime },{z}^{\prime }} \right) = ({x^{*},y^{*},z^{*}}) d, t{\prime }=t^{*}({d^{2}/\kappa _{\mathrm{T}z}}), \left( {{u}^{\prime },{v}^{\prime },{w}^{\prime }}\right)=\left( {{\varepsilon \kappa _{\mathrm{T}z} }/d} \right)\left({u^{*},v^{*},w^{*}} \right),\nonumber \\&T= ({\Delta T})T^{*}, S= \left( {\Delta S} \right)S^{*} \end{aligned}$$
(2.12)

to obtain non-dimensional equations as (on dropping the asterisks for simplicity)

$$\begin{aligned}&\left( {\nabla _1^2 +\frac{1}{\xi }\frac{\partial ^{2}}{\partial z^{2}}+Ta\frac{\partial ^{2}}{\partial z^{2}} } \right)w-Ra_\mathrm{T} \nabla _1^2 T+Ra_\mathrm{S} \nabla _1^2 S=0\end{aligned}$$
(2.13)
$$\begin{aligned}&\frac{\partial T}{\partial t}+\lambda ({\mathbf{q}\cdot \nabla })T-\lambda w=\eta \nabla _1^2 T+\frac{\partial ^{2}T}{\partial z^{2}},\end{aligned}$$
(2.14)
$$\begin{aligned}&\frac{\partial S}{\partial t}+({\mathbf{q}\cdot \nabla })S-w=\frac{1}{Le}\nabla ^{2}S+\chi ({T-S}), \end{aligned}$$
(2.15)

where \(Ra_\mathrm{T} ={\rho _0 \beta _\mathrm{T} g \Delta TdK_z }/{\mu \varepsilon \kappa _{\mathrm{T}z} }\), the Darcy–Rayleigh number, \(Ra_\mathrm{S} ={\rho _0 \beta _\mathrm{S} g\Delta SdK_z }/{ \mu \varepsilon \kappa _{\mathrm{T}z} }\), the solute Rayleigh number, both defined in terms of the vertical permeability \(K_z \), vertical thermal diffusivity \(\kappa _{\mathrm{T}z} \), and the porosity \(\varepsilon , Ta=\left( {\frac{2\Omega K_z }{\mu }} \right)^{2}\), the Darcy Taylor number, \(Le={\kappa _{\mathrm{T}z} }/{\kappa _\mathrm{S} }\), the Lewis number, \(\chi ={kd^{2}}/{\varepsilon \kappa _{\mathrm{T}z} }\), Damkohler number that measures the rate of reaction, \(\xi ={K_x }/{K_z }\), the mechanical anisotropy parameter, \(\eta ={\kappa _{\mathrm{T}x} }/{\kappa _{\mathrm{T}z} }\), the thermal anisotropy parameter, and \(\lambda =\varepsilon \frac{({\rho c})_\mathrm{f} }{({\rho c})_{m} }\), the normalized porosity parameter. The Lewis number Le is known to be much greater than unity, and the dimensionless reaction rate measured by the Damkohler number \(\chi \ge 0\). Equations (2.13–2.15) are to be solved for the stress free, isothermal, and isosolutal boundary conditions

$$\begin{aligned} w = \frac{\partial ^{2}w}{\partial z^{2}} = T = S = 0, \text{ at} z = 0, 1 \end{aligned}$$
(2.16)

The stress-free boundary conditions are chosen for mathematical simplicity, without qualitatively important physical effect being lost. The use of stress-free boundary conditions is a useful mathematical simplification but is not physically sound. The correct boundary conditions for a viscous binary fluid are to impose rigid–rigid boundary conditions but then the problem is not tractable analytically.

3 Linear Stability Analysis

In this section, we predict the thresholds of both marginal and oscillatory convections using linear theory. The eigenvalue problem defined by Eqs (2.13–2.15) subject to the boundary conditions (2.16) is solved using the time-dependent periodic disturbances in a horizontal plane. Assuming that the amplitudes of the perturbations are very small, we write

$$\begin{aligned} \left(\begin{array}{l} w \\ T \\ S \\ \end{array}\right)=\left( \begin{array}{l} W\left( z \right) \\ \Theta \left( z \right) \\ \Phi \left( z \right) \\ \end{array}\right)\exp \left[ {i\left( {lx+my} \right)+\sigma t} \right], \end{aligned}$$
(3.1)

where \(l, m\) are horizontal wavenumbers and \(\sigma \) is the growth rate. Infinitesimal perturbations of the rest state may either damp or grow depending on the value of the parameter \(\sigma \). Substituting Eq. (3.1) into the linearized version of Eqs. (2.13–2.15) we obtain

$$\begin{aligned}&\left[ {\left(\frac{D^{2}}{\xi }-a^{2}\right)+Ta D^{2}} \right] W(z)+Ra_\mathrm{T} a^{2}\Theta -Ra_\mathrm{S} a^{2}\Phi =0\end{aligned}$$
(3.2)
$$\begin{aligned}&\left[ {\sigma -\left( {D^{2}-\eta a^{2}} \right)} \right]\Theta -\lambda W=0,\end{aligned}$$
(3.3)
$$\begin{aligned}&\left[ { \sigma -\frac{1}{Le}({D^{2}-a^{2}})+\chi } \right]\Phi -\chi \Theta -W=0, \end{aligned}$$
(3.4)

where \(D={\text{ d}}/{{\text{ d}}z}\) and \(a^{2}=l^{2}+m^{2}\).

We assume the solutions of Eqs. (3.2–3.4) satisfying the boundary conditions (2.16) in the form

$$\begin{aligned} \left( {\begin{array}{l} W(z) \\ \Theta (z) \\ \Phi (z) \\ \end{array}} \right) = \left( {\begin{array}{l} W_0 \\ \Theta _0 \\ \Phi _0 \\ \end{array}} \right) {\text{ Sin}} n\pi z, (n=1,2,3,\ldots \ldots ). \end{aligned}$$
(3.5)

The most unstable mode corresponds to \(n=1\)(fundamental mode). Therefore, substituting Eq. (3.5) with \(n=1\) into Eqs. (3.2–3.4), we obtain an expression for thermal Rayleigh number in the form

$$\begin{aligned} Ra_\mathrm{T} =\frac{ \left( {\delta _{1}^{2} +\pi ^{2}Ta} \right)\left({\sigma +\delta _{2}^{2}} \right)}{\lambda a^{2}}+\frac{Ra_\mathrm{S} }{\lambda }\left({\frac{\sigma +\delta _{2}^{2} +\lambda \chi }{\sigma +\delta ^{2}Le^{-1}+\chi }}\right) \end{aligned}$$
(3.6)

where \(\delta ^{2}=\pi ^{2}+a^{2}, \delta _1^2 =\pi ^{2}\xi ^{-1}+a^{2}\) and \(\delta _2^2 =\pi ^{2}+\eta a^{2}\). The growth rate \(\sigma \) is in general a complex quantity such that \(\sigma =\sigma _r + i\sigma _\mathrm{i} \). The system with \(Re\left( \sigma \right)<0\) is always stable, while for \(Re\left( \sigma \right)>0\), it will become unstable. For neutral stability, we have \(Re (\sigma )=0\).

3.1 Stationary Mode

For the validity of principle of exchange of stabilities (i.e., steady case), we have \(\sigma =0\) (i.e.,\(\sigma _r =\sigma _i =0)\) at the margin of stability. Then the Rayleigh number at which marginally stable steady mode exists becomes

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{St} =\frac{ \left({\delta _1^2 +\pi ^{2}Ta} \right)\left( {\delta _{2}^{2} } \right)}{\lambda a^{2}}+\frac{Ra_\mathrm{S} }{\lambda }\left( {\frac{\delta _{2}^{2} +\lambda \chi }{\delta ^{2} Le^{-1}+ \chi }} \right) \end{aligned}$$
(3.7)

The minimum value of the Rayleigh number \(Ra_\mathrm{T}^\mathrm{St}\) occurs at the critical wavenumber \(a=a_\mathrm{c}^\mathrm{St} \) where \(a_\mathrm{c}^\mathrm{St} =\sqrt{r}\) satisfies a polynomial equation

$$\begin{aligned} a_0 r^{4}+a_1 r^{3}+a_2 r^{2}+a_3 r+a_4 =0, \end{aligned}$$

where \(a_0 =\eta , a_1 =2 \eta \left( {\pi ^{2}+Le \chi } \right),\)

$$\begin{aligned} a_2&= \pi ^{2}\left( {LeRa_S ({\eta -1})+\pi ^{2} ({\eta -\xi ^{-1}-Ta})} \right)+Le\eta \chi ({2\pi ^{2}+Le\chi })+Le Ra_\mathrm{S} \chi ({Le\eta -\lambda }),\\ a_3&= -2\pi ^{4}\xi ^{-1}\left( {\pi ^{2}+Le\chi } \right)\left( {1+Ta\xi } \right), \quad a_4 =-\pi ^{4}\xi ^{-1}\left( {\pi ^{2}+Le\chi } \right)^{2}\left( {1+Ta\xi } \right). \end{aligned}$$

In the absence of rotation, Eq. (3.7) reduces to

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{St} =\frac{ \left( {\delta _1^2 } \right)\left( {\delta _2^2 } \right)}{\lambda a^{2}}+\frac{Ra_\mathrm{S} }{\lambda }\left( {\frac{\delta _{2}^{2} +\lambda \chi }{\delta ^{2} Le^{-1}+ \chi }} \right), \end{aligned}$$

given by Malashetty and Biradar (2011). In the absence of a chemical reaction parameter (i.e., \(\chi =0)\), and, Further \(\left( {\lambda =1} \right)\), Eq. (3.7) reduces to

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{St} =\frac{ \left( {\delta _1^2 +\pi ^{2}Ta} \right) ({\delta _2^2 })}{ a^{2}}+ \left({\frac{\delta _2^2 Ra_\mathrm{S} }{\delta ^2 Le^{-1} }}\right). \end{aligned}$$

This is exactly the one given by Malashetty and Heera (2008). Further in absence of both rotation and chemical reaction parameter Eq. (3.7) reduces to

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{St} =\frac{1}{a^{2}}\left( {a^{2}+\frac{\pi ^{2}}{\xi }} \right)\left( {\eta a^{2}+\pi ^{2}} \right) + \left( {\frac{\eta a^{2}+\pi ^{2}}{a^{2}+\pi ^{2}}} \right)Le Ra_\mathrm{S}. \end{aligned}$$
(3.8)

This is the result obtained by Malashetty and Swamy (2010) for the onset of stationary double-diffusive convection in an anisotropic porous layer. Further, for an isotropic porous media, that is when \(\xi =\eta =1\), Eq. (3.8) reduces to the classical result of Nield and Bejan (2006)

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{St} =\frac{1}{a^{2}}({a^{2}+\pi ^{2}})^{2} +Le Ra_\mathrm{S}, \end{aligned}$$
(3.9)

with critical values \(Ra_\mathrm{T,c}^\mathrm{St} =4\pi ^{2} +Le Ra_\mathrm{S} \) and \(a_\mathrm{c}^\mathrm{St} = \pi \). In the case of single component convection in an anisotropic porous medium, \(Ra_\mathrm{S} = 0\); the expression for stationary Rayleigh number given by Eq. (3.8) reduces to

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{St} =\frac{1}{a^{2}}({a^{2}+\frac{\pi ^{2}}{\xi }}) ({\eta a^{2}+\pi ^{2}}) , \end{aligned}$$
(3.10)

which is the one obtained by Storesletten (1998) for the case of a single component fluid-saturated anisotropic porous. Further, for an isotropic porous medium, \(\xi =\eta =1\), the above Eq. (3.10) reduces to the classical result

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{St} =\frac{1}{a^{2}}\left( {a^{2}+\pi ^{2}} \right)^{2}, \end{aligned}$$

with critical values \(Ra_\mathrm{T,c}^\mathrm{St} =4\pi ^{2}\) and \(a_\mathrm{c}^\mathrm{St} = \pi \) obtained by Horton and Rogers (1945), and Lapwood (1948)

3.2 Oscillatory Mode

We now set \(\sigma = i \sigma _\mathrm{i}\), in Eq. (3.6) and clear the complex quantities from the denominator, to obtain

$$\begin{aligned} Ra_\mathrm{T} = \varDelta _1 + i \sigma _\mathrm{i} \varDelta _2 , \end{aligned}$$
(3.11)

where

$$\begin{aligned} \varDelta _1&= \frac{ \left( {\delta _1^2 +\pi ^{2}Ta} \right)\left( {\delta _2^2 } \right)}{\lambda a^{2}}+\frac{Ra_\mathrm{S} }{\lambda }\left( {\frac{\sigma _i^2 +\left( {\lambda \chi +\delta _2^2 } \right)\left( {\delta ^2 Le^{-1}+ \chi } \right)}{\sigma _{i}^{2} +\left( {\delta ^{2} Le^{-1}+ \chi } \right)^{2} }} \right),\\ \varDelta _{2}&= \frac{ \left( {\delta _{1}^{2} +\pi ^{2}Ta} \right)}{\lambda a^{2}}+\frac{Ra_S }{\lambda }\left( {\frac{\chi \left( {1-\lambda } \right)+\delta ^{2} Le^{-1}-\delta _{2}^{2} }{\sigma _{i}^{2} +\left( {\delta ^2 Le^{-1}+ \chi } \right)^{2} }} \right). \end{aligned}$$

Since \(Ra_\mathrm{T} \) is a physical quantity, it must be real. Hence, from Eq. (3.11) it follows that either \(\sigma _i =0\) (oscillatory onset) or \(\varDelta _2 =0\) (\(\sigma _i \ne 0\), oscillatory onset).

For oscillatory onset \(\varDelta _2 =0 (\sigma _i \ne 0)\) and this gives a expression for the frequency of oscillation in the form

$$\begin{aligned} \sigma _\mathrm{i}^{2} =\frac{ a^{2}Ra_\mathrm{S}}{\left( {\delta _1^2 +\pi ^{2}Ta} \right) }\left( {\delta _2^2 -\delta ^2 Le^{-1}-\chi \left( {1-\lambda } \right) } \right)-\left( {\delta ^2 Le^{-1}+\chi } \right)^{2}. \end{aligned}$$
(3.12)

Now Eq. (3.11) with \(\varDelta _{2}=0\), gives

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{Osc} =\frac{ \left( {\delta _1^2 +\pi ^{2}Ta} \right)\left( {\delta _2^2 } \right)}{\lambda a^{2}}+\frac{Ra_\mathrm{S} }{\lambda }\left( {\frac{\sigma _\mathrm{i}^2 +\left( {\lambda \chi +\delta _2^2 } \right)\left( {\delta ^2 Le^{-1}+ \chi } \right)}{\sigma _{i}^{2} +\left( {\delta ^{2} Le^{-1}+ \chi } \right)^{2} }} \right). \end{aligned}$$
(3.13)

The analytical expression for oscillatory Rayleigh number given by Eq. (3.13) is minimized with respect to the wavenumber numerically, after substituting for \(\sigma _{i}^{2} \left({>0} \right)\) from Eq. (3.12), for various values of the physical parameters in order to know their effects on the onset of oscillatory convection.

4 Finite-Amplitude Analysis

In this section, we consider the nonlinear analysis using a truncated representation of Fourier series considering only two terms. Although the linear stability analysis is sufficient for obtaining the stability condition of the motionless solution and the corresponding eigenfunctions describing qualitatively the convective flow, it can neither provide information about the values of the convection amplitudes, nor regarding the rate of heat transfer. To obtain this additional information, we perform the nonlinear analysis, which is useful to understand the physical mechanism with minimum amount of mathematics and is a step forward toward understanding the full nonlinear problem.

For simplicity of analysis, we confine ourselves to the two-dimensional rolls, so that all the physical quantities are independent of \(y\). We introduce stream function \(\psi \) such that \(u={\partial \psi }/{\partial z, w=-{\partial \psi }/{\partial x}}\) into the Eq. (2.9), eliminate pressure and non-dimensionalize the resulting equation and Eqs. (2.8–2.11) using the transformations (2.12) to obtain

$$\begin{aligned}&\left( {\frac{\partial ^{2}}{\partial x^{2}}+\frac{1}{\xi }\frac{\partial ^{2}}{\partial z^{2}}} \right)\psi -Ta^{1/2}\frac{\partial V}{\partial z} +Ra_\mathrm{T} \frac{\partial T}{\partial x}-Ra_\mathrm{S} \frac{\partial S}{\partial x} =0,\end{aligned}$$
(4.1)
$$\begin{aligned}&\left( {\frac{1}{\xi }\frac{\partial V}{\partial z}+Ta^{1/2}\frac{\partial ^{2}\psi }{\partial z^{2}}} \right)=0,\end{aligned}$$
(4.2)
$$\begin{aligned}&\frac{\partial T}{\partial t}-\left( {\eta \frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial z^{2}}} \right)T-\lambda J({\psi , T})+\lambda \frac{\partial \psi }{\partial x}=0,\end{aligned}$$
(4.3)
$$\begin{aligned}&\frac{\partial S}{\partial t}-\frac{1}{Le}\nabla ^{2}S-J({\psi ,S})+\frac{\partial \psi }{\partial x}-\chi \left( {T-S} \right)=0. \end{aligned}$$
(4.4)

Here, \(J\left( {.,.} \right)\) is the Jacobian with respect to the independent variables \(x, z\). The first effect of non-linearity is to distort the temperature and concentration fields through the interaction of \(\psi , T\) and also \(\psi , S\). The distortion of these fields will corresponds to a change in the horizontal mean, i.e. a component of the form \(\sin (2\pi z)\) will be generated. Thus a minimal Fourier series which describes the finite amplitude-free convection is given by,

$$\begin{aligned} \psi&= A(t)\sin (ax)\sin (\pi z),\end{aligned}$$
(4.5)
$$\begin{aligned} T&= B(t)\cos (ax)\sin (\pi z)+C(t)\sin (2\pi z),\end{aligned}$$
(4.6)
$$\begin{aligned} S&= D(t)\cos (ax)\sin (\pi z)+E(t)\sin (2\pi z),\end{aligned}$$
(4.7)
$$\begin{aligned} V&= F(t)\sin (ax)\cos (\pi z)+G(t)\sin (2\pi x), \end{aligned}$$
(4.8)

where the amplitudes \(A(t), B(t), C(t), E(t), F(t), and \text{ G(t)}\) are to be determined from the dynamics of the system.

Substituting Eqs. (4.5–4.8) into Eqs. (4.1–4.4) and equating the coefficients of like terms we obtain the following non-linear autonomous system of differential equations

$$\begin{aligned} \frac{{\text{ d}}A}{{\text{ d}}t}&= -\delta _1^2 A+\pi Ta^{1/2} F-aRa_\mathrm{T} B+aRa_\mathrm{S} D,\end{aligned}$$
(4.9)
$$\begin{aligned} \frac{{\text{ d}}B}{{\text{ d}}t}&= -\lambda aA-\delta _2^2 B-\lambda \pi aAC,\end{aligned}$$
(4.10)
$$\begin{aligned} \frac{{\text{ d}}C}{{\text{ d}}t}&= -4\pi ^{2}C+\frac{\pi a\lambda }{2}AB,\end{aligned}$$
(4.11)
$$\begin{aligned} \frac{{\text{ d}}D}{{\text{ d}}t}&= -Aa-\frac{\delta ^{2}D}{Le}-\pi aAE+\chi \left( {B-D} \right),\end{aligned}$$
(4.12)
$$\begin{aligned} \frac{{\text{ d}}E}{{\text{ d}}t}&= \frac{\pi aAD}{2}- \frac{4\pi ^{2}E}{Le}+\chi \left( {C-E} \right),\end{aligned}$$
(4.13)
$$\begin{aligned} \frac{{\text{ d}}F}{{\text{ d}}t}&= - \frac{F \pi }{\xi }-\pi ^{2} Ta^{1/2}A. \end{aligned}$$
(4.14)

The non-linear system of autonomous differential equations is not suitable to analytical treatment for the general time-dependent variable and we have to solve it using a numerical method. However, one can make qualitative predictions as discussed below. The system of Eqs. (4.9–4.14) is uniformly bounded in time and possesses many properties of the full problem. Thus, volume in the phase space must contract. In order to prove volume contraction, we must show that flow field has a constant negative divergence. Indeed,

$$\begin{aligned} \frac{\partial }{\partial A}\left( {\frac{{\text{ d}}A}{{\text{ d}}t}} \right)+\frac{\partial }{\partial B}\left( {\frac{{\text{ d}}B}{{\text{ d}}t}} \right)+\frac{\partial }{\partial C}\left( {\frac{{\text{ d}}C}{{\text{ d}}t}} \right)&+\frac{\partial }{\partial D}\left( {\frac{{\text{ d}}D}{{\text{ d}}t}} \right)+\frac{\partial }{\partial E}\left( {\frac{{\text{ d}}E}{{\text{ d}}t}} \right)+\frac{\partial }{\partial F}\left( {\frac{{\text{ d}}F}{{\text{ d}}t}} \right)=\nonumber \\&\quad -\left[ {\delta _1^2 \!+\!\delta _2^2 \!+\!4\pi ^{2}\!+\!\frac{1}{Le }(\delta ^{2}\!+\!4\pi ^{2})\!+\!\frac{ \pi }{\xi }\!+\!2\chi } \right],\nonumber \\ \end{aligned}$$
(4.15)

which is always negative and therefore the system is bounded and dissipative. As a result, the trajectories are attracted to a set of measure zero in the phase space; in particular they may be attracted to a fixed point, a limit cycle or, perhaps, a strange attractor. From Eq. (4.15) we conclude that if a set of initial points in phase space occupies a region \(V\) (0) at time \(t \)= 0, then after some time \(t\), the end points of the corresponding trajectories will fill a volume

$$\begin{aligned} V(t)=V(0) \exp \left[ {-\left({\delta _1^2 +\delta _2^2 +4\pi ^{2}+\frac{1}{Le }(\delta ^{2}+4\pi ^{2})+\frac{ \pi }{\xi }+2\chi } \right)t} \right]. \end{aligned}$$
(4.16)

This expression indicates that the volume decreases exponentially with time. We can also infer that, the large values of Damkohler number and very small Lewis number \((Le<1)\) tend to enhance dissipation.

From qualitative predictions we look into the possibility of an analytical solution. In the case of steady motions, Eqs. (4.1–4.3) can be solved in closed form. Setting the left hand sides of Eqs. (4.9–4.14) equal to zero, we get

$$\begin{aligned}&-\delta _1^2 A+\pi Ta^{1/2} F-aRa_\mathrm{T} B+aRa_\mathrm{S} D=0,\end{aligned}$$
(4.17)
$$\begin{aligned}&-\lambda aA-\delta _2^2 B-\lambda \pi aAC=0,\end{aligned}$$
(4.18)
$$\begin{aligned}&-4\pi ^{2}C+\frac{\pi a\lambda }{2}AB=0,\end{aligned}$$
(4.19)
$$\begin{aligned}&-Aa-\frac{\delta ^{2}D}{Le}-\pi aAE+\chi ({B-D})=0,\end{aligned}$$
(4.20)
$$\begin{aligned}&\frac{\pi aAD}{2}- \frac{4\pi ^{2}E}{Le}+\chi ({C-E})=0,\end{aligned}$$
(4.21)
$$\begin{aligned}&- \frac{F \pi }{\xi }-\pi ^{2} Ta^{1/2} A=0. \end{aligned}$$
(4.22)

Writing \(B, C, D, E, F,\) and \(G\) in terms of \(A\), using Eqs. (4.18–4.22) and substituting these in Eq. (4.17), with \(\frac{A^{2}}{8}=r\) we get

$$\begin{aligned} b_1 r^{2}+b_2 r+b_3 =0, \end{aligned}$$
(4.23)

where \(r=\frac{A_1^2 }{8}\) and

where

$$\begin{aligned} b_1&= 4a^{4}Le^{2}\pi ^{2}\lambda ^{2}({\delta _1^2 +\pi ^{2}Ta\xi }),\\ b_2&= 4a^{4}Le\pi ^{2}\lambda ({Ra_\mathrm{S} -LeRa_\mathrm{T} })+4a^{2}\pi ^{2}\lambda ^{2} ({\delta _1^2 +\pi ^{2}Ta\xi }) ({\delta ^{2}+Le\chi }) \\&+a^{2}\lambda ^{2}Le\chi ({\delta _1^2 +\pi ^{2}Ta\xi }) ({\delta ^{2}+Le\chi })+4a^{2}Le^{2}\pi ^{2}\delta _1^2 \delta _2^2, \\ b_3&= ({4\pi ^{2}\!+\!Le\chi }) ({\delta _2^2 ({\delta _1^2 \!+\!\pi ^{2}Ta\xi }) ({\delta ^{2}\!+\!Le\chi })\!+\!a^{2} ({Ra_\mathrm{S} Le({\chi \lambda \!+\!\delta _2^2 })-Ra_\mathrm{T} \lambda ( {\delta ^{2}\!+\!Le\chi })})}), \end{aligned}$$

The required root of Eq. (4.23) is given by

$$\begin{aligned} r=\frac{1}{2b_{1}}\left( {-b_{2} +\left( {b_{2}^{2} -4b_{1} b_{3}} \right)^{1/2}} \right). \end{aligned}$$
(4.24)

When we let the radical in the above equation to vanish, we obtain the expression for finite amplitude Rayleigh number \(Ra_\mathrm{T}^\mathrm{F}\), which characterizes the onset of finite-amplitude steady motions. The finite-amplitude Rayleigh number can be obtained in the form

$$\begin{aligned} Ra_\mathrm{T}^\mathrm{F} =\frac{1}{2c_1 }\left( {-c_2 +\left( {c_2 ^{2}-4c_1 c_3 } \right)^{1/2}} \right) , \end{aligned}$$
(4.25)

where the constants \({c_{j}}\,^{\prime }s\) are not presented here for brevity.

In the study of convection in fluids, the quantification of heat and mass transport is important. This is because the onset of convection, as Rayleigh number is increased, is more readily detected by its effect on the heat and mass transport. In the basic state, heat and mass transport is by conduction alone. We now proceed to find the Nusselt number and Sherwood number.

If \(H\) and \(J\) are the rate of heat and mass transport per unit area, respectively, then

$$\begin{aligned} H=-\kappa _{\mathrm{T}z} \left\langle {\frac{\partial T_\mathrm{total} }{\partial z}} \right\rangle _{z = 0} , \quad {\text{ and}} \quad J=-\kappa _\mathrm{S} \left\langle {\frac{\partial S_\mathrm{total} }{\partial z}} \right\rangle _{z = 0}, \end{aligned}$$
(4.26)

where the angular bracket corresponds to a horizontal average and

$$\begin{aligned} T_\mathrm{total} =T_0 -\Delta T\frac{z}{d}+T(x,z,t), \quad {\text{ and}} \quad S_\mathrm{total} =S_0 -\Delta S\frac{z}{d}+S(x,z,t). \end{aligned}$$
(4.27)

Substituting Eqs. (4.6) and (4.7) in Eq. (4.27) and using the resultant equations in Eq. (4.26), we get

$$\begin{aligned} H=\frac{\kappa _{\mathrm{T}z} \Delta T}{d}({1-2\pi C}) \text{ and} J=\frac{\kappa _\mathrm{S} \Delta S}{d}\left( {1-2\pi E} \right). \end{aligned}$$
(4.28)

The Nusselt number and Sherwood number are defined by

$$\begin{aligned} Nu=\frac{H}{\kappa _{\mathrm{T}z} {\Delta T}/d}=\left( {1-2\pi C} \right), \quad {\text{ and}} \quad Sh=\frac{J}{\kappa _\mathrm{S} {\Delta S}/d}=\left( {1-2\pi E} \right). \end{aligned}$$
(4.29)

Writing \(C\) and \(E\) in terms of \(A\), and substituting in Eq. (4.29), we obtain

$$\begin{aligned}&\displaystyle Nu = 1+\frac{2r}{{r+\delta _2^2 }/{a^{2}}\lambda ^{2}},\end{aligned}$$
(4.30)
$$\begin{aligned}&\displaystyle Sh = 1+2\left({\frac{4\pi ^{2}a^{2}rLe^{2}\left( {a^{2}r\lambda ^{2}+\delta _2^2 +\chi \lambda } \right)+a^{2}rLe\chi \lambda ^{2}\left( {\delta ^{2}+Le\chi } \right)}{\left( {a^{2}r\lambda ^{2}+\delta _2^2 } \right)\left( {\left( {4\pi ^{2}+Le\chi } \right)\left( {\delta ^{2}+Le\chi } \right)+4\pi ^{2}a^{2}rLe^{2}} \right)}} \right). \end{aligned}$$
(4.31)

The second-term on the right-hand side of Eq. (4.31) represent the convective contribution to heat and mass transport, respectively. The expressions for Nusselt number and Sherwood number given by Eqs. (4.30) and (4.31) are evaluated for different values of the parameters and the results are discussed in next section.

5 Results and Discussion

The effect of rotation on the onset of double-diffusive reaction–convection in an anisotropic porous layer, which is heated and salted from below, is investigated analytically using the linear and nonlinear theories. In the linear stability theory the expressions for the stationary, oscillatory Rayleigh number and for frequency of oscillation are obtained analytically. The nonlinear theory provides the quantification of heat and mass transports and also explains the possibility of the finite amplitude motions.

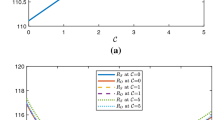
The neutral stability curves in the \(Ra_\mathrm{T}-a\) plane for Taylor number is shown in Fig. 1. From this figure it is clear that the neutral curves are connected in a topological sense. This connectedness allows the linear stability criteria to be expressed in terms of the critical Rayleigh number, \(Ra_\mathrm{Tc}\) below which the system is stable and unstable above.

Fig. 1
figure 1

Neutral stability curves for differents values of Taylor number \(Ta\)

Full size image

The effect of Taylor number Ta on the marginal stability curves for the fixed values of mechanical anisotropy parameter, thermal anisotropy parameter, Damkohler number, solute Rayleigh number, Lewis number and normalized porosity parameter, is depicted in Fig. 1. We observe from this figure that the minimum of Rayleigh number for both stationary and oscillatory states increases with the Taylor number, indicating that the effect of rotation is to enhance the stability of the system in both stationary and overstable modes.

In Figs. 2, 3, 4, 5, 6, and 7, we show the critical Rayleigh number for stationary, oscillatory, and finite-amplitude modes as function of the Taylor number for different values of the mechanical anisotropy parameter, thermal anisotropy parameter, Damkohler number, solute Rayleigh number, Lewis number, and normalized porosity parameter, respectively. We find that all of the quantities namely, the critical Rayleigh number for stationary, oscillatory, and finite-amplitude modes are increasing functions of the Taylor number. It is clear that for the parameters chosen for these figures, the steady finite-amplitude convection sets in prior to the oscillatory and stationary convection.

Fig. 2
figure 2

Variation of critical Rayleigh with Taylor number \(Ta\) for different values of mechanical anisotrpoy parameter \(\xi \)

Full size image

In Fig. 2, we display the variation of \(Ra_\mathrm{Tc}\) with Taylor number \(Ta\) for different values of mechanical anisotropy parameter \(\xi \) for the fixed values of other parameters. It is important to note that the critical Rayleigh number \(Ra_\mathrm{Tc}\) decreases with the increase of \(\xi \) for stationary and oscillatory modes. Where as it is important to note from this figure that the critical Rayleigh number \(Ra_\mathrm{Tc}\) for finite-amplitude mode decreases with the increase of \(\xi \) for small values of Taylor number \(Ta\), and for the moderate and large values of \(Ta\), the critical Rayleigh number increases with increasing \(\xi \). However, contrary to its usual influence on the onset of convection in the absence of rotation, the mechanical anisotropy parameter \(\xi \) show contrasting effect on finite amplitude at moderate and high rotation rates. Thus, the mechanical anisotropy parameter \(\xi \) has dual effect on finite-amplitude mode in the presence of rotation.

Fig. 3
figure 3

Variation of critical Rayleigh with Taylor number \(Ta\) for different values of thermal anisotrpoy parameter \(\eta \)

Full size image

The variation of the critical Rayleigh numbers for stationary, oscillatory, and finite-amplitude modes with Taylor number for different values of the thermal anisotropy parameter is shown in Fig. 3. We find that the critical Rayleigh number increases with increasing thermal anisotropy parameter for all the cases namely stationary, oscillatory, and finite-amplitude convection. Figure 4 shows the variation of critical stationary, oscillatory, and finite-amplitude Rayleigh numbers with Taylor number for different values of the Damkohler number \(\chi \). We observe from Fig. 4 that the critical Rayleigh numbers for oscillatory and finite-amplitude modes increase with Damkohler number indicating that the effect of increasing chemical reaction parameter is to inhibit the oscillatory and finite-amplitude convection. This is because the chemical reaction term couples together the temperature and concentration fields to inhibit double diffusive effects. On the other hand, increasing the chemical reaction parameter advances the onset of stationary convection.

Fig. 4
figure 4

Variation of critical Rayleigh with Taylor number \(Ta\) for different values of Damkholer number \(\chi \)

Full size image
Fig. 5
figure 5

Variation of critical Rayleigh with Taylor number \(Ta\) for different values of solute Rayleigh number \(Ra_\mathrm{S}\)

Full size image

The variation of \(Ra_\mathrm{Tc}\) with \(Ta\) for different values of solute Rayleigh number \(Ra_\mathrm{S}\) and Lewis number Le on the onset criteria is shown in Figs. 5 and 6, respectively. We observe from these figures that the effect of \(Ra_\mathrm{S}\) is to delay the onset of convection while the effect of Le is to delay stationary and finite-amplitude convection and advance the oscillatory convection. That is the solute Rayleigh number makes the system more stable while the Lewis number is responsible for the advancement of oscillatory convection.

Fig. 6
figure 6

Variation of critical Rayleigh with Taylor number \(Ta\) for different values of Lewis number \(Le\)

Full size image
Fig. 7
figure 7

Variation of critical Rayleigh with Taylor number \(Ta\) for different values of normalized porosity parameter \(\lambda \)

Full size image

Figure 7 depicts the effect of normalized porosity parameter on the critical stationary, oscillatory, and finite-amplitude Rayleigh numbers. We find that the effect of increasing the normalized porosity parameter is to decrease the critical Rayleigh number for stationary, oscillatory, and finite-amplitude mode. As normalized porosity parameter increases, the thermal “lag” effect (double-advective behavior in the terminology of Phillips (2009) is reduced. This makes advective heat transfer more effective and so makes it easier for the destabilizing thermal buoyancy gradient to produce convection.

In Fig. 8, we display the Nusselt number and the Sherwood number for different values of the governing parameter. This figure indicates that the rate of heat and mass transfer across a convective porous layer is limited in the present model by an upper bound value of 3. This limitation is due to the severely truncated two-term Fourier series representation used for the variables. Better results can only be obtained by including more terms in the Fourier series representation, which allows the variation of wavenumber as the value of Rayleigh number varies.

Fig. 8
figure 8

Variation of Nusselt number and Sherwood number with critical Rayleigh numberfor different values of Taylor number \(Ta\)

Full size image

The Taylor number reduces both heat and mass transfer and its effect is more significant on heat transfer (Fig. 8).

6 Conclusions

The onset of rotating double-diffusive reaction–convection in an anisotropic horizontal porous layer saturated with binary mixture, which is heated and salted from below, is investigated analytically using both linear and nonlinear theories. The usual normal mode technique is used to solve the linear problem. The truncated two-term Fourier series method is used to carry out the finite amplitude analysis. In the case of linear theory, the thresholds of both stationary and oscillatory convection are derived as functions of Taylor number, mechanical anisotropy parameter, thermal anisotropy parameter, Damkohler number, Lewis number, solute Rayleigh number, and normalized porosity parameter. The Taylor number \(Ta\) has a stabilizing effect on the system. When the horizontal permeability is high \((\xi >1)\), the system is more unstable; while vertical permeability is high \((\xi <1)\), the system is more stable than in the isotropic case. When the horizontal component of thermal diffusivity is dominant \((\eta >1)\), the system becomes more stable; while the vertical component of thermal diffusivity is dominant \((\eta <1)\), the system becomes more unstable. The effect of increasing the Damkohler number \(\chi \) is to advance the onset of stationary convection and delay the onset of oscillatory and finite amplitude convection. The effect of solute Rayleigh number is to delay, stationary, oscillatory, and finite-amplitude convection. It is found that the effect of increasing Lewis number is to delay the onset of stationary convection and advance the onset of oscillatory and finite-amplitude convection. The critical Rayleigh numbers for stationary, oscillatory, and steady finite-amplitude modes are increasing functions of Taylor number. Increasing the normalized porosity parameter advances stationary, oscillatory, and finite-amplitude convection. Heat and mass transfer decreases with increasing Taylor number.