Graph-based models for real-time workload: a survey

Abstract

This paper provides a survey on task models to characterize real-time workloads at different levels of abstraction for the design and analysis of real-time systems. It covers the classic periodic and sporadic models by Liu and Layland et al., their extensions to describe recurring and branching structures as well as general graph- and automata-based models to allow modeling of complex structures such as mode switches, local loops and also global timing constraints. The focus is on the precise semantics of the various models and on the solutions and complexity results of the respective feasibilty and schedulability analysis problems for preemptable uniprocessors.

1 Introduction

Real-time systems are often implemented by a number of concurrent tasks sharing hardware resources, in particular the execution processors. The designer of such systems needs to construct workload models characterizing the resource requirements of the tasks. With a formal description of the workload, a resource scheduler may be designed and analyzed. The fundamental analysis problem to solve in the design process is to check (and thus to guarantee) the schedulability of the workload, i.e., whether the timing constraints on the workload can be met with the given scheduler. In addition, the workload model may also be used to optimize the resource utilization as well as the average system performance.

In the past decades, workload models have been studied intensively in the theory of real-time scheduling (Buttazzo 2011) and other contexts, for example performance analysis of networked systems (Boudec and Thiran 2001). The research community of real-time systems has proposed a large number of models (often known as task models) allowing for the description and analysis of real-time workloads at different levels of abstraction. One of the classic works is the periodic task model due to Liu and Layland (1973), Leung and Merrill (1980), and Leung and Whitehead (1982), where tasks generate resource requests at strict periodic intervals. The periodic model was extended later to the sporadic model (Mok 1983; Baruah et al. 1990; Lehoczky et al. 1987) and multiframe models (Mok and Chen 1997; Baruah et al. 1999a) to describe non-regular arrival times of resource requests, and non-uniform resource requirements. In spite of a limited form of variation in release times and worst-case execution times, these repetitive models are highly deterministic. To allow for the description of recurring and non-deterministic behaviours, tree-like recurring models based on directed acyclic graphs are introduced (Baruah Baruah 1998a, b) and recently extended to a digraph model based on arbitrary directed graphs (Stigge et al. 2011; 2011a) to allow for modeling of complex structures like mode switches and local loops as well as global timing constraints on resource requests. With origin from formal verification of timed systems, the model of task automata (Fersman et al. 2007) was developed in the late 90s. The essential idea is to use timed automata to describe the release patterns of tasks. Due to the expressiveness of timed automata, it turns out that all the models above can be described using the automata-based model.

In addition to the expressiveness, a major concern in developing these models is the complexity of their analyses. It is not surprising that the more expressive the models are, the more difficult to analyze they tend to be. Indeed, the model of task automata is the most expressive model with the highest analysis complexity, which marks the borderline between decidability and undecidability for the schedulability analysis problem of workloads. On top of the operational models summarized above that capture the timed sequences of resource requests representing the system executions, alternative characterizations of workloads using functions on the time interval domain have also been proposed, notably demand-bound functions, request-bound functions and real-time calculus (RTC) (Thiele et al. 2000) that can be used to specify the accumulated workload over a sliding time window. They have been further used as a mathematical tool for the analysis of operational workload models.

Fig. 1

A hierarchy of task models. Arrows indicate the generalization relationship. We denote the corresponding section in parentheses

This paper is intended to serve as a survey on existing workload models for preemptable uniprocessor systems. Figure 1 outlines the relative expressive powers of the models (marked with sections where they are described). In the following sections we go through this model hierarchy and provide a brief account for each of the well-developed models.

2 Preliminaries

2.1 Terminology

We first review some terminology used in the rest of this survey. The basic unit describing workload is a job, characterized by a release time, an execution time and a type from which parameters like a deadline are derived. The higher-level structures which generate (potentially infinite) sequences of jobs are tasks. The time interval between the release time and the deadline of a job is called its scheduling window. The time interval between the release time of a job and the earliest release time of its succeeding job from the same task is its exclusion window.

A task system typically contains a set of tasks that at runtime concurrently generate sequences of jobs and a scheduler decides at each point in time which of the pending jobs to execute. We distinguish between two important classes of schedulers on preemptable uniprocessor systems:

Static priority schedulers :

Tasks are ordered by priority. All jobs generated by a task of higher priority get precedence over jobs generated by tasks of lower priority.

Dynamic priority schedulers :

Tasks are not ordered a priori; at runtime, when choosing one of the pending jobs to execute, the scheduler is not constrained to a static priority ordering between tasks.

Given suitable descriptions of a workload model and a scheduler, one of the important questions is whether all jobs that could ever be generated will meet their deadline constraints, in which case we call the workload schedulable. This is determined in a formal schedulability test which can be:

Sufficient or safe,:

if it is failed by all non-schedulable task sets,

Necessary,:

if it is satisfied by all schedulable task sets, or

Precise or exact,:

if it is both sufficient and necessary.

Workload that is schedulable with some scheduler is called feasible, determined by a feasibility test that can also be either sufficient, necessary or both.

2.2 Model hierarchy

Most workload models described in this survey are part of a model hierarchy in the sense that some are generalizations of others, cf. Fig. 1. Intuitively, a modeling formalism $\mathcal M_A$ generalizes a modeling formalism $\mathcal M_B$, if any task system expressed in terms of $\mathcal M_B$ has a corresponding task system expressed with $\mathcal M_A$ such that these two represent the same behavior. The motivation behind such a generalization concept is that more expressive models should preserve the capability of being able to analyze a given system description. That is, if a modeling formalism is being extended to increase expressiveness, the original formalism should in some way remain a subclass or special case. However, the concept as such is rather vague, which may lead to disagreements about whether one model is in fact a generalization of another.

Therefore, Stigge (2014) introduces a formalization of the notion of what it means for a modeling formalism to generalize another one within the semantic framework introduced above. Recall that we use job sequences to express the semantics of workload models. We first define an equivalence on job sequences. We remove spurious 0-jobs in this definition since they do not quantify additional workload.

Definition 1

(Job Sequence Equivalence) Two job sequences $\rho$ and $\rho '$ are equivalent, written $\rho \cong \rho '$, if they are equal after removing all jobs with execution time 0.

This equivalence is useful in order to define equivalent sets of job sequences. Two sets are equivalent if they only contain equivalent job sequences. They express the same workload demands, apart from spurious 0-jobs.

Definition 2

Two sets S and $S'$ of job sequences are equivalent, written $S \cong S'$, if for each $\rho \in S$, there is $\rho ' \in S'$ with $\rho \cong \rho '$, and vice versa.

Since we express workload model semantics as sets of job sequences, we can use this definition in order to give a formal definition of generalization. For a task system $\tau$, we write $\llbracket \tau \rrbracket$ to denote the set of job sequences generated by $\tau$.

Definition 3

(Generalization) A workload model $\mathcal M_A$ generalizes a workload model $\mathcal M_B$, written $\mathcal M_A \succcurlyeq \mathcal M_B$, if for every task system $\tau _B \in \mathcal M_B$ there is a task system $\tau _A \in \mathcal M_A$ such that $\llbracket \tau _A\rrbracket \cong \llbracket \tau _B\rrbracket$ and $\tau _A$ can be effectively constructed from $\tau _B$ in polynomial time.

This definition allows complexity results for analysis problems to carry over since modeling formalisms that have been generalized can be interpreted as special cases of more general ones. We summarize this in the following proposition.

Proposition 1

If feasibility or schedulability can be decided in pseudo-polynomial time for a workload model $\mathcal M$, then they can be decided in pseudo-polynomial time for any $\mathcal M'$ with $\mathcal M\succcurlyeq \mathcal M'$.

Further, if feasibility or schedulability are strongly $NP$- or $coNP$-hard problems for a workload model $\mathcal M$, then they are strongly $NP$- or $coNP$-hard for any $\mathcal M'$ with $\mathcal M' \succcurlyeq \mathcal M$, respectively.

Using this partial order on workload models, we outline a hierarchy of expressive power in Fig. 1. An edge $\mathcal M_A$

$\mathcal M_B$ represents the generalization relation with the arrow pointing to the more expressive model, i.e., $\mathcal M_A \succcurlyeq \mathcal M_B$. The higher a workload model is placed in the hierarchy, the higher the expressiveness, but also the more expensive feasibility and schedulability analyses.

3 From Liu and Layland tasks to GMF

In this section, we show the development of task systems from the periodic task model to different variants of the multiframe model, including techniques for their analysis.

3.1 Periodic and sporadic tasks

The first task model with periodic tasks was introduced by Liu and Layland (1973). Each periodic task $T=(P, E)$ in a task set $\tau$ is characterized by a pair of two integers: period P and worst-case execution time (WCET) E. It generates an infinite sequence $\rho = (J_0, J_1, \ldots )$ containing jobs $J_i = (R_i, e_i, v)$ which are all of the same type v with release time $R_i$ and execution time $e_i$ such that $R_{i+1} = R_i + P$ and $e_i \leqslant E$. This means that jobs are released periodically. Further, they have implicit deadlines at the release times of the next job, i.e., $d(v) = P$.

A relaxation of this model is to allow jobs to be released at later time points, as long as at least P time units pass between adjacent job releases of the same task. This is called the sporadic task model, introduced by Mok (1983). Another generalization is to add an explicit deadline D as a third integer to the task definition $T=(P, E, D)$, leading to $d(v) = D$ for all generated jobs. If $D \leqslant P$ for all tasks $T \in \tau$ then we say that $\tau$ has constrained deadlines, otherwise it has arbitrary deadlines.

This model has been the basis for many results throughout the years. Liu and Layland (1973) give a simple feasibility test for implicit deadline tasks: defining the utilization $U(\tau )$ of a task set $\tau$ as $U(\tau ) := \sum _{T_i \in \tau } E_i/P_i$, a task set is uniprocessor feasible if and only if $U(\tau )~\leqslant ~1$. As in later work, proofs of feasibility are often connected to the Earliest Deadline First (EDF) scheduling algorithm, which uses dynamic priorities and has been shown to be optimal for a large class of workload models on uniprocessor platforms, including those considered in this survey. Because of its optimality, EDF schedulability is equivalent to feasibility.

3.1.1 Demand-bound functions

For the case of explicit deadlines, Baruah et al. (1990) introduced a concept that was later called the demand-bound function: for each interval size t and task T, $dbf _T(t)$ is the maximal accumulated worst-case execution time of jobs generated by T in any interval of size t. More specifically, it counts all jobs that have their full scheduling window inside the interval, i.e., release time and deadline. The demand-bound function $dbf _\tau (t)$ of the whole system $\tau$ has the property that a task system is feasible if and only if

$$\begin{aligned} \forall t \geqslant 0: dbf _\tau (t) \leqslant t. \end{aligned}$$

(1)

This condition is a valid test for a very general class of workload models and is of great use in later parts of this survey. It holds for all models generating sequences of independent jobs. A proof was provided by Baruah et al. (1999a).

Focussing on sporadic tasks, Baruah et al. (1990) show that $dbf _\tau (t)$ can be computed with

$$\begin{aligned} dbf _\tau (t) = \sum _{T_i \in \tau } E_i \cdot \max \left\{ 0, \left\lfloor \frac{t-D_i}{P_i}\right\rfloor +1\right\} . \end{aligned}$$

(2)

This closed-form expression is motivated by the observation that periodic tasks lead to a simple form of very regular step-functions. Using this they prove that the feasibility problem is in $coNP$. Eisenbrand and Rothvoß (2010) have shown that the problem is indeed (weakly) $coNP$-hard for systems with constrained deadlines. Very recently, Ekberg and Yi (2015) have tightened this result by providing a proof of $coNP$-hardness in the strong sense.

Another contribution of Baruah et al. (1990) was to show that for the case of $U(\tau ) < c$ for some constant c, there is a pseudo-polynomial solution of the schedulability problem, by testing Condition (1) for a pseudo-polynomial number of values. Intuitively, the smaller the task set’s utilization $U(\tau )$, the smaller a value t has to be in order to be able violate Condition (1). The reason is that its left-hand side $dbf _\tau (t)$ approaches an asymptotic growth of $U(\tau )$, eventually creating a gap to its right-hand side t. Thus, if $U(\tau )$ is bounded by a $c<1$, a pseudo-polynomial bound for t can always be derived. On the other hand, for $U(\tau )=1$, a similar bound for t is not known. The existence of such a constant bound c of $U(\tau )$ (however close to 1) is a common assumption when approaching this problem since excluding utilizations very close to 1 only rules out very few actual systems.

3.1.2 Static priorities

For static priority schedulers, Liu and Layland (1973) show that the rate-monotonic priority assignment for implicit deadline tasks is optimal, i.e., tasks with shorter periods have higher priorities. They further give an elegant sufficient schedulability condition by proving that a task set $\tau$ with n tasks is schedulable with a static priority scheduler under rate-monotonic priority ordering if

$$\begin{aligned} U(\tau ) \leqslant n \cdot (2^{1/n}-1). \end{aligned}$$

(3)

For sporadic task systems with explicit deadlines, the response time analysis technique has been developed. It is based on a scenario in which all tasks release jobs at the same time instant with all following jobs being released as early as permitted. This maximizes the response time $R_i$ of the task in question, which is why the scenario is often called the critical instant. It is shown by Joseph and Pandya (1986) and independently by Audsley et al. (1991) that $R_i$ is the smallest positive solution of the recurrence relation

$$\begin{aligned} R = E_i + \sum _{j<i} \left\lceil \frac{R}{P_j}\right\rceil \cdot E_j, \end{aligned}$$

(4)

assuming that the tasks are in order of descending priority. This is based on the observation that the interference from a higher priority task $T_j$ to $T_i$ during a time interval of size R can be computed by counting the number of jobs task $T_j$ can release as $\left\lceil R/P_j\right\rceil$ and multiplying that with their worst-case duration $E_j$. Together with $T_i$’s own WCET $E_i$, the response time is derived. Solving Eq. (4) leads directly to a pseudo-polynomial schedulability test. Eisenbrand and Rothvoß (2008) show that the problem of computing $R_i$ is indeed $NP$-hard.

3.2 The multiframe model

The first extension of the periodic and sporadic paradigm for jobs of different types to be generated from the same task was introduced by Mok and Chen (1997). The motivation is as follows. Assume a workload which is fundamentally periodic but it is known that every k-th job of this task is extra long. As an example, Mok and Chen describe an MPEG video codec that uses different types of video frames. Video frames arrive periodically, but frames of large size and thus large decoding complexity are processed only once in a while. The sporadic task model would need to account for this in the WCET of all jobs, which is certainly a significant over-approximation. Systems that are clearly schedulable in practice would fail standard schedulability tests for the sporadic task model. Thus, in scenarios like this where most jobs are close to an average computation time which is significantly exceeded only in well-known periodically recurring situations, a more precise modeling formalism is needed.

To solve this problem, Mok and Chen (1997) introduce the Multiframe model. A multiframe task T is described as a pair $(P, \mathbf {E})$ much like the basic sporadic model with implicit deadlines, except that $\mathbf {E}= (E_0, \ldots , E_{k-1})$ is a vector of different execution times, describing the WCET of k potentially different frames.

3.2.1 Semantics

As before, let $\rho = (J_0, J_1, \ldots )$ be a job sequence with job parameters $J_i = (R_i, e_i, v_i)$ of release time $R_i$, execution time $e_i$ and job type $v_i$. For $\rho$ to be generated by a multiframe task T with k frames, it has to hold that $e_i \leqslant E_{(a + i) ~\mathrm {mod}~k}$ for some offset a, i.e., the worst-case execution times cycle through the list specified by vector $\mathbf {E}$. The job release times behave as before for sporadic implicit-deadline tasks, i.e., $R_{i+1} \geqslant R_i + P$. We show an example in Fig. 2.

Fig. 2

Example of a multiframe task $T=(P, \mathbf {E})$ with $P = 4$ and $\mathbf {E}= (3, 1, 2, 1)$. Note that deadlines are implicit

3.2.2 Schedulability analysis

Mok and Chen (1997) provide a schedulability analysis for static priority scheduling. They provide a generalization of Eq. (3) by showing that a task set $\tau$ is schedulable with a static priority scheduler under rate-monotonic priority ordering if

$$\begin{aligned} U(\tau ) \leqslant r \cdot n \cdot \left( (1+1/r)^{1/n} - 1 \right) . \end{aligned}$$

(5)

The value r in this test is the minimal ratio between the largest WCET $E_i$ in a task and its successor $E_{(i+1) ~\mathrm {mod}~k}$. Note that the classic test for periodic tasks in Condition (3) is a special case of Condition (5) with $r=1$.

The proof for this condition is done by carefully observing that for a class of multiframe tasks called accumulatively monotonic (AM), there is a critical instant that can be used to derive the condition (and further even for a precise test in pseudo-polynomial time by simulating the critical instant). In short, AM means that there is a frame in each task such that all sequences starting from this frame always have a cumulative execution demand at least as high as equally long sequences starting from any other frame. After showing (5) for AM tasks the authors prove that each task can be transformed into an AM task which is equivalent in terms of schedulability. The transformation is via a model called General Tasks (Mok and Chen 1996) which is an extension of multiframe tasks to an infinite number of frames and therefore of mainly theoretical interest.

Refined sufficient tests have been developed (Han 1998; Baruah et al. 1999b; Kuo et al. 2003; Lu 2007) that are less pessimistic than the test using the utilization bound in (5). They generally also allow certain task sets of higher utilization than those passing the above test to be classified as schedulable. A precise test of exponential complexity has been presented (Zuhily and Burns 2009) based on response time analysis as a generalization of (4). The authors also include results for models with jitter and blocking.

3.3 Generalized multiframe tasks

In the multiframe model, all frames still have the same period and implicit deadline. Baruah et al. (1999a) generalize this further by introducing the Generalized Multiframe (GMF) task model. A GMF task $T= (\mathbf {P}, \mathbf {E}, \mathbf {D})$ with k frames consists of three vectors:

$\mathbf {P}= (P_0, \ldots , P_{k-1})$ :

for minimum inter-release separations,

$\mathbf {E}= (E_0, \ldots , E_{k-1})$ :

for worst-case execution times, and

$\mathbf {D}= (D_0, \ldots , D_{k-1})$ :

for relative deadlines.

For unambiguous notation we write $P_i^T$, $E_i^T$ and $D_i^T$ for components of these three vectors in situations where it is not clear from the context which task T they belong to.

3.3.1 Semantics

As a generalization of the multiframe model, each job $J_i=(R_i, e_i, v_i)$ in a job sequence $\rho =(J_0, J_1, \ldots )$ generated by a GMF task T needs to correspond to a frame and the corresponding values in all three vectors. Specifically, we have for some offset a that:

• 1. $R_{i+1} \geqslant R_i + P_{(a+i) ~\mathrm {mod}~k}$

• 2. $e_i \leqslant E_{(a+i) ~\mathrm {mod}~k}$

An example is shown in Fig. 3.

Fig. 3

Example of a GMF task $T=(\mathbf {P}, \mathbf {E}, \mathbf {D})$ with $\mathbf {P}= (5, 3, 4)$, $\mathbf {E}= (3, 1, 2)$ and $\mathbf {D}= (3, 2, 3)$

3.3.2 Feasibility analysis

Baruah et al. (1999a) give a feasibility analysis method based on the demand-bound function. The different frames make it difficult to develop a closed-form expression like (2) for sporadic tasks since there is in general no unique critical instant for GMF tasks. Instead, the described method (which we sketch here with slightly adjusted notation and terminology) creates a list of pairs $\left\langle e, d \right\rangle$ of workload e and some time interval length d which are called demand pairs in later work (Stigge et al. 2011). Each demand pair $\left\langle e, d \right\rangle$ describes that a task T can create e time units of execution time demand during an interval of length d. From this information it can be derived that $dbf _T(d) \geqslant e$ since the demand bound function $dbf _T(d)$ is the maximal execution demand possible during any interval of that size.

In order to derive all relevant demand pairs for a GMF task, Baruah et al. first introduce a property called localized Monotonic Absolute Deadlines (l-MAD). Intuitively, it means that two jobs from the same task that have been released in some order will also have their (absolute) deadlines in the same order. Formally, this can be expressed as $D_i \leqslant P_i + D_{(i+1) ~\mathrm {mod}~k}$, which is more general than the classical notion of constrained deadlines, i.e., $D_i \leqslant P_i$, but still sufficient for the analysis. We assume this property for the rest of this section.

As preparation, the method by Baruah et al. (1999a) creates a sorted list $DP$ of demand pairs $\left\langle e, d \right\rangle$ for all i and j each ranging from 0 to $k-1$ with

$$\begin{aligned} e = \sum _{m=i}^{i+j} E_{m ~\mathrm {mod}~k}, \quad d = \left( \sum _{m=i}^{i+j-1} P_{m ~\mathrm {mod}~k}\right) + D_{(i+j) ~\mathrm {mod}~k}. \end{aligned}$$

For a particular pair of i and j, this computes in e the accumulated execution time of a job sequence with jobs corresponding to frames $i, \ldots , (i+j) ~\mathrm {mod}~k$. The value of d is the time from first release to last deadline of such a job sequence. With all these created demand pairs, and using shorthand notation $P_{\mathrm {sum}}:= \sum _{i=0}^{k-1} P_i$,  $E_{\mathrm {sum}}:= \sum _{i=0}^{k-1} E_i$ and $D_{\mathrm {min}}:= \min _{i=0}^{k-1} D_i$, the function $dbf _T(t)$ can be computed with

$$\begin{aligned} dbf _T(t) = {\left\{ \begin{array}{ll} 0 &{} \mathrm {if } \ t < D_{\mathrm {min}},\\ \max \left\{ e \mid \left\langle e, d \right\rangle \in DP \text { with } d \leqslant t\right\} &{} \mathrm {if } \ t \in [D_{\mathrm {min}}, P_{\mathrm {sum}}+D_{\mathrm {min}}),\\ \left\lfloor \frac{t-D_{\mathrm {min}}}{P_{\mathrm {sum}}}\right\rfloor E_{\mathrm {sum}}+ dbf _T&{}\\ \quad \big (D_{\mathrm {min}}+ (t-D_{\mathrm {min}}) ~\mathrm {mod}~P_{\mathrm {sum}}\big ) &{}\mathrm {if } \ t \geqslant P_{\mathrm {sum}}+D_{\mathrm {min}}. \end{array}\right. } \end{aligned}$$

Intuitively, we can sketch all three cases as follows: In the first case, time interval t is shorter than the shortest deadline of any frame, thus not creating any demand. In the second case, time interval t is shorter than $P_{\mathrm {sum}}+ D_{\mathrm {min}}$ which implies that at most k jobs can contribute to $dbf _T(t)$. All possible job sequences of up to k jobs are represented in demand pairs in $DP$, so it suffices to return the maximal demand e recorded in a demand pair $\left\langle e, d \right\rangle$ with $d \leqslant t$. In the third case, a job sequence leading to the maximal value $dbf _T(t)$ must include at least one complete cycle of all frames in T. Therefore, it is enough to determine the number of cycles (each contributing $E_{\mathrm {sum}}$) and looking up the remaining interval part using the second case.

Finally, Baruah et al. (1999a) describe how a feasibility test procedure can be implemented by checking Condition (1) for all t at which $dbf (t)$ changes up to a bound

$$\begin{aligned} D:= \frac{U(\tau )}{1-U(\tau )} \cdot \max _{T\in \tau } \left( P_{\mathrm {sum}}^T-D_{\mathrm {min}}^T\right) \end{aligned}$$

with $U(\tau ) := \sum _{T\in \tau } E_{\mathrm {sum}}^T/P_{\mathrm {sum}}^T$ measuring the utilization of a GMF task system. If $U(\tau )$ is bounded by a constant $c<1$ then this results in a feasibility test of pseudo-polynomial complexity. Baruah et al. include also an extension of this method to task systems without the l-MAD property, i.e., with arbitrary deadlines. As an alternative test method, they even provide an elegant reduction of GMF feasibility to feasibility of sporadic task sets by using the set $DP$ to construct a $dbf$-equivalent sporadic task set.

3.3.3 Static priorities

An attempt to solve the schedulability problem for GMF in the case of static priorities was presented by Stigge and Yi (1997). The idea is to use a function called Maximum-interference function (MIF) M(t). It is based on the request-bound function $rbf (t)$ which for each interval size t counts the accumulated execution demand of jobs that can be released inside any interval of that size. (Notice that in contrast, the demand-bound function also requires the job deadline to be inside the interval.) The MIF is a “smoother” version of that, which for each task only accounts for the execution demand that could actually execute inside the interval. We show examples of both functions in Fig. 4.

Fig. 4

Examples of request-bound function and maximum-interference function of the same task $T=(\mathbf {P}, \mathbf {E}, \mathbf {D})$ with $\mathbf {P}=\mathbf {D}=(6, 7, 10)$ and $\mathbf {E}=(3, 3, 1)$

The method uses the MIF as a generalization in the $\sum$-summation term in Eq. (4), leading to a generalized recurrence relation for computing the response time:

$$\begin{aligned} R = E_i + \sum _{j<i} M_j(R) \end{aligned}$$

(6)

Note that this expresses the response time of a job generated by one particular frame i of a GMF task with $M_j(t)$ expressing the corresponding maximum-interference functions of higher priority tasks. Computation of $M_i(t)$ is essentially the same process as determining the demand-bound function $dbf (t)$ from above.

It was discovered by Stigge and Yi (2012) that the proposed method does not lead to a precise test since the response time computed by solving Eq. (6) is over-approximate. The reason is that $M_i(t)$ over-approximates the actual interference caused by higher priority tasks. They give an example in which case the test using Eq. (6) determines a task set to be unschedulable while none of the concrete executions would lead to a deadline miss.

Stigge and Yi (2012) provide a hardness result by showing that the problem of an exact schedulability test for GMF tasks in case of static priority schedulers is strongly $coNP$-hard implying that there is no adequate replacement for $M_i(t)$. Intuitively, one single integer-valued function on the time interval domain cannot precisely capture the information needed to compute exact response times. Different concrete task sets with different resulting response times would be abstracted by identical functions, ruling out a precise test. The rather involved proof is mostly focussing on the a more general task model (Digraph Real-Time tasks, cf. Sect. 4.5) but is shown to even hold in the GMF case and in fact even applies to the MF model. Still, the MIF-based test for GMF presented by Takada and Sakamura (1997) is a sufficient test of pseudo-polynomial time complexity.

3.4 Non-cyclic GMF

The original motivation for multiframe and GMF task models was systems consisting of frames with different computational demand and possibly different deadlines and inter-release separation times, arriving in a pre-defined pattern. Consider again the MPEG video codec example where video frames of different complexity arrive, leading to applicability of the multiframe model. For the presented analysis methods, the assumption of a pre-defined release pattern is fundamental. Consider now a system where the pattern is not known a priori, for example if the video codec is more flexible and allows different types of video frames to appear adaptively, depending on the actual video contents. Similar situations arise in cases where the frame order depends on other environmental decisions, e.g. user input or sensor data. A prominent example is an engine management component in an automotive embedded real-time system. Depending on the engine speed, the tasks controlling ignition timing, fuel injection, opening of exhaust valves, etc. have different periods since the angular velocity of the crankshaft changes (Buttazzo et al. 2014). These systems cannot be modeled with the GMF task model.

Moyo et al. (2010) propose a model called Non-Cyclic GMF to capture such behavior adequately. A Non-Cyclic GMF task $T=(\mathbf {P}, \mathbf {E}, \mathbf {D})$ is syntactically identical to GMF task from Sect. 3.3, but with non-cyclic semantics. In order to define the semantics formally, let $\phi : \mathbb {N}\rightarrow \left\{ 0, \ldots , k-1\right\}$ be a function choosing frame $\phi (i)$ for the i-th job of a job sequence. Having $\phi$, each job $J_i=(R_i, e_i, v_i)$ in a job sequence $\rho =(J_0, J_1, \ldots )$ generated by a non-cyclic GMF task T needs to correspond to frame $\phi (i)$ and the corresponding values in all three vectors:

• 1. $R_{i+1} \geqslant R_i + P_{\phi (i)}$

• 2. $e_i \leqslant E_{\phi (i)}$

This contains cyclic GMF job sequences as the special case where $\phi (i) = (a+i) ~\mathrm {mod}~k$ for some offset a. An example of non-cyclic GMF semantics is shown in Fig. 5.

Fig. 5

Non-cyclic semantics of the GMF example Fig. 3

For analyzing non-cyclic GMF models, Moyo et al. (2010) give a simple density-based sufficient feasibility test. Defining $D(T):=\max _i C_i^T/D_i^T$ as the densitiy of a task T, a task set $\tau$ is schedulable if $\sum _{T\in \tau } D(T) \leqslant 1$. This generalizes a similar test for the sporadic task model with explicit deadlines. In addition to this test, Moyo et al. (2010) also include an exact feasibility test based on efficient systematic simulation. That is, they carefully extract a set of job sequences to simulate, in order to conclusively decide feasibility. A complexity bound is not given.

A different exact feasibility test is presented by Baruah (2010) for constrained deadlines using the demand-bound function as in Condition (1). A dynamic programming approach is used to compute demand pairs (see Sect. 3.3) based on the observation that $dbf _T(t)$ can be computed for larger and larger t reusing earlier values. More specifically, a function $A_T(t)$ is defined which denotes for an interval size t the accumulated execution demand of any job sequence where jobs have their full exclusion window¹ inside the interval. It is shown that $A_T(t)$ for $t>0$ can be computed by assuming that some frame i was the last one in a job sequence contributing a value to $A_T(t)$. In that case, the function value for the remaining job sequence is added to the execution time of that specific frame i. Since frame i is not known a priori, the computation has to take the maximum over all possibilities. Formally,

$$\begin{aligned} A_T(t) = \max _i \left\{ A_T(t - P_i^T) + E_i^T \mid P_i^T \leqslant t \right\} . \end{aligned}$$

(7)

Using this, $dbf _T(t)$ can be computed via the same approach by maximising over all possibilities of the last job in a sequence contributing to $dbf _T(t)$. It uses that the execution demand of the remaining job sequence is represented by function $A_T(t)$, leading to

$$\begin{aligned} dbf _T(t) = \max _i \left\{ A_T(t - D_i^T) + E_i^T \mid D_i^T \leqslant t \right\} . \end{aligned}$$

(8)

This leads to a pseudo-polynomial time bound for the feasibility test if $U(\tau )$ is bounded by a constant, since $dbf (t) > t$ implies $t < \left( \sum _{T,i} E_i^T \right) / \left( 1-U(\tau )\right)$ which is pseudo-polynomial in this case.

The same article also proves that evaluating the demand-bound function is a (weakly) $NP$-hard problem. More precisely: Given a non-cyclic GMF task T and two integers t and B it is $coNP$-hard to determine whether $dbf _T(t) \leqslant B$. The proof is via a rather straightforward reduction from the Integer Knapsack problem. Thus, a polynomial algorithm for computing $dbf (t)$ is unlikely to exist.

3.4.1 Static priorities

A recent result by Berten and Goossens (2011) proposes a sufficient schedulability test for static priorities. It is based on the request-bound function similar to Takada and Sakamura (1997) and its efficient computation. In a similar way, the function is inherently over-approximate and the test is of pseudo-polynomial time complexity.

Other recent results specifically handle the case of tasks in control applications for combustion engines. They can be modeled using the non-cyclic GMF model, but tighter results can be obtained by a more custom-tuned model which we discuss in Sect. 5.2.

4 Graph-oriented models

The more expressive workload models become, the more complicated structures are necessary to describe them. In this section we turn to models based on different classes of directed graphs. We start by recasting the definition of GMF in terms of a graph release structure.

4.1 Revisiting GMF

Recall the generalized multiframe task model from Sect. 3.3. A GMF task $T=(\mathbf {P}, \mathbf {E}, \mathbf {D})$ consists of three vectors for minimum inter-release separation times, worst-case execution times and relative deadlines of k frames. The same structure can be imagined as a directed cycle graph ² $G=(V, E)$ in which each vertex $v \in V$ represents the release of a job and each edge $(v, v') \in E$ represents the corresponding inter-release separation. A vertex v is associated with a pair $\left\langle e(v), d(v) \right\rangle$ for WCET and deadline parameters of the represented jobs. An edge (u, v) is associated with a value p(u, v) for the inter-release separation time.

The cyclic graph structure directly visualizes the cyclic semantics of GMF. In contrast, non-cyclic GMF can be represented by a complete digraph. Figure 6 illustrates the different ways of representing a GMF task with both semantics.

Fig. 6

Different ways of representing a GMF task T. The vector-representation in 6 a from Sect. 3.3 does by itself not imply cyclic or non-cyclic semantics. This is more clear with graphs in 6 b and 6 c. Note that we omit vertex and edge labels in 6 c for clarity

4.2 Recurring branching tasks

A first generalization to the GMF model was presented by Baruah (1998b), followed up by Anand et al. (2008). It is based on the observation that real-time code may include branches that influence the pattern in which jobs are released. As the result of some branch, a sequence of jobs may be released which may differ from the sequence released in a different branch. In a schedulability analysis, none of the branches may be universally worse than the others since that may depend on the context, e.g., which tasks are being scheduled together with the branching one. Thus, all branches need to be modeled explicitly and a proper representation is needed, different from the GMF release structure.

A natural way of representing branching code is a tree. Indeed, the model proposed by Baruah (1998b) is a tree representing job releases and their minimum inter-release separation times. We show an example in Fig. 7a. Formally, a Recurring Branching (RB) task T is a directed tree $G(T)=(V,E)$ in which each vertex $v \in V$ represents a type of job to be released and each edge $(u, v) \in E$ the minimum inter-release separation times. They have labels $\left\langle e(v), d(v) \right\rangle$ and p(u, v), specifying WCET, deadline and inter-release separation time parameters, respectively. In addition to the tree, each leaf u has a separation time $p(u, v_{ root })$ to the root vertex $v_{ root }$ in order to model that the behavior recurs after each traversal of the tree.

Fig. 7

Examples of RB, RRT and non-cyclic RRT task models

In order to simplify the feasibility analysis, the model is syntactically restricted in the following way. For each path $\pi = (\pi _0, \ldots , \pi _l)$ of length l from the root $\pi _0 = v_{ root }$ to a leaf $v_l$, its duration when going back to the root must be the same, i.e., the value $P := \sum _{i=0}^{l-1} p(\pi _i, \pi _{i+1}) + p(\pi _l, v_{ root })$ must be independent of $\pi$. We call P the period of T. Note that this is a generalization of GMF since GMF can be expressed as a linear tree.

4.2.1 Semantics

A job sequence $\rho = (J_0, J_1, \ldots )$ is generated by an RB task T if it corresponds to a path $\pi$ through G(T) in the following way. Path $\pi$ starts at some vertex $\pi _0$ in G(T), follows the edges to a leaf, then starts again at the root vertex, traverses G(T) again in a possibly different way, etc. (Very short $\pi$ may of course never reach a leaf.) The correspondence between $\rho$ and $\pi$ means that all jobs $J_i$ are of the form $J_i = (R_i, e_i, \pi _i)$, and the following:

• 1. $R_{i+1} \geqslant R_i + p(\pi _i, \pi _{i+1})$,

• 2. $e_i \leqslant e(\pi _i)$.

4.2.2 Feasibility analysis

The analysis presented by Baruah (1998b) is based on the concept of demand pairs as described before. We sketch the method of Baruah (1998b), slightly adjusted to fit our terminology and notation. First, a set $DP _0$ is created consisting of all demand pairs corresponding to paths not containing both a leaf and a following root vertex. This is straightforward since for each pair of vertices (u, v) in G(T) connected by a directed path $\pi$, this connecting path is unique. Thus, a demand pair $\left\langle e, d \right\rangle$ for $\pi$ can be derived by computing its total execution time and deadline. Formally, all $\left\langle e, d \right\rangle \in DP _0$ are created by enumerating all vertex pairs (u, v) and computing for their connecting path $\pi =(\pi _0, \ldots , \pi _l)$ the values

$$\begin{aligned} e := \sum _{i=0}^l e(\pi _i), \quad d := \sum _{i=0}^{l-1} p(\pi _i, \pi _{i+1}) + d(\pi _l). \end{aligned}$$

Second, all paths $\pi$ which do contain both a leaf and a following root vertex can be cut into three subpaths $\pi _{ head }$, $\pi _{ middle }$ and $\pi _{ tail }$:

$$\begin{aligned} \pi = ( \underbrace{v, \ldots , v_l}_{\pi _{ head }}, \underbrace{v_{ root }, v', \ldots , v_l', v_{ root }, v'', \ldots , v_l''}_{\pi _{ middle }}, \underbrace{v_{ root }, v''', \ldots , v'''')}_{\pi _{ tail }} \end{aligned}$$

We use $v_l$, $v_l'$, etc. for arbitrary leaf nodes. The first part $\pi _{ head }$ is the prefix of $\pi$ up to and including the first leaf in $\pi$. The second part $\pi _{ middle }$ is the middle part starting with $v_{ root }$ and ending in the last leaf which $\pi$ visits. Note that $\pi _{ middle }$ may traverse the tree several times. The third part $\pi _{ tail }$ starts with the last occurrence of $v_{ root }$ in $\pi$. For each of the three parts, a data structure is created so that demand pairs for a full path $\pi$ can be assembled easily.

In order to represent $\pi _{ head }$, a set $UP _{ leaf }$ is created. For all paths $\pi _{ head }= (\pi _0, \ldots , \pi _l)$ that end in a leaf, $UP _{ leaf }$ contains a pair $\left\langle e, p \right\rangle$ with

$$\begin{aligned} e := \sum _{i=0}^l e(\pi _i), \quad p := \sum _{i=0}^{l-1} p(\pi _i, \pi _{i+1}) + p(\pi _l, v_{ root }). \end{aligned}$$

For representing $\pi _{ middle }$, the maximal accumulated execution demand $e_{\max }$ of any path completely traversing the tree is computed. Note that all paths from the root to a leaf have the same sum of inter-release separation times and this sum is the period P of T. Finally, for representing $\pi _{ tail }$, a set $DP _{ root }$ is computed as a subset of $DP _0$ only considering paths starting at $v_{ root }$.

Using these data structures, $dbf _T(t)$ can be computed easily. If $t \leqslant P$, then a job sequence contributing to $dbf _T(t)$ either corresponds to a demand pair in $DP _0$ (not passing $v_{ root }$) or is represented by items from $UP _{ leaf }$ and $DP _{ root }$ (since it is passing $v_{ root }$ exactly once):

$$\begin{aligned} F_1(t)&:= \max \left\{ e \mid \left\langle e,d \right\rangle \in DP _0 \text { with } d \leqslant t \right\} , \\ F_2(t)&:= \max \left\{ e_1 + e_2 \mid \left\langle e_1,p \right\rangle \in UP _{leaf} \wedge \left\langle e_2, d \right\rangle \in DP _{root} \wedge p+d \leqslant t\right\} , \\ dbf _T(t)&= \max \left\{ F_1(t),~ F_2(t) \right\} \quad \text {if }t \leqslant P. \end{aligned}$$

In case $t > P$, such a job sequence must pass through $v_{ root }$ and traverses the tree completely for either $\left\lfloor t/P\right\rfloor$ or $\left\lfloor t/P\right\rfloor -1$ times. Each of the complete traversals contributes $e_{\max }$ to the total execution time sum of $\pi _{ middle }$. For the parts that are represented by $\pi _{ head }$ and $\pi _{ tail }$ of the corresponding path $\pi$, we can use $F_2$ from above, since $\pi _{ head }$ concatenated with $\pi _{ tail }$ correspond to a job sequence without a complete tree traversal but which visits $v_{ root }$. For the case of $\pi _{ middle }$ traversing the tree $\left\lfloor t/P\right\rfloor$ times, there are $t ~\mathrm {mod}~P$ time units left to consider, which is summarized in Eq. (9). Similarly, for the case of $\pi _{ middle }$ traversing the tree $\left\lfloor t/P\right\rfloor -1$ times, there are $(t ~\mathrm {mod}~P) + P$ time units left, summarized in Eq. (10). Putting it together for $t > P$:

$$\begin{aligned} F_3(t)&:= \left\lfloor \frac{t}{P}\right\rfloor \cdot e_{\max } + F_2(t ~\mathrm {mod}~P), \end{aligned}$$

(9)

$$\begin{aligned} F_4(t)&:= \left\lfloor \frac{t-P}{P}\right\rfloor \cdot e_{\max } + F_2\big ((t ~\mathrm {mod}~P) + P\big ), \\ dbf _T(t)&= \max \left\{ F_3(t),~ F_4(t) \right\} \quad \text {if } t > P.\nonumber \end{aligned}$$

(10)

Finally, in order to do the feasibility test, i.e., verify Condition (1), the demand-bound function $dbf _\tau (t) = \sum _{T \in \tau } dbf _T(t)$ is computed for all t up to a bound D derived in a similar way as for GMF in Sect. 3.3.

4.3 Recurring real-time tasks—DAG structures

In typical branching code, the control flow is joined again after the branches are completed. Thus, no matter which branch is taken, the part after the join is common to both choices. In the light of a tree release structure as in the RB task model above, this means that many vertices in the tree may actually represent the same types of jobs to be released, or even whole subtrees are equal. In order to make use of these redundancies, Baruah (1998a) proposes to use a directed acyclic graph (DAG) instead of a tree. The impact is mostly modeling efficiency: each DAG can be unrolled into a tree, but that comes at the cost of potentially exponential growth of the graph.

A Recurring Real-Time (RRT) task T is a directed acyclic graph G(T). The definition is very similar to RB tasks in the previous section, we only point out the differences. It is assumed that G(T) contains one unique source vertex (corresponding to $v_{ root }$ in an RB task) and further one unique sink vertex (corresponding to leafs in a tree). There is no explicit minimum inter-release separation time between the sink and the source vertex. Instead, an RRT task has an explicitly defined period parameter P that constrains the minimal time between two releases of jobs represented by the source vertex. An RRT task behaves just like an RB task by following paths through the DAG. We skip the details and give an example of an RRT task in Fig. 7b.

4.3.1 Feasibility analysis

Because of its close relation to RB tasks, the feasibility analysis method presented by Baruah (1998a) is very similar to the method presented above for RB tasks and we skip the details. Note that this is largely due to the general period parameter P which could be inferred in the RB model since all paths from $v_{ root }$ to $v_{ root }$ were assumed to have the same duration. However, the adapted method has exponential complexity since it enumerates paths explicitly.

Chakraborty et al. (2001) present a more efficient method based on a dynamic programming approach, leading back to pseudo-polynomial complexity. Instead of enumerating all pairs of vertices (u, v) in the DAG, the graph is traversed in a breadth-first manner. The critical observation is that all demand pairs representing a path ending in any particular vertex v can be computed from those for paths ending in all parent vertices. It is not necessary to have precise information about which the actual paths are that the demand pairs represent. Even though Chakraborty et al. consider a limited variant of the model in which paths traverse the DAG only once, the ideas can be applied in general to the full RRT model.

The feasibility problem is further shown to be $NP$-hard by Chakraborty et al. (2001) via a reduction from the Knapsack problem and the authors give a fully polynomial-time approximation scheme. For the special case where all vertices have equal WCET annotations, they show a polynomial-time solution, similar to the dynamic programming technique above.

4.3.2 Static priorities

A sufficient test for schedulability of an RRT task set with static priorities is presented by Baruah (2003). It is shown that, up to a polynomial factor, the priority assignment problem in which a priority order has to be found is equivalent to the priority testing problem where a task set with a given priority order is to be tested for schedulability. At the core of both is the test whether a given task $T \in \tau$ will meet its deadlines if it has the lowest priority of all tasks in $\tau$ (whose relative priority order does not matter). In that case T is called lowest-priority feasible.

The proposed solution gives a condition involving both the demand-bound function $dbf _T(t)$ and the request-bound function $rbf _T(t)$. It is shown that a task T is lowest-priority feasible if

$$\begin{aligned} \forall t \geqslant 0: \exists t' \leqslant t: dbf _T(t) + \sum _{T' \in \tau \setminus \left\{ T\right\} } rbf _{T'}(t') \leqslant t'. \end{aligned}$$

(11)

It is shown that $rbf _T(t)$ can be computed with just a minor modification to the computation procedure of $dbf _T(t)$ and that Condition (11) only needs to be checked for a bounded testing set of t, similar to the bound D introduced in checking Condition (1) in feasibility tests. For each t, checking the existence of a $t' \leqslant t$ is essentially identical to an iterative procedure of solving the recurrence relation in Eq. (6) of which Condition (11) is a generalization.

A tighter and more efficient test is shown by Chakraborty et al. (2001) based on a smoother variant of the request-bound function, denoted $rbf '_T(t)$. Using this, a task T is lowest-priority feasible if

$$\begin{aligned} \forall v \in G(T): \exists t' \leqslant d(v): e(v) + \sum _{T' \in \tau \setminus \left\{ T\right\} } rbf '_{T'}(t') \leqslant t'. \end{aligned}$$

(12)

This test is a more direct and tighter generalization of the sufficient test using Eq. (6) for GMF tasks.

4.3.3 Position in the model hierarchy

The RRT model is a generalization of the RB model in the sense of Definition 3. It is not the case that syntactically, every RB task is also an RRT task, because of the edges from leaves back to the root vertex in an RB task. However, Stigge (2014) demonstrates that an equivalent RRT task can be constructed as follows. Given G(T) of an RB task T, we create a new vertex v serving as a dummy sink vertex, i.e., $\left\langle e(v), d(v) \right\rangle = \left\langle 0, 0 \right\rangle$. For each leaf vertex u, we create an edge (u, v) to the sink vertex with edge label $p(u, v) := p(u, v_{ root })$ and remove edge $(u, v_{ root })$. The resulting graph is $G(T')$ of a new task $T'$ which together with a parameter P equal to the duration of any path through G(T) back to its root is now syntactically an RRT task. It is easily verified that $\llbracket T\rrbracket \cong \llbracket T'\rrbracket$.

4.4 Non-cyclic RRT

A different generalization of RB is non-cyclic RRT ³ (Baruah 2010b) where the assumption of one single sink vertex is removed. Specifically, a non-cyclic RRT task T is a DAG G(T) with vertex and edge labels as before that has a unique source vertex $v_{ source }$. Additionally, for every sink vertex v, there is a value $p(v, v_{ source })$ as before. We give an example in Fig. 7c. Note that a non-cyclic RRT task does not have a general period parameter, i.e., paths through G(T) visiting $v_{ source }$ repeatedly may do so in different time intervals when doing so through different sinks.

4.4.1 Feasibility analysis

The analysis technique presented by Baruah (2010b) is similar to the ones of RB and RRT. The author uses the dynamic programming technique of Chakraborty et al. (2001) to compute demand pairs inside the DAG in order to keep pseudo-polynomial complexity and assumes a partition of paths $\pi$ into $\pi _{ head }$, $\pi _{ middle }$ and $\pi _{ tail }$ as before. The difference here is that paths traversing G(T) completely from $v_{ source }$ to a sink may have different lengths, i.e., $\pi _{ middle }$ is not necessarily a multiple of some period P. Thus, the expressions for partial $dbf _T(t)$ computation in Eqs. (9) and (10) cannot just assume a fixed length P and a fixed computation time $e_{\max }$. The idea to solve this is to first use the technique by Chakraborty et al. (2001) to compute demand pairs for full DAG traversals. These can then be interpreted as frames with a length and an execution time requirement, which can be concatenated to achieve a certain interval length, like a very big non-cyclic GMF task. Similar to Eq. (7) for solving non-cyclic GMF feasibility, all possible paths going from source to a sink can be represented in a function $A_T(t)$ that expresses for each t the amount of execution demand these special paths may create during intervals of length t. Similar to Eq. (8), this function is integrated into Conditions (9) and (10), resulting in an efficient procedure.

The procedure is generalized in Sect. 4.5 which generalizes and unifies all feasibility tests presented so far.

4.4.2 Position in the model hierarchy

It is rather straightforward to see that the non-cyclic RRT model generalizes the RB model since a tree is a special case of a DAG. However, it is not directly obvious that non-cyclic RRT generalizes non-cyclic GMF since non-cyclic GMF does not syntactically fit into the non-cyclic RRT definition, even if interpreted as a (fully connected) digraph. Nevertheless, a transformation of a non-cyclic GMF task $T=(\mathbf {P}, \mathbf {E}, \mathbf {D})$ is given by Stigge et al. (2014). In order to create $G(T')$ for an equivalent non-cyclic RRT task $T'$, we create k vertices $v_0, \ldots , v_{k-1}$, each representing one of the k frames of T, i.e., $\left\langle e(v_i), d(v_i) \right\rangle := \left\langle E_i, D_i \right\rangle$. Further, we create a (dummy) source vertex $v_{ source }$ with $\left\langle e(v_{ source }), d(v_{ source }) \right\rangle := \left\langle 0, 0 \right\rangle$. We connect the source with the vertices $v_i$ via edges $(v_i, v_{ source })$ and $(v_{ source }, v_i)$ which have labels

$$\begin{aligned} p(v_i, v_{ source }) := P_i, \quad p(v_{ source }, v_i) := 0. \end{aligned}$$

It is clear that $T'$ is equivalent to T since all vertices $v_i$ can be visited in any order, just as the frames of T, hence $\llbracket T\rrbracket \cong \llbracket T'\rrbracket$.

4.5 Digraph real-time tasks

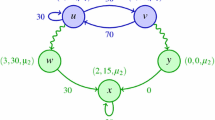
Stigge et al. (2011) observe that the non-cyclic RRT model can be generalized to any directed graph. They introduce the Digraph Real-Time (DRT) task model and describe a feasibility test of pseudo-polynomial complexity for task systems with utilization bounded by a constant. A DRT task T is described by a directed graph G(T) with edge and vertex labels as before. There are no further restrictions, any directed graph can be used to describe a task. Using any graph allows modeling of local loops which was not possible in any model presented above. Even in the non-cyclic RRT model, all cycles in that model have to pass through the source vertex. An example of a DRT task is shown in Fig. 8a.

Fig. 8

Examples for DRT and EDRT task models. The EDRT task in Fig. 8b contains two additional constraints $(u_4, u_2, 6)$ and $(u_3, u_3, 9)$, denoted with dashed arrows. Note that these dashed arrows do not represent edges that can be taken. They only denote additional timing constraints

4.5.1 Semantics

The behavior of a DRT task T is similar to earlier models. A job sequence $\rho = (J_0, J_1, \ldots )$ is generated by T if there is a path $\pi = (\pi _0, \pi _1, \ldots )$ through G(T) such that each job is of the form $J_i = (R_i, e_i, \pi _i)$ and it holds that

• 1. $R_{i+1} \geqslant R_i + p(\pi _i, \pi _{i+1})$ and

• 2. $e_i \leqslant e(\pi _i)$.

Note that this implies sporadic job releases as before. However, worst-case sequences usually release jobs as soon as permitted.

4.5.2 Feasibility analysis

Stigge et al. (2011) present a feasibility analysis method which is again based on demand pairs. However, there is no single vertex through which all paths pass and neither does the graph G(T) represent a partial order as DAGs do. Thus, earlier dynamic programming approaches can not be applied. It is not possible either to simply enumerate all paths through the graph since that would lead to an exponential procedure. Instead, the authors propose a path abstraction technique which is essentially also based on dynamic programming, generalizing earlier approaches.

For the case of constrained deadlines, each path $\pi =(v_0, \ldots , v_l)$ through $G(T) = (V, E)$ is abstracted using a demand triple $\left\langle e(\pi ), d(\pi ), v_l \right\rangle$ with

$$\begin{aligned} e(\pi ) := \sum _{i=0}^l e(v_i), \quad d(\pi ) := \sum _{i=0}^{l-1} p(v_i, v_{i+1}) + d(v_l). \end{aligned}$$

It contains as first two components a demand pair and the third component is the last vertex in the path. This abstraction allows creating all demand pairs for G(T) iteratively. The procedure starts with all demand triples that represent paths of length 0, i.e., with the set

$$\begin{aligned} \left\{ \left\langle e(v), d(v), v \right\rangle \mid v \in V \right\} . \end{aligned}$$

In each step, a triple $\left\langle e, d, v \right\rangle$ is picked from the set and extended to create new triples $\left\langle e', d', v' \right\rangle$ via

$$\begin{aligned} e' := e + e(v'), \quad d' := d - d(v) + p(v, v') + d(v'), \quad (v, v') \in E. \end{aligned}$$

This is done for all edges $(v, v') \in E$. The procedure abstracts from concrete paths since the creation of each new triple $\left\langle e', d', v' \right\rangle$ does not need the information of the full path represented by $\left\langle e, d, v \right\rangle$. Instead, the last vertex v of any such path suffices. The authors show that this procedure is efficient since it only needs to be executed once up to a bound D as before and the number of demand triples is bounded.

Further contributions of Stigge et al. (2011) include an extension of the method to arbitrary deadlines and a few optimisation suggestions for implementations. One of them is considering critical demand triples $\left\langle e, d, v \right\rangle$ for which no other demand triple $\left\langle e', d', v' \right\rangle$ exists with

• 1. $e' \geqslant e$,

• 2. $d' \leqslant d$, and

• 3. $v' = v$.

It is shown that only critical demand triples need to be stored during the procedure. All other, non-critical, demand triples can be discarded since they and all their future extensions will be dominated by others when considering contributions to the demand bound function $dbf _T(t)$. This optimization reduces the cubic time complexity of the algorithm to about quadradic in the task parameters.

The presented method is applicable to all models in the previous sections since DRT generalizes all of them. In a few special cases, custom optimizations may speed up the process. Recently, Zeng and Di Natale (2014) have proposed a clever application of max-plus algebra to the problem of computing the demand-bound function which can speed up the computation further.

4.5.3 Static priorities

Sufficient tests involving $rbf (t)$ similar to Conditions (11) and (12) can be applied to DRT as well, but no exact schedulability test for DRT with static priorities can be of pseudo-polynomial time complexity. It was shown by Stigge and Yi (2012) that the problem is strongly $NP$-hard via a reduction from the $\mathsf {3}\text {-}\mathsf {PARTITION}$ problem. Further, even fully polynomial-time approximation schemes can not exist either. The result holds for all models at least as expressive as GMF or even the multiframe model.

Despite these hardness proofs, practical schedulability tests are still desirable, even though they might have worst-case inputs for which they run in exponential time. Using an iterative refinement method, Stigge and Yi (2013) introduce a schedulability test that runs about as fast as the state-of-the-art pseudo-polynomial feasibility test on synthetically generated task sets. The idea is to abstract paths through graphs representing tasks as request functions. That is, for a task T, a path $\pi$ through G(T) is represented by a function $rf _\pi (t)$ which gives the maximal cumulative amount of workload that this task can request from the processor along $\pi$ within the first t time units. Figure 9 shows two request functions.

Fig. 9

Example of two request functions for two different paths $\pi$ and $\pi '$

Given tuples $\bar{ rf }=( rf ^{(T_{1})}, rf ^{(T_{2})}, \ldots )$ of request functions, each representing a path for a different task of higher priority, a condition can be given for a job associated with a vertex v to be able to meet its deadline as:

$$\begin{aligned} \forall \bar{ rf }: \exists t \leqslant d(v): e(v) + \sum _{T \in \tau _{ high }} rf ^{(T)} (t) \leqslant t. \end{aligned}$$

Intuitively, this condition guarantees that for all release scenarios of higher priority tasks, represented by the tuples $\bar{ rf }$, the job associated with v will be able to finish before its deadline. Compared to Conditions (11) and (12), this test is precise, but comes at the cost of testing all combinations $\bar{ rf }$ if applied naively. This can be improved by considering abstract request functions which are the point-wise maximum of request functions and thereby represent sets of behaviors. In the example in Fig. 9, consider the point-wise maximum of $rf _\pi$ and $rf _{\pi '}$ which is an over-approximation of both behaviors. The approach can be used for iterative refinement by starting with one function that represents all behaviors and is successively refined to represent smaller and smaller sets along an abstraction tree, illustrated in Fig. 10.

Fig. 10

Request function abstraction tree for request functions of some task T. The leaves are five concrete request functions. Each inner node is the point-wise maximum of all descendants and thus an abstract request function. Abstraction refinements happen downwards along the edges, starting at the root

The method refines abstractions in order to solve a combinatorial problem and is therefore called combinatorial abstraction refinement. It is a rather general idea and has been applied as well to response-time analysis of static priorities and EDF (Stigge and Yi 2014). While the problem is strongly $NP$-hard and the method’s time complexity therefore, in principle, exponential for worst-case instances, Stigge and Yi (2014) show that typical instances can be solved in time comparable to the state-of-the-art feasibility analysis described above in Sect. 4.5.2 which has pseudo-polynomial worst-case time complexity. Note that both methods are incomparable since they differ in the type of scheduler the analysis assumes, i.e., EDF versus static priorities.

4.5.4 Position in the model hierarchy

We observe that, intuitively, the DRT model generalizes all models described so far. All models are based on different classes of directed graphs which are all subsumed by the generality of the DRT model. This includes multiframe models which are essentially cycle graphs and even the sporadic task model which can be expressed using a single vertex with a self loop. Regarding the model hierarchy depicted in Fig. 1, Stigge (2014) provides more details about two aspects.

First, it is clear that non-cyclic RRT is generalized by DRT since each non-cyclic RRT task is already syntactically a DRT task. In fact, the non-cyclic RRT model is the subclass of the DRT model in which each G(T) is a strongly connected directed graph in which all cycles share a common vertex. By transitivity, all models located below non-cyclic RRT in the model hierarchy are generalized by DRT, including branching and multiframe models.

Second, the RRT model is, strictly speaking, not generalized by the DRT model. This is because the parameter P for every RRT task is a global constraint which the DRT model cannot directly express. It is a timing constraint between two successive releases of jobs associated with the source vertex. One such constraint exists per RRT task. This restriction, albeit mostly a technicality, is alleviated with the introduction of EDRT tasks in the following section. More specifically, an RRT task can be expressed by an equivalent 1-EDRT task, which in turn can be pseudo-polynomially translated into a DRT that is equivalent for most analysis purposes, as described in the following section.

4.6 Global timing constraints

In an effort to investigate the border of how far graph-based workload models can be generalized before the feasibility problem becomes infeasible, Stigge et al. (2011a) propose a task model called Extended DRT (EDRT). In addition to a graph G(T) as in the DRT model, a task T also includes a set $C(T) = \left\{ ( from _{1}, to _{1}, \gamma _{1}), \ldots , ( from _{k}, to _{k}, \gamma _{k})\right\}$ of global inter-release separation constraints. Each constraint $( from _{i}, to _{i}, \gamma _{i})$ expresses that between the visits of vertices $from _{i}$ and $to _{i}$, at least $\gamma _{i}$ time units must pass. An example is shown in Fig. 8b.

4.6.1 Feasibility analysis

The feasibility analysis problem for EDRT indeed marks the tractability borderline. In case the number of constraints in C(T) is bounded by a constant k which is a restriction called k-EDRT, Stigge et al. (2011a) present a pseudo-polynomial feasibility test. If the number is not bounded, they show that feasibility analysis becomes strongly $NP$-hard by a reduction from the Hamiltonian Path problem, ruling out pseudo-polynomial methods.

For the bounded case, we illustrate why the iterative procedure described in Sect. 4.5 for DRT can not be applied directly and then sketch a solution approach. The demand triple method can not be applied without change since the abstraction loses too much information from concrete paths. In the presence of global constraints, the procedure needs to keep track of which constraints are active. Consider path $\pi = (u_4, u_5)$ from the example in Fig. 8b, which would be abstracted with demand triple $\left\langle 2, 4, u_5 \right\rangle$. An extension with $u_2$ leading to demand triple $\left\langle 4, 7, u_2 \right\rangle$ is not correct, since the path $\pi ' = (u_4, u_5, u_2)$ includes a global constraint, separating releases of the jobs associated with $u_4$ and $u_2$ by 6 time units. A correct abstraction of $\pi '$ would therefore be $\left\langle 4, 8, u_2 \right\rangle$, but it is impossible to construct that from $\left\langle 2, 4, u_5 \right\rangle$ which lost information about the active constraint.

A solution to this problem is to integrate information about active constraints into the analysis. For each constraint $( from _{i}, to _{i}, \gamma _{i})$, the demand triple is extended by a countdown that represents how much time must pass until $to _{i}$ may be visited again. This slows down the analysis, but since the number of constraints is bounded by a constant, the slowdown is only a polynomial factor. Stigge et al. (2011a) choose to not directly integrate the countdown information into the iterative procedure but to transform each EDRT task T into a DRT task $T'$ where the countdown information is integrated into the vertices. The transformation leads to an equivalent iterative procedure and has the advantage that an already existing graph exploration engine for feasibility tests of DRT task sets can be reused without any change. The transformation is illustrated in Fig. 11.

Fig. 11

A basic example of a 1-EDRT task T being transformed into an equivalent DRT task $T'$. Only a subset of the vertices of $T'$ is shown

5 Further generalizations and extensions

We now turn to models that either extend the DRT model in other directions or are outside the hierarchy in Fig. 1 since they operate partially or entirely on a different abstraction level.

5.1 Resource sharing

Real-time systems even on uniprocessor platforms contain not only the execution processor, but often many resources shared by concurrently running jobs using a locking mechanism during their execution. Locking can introduce unwanted effects like deadlocks and priority inversion. For periodic and sporadic task systems, the Priority Ceiling (and Inheritance) Protocols (Sha et al. 1990) and Stack Resource Policy (Baker 1991) are established solutions with efficient schedulability tests. While these protocols can be used for more expressive models like DRT, the analysis methods do not necessarily apply.

Some initial work exists on extending the classical results to graph-based models. The common model extension is to consider a set of semaphores that all tasks may use, and annotate each vertex in each graph with the set of semaphores that the corresponding job may lock, together with a bound on the locking duration, cf. Fig. 12.

Fig. 12

A DRT task with resource annotations $\alpha : V \times \left\{ R_1, R_2\right\} \rightarrow \mathbb {N}$

Results of Ekberg et al. (2014) introduce an optimal protocol for GMF tasks with resources scheduled by EDF and Guan et al. (2011) develop a new protocol to deal with branching structures in the context of EDF scheduling. Recently, static priority schedulers have been considered by Zhuo (2014), in which blocking times are represented by blocking functions, similar to request functions for DRT analysis, cf. Sect. 4.5.3. Generally, the non-deterministic behaviours introduced by DRT-like models are not yet well understood in the context of resource sharing and subject of future research.

5.2 Adaptive variable-rate tasks

A model that has gained attention recently is motivated by control applications for combustion engines. In this setting, task releases are triggered by specific crankshaft rotation angles, leading to flexible inter-release separation times induced by different engine speeds. Further, execution times may be variable as well, since at higher engine speeds, certain functionality is being dropped because of a lack of time until the next task release. The resulting model contains different frames with different inter-release times and a non-trivial pattern of possible switches between frame types that can be exploited for analysis purposes. More specifically, a priori knowledge about the minimal time that one job type has to be repeatedly released until a new type can be instantiated, can lead to more exact results.

This model has been given different names, like Rate-Adaptive Tasks (Buttazzo et al. 2014), Variable Rate-Dependent Behaviour (Davis et al. 2014) or Adaptive Variable-Rate Tasks (Biondi et al. 2014). In a series of works, a few analysis methods have been developed. A sufficient utilization-based feasibility test (Buttazzo et al. 2014) was among the first known results. For static priorities, efficient but only sufficient ILP-based tests have been published (Davis et al. 2014) as well as an exact test (Biondi et al. 2014) which does an exhaustive search of all critical behaviours.

Current results are usually based on the assumption that just one task in the system does exhibit variable-rate behavior. Future work includes investigation of task systems with several such tasks for which angular velocity is correlated. Of course, this model can be over-approximated with the non-cyclic GMF model (and therefore methods for DRT analysis can be applied), but without further adaptation, corresponding analysis methods can only provide sufficient tests. The model offers an interesting research direction by investigating its relation to the DRT model and related formalisms in its hierarchy. Because of the dense set of existing frame sizes, there is no obvious one-to-one correspondence that would allow direct applicability of the methods surveyed in this article. However one may conjecture that such a mapping could be created by defining suitable equivalence classes on frame sizes, allowing definition of an equivalent graph-based model.

5.3 Task automata

A very expressive workload model called task automata is presented by Fersman et al. (2002). It is based on Timed Automata that have been studied thoroughly in the context of formal verification of timed systems (Alur and Dill 1994; Bengtsson and Yi 2003). Timed automata are finite automata extended with real-valued clocks to specify timing constraints as enabling conditions, i.e., guards on transitions. The essential idea of task automata is to use the timed language of an automaton to describe task release patterns.

In DRT terms, a task automaton (TA) T is a graph G(T) with vertex labels as in the DRT model, but labels on edges are more expressive. An edge (u, v) is labeled with a guard g(u, v) which is a boolean combination of clock comparisons of the form $x \bowtie C$ where C is a natural number and $\bowtie \in \left\{ \leqslant , <, \geqslant , >, =\right\}$. Further, an edge may be labeled with a clock reset r(u, v) which is a set of clocks to be reset to 0 when this edge is taken. Since the value of clocks is an increasing real value which represents that time passes, guards and resets can be used to constrain timing behavior on generated job sequences. We give an example of a task automaton in Fig. 13.

A task automaton has an initial vertex. In addition to resets and guards, task automata have a synchronization mechanism. This allows them to synchronize on edges either with each other or with the scheduler on a job finishing time.

Fig. 13

Example of a task automaton

Note that DRT tasks are special cases of task automata where only one clock is used. Each edge (u, v) in a DRT task with label $p(u, v) = C$ can be expressed with an edge in a task automaton with guard $x \geqslant C$ and reset $x := 0$.

Fersman et al. (2007) show that the schedulabiliy problem for a large class of systems modeled as task automata can be solved via a reduction to a model checking problem for ordinary Timed Automata. A tool for schedulability analysis of task automata is presented by Amnell et al. (2002) and Fersman et al. (2006). In fact, the feasibility problem is decidable for systems where at most two of the following conditions hold:

Preemption. :

The scheduling policy is preemptive.

Variable execution time. :

Jobs may execute for a time from an interval of possible execution times.

Task feedback. :

The finishing time of a job may influence new job releases.

However, the feasibility problem is undecidable if all three conditions are true (Fersman et al. 2007). Task automata therefore mark a borderline between decidable and undecidable problems for workload models.

Fig. 14

Example FJRT task. The fork edge is depicted with an intersecting double line, the join edge with an intersecting single line. All edges are annotated with minimum inter-release delays p(U, V). The vertex labels are omitted in this example. A possible job sequence containing jobs with their absolute release times and job types (but omitted execution times) is $\rho = [ (0, v_1), (5, v_2), (5, v_5), (6, v_4), (7, v_3), (8, v_5), (16, v_6), (22, v_1) ]$

5.4 Fork-join real-time tasks

An extension of the DRT task model to incorporate fork/join structures has been proposed recently by Stigge et al. (2013). Instead of following just one path through the graph, the behavior of a task includes the possibility of forking into different paths at certain nodes, and joining these paths later. This can be thought of as temporarily creating parallel threads which execute concurrently until they are synchronized and ultimately joined again.

Syntactically, the concept is represented using hyperedges. A hypergraph generalizes the notion of a graph by extending the concept of an edge between two vertices to hyperedges between two sets of vertices. More precisely, a hyperedge (U, V) is either a sequence edge with U and V being singleton sets of vertices, or a fork edge with U being a singleton set, or a join edge with V being a singleton set. In all cases, the edges are labeled with a non-negative integer p(U, V) denoting the minimum job inter-release separation time. The model is illustrated with an example in Fig. 14. Note that this contains the DRT model as a special case if all hyperedges are sequence edges. Since every DRT task can be interpreted as a single thread which never synchronizes with other tasks in the system, the FJRT task model is a strict generalization of the DRT task model.

As an extension of the DRT model, an FJRT task system releases independent jobs, allowing to define concepts like utilization $U(\tau )$ and demand-bound function just as before in Sect. 4.5. A task executes by following a path through the hypergraph, triggering releases of associated jobs each time a vertex is visited. Whenever a fork edge $(\left\{ u\right\} , \left\{ v_1, \ldots , v_m\right\} )$ is taken, m independent paths starting in $v_1$ to $v_m$, respectively, will be followed in parallel until joined by a corresponding join edge. In order for a join edge $(\left\{ u_1, \ldots , u_n\right\} , \left\{ v\right\} )$ to be taken, all jobs associated with vertices $u_1, \ldots , u_n$ must have been released and enough time must have passed to satisfy the join edge label. Forking can be nested, i.e., these m paths can lead to further fork edges before being joined. Note that meaningful models have to satisfy structural restrictions, e.g., each fork needs to be joined by a matching join, and control is not allowed to “jump” between parallel sections.

5.4.1 Feasibility

A complete method for analyzing FJRT task sets is not known at the time of writing. However, we sketch current approaches (Stigge et al. 2013). The usual demand-bound function based condition, i.e., checking $\forall t \geqslant 0: \sum _{T \in \tau } dbf _T(t) \leqslant t$, is applicable.

Demand tuples :

For an FJRT task T without fork and join edges, $dbf _T(t)$ can be evaluated by traversing its graph G(T) using a demand tuples abstraction as introduced in Sect. 4.5. We can extend this method to the new hyperedges by a recursive approach. Starting with “innermost” fork/join parts of the hypergraph, the tuples are merged at the hyperedges and then used as path abstractions as before. It can be shown that this method is efficient.

Utilization :

Recall that just computing $dbf _T(t)$ does not suffice for a finite test since it is also necessary to know which interval sizes t need to be checked. As for the DRT model, a bound can be derived from the utilization $U(\tau )$ of a task set $\tau$. However, it turns out that an efficient way of computing $U(\tau )$ is surprisingly difficult to find. The difficulty comes from parallel sections in tasks with loops of different periods which, when joined, exhibit the worst-case behavior in very long time intervals of not necessarily polynomial length.

6 Conclusions and outlook

This survey covers a hierarchy of graph-based workload models for hard real-time systems, together with analysis methods and related results for preemptive uniprocessor scheduling. We have provided details for all models included in a formally defined model hierarchy (cf. Fig. 1) and sketched analysis methods and complexity results for each model. Generalizations of models have been presented together with analysis methods which in turn have in most cases been generalizations as well, including previous methods as special cases. This is especially true for feasibility analysis where increased non-determinism made previous methods inapplicable. Apart from their importance in theoretical studies, we believe that these expressive models may find their applications in for example model- and component-based design for timed systems.

As a theoretical result, a classification of task models into tractable and intractable classes is shown in Fig. 15. This provides interesting insights about the precise position of the borderlines which we will discuss briefly.

Fig. 15

Classification of task models into

(pseudo-polynomial tests exist) versus

(strongly $coNP$-hard), relative to different decision problems

For EDF scheduling, the fundamental problem is to determine processor demand within time intervals. The complexity of computing this demand appears to be closely related to non-deterministic branching in task graphs. In the basic DRT model, cf. the hierarchy in Fig. 10a, computing the demand is possible in pseudo-polynomial time as long as timing constraints are either purely local or can be translated into local constraints. In this case, graph traversal algorithms can track constraints one by one when following branches. The extension from k-EDRT to EDRT causes intractability since many global constraints need to be considered together in all branches.

For SP scheduling, the source of intractability is different. In this case, actual interference patterns need to be considered, in contrast to EDF. Different interference patterns can be combined in different ways, leading to a combinatorial explosion and therefore a high complexity of the schedulability problem. Therefore, all models allowing different types of frames can be shown to lead to intractability, cf. Fig. 10b. The non-cyclic GMF model using a complete digraph for each task plays a special role in the hierarchy. Even though it allows different types of frames, it can not enforce their order. Therefore, the hardness proofs for multiframe models with static priority schedulers are not applicable to the non-cyclic GMF model. Moreover, exact pseudo-polynomial time analysis methods are not known either and left open for future work.

In preparing this paper, we have intended to cover only works on independent tasks for preemptive uniprocessors. Surveys on related topics have been published on the broad area of static-priority scheduling and analysis (Audsley et al. 1995), on scheduling and analysis of repetitive models for preemptable uniprocessors (Baruah and Goossens 2004), on real-time scheduling for multiprocessors (Davis and Burns 2011) and on the historic development of real-time systems research in general (Sha et al. 2004).

The following is a list of areas that we consider important in relation to the presented models, but did not include them in this paper for keeping the topic focused.

Real-time multiprocessor scheduling In contrast to uniprocessor systems, scheduling real-time workloads on parallel architectures is a much harder challenge. There are various scheduling strategies, e.g., global and partition-based scheduling with mostly sufficient conditions for schedulability tests. A comprehensive survey on this topic was published by Davis and Burns (2011). In the context of graph-based workload models, recent work focuses on the sporadic DAG model (Baruah et al. 2012b). Each sporadic task does not just release a single job at its activation but a set of jobs for which precedence constraints are specified with a directed acyclic graph. Results include speed-up bounds (Bonifaci et al. 2013; Li et al. 2014) and sufficient schedulability tests (Baruah 2014).

Mode switches A system may operate in different modes demonstrating different timing behaviors. In particular, the current mode is often a property of the system state, not just the task state, i.e., coordination and correlation between tasks may take place. The notion is rather general and several different concrete mode switching models are conceivable in the context of graph-based workload models like the DRT model.

• On the level of job releases, modes between tasks may be coordinated by providing synchronization possibilities on edges between job types. That is, tasks need to “take” edges together, synchronously, thereby modeling a global synchronization. Analysis methods need to be adapted in order to reflect the restricted set of behaviors. Note that many methods that are not mode-aware are still sound, but possibly over-approximate.

• On the level of job execution, modes may switch at a time instant where jobs are executing and demand that job parameters change immediately. One may consider a simple model using a directed mode-change graph where the nodes stand for modes, assigned with a set of tasks to be executed in the corresponding mode, and edges for mode switches that may be triggered by an internal or external event and guarded by a timing constraint such as a minimal separation distance. A prominent example of this kind of mode switches is the theory of mixed-criticality scheduling which has been studied intensively in recent years (Baruah et al. 2011; 2012a; Ekberg and Yi 2012). In recent work (Ekberg and Yi 2014; Ekberg et al. 2013), it has been shown that a mixed criticality task system can be modeled nicely using a chain of modes representing the criticality levels where mode switches are triggered by a task over-run that may occur at any time. The authors present a technique for scheduling the mixed criticality workload described in directed acyclic graphs. An interesting direction for future work is scheduling of mode switches in general directed graphs, which involves fixed-point computation due to cyclic structures.

An open area for research is the connection of mode switches with multiprocessor scheduling with seminal work by Li and Baruah (2012).

Tools for schedulability analysis Over the years, many models and analysis techniques have been developed. It is desirable to have a software framework that as input takes a workload description in some of the models and a scheduling policy and determines the model’s schedulability. A tool for task automata has been developed using techniques for model checking timed automata (Amnell et al. 2002). Due to the analysis complexity of timed automata, it suffers from the state-explosion problem. For the tractable models including DRT in the hierarchy of Fig. 1, a tool for schedulability analysis is currently under development in Uppsala based on the path abstraction techniques of Stigge et al. (2011) and Stigge and Yi (2013).