1 Introduction

The amount of data transmission required in modern mobile communication systems is increasing vividly. A tremendous ergodic capacities can be achieved by employing multiple antennas in data transmission and reception such as multiple input multiple output (MIMO) communication system. These systems are immune from fading channels and more reliable than single antenna communication system. The multi-user MIMO system allows a base station (BS) with multiple antennas to communicate with simple multiple users each equipped with single antenna. Every user has its different data stream which is transmitted at the same time and frequency but it is separated spatially using different precoding techniques. Multi-user massive MIMO systems enable a very large number of antennas located at the BS to jointly serve different mobile users [1–5]. It also provides greater capacity levels, advanced data rates, improved link reliability and significant energy efficiency for beyond 4G systems [6, 7].

The major drawbacks of such systems are the extra hardware costs and more computational complexity than classical multi-user MIMO systems [8, 9]. These drawbacks can be reduced by employing a reduced number of radio frequency chains (RFC) than the number of all available transmitter antennas using transmit antenna selection (TAS) techniques. These TAS techniques allow retaining most of the diversity gains which outcome from using all the available transmitting antennas [10, 11]. In order to apply TAS techniques channel state information should be acquired at the transmitter and this required downlink CSI can be attained with the uplink training and using uplink-downlink reciprocity in time division duplex (TDD) systems [12, 13]. It is well-known that the optimal antenna subset selection can be found through exhaustive search (ES)-TAS over all possible antenna subsets. Conversely, the computational complexity of such method grows exponentially with the total number of the available transmitting antennas [14]. Therefore, this method is impractical due to a large number of transmitter antennas employed in multi-user massive MIMO systems.

Particle Swarm Optimization (PSO) is one of the best commonly used optimization algorithms, and it is inspired by the social learning of birds or fishes. It is a swarm intelligence technique for optimization developed by Eberhart and Kennedy in 1995 [15]. The easiness and reduced computational complexity make this algorithm very common and commanding in resolving wide ranges of optimization problems. However, PSO always suffers from trapping in local minima and from slow convergence speeds. BPSO has been introduced for solving binary problems such as TAS. Because BPSO uses the same concepts of PSO, it also undergoes the same problems. The core part of the used BPSO is the v-shaped transfer function, which is proved to improve its performance based on the above-mentioned weaknesses [16]. Another important part in BPSO is Inertia weight, which affects the exploration-exploitation trade-off in BPSO process. Chaotic inertia weight is proved to be the best strategy for better accuracy as tested in [17].

The model scope is that a BS equipped with massive number of antennas and a fewer number of RFC need to perform data transmission to all the served users simultaneously. The number of active antennas is equal to the number of RFC. The group of active antennas is selected among the overall antennas which achieves maximum ergodic capacity. This group is selected using the discussed chaotic BPSO antenna selection algorithm. The fitness function for the evolutionary TAS is maximizing all the systems achievable ergodic capacity. The benefits from such algorithm are that it can achieve better ergodic capacity than the recent algorithms. Another benefit is that it is simpler than ES-TAS and can be easily employed in multi-user massive MIMO systems.

Recently, in [10], a large scale massive MIMO in millimeter wave band is considered. Antenna selection and beamforming are employed to achieve high-speed data transmission. An adaptive transmit and receive algorithm which relies on stochastic gradient method is studied. Also, an iterative antenna selection algorithm is considered. It can be noticed that the used algorithms complexity will grow up extremely by increasing the number of transmitting and receiving antennas as in massive MIMO case. Additionally, it is focused on point to point communication in an indoor environment with no multiuser support. While in [11], a TAS problem in measured massive MIMO channels were studied, and convex optimization was used to select the antenna subset that maximizes the capacity in the downlink which is hard to implement in real time applications. It also did not take into consideration the multiuser beamforming effect on the selection criteria. In [14], a multimode antenna selection for single user zero forcing the receiver to achieve maximum data rate is investigated. ES is compared to greedy TAS. optimization algorithms are introduced to solve the complex TAS problem. In [18], genetic optimization is used as the antenna selection method for MIMO wireless systems by maximization of the achieved instantaneous capacity. In [19], a binary particle swarm optimization (BPSO) based method is proposed for joint transmit and receive antenna selection. Both of them consider single user case, and they also consider a small number of antennas at the transmitter and receiver. Therefore, the evolutionary TAS for multi-user massive MIMO systems has not been sufficiently investigated and it is challenging to implement such evolutionary TAS algorithm for multi-user massive MIMO system.

The contribution of this paper is to study the effect of TAS on the performance of multiuser massive MIMO system. the main studied multiuser technique is zero-forcing beamforming. The chaotic BPSO-TAS is presented in order to solve selection problem. The main function of the optimized TAS is to select the near-optimal subset which maximizes the user’s achievable capacity. The optimized TAS convergence was proved by simulations. The simulation results also showed that chaotic BPSO-TAS can achieve near the optimal capacity performance of ES-TAS even with a small iteration number, and with reduced computational complexity. Thus, the proposed algorithm is important and practical for multiuser massive MIMO systems. A comprehensive comparison between relevant work and this paper scope can be abridged in Table 1.

Table 1 A comparison between relevant work and current presented work
Full size table
Fig. 1
figure 1

Multi-user massive MIMO system block diagram

Full size image

The rest of the paper is organized as follows. Section 2 describes the multiuser massive MIMO system model, and optimization problem formulation. In Sect. 3, the chaotic BPSO-TAS is described in details. Section 4 compares the proposed algorithm with other existing ones through Monte Carlo Simulation. Conclusions are presented in Sect. 5.

2 System model and formulation of the optimization problem

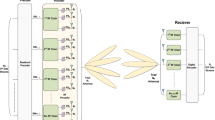
Consider a BS equipped with multiple transmitter antennas and a smaller number of RFC. The BS communicates with single-antenna users using space division multiple access (SDMA) as shown in Fig. 1. Assume that, the number of transmitter antennas is \(N_{T}\), the number of RFC is \(N_{RF}\) and the number of the users is N \(_{U}\). The number of active antennas at any given time is limited to the \(N_{RF}\) number and the other antennas are considered as not active. For such a system, a selected active downlink channel is formed between BS antennas and users’ antennas and is a subset of overall downlink channel.

The selection criterion is done using a chaotic BPSO-TAS algorithm which will be discussed intensively in the following section. Consider the data signal vector, with size F, to the user u is denoted as \(s_u \in \mathbb {C}^{F}\)and is normalized to unit power. The vector \(h_u \in \mathbb {C}^{N_T \times 1}\) is the corresponding channel vector between every user u and all transmitter antennas. The vector \(\hat{{h}}_u \in \mathbb {C}^{N_{RF} \times 1}\)is the selected corresponding channel vector between the user u and the selected transmitters using the chaotic BPSO-TAS algorithm.

We use a channel model where the channel gain from every transmitter antenna to a user u is described by a zero-mean circularly symmetric complex Gaussian random variable, which is an appropriate model for narrowband orthogonal frequency division multiplexing systems operating in a non-line-of-sight rich scattering environment [20]. The slow varying CSI is assumed to be fully known at the transmitter through channel estimation at the receiver and feedback path to the transmitter. The \(N_{U}\) different data signals are separated spatially using the linear beamforming vectors \(w_1 ,w_2 ,...,w_{N_U } \in \mathbb {C}^{N_{RF} \times 1}\), where \(w_u \)is associated to user u, and the squared norm \(\left\| {w_u } \right\| ^{2}\) is the power allocated for transmission to the same user. The received signal at that user is \(r_u \in \mathbb {C}^{F}\) and can be calculated by

$$\begin{aligned} r_u =\hat{{h}}_u^*\left( {\sum _{i=1}^{N_U } {w_i s_i } } \right) +n_u , \end{aligned}$$
(1)

where \(n_u \)is the zero mean additive receiver noise with variance \(\sigma ^{2}\), and * superscript means transpose and Hermitian of the superscripted variable. Accordingly, the signal-to-interference-and-noise-ratio (SINR) at user u is

$$\begin{aligned} SINR_u ={\left| {\hat{{h}}_u^*w_u } \right| ^{2}}/{\left( {\sum _{i\ne u} {\left| {\hat{{h}}_i^*w_i } \right| ^{2}} +\sigma ^{2}} \right) }. \end{aligned}$$
(2)

One of the well-known linear transmitting beamforming is Zero-forcing beamforming (ZFBF) and it is the counterpart of zero-forcing filtering in normal receive processing. It refers to a signal processing technique that completely eliminates interference. This can be achieved at the transmitter side by selecting beamforming vectors that are orthogonal to the channels of non-intended users. The normalized weights of the ZFBF matrix W = [\(w_1 ,w_2 ,...,w_{N_U } \)] \(\in \mathbb {C}^{N_{RF} \times N_U }\)can be calculated by [21]

$$\begin{aligned} W\mathbf{=}{\hat{{H}}^{*}(\hat{{H}}\hat{{H}}^{*})^{-1}}/{\left\| {\hat{{H}}^{*}(\hat{{H}}\hat{{H}}^{*})^{-1}} \right\| }, \end{aligned}$$
(3)

where \(\hat{{H}}=[\hat{{h}}_1^T ,\hat{{h}}_2^T ,...,\hat{{h}}^{T}_{N_U } ]^{T}\) \(\in \mathbb {C}^{N_U \times N_{RF} }\)contains the selected channel vectors from the overall antennas channel matrixH.

The main goal of this paper is to analyse the TAS optimization problem, where arbitrary fitness function \(f({ SINR}_1 ,{} { SINR}_2 ,\ldots { SINR}_{N_U } )=\sum _{u=1}^{N_U } {\log _2 (1+SINR_u )} \) is needed to be maximized. This fitness function is the summation of all users’ throughput using Shanon capacity formula [22]. This function is strictly increasing in the \(SINR_u \) of each user while the total number of selected antennas is limited to N \(_{RF}\). A binary vector \(m_i (i=1,2,...,N_T )\)with N \(_{T}\) elements needs to be defined as

$$\begin{aligned} {m_i} = \left\{ \begin{array}{ll} 1 &{}\quad i\mathrm{th}\,\textit{antenna\,\,active}\\ {0,} &{}\quad \textit{otherwise.} \end{array} \right. \end{aligned}$$
(4)

and it states which antennas are active and which are not. The first element of this vector represents the state of the first antenna, the second element represents the state of the second antenna, and so on. Every element of this vector can take two values which are “0” or “1”. If the element value is set to “0” then the corresponding antenna is not active, and its channel vector (column from H) to all the users will not exist in \(\hat{{H}}\). If the element value is set to “1” then the corresponding antenna is active, and its channel vector will exist in \(\hat{{H}}\). The algorithm which is used to construct \(\hat{{H}}\) from H is described in Fig. 2. The TAS optimization problem can be stated mathematically as

$$\begin{aligned} {\begin{array}{ll} {\max }&{} {f(SINR_1 ,SINR_2 ,...,SINR_{N_U } )} \\ {subject \,\,\, to}&{} {\sum _{i=1}^{N_T } {m_i =N_{RF} } } \\ \end{array} }, \end{aligned}$$
(5)
Fig. 2
figure 2

The flow chart of algorithm 1 which is used to construct \(\hat{H}\) from H according to selection vector m

Full size image

3 Chaotic binary particle swarm optimization

PSO is an evolutionary optimization algorithm which is inspired by the social behaviour of birds grouping. It uses a number of particles (i.e. nominee K solutions) which wing everywhere in the search space to find the global best solution. Each particle position updating should consider the current particle position, the current particle velocity, the distance between the current particle location and the particle best value location, and the distance between the current particle location and the global best value location. The particle velocity update equation can be calculated by [16]

$$\begin{aligned} {v^k}(t + 1)&= \omega (t)\,\,{v^k}(t)\nonumber \\&\quad +\, {c_1} \times rand \times \big (pbest{(t)^k} - {x^k}(t)\big ),\nonumber \\&\quad +\, {c_2} \times rand \times \big (gbest{(t)^k} - {x^k}(t)\big ) \end{aligned}$$
(6)

where \({v^k}(t)\) is the velocity of particle k at iteration t, rand is a randomly generated number that takes values between 0 and 1, \({x^k}(t)\) is the current position of particle k, \(pbest^{k}\)is the location of particle best value so far, gbest is the location of global best value. The constants \(c_1 \)and \(c_2 \)are the acceleration constants reflecting the weighting of stochastic acceleration terms that pull each particle towards \(pbest^{k}\) and gbest, respectively. The function \(\omega (t)\) is the chaotic inertia weighting function, it utilizes the nonlinear dynamics of chaos to make BPSO avoid getting into local minimum value, and it can be calculated by [17]

$$\begin{aligned} \omega (t)=(\omega _1 -\omega _ 2)\times \frac{t_{MAX} -t}{t_{MAX} }+\omega _2 \times z(t), \end{aligned}$$
(7)

where \(\omega _1 \), \(\omega _2 \) are the upper and the lower limit of the weight values consecutively, \(t_{MAX}\) is the maximum allowable iteration limit, and z(t) is the chaotic variable which is generated using logistic chaotic map. The chaotic variable generation depends on the following recursive relation

$$\begin{aligned} z(t+1)=4\times z(t)\times (1-z(t)), \end{aligned}$$
(8)

and the next position of the particle k can be calculated by

$$\begin{aligned} x^k (t+1)=x^k (t)+\nu ^k (t). \end{aligned}$$
(9)

The TAS optimization problem has a discrete binary search space in order to find the suboptimal binary vector m which is used in the selection of active antennas. This binary vector should maximize the utility function \(f({ SINR}_1 ,{} { SINR}_2 ,.....{ SINR}_{N_U } )\). In this binary search space, the PSO is dealing with only two numbers which are “0” and “1”, so the position updating process cannot be done using (9). Another method will be used to find suboptimal m which is Binary PSO. All of the K particle vectors will be divided into N \(_{T}\) bit elements. It will be denoted as \(m_i^k \)(i=1,..., N \(_{T})\) where superscript k indicates particle number and subscript i indicates element number. Every element from the proposed solution vectors will have its own velocity element \(\nu _i^k \) which will be calculated with (6). Consequently, we have to find a way to use the calculated velocities to change these elements from “0” to “1” or vice versa.

According to [23], the idea is that the probability of an element velocity will change its value and a transfer function is used to map the velocity values to the probability values for updating elements. This transfer function should be able to provide a high probability of changing the position of a large absolute value of the velocity and vice versa. It should be bounded in the interval from 0 to 1 and increasing by the increase of the velocity magnitude. A V-shaped transfer function is used in this paper, as it can improve the performance of the BPSO in terms of avoiding local minima, and convergence rate [16]. The V-shaped transfer function is defined as

$$\begin{aligned} S(\nu _i^k )=\left| {{\nu _i^k }/{\sqrt{1+(\nu _i^k )^{2}}}} \right| , \end{aligned}$$
(10)
Fig. 3
figure 3

The chaotic BPSO-TAS Algorithm

Full size image
Fig. 4
figure 4

The ergodic capacity evolution curve versus the number of iterations (t) with different \(N_{RF}\) values

Full size image

where \(\nu _i^k \) is the velocity of the particle k and element i, and the new value for every element is calculated according to (11). The steps for the applied chaotic BPSO-TAS for Multiuser Massive MIMO are described in Fig. 3.

$$\begin{aligned}&m\begin{array}{*{20}{c}} k\\ i \end{array}(t + 1) = \nonumber \\&\left\{ {} \right. \,\begin{array}{*{20}{c}} {complement\Big (m\begin{array}{*{20}{c}} k\\ i \end{array}(t)\Big )}\\ {m\begin{array}{*{20}{c}} k\\ i \end{array}(t)} \end{array}\,\,\,\begin{array}{*{20}{c}} {if}\\ {if} \end{array}\,\,\,\begin{array}{*{20}{c}} {rand() < S\Big (v\begin{array}{*{20}{c}} k\\ i \end{array}(t)\Big )}\\ {rand() \ge S\Big (v\begin{array}{*{20}{c}} k\\ i \end{array}(t)\Big )} \end{array} \end{aligned}$$
(11)

4 Numerical results and discussion

In this section, the simulations are Discussed to validate the effectiveness of the chaotic BPSO-TAS algorithm as well as to compare its performance with the optimal ES-TAS algorithm. Random antenna vector is used at the beginning of the chaotic BPSO-TAS and with no prior ordering. The parameters used in the chaotic BPSO-TAS is \(t_{MAX}=150\), \(K=30\), elements = \(N_{T}\), \(c_{1}= 1.5\), \(c_{2}=1\), \(\omega _1=0.9\), \(\omega _2=0.4\), and \(Z=0.3\) at the beginning.

The ergodic capacity evolution curve versus the number of iterations (t) with different \(N_{RF}\) values is shown in Fig. 4. The number \(N_{U}\) value is fixed to 8 users and the number \(N_{T}\) value is fixed to 64 antennas. The shown evolution curves are compared to the maximum ergodic capacity when 8 users are served by fully functioning 64 transmitter antennas. This curve shows that chaotic BPSO-TAS takes 50 iterations to improve the system’s ergodic capacity values due to improving the selection gain. After these iterations, the improvement is saturated at this sub-optimal values. It also shows that the selection gain is high when the number of used antennas is small, but it is low when a larger number of antennas are employed. Nearly half of the maximum ergodic capacity can be achieved with only 8 active transmitting antennas and 88 % of the maximum ergodic capacity is achieved when half of the antennas are employed. Figure 4 and Table 2 shows the significance of adding antenna selection to multi user massive MIMO systems as higher ergodic capacities can be achieved by employing a smaller number of RF units.

Table 2 The best achieved ergodic capacity and their percentage of the systems upper bound
Full size table
Fig. 5
figure 5

The CDF of capacities for different TAS techniques over 10,000 channel realizations

Full size image

The cumulative distribution function (CDF) of capacities for four different TAS techniques over 10,000 channel realizations is shown in Fig. 5, Namely, random (Ran)-TAS, ES-TAS, maximum norm (MN) TAS and chaotic BPSO-TAS. The Ran-TAS is done by selecting a random combination of antennas at every iteration while the ES-TAS is done by calculating the capacity with all the possible combinations and select the one that achieves maximum capacity. The MN-TAS is to choose a combination of the transmitting antennas such that it maximizes the sum of the squared magnitudes of transmitting channel gains [24]. The four TAS techniques are compared with themselves, and they are also compared to the systems which have only 8 active transmitter antennas and 64 active transmitter antennas as lower and upper bounds, consecutively.

The closer the CDF curve to the 64 active transmitting antenna, the better is the TAS algorithm. This means higher rates probability is more frequent than lower ones. The signal to noise ratio is fixed at 10 dBs at this part of the numerical analysis. The performance of the Ran-TAS is the worst one which is matching to using only 8 active transmitting antennas. The ES-TAS is the best as it searches all the possible combinations. The performance of the chaotic BPSO-TAS is shown to be matching to the optimal ES-TAS but with much smaller processing time. The chaotic BPSO-TAS average run time is only 2 % of the average runtime of the ES-TAS on the same processing unit.

Fig. 6
figure 6

The ergodic capacities for different TAS techniques and different \(N_{RF}\) values over 1000 channel realizations

Full size image

The ergodic capacities for different TAS techniques and different \(N_{RF}\) values against SNR and over 1,000 channel realizations are shown in Fig. 6. The BPSO-TAS and Ran-TAS are included in this figure. On the other hand, The ES-TAS is not included because it is very complex to implement when large numbers of transmitter antennas are employed. The figure shows that chaotic BPSO-TAS Ergodic capacity is much better than Ran-TAS due the addition of the processing gain. The Ergodic capacity differences increase with the increase in SNR values because the chaotic BPSO-TAS is able to select the active transmitting antennas with smaller noise interference. The chaotic BPSO-TAS can achieve comparable capacity performance while the TAS complexity is kept reduced. Therefore, the chaotic BPSO-TAS is more suitable for real-time implementations than the optimal ES-TAS in multi-user massive MIMO systems.

5 Conclusion and future work

In this paper, the TAS problem for multiuser massive MIMO systems using zero-forcing beamforming has been considered. The chaotic BPSO-TAS is proposed in order to maximize the achievable capacity to all the users. The addition of such technique has improved the system performance while maintaining a small number of RFC at the BS. The convergence of the algorithm is proved by numerical simulations. The numerical results also show that chaotic BPSO-TAS can achieve near the optimal capacity performance of ES-TAS even with a small number of iterations, and with reduced computational complexity. Thus, the proposed algorithm is proved to be important and practical for multiuser massive MIMO systems. However, there is a mystery question about studying the effect of using different chaotic maps generators on achievable capacities of the chaotic BPSO TAS algorithm.