Abstract
The purpose of this paper is to present a paraconsistent formal system and a corresponding intended interpretation according to which true contradictions are not tolerated. Contradictions are, instead, epistemically understood as conflicting evidence, where evidence for a proposition A is understood as reasons for believing that A is true. The paper defines a paraconsistent and paracomplete natural deduction system, called the Basic Logic of Evidence (BLE), and extends it to the Logic of Evidence and Truth (\(\textit{LET}_{J}\)). The latter is a logic of formal inconsistency and undeterminedness that is able to express not only preservation of evidence but also preservation of truth. \(\textit{LET}_{J}\) is anti-dialetheist in the sense that, according to the intuitive interpretation proposed here, its consequence relation is trivial in the presence of any true contradiction. Adequate semantics and a decision method are presented for both BLE and \(\textit{LET}_{J}\), as well as some technical results that fit the intended interpretation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The distinctive feature of paraconsistent logics is that the principle of explosion, according to which anything follows from a contradiction, does not hold, thus allowing the acceptance of contradictions within a theory without falling into triviality. Paraconsistency is the study of paraconsistent logics, both in its technical and philosophical aspects. Dialetheism is the view according to which there are true contradictions (see e.g. Priest and Berto 2013). The dialetheist claims that some contradictions are ontological in the sense that they are due to some ‘inner contradictory essence of reality’—or in other words, that reality, in order to be correctly described, demands pairs of contradictory propositions.Footnote 1 Of course, endorsing a paraconsistent logic and being a dialetheist are not the same thing: the latter implies the former, but not the other way round. One can be a paraconsistent logician without being a dialetheist, since paraconsistent logics may be studied and developed without the commitment to the truth of accepted contradictions. Another view in paraconsistency, that we call metaphysical neutrality, ‘suspends judgement’ with respect to the nature of contradictions. It is a somewhat pragmatic position: the fact that contradictions occur in several contexts of reasoning is enough to justify a non-explosive account of logical consequence, and there is no need to go into the metaphysical question about the nature of such contradictions. A third position in paraconsistency, antagonistic to dialetheism, claims that no contradiction is ontological but, rather, all contradictions that occur in scientific theories, belief systems, a number of situations in informal reasoning, and even in semantic and set theoretical paradoxes—that are, strictly speaking, results about languages with certain characteristics—have epistemic character in the sense that they are related to thought and language. This is the position endorsed by us.
It is likely that no paraconsistent logician would be opposed to epistemic contradictions. However, to the best of our knowledge, a paraconsistent formal system suited to an intuitive reading according to which only epistemic contradictions are allowed (and true contradictions are ‘prohibited’) is still lacking. Our aim here is to present a system of this kind. In order to work out such an account of paraconsistency we have to explain what it means to say that a pair of propositions A and \(\lnot A\) simultaneously ‘hold’, or ‘may be accepted’, without being true.
According to the standard view, that can be traced back to Aristotle and is to be found in virtually every book on elementary logic, the validity of an inference is a matter of necessary preservation of truth. The essential property of propositions, from the viewpoint of classical logic, is truth. Indeed, the more effective way of prohibiting true contradictions is the principle of explosion that, together with excluded middle, composes the deductive properties of classical negation. But truth is not always the only property of propositions that matters. In intuitionistic logic, for example, the property at stake is not only truth but truth together with the availability of a constructive proof. Thus, there may be a proposition A such that both A and \(\lnot A\) do not hold because there is no proof for any of them. Given the soundness of the system, a proof of A entails the truth of A, but it may be the case that A has been proved true by non-constructive means although there is no constructive proof of A. Notice that the following situation is perfectly feasible: given two propositions A and \(\lnot A\), exactly one of them is true, but from a constructivist point of view neither holds because there is no proof available for A or for \(\lnot A\). Such a view combines a realistic notion of truth with a notion of constructive proof that is essentially epistemic.Footnote 2
In the case of a non-dialetheist paraconsistent logic the situation is dual. There may be a proposition A such that it is not the case that both A and \(\lnot A\) are true, but in some sense both hold in a given context. In this case, the essential question Q is the following: Q: what property are we going to ascribe to a pair of accepted
contradictory propositions such that it would be possible
for a proposition to enjoy it without being true? Such a property has to be something weaker than truth. If we want to reject the principle of explosion together with dialetheism, without assuming a position of metaphysical neutrality, we have to give a convincing answer to Q. Our proposal is that the notion of evidence is well suited to be such an answer.
The main aim of this paper is to present a paraconsistent formal system, that we call the Logic of Evidence and Truth (\(\textit{LET}_{J}\)), and an anti-dialetheist explanation of it according to which contradictions are understood epistemically as conflicting evidence and true contradictions are not allowed. Section 2 briefly discusses the notion of evidence in order to show that it is an appropriate answer to question Q above. Section 3 presents a paracomplete and paraconsistent natural deduction system for a logic we call BLE, (the Basic Logic of Evidence), whose inference rules are intended to preserve evidence, not truth. Neither excluded middle nor explosion hold in BLE because evidence can be incomplete as well as contradictory.Footnote 3 Section 4 is dedicated to extending BLE to a logic we call \(\textit{LET}_{J}\) (Logic of Evidence and Truth based on positive intuitionistic sentential logic). \(\textit{LET}_{J}\)is a logic of formal inconsistency and undeterminedness that extends BLE by adding resources to express that a particular formula A behaves classically: a unary sentential connective \(\circ \) is added to the language of BLE, and \(\circ A\) recovers explosion and excluded middle for A. A valuation semantics, a decision method and some technical results for BLE and \(\textit{LET}_{J}\) will be presented.Footnote 4 Finally, in Sect. 5, we face some issues related to paraconsistency as preservation of evidence.
2 On the notion of evidence
There are a number of circumstances in which we have to deal with pairs of propositions A and \(\lnot A\) such that there are reasons for accepting and/or believing in both. It does not mean that both are true, nor that we actually believe that both are true. However, in such circumstances, although there may be nothing conclusive with respect to the truth-value of A, we still wish to draw inferences in the presence of both A and \(\lnot A\).Footnote 5 The acceptance of A and \(\lnot A\) can be understood as some kind of ‘conflicting information’ about A, in the sense of having non-conclusive reasons for accepting the truth as well as the falsity of A. This kind of ‘conflicting information’ we call here conflicting evidence. Let the falsity of A be represented by \(\lnot A\). So,
-
‘evidence that A is true’ means ‘reasons for believing in/accepting A’;
-
‘evidence that A is false’ means ‘reasons for believing in/accepting \(\lnot A\)’.
There may be evidence that A is true even if A is false. Conflicting evidence occurs when reasons for accepting A and \(\lnot A\) are simultaneous and non-conclusive. Conclusive evidence is evidence that establishes conclusively the truth (or the falsity) of A, and eliminates any opposed non-conclusive evidence. Typical cases of conflicting evidence, in the sense explained above, are the following. You may ask two different but reliable doctors about the cause of some symptoms and get two different and incompatible diagnoses. Another example: two witnesses may deliver two contradictory statements regarding some point that is crucial to the judge’s final decision. Supposing, again, that both are reliable, it may be said that there are reasons for believing both A and \(\lnot A\), although only one of them is true. The idea of non-conclusive versus conclusive evidence is well illustrated in theories about empirical phenomena. A good example is the conflict between classical mechanics and the theory of electromagnetic field, that are in the origin of Einstein’s special relativity (see Carnielli and Rodrigues 2016). Actually, it is not uncommon that two different scientific theories, successful in describing and predicting a class of phenomena, may yield contradictory results in some specific situations.Footnote 6
The use we make here of the notion of evidence is close to the way evidence in understood in epistemology. In Kelly (2014) we read that evidence “is the kind of thing which can make a difference to what one is justified in believing or ...what it is reasonable for one to believe” and later he adds that since “evidence is the sort of thing which confers justification ...it is natural to think that ‘reason to believe’ and ‘evidence’ are more or less synonymous.” The link between ‘evidence’ and ‘reasons to believe’ is also clear in the ‘principle of reasonable belief’, presented by Achinstein (2010a): if, in the light of background information \(\varPhi \), \(\kappa \) is evidence that A, then, given \(\varPhi \), \(\kappa \) is a good reason for believing A. Achinstein also distinguishes potential evidence from veridical evidence. Roughly speaking, an evidence \(\kappa \) for a proposition A is veridical if A is true and there is an ‘explanatory connection’ between A and \(\kappa \) (this means, as we understand it, that \(\kappa \)establishes conclusively the truth of A). On the other hand, \(\kappa \) may be potential evidence for A, even if A is false. Achinstein’s notions of potential and veridical evidence are close to what we call here, respectively, evidence simpliciter (non-conclusive) and conclusive evidence.
It is important to call attention to the fact that evidence, in the sense used here, is always external to the formal system. We are not formalizing the notion of evidence, nor will we present a ‘semantics of evidence’.Footnote 7 The aim of Sect. 3 is to give an account of the deductive behaviour of the sentential connectives from the point of view of preservation of evidence, instead of preservation of truth: an inference is taken to be valid just in case there cannot exist evidence for the premises without evidence for the conclusion. What constitutes evidence depends on the area of study and the subject matter, and this is not a problem of logic. Actually, it is not surprising that there is no unified account of what constitutes evidence for a given proposition A (see Achinstein 2010b). What kind of thing constitutes non-conclusive or conclusive evidence varies for the physicist, chemist, archaeologist and so on.
3 A logic of evidence
The aim of this section is to devise a paraconsistent formal system suited to the reading of contradictions as conflicting evidence. What we will do here has an analogy to the inference rules for intuitionistic logic, when the latter is understood epistemically as concerned with the availability of a constructive proof. Natural deduction rules are particularly well suited to expressing the intuitionistic way of constructing proofs. Roughly speaking, the basic idea of the Brouwer–Heyting–Kolmogorov (BHK) interpretation is that an inference rule is valid if it transforms constructive proofs for one or more premises into a constructive proof of the conclusion. Here, analogously, the guiding idea is the following: supposing the availability of evidence for the premises, we ask whether an inference rule yields a conclusion for which evidence is also available.
As we have seen, (i) the falsity of A is represented here by \(\lnot A\), (ii) ‘evidence that A is true’ is understood as ‘reasons for accepting/believing in A’, and (iii) ‘evidence that A is false’ means ‘reasons for accepting/believing in \(\lnot A\)’. So,
-
‘A holds’ means ‘there is evidence that A is true’;
-
‘A does not hold’ means ‘there is no evidence that A is true’;
-
‘\(\lnot A\) holds’ means ‘there is evidence that A is false’;
-
‘\(\lnot A\) does not hold’ means ‘there is no evidence that A is false’.
Accordingly, the following scenarios may be described with respect to a proposition A:
-
1.
No evidence at all: both A and \(\lnot A\) do not hold.
-
2.
Only evidence that A is true: A holds, \(\lnot A\) does not hold.
-
3.
Only evidence that A is false: \(\lnot A\) holds, A does not hold.
-
4.
Conflicting evidence: both A and \(\lnot A\) hold.
Thus, the formal system we are looking for must be not only paraconsistent but also paracomplete: neither the principle of explosion nor excluded middle should hold. The next section examines which natural deduction rules are suitable for expressing the propagation of evidence through implication, conjunction, disjunction, and negation.
3.1 A natural deduction system for preservation of evidence
Let \(L_{0}\) be a language with a denumerable set of propositional letters \(\{p_{0}, p_{1},\)\(p_{2},\ldots \}\), parentheses, and closed under the connectives in the set \(\{\lnot , \wedge ,\)\( \vee , \rightarrow \}\). The set \(S_{0}\) of formulas of \(L_{0}\) is obtained recursively in the usual way. Roman capitals stand for meta-variables for formulas of \(L_{0}\). The definition of a derivation D of A from a set \(\varGamma \) of premises is the usual one for natural deduction systems.
A complete natural deduction system for classical propositional logic is defined by adding to the introduction and elimination rules for \(\rightarrow \), \(\vee \) and \(\wedge \) the rules of explosion and excluded middle below:

By dropping the rules above and keeping only the introduction and elimination rules for \(\rightarrow \), \(\vee \) and \(\wedge \), we get positive intuitionistic propositional logic (PIL). We start with PIL, arguing that it is able to express the notion of preservation of evidence.

With respect to PIL, the availability of evidence is analogous to availability of proof. As usual in natural deduction systems, [A] means that the hypothesis A has been discharged (or canceled). An evidence-interpretation for the introduction rules for \( \wedge \) and \( \vee \) is straightforward. If \(\kappa \) and \(\kappa '\) are evidence, respectively, for A and B, \(\kappa \) and \(\kappa '\) together constitute evidence for \(A \wedge B\).Footnote 8 Similarly, if \(\kappa \) constitutes evidence for A, then \(\kappa \) is also evidence for any disjunction that has A as one disjunct. The rule \(\rightarrow I\) deserves some remarks. When the supposition that there is evidence \(\kappa \) for A leads to the conclusion that there is evidence \(\kappa '\) for B, this is itself evidence for \(A \rightarrow B\). Notice that \(\rightarrow \) does not demand any relation between the contents or meanings of A and B. If there is evidence for B, we may conclude that there is also evidence for \(A \rightarrow B\), for any A. The implication, therefore, works analogously to both classical and BHK interpretation: if B is true, \(A \rightarrow B\) is also true; if there is a construction of B, there is a construction of \(A \rightarrow B\). Up to this point, this takes care of the introduction rules.
The elimination rules may be obtained from the introduction rules. Gentzen (1935, p. 80) famously remarks that “The introductions represent, as it were, the ‘definitions’ of the symbols concerned, and the eliminations are no more, in the final analysis, than the consequences of these definitions”. Prawitz (1965, p. 33) has put this idea more precisely in the so-called inversion principle. We reformulate Prawitz’ inversion principle in terms of evidence as follows:
-
Evidence inversion principle (EIP)
Let \(\alpha \) be an application of an elimination rule that has B as consequence. Then, any \(\kappa \) that is evidence for the major premise of \(\alpha \), when combined with evidence for the minor premises of \(\alpha \) (if any), already constitutes evidence for B; the existence of evidence for B is thus obtainable directly from the existence of evidence for the premises, without the addition of \(\alpha \).
We thus easily gain the respective elimination rules which do preserve availability of evidence. For the sake of an example, let us take a look at \(\wedge E\). If some evidence \(\kappa \) for \(A \wedge B\) is available, \(\kappa \) would be, or would ‘contain’ evidence for A, as well as for B. Analogous reasoning apply to the other rules.
Up to this point we have what could be called a positive logic of preservation of evidence. PIL is well suited to express both preservation of evidence and the (positive) BHK interpretation. It is worth noting that the introduction and elimination rules for conjunction, implication and disjunction, therefore, preserve a notion stronger than truth (constructive proof) as well as a notion weaker than truth (evidence).
3.2 Negation
A central issue in paraconsistency is that of specifying a negation without (some of) the properties of classical negation but that still retains enough properties to be termed a negation. As discussed in the beginning of Sect. 3, the principle of explosion and excluded middle do not hold from the viewpoint of preservation of evidence. Another property of classical negation that must be invalid is the so-called introduction of negation:
The reason is that any extension of PIL in which introduction of negation holds is able to prove that for any A and B:
that is, from a contradiction, any negated proposition follows, which is an undesirable result for a paraconsistent system.Footnote 9 Besides, and more importantly, the introduction of negation does not fit the intuitive interpretation in terms of evidence, since there may be a circumstance such that there is evidence for B and for \(\lnot B\), and so also for \(A \rightarrow B\) and \(A \rightarrow \lnot B\), but no evidence for \(\lnot A\).
Now we turn to rules in which the conclusion is a negation of a conjunction, a disjunction or an implication. Natural deduction rules for concluding falsities may be obtained in a way similar to the rules for concluding truths. The point is that instead of asking about the conditions of assertibility, we ask about the conditions of refutability (cf. López-Escobar 1972). An example of a natural deduction rule whose conclusion is the falsity of a conjunction is the following

This rule is obtained by asking what would be sufficient conditions for refuting a conjunction. We now apply an analogous idea, asking what would be sufficient conditions for having evidence for the falsity of a conclusion. If \(\kappa \) is evidence that A is false, \(\kappa \) constitutes evidence that \(A \wedge B\) is false—mutatis mutandis for B. Analogous reasoning for \(\vee \) and \(\rightarrow \) gives the following introduction rules:

Elimination rules are obtained by applying the evidence inversion principle (EIP) mentioned above.

Indeed, let us take a look at rule \(\lnot \rightarrow E\). When \(\kappa \) is evidence that a formula \(A \rightarrow B\) is false, \(\kappa \) must also be evidence for the truth of the antecedent A and for the falsity of the consequent B.Footnote 10
The validity of double negation,

is perhaps not so clear as the other rules, but we claim that in both directions DN fits an intuitive notion of evidence. The rules above relate, in a perspicuous way, evidence that a proposition A is true and evidence that A is false. Suppose \(\kappa \) is evidence that A is true. It is reasonable to see \(\kappa \) as evidence that it is false that A is false. Now suppose, conversely, that \(\kappa \) is evidence that it is false that A is false. Again, it is reasonable that \(\kappa \) also constitutes evidence that A is true.
Let us call the logic defined by the rules DN, introduction and elimination for \(\rightarrow \), \(\vee \) and \(\wedge \), plus introduction and elimination for negated \(\rightarrow \), \(\vee \) and \(\wedge \), the Basic Logic of Evidence (BLE). BLE faithfully represents preservation of evidence when the latter is understood as reasons for believing the truth/falsity of propositions, as explained in Sect. 2 above.Footnote 11
Lemma 1
The following properties hold for BLE:
-
P1.
Reflexivity: if \(A\in \varGamma \), then \(\varGamma \vdash A\);
-
P2.
Monotonicity: if \(\varGamma \vdash B\), then \(\varGamma , A \vdash B\), for any A;
-
P3.
Transitivity (cut): if \(\varDelta \vdash A\) and \(\varGamma , A \vdash B\), then \(\varDelta ,\varGamma \vdash B\);
-
P4.
Deduction theorem: if \(\varGamma , A \vdash B\), then \(\varGamma \vdash A\rightarrow B\);
-
P5.
Compactness: if \(\varGamma \vdash A\), then there is \(\varDelta \subseteq \varGamma \), \(\varDelta \) finite such that \(\varDelta \vdash A\).
Proof
The properties P1, P2, P3 and P5 are direct consequences of the definition of a deduction of A from premises in \(\varGamma \). The deduction theorem (P4) amounts to the rule \(\rightarrow \)-introduction. \(\square \)
Since its consequence relation is reflexive, monotonic and transitive (properties P1, P2 and P3), BLE is thus a Tarskian or standard logic.
3.3 A semantics for BLE
Some logics allow for a semantics with an intuitive appeal independent of the corresponding deductive system. This is the case, for example, of the truth-tables for classical logic and the possible-worlds semantics for alethic modal logic. Indeed, these semantics do provide an insight into these logics because it really seems that the semantic clauses ‘make sense’ independently of the inference rules and/or axioms. And it is of course a relevant matter to show that the semantics and the deductive system are two different ways of determining the same set of valid inferences. On the other hand, the semantics to be presented here for BLEis not intended to have any intuitive appeal independent of the deductive system. Rather, such semantics should be seen as a mathematical tool capable of representing the inference rules in such a way that some technical results may be proved, not only for BLE but also for \(\textit{LET}_{J}\), an extension of BLE that will be seen in Sect. 4. The ‘meaning’ of the logic BLE is given by the fact that its rules preserve evidence.Footnote 12 In what follows, the values 0 and 1 are better seen as labels that intend to be faithful to the inference rules. Ascribed to a formula A, they mean, respectively, that A does not hold and that A holds. So, according to the explanation in terms of evidence given in Sect. 3,
-
\(v(A)=1\) means ‘there is evidence that A is true’;
-
\(v(A)=0\) means ‘there is no evidence that A is true’;
-
\(v(\lnot A)=1\) means ‘there is evidence that A is false’;
-
\(v(\lnot A)=0\) means ‘there is no evidence that A is false’.
The valuation semantics presented below is sound, complete, and yields a decision procedure for BLE.
Definition 2
A semivaluations for BLE is a function from the set S of formulas to \(\lbrace 0, 1 \rbrace \) such that:
-
1.
if \(s(A)=1\) and \(s(B)=0\), then \(s(A \rightarrow B)=0\);
-
2.
if \(s(B)=1\), then \(s(A \rightarrow B)=1\);
-
3.
\(s(A \wedge B)=1\) iff \(s(A)=1\) and \(s(B)=1\);
-
4.
\(s(A \vee B)=1\) iff \(s(A)=1\) or \(s(B)=1\);
-
5.
\(s(A) = 1\) iff \(s(\lnot \lnot A) = 1\);
-
6.
\(s(\lnot (A \wedge B)) = 1\) iff \(s(\lnot A) = 1\) or \(s(\lnot B) = 1\);
-
7.
\(s(\lnot (A \vee B)) = 1\) iff \(s(\lnot A) = 1\) and \(s(\lnot B) = 1\);
-
8.
\(s(\lnot (A \rightarrow B)) = 1\) iff \(s(A) = 1\) and \(s(\lnot B) = 1\);
Definition 3
A valuation for BLE is a semivaluation for which the condition below holds:
-
(Val) For all formulas of the form \(A_{1} \rightarrow (A_{2} \rightarrow \cdots \rightarrow (A_{n} \rightarrow B)\ldots )\) with B not of the form \(C \rightarrow D\):
if \(s(A_{1} \rightarrow (A_{2} \rightarrow \cdots \rightarrow (A_{n} \rightarrow B)\ldots )) = 0\), then there is a semivaluation \(s'\) such that for every i, \(1 \le i \le n\), \(s(A_{i})=1\) and \(s(B)=0\).
We say that a valuation v is a model of \(\varGamma \) (\(v \vDash \varGamma \)) if for all \(B \in \varGamma \), \(v(B)=1\); \(v \vDash A\) means that \(v(A)=1\). Logical consequence in BLE is defined as follows: \(\varGamma \vDash A\) if and only if for every valuation v, if v is a model of \(\varGamma \), then \(v(A) = 1\). It is also worth noting that this semantics shows that BLE is not compositional, in the sense that the semantic value of a complex formula is not functionally determined by the semantic values of its component parts. Indeed, this semantics may be represented by the so-called quasi-matrices.Footnote 13 Let us see an example below.
Example 4
\(A \vee (A \rightarrow B)\) is invalid in BLE.

The subformula \(A \rightarrow B \) receives 0 in the semivaluation \(s_{1}\). The latter is not excluded by condition Val (that is, it is a legitimate valuation) because there is a semivaluation s such that \(s(A)=1\) and \(s(B)=0\), namely, \(s_{4}\). Notice that the formula \(A \vee (A \rightarrow B)\), added to PIL, yields positive classical propositional logic.
The semantic clauses are intended to represent the deductive properties of the formal system in terms of the semantic values 0 and 1. It is not difficult to see a correspondence between the inference rules and the clauses 3–8 of Definition 2, for disjunction, conjunction and negation. The clauses for implication deserve some remarks. Implication is defined by clauses 1 and 2 of Definition 2 plus condition Val of Definition 3. Clause 1 expresses the fact that if \(v(A)=1\) and \(v(B)=0\), it cannot be that \(v(A \rightarrow B)=1\), since it would contradict modus ponens. Clause 2 expresses the fact that \(v(B)=1\) implies that \(v(A \rightarrow B)=1\). Clause Val establishes the equivalence between \(\varGamma , A \vDash B\) and \(\varGamma \vDash A \rightarrow B\). In order to see how this works, notice that without the clause Val we cannot guarantee the validity of \(\vDash A \rightarrow (B \rightarrow A)\).Footnote 14
Example 5
\(A\rightarrow (B\rightarrow A)\) is valid in BLE.

Some semivaluations at line 4 need to be excluded: \(s_{1}\) and \(s_{4}\) do not satisfy condition Val and therefore are not valuations. So, the formula receives 1 under every valuation (namely \(s_{2}\), \(s_{3}\), \(s_{5}\), \(s_{6}\) and \(s_{7}\)) and is thus valid.
3.3.1 Soundness
Theorem 6
If \(\varGamma \vdash A\), then \( \varGamma \vDash A\).
Proof
We show by induction on the length of a derivation D with premises in \(\varGamma \) and conclusion A, that \( \varGamma \vDash A\) holds.
Base if D has one element A, it means \(\lbrace A \rbrace \vdash A \). So, \(A \in \varGamma \), and \( \varGamma \vDash A\).
Inductive step For each rule, the inductive hypothesis says that there are sound derivations for the premise(s). The rest of the proof consists in showing that the derivation obtained by the application of the rule is sound. Details of this routine proof are left to the reader. \(\square \)
3.3.2 Completeness
Theorem 7
If \( \varGamma \vDash A\), then \(\varGamma \vdash A\).
Proof
Completeness is achieved by means of a Henkin-style proof. Suppose \(\varGamma \nvdash A\). An A-saturated set \(\varDelta \) is obtained from \(\varGamma \) by means of a Lindenbaum construction in the usual way. The following propositions, corresponding to clauses 1 to 8 of Definition 2 plus condition (Val) of Definition 3, can be proved:
- \((1')\) :
-
if \(A \in \varDelta \) and \(B \notin \varDelta \), then \(A \rightarrow B \notin \varDelta \);
- \((2')\) :
-
if \(B \in \varDelta \), then \(A \rightarrow B \in \varDelta \);
- \((3')\) :
-
\(A \wedge B \in \varDelta \) iff \(A \in \varDelta \) and \(B \in \varDelta \);
- \((4')\) :
-
\(A \vee B \in \varDelta \) iff \(A \in \varDelta \) or \(B \in \varDelta \);
- \((5')\) :
-
\(A \in \varDelta \) iff \(\lnot \lnot A \in \varDelta \);
- \((6')\) :
-
\(\lnot (A \wedge B) \in \varDelta \) iff \(\lnot A \in \varDelta \) or \(\lnot B \in \varDelta \);
- \((7')\) :
-
\(\lnot (A \vee B) \in \varDelta \) iff \(\lnot A \in \varDelta \) and \(\lnot B \in \varDelta \);
- \((8')\) :
-
\(\lnot (A \rightarrow B) \in \varDelta \) iff \(A \in \varDelta \) and \(\lnot B \in \varDelta \);
- \((Val')\) :
-
If \(\varDelta \) is A-saturated and \(A_{1} \rightarrow (A_{2} \rightarrow \cdots \rightarrow (A_{n} \rightarrow B)\ldots ) \notin \varDelta \), then there is a B-saturated set \(\varDelta '\) such that \(\varDelta \cup \lbrace A_{1}, A_{2}, \ldots A_{n} \rbrace \subseteq \varDelta '\).
The proofs of \((1')\) to \((8')\) are straightforward. In order to prove \((Val')\), suppose \(A_{1} \rightarrow (A_{2} \rightarrow \cdots \rightarrow (A_{n} \rightarrow B)\ldots ) \notin \varDelta \) and \(\varDelta \) is A-saturated. So, \(\varDelta \nvdash A_{1} \rightarrow (A_{2} \rightarrow \cdots \rightarrow (A_{n} \rightarrow B)\ldots )\), and consequently \(\varDelta \cup \lbrace A_{1}, A_{2}, \ldots A_{n} \rbrace \nvdash B\). A B-saturated set \(\varDelta '\) may be obtained from \(\varDelta \cup \lbrace A_{1}, A_{2}, \ldots A_{n} \rbrace \) by means of a Lindenbaum construction.
Consider now the characteristic function v of the set \(\varDelta \): in view of clauses \(1'\) to \(8'\) and \(Val'\), v is a valuation for BLE and v is a model for \(\varDelta \)Footnote 15. Since \(\varGamma \subseteq \varDelta \), v is also a model for \(\varGamma \). But \(v(A)=0\), so \(\varGamma \nvDash A\). By contraposition, completeness is thus obtained. \(\square \)
3.3.3 A decision procedure for BLE
In Examples 4 and 5 above we have seen how all possible valuations involved could be checked effectively by means of quasi-matrices. This depends essentially on the fact that in order to determine whether A follows from (finite) \(\varGamma \), it is enough to check a finite number of valuations involving only subformulas and negated subformulas of \(\varGamma \cup \{A\}\).
Theorem 8
Derivability in BLE is decidable.
Proof
From Lemma 1 item 5, derivability in BLE is compact. Given a derivation D of A from a (possibly infinite) set \(\varGamma \), there will always be a finite set \(\varGamma ^{0}\) such that \(\varGamma ^{0}\) contains precisely the hypotheses of D. Let \(Sub^{*}\) be the set of subformulas and negated subformulas of the formulas in \(\varGamma ^{0} \cup \{A\}\). The set \(Sub^{*}\) is finite, and a valuation depends on no more than the formulas in \(Sub^{*}\). Consequently, the corresponding quasi-matrix is finite. So, checking clauses 1–8 of Definition 2 and the clause Val of Definition 3 is clearly computable. Hence, in view of completeness and soundness, derivability in BLE is decidable. \(\square \)
There is also an interesting result about BLE that we call ‘grounding of contradictoriness’. Roughly, it says that there can be no contradiction at all, unless there is some contradiction in the atomic level.
Fact 9
A compound formula A is contradictory in a valuation v (i.e. \(v(A) = 1\) and \(v(\lnot A)=1\)) only if at least one atom p that occurs in A is contradictory in v.
Proof
Suppose there is a valuation v such that \(v(A) = v(\lnot A) = 1\). By induction on the complexity of A, we prove that there is at least one atom p that occurs in A such that \(v(p) = v(\lnot p) = 1\).
Base case\(A = p\). Clearly, \(v(A) = v(\lnot A) = v(p) = v(\lnot p) = 1\).
Inductive step We prove the case in which \(A = B \rightarrow C\).
Inductive hypothesis if \(v(B) = v(\lnot B) = 1\), then there is a p in B such that \(v(p) = v(\lnot p) = 1\); mutatis mutandis for C. Suppose \(v(B \rightarrow C) = v(\lnot (B \rightarrow C)) = 1\). So, by clauses 1 and 8 of Definition 2, \(v(B) = v(C) = v(\lnot C) = 1\). Now, apply the inductive hypothesis. We leave the remaining cases to the reader. \(\square \)
Notice, however, that the converse does not hold: there may be a contradictory atom p in a formula A without A being contradictory. Let A be the formula \(p \vee q\) and consider the valuation v such that \(v(p) = v(\lnot p) = 1\), \(v(q) = 1\) and \(v(\lnot q) = 0\). In this case, \(v(p \vee q) = 1\) but \(v(\lnot (p \vee q)) = 0\).
It is also worth noting that the dual of Fact 9 with respect to undetermined formulas does not hold: there may be compound formulas A and valuations v such that \(v(A) = 0\) and \(v(\lnot A)=0\), although there is no atom p in A such that \(v(p) = 0\) and \(v(\lnot p)=0\). For example, it may be that \(v(p \rightarrow q)=v(\lnot (p \rightarrow q)) = 0\) for \(v(p) = 0\), \(v(\lnot p)=1\), \(v(q) = 0\) and \(v(\lnot q)=1\) according to clauses 1 and 8 of Definition 2. In this aspect, BLE differs from intuitionistic logic.
Although it is almost obvious that BLE is equivalent of N4, for the sake of clarity we prove the fact below.
Fact 10
BLE is equivalent to Nelson’s logic N4.
Proof
The equivalence between N4 and BLE is straightforward from the natural deduction system for N4 presented by Wansing and Kamide (2015, Sect. 2.4). The latter slightly differs from the system we adopted in the negation rules (Sect. 3.2). Clearly, the rules \( \lnot \wedge I \), \( \lnot \vee I \), \( \lnot \rightarrow I \), \( \lnot \vee E \), \( \lnot \rightarrow E \) are respectively equivalent in each system. The only case deserving attention is the equivalence between Wansing and Kamide’s rule \( \lnot \wedge E \) (call it R1)

and ours (call it R2)

(i) In order to get R1 from R2, make \( C = \lnot A \vee \lnot B\). The latter is obtained from \( \lnot A \) (resp. \( \lnot B \)) by \( \vee I \):

(ii) On the other hand, we get R2 from R1 by means of obtaining C from \( \lnot A \vee \lnot B\) through \( \vee E \):

\(\square \)
4 A logic of evidence and truth
Although the logic BLE is able to express preservation of evidence, it is not able to express preservation of truth. However, in some contexts of reasoning we deal simultaneously with truth and evidence, that is, with propositions that we take as conclusively established as true or false, as well as others for which only non-conclusive evidence is available. On the other hand, classical logic gives a very good, maybe the best possible, account of truth preservation. Thus, we get a tool for dealing with such contexts of reasoning if we are able to restore classical logic for propositions for which there is conclusive evidence, that is, those we want to declare either true or false. If classical logic holds with respect to such propositions, we may express (with respect to them) the relation of truth-preservation. What we need is to add to BLE the means of recovering the properties of classical negation—or, more precisely, we need to restore the validity of explosion and excluded middle with respect to those formulas for which we want to recover classical logic. This will be made clear in what follows.
4.1 Logics of formal inconsistency and undeterminedness
The Logics of Formal Inconsistency (from now on, LFIs), are a family of paraconsistent logics able to express, inside the object language, the notions of ‘non-explosiveness’, ‘consistency’, or even ‘inconsistency’, as applied to formulas. This is done by means of adding a unary propositional connective \(\circ \) to the language, where \(\circ A\) means that A is consistent.Footnote 16
Explosion holds only with respect to propositions marked with \(\circ \), i.e. consistent (in some sense) propositions. Although explosion is not valid simpliciter in the sense that
-
for some \(\varGamma \), A and B: \(\varGamma , A, \lnot A \nvdash B\),
the following always holds:
-
for every \(\varGamma \), A and B: \(\varGamma , \circ A, A, \lnot A \vdash B \).
In any paraconsistent logic with few logical resources it cannot be that all contradictions are logically equivalent, otherwise the principle of explosion would hold. Indeed, suppose that for any A and B, \(A \wedge \lnot A \dashv \vdash B \wedge \lnot B\). Then, \(A \wedge \lnot A \vdash B \wedge \lnot B\), and by conjunction-elimination, \(A \wedge \lnot A \vdash B \). Rephrased contrapositively, this means that if a logic is paraconsistent, then it has some pairs of non-equivalent contradictions. This nonequivalence between contradictions fits the idea that in real-life contexts of reasoning some contradictions are more relevant than others. In such contexts, information contradicting a proposition that has been conclusively established as true is immediately rejected as false. Hence, it seems natural to have a connective able to distinguish ‘different kinds’ of contradictions, separating the contradictions that do not lead to explosion from those that do.
The idea that leads to the restriction of explosion—separating propositions into those for which some logical property holds and those for which it does not—is generalizable. In particular, excluded middle may be restricted in an analogous way. A Logic of Formal Undeterminedness (LFU) is a logic such that its language is extended by a new unary connective  , where
, where  means that A is (in some sense) determined.Footnote 17 Excluded middle does not hold, that is
means that A is (in some sense) determined.Footnote 17 Excluded middle does not hold, that is
-
for some \(\varGamma \), A and B: \(\varGamma , A \vdash B, \varGamma , \lnot A \vdash B \text{ but } \varGamma \nvdash B,\)
while the following always hold:
-
for every \(\varGamma \), A and B: if \( \varGamma , A \vdash B \text{ and } \varGamma , \lnot A \vdash B\), then
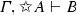 .
.
As we have seen above, it cannot be that all contradictions are equivalent in a paraconsistent logic. Similarly, in a paracomplete logic in which transitivity and \(\vee I\) hold (BLE for example), it cannot be that all instances of \(A \vee \lnot A\) are equivalent, otherwise excluded middle would be unconditionally valid. A proof of this follows. Let A be any theorem. Since \(A \vdash A \vee \lnot A\), if for any A and B, \(A \vee \lnot A \dashv \vdash B \vee \lnot B\), by transitivity it follows that \(A \vdash B \vee \lnot B\). As A is a theorem, we conclude \(\vdash B \vee \lnot B\). This, however, contradicts the definition of a paracomplete logic.
4.2 The logic \(\textit{LET}_{J}\)
An LFI and an LFU may be combined in an LFIU—a Logic of Formal Inconsistency and Undeterminedness. In a context that is at the same time paraconsistent and paracomplete, we may recover at once explosion and excluded middle with respect to a given formula A. Since consistency and determinateness are recovered simultaneously, we change the symbol  to \(\circ \). An LFIU is obtained by adding the following inference rules to the logic BLE:
to \(\circ \). An LFIU is obtained by adding the following inference rules to the logic BLE:

We call \(\textit{LET}_{J}\) the logic defined by the addition of \(EXP^{\circ }\) and \(PEM^{\circ }\) to BLE. The name \(\textit{LET}_{J}\) stands for ‘logic of evidence and truth based on positive intuitionistic propositional logic’. The language \(L_{1}\) of \(\textit{LET}_{J}\) is the language \(L_{0}\) of BLE plus the unary connective \(\circ \). The definition of the set \(S_{1}\) of formulas of \(L_{1}\), and the other definitions, are analogous. \(\textit{LET}_{J}\) enjoys properties P1 to P5 of Lemma 1, and is also a Tarskian logic. Notice that \(EXP^{\circ }\) and \(PEM^{\circ }\) may be considered elimination-rules for \(\circ \), but it is not by accident that there is no introduction-rule for \(\circ \) (we will return to this point soon).
In \(\textit{LET}_{J}\), the connective \(\circ \) works as a classicality operator in the sense that \(\circ A\) recovers classical logic for any formula that depends only on A and is formed with \(\lnot \), \(\wedge \), \(\rightarrow \) and \(\vee \) (see Fact 18 below). From ‘outside’ of the system, \(\circ A\) may be informally understood as saying that the truth-value of A has been (or may be) conclusively established. So,
-
‘\(\circ A \wedge A\) holds’ means ‘A is true’,
-
‘\(\circ A \wedge \lnot A\) holds’ means ‘A is false’.
It is important to emphasize that the particular way in which the truth or falsity of a proposition is going to be established is not a problem of logic. Truth comes from outside the formal system. The latter is no more than a tool that allows the recovering of classical consequence, and thus truth-preservation, with respect to some formulas. If classical logic holds for A, it cannot be the case that there is still conflicting evidence for A and for \(\lnot A\). If A has been established as true, any evidence for \(\lnot A\) is canceled (mutatis mutandis when A is false).
It is also worth noting that in \(\textit{LET}_{J}\) classical and paraconsistent logic coexist pacifically. \(\circ \) works like an indicator of a context switch: for formulas marked with \(\circ \) the context is classical, otherwise, the context is paraconsistent and paracomplete. There is, thus, no rivalry between classical and paraconsistent approaches, and this is made possible by the fact that, according to the proposed interpretation, classic and paraconsistent logics are ‘talking about different things’.
4.3 A semantics for \(\textit{LET}_{J}\)
In order to extend the semantics presented in Sect. 3.3 to \(\textit{LET}_{J}\) we need only to add the clause
-
9.
\(s(\circ A)=1\) implies [\(s(\lnot A)= 1\) iff \(s(A)=0\)]
to Definition 2. Clause 9 above says that if \(\circ A\) holds, we secure classical conditions for negation, but not the converse. Indeed, there may be a valuation such that \(s(\lnot A)= 1\) and \(s(A)=0\) (or vice-versa) but \(\circ A\) still does not hold. Informally, this is understood as saying that there may be evidence only for A, or only for \(\lnot A\), but such evidence is non-conclusive. The semantics so obtained is sound, complete, and yields a decision procedure for \(\textit{LET}_{J}\).
Theorem 11
Soundness and completeness: \( \varGamma \vDash _{\textit{LET}_{j}} A\) iff \(\varGamma \vdash _{\textit{LET}_{j}} A\).
Proof
In order to prove completeness, the proof of Sect. 3.3.2 is modified to include clause \(9'\) below:
- \(9'.\) :
-
\(\circ A \in \varDelta \) implies \(\lnot A \in \varDelta \) iff \(A \notin \varDelta \).
For soundness, it suffices to modify the proof of Sect. 3.3.1, showing that the rules \(EXP^{\circ }\) and \(PEM^{\circ }\) are sound with respect to clause 9 above. Details are left to the reader. \(\square \)
Theorem 12
Derivability in \(\textit{LET}_{J}\) is decidable.
Proof
The argument is similar to the proof of the decidability of BLE (Theorem 8). The set \(Sub^{*}\) is finite, so the number of valuations, and the quasi-matrices, are also finite. The only difference concerns clause 9 above. All checking procedures involved are clearly computable. Hence, in view of completeness and soundness, derivability in \(\textit{LET}_{J}\) is decidable. \(\square \)
4.4 Some facts about \(\textit{LET}_{J}\)
The logic \(\textit{LET}_{J}\) has features that fit the intuitive interpretation based on evidence and truth presented here. We show some of them below.
Fact 13
A bottom particle \(\bot \) (that is, a formula that by itself trivializes the system) is definable in \(\textit{LET}_{J}\).
Proof
Define \(\bot ~{\mathop {=}\limits ^{\text {{\tiny def }}}}~\circ A \wedge A \wedge \lnot A\). It can be proved in a few steps that \(\bot \vdash B\) for any B. \(\square \)
Fact 14
\(\textit{LET}_{J}\) has no trivial models, hence \(\textit{LET}_{J}\) does not prove \(\bot \).
Proof
Semantic clause 9 relates \(\circ \) and \(\lnot \) in such a way that trivial models are excluded. In other words, in \(\textit{LET}_{J}\) there is no valuation v such that for every formula A of \(L_{1}\), \(v(A) = 1\). As a consequence, given soundness, \(\textit{LET}_{J}\) does not prove \(\bot \), as defined in Fact 13. \(\square \)
The above result is the paraconsistent counterpart of the usual consistency proofs. Since triviality in paraconsistent logic is not equivalent to freedom from contradiction, the relevant result, tantamount to proving consistency (as freedom from contradiction) when the underlying logic is classical, is to prove that \(\bot \), or whatever would entail triviality, is not a theorem.
Fact 15
\(\lnot (A \wedge \lnot A)\) and \(A \vee \lnot A\) are logically equivalent in \(\textit{LET}_{J}\). But neither of them is logically equivalent to \(\circ A\).
Proof
Since DN (double negation) holds, \(A \vee \lnot A\) is equivalent to \(\lnot A \vee \lnot \lnot A\), and the latter, in its turn, is easily proved to be equivalent to \(\lnot (A \wedge \lnot A)\). In \(\textit{LET}_{J}\), \(\circ A \vdash \lnot (A \wedge \lnot A)\). Suppose \(\circ A\). So, \(A \vee \lnot A\). The latter implies \(\lnot A \vee \lnot \lnot A\), which is equivalent to \(\lnot (A \wedge \lnot A)\). To see that neither \(\lnot (A \wedge \lnot A)\) nor \(A \vee \lnot A\) implies \( \circ A \), take \(v(A) = 1\), \(v(\lnot A) = 0\) and \(v(\circ A) = 0\). \(\square \)
It is worth noting that the above non-equivalence fits the intuitive interpretation proposed here: it may be the case that \(\lnot (A \wedge \lnot A)\) holds even if \(\circ A\) does not hold. Accordingly, there may be a situation such that there is some non-conclusive evidence for the truth of A but no evidence for the falsity of A. In this case, \(v(\lnot (A \wedge \lnot A))=1\), although \(v(\circ A) = 0\), since the evidence available is non-conclusive. On the other hand, if \(v(\circ A) = 1\), there are only two possibilities: either \(v(A) = 1\) and \(v(\lnot A) = 0\), or \(v(A) = 0\) and \(v(\lnot A) = 1\).
Fact 16
The formulas \(A \wedge \lnot A\) and \(\circ (A \wedge \lnot A)\) jointly trivialize the consequence relation of \(\textit{LET}_{J}\).
Proof
\(A \wedge \lnot A\) implies \(\lnot A\). Applying \(\vee I\) we get \( A \vee \lnot A\), that is equivalent to \(\lnot (A \wedge \lnot A)\), and triviality follows from Fact 13, since \(A \wedge \lnot A\), \(\circ (A \wedge \lnot A)\) and \(\lnot (A \wedge \lnot A)\) define a bottom particle. \(\square \)
Given that according to the intuitive interpretation proposed here a true contradiction is expressed in \(\textit{LET}_{J}\) by \((A \wedge \lnot A) \wedge \circ (A \wedge \lnot A)\), the consequence relation of \(\textit{LET}_{J}\) trivializes in the presence of a true contradiction. Therefore, Fact 16 implies that \(\textit{LET}_{J}\) is anti-dialetheist in the sense that it cannot tolerate any true contradiction.
Fact 17
The logic \(\textit{LET}_{J}\) does not have any theorem of the form \(\circ A\).
Proof
The strategy of this proof is to show that \(\circ A\) is independent of the rules and therefore cannot be a consequence of the rules of \(\textit{LET}_{J}\). Consider for this purpose the following alternative semantics: for the connectives \(\vee \), \(\wedge \), \(\rightarrow \) and \(\lnot \), the classical conditions over \(\lbrace 0, 1\rbrace \); for \(\circ \), \(v(\circ A) = 0\) for any value of A. According to this semantics, no rule of \(\textit{LET}_{J}\) yields a conclusion with value 0 if all premises have value 1, that is, the rules are sound w.r.t. this new semantics. On the other hand, a formula \(\circ A\) receives 0 for any A. Hence, such a formula is independent of the rules, and cannot be proved in \(\textit{LET}_{J}\). \(\square \)
This result is in accordance with the intuitive idea that the attribution of \(\circ \) to a formula A may be done only from outside the formal system. It is the user of the system who establishes under which circumstances a formula may be marked with \(\circ \). That there is no introduction rule for \(\circ \) is an intentional limitation of the formal system. What constitutes evidence for a given proposition A, and whether or not such evidence is conclusive and A may be established as true, are problems that depend on the specific area of knowledge being dealt with. These problems must be kept outside the formal system.
Fact 18
If \(\circ A_{1}\), \(\circ A_{2}\), ...\(\circ A_{n}\) hold, then all formulas that depend only on \(A_{1}\), \(A_{2}\), ...\(A_{n}\) and are formed with \(\rightarrow \), \(\wedge \), \(\vee \) and \(\lnot \) behave according to classical logic.
Proof
Let \(A_{1}, A_{2}, \ldots A_{n}\) be any formulas and \(B = \phi (A_{1}, A_{2}, \ldots A_{n})\) be any composed formula formed by one or more formulas among \(A_{1}, A_{2}, \ldots A_{n}\) through \(\lnot \), \(\rightarrow \), \(\wedge \) and \(\vee \). We prove below by induction on the complexity of B that if \(\circ A_{1}, \circ A_{2}, \ldots \circ A_{n}\) hold, then the rules

hold. Therefore, all such formulas behave according to classical logic.
Base\(B = A_{i}\) (for any i). The proof is straightforward.
Inductive step
Case 1\(B = \lnot C\). We prove PEM. The inductive hypothesis is the rule below:

In order to prove that

holds, we need only an application of DN. The proof of EXP is left to the reader.
Case 2\(B = C \vee D\).
We prove EXP. The inductive hypothesis is:

The proof of PEM and the remaining cases (\(\wedge \) and \(\rightarrow \)) are left to the reader. \(\square \)
A corollary of Fact 18 is that once a formula A is marked with \(\circ \), no contradiction is allowed with respect to formulas with \(\lnot \), \(\vee \), \(\wedge \) and \(\rightarrow \) that depend only on A. However, from this, it does not follow that any formula that depends only on A is also marked with \(\circ \). Again, the point is that the attribution of \(\circ \) to any formula can be done only from outside the formal system. It must always be a proposition added to the theory at stake by means of non-logical means. Classicality does not propagate through the connectives.
It is also worth mentioning that a corollary of Fact 18 is a perspicuous form of a derivability adjustment theorem (DAT). The purpose of a DAT is to establish a relationship between two logics in the sense of restoring inferences that are lacking in one of them.Footnote 18 The basic idea is that we have to ‘add some information’ to the premises in order to restore the inferences that are otherwise lacking. The general form of a DAT is the following:
-
For all \(\varGamma \) and B, there is a \(\varDelta \) such that: \(\varGamma \vdash _{L} B\) iff \(\varGamma , \varDelta \vdash _{L*} B\).
Suppose that the logic L above is classical logic and \(L *\) is \(\textit{LET}_{J}\). The result above is tantamount to a DAT that specifies how classical logic may be recovered: the ‘information’ required (represented by the set \(\varDelta \)) consists of the atomic propositions that occur in \(\varGamma \), marked with \(\circ \).
5 On some issues related to paraconsistency as preservation of evidence
5.1 A remark on Restall’s approach to logical pluralism
What we have done here clearly indicates an approach to logical pluralism: different accounts of logical consequence may preserve different properties of propositions. We do not think that logical consequence has to be always identified with preservation of truth. Thus, classical, paracomplete (e.g. intuitionistic) and paraconsistent logics may be interpreted as being concerned with preservation of, respectively, truth, availability of a constructive proof (a notion stronger than truth) and availability of evidence (a notion weaker than truth).
Restall (2014) presents a proof-theoretic approach to logical pluralism in terms of different standards of proof based on the duality between paraconsistency and paracompleteness, a point also emphasized by us (see Carnielli and Rodrigues 2016). A detailed analysis of Restall’s arguments is outside the scope of this text. But his approach differs significantly from ours for two main reasons. First, as much as in Beall and Restall (2006), what is at stake in Restall (2014) is truth-preservation.Footnote 19 The same argument can be valid in one sense and invalid in another, but in both cases truth is the property of propositions being preserved (Restall 2014, p. 280). Second, although interesting from the technical point of view, Restall’s approach does not seem to be an attempt to represent inferences accepted in real-life argumentative scenarios.
The dual-intuitionistic logic in Restall (2014) is a paraconsistent logic obtained by restricting inference rules of classical sequent calculus in such a way that at most one formula occurs in the left hand side of a sequent (Restall 2014, p. 283). Restall’s approach sheds light on interesting features of the duality between paraconsistency and paracompleteness. But it is not clear that the paraconsistent logic so obtained really intends to correspond to real argumentative contexts. However, this does not make Restall’s dual-intuitionistic logic uninteresting; it just makes his approach different from ours. Instead, the approach to paraconsistency worked out here has tried, from the beginning, to find a way to interpret contradictions that appear in real-life contexts of reasoning. From the guiding question what does it mean to acceptAand\(\lnot A\)simultaneously without accepting their truth? we reached the notion of evidence. The next step was to find inference rules appropriate to express preservation of evidence.
The view we endorse w.r.t. the duality between paraconsistency and paracompleteness is that logics intended to represent real-life argumentative contexts have a common core (e.g. PIL) to which dual inference rules (and perhaps something else) are added. Excluded middle and explosion are dual inference rules in the sense that anything follows from \(A \wedge \lnot A\), while \(A \vee \lnot A\) follows from anything (see Carnielli and Rodrigues 2016, Sect. 2).
5.2 A remark on the problem of ‘just true, just false’
Under the intended interpretation, \(\textit{LET}_{J}\) is immune to the problem of ‘just true, just false’, faced by the so-called ‘glut-theorists’ (see, e.g. Beall 2013). We do not need to distinguish a scenario in which a formula A is just true (or just false) from a scenario in which A is both true and false because the latter is avoided in the intuitive interpretation proposed here: the simultaneous truth and falsity of A is expressed by \((A \wedge \circ A) \wedge (\lnot A \wedge \circ A)\), and this formula in \(\textit{LET}_{J}\) implies triviality. It may happen that in \(\textit{LET}_{J}\)A and \(\lnot A\) hold together, but only if \(\circ A\) does not—and in this case it does not mean that A is both true and false, but only that there is conflicting evidence w.r.t. A.
It is worth noting, however, that nothing a fortiori prevents the formal system of \(\textit{LET}_{J}\) of being interpreted differently, even in a dialetheist way. So, in such an alternative interpretation, it is remarkable that \(\textit{LET}_{J}\) would have the means to solve the problem of ‘just true, just false’ just by assuming that \(A \wedge \lnot A \) means that A is both true and false, while \(\circ A \wedge A\) (resp. \(\circ A \wedge \lnot A\)) means that A is only true (resp. only false).
5.3 Evidence versus constructive falsity
Nelson (1949), extending a proposal of Kleene (1945), suggested a constructive interpretation for the first-order number theory based on the formal system N of ‘constructible negation’. Nelson (1959) introduced a paraconsistent system called S (not yet the well-known N4), and remarked that “In both the intuitionistic and classical logic all contradictions are equivalent. This makes it impossible to consider such entities at all in mathematics” (Nelson 1959, p. 209, our emphasis). Later, Almukdad and Nelson proposed the logic \(N^-\), saying only that it is “a constructive logic which may be applied to inconsistent subject matter without necessarily generating a trivial theory” (Almukdad and Nelson 1984, p. 231). The difference between N and \(N^-\) is that explosion does not hold in the latter, but holds in the former. Following Odintsov (2003, 2008), the propositional fragments of Nelson’s logics N and \(N^-\) have been dubbed, respectively, as N3 and N4, and the latter became the standard presentation of Nelson’s paraconsistent logic.
The notion of realizability (Kleene 1945) can be understood as the formal side of the BHK interpretation of intuitionistic logic. Since in BHK the idea of proof is informal, the notion of realizability defines a formal notion of ‘proof’ by appealing to the notion of ‘realizers’ (see Rose 1953). The property of realizability is thus a kind of ‘intuitionistic notion of truth’ for intuitionistic number-theoretic statements. According to Kleene’s formulation, formulas of intuitionistic arithmetic are realized by (inductively defined) Gödel numbers of constants and of general recursive functions. Nelson (1949) extended Kleene’s approach, defining both a notion of ‘positive’ and ‘negative’ realizability. The latter adds a new feature to intuitionistic logic: formulas can also be constructively falsified.Footnote 20 So, Nelson’s motivation for proposing a constructive negation was to overcome non-constructive features of the intuitionistic negation. Indeed, negations in both N3 and N4 satisfy De Morgan’s laws, as well as the following meta-property:
It seems plausible, from the constructive viewpoint, that if \(A \wedge B\) has been proved false, then either a proof of the falsity of A or a proof of the falsity of B is available. The constructive negation of N3 (and, of course, of N4) may be also interpreted as refutability (see López-Escobar 1972). By treating constructive falsity independently of constructive truth, refutability becomes not complementary to provability—i.e. constructive falsity does not coincide with the complement of constructive truth (an ‘asymmetry’ similar to that between positive and negative evidence).
It is clear, thus, that Nelson was interested in constructive mathematics: this was the framework in which N3 and N4 were conceived. The motivation for BLE is quite different. Its inference rules have been established according to the question posed in Sect. 3: supposing the availability of evidence for the premises, we ask whether an inference rule yields a conclusion for which evidence is available.Footnote 21BLE expresses, as we have seen in Sect. 3, four different scenarios corresponding to positive evidence, absence of positive evidence, negative evidence and absence of negative evidence. On the other hand, the similarity between the intended interpretation of BLE and Nelson’s notion of constructive falsity lies in the fact that the notion of evidence for the falsity of A is not complementary to the notion of evidence for the truth of A: absence of evidence for falsity does not count as evidence for truth, and vice-versa. So, the notion of evidence for falsity is primitive in the sense that it does not coincide with the complement of evidence for truth.
BLE is not able to express, in the intended intuitive interpretation, a scenario in which the evidence for A is conclusive. This can be done by \(\textit{LET}_{J}\), by means of the classicality operator: \(A \wedge \circ A\) means that A holds and behaves classically. But in such a case, A is true—mutatis mutandis for the falsity of A, expressed in \(\textit{LET}_{J}\) by \(\lnot A \wedge \circ A\). That is precisely the point of \(\textit{LET}_{J}\): since the formulas marked with \(\circ \) behave classically, we may say that they are true (or false) and that there is conclusive evidence for their truth (or falsity). So, in \(\textit{LET}_{J}\), if \(\circ A\) holds, the notions of truth and falsity turn out to be complementary: either A is true, or A is false.
6 Final remarks
We have presented here an approach to paraconsistency that explicitly rejects dialetheism. According to the intended interpretation of \(\textit{LET}_{J}\), true contradictions are not allowed because they imply triviality (see remarks on Fact 16). There is no way to explain a context of reasoning in which a pair of propositions A and \(\lnot A\) simultaneously hold, without being dialetheist or metaphysically neutral, unless a property weaker than truth is attributed to A and \(\lnot A\). Our proposal here (our answer to question Q posed in Sect. 1) is that evidence, in the sense explained in the Sect. 2, may be such a property. Thus, the principle of explosion is rejected because a circumstance such that there is (non-conclusive) evidence for both A and \(\lnot A\), while there is no evidence for some proposition B, is completely feasible. This is an epistemic approach since evidence is an epistemic concept. But we can go one step further and say that our approach to paraconsistency is radically epistemic because true contradictions are not tolerated—as we have seen, they imply triviality as much as they do in classical logic.
We believe, however, that no philosophical, a priori argument can conclusively confirm or reject the claim that some aspects of reality need contradictory propositions in order to be described. In fact, ‘real contradictions’ seem to be quite impossible, but of course we cannot, and do not intend to, prove that. The intuitive interpretation proposed for the formal system \(\textit{LET}_{J}\) would fail if it were confirmed someday that real contradictions do exist. But in such an improbable scenario, a considerable part of science, and also of philosophy, would collapse altogether.
Notes
Although the dialetheist view has some antecedents in the history of philosophy, especially in Hegel and, according to some interpreters, also Heraclitus, the claim that there are ‘ontological contradictions’ is rather contentious, both inside and outside philosophy. It is not our aim here, however, to discuss the legitimacy of, nor argue against, dialetheism.
We defend this view in Carnielli and Rodrigues (2016). It is not unlikely that a view that accepts a non-constructive proof of the truth of a given proposition, but distinguishes such a proof from a (perhaps) more informative constructive proof, is the predominant approach to intuitionism nowadays (see Dubucs 2008).
BLE, although differently motivated, turns out to be equivalent to the well-known Nelson’s logic N4. (See also Sect. 5.3, and footnotes 11 and 21). All the technical results presented here with respect to BLE, including a valuation semantics and a decision method, also hold for N4. In a Fregian spirit, we may say that N4 and BLE are two different names, with different senses, that happen to have the same reference.
In van Benthem and Pacuit (2011) and van Benthem et al. (2015) we find a proposal of ‘evidence logics’, designed to give an account of “epistemic agents faced with possibly contradictory evidence from different sources”. Their approach is mainly semantical, in terms of ‘neighborhood semantics’ and differs from ours, motivated by proof-theoretical insights. The resulting logics proposed by them are quite different from both BLE and \(\textit{LET}_{J}\) presented here.
The logic of evidence proposed by us does not intend to represent cognitive relations between agents and propositions. It is not an account of any kind of propositional attitude. The idea is that there is some objective criterion that, when satisfied, indicates the existence of evidence for a proposition A. So, again, there can be evidence for A and an agent may be aware of such evidence and still does not believe in A. Evidence, thus, is not a name for the epistemic attitude of an agent w.r.t. a proposition. We say that our approach is epistemic because the property of propositions that is being preserved is an epistemic notion.
Melvin Fitting, in a forthcoming paper (Fitting 2017), proposes a formalization of the notion of evidence that includes an embedding of the logic BLE into the modal logic KX4, that is S4 minus \(\square A \rightarrow A\) plus \(\square \square A \rightarrow \square A\). In the well-known embedding of intuitionistic logic in S4, \(\square \) represents provability; dually, in the embedding of BLE into KX4, \(\square \) represents evidence which, in contrast to proof, permits contradictions.
The logic of evidence proposed by us is adjunctive because we want to express a notion of preservation of evidence for which \(\wedge \)-introduction holds in general. Suppose a document is (non-conclusive) evidence for the truth of A, i.e. such a document is evidence \(\kappa \) for A. Now, suppose that from another source comes another document that is (also non-conclusive) evidence for the falsity of A. The latter would be an evidence \(\kappa '\) for \(\lnot A\). We can, of course, put these two documents together, say, in a folder, or even merge them in an electronic file. These two pieces of evidence \(\kappa \) and \(\kappa '\) together are evidence that the conjunction \(A \wedge \lnot A\) is true. So, it is not the case that evidence for the latter fails when there is conflicting evidence for A. Such a situation, evidence for \(A \wedge \lnot A\), is nothing but an indication that further investigation is necessary. This is a central point of the non-dialetheist approach to paraconsistency proposed by us: it may be that evidence for a contradiction is available, but only as an indication that something is wrong and should be fixed.
A paraconsistent system in which explosion does not hold but \(A, \lnot A \vdash \lnot B\) holds is called partially explosive. An example of a partially explosive formal system is Kolmogorov’s ‘logic of judgment’ (see Kolmogorov 1925).
Notice that the negation rules exhibit a symmetry with respect to the corresponding assertion rules for the dual operators.
The rules for negation are the same as the rules for constructive falsity presented by Prawitz (1965, pp. 96–97). Although the guiding idea that led us to BLE is different, BLE can be easily proved equivalent to Nelson’s logic N4 (see Fact 10). Besides, BLE is also equivalent to the propositional fragment of refutability calculus presented by López-Escobar (1972).
In the so-called proof-theoretic semantics, the notion of proof is semantical in the sense that it gives the ‘meanings’ involved in the inferences of the formal system. Our approach has a similar spirit.
As far as we know, non-functional valuation semantics (and the respective quasi-matrices) for paraconsistent logics were presented for the first time by Costa and Alves (1977) where we find a sound and complete semantics for da Costa’s \(C_{1}\). The notion of semivaluation was introduced in Loparic (1986), where we find semantic clauses for an intuitionistic implication. In Loparic (1986) and Loparic (2010) we find adequate valuation semantics and decision procedures respectively for \(C_{\omega }\) and Heyting intuitionistic logic.
The conditions for implication are ‘global’ in the sense that one has to look at all semivaluations in order to establish whether a given semivaluation is a valuation.
Notice that v is a semivaluation that satisfies condition Val, given \(Val'\), and is thus a valuation.
The idea of expressing a metalogical notion within the object language is not new in the literature. It is found, e.g. in the \(C_{n}\) hierarchy introduced by da Costa (1963), through the idea of ‘well-behavedness’ of a formula. In da Costa’s hierarchy, however, this is done by means of a definition: in \(C_{1}\), for instance, it is expressed by \(A{}^{\circ }\), an abbreviation of \(\lnot (A\wedge \lnot A)\), which makes the ‘well-behavedness’ of A equivalent to saying that A is non-contradictory. On the other hand, in the LFIs, \(\circ A\) is introduced in such a way that allows \(\circ A\) and \(\lnot (A\wedge \lnot A)\) to be logically independent (non-equivalent). The family of LFIs incorporate a wide class of paraconsistent logics, as shown in Carnielli et al. (2007) and Carnielli and Coniglio (2016).
The notion of LFUs is introduced in Marcos (2005).
The account of logical pluralism given by Beall and Restall (2006) is based on preservation of truth, but it considers different types of cases: Tarskian models, constructions and situations that are, respectively, cases for classical, intuitionistic and relevant (i.e. paraconsistent) logics.
In Nelson (1949, p. 17), we read: “This notion of [constructive] truth will be made precise by defining a syntactical predicate ‘The natural number a P-realizes the formula A.’ At the same time a correlative concept of constructible falsity will be expressed by a predicate ‘The natural number a N-realizes the formula A’.”
The line of reasoning that lead to the logic BLE started in a modification in the logic mbC, an LFI presented in Carnielli et al. (2007). mbC is an extension of classical positive propositional logic, and excluded middle holds in mbC. In order to make mbC suitable for expressing contradictions as conflicting evidence, we presented in Carnielli and Rodrigues (2015) the logic mbCD, in which \(A \vee \lnot A\) has been replaced by the axiom \(\circ A \rightarrow (A \vee \lnot A)\), that corresponds to the rule \(PEM^\circ \). Then, in the search for a logic that could express preservation of evidence for both truth and falsity, we adopted the natural deduction system for PIL as the starting point, thus rejecting \(A \vee (A \rightarrow B)\), that holds in mbC, and we found out that, w.r.t. negation, natural deduction rules equivalent to De Morgan’s laws and double negation should hold, as well as the equivalence between \(\lnot (A \rightarrow B)\) and \(A \wedge \lnot B\). The logic so obtained is \(\textit{LET}_{J}\). BLE is \(\textit{LET}_{J}\) without the rules \(EXP^\circ \) and \(PEM^\circ \).
References
Achinstein, P. (2010a). Concepts of evidence. In Evidence, explanation, and realism. Oxford University Press.
Achinstein, P. (2010b). Why philosophical theories of evidence are (and ought to be) ignored by scientists. In Evidence, explanation, and realism. Oxford University Press.
Almukdad, A., & Nelson, D. (1984). Constructible falsity and inexact predicates. The Journal of Symbolic Logic, 49(1), 231–233.
Batens, D. (1989). Dynamic dialectical logics. In G. Priest, et al. (Eds.), Paraconsistent logic: Essays on the inconsistent (pp. 187–217). München: Philosophia Verlag.
Beall, J. (2013). Shrieking against gluts: The solution to the ‘just true’ problem. Analysis, 73(3), 438–445.
Beall, J. C., & Restall, G. (2006). Logical pluralism. Oxford: Oxford University Press.
Carnielli, W., & Rodrigues, A. (2016). Paraconsistency and duality: Between ontological and epistemological views. In P. Arazim and M. Dančák (Eds.), Logica yearbook 2015. College Publications.
Carnielli, W., & Coniglio, M. (2016). Paraconsistent logic: Consistency, contradiction and negation. New York: Springer.
Carnielli, W., Coniglio, M., & Marcos, J. (2007). Logics of formal inconsistency. In G. Gabbay (Ed.), Handbook of philosophical logic (Vol. 14). New York: Springer.
Carnielli, W., & Rodrigues, A. (2015). Towards a philosophical understanding of the logics of formal inconsistency. Manuscrito, 38, 155–184.
da Costa, N. (1963). Sistemas Formais Inconsistentes. Curitiba: Editora da UFPR.
da Costa, N. (1974). On the theory of inconsistent formal systems. Notre Dame Journal of Formal Logic, XV(4), 497–510.
da Costa, N., & Alves, E. H. (1977). A semantical analysis of the calculi Cn. Notre Dame Journal of Formal Logic, 18, 621–630.
da Costa, N., & French, S. (2003). Science and partial truth: A unitary approach to models and scientific reasoning. Oxford: Oxford University Press.
Dubucs, J. (2008). Truth and experience of truth. In M. van Atten, et al. (Eds.), One hundred years of intuitionism. Basel: Birkhäuser Verlag.
Fitting, M. (2017). Paraconsistent logic, evidence, and justification. Studia Logica, 105(6), 1149–1166.
Gentzen, G. (1935). Investigations into logical deduction. In M. E. Szabo (Ed.), The collected papers of Gerhard Gentzen. Amsterdam: North-Holland.
Kelly, T. (2014). Evidence. In: E.N. Zalta (Ed.) The Stanford encyclopedia of philosophy (Fall 2014). http://plato.stanford.edu/archives/fall2014/entries/evidence.
Kleene, S. (1945). On the interpretation of intuitionistic number theory. The Journal of Symbolic Logic, 10(4), 109–124.
Kolmogorov, A. (1925). On the principle of excluded middle. In J. van Heijenoort (Eds), From Frege to Gödel. Lincoln: toExcel Press.
Loparic, A. (1986). A semantical study of some propositional calculi. The Journal of Non-classical Logic, 3(1), 73–95.
Loparic, A. (2010). Valuation semantics for intuitionistic propositional calculus and some of its subcalculi. Principia, 14(1), 125–133.
López-Escobar, E. (1972). Refutability and elementary number theory. Indagationes Mathematicae, 34, 362–374.
Marcos, J. (2005). Nearly every normal modal logic is paranormal. Logique et Analyse, 48, 279–300.
Nelson, D. (1949). Constructible falsity. The Journal of Symbolic Logic, 14, 16–26.
Nelson, D. (1959). Negation and separation of concepts in constructive systems. In A. Heyting (Ed.), Constructivity in mathematics: Proceedings of the colloquium held at Amsterdam. Amsterdam: North-Holland.
Nickles, T. (2002). From Copernicus to Ptolemy: Inconsistency and method. In J. Meheus (Ed.), Inconsistency in Science. Dordrecht: Springer.
Odintsov, S. (2003). Algebraic semantics for paraconsistent Nelson’s logic. Journal of Logic and Computation, 13(4), 453–468.
Odintsov, S. (2008). Constructive negations and paraconsistency. New York: Springer.
Prawitz, D. (1965). Natural deduction: A proof-theoretical study. New York: Dover Publications.
Priest, G., & Berto, F. (2013). Dialetheism. In Stanford encyclopedia of philosophy. http://plato.stanford.edu/archives/sum2013/entries/dialetheism/.
Restall, G. (2014). Pluralism and proofs. Erkenntnis, 79, 279–291.
Rose, G. F. (1953). Propositional calculus and realizability. Transactions of the American Mathematical Society, 75, 1–19. http://www.ams.org/journals/tran/1953-075-01/S0002-9947-1953-0055952-4/home.html.
van Benthem, J., Fernández-Duque, D., & Pacuit, E. (2015) Evidence logic: A new look at neighborhood structures. http://www.aiml.net/volumes/volume9/Benthem-Fernandez-Duque-Pacuit.pdf.
van Benthem, J., & Pacuit, E. (2011). Dynamic logics of evidence-based beliefs. Studia Logica, 99, 61–92.
Wansing, H., & Kamide, N. (2015). Proof theory of N4-related paraconsistent logics. New York: College Publications.
Acknowledgements
We would like to thank Henrique Almeida, Antonio Coelho, Décio Krause and Wagner Sanz for some valuable comments on a previous version of this text. The first author acknowledges support from FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo, thematic project LogCons) and from a CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) research grant. The second author acknowledges support from FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais, research project 21308).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Carnielli, W., Rodrigues, A. An epistemic approach to paraconsistency: a logic of evidence and truth. Synthese 196, 3789–3813 (2019). https://doi.org/10.1007/s11229-017-1621-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-017-1621-7



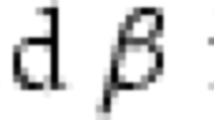

 .
.