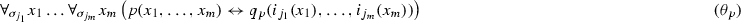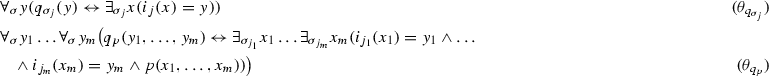Quine’s conjecture on many-sorted logic

Abstract

Quine often argued for a simple, untyped system of logic rather than the typed systems that were championed by Russell and Carnap, among others. He claimed that nothing important would be lost by eliminating sorts, and the result would be additional simplicity and elegance. In support of this claim, Quine conjectured that every many-sorted theory is equivalent to a single-sorted theory. We make this conjecture precise, and prove that it is true, at least according to one reasonable notion of theoretical equivalence. Our clarification of Quine’s conjecture, however, exposes the shortcomings of his argument against many-sorted logic.

1 Introduction

During the last century, an idea about the relationship between many-sorted logic and single-sorted logic became a piece of folklore. Many logicians endorsed the idea that many-sorted and single-sorted logic are mere “notational variants” of one another, and that the two frameworks have precisely the same expressive power. One particularly natural way to put this idea is as follows:

• Every many-sorted theory is equivalent to a single-sorted theory.

Quine was one of the most famous proponents of this claim.¹ For this reason, we call the claim Quine’s conjecture.

In this paper, we aim to capture the sense in which Quine’s conjecture is true. Although the basic idea behind the conjecture is clear, before proving it one needs to make precise what it might mean for two many-sorted theories to be “equivalent.” We consider two precise versions of Quine’s conjecture. We show that the first version of the conjecture is false, but we prove the second.

2 Preliminaries

We begin with some preliminaries about theories in many-sorted logic.² A signature $\Sigma$ is a set of sort symbols, predicate symbols, function symbols, and constant symbols. $\Sigma$ must contain at least one sort symbol, and the predicate, function, and constant symbols in $\Sigma$ are assigned arities constructed from the sorts in $\Sigma$. The only difference from the syntax of single-sorted logic is that the quantifiers $\forall _\sigma$ and $\exists _\sigma$ that appear in $\Sigma$-formulas must be indexed by sorts $\sigma \in \Sigma$.

Given a signature $\Sigma$, a $\mathbf {\Sigma }$ -theory T is a set of $\Sigma$-sentences. The sentences $\phi \in T$ are called the axioms of T. If the signature $\Sigma$ has only one sort symbol, then a $\Sigma$-theory T is called a single-sorted theory, while if $\Sigma$ has more than one sort symbol, then T is called a many-sorted theory. A $\Sigma$-structure M is a model of a $\Sigma$-theory T if $M\vDash \phi$ for all $\phi \in T$, where $\vDash$ is the standard notion of logical consequence. A theory T entails a sentence $\phi$, written $T\vDash \phi$, if $M\vDash \phi$ for every model M of T.

We begin with the following preliminary criterion for theoretical equivalence.

Definition

Theories $T_1$ and $T_2$ are logically equivalent if they have the same class of models.

One can verify that theories $T_1$ and $T_2$ are logically equivalent if and only if they entail precisely the same sentences. It is therefore easy to see that logical equivalence is too strict to capture any sense in which Quine’s conjecture is true. Theories can only be logically equivalent if they are formulated in the same signature, so no many-sorted theory is logically equivalent to a single-sorted theory.

Logical equivalence is a strict criterion for theoretical equivalence, so logicians and philosophers of science have proposed other more general criteria.³ We will begin by considering a criterion called definitional equivalence that was introduced into philosophy of science by Glymour (1971, 1977, 1980). In order to describe this criterion, we need to do some work.

Let $\Sigma \subset \Sigma ^+$ be signatures and let $p\in \Sigma ^+-\Sigma$ be a predicate symbol of arity $\sigma _1\times \cdots \times \sigma _n$. An explicit definition of p in terms of $\mathbf {\Sigma }$ is a $\Sigma ^+$-sentence of the form

$$\begin{aligned} \forall _{\sigma _1}x_1\ldots \forall _{\sigma _n}x_n\big (p(x_1, \ldots ,x_n)\leftrightarrow \phi (x_1,\ldots , x_n)\big ) \end{aligned}$$

where $\phi (x_1,\ldots , x_n)$ is a $\Sigma$-formula. Similarly, an explicit definition of a function symbol $f\in \Sigma ^+-\Sigma$ of arity $\sigma _1\times \cdots \times \sigma _n\rightarrow \sigma$ is a $\Sigma ^+$-sentence of the form

$$\begin{aligned} \forall _{\sigma _1}x_1\ldots \forall _{\sigma _n}x_n\forall _\sigma y\big ( f(x_1,\ldots , x_n)=y\leftrightarrow \phi (x_1,\ldots , x_n, y)\big ) \end{aligned}$$

(1)

and an explicit definition of a constant symbol $c\in \Sigma ^+-\Sigma$ of sort $\sigma$ is a $\Sigma ^+$-sentence of the form

$$\begin{aligned} \forall _\sigma x\big (x=c\leftrightarrow \psi (x)\big ) \end{aligned}$$

(2)

where $\phi (x_1,\ldots , x_n, y)$ and $\psi (x)$ are both $\Sigma$-formulas. Note that in all of these cases it must be that the sorts $\sigma _1,\ldots , \sigma _n, \sigma \in \Sigma$.

Although they are $\Sigma ^+$-sentences, (1) and (2) have consequences in the signature $\Sigma$. In particular, (1) and (2) imply the following sentences, respectively:⁴

$$\begin{aligned}&\forall _{\sigma _1}x_1\ldots \forall _{\sigma _n}x_n\exists _{\sigma =1}y\, \phi (x_1,\ldots , x_n, y)\\&\exists _{\sigma =1}x\,\psi (x) \end{aligned}$$

These two sentences are called the admissibility conditions for the explicit definitions (1) and (2).

We now have the resources necessary to describe the concept of a definitional extension. Let $\Sigma \subset \Sigma ^+$ be signatures and T a $\Sigma$-theory. A definitional extension of T to $\Sigma ^+$ is a $\Sigma ^+$-theory

$$\begin{aligned} T^+=T\cup \{\delta _s:s\in \Sigma ^+-\Sigma \} \end{aligned}$$

that satisfies the following two conditions. First, for each symbol $s\in \Sigma ^+-\Sigma$ the sentence $\delta _s$ is an explicit definition of s in terms of $\Sigma$, and second, if s is a constant symbol or a function symbol and $\alpha _s$ is the admissibility condition for $\delta _s$, then $T\vDash \alpha _s$.

One can think of a definitional extension of a theory as “saying no more” than the original theory (Barrett and Halvorson 2015b). It simply allows one to add “abbreviations” of old formulas to the theory. With this thought in mind, we can describe definitional equivalence.

Definition

Let $T_1$ be a $\Sigma _1$-theory and $T_2$ be a $\Sigma _2$-theory. $T_1$ and $T_2$ are definitionally equivalent if there are theories $T_1^+$ and $T_2^+$ that satisfy the following three conditions:

• $T_1^+$ is a definitional extension of $T_1$,

• $T_2^+$ is a definitional extension of $T_2$,

• $T_1^+$ and $T_2^+$ are logically equivalent $\Sigma _1\cup \Sigma _2$-theories.

One often says that $T_1$ and $T_2$ are definitionally equivalent if they have a “common definitional extension.” The intuition behind definitional equivalence is simple: $T_1$ and $T_2$ are definitionally equivalent if $T_1$ can define all of the vocabulary that $T_2$ uses, and in a compatible way, $T_2$ can define all of the vocabulary that $T_1$ uses. Definitional equivalence captures a sense in which two theories are “intertranslatable” (Barrett and Halvorson 2015a).

One can easily verify that definitional equivalence is a strictly weaker criterion than logical equivalence. Unlike logical equivalence, theories in different signatures can be definitionally equivalent. But definitional equivalence is still incapable of capturing any sense in which Quine’s conjecture is true. As we have described it, a definitional extension does not allow one to define new sorts. If $T_1$ and $T_2$ are definitionally equivalent, therefore, they must be formulated in signatures with the same sort symbols. So no many-sorted theory is definitionally equivalent to a single-sorted theory.

Fortunately, there are criteria for theoretical equivalence that are more general than definitional equivalence. The one that will be of particular interest to us is called Morita equivalence.⁵ Morita equivalence is a natural generalization of definitional equivalence. Indeed, it is essentially the same as definitional equivalence, but it allows one to define new sort symbols in addition to new predicate, function, and constant symbols.

The first version of Quine’s conjecture that we will consider is the following.

3 Quine’s conjecture 1

Every theory is Morita equivalent to a single-sorted theory.

In order to understand Quine’s conjecture 1, we need to carefully describe Morita equivalence. We begin by discussing how to define new sort symbols. Let $\Sigma \subset \Sigma ^+$ be signatures and consider a sort symbol $\sigma \in \Sigma ^+-\Sigma$. One can define the sort $\sigma$ as a product sort, a coproduct sort, a subsort, or a quotient sort. In each case one defines $\sigma$ using old sorts from $\Sigma$ and new function symbols from $\Sigma ^+-\Sigma$. These new function symbols specify how the new sort $\sigma$ is related to the old sorts in $\Sigma$. We describe in detail these four ways to define new sorts.

In order to define $\sigma$ as a product sort, one needs two function symbols $\pi _1,\pi _2\in \Sigma ^+-\Sigma$ with $\pi _1$ of arity $\sigma \rightarrow \sigma _1$, $\pi _2$ of arity $\sigma \rightarrow \sigma _2$, and $\sigma _1,\sigma _2\in \Sigma$. The function symbols $\pi _1$ and $\pi _2$ serve as the “canonical projections” associated with the product sort $\sigma$. An explicit definition of the symbols $\sigma , \pi _1$, and $\pi _2$ as a product sort in terms of $\Sigma$ is a $\Sigma ^+$-sentence of the form

$$\begin{aligned} \forall _{\sigma _1}x\forall _{\sigma _2} y\exists _{\sigma =1}z\big (\pi _1(z)=x\wedge \pi _2(z)=y\big ) \end{aligned}$$

One should think of a product sort $\sigma$ as the sort whose elements are ordered pairs, where the first element of each pair is of sort $\sigma _1$ and the second is of sort $\sigma _2$.

One can also define $\sigma$ as a coproduct sort. In this case, one needs two function symbols $\rho _1,\rho _2\in \Sigma ^+-\Sigma$ with $\rho _1$ of arity $\sigma _1\rightarrow \sigma$, $\rho _2$ of arity $\sigma _2\rightarrow \sigma$, and $\sigma _1,\sigma _2\in \Sigma$. The function symbols $\rho _1$ and $\rho _2$ are the “canonical injections” associated with the coproduct sort $\sigma$. An explicit definition of the symbols $\sigma , \rho _1$, and $\rho _2$ as a coproduct sort in terms of $\Sigma$ is a $\Sigma ^+$-sentence of the form

$$\begin{aligned} \forall _\sigma z\big (\exists _{\sigma _1=1}x(\rho _1(x)=z)\vee \exists _{\sigma _2=1} y(\rho _2(y)=z)\big ) \wedge \forall _{\sigma _1} x\forall _{\sigma _2} y\,\lnot \big (\rho _1(x) =\rho _2(y)\big ) \end{aligned}$$

One should think of a coproduct sort $\sigma$ as the disjoint union of the elements of sorts $\sigma _1$ and $\sigma _2$.

When defining a new sort $\sigma$ as a product sort or a coproduct sort, one uses two (not necessarily distinct) sort symbols $\sigma _1$ and $\sigma _2$ in $\Sigma$ and two function symbols in $\Sigma ^+-\Sigma$. The next two ways of defining a new sort $\sigma$ only require one sort symbol in $\Sigma$ and one function symbol in $\Sigma ^+-\Sigma$.

In order to define $\sigma$ as a subsort, one needs a function symbol $i\in \Sigma ^+-\Sigma$ of arity $\sigma \rightarrow \sigma _1$ with $\sigma _1\in \Sigma$. The function symbol i is the “canonical inclusion” associated with the subsort $\sigma$. An explicit definition of the symbols $\sigma$ and i as a subsort in terms of $\Sigma$ is a $\Sigma ^+$-sentence of the form

$$\begin{aligned} \forall _{\sigma _1}x\big (\phi (x)\leftrightarrow \exists _\sigma z(i(z)=x)\big ) \wedge \forall _\sigma z_1\forall _\sigma z_2\big (i(z_1)=i(z_2)\rightarrow z_1=z_2\big ) \end{aligned}$$

(3)

where $\phi (x)$ is a $\Sigma$-formula. One should think of $\sigma$ as “the things of sort $\sigma _1$ that are $\phi$.” The sentence (3) entails the following $\Sigma$-sentence:

$$\begin{aligned} \exists _{\sigma _1} x\, \phi (x) \end{aligned}$$

As above, we will call this $\Sigma$-sentence the admissibility condition for the definition (3).

Lastly, in order to define $\sigma$ as a quotient sort one needs a function symbol $\epsilon \in \Sigma ^+-\Sigma$ of arity $\sigma _1\rightarrow \sigma$ with $\sigma _1\in \Sigma$. An explicit definition of the symbols $\sigma$ and $\epsilon$ as a quotient sort in terms of $\Sigma$ is a $\Sigma ^+$-sentence of the form

$$\begin{aligned} \forall _{\sigma _1} x_1\forall _{\sigma _1}x_2\big (\epsilon (x_1)=\epsilon (x_2)\leftrightarrow \phi (x_1,x_2)\big ) \wedge \forall _\sigma z\exists _{\sigma _1}x(\epsilon (x)=z) \end{aligned}$$

(4)

where $\phi (x_1,x_2)$ is a $\Sigma$-formula. This sentence defines $\sigma$ as a quotient sort that is obtained by “quotienting out” the sort $\sigma _1$ with respect to the formula $\phi (x_1, x_2)$. The sort $\sigma$ should be thought of as the set of “equivalence classes of elements of $\sigma _1$ with respect to the relation $\phi (x_1,x_2)$,” and the function symbol $\epsilon$ is the “canonical projection” that maps an element to its equivalence class. And indeed, one can verify that the sentence (4) implies that $\phi (x_1,x_2)$ is an equivalence relation. In particular, (4) entails the following $\Sigma$-sentences:

$$\begin{aligned}&\forall _{\sigma _1}x\, \phi (x,x)\\&\forall _{\sigma _1}x_1\forall _{\sigma _1}x_2(\phi (x_1,x_2) \rightarrow \phi (x_2, x_1))\\&\forall _{\sigma _1}x_1\forall _{\sigma _1}x_2\forall _{\sigma _1} x_3\big ((\phi (x_1,x_2)\wedge \phi (x_2,x_3))\rightarrow \phi (x_1, x_3)\big ) \end{aligned}$$

These $\Sigma$-sentences are the admissibility conditions for the definition (4).

Now that we have described the four ways of defining new sort symbols, we can define the concept of a Morita extension. A Morita extension is a natural generalization of a definitional extension. The only difference is that now one is allowed to define new sort symbols. Let $\Sigma \subset \Sigma ^+$ be signatures and T a $\Sigma$-theory. A Morita extension of T to the signature $\Sigma ^+$ is a $\Sigma ^+$-theory

$$\begin{aligned} T^+=T\cup \left\{ \delta _s:s\in \Sigma ^+-\Sigma \right\} \end{aligned}$$

that satisfies the following three conditions. First, for each symbol $s\in \Sigma ^+-\Sigma$ the sentence $\delta _s$ is an explicit definition of s in terms of $\Sigma$. Second, if $\sigma \in \Sigma ^+-\Sigma$ is a sort symbol and $f\in \Sigma ^+-\Sigma$ is a function symbol that is used in the explicit definition of $\sigma$, then $\delta _f=\delta _\sigma$. (For example, if $\sigma$ is defined as a product sort with projections $\pi _1$ and $\pi _2$, then $\delta _\sigma =\delta _{\pi _1}=\delta _{\pi _2}$.) And third, if $\alpha _s$ is an admissibility condition for a definition $\delta _s$, then $T\vDash \alpha _s$.

A Morita extension of a theory again “says no more” than the original theory (Barrett and Halvorson 2015b). Like a definitional extension, it can be thought of simply as a way to add in “abbreviations” of old statements into the theory T. A Morita extension, however, allows one to abbreviate old statements using the apparatus of sorts, in addition to the apparatus of predicates, functions, and constant symbols. Our definition of Morita equivalence is perfectly analogous to definitional equivalence.

Definition

Let $T_1$ be a $\Sigma _1$-theory and $T_2$ a $\Sigma _2$-theory. $T_1$ and $T_2$ are Morita equivalent if there are theories $T_1^1, \ldots , T_1^n$ and $T_2^1,\ldots , T_2^m$ that satisfy the following three conditions:

• Each theory $T_1^{i+1}$ is a Morita extension of $T_1^{i}$,

• Each theory $T_2^{i+1}$ is a Morita extension of $T_2^i$,

• $T_1^n$ and $T_2^m$ are logically equivalent $\Sigma$-theories with $\Sigma _1\cup \Sigma _2\subset \Sigma$.

The intuition behind Morita equivalence is the same as that behind definitional equivalence: $T_1$ and $T_2$ are Morita equivalent if they each can, in compatible ways, define all of the vocabulary that the other uses.

One small clarification should be made about this definition. In order to show that two theories are Morita equivalent, one is allowed to take a finite number n of Morita extensions of $T_1$ and a finite number m of Morita extensions of $T_2$. One might wonder whether any generality is lost if we were to instead define Morita equivalence as follows:

• ($\star$) $T_1$ and $T_2$ are Morita equivalent if there are logically equivalent theories $T_1^+$ and $T_2^+$ that are Morita extensions of $T_1$ and $T_2$, respectively.

The following example shows that the proposal $(\star )$ is significantly less general than the standard definition of Morita equivalence provided above.

Example

Let $\sigma _1$ and $\sigma _2$ be sort symbols, with c a constant symbol of sort $\sigma _1$, d a constant symbol of sort $\sigma _2$, and i a function symbol of arity $\sigma _2\rightarrow \sigma _1$. We define the signatures $\Sigma _1=\{\sigma _1, c\}$, $\Sigma _2=\{\sigma _1, c, \sigma _2, i\}$, and $\Sigma _3=\{\sigma _1, c, \sigma _2, i, d\}$ and consider the following three theories:

$$\begin{aligned} T_1= & {} \emptyset \\ T_2= & {} \left\{ \forall _{\sigma _1}x\big (x=c\leftrightarrow \exists _{\sigma _2} y(i(y)=x)\big )\wedge \forall _{\sigma _2}y_1\forall _{\sigma _2}y_2 \big (i(y_1)=i(y_2)\rightarrow y_1=y_2\big )\right\} \\ T_3= & {} T_2\cup \left\{ \forall _{\sigma _2}y\big (y=d\leftrightarrow i(y)=c\big )\right\} \end{aligned}$$

It is easy to see that the $\Sigma _2$-theory $T_2$ is a Morita extension of the $\Sigma _1$-theory $T_1$, and that the $\Sigma _3$-theory $T_3$ is a Morita extension of $T_2$. The theory $T_2$ defines the sort $\sigma _2$ as a subsort containing just the “thing that is c,” and $T_3$ then defines the constant d in such a way that it applies to this new thing. So naturally, one would like to consider $T_1$ and $T_3$ equivalent. After all, $T_3$ is obtained from $T_1$ simply by defining some new vocabulary.

Although $T_1$ and $T_3$ are Morita equivalent according to the standard definition, they are not equivalent according to the proposal $(\star )$. The axiom of $T_3$ that defines d in terms of $\Sigma _2$ is not a definition of d in terms of $\Sigma _1$. And indeed, there simply is no definition of the constant symbol d in terms of $\Sigma _1$. Such a definition would have to be a sentence of the form $\forall _{\sigma _2}y\,(y=d\leftrightarrow \psi (y))$, where $\psi$ is a $\Sigma _1$-formula. This expression, however, is not well-formed. The constant d and variable y are of sort $\sigma _2$, which is not in $\Sigma _1$, so $\psi$ cannot be a $\Sigma _1$-formula. This means that there is no Morita extension of $T_1$ that defines the constant symbol d; it takes two Morita extensions of $T_1$ to define d.

The proposal $(\star )$ would therefore not be a satisfactory definition of Morita equivalence, so we use the standard definition for the remainder of this paper.

One can easily verify that Morita equivalence is a strictly weaker criterion than definitional equivalence. If two theories are definitionally equivalent, then they are Morita equivalent. But in general the converse does not hold. As the above example shows, theories can be Morita equivalent even if they are formulated in signatures with different sort symbols.

We now consider Quine’s conjecture 1 and show that it is false. The following theorem provides an example of a theory that is not Morita equivalent to any single-sorted theory.

Theorem 1

Let $\Sigma _1=\{\sigma _1,\sigma _2,\ldots \}$ be a signature containing a countable infinity of sort symbols. The $\Sigma _1$-theory $T_1=\emptyset$ is not Morita equivalent to any single-sorted theory.

The idea behind Theorem 1 is simple. One can think of the theory $T_1$ as saying the following: “Every element is either of kind$_1$ or of kind$_2$ or of kind$_3$ or..., no element is of more than one kind, and there is at least one element of every kind.” A single-sorted theory in first-order logic simply does not have the expressive power to say this. (In particular, it cannot express the first conjunct.) The theory $T_1$ should therefore not be Morita equivalent to any single-sorted theory. Before proving this we need a simple lemma and some notation.

Lemma

Let $\Sigma \subset \Sigma ^+$ be signatures and T a $\Sigma$-theory. Suppose that A is a model of T with $A_\sigma$ a finite set for every sort $\sigma \in \Sigma$. Let $T^+$ be a Morita extension of T to a signature $\Sigma ^+$ and $A^+$ a model of $T^+$ such that $A^+|_\Sigma =A$.⁶ Then $A^+_\sigma$ is a finite set for every $\sigma \in \Sigma ^+$.

Proof

Let $\sigma \in \Sigma ^+-\Sigma$ be a sort symbol. We show that $A^+_\sigma$ is a finite set in the cases where $\sigma$ is defined as a product sort or a subsort. If $T^+$ defines $\sigma$ as a product sort of $\sigma _1$ and $\sigma _2$, then $A^+_\sigma$ has exactly as many elements as $A_{\sigma _1}\times A_{\sigma _2}$, which is finite by assumption. If $T^+$ defines $\sigma$ as a subsort of $\sigma _1\in \Sigma$, then the cardinality of $A^+_\sigma$ is less than or equal to the cardinality of $A_{\sigma _1}$, which is also finite. The coproduct and quotient cases follow analogously. $\square$

Our proof of Theorem 1 will expedited by using the following simple category-theoretic machinery.⁷ A first-order theory T has a category of models. A category C is a collection of objects with arrows between the objects that satisfy two basic properties. First, there is an associative composition operation $\circ$ defined on the arrows of C, and second, every object c in C has an identity arrow $1_c:c\rightarrow c$. We will use the notation $\text {Mod}(T)$ to denote the category of models of T. An object in $\text {Mod}(T)$ is a model M of T, and an arrow $f:M\rightarrow N$ between objects in $\text {Mod}(T)$ is an elementary embedding $f:M\rightarrow N$ between the models M and N. One can easily verify that $\text {Mod}(T)$ is a category.

A functor $F:C\rightarrow D$ between categories C and D is a map from objects and arrows of C to objects and arrows of D that satisfies

$$\begin{aligned} F(f:a\rightarrow b)=Ff:Fa\rightarrow Fb\qquad F(1_c)=1_{Fc}\qquad F(g\circ h)=Fg\circ Fh \end{aligned}$$

for every arrow $f:a\rightarrow b$ in C, every object c in C, and every composable pair of arrows g and h in C. Functors are the “structure-preserving maps” between categories; they preserve domains, codomains, identity arrows, and the composition operation. A functor $F:C\rightarrow D$ is full if for all objects $c_1, c_2$ in C and arrows $g:Fc_1\rightarrow Fc_2$ in D there exists an arrow $f:c_1\rightarrow c_2$ in C with $Ff=g$. F is faithful if $Ff=Fg$ implies that $f=g$ for all arrows $f:c_1\rightarrow c_2$ and $g:c_1\rightarrow c_2$ in C. F is essentially surjective if for every object d in D there exists an object c in C such that $Fc\cong d$. A functor $F:C\rightarrow D$ that is full, faithful, and essentially surjective is called an equivalence of categories.

We now turn to the proof of Theorem 1.

Proof of Theorem 1

Suppose for contradiction that there is a single-sorted theory $T_2$ that is Morita equivalent to $T_1$. This means that $T_2$ is a $\Sigma _2$-theory with $\sigma \in \Sigma _2$ the unique sort symbol. Let T be the “common Morita extension” of $T_1$ and $T_2$ to a signature $\Sigma \supset \Sigma _1\cup \Sigma _2$. We consider the model A of $T_1$ defined by $A_{\sigma _i}=\{i, i'\}$ for each $i\in \mathbb {N}$. For every $i\in \mathbb {N}$ there is an isomorphism $f_i:A\rightarrow A$ that is the identity on $A_{\sigma _j}$ for $j\ne i$, but on $A_{\sigma _i}$ maps $f_i:i\mapsto i'$ and $f_i:i'\mapsto i$. The $f_i:A\rightarrow A$ are isomorphisms, and so are elementary embeddings. This implies that there are infinitely many arrows $f:A\rightarrow A$ in the category $\text {Mod}(T_1)$.

Since $T_1$ and $T_2$ are Morita equivalent, there is an equivalence of categories $F:\text {Mod}(T_1)\rightarrow \text {Mod}(T_2)$ such that for every model M of $T_1$

$$\begin{aligned} F(M)=M^+|_{\Sigma _2} \end{aligned}$$

for some model $M^+$ of T that is isomorphic to an expansion of M (Barrett and Halvorson 2015b, Theorem 5.1). We consider the model $A^+$ of T. The Lemma implies that $A^+_\sigma$ is a finite set. This implies that $F(A)_\sigma$ is a finite set. Since $\Sigma _2$ contains only the sort $\sigma$ and $F(A)_\sigma$ is finite, there can be at most finitely many arrows $g:F(A)\rightarrow F(A)$ in the category $\text {Mod}(T_2)$. But since F is an equivalence and therefore full and faithful, this cannot be the case. $\square$

Theorem 1 immediately implies that Quine’s conjecture 1 is false. It is not the case that every many-sorted theory is Morita equivalent to a single-sorted theory. This disproof of Quine’s conjecture 1, however, suggests the following slight modification of the conjecture.

4 Quine’s conjecture 2

If $\Sigma$ is a signature with finitely many sorts, then every $\Sigma$ -theory is Morita equivalent to a single-sorted theory.

This second version of Quine’s conjecture is true. One proves Quine’s conjecture 2 by explicitly constructing a “corresponding” single-sorted theory ${\widehat{T}}$ for every many-sorted theory T. The basic idea behind the construction is intuitive. The theory ${\widehat{T}}$ simply replaces the sort symbols that the theory T uses with predicate symbols.⁸ It takes some work, however, to make this idea precise.

Let $\Sigma$ be a signature with finitely many sort symbols $\sigma _1,\ldots , \sigma _n$. We begin by constructing a corresponding signature ${\widehat{\Sigma }}$ that contains one sort symbol $\sigma$. The symbols in ${\widehat{\Sigma }}$ are defined as follows. For every sort symbol $\sigma _j\in \Sigma$ we let $q_{\sigma _j}$ be a predicate symbol of sort $\sigma$. For every predicate symbol $p\in \Sigma$ of arity $\sigma _{j_1}\times \cdots \times \sigma _{j_m}$ we let $q_p$ be a predicate symbol of arity $\sigma ^m$ (the m-fold product of $\sigma$). Likewise, for every function symbol $f\in \Sigma$ of arity $\sigma _{j_1}\times \cdots \times \sigma _{j_m}\rightarrow \sigma _j$ we let $q_f$ be a predicate symbol of arity $\sigma ^{m+1}$. And lastly, for every constant symbol $c\in \Sigma$ we let $d_c$ be a constant symbol of sort $\sigma$. The single-sorted signature ${\widehat{\Sigma }}$ corresponding to $\Sigma$ is then defined to be

$$\begin{aligned} {\widehat{\Sigma }}=\{\sigma \}\cup \{q_{\sigma _1},\ldots , q_{\sigma _n}\}\cup \{q_p: p\in \Sigma \}\cup \{q_f: f\in \Sigma \}\cup \{d_c: c\in \Sigma \} \end{aligned}$$

We can now describe a method of “translating” $\Sigma$-theories into ${\widehat{\Sigma }}$-theories. Let T be an arbitrary $\Sigma$-theory. We define a corresponding ${\widehat{\Sigma }}$-theory ${\widehat{T}}$, and then show that ${\widehat{T}}$ is Morita equivalent to T.

We begin by translating the axioms of T into the signature ${\widehat{\Sigma }}$. This will take two steps. First, we describe a way to translate the $\Sigma$-terms into ${\widehat{\Sigma }}$-formulas. Given a $\Sigma$-term $t(x_1,\ldots , x_n)$, we define the ${\widehat{\Sigma }}$-formula ${\widehat{\psi }}_t(y_1,\ldots , y_n, y)$ recursively as follows.

• If $t(x_1,\ldots , x_n)$ is the variable $x_i$, then ${\widehat{\psi }}_t$ is the ${\widehat{\Sigma }}$-formula $y_i=y$.

• If $t(x_1,\ldots , x_n)$ is the constant c, then ${\widehat{\psi }}_t$ is the ${\widehat{\Sigma }}$-formula $d_{c}=y$.

• Suppose that $t(x_1,\ldots , x_n)$ is the term $f(t_1(x_1,\ldots , x_n),\ldots , t_k(x_1,\ldots , x_n))$ and that each of the ${\widehat{\Sigma }}$-formulas ${\widehat{\psi }}_{t_i}(y_1,\ldots , y_n, y)$ have been defined. Then ${\widehat{\psi }}_t(y_1,\ldots , y_n, y)$ is the ${\widehat{\Sigma }}$-formula

  $$\begin{aligned} \exists _{\sigma }z_1\ldots \exists _\sigma z_k\big ({\widehat{\psi }}_{t_1}(y_1,\ldots , y_n, z_1)\wedge \ldots \wedge {\widehat{\psi }}_{t_k}(y_1,\ldots , y_n, z_k)\wedge q_{f}(z_1,\ldots , z_k, y)\big ) \end{aligned}$$

One can think of the formula $\psi _t(y_1,\ldots , y_n, y)$ as the translation of the expression “$t(x_1,\ldots , x_n)=x$” into the signature ${\widehat{\Sigma }}$.

Second, we use this map from $\Sigma$-terms to ${\widehat{\Sigma }}$-formulas to describe a map from $\Sigma$-formulas to ${\widehat{\Sigma }}$-formulas. Given a $\Sigma$-formula $\psi (x_1,\ldots , x_n)$, we define the ${\widehat{\Sigma }}$-formula ${\widehat{\psi }}(y_1,\ldots , y_n)$ recursively as follows.

• If $\psi (x_1,\ldots , x_n)$ is $t(x_1,\ldots , x_n) =s(x_1,\ldots , x_n)$, where s and t are $\Sigma$-terms of sort $\sigma _i$, then ${\widehat{\psi }}(y_1,\ldots , y_n)$ is the ${\widehat{\Sigma }}$-formula

  $$\begin{aligned} \exists _\sigma z\big ({\widehat{\psi }}_{t}(y_1,\ldots , y_n, z)\wedge {\widehat{\psi }}_{s}(y_1,\ldots , y_n, z)\wedge q_{\sigma _i}(z)\big ) \end{aligned}$$

• If $\psi (x_1,\ldots , x_n)$ is $p(t_1(x_1,\ldots , x_n),\ldots , t_k(x_1,\ldots , x_n))$, where $p\in \Sigma$ is a predicate symbol, then ${\widehat{\psi }}(y_1,\ldots , y_n)$ is the ${\widehat{\Sigma }}$-formula

  $$\begin{aligned} \exists _\sigma z_1\ldots \exists _\sigma z_k\big ({\widehat{\psi }}_{t_1}(y_1,\ldots , y_n, z_1)\wedge \ldots \wedge {\widehat{\psi }}_{t_k}(y_1,\ldots , y_n, z_k)\wedge q_{p}(z_1,\ldots , z_k)\big ) \end{aligned}$$

• This definition extends to all $\Sigma$-formulas in the standard way. We define the ${\widehat{\Sigma }}$-formulas ${\widehat{\lnot \psi }}:=\lnot {{\widehat{\psi }}}$, ${\widehat{\psi _1\wedge \psi _2}}:={\widehat{\psi _1}} \wedge {\widehat{\psi _2}}$, ${\widehat{\psi _1\vee \psi _2}}:={\widehat{\psi _1}} \vee {\widehat{\psi _2}}$, and ${\widehat{\psi _1\rightarrow \psi _2}}:={\widehat{\psi _1}} \rightarrow {\widehat{\psi _2}}$. Furthermore, if $\psi (x_1,\ldots , x_n, x)$ is a $\Sigma$-formula, then we define both of the following:

  $$\begin{aligned} {\widehat{\forall _{\sigma _i}} x \psi }&{:}{=}&\forall _\sigma y(q_{\sigma _i} (y)\rightarrow {\widehat{\psi }}(y_1,\ldots , y_n, y))\\ {\widehat{\exists _{\sigma _i} x\psi }}&{:}{=}&\exists _\sigma y(q_{\sigma _i} (y)\wedge {\widehat{\psi }}(y_1,\ldots , y_n, y)) \end{aligned}$$

One should think of the formula ${\widehat{\psi }}$ as the translation of the $\Sigma$-formula $\psi$ into the signature ${\widehat{\Sigma }}$.

This allows us to consider the translations ${\widehat{\alpha }}$ of the axioms $\alpha \in T$. The single-sorted theory ${\widehat{T}}$ will have the ${\widehat{\Sigma }}$-sentences ${\widehat{\alpha }}$ as some of its axioms. But ${\widehat{T}}$ will have more axioms than just the sentences ${\widehat{\alpha }}$. It will also have some auxiliary axioms. These auxiliary axioms will guarantee that the symbols in ${\widehat{\Sigma }}$ “behave like” their counterparts in $\Sigma$. We define auxiliary axioms for the predicate symbols $q_{\sigma _1},\ldots , q_{\sigma _n}\in {\widehat{\Sigma }}$, $q_{p}\in {\widehat{\Sigma }}$, and $q_f\in {\widehat{\Sigma }}$, and for the constant symbols $d_c\in {\widehat{\Sigma }}$. We discuss each of these four cases in detail.

We first define auxiliary axioms to guarantee that the symbols $q_{\sigma _1},\ldots , q_{\sigma _n}$ behave like sort symbols. The ${\widehat{\Sigma }}$-sentence $\phi$ is defined to be $\forall _\sigma y(q_{\sigma _1}(y)\vee \ldots \vee q_{\sigma _n}(y))$.⁹ Furthermore, for each sort symbol $\sigma _j\in \Sigma$ we define the ${\widehat{\Sigma }}$-sentence $\phi _{\sigma _j}$ to be

$$\begin{aligned} \exists _\sigma y (q_{\sigma _j}(y))\wedge \forall _\sigma y \big (q_{\sigma _j}(y)&\rightarrow (\lnot q_{\sigma _1}(y)\wedge \ldots \wedge \lnot q_{\sigma _{j-1}}(y)\\&\quad \,\wedge \lnot q_{\sigma _{j+1}}(y)\wedge \ldots \wedge \lnot q_{\sigma _n}(y))\big ) \end{aligned}$$

One can think of the sentences $\phi _{\sigma _1},\ldots , \phi _{\sigma _n}$, and $\phi$ as saying that “everything is of some sort, nothing is of more than one sort, and every sort is nonempty.”

Next we define auxiliary axioms to guarantee that the symbols $q_p$, $q_f$, and $d_c$ behave like their counterparts p, f, and c in $\Sigma$. For each predicate symbol $p\in \Sigma$ of arity $\sigma _{j_1}\times \cdots \times \sigma _{j_m}$, we define the ${\widehat{\Sigma }}$-sentence $\phi _{p}$ to be

$$\begin{aligned} \forall _\sigma y_1\ldots \forall _\sigma y_m\left( q_{p}(y_1,\ldots , y_m)\rightarrow \left( q_{\sigma _{j_1}}(y_1)\wedge \ldots \wedge q_{\sigma _{j_m}}(y_m)\right) \right) \end{aligned}$$

This sentence restricts the extension of $q_p$ to the subdomain of n-tuples satisfying $q_{\sigma _{j_1}},\dots ,q_{\sigma _{j_m}}$, guaranteeing that the predicate $q_p$ has “the appropriate arity.” Consider, for example, the case of a unary predicate p of sort $\sigma _i$. In that case, $\phi _p$ says that

$$\begin{aligned} \forall _\sigma y (q_p(y)\rightarrow q_{\sigma _i}(y)) , \end{aligned}$$

which means that nothing outside the subdomain $q_{\sigma _i}$ satisfies $q_p$. Note, however, that here we have made a conventional choice. We could just as well have stipulated that $q_p$ applies to everything outside of the subdomain $q_{\sigma _i}$. All that matters here is that $q_p$ is trivial (either trivially true, or trivially false) except on the subdomain of objects satisfying $q_{\sigma _i}$.

For each function symbol $f\in \Sigma$ of arity $\sigma _{j_1}\times \cdots \times \sigma _{j_m}\rightarrow \sigma _j$ we define the ${\widehat{\Sigma }}$-sentence $\phi _{f}$ to be the conjunction

$$\begin{aligned}&\forall _\sigma y_1\ldots \forall _\sigma y_m \forall _\sigma y\big (q_{f}(y_1,\ldots , y_m, y)\rightarrow (q_{\sigma _{j_1}}(y_1)\wedge \ldots \wedge q_{\sigma _{j_m}}(y_m)\wedge q_{\sigma _j}(y))\big )\\&\quad \wedge \forall _\sigma y_1\ldots \forall _\sigma y_m\big ((q_{\sigma _{j_1}}(y_1)\wedge \ldots \wedge q_{\sigma _{j_m}}(y_m))\rightarrow \exists _{\sigma =1} y(q_{f}(y_1,\ldots , y_m, y))\big ) \end{aligned}$$

The first conjunct guarantees that the symbol $q_{f}$ has “the appropriate arity,” and the second conjunct guarantees that $q_f$ behaves like a function. Lastly, if $c\in \Sigma$ is a constant symbol of arity $\sigma _j$, then we define the ${\widehat{\Sigma }}$-sentence $\phi _{c}$ to be $q_{\sigma _j}(d_{c})$. This sentence guarantees that the constant symbol $d_{c}$ also has “the appropriate arity.”

We now have the resources to define a ${\widehat{\Sigma }}$-theory ${\widehat{T}}$ that is Morita equivalent to T.

$$\begin{aligned} {\widehat{T}}=\{{\widehat{\alpha }}: \alpha \in T\}&\cup \{\phi , \phi _{\sigma _1},\ldots ,\phi _{\sigma _n}\}\\&\cup \{\phi _{p}: p\in \Sigma \}\\&\cup \{\phi _{f}: f\in \Sigma \}\\&\cup \{\phi _{c}: c\in \Sigma \} \end{aligned}$$

The theory ${\widehat{T}}$ has two kinds of axioms, the translated axioms of T and the auxiliary axioms. These axioms allow ${\widehat{T}}$ to imitate the theory T in the signature ${\widehat{\Sigma }}$. Indeed, one can prove the following result.

Theorem 2

The theories T and ${\widehat{T}}$ are Morita equivalent.

The proof of Theorem 2 requires some work, and has therefore been placed in an appendix. But the idea behind the proof is simple. The theory T needs to define symbols in ${\widehat{\Sigma }}$. It defines the sort symbol $\sigma$ as a “universal sort,” by taking the coproduct of the sorts $\sigma _1,\ldots , \sigma _n\in \Sigma$. The theory T then defines the symbols $q_p$, $q_f$, and $d_c$ in ${\widehat{\Sigma }}$ simply by using the corresponding symbols p, f, and c in $\Sigma$. Likewise, the theory ${\widehat{T}}$ needs to define the symbols in $\Sigma$. It defines the sort symbol $\sigma _j$ as the subsort of “things that are $q_{\sigma _j}$” for each $j=1,\ldots , n$. And ${\widehat{T}}$ defines the symbols p, f, and c again by using the corresponding symbols $q_p$, $q_f$, and $d_c$.

Since the theory T was arbitrary, Theorem 2 immediately implies that Quine’s conjecture 2 is true.

5 Philosophical implications

Our proof of Quine’s conjecture 2 substantiates Quine’s original thought about the relationship between many-sorted logic and single-sorted logic. It captures a precise sense in which single-sorted logic has exactly the same expressive power as (finitely) many-sorted logic.

In capturing this relationship, our results provide a reason to prefer Morita equivalence over definitional equivalence. The original motivation for taking definitional equivalence as the standard for theoretical equivalence is intuitive: Definitional equivalence captures a sense in which two theories are intertranslatable. If $T_1$ and $T_2$ are definitionally equivalent, then there are two precise ways to translate between the theories.

• The first way of translating between $T_1$ and $T_2$ is purely syntactic. Formulas of $T_1$ can be translated into the signature of $T_2$, and vice versa, and these translations have some nice features. In particular, theorems are translated into theorems, and the two translations are “almost inverse” to one another (Barrett and Halvorson 2015a, Theorem 1).¹⁰

• The second way of translating is semantic. Models of $T_1$ can be translated into models of $T_2$, and vice versa, and these translations also have some nice features. In particular, the two translations induce a categorical equivalence between the categories of models of the two theories (Barrett and Halvorson 2015b, Theorems 3.1 and 5.1).

Morita equivalence also captures a sense in which two theories are intertranslatable. Indeed, if two theories are Morita equivalent, then one can again translate formulas and convert models between them (Barrett and Halvorson 2015b, Theorems 4.3 and 5.1).

The motivation for taking definitional equivalence as the standard for theoretical equivalence therefore carries over to Morita equivalence. But our results show that Morita equivalence has a virtue that definitional equivalence lacks. In particular, if one follows Glymour (1971, 1977, 1980) in taking definitional equivalence as the standard for theoretical equivalence, then one cannot recover any sense in which Quine’s conjecture is true. If one wants to substantiate Quine’s conjecture and capture the relationship between the many-sorted and single-sorted frameworks, one needs to move to Morita equivalence.

Our discussion also yields a cautionary remark concerning a particular argument of Quine’s. One might be tempted to conclude from Theorem 2 that many-sorted logic is dispensable. In fact, this is precisely the conclusion that Quine himself drew. Quine says that explicitly naming sorts and specifying the sorts of the vocabulary in the signature of a theory is an “artificial device” (Quine and Carnap 1990, p. 409), and that we are licensed to ignore it. He sums up his negative stance on many-sorted logic as follows:

All in all, I find an overwhelming case for a single unpartitioned universe of values of bound variables, and a simple grammar of predication which admits general terms all on an equal footing. Subsidiary distinctions can still be drawn as one pleases, both on methodological considerations and on considerations of natural kind; but we may think of them as distinctions special to the sciences and unreflected in the structure of our notation (Quine 1960, p. 229).¹¹

Quine’s reasoning here may be seductive, but it is nonetheless misleading. We have shown that for each theory T in a signature $\Sigma$ with finitely many sorts, there is a Morita equivalent single-sorted theory ${\widehat{T}}$. This result does not imply that we can ignore sorts altogether. There are a number of reasons for this.

First, Quine’s argument against many-sorted logic is circular. It relies on a theorem that can only be stated in the framework of many-sorted logic. In capturing the sense in which Quine’s conjecture is true, one employs Morita equivalence, a standard of equivalence that is itself inherently many-sorted. If one does away with the many-sorted framework altogether, one can no longer capture this equivalence; the single-sorted framework simply does not provide one with a criterion for equivalence that is capable of substantiating Quine’s conjecture.

The many-sorted framework simply allows us to better recognize the variety of ways in which theories might be equivalent. For example, one might want to consider Euclidean geometry formulated using lines to be equivalent to Euclidean geometry formulated using points. Although both of these theories are single-sorted, the single-sorted framework does not allow one to consider them equivalent. With Morita equivalence in hand, however, the many-sorted framework does allow one capture this equivalence (Barrett and Halvorson 2016). The issue here is that two single-sorted theories might have different sorts, in which case there is a non-trivial question about whether these sorts can be defined from each other. One theory’s single sort might, for example, be definable as a product of another theory’s single sort. In particular, this means that two single-sorted theories can be Morita equivalent even if they are not definitionally equivalent. The following simple example serves to illustrate this fact.

Example

Consider the signatures $\Sigma _1=\{\sigma _1\}$ and $\Sigma _2=\{\sigma _2, p\}$, where $\sigma _1$ and $\sigma _2$ are sort symbols, and p is a unary predicate of sort $\sigma _2$. We define the following two theories.

$$\begin{aligned} T_1= & {} \{\exists _{\sigma _1=1}x\,(x=x)\}\\ T_2= & {} \{\exists _{\sigma _2=2}y\,(y=y), \exists _{\sigma _2=1}y\,p(y)\} \end{aligned}$$

The $\Sigma _1$-theory $T_1$ says “there is only one thing”, while the $\Sigma _2$-theory $T_2$ says “there are exactly two things, the first is p, and the second is $\lnot p$.” These two theories are Morita equivalent. In order to prove this, one shows that $T_1$ can define all of the symbols that $T_2$ uses, and vice versa. The theory $T_1$ defines the sort symbol $\sigma _2$ as the coproduct of the sort $\sigma _1$ with itself, and then defines the predicate p to hold of the element in the image of the canonical injection $\rho _1$ that is associated with the new coproduct sort $\sigma _2$. And on the other hand, the theory $T_2$ defines the sort symbol $\sigma _1$ as the subsort of “things that are p.” $T_1$ and $T_2$ are therefore Morita equivalent.

Suppose, however, that we were to follow Quine and ignore the apparatus of sorts when considering these theories $T_1$ and $T_2$. That is, suppose that we were to treat $T_1$ and $T_2$ as if they were both formulated using the same single sort symbol. The single-sorted framework then gives us no way of recognizing any sense in which these theories are equivalent. The theory $T_1$ implies that “there is one thing”, while the theory $T_2$ implies that “there are two things.” These implications contradict one another, so $T_1$ and $T_2$ do not even have a common conservative extension, let alone a common definitional extension.¹² They are therefore not definitionally equivalent. If we ignore the apparatus of sorts when considering the theories $T_1$ and $T_2$, then we are also forced to forget a natural sense in which they are equivalent theories.¹³

When Quine argues that nothing of philosophical significance turns on the use of many-sorted as opposed to single-sorted logic, therefore, he is mistaken. Indeed, recall that Quine used the fact that many-sorted logic could be reduced to single-sorted logic as a tool in his debates with Carnap. While Carnap finds many-sorted logic helpful for capturing the phenomenon of category mistakes, Quine claims that it is more convenient to say that sentences committing category mistakes are meaningful, but trivially false:

[...] the many-sorted is translatable into one-sorted. Generally such translation has the side effect of admitting as meaningful some erstwhile meaningless predications. E.g., if the predicate “divisible by 3” is henceforth to be trained on general variables instead of number variables, we must make sense of calling things other than numbers divisible by 3. But this is easy; we may count such attributions as false instead of meaningless (Quine 1969, p. 96).

Quine has again missed a beat here. Recall that in eliminating sort distinctions, we had to make a conventional choice.¹⁴ For a predicate that originally was restricted to things of a particular sort, what should we say about its application to things of another sort? Should we say that it applies to all such things, or to no such things? There is no default answer here because we have to consider the question both for a predicate and for its negation (in which case our answers will be opposite to each other).

Consider a particular example. The predicates “prime” and “composite” are defined on the domain of natural numbers. Now suppose that we unify the domain of natural numbers with the domain of 20th century philosophers. Following Quine’s suggestion, we should count the attribution of “prime” to philosophers as false, e.g. “Carnap is prime,” is considered false. By the same reasoning, we also count the attribution of “composite” (i.e. “not prime”) to philosophers as false, e.g. “Carnap is composite,” is considered false. But then Carnap is neither prime nor not-prime, which cannot be tolerated within the framework of classical logic.

Quine is therefore wrong when he claims that “we may count such attributions as false.” If we count all such attributions as false, then we land ourselves in a contradiction. We have to choose which attributions are true, and which are false. The many-sorted framework allows us to refrain from making such conventional choices, which could easily be mistaken for assertions. And this is an advantage of the framework. It does not force us to apply predicates in cases where we have no good reason to say that they do (or do not) hold of the items in question.

Recent philosophical literature has devoted significant attention to logic and quantifiers, but relatively little to the device of sorts.¹⁵ Some of us felt justified to ignore sorts because we believed Quine when he claimed that every theory can be replaced by a single-sorted variant. But when we look at the actual mechanics of how this replacement works, it becomes clear that Quine was mistaken about the philosophical upshot of the logical facts. Many-sorted theories are eliminable only to the extent that Morita equivalence is a reasonable notion of equivalence, and Morita equivalence only makes sense in the framework of many-sorted logic. When we forget the apparatus of sorts, we are also foced forget a particularly natural and useful criterion for theoretical equivalence. And in addition, eliminating sort distinctions forces us to make unnecessary conventional choices about how to extend predicates beyond their original range of application.

Through a bit of logical legerdemain, Quine convinced a generation of philosophers that formal logic can do without the apparatus of sorts. But the formal result — that each theory can be replaced with a single-sorted variant — does not support the philosophical conclusion. If we forget about the apparatus of sorts and replace each theory with a single-sorted variant, then philosophical questions will be begged and an interesting point of view will be lost.

Appendix

The objective of this appendix is to prove Theorem 2. We prove a special case of the result for convenience. We will assume that $\Sigma$ has only three sort symbols $\sigma _1, \sigma _2,\sigma _3$ and that $\Sigma$ does not contain function or constant symbols. A perfectly analogous (though more tedious) proof goes through in the general case.

We prove the result by explicitly constructing a “common Morita extension” $T_{4}\cong {\widehat{T}}_{4}$ of T and ${\widehat{T}}$ to the following signature.

$$\begin{aligned} \Sigma ^+=\Sigma \cup {\widehat{\Sigma }}&\cup \{\sigma _{12}\} \cup \{\rho _1, \rho _2, \rho _{12}, \rho _3\} \cup \{ i_1,i_2, i_3\} \end{aligned}$$

The symbol $\sigma _{12}\in \Sigma ^+$ is a sort symbol. The symbols denoted by subscripted $\rho$ are function symbols. Their arities are expressed in the following figure.

The symbols $i_1$, $i_2$, and $i_3$ are function symbols with arity $\sigma _1\rightarrow \sigma$, $\sigma _2\rightarrow \sigma$, and $\sigma _3\rightarrow \sigma$, respectively.

We now turn to the proof.

Proof of Theorem 2

The following figure illustrates how our proof will be organized.

Steps 1–3 define the theories ${\widehat{T}}_1,\ldots , {\widehat{T}}_{4}$, steps 4–6 define $T_1,\ldots , T_{4}$, and step 7 shows that $T_{4}$ and ${\widehat{T}}_{4}$ are logically equivalent.

• Step 1 We begin by defining the theory ${\widehat{T}}_1$. For each sort $\sigma _j\in \Sigma$ we consider the following sentence.

  

  The sentence $\theta _{\sigma _j}$ defines the symbols $\sigma _j$ and $i_j$ as the subsort of “things that are $q_{\sigma _j}$.” The auxiliary axioms $\phi _{\sigma _j}$ of ${\widehat{T}}$ guarantee that the admissibility conditions for these definitions are satisfied. The theory ${\widehat{T}}_1={\widehat{T}}\cup \{\theta _{\sigma _1}, \theta _{\sigma _2},\theta _{\sigma _3}\}$ is therefore a Morita extension of ${\widehat{T}}$ to the signature ${\widehat{\Sigma }}\cup \{\sigma _1,\sigma _2,\sigma _3, i_1,i_2,i_3\}$.

• Step 2 We now define the theories ${\widehat{T}}_2$ and ${\widehat{T}}_3$. Let $\theta _{\sigma _{12}}$ be a sentence that defines the symbols $\sigma _{12}, \rho _1, \rho _2$ as a coproduct sort. The theory ${\widehat{T}}_2={\widehat{T}}_1\cup \{\theta _{\sigma _{12}}\}$ is clearly a Morita extension of ${\widehat{T}}_1$.

  We have yet to define the function symbols $\rho _{12}$ and $\rho _3$. The following two sentences define these symbols.

  

  The sentence $\theta _{\rho _3}$ simply defines $\rho _3$ to be equal to the function $i_3$. For the sentence $\theta _{\rho _{12}}$, we define the formula $\psi (x,y)$ to be

  $$\begin{aligned} \exists _{\sigma _{1}} z_1 \big ( \rho _{1}(z_1)=x\wedge i_{1}(z_1)=y\big ) \vee \exists _{\sigma _{2}} z_2\big ( \rho _{2}(z_2)=x\wedge i_{2}(z_2)=y\big ) \end{aligned}$$

  We should take a moment here to understand the definition $\theta _{\rho _{12}}$. We want to define what the function $\rho _{12}$ does to an element a of sort $\sigma _{12}$. Since the sort $\sigma _{12}$ is the coproduct of the sorts $\sigma _1$ and $\sigma _2$, the element a must “actually be” of one of the sorts $\sigma _1$ or $\sigma _2$. (The disjuncts in the formula $\psi (x,y)$ correspond to these possibilities.) The definition $\theta _{\rho _{12}}$ stipulates that if a is “actually” of sort $\sigma _j$, then the value of $\rho _{12}$ at a is the same as the value of $i_j$ at a. One can verify that ${\widehat{T}}_{2}$ satisfies the admissibility conditions for $\theta _{\rho _3}$ and $\theta _{\rho _{12}}$, so the theory ${\widehat{T}}_3={\widehat{T}}_{2}\cup \{\theta _{\rho _3}, \theta _{\rho _{12}}\}$ is a Morita extension of ${\widehat{T}}_{2}$ to the signature

  $$\begin{aligned} {\widehat{\Sigma }}\cup \{\sigma _1,\sigma _2, \sigma _3, \sigma _{12}, i_1,i_2, i_3, \rho _1, \rho _2,\rho _3, \rho _{12}\} \end{aligned}$$

• Step 3 We now describe the $\Sigma ^+$-theory ${\widehat{T}}_{4}$. This theory defines the predicates in the signature $\Sigma$. Let $p\in \Sigma$ be a predicate symbol of arity $\sigma _{j_1}\times \cdots \times \sigma _{j_m}$. We consider the following sentence.

  

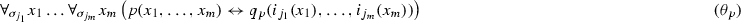
  The theory ${\widehat{T}}_{4}={\widehat{T}}_3\cup \{\theta _{p}:p\in \Sigma \}$ is therefore a Morita extension of ${\widehat{T}}_3$ to the signature $\Sigma ^+$.

• Step 4 We turn to the left-hand side of our organizational figure and define the theories $T_1$ and $T_{2}$. We proceed in an analogous manner to the first part of Step 2. The theory $T_1=T\cup \{\theta _{\sigma _{12}}\}$ is a Morita extension of T to the signature $\Sigma \cup \{\sigma _{12}, \rho _1,\rho _2\}$. Now let $\theta _\sigma$ be the sentence that defines the symbols $\sigma , \rho _{12}, \rho _3$ as a coproduct sort. The theory $T_{2}=T_{1}\cup \{\theta _{\sigma }\}$ is a Morita extension of $T_{1}$ to the signature $\Sigma \cup \{\sigma _{12}, \sigma , \rho _1, \rho _2, \rho _3, \rho _{12}\}$.

• Step 5 This step defines the function symbols $i_1$, $i_2$, and $i_3$. We consider the following sentences.

  

  The sentence $\theta _{i_3}$ defines the function symbol $i_3$ to be equal to $\rho _3$. The sentence $\theta _{i_{2}}$ defines the function symbol $i_{2}$ to be equal to the composition “$\rho _{12}\circ \rho _{2}$.” Likewise, the sentence $\theta _{i_{1}}$ defines the function symbol $i_{1}$ to be “$\rho _{12}\circ \rho _{1}$.” The theory $T_3=T_{2}\cup \{\theta _{i_1},\theta _{i_2}, \theta _{i_3}\}$ is a Morita extension of $T_{2}$ to the signature $\Sigma \cup \{\sigma _{12}, \sigma , \rho _1, \rho _2, \rho _3, \rho _{12}, i_1, i_2, i_3\}$.

• Step 6 We still need to define the predicate symbols in ${\widehat{\Sigma }}$. Let $\sigma _j\in \Sigma$ be a sort symbol and $p\in \Sigma$ a predicate symbol of arity $\sigma _{j_1}\times \cdots \times \sigma _{j_m}$. We consider the following sentences.

  

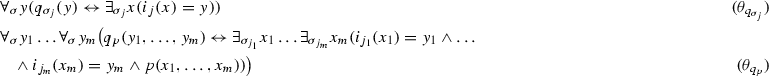
  These sentences define the predicates $q_{\sigma _j}\in {\widehat{\Sigma }}$ and $q_p\in {\widehat{\Sigma }}$. One can verify that $T_3$ satisfies the admissibility conditions for the definitions $\theta _{q_{\sigma _j}}$. And therefore the theory $T_{4}=T_3\cup \{\theta _{q_{\sigma _1}}, \theta _{q_{\sigma _2}}, \theta _{q_{\sigma _3}}\}\cup \{\theta _{q_{p}}: p\in \Sigma \}$ is a Morita extension of $T_3$ to the signature $\Sigma ^+$.

• Step 7 It only remains to show that the $\Sigma ^+$-theories $T_{4}$ and ${\widehat{T}}_{4}$ are logically equivalent. One can verify by induction on the complexity of $\psi$ that

  $$\begin{aligned} T_{4}\vDash \psi \leftrightarrow {\widehat{\psi }}\text { and } {\widehat{T}}_{4}\vDash \psi \leftrightarrow {\widehat{\psi }}. \end{aligned}$$

  (5)

  for every $\Sigma$-sentence $\psi$. One then uses (5) to show that $\text {Mod}(T_{4})=\text {Mod}({\widehat{T}}_{4})$. The argument involves a number of cases, but since each case is straightforward we leave them to the reader to verify. The theories $T_{4}$ and ${\widehat{T}}_{4}$ are logically equivalent, which implies that T and ${\widehat{T}}$ are Morita equivalent. $\square$