1 Introduction

In the 1960s, inspired by bionics, metaheuristic optimization algorithms, which take inspiration from random phenomena in nature and combine stochastic algorithms with local algorithms, emerged. Metaheuristic optimization algorithms can solve large-scale complex problems quickly and do not have any requirement on the objective function and are not limited to specific problems, and these make them one of the hot problems in the research of optimization problems. The core of the metaheuristic algorithm is exploration and exploitation, where exploration means exploring the entire search space. And exploitation means to use the information obtained from exploration to approach the optimal solution step by step. In general, a metaheuristic algorithm with good performance will usually maintain a balance between exploration and exploitation [1, 2].

The marine predators algorithm (MPA) is a nature-based metaheuristic algorithm proposed by Faramarzi et al. in 2020, with the main revelation being the widely adopted foraging strategies Levy and Brownian motion of marine predators [3]. It is proven to be an optimization algorithm with good performance. However, the whole optimization process is divided into three fixed phases according to the iteration number, and each phase has a specific location update formula. In each iteration phase, a specific location update formulas of search agents are defined. In other words, the position of the search agents will be updated in a fixed way according to the iterative process. Such an update strategy is not flexible and specific. When facing different optimization problems, such a solidified search agent position update strategy may affect the balance between exploration and exploitation in the optimization process, and the phenomenon of premature convergence may occur, thus affecting the optimization performance. According to the No Free Lunch Theorem [4], there does not exist any optimization algorithm that performs better than other optimization algorithms on all problems. Therefore, the search agent location update formula of the algorithm must be adaptively adjusted to the characteristics of the problem, as well as to the optimization situation. Maintaining a balance between exploration and exploitation during the optimization process and avoiding premature convergence will enable the algorithm to have better performance.

In this study, a novel modified Marine Predators Algorithm hybridizing by Q-learning (QMPA) is proposed, which adaptively adjusts the update strategies of different search agents at different iteration phases. This will avoid the imbalance between exploitation and exploration, effectively improving the ability to search globally and optimizing performance. The main contributions of this paper are as follows:

  • An adaptive control strategy based on reinforcement learning is proposed.

  • A novel MPA algorithm for search agent adaptive selection of location update method is proposed.

  • Based on 10 classical benchmark functions, QMPA and MPA are compared in three dimensions 10, 30, and 50.

  • Comparative experiments of QMPA and other algorithms are conducted on the CEC2014 test function set and two engineering problems.

The remaining part of the paper is structured as follows: A review of related work is given in Sect. 2, and Sect. 3 provides basic information about the MPA and the fundamentals of Q-learning. In Sect. 4, the proposed QMPA is illustrated in detail. Section 5 provides the experiments and the related results. Section 6 describes the threats to validity. The conclusion of the whole paper and recommendations for future related work are summarized in Sect. 7.

2 Related work

Since the proposed method is based on the adaptive control of the metaheuristic algorithm, this section will review both the metaheuristic algorithm and its adaptive control, respectively, to better highlight the existing research results and deficiencies.

Metaheuristic algorithms have developed rapidly in recent years and many algorithms have emerged. Among them, there are three main categories, which are swarm intelligence algorithms, physics-based and evolutionary algorithms. Algorithms such as genetic algorithm [5] and differential evolution algorithm [6] belong to evolutionary algorithms. Simulated annealing [7] and gravitational search [8] belong to the physics-based algorithms. The swarm intelligence algorithms include particle swarm optimization (PSO) [9], grey wolf optimizer (GWO) [10] and MPA [3], etc. Meanwhile, metaheuristic optimization algorithms have a wide range of applications in the fields of medical [11], mechanical design [12], parametric optimization [13] and image processing [14], and have good performance.

Although these metaheuristic algorithms may be able to solve relatively complex optimization problems in different scenarios, finding the global optimal solution is still a challenging task. This is because these algorithms usually converge prematurely and fall into local optimum due to the imbalance between exploitation and exploration [15]. The same problem exists for MPA. When MPA faces multimodal and nonlinear problems, it usually encounters with stagnation and falling into local optimum [16]. Literature [17] points out premature convergence is a problem for MPA, which divides the optimization iteration phase into three phases, namely, exploration phase, exploration to exploitation phase, and exploitation phase. It may lead to falling into a local optimum. In the scheduling optimization of charging and discharging, the problem of falling into local optimum of MPA is also pointed out in the literature [18]. Similarly, literatures [19,20,21] also illustrate the shortcomings of MPA such as lacking of population diversity and the tendency to converge prematurely in the last optimization stage.

Facing the problem that metaheuristic algorithms tend to converge too early and fall into local optimum, many scholars have proposed some solutions. For example, hybrid algorithms are constructed by hybridizing multiple methods, which can effectively improve the phenomenon of premature convergence. Emperor Penguins Colony algorithm combined with genetic operators has shown good performance in community detection in complex networks [22]. Integration of particle swarm algorithm with a genetic algorithm can solve the vehicle path optimization problem well [23]. Literature [24] combines ant colony algorithm with a genetic algorithm to better solve the delivery scheduling optimization problem. In the problem of determining optimal design parameters of model predictive control, the hybrid firefly–whale optimization algorithm showed good performance [25]. In the literature [26], a hybrid algorithm combining particle swarm optimization algorithm and bat algorithm is proposed for solar PV microgrid capacity configuration optimization. To improve the performance of the MPA algorithm in the optimal design of automotive components, literature [27] hybridized the Nelder-Mead algorithm with MPA. Although the hybrid algorithm has good performance in a certain area, it is designed for a specific problem, which makes the application of the algorithm possess some limitations.

In order to make the metaheuristic optimization algorithm have good performance facing different complex problems, some scholars have improved the algorithm using adaptive control strategies. As studied by some scholars, there are two main improvement mechanisms: automatic adjustment and feedback adjustment. Automatic adjustment is the search for the optimal solution along with the search for parameters. In the literature [28], three parameters of the inertial weight and two cognition acceleration coefficients of PSO are updated together with the particles, improving the performance of the algorithm. In the literature [29], two fixed parameters in the differential evolution algorithm are iteratively searched in the specified range, enhancing the convergence velocity and its performance. However, automatic adjustment is a way of implicit parameter adjustment, which is not conducive to understanding and analysis. Feedback adjustment is used to guide parameter adjustment through the feedback on algorithm performance changes. An adaptive parameter control model is proposed in the literature [30]. The parameters of the particle swarm optimization algorithm are adjusted based on a linearly decreasing ideal velocity profile [31]. In the literature [32], the parameters of fruit fly optimization algorithm are controlled by feedback based on the state of the already generated solution. The literature [33] redefines a nonlinear step-factor parameter control strategy in order to improve the self-adaptability of MPA. The literature [34] set a strategy for the selection of exploration and exploitation phases of the MPA optimization process according to the iterative process, which has a certain improvement on the performance of the MPA algorithm. However, this strategy is limited by the fact that it is only related to the iterative process, and has some limitations on performance improvement. The literature [35] improves the exploration and exploitation capability of MPA by an adaptive update formula, which is based on the global optimal fitness. However, this adaptive update formula is only related to the current search state and cannot avoid falling into local optimum. Unlike automatic adjustment, feedback adjustment is performed by displaying parameters, which facilitates understanding and analysis, but is not conducive to controlling the direction and degree of adjustment.

As mentioned above, many metaheuristic optimization algorithms always suffer from premature convergence, and this is also true for MPA. Although there are many studies to improve MPA, they are mainly oriented to specific problems. In addition, there are limitations in studies targeting the combination of MPA and adaptive strategies. The performance of the MPA is limited when faced with different complex optimization problems, while the existing adaptive control strategies have some drawbacks. For MPA, the key to achieving good performance is to strike a balance between exploration and exploitation. On the one hand, the algorithm needs to search extensively for regions with exploitation prospects. On the other hand, the algorithm also needs to perform further in-depth exploitation within the regions with exploitation prospects searched in the earlier stage. It is known that reinforcement learning has a long-term perspective, and it is widely used to guide the selection of actions based on the outcome of future trials [36,37,38]. In this study, reinforcement learning is combined with the MPA algorithm to adaptively adjust the update method of different search agents at different iteration stages by Q-learning. Specifically, the choice of update method is based on a Q-table that has been matured through multiple training cycles. The Q-table consists of two dimensions, including the action and the state. The action is the four update formulas defined in the standard MPA, and the state reflects the difference between the search agents and the optimum solution. Each search agent has a different Q-table at various iteration stages, and each search agent updates the Q-table by training it several times in each iteration. The Q-table updates are based on a reward function, which is set considering both different iteration stages and different search agents. The whole adaptive adjustment process is based on the feedback of reinforcement learning for future exploration, which is real-time, targeted and effective. At the same time, this adaptive adjustment mechanism is easy to understand and control. The approach proposed in this paper can enhance the balance between exploitation and exploration, avoid the phenomenon of premature convergence, and improve the performance in the face of different complex optimization problems.

3 Briefing on the MPA and Q-learning

For more effective discussion, the ideas of the MPA and Q-learning are firstly briefed.

3.1 MPA

The marine predators algorithm is a metaheuristic optimization algorithm proposed based on the foraging law of marine predators [3]. It is mainly inspired by the predatory behaviors and foraging strategies of marine organisms such as sharks, sunfish, and swordfish, and solves the optimization problem by simulating the laws of these marine organisms in predation on their prey. Among them, the foraging strategies mainly include two categories of Levy flight and Brownian motion. In the optimization process, foraging strategies are selected according to the different movement speeds between predator and prey. The probability of encounter between predator and prey is maximized by weighing the choice of two foraging strategies, Levy flight, and Brownian motion, at different stages.

Like most other algorithms, the initial solution of MPA is uniformly distributed:

$$X_{0} = X_{{{\text{lb}}}} + \, rd \, \left( {X_{{{\text{ub}}}} - X_{{{\text{lb}}}} } \right)$$
(1)

where \(rd\) is a random vector, uniformly distributed between 0 and 1, \(X_{{{\text{lb}}}}\) is the minimal boundary of the variables, and \(X_{{{\text{ub}}}}\) is the maximal boundary of the variables.

After initialization, a matrix named \({\text{Pre}}\) will be constructed and the predators’ positions update will be based on this matrix. In addition, the best search agents are selected in each iteration to form the Eli matrix, which has the same dimensions as the \({\text{Pre}}\) matrix, and the search agents in the Eli matrix is called the top predator.

$${\text{Pre }} = \left[ {\begin{array}{*{20}c} {X_{1,1} } & {X_{1,2} } & \cdots & {X_{{1,\;{\text{Dim}}}} } \\ {X_{2,1} } & {X_{2,2} } & \cdots & {X_{{2,\;{\text{Dim}}}} } \\ \vdots & \vdots & \vdots & \vdots \\ {X_{n,1} } & {X_{n,2} } & {X_{n,2} } & {X_{{n,\;{\text{Dim}}}} } \\ \end{array} } \right]_{{n\; \times \;{\text{Dim}}}}$$
(2)

where \(X_{i,j}\) presents the jth dimension of ith prey, \({\text{Dim}}\) is the dimension of search agents, and n means the number of search agents.

Considering the speed between predator and prey, the search agents’ search for superiority is divided into three stages. Each process corresponds to a different position update strategy.

Phase1: In the early phase of optimization, exploration is significant. Generally, the prey at this stage moves faster than the predator, and staying still is the better way for predators, and the position is updated in the following way.

$${\text{While}}\;t \le \frac{1}{3}t_{\max }$$
$$\begin{gathered} \overrightarrow {{{\text{ step}}_{i} \, }} = \overrightarrow {{M_{B} }} \otimes \left( {\overrightarrow {{{\text{ Eli}}_{i} \, }} - \overrightarrow {{M_{B} }} \otimes \overrightarrow {{{\text{Pre}}_{i} }} } \right),\;i = 1, \ldots n \\ \overrightarrow {{{\text{ Pre}}_{i} \, }} = \overrightarrow {{{\text{Pre}}_{i} }} + C * \overrightarrow {{{\text{rand}}}} \otimes \overrightarrow {{{\text{ step}}_{i} \, }} \\ \end{gathered}$$
(3)

where \(\overrightarrow {{M_{B} }}\) is a vector representing the Brownian motion, \(C\) is a constant number, \(\otimes\) is entry-wise multiplications, \(\overrightarrow {{{\text{rand}}}}\) is a vector that is randomly and uniformly distributed from 0 to 1.

Phase2: During the intermediate phase of optimization, the speed of movement of prey and predator is very close, and at this time exploration and exploitation are equally important. Dividing the search agents into two parts, one for exploration and the other for exploitation, the detailed position update is shown as follows:

$${\text{While }}\frac{1}{3}t_{\max } < t < \frac{2}{3}t_{\max }$$

For the first half of the search agents

$$\begin{gathered} \overrightarrow {{{\text{ step}}_{i} \, }} = \overrightarrow {{M_{L} }} \otimes \left( {\overrightarrow {{{\text{ Eli}}_{i} \, }} - \overrightarrow {{M_{L} }} \otimes \overrightarrow {{{\text{Pre}}_{i} }} } \right){, }i = 1, \ldots {n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2} \\ \overrightarrow {{{\text{ Pre}}_{i} \, }} = \overrightarrow {{{\text{Pre}}_{i} }} + C * \overrightarrow {{{\text{rand}}}} \otimes \overrightarrow {{{\text{ step}}_{i} \, }} \\ \end{gathered}$$
(4)

where \(\overrightarrow {{M_{L} }}\) is a vector representing the Levy movements.

For another half of the search agents

$$\begin{gathered} \overrightarrow {{\text{ step}}}_{i} = \overrightarrow {{M_{B} }} \otimes \left( {\overrightarrow {{M_{B} }} \otimes \overrightarrow {{{\text{ Eli}}_{i} \, }} - \overrightarrow {{{\text{Pre}}_{i} }} } \right){,}\; \, i = {n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2} + 1,...n \\ \overrightarrow {{{\text{ Pre}}_{i} \, }} = \overrightarrow {{{\text{Eli}}_{i} }} + C * CF \otimes \overrightarrow {{{\text{ step}}_{i} \, }} \\ \end{gathered}$$
(5)

where \({\text{CF}}\) is a parameter that is used in the optimization process to control the step size, and the formula of mathematics is shown as follows:

$${\text{CF}} = \left( {1 - {\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t {t_{\max } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${t_{\max } }$}}} \right)^{{\left( {{\raise0.7ex\hbox{${2t}$} \!\mathord{\left/ {\vphantom {{2t} {t_{\max } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${t_{\max } }$}}} \right)}}$$
(6)

Phase3: At the end of the optimization phase, prey is not as fast as predators. It is usually associated with high exploitation, and the position is updated in the following way.

$${\text{While}}\; \, t \ge \frac{2}{3}t_{Max}$$
$$\begin{gathered} \overrightarrow {{\text{ step}}}_{i} = \overrightarrow {{M_{L} }} \otimes \left( {\overrightarrow {{M_{L} }} \otimes \overrightarrow {{{\text{ Eli}}_{i} \, }} - \overrightarrow {{{\text{Pre}}_{i} }} } \right){, }i = 1, \ldots n \\ \overrightarrow {{{\text{ Pre}}_{i} \, }} = \overrightarrow {{{\text{Eli}}_{i} }} + C * {\text{CF}} \otimes \overrightarrow {{{\text{ step}}_{i} \, }} \\ \end{gathered}$$
(7)

In addition, some environmental changes may affect predator behavior. For example, sharks are distributed around the fish aggregating devices (FADs) most of the time [39]. The FADs are usually viewed as local optima and considering longer jumps can avoid falling into local optima. The mathematical expression for FADs is given as follows:

$$\overrightarrow {{{\text{Pre}}_{i} }} = \left\{ {\begin{array}{*{20}l} {\overrightarrow {{{\text{Pre}}_{i} }} + {\text{CF}}\left[ {\vec{X}_{{{\text{lb}}}} + \overrightarrow {{{\text{rand}}}} \otimes \left( {\vec{X}_{{{\text{ub}}}} - \vec{X}_{{{\text{lb}}}} } \right)} \right] \otimes \vec{U},} \hfill & {{\text{if}}\; \, r \le {\text{FADs}}} \hfill \\ {\overrightarrow {{{\text{Pre}}_{i} }} + [{\text{FADs}}(1 - r) + r]\left( {\overrightarrow {{{\text{Pre}}_{r1} }} - \overrightarrow {{{\text{Pre}}_{r2} }} } \right),} \hfill & {{\text{if}}\; \, r > {\text{FADs}}} \hfill \\ \end{array} } \right.$$
(8)

where \(r\) is a number, randomly distributed from 0 to 1.\(\vec{U}\) is a vector containing only 0 and 1. \(r_{1}\) and \(r_{2}\) represent random indexes.

The pseudo-code of the MPA is given as follows:

figure a

The original algorithm divides the entire iterative cycle into three phases equally, and in the second phase, the search agents is fixed into two parts. Each phase adopts a corresponding update strategy. This fixed division is not conducive to a more efficient and targeted search agent search.

3.2 Q-learning

Reinforcement learning is a popular machine learning technique in recent years and has achieved remarkable results in many fields [36,37,38]. Q-learning is a value-based algorithm in RL, proposed by Watkins in 1989. The iterative formula for Q-learning is shown in Eq. (9).

$$Q(s_{m + 1} ,a_{m + 1} ) = (1 - \alpha )Q(s_{m} ,a_{m} ) + \alpha \left[ {R(s_{m} ,a_{m} ) + \gamma \mathop {\max }\limits_{a} Q(s_{m + 1} ,a)} \right]$$
(9)

where \(\gamma\) represents the discount factor, \(\alpha\) denotes the learning rate, \(R(s_{m} ,a_{m} )\) is the reward obtained by the agent for performing the action \(a_{m}\) in the state \(s_{m}\) and \(Q(s_{m} ,a_{m} )\) is the cumulative reward earned by the agent at time \(m\).

A Q value table is first created in Q-learning. The agent gets feedback through continuous interaction in the hell environment and forms a reward value for the agent's state-action pair. Through continuous iterative modification of the Q table, the positive reward action will be chosen by the search agent, and the probability of the corresponding action will increase. After several iterations, the optimal set of Actions is formed. Figure 1 demonstrates the model of Q-learning.

Fig. 1
figure 1

The model of Q-learning

Full size image

4 The proposed QMPA

QMPA is a new algorithm based on the standard MPA by Q-learning proposed in this paper. The algorithm mainly consists of four important components: action, state, reward, and Q table, as Fig. 2 shows, where the Q table is the core, which guides the search agent in which state to take which action, and its update is in turn based on the reward generated by the action taken by the search agent. This section will describe the components of QMPA in detail.

Fig. 2
figure 2

The important elements in the QMPA

Full size image

4.1 State and action

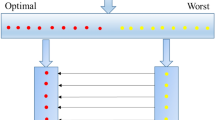
To distinguish the state that each search agent is in, this paper divides the whole search agent into four states according to the fitness, which are Largest, Larger, Smaller, and Smallest, as shown in Table 1, representing the relative performance concerning the global worst and the best, respectively. The global worst fitness and the best fitness are set as two extremes, and the difference between these two extremes is the average division into four parts, which are four different states. Each search agent determines the state based on the fitness. In the standard MPA, four update formulas are defined according to different stages, however, in this paper, these four update formulas are defined as four kinds of actions.

Table 1 The definition of state
Full size table

4.2 Q table

The next step is the design of the Q table, a two-dimensional table with rows representing state and action. When the search agent is judged to be in the state, it can select the corresponding row and then select the action that generates the largest Q value in this row.

4.3 Reward function

First, it is necessary to decide whether a search agent is rewarded or punished. If the fitness of a search agent after taking an action has improved compared with the previous one, it is rewarded and its corresponding Q value is increased. Conversely, if the fitness has decreased, it is punished and its corresponding Q value is decreased.

Determining the level of the reward or punishment will be the next step to be taken. In the standard MPA, it divides the entire iteration cycle into three parts, where the search agent is encouraged to do exploration during the first one-third of the iteration cycle, and all search agents take Eq. (3) for updating. In the middle third of the iteration cycle, half of the search agents are encouraged to exploit and updated using Eq. (4), and the other half of the search agents are updated using Eq. (5) to continue the exploration. In the final stage of the iteration, all search agents are encouraged to exploitation and updated using Eq. (7). Inspired by the standard MPA, this paper will set the reward and punishment intensity with the period of iteration and the different search agents, and the reward and punishment intensity formula are shown in Eq. (10).

$$\begin{gathered} \left\{ {\begin{array}{*{20}l} {R_{A1} (t) = 500 - \frac{500}{{t_{\max } }}t} \hfill \\ {R_{A2} (t) = \left\{ {\begin{array}{*{20}c} {250 + \frac{500}{{t_{\max } }}t - \frac{167}{n}i,t \le \frac{{t_{\max } }}{2} \, (i = 1,2, \cdots n)} \\ {750 - \frac{500}{{t_{\max } }}t - \frac{167}{n}i,t > \frac{{t_{\max } }}{2} \, (i = 1,2, \cdots n)} \\ \end{array} } \right.} \hfill \\ {R_{A3} (t) = \left\{ {\begin{array}{*{20}c} {83 + \frac{500}{{t_{\max } }}t + \frac{167}{n}i,t \le \frac{{t_{\max } }}{2} \, (i = 1,2, \cdots n)} \\ {583 - \frac{500}{{t_{\max } }}t + \frac{167}{n}i,t > \frac{{t_{\max } }}{2} \, (i = 1,2, \cdots n)} \\ \end{array} } \right.} \hfill \\ {R_{A4} (t) = \frac{500}{{t_{\max } }}t} \hfill \\ \end{array} } \right. \hfill \\ P_{{{\text{Ak}}}} (t) = R_{{{\text{Ak}}}} (t) - 500 \, (k = 1,2,3,4) \hfill \\ \end{gathered}$$
(10)

where \(R_{{{\text{Ak}}}}\) denotes the reward value of the \(k\) th action, \(P_{{{\text{Ak}}}}\) represents the punishment value of the \(k\) th action, and \(n\) means the number of search agents.

As shown in Fig. 3, for rewards, actions A1 and A4 produce monotonically increasing and monotonically decreasing reward values, respectively, and are the same for all search agents. The reward values generated by actions A2 and A3 are a dashed line and are different for different search agents, varying in the blue shaded area. All n search agents are sorted sequentially, with the first search agent corresponding to the A2 action producing a reward value at the top of the blue area, and the A3 action producing a reward value at the bottom of the blue area. As the search agent number increases, the reward value created by the A2 action gradually moves downward, while the reward value created by the A3 action gradually moves upward. For the n/2nd search agent, the reward values generated by actions A2 and A3 are equal, and for the nth search agent, the reward value generated by action A2 is located at the bottom of the blue area, while the reward value generated by action A3 is located at the top of the blue area. For the punishment, the punishment value is set similarly to the reward value, by subtracting 500 from the corresponding reward value.

Fig. 3
figure 3

Reward mechanism

Full size image

In general, at the beginning of the iteration, action A1 yields the highest reward, indicating that the execution of action A1 is more encouraged at the beginning of the iteration. In the middle stage of the iteration, the reward values corresponding to actions A2 and A3 are shifted, with half of the search agents executing action A2 with a higher reward value and the other half executing action A3 with a higher reward value. In the final stages of the iteration, action A4 yields the strongest reward. The reason for setting such a reward mechanism is that in the early stage of optimization, the search agent needs more exploration ability to discover more potential regions. However, in the middle stage, exploration and exploitation are equally important in order to discover the optimal solution while jumping out of the local optimum. In the late stage of optimization, it needs more exploitation ability to find the optimal solution locally. Unusually, the reward mechanism set in this paper is dynamic, and it is related to the number of iterations and search agents. This flexible setting allows the algorithm to better maintain a balance between exploration and exploitation capabilities during the optimization process.

4.4 The flowchart of QMPA

The flowchart of the QMPA is presented in Fig. 4, where t denotes the current number of iterations, \(t_{\max }\) denotes the maximum number of iterations, \(epi\) is the maximum number of steps that Q-learning can explore in the future, and q denotes the number of steps that Q-learning currently explores. First, initialize the search agents, \(t_{\max }\), \(n\), \(epi\), then calculate the fitness. Next, the search agent position is updated, and the whole iteration cycle is divided into two parts. When running the first 80% of the iterative process, adaptive learning is performed by Q-learning to select the best position update formula for each search agent in each iteration. However, when the number of iterations is the last 20%, the position update is performed by Eq. (7). The reason for this setup is that later in the optimization phase, the global search needs to be stopped and a local search is performed when exploitation is very important. Therefore, it is very appropriate to use Eq. (7) to change the position of the search agent at the late stage of optimization. In Q-learning adaptive learning, firstly, the Q table is initialized. Then, the initial state S is determined according to the fitness of the search agent. Thirdly, the action is selected under the current state by the Q table. Fourthly, the fitness after performing the action is calculated and the next state S' is determined. Fifthly, the Q table is updated according to the reward function, and finally the current state is S' and the next cycle is continued. Until all the cycle counts are completed, a mature Q table is obtained, and then the Q table is used for position updating. The multiple cycles are designed to allow the search agent to explore \(epi\) steps forward, and a mature Q table can bring out future actions that maximize long-term benefits. Repeat the whole process for each search agent of each iteration to finish updating the position. Continue repeating the next iteration until the whole iteration process is completed. Algorithm 2 presents the pseudo-code of QMPA.

Fig. 4
figure 4

The flowchart of the QMPA

Full size image
figure b

5 Numerical experiment

To evaluate the proposed QMPA with the standard MPA as well as other algorithms, three different experiments were set up in this study. Experiment 1 was performed on 10 classical test functions, the second set of experiment was performed on the challenging CEC2014 test suite, and the third set of experiment was optimized for two engineering problems.

5.1 Experiment 1

In the first experiment, the behavior of QMPA and MPA in different dimensions is compared by commonly used classic test functions. These classic test functions include unimodal and multimodal functions and their properties are shown in Table 2. The unimodal functions are mainly designed to test the exploitation capability, while the exploration performance is experimented with by the multimodal functions. Figure 5 shows two-dimensional images of these functions. These functions will be tested in 10, 30, and 50 dimensions (Dim) using MPA respectively. Each test took 500 iterations, and the number of population was 25. To make the results more meaningful, each test function ran 31 times independently. The common parameter \(P = 0.5\) and \(FADs = 0.2\) in the algorithm, and the number of cycles(\(epi\)) in QMPA was set to 10.

Table 2 Mathematical formulation and properties of classic test functions
Full size table
Fig. 5
figure 5

Two-dimensional view of classic test functions

Full size image

Table 3 presents the results of tests for Dim = 10, and the comparison results for Dim = 30 and Dim = 50 are in Tables 4 and 5, and the optimal value among them is bolded. Table 3 demonstrates that the QMPA performs better than MPA for seven of the ten functions when the dimension is 10. However, the performance is close for the remaining three functions. The Wilcoxon signed-rank test was used to express more clearly the advantages and disadvantages of the algorithms. The “Test” column in Table 3 presents the results. “ + ” and “-” indicate that one algorithm is significantly more or less good than the other, respectively, and “≈” indicates that one algorithm is equal to the other. The test results show significant differences in the performance of these two algorithms; QMPA performs significantly better than MPA in seven functions and equally well in the remaining three functions.

Table 3 Comparison of MPA and QMPA on classic test functions ( Dim = 10)
Full size table
Table 4 Comparison of MPA and QMPA on classic test functions (Dim = 30)
Full size table
Table 5 Comparison of MPA and QMPA on classic test functions (Dim = 50)
Full size table

The QMPA also has excellent performance in high dimensions. The results for dimensions 30 and 50 are presented in Tables 4 and 5, respectively. Table 4 demonstrates that the QMPA gives much better solutions compared with the MPA for seven functions and has similar performance to MPA for the other three functions. The performance of QMPA is worse than MPA in the TF3 function, better than MPA on five functions, and close to MPA in the remaining four functions in Table 5.

Figures 6, 7, 8 show the convergence curves of MPA and QMPA from low to high dimensions, respectively. The convergence curves in the figures are obtained as the average of 31 runs, which makes the results more credible. From the graphs, we can find that the QMPA has a good representation in most of the functions. Specifically, from Fig. 6, it can be found that MPA appears premature over TF1, TF2, TF3, TF4, and TF7. And in TF5, TF6, and TF8, the lack of exploitation capacity of MPA in the later stage is exposed. Similarly, in Figs. 7 and 8, MPA appears to converge prematurely over TF1, TF2, TF4, and TF8. And the lack of exploitation capability is reflected in TF5, TF6, and TF9. In contrast, QMPA behaves differently, both in low and high dimensions. On the one hand, QMPA can effectively jump away from the local optimum, and in addition, it has a better exploitation ability in the later stage of optimization.

Fig. 6
figure 6

Convergence Graphics (Dim = 10)

Full size image
Fig. 7
figure 7

Convergence Graphics (Dim = 30)

Full size image
Fig. 8
figure 8

Convergence Graphics (Dim = 50)

Full size image

The unimodal functions provide a good assessment of the algorithm's ability to exploitation because it has a single optimal solution within the globe. From the results, the QMPA has an overall dominance over the unimodal functions. In contrast, the multimodal functions are different and have lots of local optimums that grow exponentially with the number of dimensions. For assessing the exploratory ability of an algorithm, the multimodal function is very suitable. The results show that the QMPA outperforms MPA on some multimodal functions. That is, the QMPA is superior to the MPA in terms of both exploitation ability and exploration ability. This is due to the adaptive adjustment of the search agent update method, which allows the search agent in different states to take the most suitable update method. When faced with different problems, QMPA can effectively maintain the balance between exploitation and exploration in the optimization process and avoid the phenomenon of premature aging.

5.2 Experiment 2

In the second experiment, the more challenging CEC2014 test suite [40] will be selected to assess the performance of the QMPA. The CEC2014 test suite contains a total of 30 test functions in four categories, including simple functions, such as unimodal and simple multimodal functions, and also more complex functions, such as hybrid and composition functions.

In this experiment, we will not only prove that the QMPA is superior to the MPA but also better than some commonly used optimization algorithms, such as GWO, PSO, Slime Mould Algorithm(SMA) [41], Sine Cosine Algorithm (SCA) [42], Reptile Search Algorithm(RSA) [43], and Aquila Optimizer(AO) [44]. The parameters of QMPA and MPA in this experiment are the same as those in the first experiment. The detailed parameter settings of GWO, PSO, SMA, SCA, RSA, and AO are shown in Table 6.

Table 6 Parameter settings of GWO, PSO, SMA, SCA, RSA, and AO
Full size table

To make the comparative analysis meaningful, all algorithms are compared in the same environment. The number of population was 25, the dimension was 10, and the iteration time was set to 500. To avoid randomness, the mean of the results of 31 independent runs is taken as the comparison result.

Table 7 presents the results of the comparison of QMPA with the competing algorithms, which includes the standard deviation (Std) and mean of the results of 31 runs. Furthermore, to clearly demonstrate the excellent performance of QMPA, pairwise statistical tests are performed for QMPA with MPA, GWO, PSO, SMA, SCA, RSA, and AO. The results of 31 runs of each algorithm were subjected to the Wilcoxon signed-rank test with statistical significance \(\alpha = 0.05\), and are shown in Table 8.

Table 7 Results of the CEC2014 test suite
Full size table
Table 8 Wilcoxon Signed-Rank Test Results for QMPA and Other Algorithms on the CEC2014 Test Suite
Full size table

Table 7 shows the test results, and the last row counts the performance of each algorithm in achieving the optimal value on the CEC2014 test suite. For unimodal functions (F1-F3), have only one optimal solution, making them the best candidates for assessing algorithm exploitation capabilities. The mean of the QMPA received 1st place over the F1 and F2 functions, and for F3, QMPA tied with MPA for 1st place. The QMPA also achieved two 1st places and one 2nd place in the comparison of standard deviations. It reflects that QMPA has good exploitation ability and robustness.

The second class is simple multimodal functions (F4-F16) with two or more local optimal solutions. Therefore, it is very appropriate to use such functions to evaluate the ability of QMPA and other algorithms to move away from local optima and exploration. From the results, QMPA is an excellent algorithm and achieves the 1st place in the mean for 12 of the 13 tested functions.

For the last two categories, hybrid functions (F17-F22) have a lot of local optima, as do the composition functions (F23-F30), and test functions with such characteristics are useful for assessing the ability of an algorithm to escape from local minima. Among the hybrid functions, QMPA obtains the best average values of F17, F18, F19, F20, and F21, and only performs worse than MPA in F22. In the composite function, the QMPA has an ordinary performance, with the best average value obtained only on F26 and F30.

Based on these results, the QMPA proposed in this paper obtained the best mean value on 22 functions and the best standard deviation value on 16 functions in the CEC2014 test suite. In contrast, the original algorithm MPA obtained only 7 best values on the mean performance. In other words, QMPA obtained the best overall performance and outperformed the other algorithms, even standard MPA, in balancing exploration and exploitation capabilities and getting rid of local optimizations.

Furthermore, this chapter presents the convergence analysis of QMPA with MPA, GWO, PSO, SMA, SCA, RSA, and AO for some of the tested functions based on the average of 31 independent runs, and the results are demonstrated in Fig. 9. QMPA achieves stable behavior for all functions, indicating that the algorithms are convergent. QMPA exhibits two advantages over other algorithms. One of them is that it does not converge prematurely. From Fig. 9, it can be found that RSA has obvious premature phenomenon, which appears in most test functions, while QMPA has a completely different performance. The second is the ability to ensure a balance between exploration and exploitation throughout the optimization process. For the whole optimization process, a strong exploration capability is required in the early stage, while the later stage of optimization requires a higher algorithm exploitation capability. Obviously, the fitness of QMPA decreases faster in the early stage, and the convergence value is better in the later stage on F3, F5, F6, F8, F10, F12, F13, and F16. In other words, QMPA is able to control the balance between exploration and exploitation at different stages of optimization, and also this is the guarantee of having good optimization performance.

Fig. 9
figure 9

Convergence curves of QMPA and other algorithms over CEC2014 functions

Full size image

For further analysis of the test results, some boxplots are given in Fig. 10. The boxplot is drawn using the results of each independent run of each algorithm and shows the distribution of the results of 31 independent runs well. Compared with MPA and other competing algorithms, QMPA is narrower and more to the left in the distribution of boxplot for most functions. This also reflects that the QMPA possesses stronger robustness and better optimization performance. It is further proved that the adaptive control strategy of search agent position updating method proposed in this paper helps QMPA to have stable and excellent performance when facing different complex optimization problems.

Fig. 10
figure 10

Boxplots of QMPA and competitor algorithms

Full size image

In addition, for further comparative analysis, paired statistical tests were performed for QMPA and MPA, GWO, PSO, SMA, SCA, RSA, and AO, respectively. The results of 31 runs of each algorithm were subjected to the Wilcoxon sign-rank test for statistical significance \(\alpha { = 0}{\text{.05}}\). The null hypothesis of this test is that "No differences are found between QMPA and the other algorithms in terms of the median number of optimal solutions obtained with the same test function."

The statistical test results are illustrated in Table 8. Where " + " indicates that QMPA outperforms the comparison algorithm at the 95% significance level, while "-" is the opposite, indicating that QMPA is worse than the comparison algorithm. " = " means the results of QMPA are not significantly different from those of the comparison algorithm. The last row summarizes the performance of QMPA and other algorithms in the " + ", " = ", and "-" cases. It is obvious that QMPA performs much well than other optimization algorithms. Compared with the standard MPA, the QMPA performs better on 19 functions, and they are comparable on 8 functions.

5.3 Experiment 3

In this section, two commonly used real-world engineering problems are chosen to perform performance tests of the QMPA. There are some equations or inequality constraints in their optimization models, and in this experiment, the constrained problem will be transformed into an unconstrained one using a simple penalty function method. The constraints and optimization model can be found in [45]. The maximum number of iterations was set as 500, with a total of 25 populations and 31 independent runs.

5.3.1 Tension/compression spring design

Finding the minimum weight is the optimization objective of this engineering problem. The three-dimensional physical drawing is shown in Fig. 11, and the optimization variables involved are mean coil diameter (D), the number of active coils(N), and wire diameter(d).

Fig. 11
figure 11

Description of the tension/compression spring design example

Full size image

This problem has been studied in many literatures using some optimization algorithms, such as CA [46], GSA [8], BFOA [47], and PFA [48]. Table 9 presents the optimization results using different algorithms. The optimal results of the PFA, MPA, and QMPA are very close, but the QMPA results are slightly better.

Table 9 The best results were obtained
Full size table

5.3.2 Welded beam design

The target of the optimization of this optimization problem is to obtain the lowest manufacturing cost of the welded beam. As it is shown in Fig. 12, this optimization model has four optimization variables, that are the thickness of weld (h), length of the attached part of the bar (l), the height of the bar (m), and thickness of the bar (b).

Fig. 12
figure 12

Description of the welded beam design example

Full size image

The optimization results of this issue were compared and analyzed by selecting the results of other literature, including SA [49], HS [50], HAS-GA [51], and GSA [8], as shown in Table 10. It is clear that the QMPA gives the most optimal results, which has clearly validated the excellent performance of the QMPA again.

Table 10 The best results were obtained
Full size table

6 Threats to validity

Threats to validity are generally classified as threats to internal validity and threats to external validity. In this paper, the threats to internal validity mainly come from the implementation of the QMPA and the comparison algorithm used in the comparison tests. For the implementation of the QMPA, programming based on the source code of MPA, along with testing and analysis in a variety of simple problems to ensure the correctness of the algorithm code; For the implementation of the comparison algorithms, the open source code provided by the original author of the corresponding algorithm is used, and the best parameters proposed in the original article are followed for experiments. Throughout the process, all the codes are carefully checked to ensure error-free. The threats to external validity mainly come from the test functions and engineering optimization problems used in this paper. To reduce the threats to external validity, the test functions and engineering optimization problems selected in this paper are widely used in many papers and competitions, and their correctness and reasonableness have a certain degree of confidence. Also, the corresponding scripts are carefully checked for correctness.

7 Conclusion

A novel modified marine predators algorithm hybridizing by Q-learning (QMPA) is proposed to improve the ability of MPA to find the global optimal solution by adaptively adjusting the search agent position update strategy in different iteration stages and states. The adaptive update strategy selection of the MPA is finally achieved with the help of Q-learning by processes of determining states and actions, designing Q tables, and choosing reward functions. The statistical results of different experiments demonstrate that the QMPA has a better optimization capability compared with the standard MPA and other optimization algorithms.

In this paper, only two engineering problems are studied to test the proposed algorithm, which can be employed in different fields to solve complex engineering real-world problems in future work. Also, it is anticipated the proposed adaptive control strategy can be applied to other metaheuristic optimization problems.