Multi-objective workflow grid scheduling using $\varepsilon$-fuzzy dominance sort based discrete particle swarm optimization

Abstract

With the rapid development of networking technology, grid computing has emerged as a source for satisfying the increasing demand of the computing power of scientific computing community. Mostly, the user applications in scientific and enterprise domains are constructed in the form of workflows in which precedence constraints between tasks are defined. Scheduling of workflow applications belongs to the class of NP-hard problems, so meta-heuristic approaches are preferred options. In this paper, $\varepsilon$-fuzzy dominance sort based discrete particle swarm optimization ($\varepsilon$-FDPSO) approach is used to solve the workflow scheduling problem in the grid. The $\varepsilon$-FDPSO approach has never been used earlier in grid scheduling. The metric, fuzzy dominance which quantifies the relative fitness of solutions in multi-objective domain is used to generate the Pareto optimal solutions. In addition, the scheme also incorporates a fuzzy based mechanism to determine the best compromised solution. For the workflow applications two scheduling problems are solved. In one of the scheduling problems, we addressed two major conflicting objectives, i.e. makespan (execution time) and cost, under constraints (deadline and budget). While, in other, we optimized makespan, cost and reliability objectives simultaneously in order to incorporate the dynamic characteristics of grid resources. The performance of the approach has been compared with other acknowledged meta-heuristics like non-dominated sort genetic algorithm and multi-objective particle swarm optimization. The simulation analysis substantiates that the solutions obtained with $\varepsilon$-FDPSO deliver better convergence and uniform spacing among the solutions keeping the computation overhead limited.

1 Introduction

Grid computing infrastructure has emerged as a next generation of high performance computing by providing availability of vast heterogenous resources. To achieve the promising potential of distributed resources, effective and efficient scheduling algorithms are required. The grid scheduling problem is to coordinate and allocate the resources to grid applications. Many important grid applications in e-science and e-business fall in the category of workflow applications modeled by directed acyclic graphs (DAG). Workflow scheduling is one of the key challenges, which deals with assigning different grid services to the workflow tasks while maintaining the task precedence constraints. Depending upon the user demands and objective functions of resource providers, several issues arise such as minimization of makespan, total cost and maximization of system reliability, etc. Many list heuristics have been devoted to this problem, typically restricted to optimizing single objective, namely minimizing execution time (makespan)  [1–3], total cost  [4, 5] or reliability  [6]. Some isolated approaches try to optimize across two criteria. A linear programming based technique is proposed in  [7] which considers one objective at a time. It provides a single solution to the user but fails to produce the trade-off front.

In recent years, to achieve better solution quality, most research focus on developing nature inspired meta-heuristic algorithms to solve the scheduling problem, like simulated annealing (SA)  [8], genetic algorithm (GA)  [9, 10], ant colony optimization (ACO)  [11], tabu search  [12] and particle swarm optimization (PSO)  [13]. Mostly, the research on multi-objective grid scheduling problem as in References  [14–16], linearly combine the different objectives into a scalar cost function using the weight factors, which convert the problem into a single objective problem prior to optimization. The weight selection method being abstract and empirical, in general, it is very difficult to accurately select these weights, as small perturbations in weights lead to different solutions. Hence, in this study, we proposed the use of multi-objective optimization approach to generate Pareto optimal solutions for grid workflow (dependent tasks) scheduling. Pareto optimal solutions are preferred over single solution in real life applications.To generate the Pareto optimal solutions through the aforementioned approaches, multiple runs of the algorithm is needed to be executed after varying the weights, which requires considerably large time.

In this paper, we developed the multi-objective discrete particle swarm optimization algorithm using $\varepsilon$-fuzzy dominance  [17, 18] based sorting procedure ($\varepsilon$-FDPSO) to solve the grid scheduling problem for workflow tasks. We considered the three conflicting objectives of makespan, total cost and reliability under deadline and budget constraints. The metric fuzzy dominance is used to measure the relative fitness of solutions in multi-objective domain. The approach has proven to be highly effective, and providing faster convergence for most difficult multi-objective problems especially when number of objectives are large. In this study, we also select the best compromised solution from the obtained Pareto front based on fuzzy approach. The efficacy and applicability of the approach used for grid workflow scheduling is demonstrated through varying sized application task graphs and comparing it with well known meta-heuristics NSGA-II  [19], and multi-objective particle swarm optimization (MOPSO) [20].

In the remainder of the paper, we briefly mention the related work in Sect. 2. Section 3, specifies the problem formulation. Thereafter, in Sect. 4, we briefly introduced the approach of multi-objective optimization. In Sect. 5, we explain the $\varepsilon$-fuzzy dominance based discrete particle swarm optimization algorithm. Section 6, describes the multi-objective workflow grid scheduling algorithm proposed. Sections 7 and 8 discusses the simulation strategy and result analysis respectively. Finally Sect. 9, gives the conclusion.

2 Related work

The problem of Grid scheduling, for DAG-based task graph, has already been addressed in the literature. Most of the related work attempt to achieve execution time (makespan) or total cost as two independent scheduling criteria. To schedule scientific workflow applications in grid, Wieczorek et al.  [5] uses Heterogeneous Earliest Finish Time (HEFT) and GAs with extension by the ASKALON project. The heuristic in  [4], addressed a similar problem of bi-criteria budget-constrained workflow scheduling, by applying a two-phase optimization. The first phase optimizes the schedule for a single criterion only; the second phase produces the final solution for both criteria, keeping the budget within the defined constraint. A guided local optimization approach is applied to transform the intermediate solution to the final solution. Depending on the criterion used to optimize in the first phase (either execution time or economic cost), one of two proposed versions of the scheduling algorithm is used (called LOSS and GAIN respectively). Work in  [7], proposes a new bi criterion workflow scheduling algorithm that performs optimization based on a flexible sliding constraint, and they apply a dynamic programming method to the entire workflow to enable an extensive exploration of the search space within the optimization process.

The paper  [16] proposed a multi-objective optimization approach called Multi-objective Resource Scheduling Approach (MORSA) to optimize the flow time and the total execution cost simultaneously. In paper  [21], the author proposed a workflow execution planning approach using Multi-objective Differential Evolution (MODE) to generate a set of trade-off schedules within the user specified constraints (deadline and budget), which will offer more choices to user when estimating QOS requirements. The work presented by  [6], addresses tradeoff between execution time and reliability. The authors propose two workflow scheduling algorithms; one of which is called BDLS and the second one called BGA which is a GA. A sophisticated reliability model concerning both computation and communication is proposed. For independent task scheduling in grid, Abraham et al.  [22] used the fuzzy particle swarm optimization and Izakian et al.  [15], used the discrete PSO using the weighted sum method. However, tradeoff between makespan, cost and reliability is difficult to obtain through the above mentioned approaches. In our previous work  [23], we addressed the problem of workflow scheduling with the aim to provide the preference set of solutions to the decision maker near his/her specified regions of interest using evolutionary algorithms (R-NSGA-II, R-$\varepsilon$-MOEA). There we applied the non-domination sorting to rank the solutions.

In the present work, we proposed the use of discrete particle swarm optimization using $\varepsilon$-fuzzy dominance based sorting to obtain the entire Pareto optimal set.

3 Problem formulation

Workflow application is represented as DAG, $G = (V, E)$ where V is the set of vertices representing n different tasks $t_{i}\in V, (1 \le i \le n)$ that can be executed on any available processor. E is the set of edges $e_{ij} = (t_{i}, t_{j})\in E, (1 \le i \le n, 1 \le j \le n, i \ne j)$ representing dependencies among the tasks $t_{i}$ and $t_{j}$ with $t_{i}$ as parent task and $t_{j}$ as child task. A task without any predecessor is called an entry task and a task without any successor is called an exit task. The weight w($t_{i}$) is assigned to task $t_{i}$ represents the number of instructions to be executed for the task and weight w($e_{ij}$) assigned to edge $e_{ij}$ represents the amount of data required to send from task $t_{i}$ to $t_{j}$ if they are not executed on the same resource.

We consider the grid computing system represented as set $R = \{r_{1}, r_{2}, \ldots , r_{m}\}$, consisting of m number of computing resources interconnected by fully connected communication links where communication is assumed to be performed without contention. The resources may have different memory sizes, processing capabilities delivered at different prices and failure rates. Similarly communication links may have different bandwidth. Task executions once started on the processor is considered to be non-preemptive. Further, to consider bandwidth linkage between two resources, a $m \times m$ Data Transfer Time matrix between two resources are stored, where each entry $B_{s,t}$ is used to store the time required to transfer a unit data from processor $r_{s}$ to $r_{t}$. Furthermore, each resource $r_{j}$ is associated with values: (i) $\gamma _{j}$ represents the computing speed illustrated by the unitary instruction execution time, (ii) $c_{j}$, its economic cost which specifies cost of using the resource $r_{j}$ per unit of time, (iii) $\lambda _{j}$, its failure rate. The failure of resource is assumed to follow the Poisson process. The failure rate can be derived from the past performance (system log) or statistical prediction technique.

We define the workflow grid scheduling as the problem of assigning various precedence constrained tasks in the workflow to different available grid resources. In this work, each schedule (solution) is represented as the task assignment string corresponding to the scheduling order string. Task assignment string is the allocation of each task to the available time slot of the resource capable of executing the task, and the scheduling order string encodes the order to schedule tasks. The ordering of tasks in the scheduling order string must satisfy the task dependencies. To describe schedule $S: V \rightarrow R$ which maps every task $t_{i}$ onto a suitable resource $r_{j}$ we define some attributes EST$(t_{i})$, as earliest execution start time and EFT$(t_{i})$ as earliest finish time of a task $t_{i}$ on some resource $r_{j}$ respectively. These are formally defined as follows:

$$\begin{aligned} \mathrm{EST}(t_{i})&= {^\mathrm{max}_{t_{p}\in \mathrm{pred}(t_{i})}}\{ \mathrm{EFT}(t_{p})+\mathrm{DCT}_{p,i}\}\end{aligned}$$

(1)

$$\begin{aligned} \mathrm{EFT}(t_{i})&= \mathrm{EST}(t_{i})+w(t_{i})\cdot \gamma _{j} \end{aligned}$$

(2)

where pred$(t_{i})$ is the set of immediate predecessor tasks of task $t_{i}$ and DCT$_{p,i}$ is the total communication time required to transfer data units from task $t_{p}$ (scheduled on resource $r_{s}$) to task $t_{i}$ (scheduled on resource $r_{j}$), which is calculated as follows:

$$\begin{aligned} \mathrm{DCT}_{p,i}= w(e_{pi})\cdot B_{s,j} \end{aligned}$$

(3)

For the entry task $t_\mathrm{entry}$, the EST is defined by:

$$\begin{aligned} \mathrm{EST}(t_\mathrm{entry})=0 \end{aligned}$$

(4)

For the other tasks in the task graph, the starting time and finish time are computed recursively, starting from the entry task, as shown in Eqs. (1) and (2), respectively.

Let k number of tasks has been executed on a resource $r_{j}$, then let FT$_{j}$ represents the finish time of last completed task on resource $r_{j}$ and is defined as

$$\begin{aligned} \mathrm{FT}_{j}={^\mathrm{max}_{1,2, \ldots , k}} \{ \mathrm{EFT}(t_{k})\} \end{aligned}$$

(5)

For the economic cost, we used the “pay per use” paradigm  [24] , where users have to pay fixed price per time unit of the resource usage. Let $C_{i,j}$ is the cost of executing a task $t_{i}$ on resource $r_{j}$ and is calculated as follows:

$$\begin{aligned} C_{i,j}=c_{j}\cdot w(t_{i})\cdot \gamma _{j} \end{aligned}$$

(6)

Bi-objective workflow scheduling problem: In order to solve the bi-objective grid workflow scheduling problem, we consider two conflicting objectives of minimization of execution time and total cost. Therefore grid workflow scheduling problem is formulated as:

$$\begin{aligned} \mathrm{Minimize\, Time (S)}&= \mathrm{EFT}(t_\mathrm{exit})\end{aligned}$$

(7)

$$\begin{aligned} \mathrm{Minimize\, Cost (S)}&= \sum C_{i,j} \end{aligned}$$

(8)

Subject to Cost (S)$< B \;\mathrm{and \; Time (S)} < D$

where B is the cost constraint (Budget) and D is the time constraint (Deadline) required by users for workflow execution.

Tri-objective workflow scheduling problem: In dynamic environment of grid where resources can fail inevitably, a scheduling decision is still challenging area and it should consider reliability of resources while generating schedule (S) in addition to makespan and cost objectives. Failure of resources can have adverse effects on the performance of workflow application, so we have optimized another objective called reliability along with two already discussed objectives of makespan and cost.

Reliability of a workflow application is the probability that all the tasks over the assigned processors complete successfully. Thus, it is given by the probability that each processor is working untill all the tasks assigned to them are completed. As $\lambda _{j}$ repersents the failure rate of resource $r_{j}$, thus the probability that resource $r_{j}$ can complete all its assigned tasks in schedule S successfully is $R{^{j}_\mathrm{S}}=\exp ^{-\lambda _{j}\cdot \mathrm{FT}_{j}}$. Thus the reliability $R_\mathrm{S}$ of an application in schedule S is given by the product of probabilities of successful completion of tasks to all the resources.

$$\begin{aligned} R{_\mathrm{S}}={\Pi _{j=1}^{m}}R{^{j}_\mathrm{S}} = {\exp ^{{-\sum _{j=1}^{m}}\lambda _{j}\cdot \mathrm{FT}_{j}}} \end{aligned}$$

(9)

To maximize the reliability, we need to minimize the Reliability Index (RI) for schedule S which is given by

$$\begin{aligned} \mathrm{RI}= {\sum _{j=1}^{m}}\lambda _{j}\cdot \mathrm{FT}_{j} \end{aligned}$$

(10)

Therefore, we formulated maximization of reliability in terms of minimization of Reliability Index, represented as below

$$\begin{aligned} \mathrm{Minimize \, Reliability\, Index \, (S)}=\mathrm{RI} \end{aligned}$$

(11)

4 Multi-objective optimization: a brief overview

Conventionally, multi-objective optimization problem (MOP)  [25], can be defined as the simultaneous optimization of multiple conflicting objectives. The aim is to determine the trade-off surface, which is a set of non-dominated solutions known as Pareto optimal solutions. Every individual in this set is an acceptable solution. Mathematically a minimization problem can be formulated as follows:

$$\begin{aligned} \mathrm{Minimize} \; f{_i}(s) \ i=1,2,\ldots ,M \end{aligned}$$

(12)

where $f_{i}$ is the $i$th objective function, s is a decision vector that represents a solution; M is the number of objectives. There are two relations in MOP called usual Pareto Dominance and $\varepsilon$-Pareto Dominance, which are stated as:

Usual Pareto Dominance: Let $f(s) = (f_{1}(s), f_{2}(s),\ldots , f_{M}(s))$ consists of M objectives. Consider two solution vectors $s_{1}$ and $s_{2}$. Then solution $s_{1}$ is said to dominate $s_{2}$ (also written as $s_{1}\prec s_{2})$ iff following two conditions hold:

• 1. $\forall i\in \{1,2,\ldots ,M\}\ :f_{i}(s_{1})\le f_{i}(s_{2})$

• 2. $\exists j\in \{1,2,\ldots ,M\}\ :f_{j}(s_{1})< f_{j}(s_{2})$ $\varepsilon$-Pareto Dominance: Solution $s_{1}$ is said to $\varepsilon$-Dominate $s_{2}$ iff following two conditions hold:

• 1. $\forall i\in \{1,2,\ldots ,M\}\ :{\lfloor {f_{i}(s_{1}){\setminus }\varepsilon _{i}}\rfloor } \le {\lfloor {f_{i}(s_{2}){\setminus } \varepsilon _{i}}\rfloor }$

• 2. $\exists j\in \{1,2,\ldots ,M\}\ :{\lfloor {f_{j}(s_{1}){\setminus } \varepsilon _{j}}\rfloor } < {\lfloor {f_{j}(s_{2}){\setminus } \varepsilon _{j}}\rfloor }$

The solutions which are non-dominated by other solution from a given set are known as non-dominated solutions regarding that set. The front obtained by mapping these non-dominated solutions into objective space is called Pareto optimal front (POF). Due to the high computational complexity and memory constraints, finding the complete POF is infeasible, so diverse set of solutions are desired covering the maximum possible region of POF.

5 $\varepsilon$-Fuzzy dominance sort based discrete particle swarm optimization algorithm

Particle Swarm Optimization is a technique  [26] influenced by the study of social behavior of insects and animals. It consists of swarm of particles, initialized with a population of random candidate solutions. Each particle is represented by a position vector and a velocity vector. The movement of each particle at any instance of time is guided by its own experience (local best) and the experience of its most successful particle (global best) in the swarm. The performance of a particle is measured by the fitness value, which is problem specific. Due to the success of PSO in single objective optimization, in recent years, more and more attempts have been made to extend PSO to the domain of multi-objective problems, see e.g.  [20, 27, 28]. The main challenge in MOPSO is to select the global and local attractors such that the swarm is guided towards the Pareto optimal front and maintains sufficient diversity.

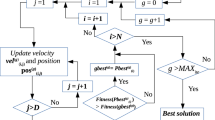
In this paper, to solve grid scheduling problem, we have used the $\varepsilon$-fuzzy dominance based sorting procedure to select the global attractor. During the velocity update, particles move towards the particle (global attractor) with lower rank based on $\varepsilon$-fuzzy dominance. In this way, new positions for the population are generated and previous positions are stored in memory (Archive). The proposed $\varepsilon$-fuzzy dominance sort based discrete particle swarm optimization ($\varepsilon$-FDPSO) is explained in the following section.

5.1 Discrete PSO

PSO has been proved to be an excellent method for continuous numeric optimization problems. But it is obvious that standard PSO can’t be used to solve discrete problems directly. So, much effort has been devoted to solve discrete optimization problems by using discrete PSO. A variant of discrete PSO (DPSO)  [15] was proposed for grid scheduling.

Problem encoding: For optimization of grid workflow scheduling problem, we have generated task assignment string S, which maps every task $t_{i}$ onto a suitable resource $r_{j}$. Figure 1a, shows an example of workflow application as (DAG), where the weight on the edges represents the inter-task communication cost among six tasks. Further, a feasible task assignment string corresponding to given DAG is also shown.

Fig. 1

a Workflow application and its task assignment string and b mapping of task assignment string to particle position matrix

Task assignment string, is then mapped to the $m \times n$ matrix, called position matrix where m is the number of available resources and n is the number of tasks. Let $X^{k}()$ is the position matrix of $k$th swarm particle where $X^{k}()=[ X_{(i,j)}^{k}]$ then

$$\begin{aligned} {X_{(i,j)}^{k}}( )\in \{0,1\}(\forall i,j),\quad i\in \{1,2, \ldots ,m\}, j\in \{1,2, \ldots ,n\} \end{aligned}$$

(13)

where ${X_{(i,j)}^{k}} = 1$ means that $j$th task is performed by $i$th resource. Hence, in each column of the matrix only single element is 1 and others are 0. Figure 1b shows a mapping of task assignment string to the particle position matrix in PSO domain.

Velocity matrix of of $k$th particle is $V^{k}()=[ V_{(i,j)}^{k}]$, so

$$\begin{aligned} {V_{(i,j)}^{k}}( )\in [-V_\mathrm{max}, V_\mathrm{max}],\quad (\forall i,j),\,i\in \{1,2, \ldots ,m\},\, j\in \{1,2, \ldots ,n\}\qquad \quad \end{aligned}$$

(14)

The best position that $k$th particle has visited since the initial time step is denoted as Pbest${_{(i,j)}^{k}}( )$ and Gbest${_{(i,j)}^{k}}( )$ represents the best position that $k$th particle and its neighbors have visited since the algorithm was initiated. To update Pbest${^{k}}$ and Gbest${^{k}}$ in each time stamp we are using the $\varepsilon$-fuzzy dominance sorting approach as mentioned in Sect. 6.3.

Velocity update: For particle updating, we are first updating velocity matrix according to (15) and then finally position matrix is updated using (16).

$$\begin{aligned} V_{(i,j)}^{k}(t+1)\!&= \!\omega \cdot V_{i,j} ^{k}(t)\!+\! c_{1}r_{1}(\mathrm{Pbest}_{i,j}^{k}(t)-X_{i,j}^{k}(t))\!+\! c_{2}r_{2}(\mathrm{Gbest}_{i,j}^{k}(t)-X_{i,j}^{k}(t))\end{aligned}$$

(15)

$$\begin{aligned} X_{i,j} ^{k}(t+1)&= \left\{ \begin{array}{l@{\quad }l} 1 &{} \mathrm{if}\; V_{i,j} ^{k}(t+1)= \mathrm{max} \{V_{i,j} ^{k}(t+1)\}, \, \forall i\in \{1,2,\ldots , m\}\\ 0 &{} \mathrm{otherwise}\\ \end{array} \right. \end{aligned}$$

(16)

where $c_{1}$ and $c_{2}$ are the cognitive and interaction coefficients. The higher value of $c_{1}$ ensures large deviation of particle in search space while higher value of $c_{2}$ specifies the convergence towards its global best. To have the compromise between exploration and exploitation time varying coefficients have been introduced  [29]. It is proposed that $c_{1}$ decreases linearly over time, while $c_{2}$ increases linearly. The values of $c_{1}$ and $c_{2}$ at iteration t is evaluated as

$$\begin{aligned} {c_{1}}= (c_{1\mathrm{f}}-c_{1\mathrm{i}}) \frac{t}{\max \_t}+c_{1\mathrm{i}}\end{aligned}$$

(17)

$$\begin{aligned} {c_{2}}= (c_{2\mathrm{f}}-c_{2\mathrm{i}}) \frac{t}{\max \_t}+c_{2\mathrm{i}} \end{aligned}$$

(18)

where $c_{1\mathrm{f}}$ , $c_{2\mathrm{f}}$ are final values and $c_{1\mathrm{i}}$ ,$c_{2\mathrm{i}}$ are initial values of coefficients respectively. The random numbers $r_{1}$ and $r_{2}$ are generated independently in range [0, 1]. The parameter $\omega$ (inertia weight) controls the momentum of particles by weighing the contribution of previous velocity. The value of $\omega$ is important to ensure convergent behavior, and to optimize the tradeoff between exploration and exploitation. The higher value of $\omega$ helps in global exploration, so it is desired at the initial stages while lower values help in local search and is needed in the later stages. So the inertial weighing function is utilized as

$$\begin{aligned} {\omega }= ({\omega _\mathrm{max}}-{\omega _\mathrm{min}}) \frac{\mathrm{max}\_t-t}{\mathrm{max}\_t}+{\omega _\mathrm{min}} \end{aligned}$$

(19)

Using Eq. (16), in each column of position matrix, the value 1 is assigned to the element whose corresponding element in velocity matrix has maximum value in its corresponding column. If in a column of velocity matrix there are more than one element with max value, then one of these elements is selected randomly and 1 is assigned to its corresponding element in the position matrix.

Fitness functions: In this paper, multiple objectives of makespan (execution time), total cost and reliability are considered for the evaluation of workflow scheduling algorithm. The fitness functions$F_\mathrm{time}$ (S), $F_\mathrm{cost}$ (S) and $F_\mathrm{rel\_index}$ (S) are formed in order to evaluate individuals and are calculated from Eqs. (7), (8) and (11) respectively by adding the penalty value. On the violation of deadline and budget constraints, penalty is added to the respective objective function, otherwise not.

5.2 $\varepsilon$-Fuzzy dominance

In multi-objective problems, it is impossible to find a solution that is best with respect to all the objectives. Also, it makes the problem of requirements specification a real challenge. Under these circumstances, the concept of Pareto optimality is used. Since all the solutions in the Pareto set are non-dominated, they must be treated as all equally good. The ranking based on non-dominance sorting algorithm has the drawback of not providing a complete framework for easy implementation of new methods, as it does not measure the extents by which one solution dominates another. This yields the new measure called fuzzy dominance  [17] which correlates with the crisp definition of dominance.

Let us assume the MOP with the aim to minimize M number of objectives functions $f_{i}(s), \ i=1,\ldots ,M$. The solution set (containing set of all possible solution vectors) is denoted as $\Psi \subset R^n$ where n is the dimensionality.

Fuzzy i-dominance by a solution: Given a monotonically non-decreasing function $\mu _i^\mathrm{dom}(.)$, whose range is in [0, 1], $i \in \{1, 2,\ldots , M \}$, a solution $u \in \Psi$ is said to i dominate solution $v \in \Psi$, if and only if $f_{i}(u)<f_{i}(v)$. This relationship will be denoted as $u{\succ _{i}^{F}}v$. If $u{\succ _{i}^{F}}v$, the degree of fuzzy i dominance is equal to ${\mu _{i}^\mathrm{dom}}(f_{i}(v)-f_{i}(u))\equiv {\mu _{i}^\mathrm{dom}}\left( u{\succ _{i}^{F}}v\right)$. Fuzzy dominance can be regarded as fuzzy relationship $u{\succ _{i}^{F}}v$ between u and v.

Fuzzy dominance by a solution: Solution $u \in \Psi$ is said to fuzzy dominate solution $v \in \Psi$ if and only if $\forall i \in \{1, 2,\ldots , M\}, u{\succ _{i}^{F}}v$ holds. This relationship can be denoted as $u{\succ ^{F}}v$. The degree of fuzzy dominance can be defined by invoking the concept of fuzzy intersection and using t-norm, and is computed as

$$\begin{aligned} {\mu ^\mathrm{dom}\left( u{\succ ^{F}}v\right) }= \mathop {\bigcap }_{i=1}^{M}{\mu _{i}^\mathrm{dom}\left( u{\succ _{i}^{F}}v\right) } \end{aligned}$$

(20)

In the previous implementation of fuzzy dominance  [17], the membership functions ${\mu _{i}^{dom}}(.)$ used to compute the fuzzy i dominance were defined to be zero for negative arguments. So if $f_{i}(u)>f_{i}(v)$, the degree of fuzzy dominance $u{\succ _{i}^{F}}v$ was necessarily zero. Here we allow non-zero values. With the use of $\varepsilon$, non-dominated solutions may not necessarily be assigned zero values. The membership functions used are trapezoidal, yielding non-zero values whenever their arguments are to the right of threshold $\varepsilon$. Mathematically the membership function ${\mu _{i}^\mathrm{dom}\left( u{\succ _{i}^{F}}v\right) }$ are defined as:

$$\begin{aligned} \mu _{i}^\mathrm{dom}(\Delta f_{i})=\left\{ \begin{array}{l@{\quad }l} 0, \ &{} \Delta f_{i}\le -\varepsilon \\ \frac{\Delta f_{i}}{\Delta _{i}},\ &{} -\varepsilon <\Delta f_{i}<\Delta _{i}-\varepsilon \\ 1,\ &{}\Delta f_{i}\ge \Delta _{i}-\varepsilon \end{array}\right. \end{aligned}$$

(21)

where $\Delta f_{i} = f_{i}(v)- f_{i}(u)$.

Fuzzy dominance in a population: Given a population of solutions $S \in \Psi$, a solution $v \in S$ is said to be fuzzy dominated in S iff it is fuzzy dominated by any other solution $u \in S$. In this case the degree of fuzzy dominance can be computed by performing a union operation over every possible ${\mu ^\mathrm{dom}\left( u{\succ ^{F}}v\right) }$, carried out using t-co norms as:

$$\begin{aligned} {\mu ^\mathrm{dom}(S{\succ ^{F}}v)}= \mathop {\bigcup }\limits _{{u \in S}}{\mu ^\mathrm{dom}\left( u{\succ ^{F}}v\right) } \end{aligned}$$

(22)

In this manner, each solution is assigned a single measure to reflect the amount it dominates the others in a population. Better solutions within the set are assigned lower fuzzy dominance values. This sorting procedure is used to select the best global particle available after each iterative step.

In order to find the fuzzy dominance by a solution we need to compare it with other solution M times corresponding to M number of objectives. Then to obtain fuzzy dominance in a population, the solution is compared to every other solution of the population. It requires MN number of comparisons, where N is the size of the population. Finally to assign fuzzy dominance for solutions corresponding to population of size N, the total complexity is ${O(MN^{2})}$.

6 Proposed multi-objective workflow scheduling algorithm ($\varepsilon$-FDPSO)

In order to solve the multi-objective workflow scheduling problem, the $\varepsilon$-FDPSO algorithm is used as follows:

• 1. Initialize population of Size N. Set iteration counter $t=0$.

  • Randomly initialize the $m\times n$ dimensional swarm particles. $X_{(i,j)}^{k} (0) \forall k \in \{1, 2,\ldots , N \}$.

  • Initialize all particle velocities $V_{(i,j)}^{k} (0)$ to zeros and personal best position Pbest$_{{i,j}}^{k} (0)$ is set to $X_{(i,j)}^{k} (0)$.

• 2. Evaluate the particles of the swarm according to the values of its objective (fitness) functions. Sort the particle of the swarm on the basis of $\varepsilon$-fuzzy dominance and perimeter. Then initialize the archive $A_{(i,j)}^{k} (0)$ with it.

• 3. $t=t+1$.

• 4. Repeat the loop (step through the PSO operators)

  • Initialize the global best position for $k$th particle Gbest$_{(i,j)}^{k} (0)$ from the archive with binary tournament selection.

  • Update the velocity of $k$th particle $V_{(i,j)}^{k} (t)$ according to Eq. (15).

  • Update particle position $X_{(i,j)}^{k} (t)$ according to Eq. (16).

  • Mutate the particle position with adaptive mutation.

  • Repeat the loop for all the particles.

• 5. Evaluate each particle $X_{(i,j)}^{k} (t)$ in the population.

• 6. Make the union of current particle positions and archive particles positions from previous iteration to have total of 2N particle positions. Select the best N solutions on the basis of $\varepsilon$-fuzzy dominance sort and perimeter and finally update the archive as mentioned in Sect. 6.1.

• 7. Update each particles Pbest$_{(i,j)}^{k} (t)$ and Gbest$_{(i,j)}^{k} (t)$ as mentioned in Sect. 6.3.

• 8. Increment the loop counter. If it is less than max _t of iteration then go to step 3, otherwise output the $\varepsilon$-fuzzy dominant solutions from the archive.

The main operators used in this algorithm are explained below.

6.1 Updating external archive

In multi-objective algorithms use of elite archive is common  [20] that is used to store the non-dominated particles found along the search process. After the evaluation of objective functions, each particle is checked for its $\varepsilon$-fuzzy dominance with other members of the population. The archive stores the best N (size of archive) $\varepsilon$-fuzzy dominated solutions found so far by the $\varepsilon$-FDPSO. This is obtained by making the union of solutions from the current generation and the solutions from the archive of previous generations. Then these 2N solutions are sorted in ascending order of $\varepsilon$-fuzzy dominance. If multiple solutions are having the same value of $\varepsilon$-fuzzy dominance, then perimeter (I(.)) is assigned to each such solution and the solution having higher value of I(.) is preferred. From these 2N solutions sorted on the basis of $\varepsilon$-fuzzy dominance and perimeter, the best N solutions are selected to update the archive.

6.2 Perimeter assignment

When multiple solutions are having the same $\varepsilon$-fuzzy dominance value, then we use the diversity fitness function equal to the perimeter of the largest M dimensional hypercube in the objective space  [30]. The value of perimeter $I (v)$ for any solution v is given by:

$$\begin{aligned} I(v)=\mathop {\sum }\limits _{i=1}^{M}( f_{i}(u)- f_{i}(w))/(\mathrm{max}(f_{i})-\mathrm{min}(f_{i})) \end{aligned}$$

(23)

where u and w are solutions adjacent to v, when merged population is sorted in ascending order according to $i$th objective. Boundary solutions are assigned infinite value. Solution with higher value of $I(v)$ is preferred because it indicates the region of sparseness along solution v, which ultimately maintains the diversity of the solutions. Here we have to sort at most N solutions corresponding to M objective functions. Therefore, perimeter assignment has O(M N log N) complexity.

6.3 Updating particles memory (Pbest and Gbest)

The Gbest solution is selected by binary tournament selection from individuals of the current archive which are sorted on the basis of $\varepsilon$-fuzzy dominance and perimeter. For the Pbest, we compare particle current position with the best position of particle from the previous generation. The non-dominating solution is assigned as the current Pbest. If the solutions are mutually non-dominating to each other, then the current position of particle is selected as current Pbest.

6.4 Adaptive mutation

The use of mutation operator is needed in multi-objective PSO  [31] to avoid getting stuck into local minima and to efficiently explore the search space. Here, we reduce the percentage of mutation as it progress to make a balance between exploration and exploitation.

$$\begin{aligned} P(\mathrm{Mutation}) = 1- t/\mathrm{max}\_t \end{aligned}$$

(24)

where t represents the current iteration and max_t representing the maximum number of iterations taken. For every particle a random number (m_rand) in range [0, 1] is taken. If $m$_rand $<$ $P$(Mutation), then randomly a task is selected from the particle for mutation. Here, we are using the replacing mutation operator.

The complexity of one iteration of the proposed algorithm is dominated by the basic operations of : (1) fuzzy dominance assignment ${O(MN^{2})}$, 2) perimeter assignment $(O(M N \mathrm{log} N))$ and sorting on 2N solutions $(O(2N \mathrm{log} (2N))$ as mentioned in step 6 of the algorithm. Therefore, the overall complexity of the proposed algorithm is ${O(MN^{2})}$ due to the fuzzy dominance assignment.

7 Simulation strategy

We used GridSim  [32] toolkit in our experiment to simulate the scheduling of workflow tasks. GridSim is a java based toolkit for modeling and simulation of resource and application scheduling in large-scale parallel and distributed computing environment such as Grid. It is flexible to support simulation of grid entities like resources, users, application tasks, resource brokers or schedulers and their behavior using discrete events.

7.1 Simulation model

To simulate precedence constraint tasks in workflows, we used the different workflow models represented by randomly generated task graphs and task graph corresponding to real world problems such as Gaussian elimination and Fast Fourier Transforms as in  [21]. We also varied the size of the task graph by taking the different number of tasks as taken in [33].

The resources were eight virtual nodes, where each virtual nodes consists of heterogeneous distributed computer systems with eight number of processors. Links between resources are established through a router so that direct communication can take place between resources. Computational rating (million instructions per second) of processing elements varies from pentium II to pentium IV and computational cost (in dollars) of each resource is generated randomly where cost is inversely proportional to computational rating. The failure rate of the resources has been considered between $10^{-5}$ and $10^{-7}$ failures/s.

In order to generate a valid schedule which can meet both deadline and budget constraints specified by the user, two algorithms HEFT  [34] and Greedy Cost were used to make deadline and budget effectively. HEFT is a time optimization scheduling algorithm in which workflow tasks are scheduled on minimum execution time heterogeneous resources irrespective of utility cost of resources. So HEFT gives minimum makespan (Time$_\mathrm{min}$) and maximum total cost (Cost$_\mathrm{max}$) of the workflow schedule. Greedy Cost is a cost optimized scheduling algorithm in which workflow tasks are scheduled on cheapest heterogeneous resources irrespective of the task execution time. Thus Greedy Cost gives maximum makespan (Time$_\mathrm{max}$) and minimum total cost (Cost$_\mathrm{min}$) of the workflow schedule Thus Deadline (D) and Budget (B) are specified as:

$$\begin{aligned} D&= \mathrm{Time}_\mathrm{max} - 0.1(\mathrm{Time}_\mathrm{max} -\mathrm{Time}_\mathrm{min})\end{aligned}$$

(25)

$$\begin{aligned} B&= \mathrm{Cost}_\mathrm{max} - 0.1(\mathrm{Cost}_\mathrm{max} - \mathrm{Cost}_\mathrm{min}) \end{aligned}$$

(26)

We considered the small value of budget and deadline (tight constraints)  [23], as it is challenging to get schedule under tight constraints.

At present, the most popular techniques to solve MOP are the probabilistic GA based non-dominated sort genetic algorithm (NSGA-II)  [19], MOPSO [20]. Thus, to measure the effectiveness and validity of $\varepsilon$-FDPSO algorithm for multi-objective workflow scheduling problem in grid, we have implemented the highly competitive techniques: NSGA-II, MOPSO (with time variant inertia and acceleration coefficients  [29]). To implement the NSGA-II we have taken binary tournament selection, two point crossover and replacing mutation.

The parameter values used for $\varepsilon$-FDPSO, MOPSO and GA are optimally tuned by trial and error experiments to let the competing algorithms perform at their best level. To be specific, the parameter setting used by $\varepsilon$-FDPSO and MOPSO is (population size = thrice the number of tasks, $c_{1}=2.5\rightarrow 0.5$ and $c_{2}=0.5\rightarrow 2.5$, inertia weight $(\omega = 0.9\rightarrow 0.1)$ and GA (population size = thrice the number of tasks, crossover rate $=$ 0.8, mutation rate $=$ 0.5). Furthermore, in $\varepsilon$- FDPSO, the $\varepsilon$-values of makespan, cost and reliability objective were varied from 0.010 to 0.015, 0.010– 0.015 and 0.0003–0.0009 in order to control the diversity and extent of obtained solutions respectively.

The performance of scheduling algorithm was evaluated considering different test suits representing workflow applications in bi-objective and tri-objective workflow scheduling.

• (i) Test suit of randomly generated task graph.

• (ii) Test suit of task graph corresponding to real world problems such as Gaussian elimination, Fast Fourier Transform.

7.2 Comparative performance

To evaluate the performance of the proposed approach for multi-objective workflow scheduling, various issues are taken into consideration: (1) we need to minimize the distance of the Pareto front produced to the global Pareto front (reference front). (2) The spread of the solutions should be smooth and uniform i.e. all the members of the Pareto front should be equally spaced. (3) Computational time should be minimum. Based on these issues, we used three metrics Generational Distance (GD), Spacing [35] and Computational Time. GD is the well known convergence metric to evaluate the quality of an algorithm against the reference front P*. The reference front P* was obtained by merging solutions of algorithms over 10 runs. On the other side, Spacing metric was used to evaluate diversity among the solutions. Mathematically GD and Spacing metric are expressed as:

$$\begin{aligned} \mathrm{GD}&= \frac{(\sum _{i=1}^{|Q|} d_{i}^{2})^{1/2}}{|Q|}\end{aligned}$$

(27)

$$\begin{aligned} \mathrm{Spacing}&= \sqrt{{\frac{1}{|Q|}}{\sum \nolimits _{i=1}^{|Q|}}( d_{i}-\overline{d})^{2}} \end{aligned}$$

(28)

In Eq. (27), $d_{i}$ is the Euclidean distance between the solution of Q and the nearest solution of P*. Q is the front obtained using an algorithm for which we calculate GD metric. In Eq. (28), $d_{i}$ is the distance between the solution and its nearest solution of Q and it is different from Euclidean distance. And, $\overline{d_{i}}$ is the mean value of the distance measures $d_{i}$. The small value of both GD and Spacing metric is desirable for an evolutionary algorithm. Further, we normalized Euclidean distance and distance value before using them in Eqs. (27) and (28) because all objectives in our problem are on different scale. We also present the computational time needed to run each algorithm.

7.3 Best compromise solution

The Pareto optimal set obtained by applying $\varepsilon$-FDPSO comprises of solutions that satisfy different goals to some extent. A Fuzzy-based approach  [36] is then applied to select the best compromised solution from the obtained Pareto set which can be offered to the decision maker. In this, a simple linear membership function was considered for each of the objective functions as follows:

$$\begin{aligned} \mu _{k}=\left\{ \begin{array}{l@{\quad }l} 1, \ &{} f_{k}\le f_\mathrm{min}\\ \frac{{f_{k}^\mathrm{max}}-f_{k}}{{f_{k}^\mathrm{max}}-{f_{k}^\mathrm{min}}}&{} \ {f_{k}^\mathrm{min}} <f_{k}<{f_{k}^\mathrm{max}}\\ 0,\ &{} f_{k}>{f_{k}^\mathrm{max}} \end{array}\right. \end{aligned}$$

(29)

where ${f_{k}^\mathrm{max}}$ and ${f_{k}^\mathrm{min}}$ are the maximum and minimum values of the $k$th objective function, among all Pareto optimal solutions respectively. The normalized membership function $\mu ^{i}$ corresponding to $i$th non-dominated solution is defines as

$$\begin{aligned} \mu ^{i}=\frac{\Sigma _{k=1}^{M}\mu _{k}^{i}}{\Sigma _{i=1}^{N}\Sigma _{k=1}^{M}\mu _{k}^{i}} \end{aligned}$$

(30)

where M is the number of objectives functions and N is the number of non-dominated solutions in the Pareto front. The solution having the maximum membership value $\mu ^{i}$ in the fuzzy set is considered as the best compromised solution.

8 Simulation results

8.1 Test suit 1

In this test suit, we used the workflow model represented by randomly generated task graph (Random). The size of random task graph was varied by considering the different number of nodes as 20, 50 and 100 to represent the small, medium and large size parallel application. The cost of each edge was selected randomly from the uniform distribution across the mean equal to the product of average computation cost and the communication to computation ratio (CCR). Here CCR is taken as 0.5 to represent the computation intensive application. The computation cost of each task $t_{i}$ on resource $r_{j}$ is selected randomly by the uniform distribution with the mean equal to the twice of specified average computation cost.

In bi-objective workflow scheduling, the makespan and cost of the schedules are considered. The Pareto optimal solutions obtained with $\varepsilon$-FDPSO, MOPSO and NSGA-II for bi-objective problem, obtained after 200 iterations are shown in Figs. 2, 3 and 4 for the first test suit chosen. From the typical run shown in Figs. 2, 3 and 4, we can see that most of the solutions obtained with $\varepsilon$-FDPSO are lying on the better front while preserving almost uniform spacing among solutions. This may be attributed as the fuzzy dominance sorting allows the selection of solutions which are closer to non-dominated front with less $\varepsilon$-fuzzy domination and $\varepsilon$-domination maintains the $\varepsilon$-value gap between solutions.

Fig. 2

Performance of the algorithms in bi-objective workflow scheduling for the test suit 1 (number of task $=$ 20)

Fig. 3

Performance of the algorithms in bi-objective workflow scheduling for the test suit 1 (number of task $=$ 50)

Fig. 4

Performance of the algorithms in bi-objective workflow scheduling for the test suit 1 (number of task $=$ 100)

Table 1 shows the comparison result among the three algorithms on the basis of metrics described previously. The results are obtained by taking the average over the 10 runs. The value of convergence metric GD corresponding to $\varepsilon$-FDPSO is less as compared to other algorithms considered for all the three cases. It clearly specifies that performance of the proposed algorithm is better and reaches a solution set very close to true Pareto front. Further, with the increase in the number of tasks performance of the algorithm increases due to occurrence of large number of non-dominated solutions (from large sample space). With the help of fuzzy dominance sorting, solutions which are closer to non-dominated front are selected and thus provides better convergence.

Table 1 GD, spacing and computational time metric results of the algorithms in bi-objective workflow scheduling for the test suit 1

Regarding spread of solutions, measured by spacing metric shows that $\varepsilon$-FDPSO performs better (showed by lower values for the spacing metric) because of perimeter assignment operator and $\varepsilon$-domination. Finally, it is interesting to note that, proposed algorithm provides better convergence and uniform spacing in relatively small computational time.

In tri-objective workflow scheduling problem, we considered the three conflicting objectives of makespan, cost and reliability. In order to obtain Pareto optimal set of solutions, we have run $\varepsilon$-FDPSO, MOPSO and NSGA-II algorithms over 400 iterations. The Pareto solutions of each algorithm at different number of tasks graphs considered in this test suit are shown in Figs. 5, 6 and 7. The results clearly specify that most of the solutions corresponding to $\varepsilon$-FDPSO are falling in the better minimization region as compared to MOPSO and NSGA-II with more uniform spacing. Table 2 shows the comparison of results among three algorithms corresponding to metrics considered previously. It can be seen that $\varepsilon$-FDPSO converges with small computational time and provides uniform spacing.

Fig. 5

Performance of the algorithms in tri-objective workflow scheduling for the test suit 1 (number of task $=$ 20)

Fig. 6

Performance of the algorithms in tri-objective workflow scheduling for the test suit 1 (number of task $=$ 50)

Fig. 7

Performance of the algorithms in tri-objective workflow scheduling for the test suit 1 (number of task $=$ 100)

Table 2 GD, spacing and computational time metric results of the algorithms in tri-objective workflow scheduling for the test suit 1

The best compromised solutions obtained by the proposed algorithm for test suit 1 in bi-objective and tri-objective workflow scheduling problems are shown in Table 3 respectively.

Table 3 Compromised solutions obtained by $\varepsilon$-FDPSO for the test suit 1 in bi-objective and tri-objective workflow scheduling

8.2 Test suit 2

In this test suit, we generated the task graphs corresponding to real life problems such as Gaussian Elimination (GE) and Fast Fourier Transform (FFT). The structure of these task graphs is fixed. The numbers of nodes chosen are 27 and 39 (medium size task graph) respectively. The cost of each edge was selected randomly from the uniform distribution with mean equal to the product of average computation cost and the communication to computation ratio (CCR). Here CCR is taken as 0.5 to represent the computation intensive application. The computation cost of each task $t_{i}$ on resource $r_{j}$ is selected randomly by the uniform distribution with the mean equal to the twice of specified average computation cost. In multi-objective workflow scheduling, Figs. 8, 9 (corresponding to Bi-objective problem) and Figs. 10, 11 (corresponding to Tri-objective problem) shows the Pareto optimal solutions produced by the algorithms considered for the chosen second test suit. The graphs clearly specifies that solutions obtained with $\varepsilon$-FDPSO are lying on the better front compared to other algorithms, while preserving uniform diversity between solutions. The results obtained with GD and Spacing metric along with computation time by the three algorithms for second test suit in Bi-objective and Tri-objective workflow grid scheduling problem are shown by Tables 4 and 5 respectively. The trends are similar to test suit 1. It can be seen that the performance of $\varepsilon$-FDPSO is best with respect to convergence and spacing with small computation time.

Fig. 8

Performance of the algorithms in bi-objective workflow scheduling for the test suit 2 (GE)

Fig. 9

Performance of the algorithms in bi-objective workflow scheduling for the test suit 2 (FFT)

Fig. 10

Performance of the algorithms in tri-objective workflow scheduling for the test suit 2 (GE)

Fig. 11

Performance of the algorithms in tri-objective workflow scheduling for the test suit 2 (FFT)

Table 4 GD, spacing and computational time metric results of the algorithms in bi-objective workflow scheduling for the test suit 2

Table 5 GD, spacing and computational time metric results of the algorithms in tri-objective workflow scheduling for the test suit 2

The convergence of $\varepsilon$-FDPSO is relatively high in case of tri objective workflow scheduling for both test cases considered, because as the number of objectives are increasing, density of non-dominated solutions close to the Pareto set increases. In algorithms NSGA-II and MOPSO they treat all the non-dominated set of solutions as equally good solutions, as they do not quantify the extent by which one solution dominates other or how close it is to the Pareto set. So there are chances of selecting the solutions in the next iteration which are non-dominated to each other but level of their non-dominance may not be very high. On the other hand in our proposed algorithm, we are able to discriminate solutions which are closer to the non-dominated set (Pareto set) from those further behind with the help of $\varepsilon$-fuzzy dominance so better solutions will definitely be picked up for the next iteration. Thus with the help of $\varepsilon$-fuzzy dominance sort based selection, the speed of convergence increases. This specifies that $\varepsilon$-FDPSO is the better choice for multi-objective workflow grid scheduling problem especially when number of objectives are large.

Table 6 shows the best compromised solutions obtained by the proposed algorithm for the current test cases in bi-objective and tri-objective workflow scheduling problems, respectively.

Table 6 Compromised solutions obtained by $\varepsilon$-FDPSO for the test suit 2 in bi-objective and tri-objective workflow scheduling

9 Conclusion and future work

Over the years, researchers have focused their attention on grid scheduling problem with a single objective. However, the goal of decision maker is multi-fold and prefers the set of Pareto optimal solutions when considering real life applications. The current work emphasizes on the planning and optimizing the workflow scheduling in the grid with conflicting objectives of minimization of execution time (makespan), cost and maximization of reliability. Here, we have used DPSO using $\varepsilon$-fuzzy dominance based sorting ($\varepsilon$-FDPSO) approach to solve the problem. Although, the approach was introduced earlier, it has never been applied to the problem studied in this paper. The simulation experiments, using randomly generated task graphs and task graphs corresponding to real world problems, exhibit that $\varepsilon$-FDPSO performs better for grid workflow task scheduling in terms of the convergence towards the true Pareto optimal front and uniformly distributed solutions with small computation overhead. In case of tri-objective workflow scheduling, relative performance of the candidate algorithm is high, due to use of fuzzy dominance rather than simple non-dominance for selection of solutions in the Pareto set. A good course of future research may be to develop the hybrid multi-objective optimization techniques to solve the workflow grid scheduling problem and compare their performance with $\varepsilon$-FDPSO.