Introduction

Understanding of the structure and symmetry of quasicrystals is one of the major unsolved problems in modern solid-state physics and chemistry. Discovery of quasicrystals by Shechtman et al. [1] led to the revision of the basic principles which underlay the packing of atoms and molecules in solids. The mere fact of the existence of quasicrystals was extremely controversial to the fundamentals of crystallography and dominating scientific opinions. Since the discovery of the X-ray diffraction in crystals, the terms order and periodicity have been meant to be synonymous. The discovery of quasicrystals has seriously challenged this understanding. It has become obvious that all special features which were previously meant to be associated with the notion of a crystal (i.e., the strict long-range order, the discreteness of diffraction patterns, the perfect external faceting, and the anisotropy of properties) do not require obligatory periodicity.

The two-dimensional aperiodic tiling invented by Penrose [2] has for a long time inspired mathematicians, physicists, and chemists to look for a new state of matter. Even before the quasicrystals were actually experimentally discovered, Mackay had showed [3] that the aperiodic distribution of atoms may have an essentially discrete diffraction pattern, despite the lack of lattice periodicity. The importance of his work cannot be overestimated. The discreteness of the diffraction pattern is now adopted as a basis for the new definition of the notion of a crystal. After Steinhardt et al. [4–6] introduced the term quasicrystal and offered a theoretical explanation of icosahedral quasicrystals, based on the grid projection technique from six-dimensional hypercubic lattice, a new scientific discipline has been developed—namely, quasicrystallography. We do not pretend to make a balanced review here but rather refer the reader to the more detailed descriptions of the modern viewpoints on the structure and properties of quasicrystals, which may be found in literature [7–23].

Despite the significant advances in the structural characterization of quasicrystals, the problem is still far from being completely solved. The first question is: What is, in fact, a quasicrystal? According to Senechal [24], no one is sure. The definition of a quasicrystal as a solid with forbidden symmetry appeals to the crystallographic restriction theorem in a mutually exclusive manner. If they are really forbidden, then why do they exist? If they do exist, then who forbade them and why? Thus, the old definition appealing to the forbidden symmetry is incorrect. On the other hand, when one recedes from the crystallographic restriction theorem, another question arises. Do quasicrystals comply with some restrictions in place of the rejected ones? Of course, we are familiar with the claim by Steinhardt et al. [5] that “in fact, they [quasicrystals] can have arbitrary orientational symmetries disallowed for crystals corresponding to any star of symmetry vectors.”

The Commission on Aperiodic Crystals decided on a temporary working definition whereby a crystal is “any solid having an essentially discrete diffraction diagram,” because the Commission was not ready to give precise microscopic descriptions of all the ways in which order can be achieved. The arguments pro and contra have been adduced by Lifshitz [25, 26]. So, the new definition adopted by the International Union of Crystallography states that an aperiodic crystal is meant to be a structure with sharp diffraction peaks, but without lattice periodicity.

Dyson [27] proposed the following mathematical definition: “A quasicrystal is a distribution of discrete point masses whose Fourier transform is a distribution of discrete point frequencies. Or to say it more briefly, a quasicrystal is a pure point distribution that has a pure point spectrum. This definition includes as a special case the ordinary crystals, which are periodic distributions with periodic spectra.” Next, he described an example of the very special kind of non-periodic structure, which perhaps meets all the other mentioned conditions. Particularly, Dyson wrote [27]: “Here comes the connection of the one-dimensional quasicrystals with the Riemann hypothesis. If the Riemann hypothesis is true, then the zeros of the zeta-function form a one-dimensional quasicrystal according to the definition. They constitute a distribution of point masses on a straight line, and their Fourier transform is likewise a distribution of point masses, one at each of the logarithms of ordinary prime numbers and prime-power numbers.” On the one hand, such an artificial solid is hardly to imagine because the interatomic distances are determined by the nature of the chemical bonds. On the other hand, we can easily imagine or even construct a corresponding photonic crystal using modern technologies [28]. Perhaps this may result in the creation of a new exotic kind of photonic aperiodic crystals with unique properties. Recall that the Fourier transform is a reversible linear transformation. Thus, we can imagine another artificial solid or construct a certain photonic crystal following the rules of the prime number distribution. Perhaps this will result in another kind of aperiodic crystals, which may also reveal some unique properties. However, all of these are not quasicrystals or, strictly speaking, they are not those, which were previously meant to be as quasicrystals. When the mere term quasicrystals was introduced, Levine and Steinhard [4] especially emphasized the self-similar arrangement of atoms in real space, the self-similar arrangement of Bragg peaks in reciprocal space, and the self-similar sequence of gaps in both electronic density of states and phonon spectrum. So, we would like to keep the term quasicrystal reserved for those of aperiodic crystals which exhibit the multiple self-similarity.

The most successful approach to describe the structure of quasicrystals is now associated with the high-dimensional crystallographic methodology. Within the frameworks of the higher-dimensional approach [9], diffraction pattern in the form of aperiodic set of δ-peaks can be indexed by the usual way. If the number of basic vectors n is taken to be greater than the real space dimensionality, it causes the necessity of a nD reciprocal space. Consequently, this becomes a direct space of the same dimensionality—the embedding space. The respective cut-and-project procedure provides the correspondence between physical and embedding spaces based on the fact that the actual quasiperiodic structure in 3D physical space can be obtained by slicing higher-dimensional lattice by irrational hyperplanes and projecting the resulting strip from the embedding space. Thus, the aperiodic 3D crystal structure consisting of real 3D atoms results from a cut of a periodic nD lattice decorated with nD hyperatoms. Electron density distribution functions of fictitious nD hyperatoms as well as their scattering factors and exact positions in the embedding space can be calculated directly from the observed diffraction pattern [19, 23].

We are strongly convinced that a three-dimensional description is always preferable for a three-dimensional object. This may be exemplified by the quotation from the monograph by Hyde et al. [29]: “The problem is to relate observed diffraction patterns with non-standard, supposedly disallowed, crystallographic symmetries, to the atomic distributions that cause them. That problem remains. Because while a physicist living in world made up of equations and group theory has no difficulty in constructing the universe, its scaling laws, and singularities like black holes, as a realization of a sixteen dimensional group say, the chemist is more narrowly constrained. A three-dimensional atom has a certain pedestrian reality that does not so easily lend itself to a mapping onto six dimensions.”

If the suitable substitution rules were available for the three-dimensional quasicrystalline packings, the inflation/deflation procedure, applied iteratively, could represent an alternative to the higher-dimensional approach in order to fill the entire space by a quasicrystalline manner. To our knowledge, no attempts have been made to formulate the substitution rules for icosahedral packings. The goal of the present paper is to describe the icosahedral quasicrystals without appealing to higher dimensions.

Fractal approach

Before proceeding with the three-dimensional packings, we would like to explain the key features of our approach using the two-dimensional Penrose tiling as an example.

Earlier, we have assumed that “unusual” structures may have idealized prototypes in non-Euclidean spaces [30]. After being mapped into the real space, “unusual” structures inherit partially the non-Euclidean symmetry, which becomes not quite evident or “hidden.” The main task is to estimate the hidden symmetry of quasicrystals and to define their structure through their symmetry groups. This is not a slip of the tongue. We would like to abandon the widely accepted point of view that quasicrystals have only the point symmetry and that their whole structure is described by groupoids instead of groups. If both inflation and deflation procedures are performed infinitely many times, the resulting structure becomes a fractal. All locally isomorphic tilings converge to the common infinitely fragmented fractal parent, which may be described in terms of the group theory by the usual manner. It is reasonable to refer the symmetry group of such fractal tiling to any aperiodic crystal belonging to the corresponding Penrose local isomorphism class.

The concept of the fractal Penrose tiling has been introduced by Bandt and Gummelt [31], who were, perhaps, ready to encounter some skepticism, especially emphasizing that “…some readers will find [it] inconvenient to work with such tiles.” They investigated the kites-and-darts Penrose tiling and proposed to replace the basic tiles by corresponding tiles with fractal boundaries that were obtained iteratively by multiple application of the deflation procedure. The proper matching rules were derived from the shape of initial tiles, which were referred to as “natural” matching rules. Fractal boundaries reflected the self-similarity in a very natural way.

Recently, we applied the concept of infinite fragmentation to the rhombus Penrose tiling [32, 33]. We have shown that the tiling may be considered as an equivalent covering by overlapping resized copies of some unique fractal island, which are in turn covered by smaller islets, and so forth. On the other hand, we can take the conventional tiling into thick and thin rhombuses, perform the deflation infinitely many times, and superimpose the initial conventional tiling over the fractal. After that, we can consider the fractal tiling in the usual way but bearing in mind that every usual tile contains a fractal dust of quasilattice sites inside. The true symmetry of the fractal tiling is much higher than the apparent symmetry of that represented by finite-sized tiles. Fractal tilings have the special features of being self-similar and self-inverse. There has been exhaustive discussion as to why the multiple self-similarity does not conflict with crystallinity [32].

It is universally accepted that eight inequivalent sites exist in the rhombus Penrose tiling [7, 8, 20, 23]. Consider the thick and thin rhombuses and perform the deflation several times. We have to emphasize that the conventional operations should be applied twice in a row (Fig. 1). Inequivalent rhombus sides are, as usual, marked with single and double arrows. Choose an arbitrary vertex and apply both inflation and deflation procedures to its local environment. Apply both operations repeatedly making a pause after each even iteration and comparing results. The local environment of any vertex ceases or will cease to change in the end coinciding with one of two possible self-similar arrangements.

Fig. 1
figure 1

Deflation of the thick (a) and thin (b) rhombuses of the Penrose tiling. Only two vertex types exist in the infinitely fragmented fractal “parent” (designated by open and solid circles, respectively). Only even iterations of the standard deflation procedure do not permute the vertices of alternative types

Full size image

If in the same manner we would operate with an infinitely fragmented tiling represented by finite-sized tiles that are filled with a fractal dust, we could reveal that the tiling itself remains unchanged in this case. This only leads to an increase of the scale of consideration, as if the details of the picture are examined through a very large magnifying glass. The regions initially surrounding the chosen site, in the limiting case, become removed infinitely far away. Therefore, in the corresponding fractal tiling, there exist only two types of vertices that are invariant with respect to the self-similarity. All vertices, toward which the double-arrows point and which were marked with dots by de Bruijn [7, 8], belong to the first type. All the rest vertices belong to the second type. Two inequivalent types of vertices are referred by us to as the A and B types, and designated by open and solid circles, respectively.

Based on the fact that only even iterations of the conventional deflation procedure do not permute the inequivalent vertices [32], we restated the natural matching rules for the rhombus Penrose tiling (Fig. 2). When considering deflation rules, we cover the thick and thin rhombuses with their own copies reduced in τ 2 times, where τ is the golden mean. We highlight that, contrary to the widely accepted view, we use the inflation factor of τ 2 but not of τ. For any rhombus, one out of the four vertices corresponds to the first type of locally inequivalent sites, while the other three vertices correspond to the second type. The edge marked with the single arrow connects two vertices, which are both of the second type. The edge marked with the double arrow connects two alternate vertices. After deflation, the additional A-type vertex divides the [BB]-type edge into two unequal parts in the τ:1 ratio, whereby the single-arrow edge decomposes into the reduced copy of the double-arrow edge and the reduced copy of the thick rhombus. The additional B-type vertex divides the [AB]-type edge into two unequal parts in the τ:1 ratio, whereby the double-arrow edge decomposes into the reduced copy of the thick rhombus and the reduced copy of the single-arrow edge. The diagonal of the thick rhombus decomposes into: the small copy of the double-arrow edge, two thick rhombuses reduced in τ 4 and τ 2 times, respectively, and the small copy of the single-arrow edge. The diagonal of the thin rhombus turns into the diagonal of the τ 2 times reduced thick rhombus.

Fig. 2
figure 2

Restated inflation/deflation rules for the rhombus Penrose tiling by using the inflation factor of τ 2. a Deflation of the thick and thin rhombuses. b Decomposition of inequivalent edges and diagonals of thick and thin rhombuses. c Natural local matching rules as a consequence of the multiple self-similarity of the fractal islands

Full size image

Let us generate fractal islands. For this purpose, we deflate thick and thin rhombuses infinitely many times. After the first iteration (i.e., the 2nd conventional), some of the reduced copies of the thick rhombus belong to the initial regions only by half since the edges of the initial rhombuses pass along the diagonals of the reduced copies. We expand the initial rhombuses, so that the regions, thus obtained, will contain all the reduced copies entirely. By applying the second iteration (i.e., the 4th conventional), we again find that some of the copies of even smaller sizes partially project beyond the considered regions. Next, we expand the regions, so that they will include smaller rhombuses located at the boundaries and continue this procedure to infinity. As a result, we obtain the “islands” with fractal boundaries instead of rhombuses. When the overlapping fractal islands are finally combined according to the restated inflation/deflation rules, one can easily reveal that the shared regions represent nothing but the smaller and smaller copies of the initial thick fractal island, so that the multiple self-similarity becomes obvious.

Self-similarity, in general, is described as the rotational homothety conjugated with translation. Improper rotations or rotoreflections combined with rescalings and shifts should also be taken into account. It is important to emphasize that self-similarity should be considered as the true group automorphism and not as the repeating structural motifs in solids or substitution rules for tilings (Fig. 3). Logarithmic spirals represent the geodesic lines of the rotational homothety. Point-to-point correspondence for the equivalent vertices is depicted in the figure. Note again that the self-similarity group operations, thus defined, do not permute the vertices of alternative types.

Fig. 3
figure 3

Two self-similar plane tilings with complete fivefold point symmetry (a, b). Logarithmic spirals represent the geodesic lines of the rotational homothety

Full size image

Compare the two above plane tilings with the complete fivefold point symmetry. Both their “parent” fractals reveal the true self-similarity, because they coincide with themselves as a whole when mapping the entire space onto itself by corresponding affine transformation composed with rotation. The question then arises as how to combine self-similarities with different fixed points. The affine transformation has the only singular fixed point. It cannot move. The solution is indeed so simple that it seems almost absurd: It is necessary to consider another topological space instead of the Euclidean plane.

We should simply replace the Euclidean plane with the extended complex plane. What is the secret of the trick? Imagine the Penrose tiling covering the entire plane and draw two axes indicating the real and imaginary parts of the complex variable (Fig. 4). It seems as nothing has changed. The Penrose tiling itself looks like before. But for now the problem of combining self-similarities with different fixed points is no longer the case. The first self-similarity operation that is acting on the fixed point of the second self-similarity operation produces the infinite set of “fixed” points when it is performed repeatedly and vice versa. The resulting infinitely fragmented fractal tiling may be described as usual in terms of the group theory, in contradistinction to the quasicristalline plane tiling from which it has been obtained.

Fig. 4
figure 4

Combining self-similarities with different fixed points in the complex plane

Full size image

Consider the following group automorphisms g k defined in terms of the complex plane mappings \(z \mapsto w\):

$$g_{1} :\quad w = \tau^{ - 2} \text{e}^{i \cdot 2\pi /10} z,$$
$$g_{2} :\quad w = \tau^{ - 2} \text{e}^{i \cdot 2\pi /10} \left( {z - \tau} \right) + \tau,$$
$$g_{3} :\quad w = \tau^{ - 2} \left( {z - 1} \right) + 1,$$
$$g_{4} :\quad w = \tau^{ - 2} \text{e}^{ - i \cdot 2\pi /10} z,$$
$$g_{5} :\quad w = \tau^{ - 2} \text{e}^{ - i \cdot 2\pi /10} \left( {z - \tau } \right) + \tau ,$$
$$g_{6} :\quad w = \tau^{ - 2} \text{e}^{i \cdot 2\pi /10} \left( {z - 1 - \tau } \right) + 1 + \tau ,$$
$$g_{7} :\quad w = \tau^{ - 2} \text{e}^{ - i \cdot 2\pi /10} \left( {z - 1 - \tau } \right) + 1 + \tau ,$$
$$g_{8} :\quad w = \frac{{\tau^{2} }}{z} + \tau ,$$

and, optionally, the complex conjugation:

$$g_{9} :\quad w = z^{*}.$$

All these symmetry elements represent some conformal transformations of the complex plane and, therefore, they are mutually compatible with each other. The elements \(g_{1} g_{4}^{ - 1}\) and \(g_{2} g_{5}^{ - 1}\) exemplify two different coexisting fivefold rotations around different points. The elements \(g_{1} g_{4}\) and \(g_{2} g_{5}\) represent two single affine transformations with different fixed points—dilatations with the scale factor of τ 4. Let us specify right away that not all of the above elements are necessarily independent.

We desire to draw special attention to the fact that is usually missed in most textbooks. Besides self-similarity, the logarithmic spiral has an additional “hidden” symmetry! The “golden” spiral coincides with itself after an inversion in a circle.

Imagine a fivefold rotation axis normal to the plane. It generates a unique center of global fivefold symmetry in the Euclidean plane as well as in the affine plane. On the contrary, at least two different centers of global fivefold symmetry emerge in the extended complex plane: one at the origin and another at the infinitely distant point. Recall that the complex plane may be brought into correspondence with a sphere by stereographic projection, so that the origin corresponds to the south pole, whereas the infinitely distant point corresponds to the north pole. The logarithmic spirals, which represent the geodesic lines for the rotational homothety in the plane, may be brought into correspondence with loxodromes on the sphere (Fig. 5). When the original representing points move along the logarithmic spirals in consequence of the complex plane self-similarity transformations, their images move along the loxodromes twisting around the opposite poles of the sphere.

Fig. 5
figure 5

Hidden symmetry of the Penrose tiling. a The complex plane brought into correspondence with a Riemann sphere by stereographic projection. The logarithmic spirals correspond to the loxodromes on the sphere. b The opposite poles represent two alternative vertex types

Full size image

The opposite poles look very much alike. They represent two alternative vertex types [33]. Indeed, let us place the initial fractal plane tiling tangent to the south pole, then perform the inverse stereographic projection, next place the second tangent plane and perform the stereographic projection once again but now from the south pole onto the plane that is tangent to the north pole, and finely compare the resulting fractals. Both have the common “parent,” both have the centers of fivefold symmetry, and both are characterized by twisting logarithmic spirals. Now, one can easily trace the point-to-point correspondence between corresponding geodesics. The poles become interchanged when the sphere is reflected in the equatorial plane. In the tangent plane, such transformation corresponds to the inversion in a circle. Single inversion, in the ordinary sense of this term, exchanges the interior of the circle with its own exterior, replacing the origin by the infinitely distant point. For example, the Apollonian gaskets reveal such kind of symmetry. The self-inversion of fractal aperiodic tilings should be considered in a broadened sense as a composition of the inversion with rotations, rescalings, and translations, whereas the pure reflection by itself in a circle can be absent as an independent symmetry element. The generalized inversion swaps the interior and the exterior of circles that are drawn around vertices of two alternative types [33]. This property can be clarified when taking into account the local isomorphism of the Penrose tiling and the analytic continuation for functions of the complex variable. Indeed, if a certain analytic function maps the exterior of some Jordan curve, drawn around the origin, exactly onto the interior of its image drawn around the vertex of the alternative type, then it maps the entire complex plane onto itself and represents the automorphism of the resulting fractal. So, the “hidden” inversive symmetry of the fractal Penrose tiling may permute the vertices of alternative types.

The inversion in the unit circle may be represented as the Möbius involution combined with the complex conjugation and vice versa: The Möbius involution may be represented as the inversion in the unit circle combined with the complex conjugation. The ordinary inversion swaps the interior with the exterior, whereby the clockwise twisted logarithmic spirals turn into the counterclockwise twisted spirals. The Möbius involution swaps the interior with the exterior without reflecting spirals. It is the orientation-preserving operation. Now, we can offer a conjecture:

Conjecture: All orientation-preserving symmetries of the fractal Penrose tiling may be expressed in terms of the Möbius transformations, whereby the symmetry group of the resulting fractal exemplifies the symmetry of a certain discrete subgroup of the continuous group of the linear fractional transformations. The full symmetry group may be obtained by adding the complex conjugation to the group generators.

Within the frameworks of the classical crystallography, the following well-known statements for periodic crystals are known: The composition of two reflections in parallel mirrors is equivalent to the translation, and the composition of two reflections in mutually intersecting mirrors is equivalent to the rotation. The corresponding statement for aperiodic crystals can be formulated as follows: The product of inversions with a common center but with different radii is equivalent to the similarity. Thus, any operation of the similarity can be expressed as a composition of inversions.

Let us draw two nonintersecting circles around vertices of different types, each of which passes through ten alternating sites. Then, we can establish the Möbius transformation that maps the interior of the first circle onto the exterior of the second circle, and vice versa. This mapping will serve as the first generating element. Next, instead of one of the circles, we take another circle, which radius is τ 2 fold less. Such inversion will serve as the second generating element. Similarly, we can choose the second pair of sites and obtain the next generating elements. Finally, we can continue this procedure until the group is completely defined. Note that the described procedure is nothing but the generation of the Schottky group [34].

The Schottky groups represent the special kind of the finitely generated free Kleinian groups. All of their non-trivial generating elements are loxodromic. These groups are very diverse, extremely intricate, and rather complex. Their systematic investigation has been hampered for a long time. Growing computational capabilities of computer graphics have broken the deadlock. The essence of the problem can be clarified by the quote from the monograph by Mumford et al. [34], who noted that this kind of symmetry is characteristic for “…a family of unusually symmetrical shapes, which arise when two spiral motions of a very special kind are allowed to interact” and that “these shapes display intricate ‘fractal’ complexity on every scale from very large to very small.” The visualization of the Schottky groups forms part of a century-old dream conceived by the great German geometer Felix Klein. Sometimes, the interaction of the two spiral motions is quite regular and harmonious, sometimes it is total disorder, and sometimes—and this is the most intriguing case—it has layer upon layer of structure teetering on the very brink of chaos. Simply put, these groups describe the interaction of spiral motions on the plane or, in other words, the multiple self-similarity.

Fractal self-similar tilings necessarily exhibit the circular property. Any of their symmetry operations maps the given circle again into a circle. Thus, the problem of quasicrystalline order is closely related to the problem raised by Coxeter [35]: “…how Euclidean geometry, in which lines and planes play a fundamental role, can be extended to inversive geometry, in which this role is taken over by circles and spheres.” Another remarkable property is that the Clifford cross-ratio, also called a double ratio or anharmonic ratio of four points, is an invariant of the transformation. One can completely define a specific symmetry transformation by setting three points and their images. This holds true for any symmetry transformation of self-similar and self-inverse aperiodic crystals. Thus, the equivalent representation of the Penrose tiling by Robinson triangles [36] may be rewritten in terms of the Möbius transformations by simply using the Clifford cross-ratio for corresponding triangles. The infinitely fragmented fractal “parent” of Conway’s pinwheel tiling [37, 38] may be also introduced in exactly the same elementary way taking into account the Clifford cross-ratio preservation for corresponding triangles.

So, the fractal approach makes it possible to find out the hidden, sometimes unexpected symmetry, as well as to derive the natural local matching rules that are stated not as formal designations by colors and other marks but as the order of sequence of the smaller units along the boundaries of the larger ones, which naturally reflects the self-similarity. Recent advances in the theoretical explanation of substitution tilings and their matching rules are surveyed in the literature [37–45]. Particularly, Goodman-Strauss [39] proved that, subject to relatively mild conditions, one can construct local rules for any substitution tiling in nD Euclidean space, which force the desired global structure to emerge. Fernique and Ollinger [40] showed that tilings with a strong hierarchical structure can be enforced by finitely many local constraints, concerning especially to the Rauzy fractal [41]. Note that the most general universal solution does not always represent the best way to handle the specific problem. Moreover, it is not yet known whether the similar ideas are applicable for the structural characterization of actual quasicrystals. We are just going to show that icosahedral quasicrystals represent examples of the 3D substitution tilings with corresponding local matching rules.

Inflation/deflation rules for icosahedral quasicrystals

Of course, the skeptical reader may claim that this problem has been already solved by Steinhardt et al. [5, 6]. Indeed, this assertion is not too far from the truth. Socolar and Steinhardt [6] described the special features of icosahedral tilings, decoration of unit cells by intersecting Ammann planes, and deflation decoration procedure of unit cells with detailed subtiling specification. Unfortunately, because each cell is divided into such small pieces and the specification of the Ammann plane decoration of the unit cells is very complicated, these small pieces may be tracked in the integral structure only with serious difficulties hindering the accurate analysis and practical use of the algorithm.

First of all, we would like to give a relatively long word-for-word quotation from the fundamental paper by Socolar and Steinhardt [6]:

  1. 1.

    “Four types of unit cells appear; the triacontahedron, the icosahedron, the dodecahedron, and the prolate rhombohedron, with volumes in the ratios 10τ:5τ:2τ:1.

  2. 2.

    There are three complete packings with a (single) center of icosahedral point symmetry. One of these has a triacontahedron at its center, the next shell being composed of thirty dodecahedra. The other two have a star at their centers, one having twelve icosahedra as the next shell, the other having twelve triacontahedra.

  3. 3.

    There is a homogeneity about the packings reminiscent of the Penrose tilings. Given any finite region, there are others identical to it relatively close by.”

Now, we would like to show how these basic principles may be reformulated in a very elegant way taking into account the fractal approach.

The inflation/deflation procedure must obey the composition–decomposition rule [46]. Tiles that match together must have decompositions that also match together. This rule makes it possible to construct the tiling of larger and larger size, eventually covering the whole space by repeatedly applying the inflation step with subsequent deflation step, so that the size of the original tiles remains unchanged. Thus, it is preferable not to divide the unit cells into small pieces but inflate four original unit cells and deflate the enlarged cells back to their own copies. We have found that in order not to divide the tiles into smithereens, the original unit cells should be increased by a factor of τ 3. In that case, all vertices of the inflated unit cells coincide with some of vertices of the original quasilattice built by conventional rules [6]. Even though it was difficult to operate with such giant inflated cells containing hundreds of polyhedra, our efforts were rewarded by the unification and simplification of matching rules.

The inflation/deflation rules for the icosahedral tiling are presented in Fig. 6. Four types of unit cells are: the “golden” zonohedra–rhombohedron γ3 (3 zones, 6 faces), rhombic dodecahedron γ4 (4 zones, 12 faces), rhombic icosahedron γ5 (5 zones, 20 faces), and rhombic triacontahedron γ6 (6 zones, 30 faces). Any zonohedron may be described as the three-dimensional projection of the corresponding hypercube, thus the Coxeter designations for polytopes [47] are used. Particularly, γ4 designates the tesseract. Golden zonohedra are inflated by a factor of τ 3 and uniquely decorated by the tiles of the original size (compare with [6, 22, 48]).

Fig. 6
figure 6

Inflation/deflation rules for icosahedral tilings. Four types of “golden” zonohedra serving as “unit cells” for icosahedral quasicrystals are inflated by a factor of τ 3 and uniquely decorated by the tiles of the original size. a–d Inflation/deflation rules for the prolate rhombohedron, rhombic dodecahedron, rhombic icosahedron, and rhombic triacontahedron, respectively

Full size image

Some of the small units partially exceed the bounds of the inflated cells. They fit together like key to lock providing the integrity of the whole tiling. Inflated cells, in turn, have to be assembled face-to-face into the larger cells sharing their own reduced copies on the boundaries.

Figure 7 represents the deflation rule for the rhombic triacontahedron. This procedure generates one out of three possible Euclidean packings with exact icosahedral point symmetry. There is a triacontahedron at the center. The next shell is composed of thirty rhombic dodecahedra placed on the twofold axes. Next, twenty prolate rhombohedra are placed on the threefold axes, and additional twelve clusters of ten rhombohedra, in the form of incomplete stars, are placed on the fivefold axes. Thirty triacontahedra are placed on the twofold axes with twelve rhombic icosahedra on the fivefold axes. Next, twenty clusters of ten rhombohedra in the form of an incomplete star are placed on the threefold axes, and additionally, the rhombic icosahedra on the fivefold axes are capped by twelve clusters of five rhombohedra in the form of an unfinished star. Finally, sixty rhombic icosahedra are placed in the middle of each edge of the inflated cell. The decomposition rule may be formally written as follows:

$$\gamma_{6} \times \tau^{9} \to \gamma_{6} + 30\gamma_{4} + 20\gamma_{3} + 12 \cdot 10\gamma_{3} + 30\gamma_{6} + 12\gamma_{5} +\,20 \cdot \left( {4 + 6 \cdot \frac{1}{2}} \right)\gamma_{3} + 12 \cdot 5\gamma_{3} + 60 \cdot \frac{2}{5}\gamma_{5}$$
Fig. 7
figure 7

Deflation of the rhombic triacontahedron. a–i Consecutive steps of the deflation procedure

Full size image

Fractions reflect the fact that the corresponding polyhedra belong to the inflated cell only partially. Note that if the cell is enlarged with a linear scale factor of τ 3, its volume increases by a factor of τ 9.

The deflation rules for rhombic icosahedron, rhombic dodecahedron, and golden rhombohedron may be derived from the corresponding deflation rule for triacontahedron in a unique way, due to the hypothesis on the circular property. For the fractal icosahedral tiling, there needs to be an equivalent representation by overlapping spheres, whereby the shared regions must have identical decompositions. Hence, when an image of one of the inflated zonohedra is properly superimposed onto an existing inflated and deflated rhombic icosahedron, the desired deflation rule may be derived by the duplication of intersecting area.

The deflation rule for the rhombic icosahedron is shown in Fig. 8. It is essential to emphasize that the opposite vertices on the fivefold axis of this polyhedron correspond to the alternative types, and the opposite sides are not equivalent. One side inherits the outer surface of the inflated triacontahedron and is characterized by rhombic icosahedra placed in the middle of each edge. The opposite side is characterized by the ring of ten triacontahedra arranged face-to-face around the fivefold axis.

Fig. 8
figure 8

Deflation of the rhombic icosahedron. a Initiate rhombic icosahedron, b–k consecutive steps of the deflation procedure

Full size image

Figure 9 represents the deflation rule for the rhombic dodecahedron. Such polyhedra usually appear in the final tiling along the local twofold axes next to the triacontahedra. Note that the rhombic dodecahedron has no symmetry plane perpendicular to that axis. Only two mutually perpendicular planes exist in the deflated rhombic dodecahedron.

Fig. 9
figure 9

Deflation of the rhombic dodecahedron. a Initiate rhombic dodecahedron, b–j consecutive steps of the deflation procedure

Full size image

The deflation rule for single rhombohedron is last but not least (Fig. 10). The opposite vertices on the threefold axis of the rhombohedron correspond to the alternative types. One of the vertices is surrounded by rhombic icosahedra in the second shell, whereas the other vertex is surrounded by triacontahedra. The arrangement of cells in the middle of the inflated rhombohedron is also asymmetric. The deflated rhombohedron does not possess the central symmetry.

Fig. 10
figure 10

Deflation of the prolate rhombohedron. a–g Consecutive steps of the deflation procedure

Full size image

The derived rules may be applied repeatedly. Both inflation and deflation procedures may be performed infinitely many times by turning the initial tiling into a fractal tiling, eventually covering the whole space. Consider the resulting fractal. It may be mentally divided into the tiles of the original size. Such tiling looks like the usual icosahedral tiling by golden zonohedra. The only difference is that now there are infinitely many quasilattice sites within any tile. Choose an arbitrary vertex and examine its local environment. After sufficient magnification, the local environment of any site exactly coincides with one of two possible tilings with the complete icosahedral point symmetry. Both of these tilings are characterized by a star of twenty rhombohedra at the center and differ by the arrangement of cells starting with the second shell. Thus, in the corresponding fractal tiling, only two types of vertices exist, which are invariant with respect to the self-similarity. Two types of inequivalent sites are denoted in Fig. 6 by the open and solid circles, respectively. For example, in the rhombic triacontahedron, the vertices, lying on the fivefold axes, belong to the first type, whereas the vertices, lying on the threefold axes, belong to the second type. It does not quite mean that the first vertices have the fivefold symmetry, whereas the second ones have the threefold symmetry. We have to highlight once again that all vertices have complete icosahedral symmetry!

Natural local matching rules

Bandt and Gummelt [31] clearly illustrate the essence of the problem: “In general, however, the connection between matching rules and self-similarity is far from being understood. It is not known whether aperiodic sets of tiles can be constructed without inflation arguments. Moreover, it is not clear how to define matching rules for a given set of self-similar prototiles which force tilings to admit a unique inflation.” We present our case with the firmly held conviction that there is a direct connection between matching rules and self-similarity.

Imagine a tiling with the complete icosahedral point symmetry that covers the whole space. Enlarge it with a linear scale factor of τ 3, superimpose the enlarged copy of the tiling over the initial one, and return to the initial scale of consideration. One can see that the basic unit cells share their own reduced copies on the common faces and along common edges. The alternating order of the reduced copies of the initial unit cells on the common faces and along common edges uniquely predefines the natural local matching rules. On the other hand, such rescaling is equivalent to the inflation/deflation procedure and may be performed infinitely many times. It is also equivalent to the true operation of self-similarity considered as the group automorphism when bearing in mind that every cell contains infinitely many sites.

The local matching rules for icosahedral tiling are depicted in Fig. 11. There are only two types of inequivalent sites. Take an arbitrary vertex and perform the inflation/deflation procedure to the local environment of the chosen vertex. If, after several iterations, the chosen vertex becomes the center of the star surrounded by rhombic icosahedra, then it belongs to the A type. If the vertex becomes the center of the star surrounded by rhombic triacontahedra, then the chosen vertex belongs to the B type.

Fig. 11
figure 11

Local matching rules for icosahedral tilings. a Two types of inequivalent sites. Type A corresponds to the vertex in the center of star of twenty rhombohedra surrounded by twelve rhombic icosahedra. Type B corresponds to the vertex in the center of star of twenty rhombohedra surrounded by twelve rhombic triacontahedra. b Two types of edges. The first type edge decomposes into the reduced copy of the second type edge, the rhombic icosahedron, and the reduced copy of the first type edge itself. The second type edge decomposes into the its own reduced copy and the rhombic triacontahedron. c Three types of faces

Full size image

In the whole tiling, there are no edges connecting equivalent vertices, but only the vertices of two alternative types may be connected by edges. There are exactly two types of edges. The first type edge [BA]1 decomposes after deflation into the reduced copy of the second type edge [BA]2, the rhombic icosahedron with opposite vertices A and B, and into the reduced copy of the first type edge itself [BA]1. The second type edge [BA]2 decomposes after deflation into its own reduced copy [BA]2, and into the rhombic triacontahedron with equal opposite vertices A and A. We have marked the second type edge by an arrow directed to the A-type vertex, indicating the position of the triacontahedron after deflation. These rules form an indivisible recursive algorithm:

$$[BA]_{1} \times \tau^{3} \to [BA]_{2} + \gamma_{5} + [BA]_{1}$$
$$[BA]_{2} \times \tau^{3} \to [BA]_{2} + \gamma_{6}$$

There are exactly three types of inequivalent faces. The Steinhardt designations for faces [6] are specifically depicted in Fig. 11 for further understanding.

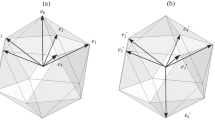
Let us return to the investigation of inequivalent sites or, in other words, to the question of how to construct the two remaining packings with the complete point icosahedral symmetry. In order to obtain the packing, one should arrange twenty rhombohedra in a star and perform the inflation/deflation procedure according to the deflation rules described above. This results in a decorated star—τ 3 as large as the original star. Then, the inflation/deflation procedure may be performed repeatedly until the star, many times enlarged, eventually covers the whole space. However, the opposite vertices of the single rhombohedron belong to two different types. Thus, the two different packings with the complete point icosahedral symmetry may be constructed according to the common algorithm. The first packing may be derived by assembling twenty rhombohedra around the A-type vertex and performing the inflation/deflation procedure. The second packing, similarly, may be derived by assembling the same twenty rhombohedra around the opposite vertex of the B type. The desired packings are presented in Figs. 12 and 13, respectively.

Fig. 12
figure 12

Inflation/deflation rules for the star of rhombohedra around the A–type vertex. a–j Consecutive steps of the deflation procedure

Full size image
Fig. 13
figure 13

Inflation/deflation rules for the star of rhombohedra around the B–type vertex. a–j Consecutive steps of the deflation procedure

Full size image

Generating the aperiodic structure from an arbitrary tile

Any tile may be used to generate a locally isomorphic tiling inflated to infinity, as well as any finite cluster of tiles cut from the properly decorated cell can serve for the same purpose. Recall that two quasicrystals are in the same local isomorphism class if and only if, every finite configuration of unit cells occurs each inside the other [5]. Consider two locally isomorphic tilings, deflate both tilings infinitely many times, and compare the results. The question arises whether or not the final infinite fractal tiling depends on the shape of the initial tile from which it has been derived. If not, then the infinite fractal tiling is the unique object that characterizes the corresponding local isomorphism class as a whole. In essence, we have already pointed out that this question can be reduced to another one, namely whether or not it is allowed to combine self-similarities with different singular points. Physicists might reject this possibility based on the apparent inconsistence with atomicity. As for us, we do not see any contradictions.

The problem of the single prototile is known in the literature [49–52]. If our hypothesis on the Schottky groups holds true, then it makes no difference as to which tile is originally chosen to fill the whole space in a self-similar manner. Even a ball can serve as a suitable fundamental domain, no matter how seemingly inconvenient it appears for crystals. A spherical shell, within two spheres with the outer sphere of radius τ 3 times of the inner sphere, exemplifies another possibility.

We will now illustrate how an infinite self-similar rod may be constructed starting from a single line segment (Fig. 14). Consider an arbitrary edge [AB], namely, the one which is not marked by an arrow. Let us assume, for specificity’s sake, that the edge has the unit length. Inflate it to τ 3 times of its original size and deflate. The inflation moves the image of the point B to the new position at the distance of τ 3 = 1 + 2τ from the origin as the first iteration, whereas the deflation generates two additional points within the inflated edge. The second iteration creates another image of the initial point B at the distance of τ 6 = 5 + 8τ, the third iteration (Fig. 15) creates the image at the distance of τ 9 = 21 + 34τ, and so forth. As a result, the quasi-unit cells become strongly ordered along the fivefold symmetry axis of an icosahedral quasicrystal and form a highly symmetrical self-similar rod.

Fig. 14
figure 14

Generating self-similar rod from single line segment. First two iterations of the inflation/deflation procedure are applied to the single line segment represented by the edge of first type. Arrows indicate new positions of the initiate points after performing the self-similarity operations

Full size image
Fig. 15
figure 15

Self-similar rod with fivefold symmetry corresponding to a τ 9 times enlarged image of the initiate single edge

Full size image

Plane sheets, spreading out to infinity in all directions, may be derived from a single quasi-unit cell within the same manner. Another fine example of iteratively performed self-similarity is a lot of possible hollow cage superclusters of triacontahedra arranged face-to-face in a manner that is reminiscent of the Matryoshka, Russian doll.

Just as single bricks within a wall of bricks occupy positions, which are predetermined by the translational invariance, so the quasi-unit cells occupy positions, which are predetermined by the self-similarity. Quasicrystals surely are not twins [53, 54]. They represent another kind of ordering and nothing more.

Discussion

First of all, we would like to draw the reader’s attention to the fact that one of the fundamental unsolved problems in the solid-state chemistry, namely the description of the structure and symmetry of quasicrystals, should be considered as a part of the Hilbert’s 18th problem.

The Hilbert’s 18th problem [55], namely Building up of space from congruent polyhedra, is assumed to be completely resolved. It is widely believed that the 18th problem, in essence, may be reduced to the counting discrete subgroups of the continuous group of rigid motions. In other words, in order to fill a certain space with congruent polyhedra, we should consider its isometries, but aren’t we at risk of falling into a logic trap by restricting ourselves only to isometries of the same space? The second part of the 18th problem, as it is usually restated in terms of anisohedral tilings, is also declared to be solved just after some examples of such tilings have been found. Let us go back and reread the Hilbert’s original statement: “A fundamental region of each group of motions, together with the congruent regions arising from the group, evidently fills up space completely. The question arises: whether polyhedra also exist which do not appear as fundamental regions of groups of motions, by means of which nevertheless by a suitable juxtaposition of congruent copies a complete filling up of all space is possible.” Thus, the initial question begins with the phrase that there exists at least one evident way to resolve the problem. In the second phrase, Hilbert asked whether there may be more than one way to resolve it. Obviously, he challenged us to develop an alternative.

So, we have offered an algorithm that describes the way how to fill the entire space with congruent copies of golden zonohedra, based on the ordering principles that are convenient for quasicrystals. We do not see any principal differences, on the one hand, between filling the space by congruent copies of the unit cell, according to the rules of classical crystallography, and on the other hand, filling the same space by congruent copies of quasi-unit cells, according to the well-defined iterative and recursive algorithm somewhere from beyond the comprehensively developed scientific discipline. The question is whether our arguments comply fully with the conditions of the Hilbert’s 18th problem. In our opinion, the offered algorithm represents a particular solution of the problem under consideration. Except for the one described, one might ask: “How many other solutions exist for this problem, which has allegedly been reduced to the crystallographic groups and declared to be completely solved?” This is not an idle question. In fact, this problem is nothing more than the classification of quasicrystals according to their symmetry.

We see our work as a contribution to the better scientific understanding of the structure and formation of quasicrystals. Despite the challenging work by Steinhardt et al. [5, 6], no consensus has been reached on how the structure of icosahedral quasicrystal is formed. For example, Abe et al. [56] postulated that “quasicrystals cannot be defined as packing of identical unit cells,” so that their structures can be effectively viewed only in terms of packing by overlapping clusters that are the most stable, energetically favored atomic configurations.

On the contrary, we believe that quasicrystals may be described as packing of unit cells side by side without overlapping with the only exception—there are four types of cells. In both crystalline and quasicrystalline idealized structures, every unit cell is obliged to occupy exactly the predefined position. In essence, we can imagine a substitutional packing irrelative of the cluster energetics at all, exactly in the same manner as crystallographers describe the Bravais lattices irrelative of the fact, whether some positions are occupied by atoms or not. After that, we can fill the unit cells by atoms in an almost arbitrary manner and multiply them respecting the matching rules. The artificial structure thus obtained would surely exhibit quasicrystallinity. Next question appears right away. How to fill four basic unit cells with specific atoms and clusters in order to get the consistent structure with given local atomic arrangement characteristic of an actual quasicrystal? Is it possible to incorporate these ideas into the practical refinement procedure? In general, this problem remains open, but just a simple comparison of the described packings with the known typical structures of crystalline approximants [16, 17, 48, 57–62] allows us to hope that the substitutional algorithm may bring a new perspective to the multiple cells formalism.

As a conclusion, we offer the clear substitution rules for icosahedral packings that make it possible to fill the entire space with golden zonohedra in a strictly regular manner without addressing to higher dimensions. It is important to highlight that our description remains principally three-dimensional, whereby the natural local matching rules may be formulated without addressing to Ammann planes. The proposed algorithm does not contradict the standard cut-and-project scheme, but further investigations are necessary to establish the exact interrelations.