1 Introduction

The Helioseismic and Magnetic Imager (HMI) on board the Solar Dynamics Observatory (SDO) provides us with measurements based on which the photospheric magnetic field vector can be derived (Schou et al. 2012). In this work we describe how these measurements can be extrapolated into the solar corona under the assumption that the coronal magnetic field is force-free, which means that the Lorentz force vanishes. We compare the resulting magnetic field models with observations of the coronal plasma from the Atmospheric Imaging Assembly (AIA), which is also on board the SDO.

The force-free field equations are given by

(1)
(2)

subject to the boundary condition

$$\mathbf{B} = \mathbf{B}_\mathrm{obs}\quad \mathrm{on \, the \, bottom \, boundary}, $$
(3)

where B is the three-dimensional (3D) magnetic field and B obs the measured magnetic field vector in the photosphere. Bineau (1972) and Amari, Boulmezaoud, and Aly (2006) investigated the mathematical structure of these equations regarding existence, uniqueness, and well-posedness. Boulmezaoud and Amari (2000) proved the existence of force-free solutions for simple and multiple connected domains, and Aly (2005) proved uniqueness of force-free fields for a special cylindrical configuration. Several methods have been developed to solve these equations numerically. For reviews see Sakurai (1989), Aly (1989), Amari et al. (1997), and Wiegelmann (2008). Within the last few years the different numerical codes have been intensively tested, evaluated, and compared in Schrijver et al. (2006), Metcalf et al. (2008), and Schrijver et al. (2008). A joint study (DeRosa et al. 2009) has concluded that a successful application of nonlinear force-free field (NLFFF) extrapolation methods requires:

  1. i)

    Large model volumes at high resolution, which accommodate most of the magnetic connectivities within an active region and to its surroundings.

    The field of view of the isolated active region (AR) 11158, as shown in Figures 1 and 2, seems a suitable candidate to fulfill this requirement.

    Figure 1
    figure 1

    Left: Full-disk SDO/HMI magnetogram, Right: Full-disk AIA 171 Å image. Both data sets were obtained on February 14, 2011 at 20:34 UT and have been co-aligned as described in the SDO data analysis guide (DeRosa and Slater 2011). The rectangle outlines the subregion (AR 11158) in the vector magnetogram which is used for the force-free field modeling.

    Full size image
    Figure 2
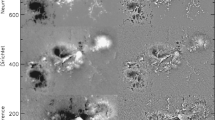
    figure 2

    Top left: B los cut from full-disk HMI magnetogram. Top right: B z from vector magnetogram. To align the vector magnetogram with the line-of-sight magnetogram and AIA we carried out a correlation analysis; the correlation between B los and B z is 92 %. Bottom: Same field of view seen in AIA 171 Å. In the right picture we over-plotted contour lines of B z (same color code as in the images above).

    Full size image
  2. ii)

    Accommodation of measurement uncertainties in the transverse field component.

    This has been implemented in recent updates of different NLFFF extrapolation codes; see Wheatland and Régnier (2009), Wiegelmann and Inhester (2010), Amari and Aly (2010), Wheatland and Leka (2011), and Tadesse et al. (2011).

  3. iii)

    Preprocessing of the photospheric vector field for a realistic approximation of the upper chromospheric, nearly force-free field.Footnote 1

    As we will see in Section 2.1, the HMI vector magnetogram shown in Figure 3 is almost force-free. Tools for implementing the measurement errors (previous item) can also deal with the remaining small forces. For comparison we also investigate preprocessed data.

    Figure 3
    figure 3

    SDO/HMI vector magnetogram observed on February 14, 2011, at 20:34 UT. The rectangular area marks the inner box, where w f=w d=1; see Section 3 for details.

    Full size image
  4. iv)

    Force-free models should be compared with coronal observations.

    In Figures 5 and 6 and in Table 2 we compare the force-free models with coronal images observed with SDO/AIA.

2 Instrumentation and Data Set

The HMI instrument (Scherrer et al. 2012; Schou et al. 2012) on SDO observes the full Sun at six wavelengths in the Fe i 6173 Å absorption line. Filtergrams with a plate scale of 0.5′′ pixels are collected and converted to observable quantities like Dopplergrams, continuum filtergrams, and line-of-sight and vector magnetograms. For vector data, each set of filtergrams takes 135 seconds to be completed, and the filtergrams are then averaged over a period of about 12 minutes (see Hoeksema et al. (2012; to be submitted to Solar Phys.) and the HMI homepage for details: http://hmi.stanford.edu/ ). To generate the vector magnetograms, Stokes parameters are derived from the averaged filtergrams and inverted with the help of a Milne–Eddington algorithm, an advanced version of the Very Fast Inversion of the Stokes Vector (VFISV) (Borrero et al. 2011). The magnetic filling factor is set to be one in the inversion. With the amount of information HMI provides about the line profile, this produces the most stable results. One could determine the filling factor in strong field regions, where it is expected to be close to unity. However, in weak field regions, it is difficult to resolve the filling factor as well as the field strength. The 180∘ azimuthal ambiguity in the transverse field is resolved by an improved version of the minimum energy algorithm (Metcalf 1994; Metcalf et al. 2006; Leka et al. 2009). HMI vector field uncertainties depend on field strength, disk position, and orbital velocity. Formal uncertainties due to the inversion are computed for each pixel as part of the normal processing. Conservatively, the random errors in the line-of-sight component are about 5 G, while the uncertainty in the transverse field is as much as 200 G in weak field regions and as little as 70 G where the field is strong. The zero point uncertainty in the longitudinal direction is < 0.1 G. Additional uncertainties arise because of the disambiguation and systematic errors that are not as well quantified.

Regions of interest (ROIs) containing strong magnetic fluxes are automatically identified (Turmon et al. 2010). Figure 3 shows a vector magnetogram containing AR 11158 observed on February 14, 2011 at 20:34 UT. After correcting for projection effects (Gary and Hagyard 1990), the data have been mapped to a local Cartesian coordinate using Lambert equal area projection (Calabretta and Greisen 2002). An overview on the processing of HMI vector magnetograms can be found at http://jsoc.stanford.edu/jsocwiki/VectorMagneticField/ . For the magnetic field extrapolation, we bin the data to 720 km (about 1′′) and use a computational box of 300×300×160 grid points.

2.1 Quality of the HMI Vector Magnetogram

To serve as a suitable lower boundary condition for a force-free modeling, vector magnetograms must be approximately flux balanced, and the net force and net torque have to vanish. Wiegelmann, Inhester, and Sakurai (2006) introduced three dimensionless parameters, the flux balance ϵ flux, net force balance ϵ force, and net torque balance ϵ torque:

where the integrals in ϵ force and ϵ torque correspond to the Maxwell stress tensor and its first moment, respectively (see Molodensky 1969, 1974; Aly 1989). For perfectly force-free consistent boundary conditions these three quantities are zero, while for real observed data this is hardly the case. However, for practical computations, it is sufficient that these quantities become small, e.g., ϵ flux,ϵ force,ϵ torque≪1. In Table 1 we list the values for the used HMI data set in the first row. All three quantities are well below unity, which gives us some confidence that the data might serve as a suitable boundary condition for a force-free modeling.

Table 1 Values of the three dimensionless parameters defined in Section 2.1 following Wiegelmann, Inhester, and Sakurai (2006), for different data sets.
Full size table

To deal with vector magnetogram data being inconsistent with the force-free assumption, we developed a preprocessing routine (Wiegelmann, Inhester, and Sakurai 2006), which derives suitable boundary conditions for force-free modeling from the measured photospheric data. Applying this procedure to HMI further reduces ϵ force and ϵ torque significantly (second row). Note that the values of about 0.05 for ϵ force and ϵ torque for the original HMI vector magnetogram (first row) are significantly lower than those observed for vector magnetograms from other ground-based and space-borne missions (rows 3 – 5) like the Solar Flare Telescope (SFT), Hinode, and SOLIS.Footnote 2 For detailed investigations of these data sets, see Wiegelmann, Inhester, and Sakurai (2006), Schrijver et al. (2008), and Thalmann, Wiegelmann, and Raouafi (2008), respectively.

3 Nonlinear Force-Free Field Modeling

We solve the force-free Equations (1)–(3) by using an optimization principle as proposed by Wheatland, Sturrock, and Roumeliotis (2000) and extended by Wiegelmann (2004) and Wiegelmann and Inhester (2010) in the form

(4)

where ν is a Lagrangian multiplier which controls the injection speed of the boundary conditions. w f and w d are weighting functions, which are one in the region of interest (inner 236×236×128 physical box) and drop to zero in a 32 pixel boundary layer toward the lateral and top boundaries of the full 300×300×160 computational domain. W is a space-dependent diagonal matrix whose elements are inversely proportional to the estimated squared measurement error of the respective field component. In principle, one could compute W from the measurement noise and errors obtained from the inversion of measured Stokes profiles to field components. Until these quantities become available, a reasonable assumption is that the magnetic field is measured in strong field regions more accurately than in the weak field and that the error in the photospheric transverse field is at least one order of magnitude higher than the line-of-sight component. Appropriate choices to optimize ν and W for use with SDO/HMI magnetograms are investigated in this paper. For a detailed description of the current code implementation and tests we refer to Wiegelmann (2004) for the basic code and Wiegelmann and Inhester (2010) for a description and tests of slow boundary injection and the consideration of measurement errors. For the first time we combine the above described algorithm with a multiscale approach as described in Wiegelmann (2008). For this work we apply our code with a three-level multiscale approach to an SDO/HMI data set with 300×300 points in x and y and extrapolate 160 pixels in height in the z direction.

3.1 Quality of the Reconstructed 3D Fields

To evaluate how well the force-free and divergence-free conditions are satisfied by the reconstructed 3D fields, we monitor the following expressions:

(5)
(6)
(7)
(8)
(9)

where L 1 and L 2 correspond to the first and second terms in Equation (4), respectively, with the difference that the integral is carried out in the inner 236×236×128 physical box, where w f≡w d≡1, excluding the buffer boundary of 32 pixels toward the lateral and top boundary of the computational box. For potential and linear force-free fields, the values correspond to the discretization error. Also investigated in the inner box is the sine of the current weighted average angle σ j between the magnetic field and electric current (see Wheatland, Sturrock, and Roumeliotis (2000) and Schrijver et al. (2006) for details) and L 1∞ and L 2∞, which are the L ∞ norms for the Lorentz force and divergence, respectively.

3.2 Code setup and choice of free parameters

Before we perform nonlinear force-free extrapolations, we use the vertical component B z of the HMI data to compute a potential and a linear force-free field (αL=2.5, α=1.16×10−8 m−1) with a Fourier transform method (Alissandrakis 1981). Here, α is the linear force-free parameter (∇×B=α B), which is 0 for a potential field. For a linear force-free field we calculate, as suggested by Hagino and Sakurai (2004), an averaged value \(\alpha= \sum {\mu_{0} J_{z} \operatorname {sign}(B_{z})}/ \sum{|B_{z}|}\), where \(J_{z}=\frac{1}{\mu_{0}}(\frac{\partial B_{y}}{\partial x}-\frac{\partial B_{x}}{\partial y} )\) is the vertical current in the photosphere.

For nonlinear force-free fields (NLFFFs) we minimize the function (4), and we vary the Lagrangian multiplier ν and the mask W, which we want to optimize. In the first column in Table 2 we name case studies with different parameter sets (as specified in columns 2 and 3) with letters (A to N). For cases A – H we choose W=B T/max(B T). This seems to be a reasonable choice, as the measurement error in the transverse field is higher in weak field regions. We vary the Lagrangian multiplier ν between 0.1 and 0.0001 for cases A – F. The lower the value of ν, the slower the observed boundary becomes injected, so that the code has more time to relax toward a force-free state. The computing time increases with a power law when ν decreases (Time [h]∼0.013 h⋅ν −0.88); see Figure 4a and column 10 in Table 2. The relation between ν and \(\operatorname {asin}(\sigma_{j})\) can also be approximated by a power law \((\operatorname {asin}(\sigma_{j})\,[\mathrm{degree}] \sim 45.7^{\circ} \cdot \nu^{0.28})\); see Figure 4b. The values for force- and divergence-freeness L 1 and L 2 are slightly higher for ν=10−4 than for 10−3, but the general trend is that L 1 and L 2 decrease with decreasing ν in the form of a power law, L∼98⋅ν 0.46, with L=L 1+L 2; see Figure 4c. It seems that the choice ν=0.001 is optimal, as higher values of ν correspond to worse fulfillment of all force-free consistency criteria (σ j ,L 1,L 2), and a lower ν only increases the computing time drastically, but does not or hardly improves the solution.

Figure 4
figure 4

Relation between the Lagrangian multiplier ν and computing time (panel a), \(\operatorname {asin}(\sigma_{j})\) (panel b), and L=L 1+L 2 (panel c). Panel d shows the relation of computing time in hours to \(\operatorname {asin}(\sigma_{j})\). The values correspond to NLFFF cases A – F in Table 2. The dashed lines show power law fits in all panels (in panel c the lowest value ν=0.0001 has been excluded from the power law fit).

Full size image
Table 2 Evaluation of force-free field models. The first column names the model and in columns 2 and 3 we show the model parameters. Columns 4 to 8 show different force-free consistency evaluations, column 9 the magnetic energy compared with a potential field, and column 10 the computing time on one processor. In the last three columns we compare magnetic field lines in different regions (denoted red, white, green; see also Figure 6) with an AIA image.
Full size table

In cases G and H we investigate the influence of preprocessing on the result. We used a standard preprocessing parameter set μ 1=μ 2=1,μ 3=0.001,μ 4=0.01. These parameters control the amount of force-freeness, torque-freeness, nearness to the actually observed data, and smoothing, respectively (see Wiegelmann, Inhester, and Sakurai (2006) for details on preprocessing). NLFFF extrapolations have been carried out here for ν=0.01 and ν=0.001, and we find that L 1 and L 2 are smaller for extrapolations from preprocessed data. Similarly to the unprocessed case, L 1,L 2,σ j decrease with decreasing ν, while the computing time increases. The computing time for preprocessed data is about a factor of three (ν=0.01) or two (ν=0.001) higher compared with the unprocessed cases. However, the angle between the magnetic field and current \(\operatorname {asin}(\sigma_{j})\) does not improve, and becomes worse (by a factor 1.3) for ν=0.001. A reason for the L-values becoming lower, while σ j remains the same, might be that some strong current peaks are smoothed out by preprocessing. If we consider that without preprocessing (case E) L 1 and L 2 are already of the order of the discretization error of the potential field, the lower value σ j , and the shorter computing times, we conclude that preprocessing is not necessary for this data set.

In cases I – L we investigate the effect of different mask functions. We choose a unique mask in cases I and J, which means that we do not consider different errors in high and low field strength regions in the photospheric vector magnetogram. As one can see (in comparison with cases B and E) all three force-free consistency criteria are worse; consequently, one should not use a unique mask. Interesting cases are K and L, where we choose the mask W=(B T/max(B T))2. This choice gives more weight to strong than to weak regions, similarly as in the linear cases A – H, but prefers strong regions significantly more. For ν=0.01 (case K compared with B) L 1 and L 2 are better and σ j worse. For ν=0.001 (case L compared with E) all three criteria are fulfilled somewhat better for the quadratic mask function. However, the computing time is a factor of 1.6 longer for the quadratic case (L). We conclude that, if ν is sufficiently low, than the final equilibrium is quite robust regarding the exact choice of the mask function profile.

For comparison we also extrapolated the magnetogram with the old code version, which uses a fixed lower boundary and does not contain a mask and Lagrangian multiplier (cases M and N without and with preprocessing, respectively). Without preprocessing, all three force-free consistency criteria are fulfilled worse than for the new code, because the old code has no ability to correct for inconsistencies in the magnetograms. Preprocessing improves the result for L 1 and L 2 by about a factor of four, but σ j hardly improves. However, the computing time for the old code (case N) is significantly lower (by a factor of five and nine compared to E and L, respectively), as for the best runs with the new code. If we compare results of the old code (case N, after preprocessing) with results from the new code with similar computing times (cases C and G), the performances are similar. Higher computing times are the price we pay to get better force-free consistent equilibria.

In column 9 in Table 2 we present the ratio of the total magnetic energy to the energy of a potential field E/E 0. While the correct value is a priori unknown, this criterion cannot serve directly as a quality measure of the reconstructed NLFFFs, except that E/E 0 should be greater than unity. E/E 0 is an important quantity, as it defines an upper limit for the free magnetic energy, which could become converted in kinetic and thermal energy during eruptions. Taking the average of all 14 NLFFF models we find E/E 0=1.20±0.06, and if we consider only the best cases, say where \(\operatorname {asin}(\sigma_{j}) < 10^{\circ}\) (cases D, E, F, H, J, L), one finds E/E 0=1.24±0.03. For long time series it will probably not be possible to extrapolate all magnetograms with several different parameter sets, but we propose to do this for some magnetograms within a time series to derive an error estimation for E/E 0. We find that this quantity is not significantly influenced by the chosen parameter set (value of Lagrangian multiplier ν, mask function profile W, preprocessing) if the force-free consistency criteria L 1,L 2,σ j are fulfilled, and one should check them for each extrapolation from vector magnetograms. We find that the L ∞ norms for Lorentz force and divergence behave very similarly to the integral forms. Therefore, both norms can alternatively be used to evaluate the quality of the extrapolated field.

4 Comparison with AIA Images

As pointed out in DeRosa et al. (2009), force-free field models should be compared with coronal observations in order to quantify to what extent they correctly reproduce the coronal magnetic field configuration. In Figure 5 we show some arbitrarily chosen force-free field lines (from NLFFF model E) in comparison with AIA images in different wavelengths (see Lemen et al. (2012) for an overview of AIA). Qualitatively the field lines seem to reasonably agree with the observed plasma loops, but deviations are also clearly recognizable. In the following we aim to estimate the difference between force-free field lines and plasma loops quantitatively. While stereoscopic reconstructed loops in 3D as used in DeRosa et al. (2009) and Conlon and Gallagher (2010) are not available, we compare our results with an AIA image from one viewpoint. A basic assumption is that the plasma is frozen into the magnetic field; hence the plasma loops outline the magnetic field lines. Consequently, the gradient of the intensity parallel to the magnetic field lines should be small. We want to detect bright loops (high intensity) and to quantify the deviation of projected field lines (computed from the NLFFF models) and plasma loops (as visible in AIA images) as

$$C=\frac{\sqrt{\int_S (\nabla I(s))^2} \,\mathrm{d}s}{\int_S I(s) \,\mathrm{d}s},$$
(10)

where I(s) is the intensity along a projected magnetic field line.Footnote 3 This criterion finds loops of high I(s) with small intensity gradients along the loops (low ∇I(s)). For other possibilities to define the penalty function C, see Wiegelmann et al. (2005) and Conlon and Gallagher (2010).

Figure 5
figure 5

AIA images of AR 11158 in different wavelengths, observed on February 14, 2011 at 20:34 UT. Over-plotted are some selected field lines from NLFFF model E.

Full size image

For a quantitative comparison, we compute a number of field lines, originating ± 5 pixels around previously chosen locations: P 1=(80,30),P 2=(85,100), and P 3=(225,185). Field lines not closing within the extrapolation domain are excluded from the quantitative comparison, and the ten field lines giving the lowest values of C are considered for further analysis. The average and standard deviation of C for these ten field lines in each region are displayed in the last three columns of Table 2, respectively. The field lines originating from ± 5 pixels around P 1,P 2, and P 3 are shown as red, white, and green curves, respectively for some of the models in Figure 6. The field lines corresponding to the potential field model, the NLFFF models E and L (which best performed for the force-free consistency criteria, see last section), and the old (fixed boundary, model M) NLFFF code are shown in Figure 6.

Figure 6
figure 6

AIA 171 Å images with field lines as computed from selected models. The red, white, and green loops here correspond to AIA-red, AIA-white, and AIA-green in Table 2.

Full size image

The white loops in Figure 6 seem to agree reasonably well with AIA for all models, even those of the potential field model. The average penalty function for these loops is in the range 200 – 300 for all models. However, the red S-shaped coronal loops cannot be identified with a potential or linear-force free model (the linear model performing even worse than the potential one). All NLFFF models show a much better agreement, with the penalty function (about 165 – 265) being in most cases less than half as large as for the potential field. The penalty function for the green loops is higher for all models, but the penalty function for the best NLFFF models is about a factor of two better than for the potential field. It seems that these green loops are the most challenging loops to reconstruct, and the old NLFFF code, which used a fixed boundary for the transverse potential field, performs only slightly better than the potential field. However, the best NLFFF models (in the sense of being more force-free, in particular cases E and L shown in Figure 6) indicate the correct field topology also for the green loops. Using the penalty function C to evaluate the quality of the reconstruction clearly favors NLFFF models over potential and linear FF models, but this criterion is not sensitive enough to definitely favor one of the NLFFF models. In the future one should consider a more sophisticated comparison between magnetic field models and coronal images, e.g., by applying different penalty functions, using loops or structures extracted from the images, and doing comparisons in different AIA wavelengths. For earlier observations from SDO (for which vector magnetograms have not yet been released) one could also compare the results with images taken from vantage points with one or both of the Solar TErrestrial RElations Observatory (STEREO) spacecraft or compare them directly with stereoscopic reconstructed 3D loops. However, this cannot be implemented as a standard diagnostic for NLFFF models, as the angle between the two STEREO spacecraft and SDO becomes too large for stereoscopy.

5 Conclusions and Outlook

In this work we have carried out nonlinear force-free coronal field extrapolations of an isolated active region based on data from SDO/HMI. The vector magnetogram is almost perfectly flux balanced, and the field of view is large enough to also cover the weak field surrounding the active region. Both conditions are necessary in order to carry out meaningful force-free computations. We also found that the photospheric magnetogram satisfied the force-free criteria. The net force and torque are considerably smaller than in earlier measurements of other active region fields with SFT, Hinode, and SOLIS; however, we do not know for sure if this is a general property of HMI or if it is only true for this particular isolated active region. A comparison of an active region measurement with different instruments is planned. The data could be used directly as the boundary condition for nonlinear force-free field computation; preprocessing of the photospheric field was not necessary.

The new code version takes into account errors in the measurements, in particular in the transverse field, and injects the boundary data slowly, controlled by a Lagrangian multiplier ν. The error incorporation is controlled by using a mask function, which is one for the most trustworthy data and 0 where one cannot trust the data. Unless an exact error computation becomes available from inversion and ambiguity removal of the photospheric magnetic field vector, a reasonable assumption is that the field is measured more accurately in strong field regions, and we carried out computations with the mask ∝B T and \(\propto B_{\mathrm{T}}^{2}\). For a sufficiently small Lagrangian multiplier ν=0.001 we found that the resulting coronal fields are force-free and divergence-free in the sense that the remaining residual forces are of the order of the discretization error of potential and linear force-free fields. The weighted angle between magnetic field and electric current is about 5 – 6∘. The resulting field is almost identical for both masks, but computations with the \(\propto B_{\mathrm{T}}^{2}\) mask take significantly longer (9 h 13 min versus 5 h 46 min for the ∝B T mask). Injecting the boundary faster by choosing a higher Lagrangian multiplier (say ν=0.01) speeds up the computation (a run takes only half an hour), but the residual forces are higher, and the current and field are not well aligned. Inserting the boundary even more slowly (say ν=0.0001) leads to much longer computing times (more than 50 h), but does not improve the solution. We conclude that the choice ν=0.001 and a mask ∝B T or \(\propto B_{\mathrm{T}}^{2}\) are the optimal choices for this data set.

The computations have been performed on one processor on a Linux PC. Our code has been parallelized with OpenMP, but rather than processing a single magnetogram with a parallelized code, it is planned to process different magnetograms of a time series simultaneously. While the time cadence of HMI vector magnetograms is about 12 min, NLFFF computations for one magnetogram on one processor take about 6 h. Consequently, the requirement is about 50 processors (for each active region) in order for the NLFFF tools to catch up with the data stream from HMI.

An important question is to what extent the optimum parameters for this data set can also be applied to other active regions from SDO/HMI. A key point is to monitor the consistency criteria of the magnetogram as well as the remaining residual forces and alignment of fields and currents in the reconstructed 3D field. A comparison of the magnetic field model with AIA images should also always be done. We used the 171 Å channel here, because loops are well visible in this wavelength. However, the question of how coronal magnetic field models can be validated best by coronal observations should be further investigated. Magnetic field lines are 3D structures; many field lines might not be filled with plasma and thus not visible in EUV images. Also, the question of how/if one can use the different wavelengths in AIA to validate coronal field models is not trivial.

A stumbling stone for AR-NLFFF models could be that other active regions are not as well isolated as AR 11158 investigated here, but might be magnetically connected to other active regions and the quiet Sun. This situation requires full-disk vector magnetograms and force-free computations in spherical geometry, as for example carried out from full-disk SOLIS measurements in Tadesse et al. (2012). Due to their nature, extrapolations from full-disk magnetograms must be calculated with a reduced spatial resolution, or one has to accept significantly longer computing times. Global force-free coronal magnetic field models can also be used to specify the lateral boundaries for active region modeling for nonisolated active regions.