1 Introduction

In the last decade we observe the fast development of a new branch of solar physics called coronal seismology (e.g. Aschwanden 2006; Nakariakov and Melnikov 2009; Erdélyi and Goossens 2011). Coronal seismology was first suggested by Uchida (1970), Rosenberg (1970) and Roberts, Edwin, and Benz (1984), but its fast progress is related to the launch of recent space missions like TRACE, SOHO and Hinode. The aim of coronal seismology is to obtain information about properties of a medium from observations of waves and oscillations in this medium. The initial advances of coronal seismology are mainly related to observations of different wave modes in coronal magnetic loops. In particular, observations of kink oscillations of coronal magnetic loops enabled theorists to estimate the magnetic field strength in coronal loops (e.g. Nakariakov and Ofman 2001) and the atmospheric scale height in the corona (e.g. Andries, Arregui, and Goossens 2005; Dymova and Ruderman 2006; Arregui et al. 2007; Van Doorsselaere, Nakariakov, and Verwichte 2007; Goossens 2008; Verth, Erdelyi, and Jess 2008; Andries et al. 2009). Recently significant progress has been made in prominence seismology (e.g. Terradas et al. 2008; Soler et al. 2010; Diaz, Oliver, and Ballester 2010; Arregui and Ballester 2011; Arregui et al. 2011).

To obtain information about the coronal plasma and magnetic field from the observations of waves and oscillations one needs theoretical models of these waves and oscillations. In particular, one needs theoretical models of coronal loop oscillations. Traditionally coronal magnetic loops have been modeled as monolithic magnetic cylinders, although recently more sophisticated models have been developed (see, e.g., the review by Ruderman and Erdélyi 2009).

One more type of oscillations important for coronal seismology are quasi-periodic pulsations (QPPs) of electromagnetic emission generated by solar flares. The periods of these pulsations range from a fraction of a second to a few tens of seconds. At present there are two main mechanisms suggested for their explanations. The first one is related to MHD auto-oscillations, in particular to oscillatory regimes of magnetic reconnection (e.g. Inglis, Nakariakov, and Melnikov 2008; Inglis and Nakariakov 2009; Nakariakov et al. 2010a, 2010b). The second mechanism is the modulation of the electromagnetic emission by fast sausage modes in magnetic tubes (Rosenberg 1970; Kopylova, Stepanov, and Tsap 2002; Nakariakov, Melnikov, and Reznikova 2003; Kopylova et al. 2007; Nakariakov and Melnikov 2009). An important property of fast sausage modes in a straight homogeneous magnetic tube with axial magnetic field is that they are trapped waves when their wavelength is smaller than the cut-off wavelength, while they become leaky (i.e. we have radiation pulsations) when the wavelength is larger than the cut-off wavelength (e.g. Zaitsev and Stepanov 1975; Meerson, Sasorov, and Stepanov 1978; Wilson 1980; Spruit 1982; Edwin and Roberts 1983; Inglis et al. 2009). The typical cut-off wavelength is of the order of the tube radius. Since the typical radii of coronal magnetic loops are much smaller than their lengths, this implies that only harmonics of fast sausage modes with high axial numbers can exist in the form of trapped waves. The only exceptions are flaring loops with the very large ratio of plasma densities inside and outside the loop. This fact does not cause any difficulty when applying fast sausage modes for interpretation of radiation pulsations with periods of a few seconds. However, oscillations with longer periods, of the order of tens of seconds, have been also observed (e.g. Trottet, Pick, and Heyvaerts 1979; Aschwanden 1987; Kupriyanova et al. 2010). Recently Foullon et al. (2010) reported observations of radiation pulsations with larger periods, up to 10 min. Fast sausage waves with such periods in a straight homogeneous magnetic tube are leaky unless we assume that the density ratio is very large. As a result it is problematic to use fast sausage waves for the interpretation of these observations. Hence, it is desirable to develop new models of coronal magnetic loops that will describe trapped long-period fast sausage waves.

Parker (1979) considered a quasi-static expansion of twisted magnetic tubes in the solar atmosphere. He showed that, during this process, the magnetic flux in the tube is redistributed in such a way that the azimuthal flux is concentrated at the peripheral part of the tube, and the axial flux in the tube core. As a result a tube consisting of two parts is formed. In the internal or core part of this tube the magnetic field is predominantly axial, while it is predominantly azimuthal in the annulus encircling the core region. One can expect that the formation of such magnetic flux tubes consisting of two parts is a natural result of the evolution of twisted magnetic tubes transported in the solar atmosphere from the convection zone. This observation puts studying waves and oscillations of magnetic tubes consisting of two parts on the agenda.

Standing waves in a magnetic tube consisting of two parts have been already studied by Mikhalyaev and Solov’ev (2005) (see also the review by Ruderman and Erdélyi 2009). However, in the model of a magnetic tube studied in this paper the magnetic field was axial both in the core region and annulus. Erdélyi and Carter (2006) and Carter and Erdélyi (2008) studied the wave propagation in a tube consisting of the core with the axial magnetic field and the annulus with the twisted magnetic field.

The aim of this paper is to study standing waves in a tube consisting of the core region with the axial magnetic field and the annulus with the purely azimuthal magnetic field. We show that such a tube can support trapped fast sausage standing waves corresponding to the fundamental mode and the low-order overtones in the axial direction. The paper is organized as follows. In the next section we formulate the problem. In Section 3 we derive the dispersion equation for fast sausage waves. In Section 4 we study the dispersion equation analytically in the long wavelength approximation and numerically for arbitrary wavelength. Section 5 contains the summary of the obtained results and our conclusions.

2 Problem Formulation

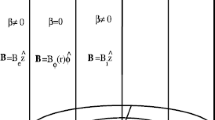
The solar corona is strongly dominated by the magnetic field with the magnetic pressure being much larger than the plasma pressure. This implies that we can use the cold plasma approximation to describe fast wave modes. We consider standing waves in a model magnetic tube first suggested by Mikhalyaev (2005). This model magnetic tube consists of a core region with axial magnetic field and the annulus with purely azimuthal magnetic field. The external magnetic field is once again axial. Hence, in cylindrical coordinates r, φ, z with the z -axis coinciding with the tube axis the background magnetic field is given by

$$ \mathbf{B}(r) = \left\{ \begin{array}{@{}l@{\quad}l} B_{\mathrm{i}}\mathbf{e}_z, & r < b,\\[1mm] (B_0/\alpha r)\mathbf{e}_\varphi, & b < r < a, \\[1mm] B_{\mathrm{e}}\mathbf{e}_z, & a < r , \end{array} \right. $$
(1)

where a is the radius of the tube, b is the radius of the core region, B i, B e, B 0 and α are constants, and e φ and e z are the unit vectors in the azimuthal and axial directions. The magnetic field has to satisfy the equilibrium conditions, which are the conditions of the magnetic pressure balance at the boundaries r=a and r=b,

$$ B_{\mathrm{i}}^2 = \frac{B_0^2}{(\alpha b)^2}, \qquad B_{\mathrm{e}}^2 = \frac {B_0^2}{(\alpha a)^2} . $$
(2)

It follows from this equation that bB i=aB e. Since the magnetic field is discontinuous at the tube and core boundaries, there are surface currents on these boundaries with the components given by

$$ j_\varphi(b) = j_z(b) = \frac{B_{\mathrm{i}}}{\mu_0}, \qquad j_\varphi(a) = j_z(a) = -\frac{B_{\mathrm{e}}}{\mu_0}, $$
(3)

where μ 0 is magnetic permeability of free space. It is straightforward to see that the total current in the loop is zero, so the loop is current-neutral. Note that, at present, the data on the current distribution in coronal loops are sparse. Melrose (1991) argued that some of coronal loops might not be current-neutral.

We assume that the background density is given by

$$ \rho(r) = \left\{ \begin{array}{@{}l@{\quad}l} \rho_{\mathrm{i}}, & r < b, \\[1mm] \rho_0/(\alpha r)^2, & b < r < a,\\[1mm] \rho_{\mathrm{e}}, & a < r . \end{array} \right. $$
(4)

Then the Alfvén speed, \(V_{\mathrm{A}}(r) = B(r)/\sqrt{\mu_{0}\rho(r)}\), is a piece-wise constant function. To simplify the analysis we assume in what follows that ρ 0/(αa)2=ρ e. The dependence of the background density on r is shown in Figure 1. Now the Alfvén speed is the same in the annulus and outside the tube, V A0=V Ae. It is not very difficult to extend the analysis to the general case where V A0≠V Ae. The qualitative behavior of fast sausage waves remains the same. It follows from the first condition in Equation (2) that

$$ \rho_{\mathrm{i}}V_{\mathrm{Ai}}^2 = \frac{\rho_0 V_{\mathrm{A}0}^2}{(\alpha b)^2} = \frac{a^2\rho_{\mathrm{e}}V_{\mathrm{Ae}}^2}{b^2}. $$
(5)

We assume that V Ai<V A0, which implies that ρ i/ρ e>(a/b)2.

Figure 1
figure 1

The dependence of the background density on the radial coordinate r.

Full size image

Usually the density variation in the radial direction causes the wave energy to be resonantly absorbed. However, this is not the case in our study. The general reason for this is that there is no Alfvén resonance for axisymmetric motion. The sausage waves can be subject to slow resonance only (e.g. Goossens, Erdélyi, and Ruderman 2011). There is no slow resonance in a cold plasma approximation. Even if we take the plasma pressure into account, the phase speed of fast waves is much larger than the slow magnetosonic speed in a low-beta plasma, which makes the slow resonance impossible. Further, in the particular equilibrium that we consider here, there is no resonant absorption even for non-axisymmetric waves because, for a wave mode with the wavenumber k, the Alfvén spectrum consists of only two points: V A0 k and V Ai k. Hence, there is no Alfvén continuum.

The plasma and magnetic field perturbations are described by the linearized magnetohydrodynamic (MHD) equations for ideal cold (i.e. zero-beta) plasmas,

$$ \rho\frac{\partial^2\boldsymbol{\xi}}{\partial t^2} = \frac{1}{\mu_0}(\nabla\times\mathbf{b})\times\mathbf{B}, $$
(6)
(7)

where B=B φ e φ +B z e z , ξ=(ξ r ,ξ φ ,ξ z ) is the plasma displacement and b=(b r ,b φ ,b z ) the magnetic field perturbation. We do not write the mass conservation equation, because it is not used in what follows. We also have to impose boundary conditions at the boundaries of the annulus. At these boundaries the radial plasma displacement and the Lagrangian magnetic pressure perturbation have to be continuous. Hence, we have (e.g. Bennett, Roberts, and Narain 1999)

$$ \xi_{r\mathrm{i}}(b) = \xi_{r0}(b), \qquad\xi_{r0}(a) = \xi_{r\mathrm{e}}(a), $$
(8)
$$ P_{\mathrm{i}}(b) = P_0(b) - \frac{\rho_0 V_{\mathrm{A}0}^2}{\alpha^2 b^3}\xi _{r0}(b), \qquad P_0(a) - \frac{\rho_0 V_{\mathrm{A}0}^2}{\alpha^2 a^3}\xi_{r0}(a) = P_{\mathrm{e}}(a) , $$
(9)

where P=b⋅B/μ 0 is the magnetic pressure perturbation.

Equations (6) and (7), and the boundary conditions (8) and (9) are used in the next section to derive the dispersion equation for fast sausage waves.

3 Derivation of Dispersion Equation

Since the background density and magnetic field are axisymmetric and independent of z, we can look for a solution to Equations (6) and (7) that is independent of φ and Fourier-analyze this solution with respect to z. In addition, we are looking for eigenmodes. Hence, we take perturbations of all variables to be proportional to exp[i(kz−ωt)]. Then Equations (6) and (7) reduce to the system of ordinary differential equations describing the dependence of perturbations on r. It is straightforward to show that ξ φ =ξ z =b φ =0. Hence, in the fast sausage waves, only ξ r , b r and b z are non-zero. The system of equations describing the dependence of perturbations of r can be reduced to a system of two equations for ξ r and P (Appert, Gruber, and Vaclavik 1974). In the particular case of cold plasma and sausage waves this system takes the form

$$ D\frac{\mathrm{d}(r\xi_r)}{\mathrm{d}r} = rC_1\xi_r - rC_2 P , $$
(10)
$$ D\frac{\mathrm{d}P}{\mathrm{d}r} = C_3\xi_r - C_1 P, $$
(11)

where

$$ D = \rho\omega^2 - \frac{k^2 B_z^2}{\mu_0} , \qquad C_1 = \frac{2\rho\omega^2 B_\varphi^2}{rB^2}, \qquad C_2 = \frac{\omega^2}{V_{\mathrm{A}}^2} - k^2 , $$
(12)
$$ C_3 = D \biggl(D + \frac{2B_\varphi}{\mu_0}\frac{\mathrm{d}}{\mathrm{d}r} \frac{B_\varphi }{r} \biggr) + \biggl(\frac{2B_\varphi}{r\mu_0} \biggr)^2 \biggl( \frac{\omega^2 B_\varphi^2}{V_{\mathrm{A}}^2} - k^2 B_z^2 \biggr). $$
(13)

Eliminating ξ r we obtain the equation for P ,

$$ \frac{\mathrm{d}^2P}{\mathrm{d}r^2} + \frac{C_3}{rD} \frac{\mathrm{d}}{\mathrm{d}r} \biggl(\frac{rD}{C_3} \biggr)\frac{\mathrm{d}P}{\mathrm{d}r} + \biggl[\frac{C_3}{rD}\frac{\mathrm{d}}{\mathrm{d}r} \biggl( \frac{rC_1}{C_3} \biggr) + \frac{C_2C_3-C_1^2}{D^2} \biggr]P=0. $$
(14)

In regions r<b and r>a , where the background magnetic field is purely axial, Equations (11) and (14) reduce to

$$ \frac{\mathrm{d}^2 P}{\mathrm{d}r^2} + \frac{1}{r}\frac{\mathrm{d}P}{\mathrm{d}r} + k_r^2 P = 0, \quad k_r^2 = \frac{\omega^2}{V_{\mathrm{A}}^2} - k^2 , $$
(15)
$$ \xi_r = \frac{1}{\rho(\omega^2 - V_{\mathrm{A}}^2 k^2)}\frac{\mathrm{d}P}{\mathrm{d}r}. $$
(16)

In what follows we consider trapped waves with the amplitude decaying exponentially with the distance from the tube. When \(k_{r\mathrm{e}}^{2} > 0\), the solution to Equation (15) in the external region is expressed in terms of Bessel functions that decay only as r −1/2 when r increases. We can have a solution decaying exponentially in the external region only when \(k_{r\mathrm{e}}^{2} < 0\). In that case the solution in the external region is given by

$$ P_{\mathrm{e}} = A_{\mathrm{e}}K_0(\lambda r), \qquad\xi_{r\mathrm{e}} = \frac{A_{\mathrm{e}}\lambda K_1(\lambda r)}{\rho_{\mathrm{e}}(V_{\mathrm{A}e}^2 k^2 - \omega^2)}, $$
(17)

where

$$ \lambda^2 = -k_{r\mathrm{e}}^2 = -k_{r0}^2= k^2 - \frac{\omega^2}{V_{\mathrm{A}0}^2}, $$
(18)

A e is a constant, and K 0 and K 1 are the modified Bessel functions of the second kind (McDonald functions), and the zero and first order. When \(\omega^{2} > V_{\mathrm{A}i}^{2} k^{2}\) we have \(k_{r\mathrm{i}}^{2} > 0\), so the corresponding wave mode is a body wave (Edwin and Roberts 1983). In this case the solution in the core region regular at r=0 is given by

$$ P_{\mathrm{i}} = A_{\mathrm{i}}J_0(\kappa r), \qquad\xi_{r\mathrm{i}} = \frac{A_{\mathrm{i}}\kappa J_1(\kappa r)}{\rho_{\mathrm{i}}(V_{\mathrm{Ai}}^2 k^2 - \omega^2)}, $$
(19)

where A i is a constant, J 0 and J 1 are the Bessel functions of the zero and first order, and κ=k ri. When \(\omega^{2} < V_{\mathrm{Ai}}^{2} k^{2}\) we have \(k_{r\mathrm{i}}^{2} < 0\), so the corresponding wave mode is a surface wave. To obtain the solution in the core region regular at r=0 in this case we have to substitute I 0(|κ|r) and I 1(|κ|r) for J 0(κr) and J 1(κr), respectively, in Equation (19), where I 0 and I 1 are the modified Bessel functions of the first kind, and the zero and first order.

In the annulus (b<r<a), where the background magnetic field is purely azimuthal, Equations (11) and (14) reduce to

$$ \frac{\mathrm{d}^2 P}{\mathrm{d}r^2} + \frac{3}{r}\frac{\mathrm{d}P}{\mathrm{d}r} + \lambda^2 P = 0, $$
(20)
$$ \xi_r = \frac{\alpha^2 r}{\rho_0\omega^2} \biggl(r\frac{\mathrm{d}P}{\mathrm{d}r} + 2P \biggr). $$
(21)

Using the variable substitution P=S/r we transform Equation (20) to the modified Bessel equation of order one,

$$ \frac{\mathrm{d}^2 S}{\mathrm{d}r^2} + \frac{1}{r}\frac{\mathrm{d}S}{\mathrm{d}r} - \biggl(\lambda^2 + \frac{1}{r^2} \biggr)S = 0. $$
(22)

Hence, in the annulus, the solution is given by

$$ P_0 = \frac{1}{r} \bigl[A_1 I_1(\lambda r) + A_2 K_1(\lambda r) \bigr], \qquad \xi_{r0} = \frac{\alpha^2\lambda r}{\rho_0\omega^2} \bigl[A_1 I_0(\lambda r) - A_2 K_0(\lambda r) \bigr] , $$
(23)

where A 1 and A 2 are constants. When deriving Equations (17), (19), and (23) we have used the recurrent relations for Bessel functions and modified Bessel functions (e.g. Abramowitz and Stegun 1964). Substituting Equations (17), (19), and (23) in the boundary conditions (8) and (9) we obtain the system of four linear homogeneous algebraic equations for the quantities A i, A e, A 1 and A 2. This system has non-trivial solutions only when its determinant is equal to zero. This condition results in the dispersion equation for fast sausage waves,

$$ WZ - XY = 0, $$
(24)

where

$$ W = J_0(\kappa b)I_0(\lambda b) - \frac{J_1(\kappa b)}{\kappa b} \biggl(I_0(\lambda b) - \frac{b\omega^2}{ \lambda V_{\mathrm{A}0}^2}I_1(\lambda b) \biggr), $$
(25)
$$ X = J_0(\kappa b)K_0(\lambda b) - \frac{J_1(\kappa b)}{\kappa b} \biggl(K_0(\lambda b) + \frac{b\omega^2}{ \lambda V_{\mathrm{A}0}^2}K_1(\lambda b) \biggr), $$
(26)
$$ Y = I_0(\lambda a)K_0(\lambda a) + \frac{K_1(\lambda a)}{\lambda a} \biggl(I_0(\lambda a) - \frac{a\omega^2}{ \lambda V_{\mathrm{A}0}^2}I_1(\lambda a) \biggr), $$
(27)
$$ Z = K_0^2(\lambda a) + \frac{K_1(\lambda a)}{\lambda a} \biggl(K_0(\lambda a) + \frac{a\omega^2}{ \lambda V_{\mathrm{A}0}^2}K_1(\lambda a) \biggr). $$
(28)

The dispersion equation (24) is valid for body waves, i.e. when ω/k>V Ai. To obtain the dispersion equation for surface waves we have to substitute |κ| for κ, and I 0 and I 1 for J 0 and J 1 in this equation. The dispersion equation (24) is used in the next section to study fast sausage waves.

4 Fast Sausage Waves in Coronal Loops

In this section we study the properties of fast sausage waves in a model coronal loop described in Section 2. We start our analysis from the long wavelength approximation and assume that ka≪1. Then, using the expansions of Bessel functions and modified Bessel functions for small values of the argument (e.g. Abramowitz and Stegun 1964), we obtain, in the thin tube approximation, the solution for the dispersion equation (24):

$$ \omega^2 = k^2 V_{\mathrm{A}0}^2 \frac{\ln(a/b)}{2 + \ln(a/b)} . $$
(29)

Obviously \(\omega^{2} < k^{2} V_{\mathrm{A}0}^{2}\), so λ 2>0 and the dispersion equation (29) corresponds to a trapped mode. This mode is a body wave (κ 2>0) when

$$ \frac{\rho_{\mathrm{i}}}{\rho_{\mathrm{e}}} > \frac{a^2[2 +\ln(a/b)]}{b^2\ln (a/b)} , $$
(30)

and it is a surface wave (κ 2<0) otherwise.

We have also studied the dispersion equation (24) numerically. If we rewrite this dispersion equation in terms of dimensionless quantities \(\tilde{\omega} = \omega/kV_{\mathrm{Ai}}\) and \(\tilde{k} = bk\), then we will see that the dimensionless dispersion equation contains only two parameters: a/b and \(V_{\mathrm{A}0}/V_{\mathrm{Ai}} = (b/a)\sqrt{\rho_{\mathrm{i}}/ \rho_{\mathrm{e}}}\). In Figure 2 the numerically calculated dispersion curves are shown for a=2b and V A0=3V Ai. The numbers at the curves are the radial numbers of the modes, which are the numbers of nodes in the radial direction. We see that only the principal mode that has no nodes in the radial direction can exist in the long wavelength approximation. All other modes have cut-off wavenumbers and can be supported by the tube only if the wavenumber is larger than the cut-off wavenumber. We also see that the frequency of the principal mode tends to the value given by Equation (29) when bk→0. On the other hand, ω≈kV Ai for large values of bk that can be considered as the thick tube approximation. For comparison, in Figure 3, we have also shown the dispersion curves for fast sausage modes of a homogeneous magnetic tube with V A0=3V Ai. We see that, in this case, all modes including the principal one have cut-off wavenumbers.

Figure 2
figure 2

The dispersion curves for fast sausage waves in a complex current-carrying loop with a/b=2 and V A0/V Ai=3. The numbers at the curves indicate the number of nodes in the radial direction.

Full size image
Figure 3
figure 3

The dispersion curves for fast sausage waves in a homogeneous loop with V A0/V Ai=3. The numbers at the curves indicate the number of nodes in the radial direction.

Full size image

The cut-off wave number k c is determined by the condition that the mode phase speed becomes equal to the external Alfvén speed when k=k c. When k<k c, the phase speed is larger than the external Alfvén speed, and the corresponding mode is leaky. Introducing the intermediate region with purely azimuthal magnetic field reduces the mode phase speed, thus decreasing the cut-off wave number. This effect is clearly seen when comparing Figures 2 and 3. In the case of the principal mode this phase speed reduction is so strong that its phase speed never exceeds the external Alfvén speed, and thus there is no cut-off wave number for this mode.

Let us now apply the theoretical results obtained in this paper to quasi-periodic pulsations of microwave emission generated in a single flaring loop observed with the Nobeyama Radioheliograph and Nobeyama radio polarimeters on 21 May 2004. This observation has been reported by Kupriyanova et al. (2010). In this observation the loop length was L=25 Mm and the pulsation period P=30 – 40 s. Flaring loops are relatively thick, so we take the radius of the loop cross-section R=2.5 Mm. First we apply the theory of fast sausage waves in homogeneous magnetic tubes. For the principal mode the cut-off wave number is given by (Edwin and Roberts 1983; Aschwanden, Nakariakov, and Melnikov 2004)

$$ k_{\mathrm{c}} R \approx2.4(V_{\mathrm{Ai}}/V_{\mathrm{Ae}}). $$
(31)

Assuming that the pulsations of microwave emission were caused by the fast sausage mode fundamental in the longitudinal direction, we obtain kR=π(R/L)≈0.31. The condition k c R≤0.31 is equivalent to V Ai/V Ae<0.13. If we assume that the magnetic field magnitude inside and outside the loop is the same, then we can rewrite this inequality as ρ i/ρ e>60. We see that the loop could support the trapped fundamental fast sausage mode only if the density contrast is very large, although it is not completely unrealistic because the density contrast in flaring loops can be very large (Aschwanden, Nakariakov, and Melnikov 2004).

The estimate for the phase speed is 2L/P=625 – 830 km s−1. For k close to k c the phase speed is close to V Ae. The typical value of the number density of coronal plasma surrounding the loop is 3×1014 m−3. Then, for V Ae≤830 km s−1, we obtain B≲7 G (gauss), which is too small for flaring loops. Of course, we can increase this estimate by decreasing k c and, consequently, making the phase velocity closer to V Ai. However, for this we have to increase further the density ratio. We see that fast sausage modes in homogeneous magnetic tubes can explain the observed modulation of microwave emission, but only under fairly extreme assumptions about plasma parameters and magnetic field.

In contrast, the theory of fast sausage waves in current-carrying coronal loops can easily explain the observed microwave emission modulation without making any extreme assumptions. Let us, for definiteness, take P=40 s. Then it follows from Equation (29) that

$$V_{\mathrm{A}0} \approx1.25\times10^6\sqrt{\frac{2 + \ln(a/b)}{\ln(a/b)}}~\mathrm{m}\,\mathrm{s}^{-1}. $$

Once again taking the number density of the surrounding plasma equal to 3×1014 m−3, we arrive at

$$B_{\mathrm{e}} \approx10\sqrt{\frac{2 + \ln(a/b)}{\ln(a/b)}}~\mathrm{G}. $$

If now we take B e=50 G, which is a realistic value for flaring loops, then we obtain from this equation a/b≈1.087, so we need a very thin annulus with the azimuthal magnetic field to obtain the correct values for parameters of the flaring loop. In accordance with Equation (4), ρ i/ρ e>(a/b)2≈1.18. This is the only restriction imposed on the density ratio. In particular, we can take ρ i/ρ e=3, which sometimes is considered as a typical value in non-flaring loops.

5 Summary and Conclusions

The first steps of coronal seismology were based on the use of the simplest model of a coronal loop, which is a straight homogeneous magnetic tube. Depending on the phase velocity, trapped waves that can propagate in such a tube are divided in fast and slow ones. Another classification is related to the azimuthal dependence of perturbations. The waves are divided in sausage, kink and fluting. The third classification is based on the radial dependence of perturbations. In particular, the wave mode that does not have nodes in the radial direction is called principal. The principal kink and fluting modes are the only fast modes that can have arbitrary wavelength. All other fast wave modes have cut-off wavelengths. Typically these wavelengths are of the order of the radius of the tube cross-section, but sometimes they can be substantially larger.

The principal fast sausage mode is used for the description of pulsations of microwave radiation observed in flaring and post-flaring coronal loops. This application of the sausage mode was very successful when the periods of pulsations did not exceed a few seconds. However, the attempts to extend this model to pulsations with periods of a few tens of seconds encounter serious difficulties related to the existence of the cut-off wavelength.

These difficulties can be easily overcome using the model of a complex magnetic tube studied in this paper. In this model the tube consists of the core region with the axial magnetic field and the annulus with the azimuthal magnetic field. The magnetic field in the external plasma is also axial. The most important difference between this model and the model of a homogeneous magnetic tube is that the principal fast sausage mode in a complex tube can have any wavelength. There is no cut-off wavelength for this mode. It has been shown that this model can successfully describe pulsations of microwave radiations with periods of a few tens of seconds without making any extreme assumptions about the plasma and magnetic field parameters.

Here we need to make one important comment. The theory of fast sausage MHD waves is applied for interpretation of pulsations of microwave radiation in flaring and post-flaring coronal loops. This theory has been developed under the assumption that waves propagate on a static background. However, in fact, the background is not static at all. In the model suggested in this paper it is assumed that a complex magnetic tube is formed during the quasi-static expansion of a twisted magnetic tube, which, once again, suggests that the background is not static. Hence, strictly speaking, we have to study wave propagation on a dynamic background before applying the results to interpretation of microwave radiation pulsations.

The theory of waves and oscillation on a dynamic background is only making its first steps. Recently kink oscillations of coronal magnetic loops with the density varying due to cooling have been studied (Morton and Erdélyi 2009, 2010; Ruderman 2011a, 2011b). It turns out that, in the case of the dynamic background, the oscillation frequencies are determined by the same boundary value problem as in the static case, where the time is present as a parameter. As a result, the frequency varies with time. Hence, studying the dispersion equation (24) is the starting point in investigating fast sausage waves on a dynamic background. It is quite possible that the observed variation of frequency of microwave radiation pulsations is related to the dynamic nature of the background. But this is a problem for future study.