Estimating FARIMA models with uncorrelated but non-independent error terms

Abstract

In this paper we derive the asymptotic properties of the least squares estimator (LSE) of fractionally integrated autoregressive moving-average (FARIMA) models under the assumption that the errors are uncorrelated but not necessarily independent nor martingale differences. We relax the independence and even the martingale difference assumptions on the innovation process to extend considerably the range of application of the FARIMA models. We propose a consistent estimator of the asymptotic covariance matrix of the LSE which may be very different from that obtained in the standard framework. A self-normalized approach to confidence interval construction for weak FARIMA model parameters is also presented. All our results are done under a mixing assumption on the noise. Finally, some simulation studies and an application to the daily returns of stock market indices are presented to corroborate our theoretical work.

1 Introduction

Long memory processes takes a large part in the literature of time series (see for instance Granger and Joyeux (1980), Fox and Taqqu (1986), Dahlhaus (1989), Hosking (1981), Beran et al. (2013), Palma (2007), among others). They also play an important role in many scientific disciplines and applied fields such as hydrology, climatology, economics, finance, to name a few. To model the long memory phenomenon, a widely used model is the fractional autoregressive integrated moving average (FARIMA, for short) model. Consider a second order centered stationary process $X:=(X_t)_{t\in {\mathbb {Z}}}$ satisfying a FARIMA$(p,d_0,q)$ representation of the form

$$\begin{aligned} a_0(L)(1-L)^{d_0}X_t=b_0(L)\epsilon _t, \end{aligned}$$

(1)

where $d_0\in \left]-1/2,1/2\right[$ is the long memory parameter, L stands for the back-shift operator and $a_0(L)=1-\sum _{i=1}^pa_{0i}L^i$ is the autoregressive (AR for short) operator and $b_0(L)=1-\sum _{i=1}^qb_{0i}L^i$ is the moving average (MA for short) operator (by convention $a_{00}=b_{00}=1$). The operators $a_0$ and $b_0$ represent the short memory part of the model. Process $\epsilon :=(\epsilon _t)_{t\in {\mathbb {Z}}}$ can be interpreted as in Francq and Zakoïan (1998) as the linear innovation of X, i.e. $\epsilon _t=X_t-{\mathbb {E}}[X_t|{\mathbf {H}}_X(t-1)]$, where ${\mathbf {H}}_X(t-1)$ is the Hilbert space generated by $(X_s, s<t)$. The innovation process $\epsilon$ is assumed to be a stationary sequence satisfying

(A0)::

${\mathbb {E}}\left[ \epsilon _t\right] =0, \ \mathrm {Var}\left( \epsilon _t\right) =\sigma _{\epsilon }^2 \text { and } \mathrm {Cov}\left( \epsilon _t,\epsilon _{t+h}\right) =0$ for all $t\in {\mathbb {Z}}$ and all $h\ne 0$.

Under the above assumptions the process $\epsilon$ is called a weak white noise. Different sub-classes of FARIMA models can be distinguished depending on the noise assumptions. It is customary to say that X is a strong FARIMA$(p,d_0,q)$ representation and we will do this henceforth if in (1) $\epsilon$ is a strong white noise, namely an independent and identically distributed (iid for short) sequence of random variables with mean 0 and common variance. A strong white noise is obviously a weak white noise because independence entails uncorrelatedness. Of course the converse is not true. Note that the independence hypothesis on the innovation can be tested using the distance correlation (see for instance Székely et al. (2007), Davis et al. (2018) and Aknouche and Francq (2021)). Between weak and strong noises, one can say that $\epsilon$ is a semi-strong white noise if ${\epsilon }$ is a stationary martingale difference, namely a sequence such that ${\mathbb {E}}(\epsilon _{t}|\epsilon _{t-1},\epsilon _{t-2},\dots )=0$. An example of semi-strong white noise is the generalized autoregressive conditional heteroscedastic (GARCH) model (see Francq and Zakoïan (2019)). Martingale difference hypothesis can be tested using the procedures introduced for instance in Dominguez and Lobato (2003), Escanciano and Velasco (2006) and Hsieh (1989). If $\epsilon$ is a semi-strong white noise in (1), X is called a semi-strong FARIMA$(p,d_0,q)$. If no additional assumption is made on $\epsilon$, that is if $\epsilon$ is only a weak white noise (not necessarily iid, nor a martingale difference), the representation (1) is called a weak FARIMA$(p,d_0,q)$. It is clear from these definitions that the following inclusions hold:

$$\begin{aligned}&\left\{ \text {strong FARIMA}(p,d_0,q) \right\} \subset \left\{ \text {semi-strong FARIMA}(p,d_0,q) \right\} \\&\subset \left\{ \text {weak FARIMA}(p,d_0,q)\right\} . \end{aligned}$$

Nonlinear models are becoming more and more employed because numerous real time series exhibit nonlinear dynamics. For instance conditional heteroscedasticity can not be generated by FARIMA models with iid noises.¹ As mentioned by Francq and Zakoïan (2005, 1998) in the case of ARMA models, many important classes of nonlinear processes admit weak ARMA representations in which the linear innovation is not a martingale difference. The main issue with nonlinear models is that they are generally hard to identify and implement. These technical difficulties certainly explain the reason why the asymptotic theory of FARIMA model estimation is mainly limited to the strong or semi-strong FARIMA model.

Now we present some of the main works about FARIMA model estimation when the noise is strong or semi-strong. For the estimation of long-range dependent processes, the commonly used estimation method is based on the Whittle frequency domain maximum likelihood estimator (MLE) (see for instance Dahlhaus (1989), Fox and Taqqu (1986), Taqqu and Teverovsky (1997), Giraitis and Surgailis (1990)). The asymptotic properties of the MLE of FARIMA models are well-known under the restrictive assumption that the errors $\epsilon _t$ are independent or martingale difference (see Beran (1995), Beran et al. (2013), Palma (2007), Baillie et al. (1996), Ling and Li (1997), Hauser and Kunst (1998), among others). Hualde and Robinson (2011), Nielsen (2015) and Cavaliere et al. (2017) have considered the problem of conditional sum of squares estimation (see Klimko and Nelson (1978)) and inference on parametric fractional time series models driven by conditionally (unconditionally) heteroskedastic shocks. All the works mentioned above assume either strong or semi-strong innovations. In the modeling of financial time series, for example, the GARCH assumption on the errors is often used (see for instance Baillie et al. (1996), Hauser and Kunst (1998)) to capture the conditional heteroscedasticity. The GARCH models are generally martingale differences. Various research works were devoted to testing the martingale difference hypothesis (see for example Dominguez and Lobato (2003), Escanciano and Velasco (2006) and Hsieh (1989)). In financial econometrics, the returns are often assumed to be martingale increments (though they are not generally independent sequences). However, many works have shown that for some exchange rates, the martingale difference assumption is not satisfied (see for instance Escanciano and Velasco (2006)). There is no doubt that it is important to have a soundness inference procedure for the parameter in the FARIMA model when the (possibly dependent) error is subject to unknown conditional heteroscedasticity. Little is thus known when the martingale difference assumption is relaxed. Our aim in this paper is to consider a flexible FARIMA specification and to relax the independence assumption (and even the martingale difference assumption) in order to be able to cover weak FARIMA representations of general nonlinear models.

A very few works deal with the asymptotic behavior of the MLE of weak FARIMA models. To our knowledge, Shao (2012, 2010b) are the only papers on this subject. Under weak assumptions on the noise process, the author has obtained the asymptotic normality of the Whittle estimator (see Whittle (1953)). Nevertheless, the inference problem is not fully addressed. This is due to the fact that the asymptotic covariance matrix of the Whittle estimator involves the integral of the fourth-order cumulant spectra of the dependent errors $\epsilon _t$. Using non-parametric bandwidth-dependent methods, one builds an estimation of this integral but there is no guidance on the choice of the bandwidth in the estimation procedures (see Shao (2012), Taniguchi (1982), Keenan (1987), Chiu (1988) for further details). The difficulty is caused by the dependence in $\epsilon _t$. Indeed, for strong noise, a bandwidth-free consistent estimator of the asymptotic covariance matrix is available. When $\epsilon _t$ is dependent, no explicit formula for a consistent estimator of the asymptotic variance matrix seems to be provided in the literature (see Shao (2012)).

In this work we propose to adopt for weak FARIMA models the estimation procedure developed in Francq and Zakoïan (1998) so we use the least squares estimator (LSE for short). We show that a strongly mixing property and the existence of moments are sufficient to obtain a consistent and asymptotically normally distributed least squares estimator for the parameters of a weak FARIMA representation. For technical reasons, we often use an assumption on the summability of cumulants. This can be a consequence of a mixing and moments assumptions (see Doukhan and León (1989), for more details). These kind of hypotheses enable us to circumvent the problem of the lack of speed of convergence (due to the long-range dependence) in the infinite AR or MA representations. We fix this gap by proposing rather sharp estimations of the infinite AR and MA representations in the presence of long-range dependence (see Sect. 6.1 for details).

In our opinion there are three major contributions in this work. The first one is to show that the estimation procedure developed in Francq and Zakoïan (1998) can be extended to weak FARIMA models. This goal is achieved thanks to Theorems 1 and 2 in which the consistency and the asymptotic normality are stated. The second one is to provide an answer to the open problem raised by Shao (2012) (see also Shao (2010b)) on the asymptotic covariance matrix estimation. We propose in our work a weakly consistent estimator of the asymptotic variance matrix (see Theorem 5). Thanks to this estimation of the asymptotic variance matrix, we can construct a confidence region for the estimation of the parameters. Finally another method to construct such confidence region is achieved thanks to an alternative method using a self normalization procedure (see Theorem 8).

The paper is organized as follows. Section 2 shows that the least squares estimator for the parameters of a weak FARIMA model is consistent when the weak white noise $(\epsilon _t)_{t\in {\mathbb {Z}}}$ is ergodic and stationary, and that the LSE is asymptotically normally distributed when $(\epsilon _t)_{t\in {\mathbb {Z}}}$ satisfies mixing assumptions. The asymptotic variance of the LSE may be very different in the weak and strong cases. Section 3 is devoted to the estimation of this covariance matrix. We also propose a self-normalization-based approach to construct a confidence region for the parameters of weak FARIMA models which avoids to estimate the asymptotic covariance matrix. We gather in Section 7 all our figures and tables. These simulation studies and illustrative applications on real data are presented and discussed in Sect. 4. The proofs of the main results are collected in Sect. 6.

In all this work, we shall use the matrix norm defined by $\Vert A\Vert =\sup _{\Vert x\Vert \le 1}\Vert Ax\Vert =\rho ^{1/2}( A^{'}A)$, when A is a ${\mathbb {R}}^{k_1\times k_2}$ matrix, $\Vert x\Vert ^2=x'x$ is the Euclidean norm of the vector $x\in {\mathbb {R}}^{k_2}$, and $\rho (\cdot )$ denotes the spectral radius.

2 Least squares estimation

In this section we present the parametrization and the assumptions that are used in the sequel. Then we state the asymptotic properties of the LSE of weak FARIMA models.

2.1 Notations and assumptions

We make the following standard assumption on the roots of the AR and MA polynomials in (1).

(A1)::

The polynomials $a_0(z)$ and $b_0(z)$ have all their roots outside of the unit disk with no common factors.

Let $\varTheta ^{*}$ be the space

$$\begin{aligned} \varTheta ^{*}:=&\Big \{(\theta _1,\theta _2,\ldots ,\theta _{p+q}) \in {\mathbb {R}}^{p+q},\text { where } a_{\theta }(z)=1-\sum _{i=1}^{p}\theta _{i}z^{i}\, \text { and } b_{\theta }(z)=1-\sum _{j=1}^{q}\theta _{p+j}z^{j} \\&\quad \text { have all their zeros outside the unit disk}\Big \}\ . \end{aligned}$$

Denote by $\varTheta$ the Cartesian product $\varTheta ^{*}\times \left[ d_1,d_2\right]$, where $\left[ d_1,d_2\right] \subset \left] -1/2,1/2\right[$ with $d_1-d_0>-1/2$. The unknown parameter of interest $\theta _0=(a_{01},a_{02},\ldots ,a_{0p},b_{01},b_{02},\ldots ,b_{0q},d_0)^\prime$ is supposed to belong to the parameter space $\varTheta$.

The fractional difference operator $(1-L)^{d_0}$ is defined, using the generalized binomial series, by

$$\begin{aligned} (1-L)^{d_0}=\sum _{j\ge 0}\alpha _j(d_0)L^j, \end{aligned}$$

where for all $j\ge 0$, $\alpha _j(d_0)=\varGamma (j-d_0)/\left\{ \varGamma (j+1)\varGamma (-d_0)\right\}$ and $\varGamma (\cdot )$ is the Gamma function. Using the Stirling formula we obtain that for large j, $\alpha _j(d_0)\sim j^{-d_0-1}/\varGamma (-d_0)$ (one refers to Beran et al. (2013) for further details).

For all $\theta \in \varTheta$ we define $( \epsilon _t(\theta )) _{t\in {\mathbb {Z}}}$ as the second order stationary process which is the solution of

$$\begin{aligned} \epsilon _t(\theta )=\sum _{j\ge 0}\alpha _j(d)X_{t-j}-\sum _{i=1}^p\theta _i\sum _{j\ge 0}\alpha _j(d)X_{t-i-j}+\sum _{j=1}^q\theta _{p+j}\epsilon _{t-j}(\theta ). \end{aligned}$$

(2)

Observe that, for all $t\in {\mathbb {Z}}$, $\epsilon _t(\theta _0)=\epsilon _t$ a.s. Given a realization $X_1,\dots ,X_n$ of length n, $\epsilon _t(\theta )$ can be approximated, for $0<t\le n$, by ${\tilde{\epsilon }}_t(\theta )$ defined recursively by

$$\begin{aligned} {\tilde{\epsilon }}_t(\theta )=\sum _{j=0}^{t-1}\alpha _j(d)X_{t-j} -\sum _{i=1}^p\theta _i\sum _{j=0}^{t-i-1}\alpha _j(d)X_{t-i-j} +\sum _{j=1}^q\theta _{p+j}{\tilde{\epsilon }}_{t-j}(\theta ), \end{aligned}$$

(3)

with ${\tilde{\epsilon }}_t(\theta )=X_t=0$ if $t\le 0$. It will be shown that these initial values are asymptotically negligible and, in particular, that $\epsilon _t(\theta )-{\tilde{\epsilon }}_t(\theta )\rightarrow 0$ in ${\mathbb {L}}^2$ as $t\rightarrow \infty$ (see Remark 12 hereafter). Thus the choice of the initial values has no influence on the asymptotic properties of the model parameters estimator.

Let $\varTheta ^{*}_{\delta }$ denote the compact set

$$\begin{aligned} \varTheta ^{*}_{\delta }=\left\{ \theta \in {\mathbb {R}}^{p+q}; \text { the roots of the polynomials } a_{\theta }(z) \text { and } b_{\theta }(z) \text { have modulus } \ge 1+\delta \right\} . \end{aligned}$$

We define the set $\varTheta _{\delta }$ as the Cartesian product of $\varTheta ^{*}_{\delta }$ by $\left[ d_1,d_2\right]$, i.e. $\varTheta _{\delta }=\varTheta ^{*}_{\delta }\times \left[ d_1,d_2\right]$, where $\delta$ is a positive constant chosen such that $\theta _0$ belongs to $\varTheta _{\delta }$.

The random variable ${\hat{\theta }}_n$ is called least squares estimator if it satisfies, almost surely,

$$\begin{aligned} {\hat{\theta }}_n=\underset{\theta \in \varTheta _{\delta }}{\mathrm {argmin}} \ Q_n(\theta ), \text { where }Q_n(\theta )=\frac{1}{n}\sum _{t=1}^n{\tilde{\epsilon }}_t^2(\theta ). \end{aligned}$$

(4)

Our main results are proven under the following assumptions:

(A2)::

The process $(\epsilon _t)_{t\in {\mathbb {Z}}}$ is strictly stationary and ergodic.

The consistency of the least squares estimator will be proved under the three above assumptions ((A0), (A1) and (A2)). For the asymptotic normality of the LSE, additional assumptions are required. It is necessary to assume that $\theta _0$ is not on the boundary of the parameter space ${\varTheta _\delta }$.

(A3)::

We have $\theta _0\in \overset{\circ }{\varTheta _\delta }$, where $\overset{\circ }{\varTheta _\delta }$ denotes the interior of $\varTheta _\delta$.

The stationary process $\epsilon$ is not supposed to be an independent sequence. So one needs to control its dependency by means of its strong mixing coefficients $\left\{ \alpha _{\epsilon }(h)\right\} _{h\ge 0}$ defined by

$$\begin{aligned} \alpha _{\epsilon }\left( h\right) =\sup _{A\in {\mathcal {F}}_{-\infty }^t,B \in {\mathcal {F}}_{t+h}^{+\infty }}\left| {\mathbb {P}}\left( A\cap B\right) -{\mathbb {P}}(A){\mathbb {P}}(B)\right| , \end{aligned}$$

where ${\mathcal {F}}_{-\infty }^t=\sigma (\epsilon _u, u\le t )$ and ${\mathcal {F}}_{t+h}^{+\infty }=\sigma (\epsilon _u, u\ge t+h)$.

We shall need an integrability assumption on the moments of the noise $\epsilon$ and a summability condition on the strong mixing coefficients $(\alpha _{\epsilon }(h))_{h\ge 0}$.

(A4)::

There exists an integer $\tau \ge 2$ such that for some $\nu \in ]0,1]$, we have ${\mathbb {E}}|\epsilon _t|^{\tau +\nu }<\infty$ and $\sum _{h=0}^{\infty }(h+1)^{k-2} \left\{ \alpha _{\epsilon }(h)\right\} ^{\frac{\nu }{k+\nu }}<\infty$ for $k=1,\dots ,\tau$.

Note that (A4) implies the following weak assumption on the joint cumulants of the innovation process $\epsilon$ (see Doukhan and León (1989), for more details).

(A4’)::

There exists an integer $\tau \ge 2$ such that $C_\tau :=\sum _{i_1,\dots ,i_{\tau -1}\in {\mathbb {Z}}}|\mathrm {cum} (\epsilon _0,\epsilon _{i_1},\dots ,\epsilon _{i_{\tau -1}})|<\infty \ .$

In the above expression, $\mathrm {cum}(\epsilon _0,\epsilon _{i_1},\dots ,\epsilon _{i_{\tau -1}})$ denotes the $\tau -$th order cumulant of the stationary process. Due to the fact that the $\epsilon _t$’s are centered, we notice that for fixed (i, j, k)

$$\begin{aligned} \mathrm {cum}(\epsilon _0,\epsilon _i,\epsilon _j,\epsilon _k)={\mathbb {E}} \left[ \epsilon _0\epsilon _i\epsilon _j\epsilon _k\right] -{\mathbb {E}} \left[ \epsilon _0\epsilon _i\right] {\mathbb {E}}\left[ \epsilon _j\epsilon _k \right] -{\mathbb {E}}\left[ \epsilon _0\epsilon _j\right] {\mathbb {E}}\left[ \epsilon _i\epsilon _k\right] -{\mathbb {E}} \left[ \epsilon _0\epsilon _k\right] {\mathbb {E}} \left[ \epsilon _i\epsilon _j\right] . \end{aligned}$$

Assumption (A4) is a usual technical hypothesis which is useful when one proves the asymptotic normality (see Francq and Zakoïan (1998) for example). Let us notice however that we impose a stronger convergence speed for the mixing coefficients than in the works on weak ARMA processes. This is due to the fact that the coefficients in the AR or MA representation of $\epsilon _t(\theta )$ have no more exponential decay because of the fractional operator (see Sect. 6.1 for details and comments).

As mentioned before, Hypothesis (A4) implies (A4’) which is also a technical assumption usually used in the fractionally integrated ARMA processes framework (see for instance Shao (2010c)) or even in an ARMA context (see Francq and Zakoïan (2007); Zhu and Li (2015)). One remarks that in Shao (2010b), the author emphasized that a geometric moment contraction implies (A4’). This provides an alternative to strong mixing assumptions but, to our knowledge, there is no relation between this two kinds of hypotheses.

2.2 Asymptotic properties

The asymptotic properties of the LSE of the weak FARIMA model are stated in the following two theorems.

Theorem 1

(Consistency) Assume that $(\epsilon _t)_{t\in {\mathbb {Z}}}$ satisfies (1) and belongs to ${\mathbb {L}}^2$. Let $( {\hat{\theta }}_n)_{n\ge 1}$ be a sequence of least squares estimators. Under Assumptions (A0), (A1) and (A2), we have

$$\begin{aligned} {\hat{\theta }}_n\xrightarrow [n\rightarrow \infty ]{{\mathbb {P}}} \, \theta _0. \end{aligned}$$

The proof of this theorem is given in Sect. 6.2.

In order to state our asymptotic normality result, we define the function

$$\begin{aligned} O_n(\theta )&=\frac{1}{n}\sum _{t=1}^n\epsilon _t^2(\theta ), \end{aligned}$$

(5)

where the sequence $\left( \epsilon _t(\theta )\right) _{t\in {\mathbb {Z}}}$ is given by (2). We consider the following information matrices

$$\begin{aligned} I(\theta )=\lim _{n\rightarrow \infty }Var\left\{ \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta )\right\} \text { and } J(\theta )=\lim _{n\rightarrow \infty }\left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}O_n(\theta )\right] \text {a.s.} \end{aligned}$$

The existence of these matrices are proved when one demonstrates the following result.

Theorem 2

(Asymptotic normality) We assume that $(\epsilon _t)_{t\in {\mathbb {Z}}}$ satisfies (1). Under (A0)–(A3) and Assumption (A4) with $\tau =4$, the sequence $( \sqrt{n}( {\hat{\theta }}_n-\theta _0)) _{n\ge 1}$ has a limiting centered normal distribution with covariance matrix $\varOmega :=J^{-1}(\theta _0)I(\theta _0)J^{-1}(\theta _0)$.

The proof of this theorem is given in Sect. 6.3.

Remark 3

Hereafter (see more precisely (55)), we will be able to prove that

$$\begin{aligned} J(\theta _0)= 2{\mathbb {E}}\left[ \frac{\partial }{\partial \theta }\epsilon _t(\theta _0)\frac{\partial }{\partial \theta '}\epsilon _t(\theta _0)\right] \ \text {a.s.} \end{aligned}$$

Thus the matrix $J(\theta _0)$ has the same expression in the strong and weak FARIMA cases (see Theorem 1 of Beran (1995)). On the contrary, the matrix $I(\theta _0)$ is in general much more complicated in the weak case than in the strong case.

Remark 4

In the standard strong FARIMA case, i.e. when (A2) is replaced by the assumption that $(\epsilon _t)_{t\in {\mathbb {Z}}}$ is iid, we have $I(\theta _0)=2\sigma _{\epsilon }^2J(\theta _0)$. Thus the asymptotic covariance matrix is then reduced as $\varOmega _S:=2\sigma _{\epsilon }^2J^{-1}(\theta _0)$. Generally, when the noise is not an independent sequence, this simplification can not be made and we have $I(\theta _0)\ne 2\sigma _{\epsilon }^2J(\theta _0)$. The true asymptotic covariance matrix $\varOmega =J^{-1}(\theta _0)I(\theta _0)J^{-1}(\theta _0)$ obtained in the weak FARIMA framework can be very different from $\varOmega _S$. As a consequence, for the statistical inference on the parameter, the ready-made softwares used to fit FARIMA do not provide a correct estimation of $\varOmega$ for weak FARIMA processes because the standard time series analysis softwares use empirical estimators of $\varOmega _S$. The problem also holds in the weak ARMA case (see Francq and Zakoïan (2007) and the references therein).This is why it is interesting to find an estimator of $\varOmega$ which is consistent for both weak and (semi-)strong FARIMA cases.

Based on the above remark, the next section deals with two different methods in order to find an estimator of $\varOmega$.

3 Estimating the asymptotic variance matrix

For statistical inference problem, the asymptotic variance $\varOmega$ has to be estimated. In particular Theorem 2 can be used to obtain confidence intervals and significance tests for the parameters.

First of all, the matrix $J(\theta _0)$ can be estimated empirically by the square matrix ${\hat{J}}_n$ of order $p+q+1$ defined by:

$$\begin{aligned} {\hat{J}}_n=\frac{2}{n}\sum _{t=1}^n\left\{ \frac{\partial }{\partial \theta }{\tilde{\epsilon }}_t \left( {\hat{\theta }}_n\right) \right\} \left\{ \frac{\partial }{\partial \theta ^{'}}{\tilde{\epsilon }}_t \left( {\hat{\theta }}_n\right) \right\} . \end{aligned}$$

(6)

The convergence of ${\hat{J}}_n$ to $J(\theta _0)$ is classical (see Lemma 17 in Sect. 6.3 for details).

In the standard strong FARIMA case, in view of remark 4, we have ${\hat{\varOmega }}_S:=2{\hat{\sigma }}_{\epsilon }^2{\hat{J}}_n^{-1}$ with ${\hat{\sigma }}_{\epsilon }^2=Q_n({\hat{\theta }}_n)$. Thus ${\hat{\varOmega }}_S$ is a consistent estimator of $\varOmega _S$. In the general weak FARIMA case, this estimator is not consistent when $I(\theta _0)\ne 2\sigma _{\epsilon }^2J(\theta _0)$. So we need a consistent estimator of $I(\theta _0)$.

3.1 Estimation of the asymptotic matrix $I(\theta _0)$

For all $t\in {\mathbb {Z}}$, let

$$\begin{aligned} H_t(\theta _0)&=2\epsilon _t(\theta _0)\frac{\partial }{\partial \theta }\epsilon _t(\theta _0) =\left( 2\epsilon _t(\theta _0)\frac{\partial }{\partial \theta _1} \epsilon _t(\theta _0),\dots ,2\epsilon _t(\theta _0)\frac{\partial }{\partial \theta _{p+q+1}}\epsilon _t(\theta _0)\right) ^{'}. \end{aligned}$$

(7)

We shall see in the proof of Lemma 18 that

$$\begin{aligned} I(\theta _0)&=\lim _{n\rightarrow \infty }\mathrm {Var}\left( \frac{1}{\sqrt{n}}\sum _{t=1}^nH_t(\theta _0)\right) = \sum _{h=-\infty }^{+\infty }\mathrm {Cov}\left( H_t(\theta _0),H_{t-h}(\theta _0)\right) . \end{aligned}$$

Following the arguments developed in Boubacar Mainassara et al. (2012), the matrix $I(\theta _0)$ can be estimated using Berk’s approach (see Berk (1974)). More precisely, by interpreting $I(\theta _0)/2\pi$ as the spectral density of the stationary process $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ evaluated at frequency 0, we can use a parametric autoregressive estimate of the spectral density of $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ in order to estimate the matrix $I(\theta _0)$.

For any $\theta \in \varTheta$, $H_t(\theta )$ is a measurable function of $\left\{ \epsilon _s,s\le t\right\}$. The stationary process $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ admits the following Wold decomposition $H_t(\theta _0)=u_t+\sum _{k=1}^{\infty }\psi _ku_{t-k}$, where $(u_t)_{t\in {\mathbb {Z}}}$ is a $(p+q+1)-$variate weak white noise with variance matrix $\varSigma _u$.

Assume that $\varSigma _u$ is non-singular, that $\sum _{k=1}^{\infty }\left\| \psi _k\right\| <\infty$, and that $\det (I_{p+q+1}+\sum _{k=1}^{\infty }\psi _kz^k)\ne 0$ if $\left| z\right| \le 1$. Then $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ admits a weak multivariate $\mathrm {AR}(\infty )$ representation (see Akutowicz (1957)) of the form

$$\begin{aligned} \varPhi (L)H_t(\theta _0):=H_t(\theta _0)-\sum _{k=1}^{\infty }\varPhi _kH_{t-k} (\theta _0)=u_t, \end{aligned}$$

(8)

such that $\sum _{k=1}^{\infty }\left\| \varPhi _k\right\| <\infty$ and $\det \left\{ \varPhi (z)\right\} \ne 0$ if $\left| z\right| \le 1$.

Thanks to the previous remarks, the estimation of $I(\theta _0)$ is therefore based on the following expression

$$\begin{aligned} I(\theta _0)=\varPhi ^{-1}(1)\varSigma _u\varPhi ^{-1}(1). \end{aligned}$$

Consider the regression of $H_t(\theta _0)$ on $H_{t-1}(\theta _0),\dots ,H_{t-r}(\theta _0)$ defined by

$$\begin{aligned} H_t(\theta _0)=\sum _{k=1}^{r}\varPhi _{r,k}H_{t-k}(\theta _0)+u_{r,t}, \end{aligned}$$

(9)

where $u_{r,t}$ is uncorrelated with $H_{t-1}(\theta _0),\dots ,H_{t-r}(\theta _0)$. Since ${H}_t(\theta _0)$ is not observable, we introduce ${\hat{H}}_t\in {\mathbb {R}}^{p+q+1}$ obtained by replacing $\epsilon _t(\cdot )$ by ${\tilde{\epsilon }}_t(\cdot )$ and $\theta _0$ by ${\hat{\theta }}_n$ in (7):

$$\begin{aligned} {{\hat{H}}}_t&=2{{\tilde{\epsilon }}}_t({{\hat{\theta }}}_n) \frac{\partial }{\partial \theta }{{\hat{\epsilon }}}_t(\theta _n) \ . \end{aligned}$$

(10)

Let ${\hat{\varPhi }}_r(z)=I_{p+q+1}-\sum _{k=1}^r{{\hat{\varPhi }}}_{r,k}z^k$, where ${{\hat{\varPhi }}}_{r,1},\dots ,{{\hat{\varPhi }}}_{r,r}$ denote the coefficients of the LS regression of ${\hat{H}}_t$ on ${\hat{H}}_{t-1},\dots ,{\hat{H}}_{t-r}$. Let ${\hat{u}}_{r,t}$ be the residuals of this regression and let ${\hat{\varSigma }}_{{\hat{u}}_r}$ be the empirical variance (defined in (11) below) of ${\hat{u}}_{r,1},\dots ,{\hat{u}}_{r,r}$. The LSE of ${\underline{\varPhi }}_r=\left( \varPhi _{r,1},\dots ,\varPhi _{r,r}\right)$ and $\varSigma _{u_r}=\mathrm {Var}(u_{r,t})$ are given by

$$\begin{aligned} \underline{{\hat{\varPhi }}}_r={\hat{\varSigma }}_{{\hat{H}}, \underline{{\hat{H}}}_r}{\hat{\varSigma }}_{\underline{{\hat{H}}}_r}^{-1} \ \text { and } \ {\hat{\varSigma }}_{{\hat{u}}_r}=\frac{1}{n}\sum _{t=1}^n\left( {\hat{H}}_t -\underline{{\hat{\varPhi }}}_r \underline{{\hat{H}}}_{r,t}\right) \left( {\hat{H}}_t-\underline{{\hat{\varPhi }}}_r \underline{{\hat{H}}}_{r,t}\right) ^{'}, \end{aligned}$$

(11)

where

$$\begin{aligned} \underline{{\hat{H}}}_{r,t}=( {\hat{H}}_{t-1}^{'},\dots ,{\hat{H}}_{t-r}^{'}) ^{'},\quad {\hat{\varSigma }}_{{\hat{H}},\underline{{\hat{H}}}_r} =\frac{1}{n}\sum _{t=1}^n{\hat{H}}_t\underline{{\hat{H}}}_{r,t}^{'} \text { and } {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}=\frac{1}{n}\sum _{t=1}^n \underline{{\hat{H}}}_{r,t}\underline{{\hat{H}}}_{r,t}^{'}, \end{aligned}$$

with by convention ${\hat{H}}_t=0$ when $t\le 0$. We assume that ${\hat{\varSigma }}_{\underline{{\hat{H}}}_r}$ is non-singular (which holds true asymptotically).

In the case of linear processes with independent innovations, Berk (see Berk (1974)) has shown that the spectral density can be consistently estimated by fitting autoregressive models of order $r=r(n)$, whenever r tends to infinity and $r^3/n$ tends to 0 as n tends to infinity. There are differences with Berk (1974): $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ is multivariate, is not directly observed and is replaced by $({\hat{H}}_t)_{t\in {\mathbb {Z}}}$. It is shown that this result remains valid for the multivariate linear process $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ with non-independent innovations (see Boubacar Mainassara et al. (2012); Boubacar Mainassara and Francq (2011), for references in weak (multivariate) ARMA models). We will extend the results of Boubacar Mainassara et al. (2012) to weak FARIMA models.

The asymptotic study of the estimator of $I(\theta _0)$ using the spectral density method is given in the following theorem.

Theorem 5

We assume (A0)-(A3) and Assumption (A4’) with $\tau =8$. In addition, we assume that the innovation process $(\epsilon _t)_{t\in {\mathbb {Z}}}$ of the FARIMA$(p,d_0,q)$ model (1) is such that the process $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ defined in (7) admits a multivariate AR$(\infty )$ representation (8), where $\Vert \varPhi _k\Vert =\mathrm {o}(k^{-2})$ as $k\rightarrow \infty$, the roots of $\det (\varPhi (z))=0$ are outside the unit disk, and $\varSigma _u=\mathrm {Var}(u_t)$ is non-singular. Then, the spectral estimator of $I(\theta _0)$

$$\begin{aligned} {\hat{I}}^{\mathrm {SP}}_n:={\hat{\varPhi }}_r^{-1}(1) {\hat{\varSigma }}_{{\hat{u}}_r}{\hat{\varPhi }}_r^{'-1}(1)\xrightarrow []{} I(\theta _0)=\varPhi ^{-1}(1)\varSigma _u\varPhi ^{-1}(1) \end{aligned}$$

in probability when $r=r(n)\rightarrow \infty$ and $r^5(n)/n^{1-2(d_0-d_1)}\rightarrow 0$ as $n\rightarrow \infty$ (remind that $d_0\in [ d_1{,}d_2]\subset ] -1/2{,}1/2[$).

The proof of this theorem is given in Sect. 6.4.

A second method to estimate the asymptotic matrix (or rather avoiding estimate it) is proposed in the next subsection.

3.2 A self-normalized approach to confidence interval construction in weak FARIMA models

We have seen previously that we may obtain confidence intervals for weak FARIMA model parameters as soon as we can construct a convergent estimator of the variance matrix $I(\theta _0)$ (see Theorems 2 and 5 ). The parametric approach based on an autoregressive estimate of the spectral density of $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ that we used before has the drawback of choosing the truncation parameter r in (9). This choice of the order truncation is often crucial and difficult. So the aim of this section is to avoid such a difficulty.

This section is also of interest because, to our knowledge, it has not been studied for weak FARIMA models. Notable exception is Shao (2012) who studied this problem in a short memory case (see Assumption 1 in Shao (2012) that implies that the process X is short-range dependent).

We propose an alternative method to obtain confidence intervals for weak FARIMA models by avoiding the estimation of the asymptotic covariance matrix $I(\theta _0)$. It is based on a self-normalization approach used to build a statistic which depends on the true parameter $\theta _0$ and which is asymptotically distribution-free (see Theorem 1 of Shao (2012) for a reference in weak ARMA case). The idea comes from Lobato (2001) and has been already extended by Boubacar Maïnassara and Saussereau (2018); Kuan and Lee (2006); Shao (2010c, 2010a, 2012) to more general frameworks. See also Shao (2015) for a review on some recent developments on the inference of time series data using the self-normalized approach.

Let us briefly explain the idea of the self-normalization.

By a Taylor expansion of the function $\partial Q_n(\cdot )/ \partial \theta$ around $\theta _0$, under (A3), we have

$$\begin{aligned} 0=\sqrt{n}\frac{\partial }{\partial \theta }Q_n({\hat{\theta }}_n) =\sqrt{n}\frac{\partial }{\partial \theta }Q_n(\theta _0) +\left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) \right] \sqrt{n}\left( {\hat{\theta }}_n-\theta _0\right) , \end{aligned}$$

(12)

where the $\theta ^*_{n,i,j}$’s are between ${\hat{\theta }}_n$ and $\theta _0$. Using the following equation

$$\begin{aligned}&\sqrt{n}\left( \frac{\partial }{\partial \theta }O_n(\theta _0) -\frac{\partial }{\partial \theta }Q_n(\theta _0)\right) =\sqrt{n} \frac{\partial }{\partial \theta }O_n(\theta _0)\\&\quad +\left\{ \left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n(\theta ^{*}_{n,i,j}) \right] -J(\theta _0) +J(\theta _0)\right\} \sqrt{n}({\hat{\theta }}_n-\theta _0), \end{aligned}$$

we shall be able to prove that (12) implies that

$$\begin{aligned} \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0)+J(\theta _0)\sqrt{n} ({\hat{\theta }}_n-\theta _0)=\mathrm {o}_{{\mathbb {P}}}\left( 1\right) . \end{aligned}$$

(13)

This is due to the following technical properties:

• the convergence in probability of $\sqrt{n}\partial Q_n(\theta _0)/\partial \theta -\sqrt{n}\partial O_n(\theta _0)/\partial \theta$ to 0 (see Lemma 15 hereafter),

• the convergence in probability of $[\partial ^2 Q_n(\theta _{n,i,j}^{*})/\partial \theta _i\partial \theta _j]$ to $J(\theta _0)$ (see Lemma 17 hereafter),

• the tightness of the sequence $(\sqrt{n}({\hat{\theta }}_n-\theta _0))_{n\ge 1}$ (see Theorem 2) and

• the existence and invertibility of the matrix $J(\theta _0)$ (see Lemma 16 hereafter).

Thus we obtain from (13) that

$$\begin{aligned} \sqrt{n}({\hat{\theta }}_n-\theta _0)=\frac{1}{\sqrt{n}}\sum _{t=1}^nU_t +\mathrm {o}_{{\mathbb {P}}}\left( 1\right) , \end{aligned}$$

where (remind (7))

$$\begin{aligned} U_t=-J^{-1}(\theta _0)H_t(\theta _0). \end{aligned}$$

At this stage, we do not rely on the classical method that would consist in estimating the asymptotic covariance matrix $I(\theta _0)$. We rather try to apply Lemma 1 in Lobato (2001). So we need to check that a functional central limit theorem holds for the process $U:=(U_t)_{t\ge 1}$. For that sake, we define the normalization matrix $P_{p+q+1,n}$ of ${\mathbb {R}}^{(p+q+1)\times (p+q+1)}$ by

$$\begin{aligned} P_{p+q+1,n}=\frac{1}{n^2}\sum _{t=1}^n\left( \sum _{j=1}^t( U_j-{\bar{U}}_n)\right) \left( \sum _{j=1}^t (U_j-{\bar{U}}_n)\right) ^{'} , \end{aligned}$$

(14)

where ${\bar{U}}_n = (1/n)\sum _{i=1}^n U_i$. To ensure the invertibility of the normalization matrix $P_{p+q+1,n}$ (it is the result stated in the next proposition), we need the following technical assumption on the distribution of $\epsilon _t$.

(A5)::

The process $(\epsilon _t)_{t\in {\mathbb {Z}}}$ has a positive density on some neighborhood of zero.

Proposition 6

Under the assumptions of Theorem 2 and (A5), the matrix $P_{p+q+1,n}$ is almost surely non singular.

The proof of this proposition is given in Sect. 6.5.

Let $(B_m(r))_{r\ge 0}$ be a m-dimensional Brownian motion starting from 0. For $m\ge 1$, we denote by ${\mathcal {U}}_m$ the random variable defined by:

$$\begin{aligned} {\mathcal {U}}_m=B_m^{'}(1)V_m^{-1}B_m(1), \end{aligned}$$

(15)

where

$$\begin{aligned} V_m=\int _0^1\left( B_m(r)-rB_m(1)\right) \left( B_m(r)-rB_m(1)\right) ^{'}dr. \end{aligned}$$

(16)

The critical values of ${\mathcal {U}}_m$ have been tabulated by Lobato (2001).

The following theorem states the self-normalized asymptotic distribution of the random vector $\sqrt{n}({\hat{\theta }}_n-\theta _0)$.

Theorem 7

Under the assumptions of Theorem 2 and (A5), we have

$$\begin{aligned} n ({\hat{\theta }}_n-\theta _0)^{'}P_{p+q+1,n}^{-1}({\hat{\theta }}_n -\theta _0)\xrightarrow [n\rightarrow \infty ]{\text {in law}}{\mathcal {U}}_{p+q+1}. \end{aligned}$$

The proof of this theorem is given in Sect. 6.6.

Of course, the above theorem is useless for practical purpose because the normalization matrix $P_{p+q+1,n}$ is not observable. This gap will be fixed below when one replaces the matrix $P_{p+q+1,n}$ by its empirical or observable counterpart

$$\begin{aligned} {\hat{P}}_{p+q+1,n}=\frac{1}{n^2}\sum _{t=1}^n\left( \sum _{j=1}^t( {{\hat{U}}}_j- {\frac{1}{n} \sum _{k=1}^n {{\hat{U}}}_k})\right) \left( \sum _{j=1}^t( {{\hat{U}}}_j- {\frac{1}{n} \sum _{k=1}^n {{\hat{U}}}_k})\right) ^{'}\text { where }{\hat{U}}_j=-{\hat{J}}_n^{-1}{\hat{H}}_j.\nonumber \\ \end{aligned}$$

(17)

The above quantity is observable and we are able to state our Theorem which is the applicable version of Theorem 7.

Theorem 8

Under the assumptions of Theorem 2 and (A5), we have

$$\begin{aligned} n ({\hat{\theta }}_n-\theta _0)^{'}{{\hat{P}}}_{p+q+1,n}^{-1} ({\hat{\theta }}_n-\theta _0)\xrightarrow [n\rightarrow \infty ]{\text {in law}}{\mathcal {U}}_{p+q+1}. \end{aligned}$$

The proof of this theorem is given in Sect. 6.7.

At the asymptotic level $\alpha$, a joint $100(1-\alpha )\%$ confidence region for the elements of $\theta _0$ is then given by the set of values of the vector $\theta$ which satisfy the following inequality:

$$\begin{aligned} n({\hat{\theta }}_n-\theta )^{'}{\hat{P}}_{p+q+1,n}^{-1}({\hat{\theta }}_n -\theta )\le {\mathcal {U}}_{p+q+1,\alpha }, \end{aligned}$$

where ${\mathcal {U}}_{p+q+1,\alpha }$ is the quantile of order $1-\alpha$ for the distribution of ${\mathcal {U}}_{p+q+1}$.

Corollary 9

For any $1\le i\le p+q+1$, a $100(1-\alpha )\%$ confidence region for $\theta _0(i)$ is given by the following set:

$$\begin{aligned} \left\{ x\in {\mathbb {R}}\ {;} \ n\big ({\hat{\theta }}_n(i)-x\big )^{2}{\hat{P}}_{p+q+1,n}^{-1}(i,i)\le {\mathcal {U}}_{1,\alpha }\right\} , \end{aligned}$$

where ${\mathcal {U}}_{1,\alpha }$ denotes the quantile of order $1-\alpha$ of the distribution for ${\mathcal {U}}_{1}$.

The proof of this corollary is similar to that of Theorem 8 when one restricts ourselves to a one dimensional case.

4 Numerical illustrations

In this section, we investigate the finite sample properties of the asymptotic results that we introduced in this work. For that sake we use Monte Carlo experiments. The numerical illustrations of this section are made with the open source statistical software R (see R Development Core Team, 2017) or (see http://cran.r-project.org/).

4.1 Simulation studies and empirical sizes for confidence intervals

We study numerically the behavior of the LSE for FARIMA models of the form

$$\begin{aligned} (1-L)^d\left( X_t-aX_{t-1}\right) =\epsilon _t-b\epsilon _{t-1}, \end{aligned}$$

(18)

where the unknown parameter is taken as $\theta _0=(a,b,d)=(-0.7,-0.2,0.4)$. First we assume that in (18) the innovation process $(\epsilon _t)_{t\in {\mathbb {Z}}}$ is an iid centered Gaussian process with common variance 1 which corresponds to the strong FARIMA case. In two other experiments we consider that in (18) the innovation processes $(\epsilon _t)_{t\in {\mathbb {Z}}}$ are defined respectively by

$$\begin{aligned} \left\{ \begin{array}{l}\epsilon _{t}=\sigma _t\eta _{t}\\ \sigma _t^2=0.04+0.12\epsilon _{t-1}^2 +0.85\sigma _{t-1}^2 \end{array}\right. \end{aligned}$$

(19)

and

$$\begin{aligned} \epsilon _{t}&=\eta _{t}^2\eta _{t-1}, \end{aligned}$$

(20)

where $(\eta _t)_{t\ge 1}$ is a sequence of iid centered Gaussian random variables with variance 1. Note that the innovation process in (20) is not a martingale difference whereas it is the case of the noise defined in (19). The noise defined by (20) is an extension of a noise process in Romano and Thombs (1996).

We simulated $N=1,000$ independent trajectories of size $n=2,000$ of Model (18) in the three following case: the strong Gaussian noise, the semi-strong noise (19) and the weak noise (20).

Fig. 1

LSE of $N=1,000$ independent simulations of the FARIMA(1, d, 1) model (18) with size $n=2,000$ and unknown parameter $\theta _0=(a,b,d)=(-0.7,-0.2,0.4)$, when the noise is strong (left panel), when the noise is semi-strong (19) (middle panel) and when the noise is weak of the form (20) (right panel). Points (a)-(c), in the box-plots, display the distribution of the estimation error ${\hat{\theta }}_n(i)-\theta _0(i)$ for $i=1,2,3$

Fig. 2

LSE of $N=1,000$ independent simulations of the FARIMA(1, d, 1) model (18) with size $n=2,000$ and unknown parameter $\theta _0=(a,b,d)=(-0.7,-0.2,0.4)$. The top panels present respectively, from left to right, the Q-Q plot of the estimates ${\hat{a}}_n$, ${\hat{b}}_n$ and ${\hat{d}}_n$ of a, b and d in the strong case. Similarly the middle and the bottom panels present respectively, from left to right, the Q-Q plot of the estimates ${\hat{a}}_n$, ${\hat{b}}_n$ and ${\hat{d}}_n$ of a, b and d in the semi-strong and weak cases

Fig. 3

LSE of $N=1,000$ independent simulations of the FARIMA(1, d, 1) model (18) with size $n=2,000$ and unknown parameter $\theta _0=(a,b,d)=(-0.7,-0.2,0.4)$. The top panels present respectively, from left to right, the empirical distribution of the estimates ${\hat{a}}_n$, ${\hat{b}}_n$ and ${\hat{d}}_n$ of a, b and d in the strong case. Similarly the middle and the bottom panels present respectively, from left to right, the empirical distribution of the estimates ${\hat{a}}_n$, ${\hat{b}}_n$ and ${\hat{d}}_n$ of a, b and d in the semi-strong and weak cases. The kernel density estimate is displayed in full line, and the centered Gaussian density with the same variance is plotted in dotted line

Figures 1, 2 and 3 compare the empirical distribution of the LSE in these three contexts. The empirical distributions of ${\hat{d}}_n$ are similar in the three cases whereas the LSE ${\hat{a}}_n$ of a is more accurate in the weak case than in the strong and semi-strong cases. This last remark on the empirical distribution of ${\hat{a}}_n$ is in accordance with the results of Romano and Thombs (1996) who showed that, with weak white noises similar to (20), the asymptotic variance of the sample autocorrelations can be greater or less than 1 as well (1 is the asymptotic variance for strong white noises). The empirical distributions of ${\hat{b}}_n$ are more accurate in the strong case than in the weak case. Remark that in the weak case the empirical distributions of ${\hat{b}}_n$ are more accurate than the semi-strong ones.

Figure 4 compares standard estimator ${\hat{\varOmega }}_S=2{{\hat{\sigma }}}_\epsilon ^2{\hat{J}}_n^{-1}$ and the sandwich estimator ${\hat{\varOmega }}={\hat{J}}_n^{-1}{\hat{I}}^{\mathrm {SP}}_n{\hat{J}}_n^{-1}$ of the LSE asymptotic variance $\varOmega$. We used the spectral estimator ${\hat{I}}^{\mathrm {SP}}_n$ defined in Theorem 5. The multivariate AR order r (see (9)) is automatically selected by AIC (we use the function VARselect() of the vars R package). In the strong FARIMA case we know that the two estimators are consistent. In view of the two upper subfigures of Fig. 4, it seems that the sandwich estimator is less accurate in the strong case. This is not surprising because the sandwich estimator is more robust, in the sense that this estimator remains consistent in the semi-strong and weak FARIMA cases, contrary to the standard estimator (see the middle and bottom subfigures of Fig. 4). The estimated asymptotic standard errors obtained from Theorem 2 of the estimated parameters are given by: 0.0308 in the strong case, 0.0465 in the semi-strong case and 0.0300 in the weak case for ${\hat{a}}_n$, 0.0539 in the strong case, 0.0753 in the semi-strong case and 0.0666 in the weak case for ${\hat{b}}_n$ and 0.0253 in the strong case, 0.0364 in the semi-strong case and 0.0264 in the weak case for ${\hat{d}}_n$.

Fig. 4

Comparison of standard and modified estimates of the asymptotic variance $\varOmega$ of the LSE, on the simulated models presented in Fig. 1. The diamond symbols represent the mean, over $N=1,000$ replications, of the standardized errors $n({\hat{a}}_n+0.7)^2$ for (a) (1.90 in the strong case and 4.32 (resp. 1.80) in the semi-strong case (resp. in the weak case)), $n({\hat{b}}_n+0.2)^2$ for (b) (5.81 in the strong case and 11.33 (resp. 8.88) in the semi-strong case (resp. in the weak case)) and $n({\hat{d}}_n-0.4)^2$ for (c) (1.28 in the strong case and 2.65 (resp. 1.40) in the semi-strong case (resp. in the weak case))

Fig. 5

A zoom of the left-middle and left-bottom panels of Fig. 4

Fig. 6

A zoom of the right-middle and right-bottom panels of Fig. 4

Figure 5 (resp. Fig. 6) presents a zoom of the left(right)-middle and left(right)-bottom panels of Fig. 4. It is clear that in the semi-strong or weak case $n({\hat{a}}_n-a)^2$, $n({\hat{b}}_n-b)^2$ and $n({\hat{d}}_n-d)^2$ are, respectively, better estimated by ${\hat{J}}_n^{-1}{\hat{I}}^{\mathrm {SP}}_n{\hat{J}}_n^{-1}(1,1)$, ${\hat{J}}_n^{-1}{\hat{I}}^{\mathrm {SP}}_n{\hat{J}}_n^{-1}(2,2)$ and ${\hat{J}}_n^{-1}{\hat{I}}^{\mathrm {SP}}_n{\hat{J}}_n^{-1}(3,3)$ (see Fig. 6) than by $2{{\hat{\sigma }}}_\epsilon ^2{\hat{J}}_n^{-1}(1,1)$, $2{{\hat{\sigma }}}_\epsilon ^2{\hat{J}}_n^{-1}(2,2)$ and $2{{\hat{\sigma }}}_\epsilon ^2{\hat{J}}_n^{-1}(3,3)$ (see Fig. 5). The failure of the standard estimator of $\varOmega$ in the weak FARIMA framework may have important consequences in terms of identification or hypothesis testing and validation.

Now we are interested in standard confidence interval and the modified versions proposed in Sects. 3.1 and 3.2 . Table 1 displays the empirical sizes in the three previous different FARIMA cases. For the nominal level $\alpha =5\%$, the empirical size over the $N=1,000$ independent replications should vary between the significant limits 3.6% and 6.4% with probability 95%. For the nominal level $\alpha =1\%$, the significant limits are 0.3% and 1.7%, and for the nominal level $\alpha =10\%$, they are 8.1% and 11.9%. When the relative rejection frequencies are outside the significant limits, they are displayed in bold type in Table 1. For the strong FARIMA model, all the relative rejection frequencies are inside the significant limits for n large. For the semi-strong FARIMA model, the relative rejection frequencies of the standard confidence interval are definitely outside the significant limits, contrary to the modified versions proposed. For the weak FARIMA model, only the standard confidence interval of ${\hat{b}}_n$ is outside the significant limits when n increases. As a conclusion, Table 1 confirms the comments done concerning Fig. 4.

4.2 Application to real data

We now consider an application to the daily returns of four stock market indices (CAC 40, DAX, Nikkei and S&P 500). The returns are defined by $r_t=\log (p_t/p_{t-1})$ where $p_t$ denotes the price index of the stock market indices at time t. The observations cover the period from the starting date (March 1st 1990 for CAC 40, December 30th 1987 for DAX, January 5th 1965 for Nikkei and January 3rd 1950 for S&P 500) of each index to February 13th 2019. The sample size is 7,341 for CAC 40; 7,860 for DAX; 13,318 for Nikkei and 17,390 for S&P 500.

Table 1 Empirical size of standard and modified confidence interval: relative frequencies (in %) of rejection

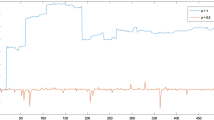
In Financial Econometrics the returns are often assumed to be a white noise. In view of the so-called volatility clustering, it is well known that the strong white noise model is not adequate for these series (see for instance Francq and Zakoïan (2019); Lobato et al. (2001); Boubacar Mainassara et al. (2012); Boubacar Maïnassara and Saussereau (2018)). A long-range memory property of the stock market returns series was largely investigated by Ding et al. (1993) which shows that there are more correlation between power transformation of the absolute return $|r_t|^v$ ($v>0$) than returns themselves (see also Beran et al. (2013), Palma (2007), Baillie et al. (1996) and Ling and Li (1997)). We choose here the case where $v=2$ which corresponds to the squared returns $(r_t^2)_{t\ge 1}$ process. This process have significant positive autocorrelations at least up to lag 100 (see Fig. 9) which confirm the claim that stock market returns have long-term memory (see Ding et al. (1993)).

We fit a FARIMA(1, d, 1) model to the squares of the 4 daily returns. As in Ling (2003), we denote by $(X_t)_{t\ge 1}$ the mean corrected series of the squared returns and we adjust the following model

$$\begin{aligned} (1-L)^d\left( X_t-aX_{t-1}\right) =\epsilon _t-b\epsilon _{t-1} . \end{aligned}$$

Fig. 7

Closing prices of the four stock market indices from the starting date of each index to February 13th 2019

Fig. 8

Returns of the four stock market indices from the starting date of each index to February 13th 2019

Fig. 9

Sample autocorrelations of squared returns of the four stock market indices

Figure 7 (resp. Fig. 8) plots the closing prices (resp. the returns) of the four stock market indices. Figure 9 shows that squared returns $(X_t)_{t\ge 1}$ are generally strongly autocorrelated. Table 2 displays the LSE of the parameter $\theta =(a,b,d)$ of each squared of daily returns. The p-values of the corresponding LSE, ${{\hat{\theta }}}_n=({\hat{a}}_n,{\hat{b}}_n,{\hat{d}}_n)$ are given in parentheses. The last column presents the estimated residual variance. Note that for all series, the estimated coefficients $|{\hat{a}}_n|$ and $|{\hat{b}}_n|$ are smaller than one and this is in accordance with our Assumption (A1). We also observe that for all series the estimated long-range dependence coefficients ${\hat{d}}_n$ are significant for any reasonable asymptotic level and are inside $]-0.5{,}0.5[$. We thus think that the assumption (A3) is satisfied and thus our asymptotic normality theorem can be applied. Table 3 then presents for each series the modified confidence interval at the asymptotic level $\alpha =5\%$ for the parameters estimated in Table 2.

5 Conclusion

Taking into account the possible lack of independence of the error terms, we show in this paper that we can fit FARIMA representations of a wide class of nonlinear long memory times series. This is possible thanks to our theoretical results and it is illustrated in our real cases and simulations studies.

This standard methodology (when the noise is supposed to be iid), in particular the significance tests on the parameters, needs however to be adapted to take into account the possible lack of independence of the errors terms. A first step has been done thanks to our results on the confidence intervals. In future works, we intent to study how the existing identification (see Boubacar Maïnassara (2012), Boubacar Maïnassara and Kokonendji (2016)) and diagnostic checking (see Boubacar Maïnassara and Saussereau (2018), Francq et al. (2005)) procedures should be adapted in the presence of long-range dependence framework and dependent noise.

It would also be interesting to study the adaptation of the exact maximum likelihood method of Sowell (1992) or the self-weighted LSE considered in Zhu and Ling (2011) to the case of weak FARIMA models.

6 Proofs

In all our proofs, K is a positive constant that may vary from line to line.

6.1 Preliminary results

In this subsection, we shall give some results on estimations of the coefficient of formal power series that will arise in our study. Some of them are well know and some others are new to our knowledge. We will make some precise comments hereafter.

We begin by recalling the following properties on power series. If for $|z|\le R$, the power series $f(z)=\sum _{i\ge 0}a_iz^i$ and $g(z)=\sum _{i\ge 0}b_iz^i$ are well defined, then one has $(fg)(z)= \sum _{i\ge 0} c_iz^i$ is also well defined for $|z|\le R$ with the sequence $(c_i)_{i\ge 0}$ which is given by $c=a*b$ where $*$ denotes the convolution product between a and b defined by $c_i=\sum _{k=0}^i a_kb_{i-k}=\sum _{k=0}^i a_{i-k}b_{k}$. We will make use of the Young inequality that states that if the sequence $a\in \ell ^{r_1}$ and $b\in \ell ^{r_2}$ are such that $\frac{1}{r_1}+\frac{1}{r_2}=1+\frac{1}{r}$ with $1\le r_1,r_2,r \le \infty$, then

$$\begin{aligned} \left\| a*b \right\| _{\ell ^r} \le \left\| a \right\| _{\ell ^{r_1}} \times \left\| b \right\| _{\ell ^{r_2}} . \end{aligned}$$

Now we come back to the power series that arise in our context. Remind that for the true value of the parameter,

$$\begin{aligned} a_{\theta _0}(L)(1-L)^{d_0}X_t=b_{\theta _0}(L)\epsilon _t. \end{aligned}$$

(21)

Thanks to the assumptions on the moving average polynomials $b_\theta$ and the autoregressive polynomials $a_\theta$, the power series $a_\theta ^{-1}$ and $b_\theta ^{-1}$ are well defined.

Table 2 Fitting a FARIMA(1, d, 1) model to the squares of the 4 daily returns considered

Table 3 Modified confidence interval at the asymptotic level $\alpha =5\%$ for the parameters estimated in Table 2

Thus the functions $\epsilon _t(\theta )$ defined in (2) can be written as

$$\begin{aligned} \epsilon _t(\theta )&= b^{-1}_{\theta }(L) a_{\theta }(L)(1-L)^{d}X_t \end{aligned}$$

(22)

$$\begin{aligned}&=b^{-1}_{\theta }(L) a_{\theta }(L)(1-L)^{d-d_0}a^{-1}_{\theta _0}(L) b_{\theta _0}(L)\epsilon _t \end{aligned}$$

(23)

and if we denote $\gamma (\theta )=(\gamma _i(\theta ))_{i\ge 0}$ the sequence of coefficients of the power series $b^{-1}_{\theta }(z) a_{\theta }(z)(1-z)^{d}$, we may write for all $t\in {\mathbb {Z}}$:

$$\begin{aligned} \epsilon _t(\theta )&=\sum _{i\ge 0}\gamma _i(\theta )X_{t-i}. \end{aligned}$$

(24)

In the same way, by (22) one has

$$\begin{aligned} X_t&= (1-L)^{-d}a^{-1}_{\theta }(L) b_{\theta }(L)\epsilon _t(\theta ) \end{aligned}$$

and if we denote $\eta (\theta )=(\eta _i(\theta ))_{i\ge 0}$ the coefficients of the power series $(1-z)^{-d}a^{-1}_{\theta }(z) b_{\theta }(z)$ one has

$$\begin{aligned} X_t&= \sum _{i\ge 0}\eta _i(\theta )\epsilon _{t-i}(\theta ) \ . \end{aligned}$$

(25)

We strength the fact that $\gamma _0(\theta )=\eta _0(\theta )=1$ for all $\theta$.

For large j, Hallin et al. (1999) have shown that uniformly in $\theta$ the sequences $\gamma (\theta )$ and $\eta (\theta )$ satisfy

$$\begin{aligned} \frac{\partial ^k\gamma _j(\theta )}{\partial \theta _{i_1}\cdots \partial \theta _{i_k}}=\mathrm {O}\left( j^{-1-d}\left\{ \log (j)\right\} ^k\right) ,\text { for }k=0,1,2,3, \end{aligned}$$

(26)

and

$$\begin{aligned} \frac{\partial ^k\eta _j(\theta )}{\partial \theta _{i_1}\cdots \partial \theta _{i_k}}=\mathrm {O}\left( j^{-1+d}\left\{ \log (j)\right\} ^k\right) , \text { for }k=0,1,2,3. \end{aligned}$$

(27)

One difficulty that has to be addressed is that (24) includes the infinite past $(X_{t-i})_{i\ge 0}$ whereas only a finite number of observations $(X_t)_{1\le t\le n}$ are available to compute the estimators defined in (4). The simplest solution is truncation which amounts to setting all unobserved values equal to zero. Thus, for all $\theta \in \varTheta$ and $1\le t\le n$ one defines

$$\begin{aligned} {\tilde{\epsilon }}_t(\theta )=\sum _{i=0}^{t-1}\gamma _i(\theta )X_{t-i}= \sum _{i\ge 0} \gamma _i^t(\theta ) X_{t-i} \end{aligned}$$

(28)

where the truncated sequence $\gamma ^t(\theta )= ( \gamma _i^t(\theta ))_{i\ge 0}$ is defined by

$$\begin{aligned} \gamma _i^t(\theta )=\left\{ \begin{array}{rl} \gamma _i(\theta ) &{}\text { if } \ 0\le i\le t-1\ , \\ 0&{} \text { otherwise.} \end{array}\right. \end{aligned}$$

Since our assumptions are made on the noise in (1), it will be useful to express the random variables $\epsilon _t(\theta )$ and its partial derivatives with respect to $\theta$, as a function of $(\epsilon _{t-i})_{i\ge 0}$.

From (23), there exists a sequence $\lambda (\theta )=(\lambda _i(\theta ))_{i\ge 0}$ such that

$$\begin{aligned} \epsilon _t(\theta )=\sum _{i=0}^{\infty }\lambda _i\left( \theta \right) \epsilon _{t-i} \end{aligned}$$

(29)

where the sequence $\lambda (\theta )$ is given by the sequence of the coefficients of the power series $b^{-1}_{\theta }(z) a_{\theta }(z)(1-z)^{d-d_0}a^{-1}_{\theta _0}(z) b_{\theta _0}(z)$. Consequently $\lambda (\theta ) = \gamma (\theta )*\eta (\theta _0)$ or, equivalently,

$$\begin{aligned} \lambda _i( \theta )&=\sum _{j=0}^i\gamma _j(\theta )\eta _{i-j}(\theta _0). \end{aligned}$$

(30)

As in Hualde and Robinson (2011), it can be shown using Stirling’s approximation that there exists a positive constant K such that

$$\begin{aligned} \sup _{\theta \in \varTheta _{\delta }}\left| \lambda _i(\theta )\right| \le K\sup _{d\in [d_1,d_2]} i^{-1-(d-d_0)}\le K i^{-1-(d_1-d_0)} \ . \end{aligned}$$

(31)

Equations (29) and (31) imply that for all $\theta \in \varTheta$ the random variable $\epsilon _t(\theta )$ belongs to ${\mathbb {L}}^2$, that the sequence $(\epsilon _t(\theta ))_t$ is an ergodic sequence and that for all $t\in {\mathbb {Z}}$ the function $\epsilon _t(\cdot )$ is a continuous function. We proceed in the same way as regard to the derivatives of $\epsilon _t(\theta )$. More precisely, for any $\theta \in \varTheta$, $t\in {\mathbb {Z}}$ and $1\le k,l \le p+q+1$ there exists sequences $\overset{\mathbf{. }}{\lambda }_{k}(\theta )= (\overset{\mathbf{. }}{\lambda }_{i,k}(\theta ))_{i\ge 1}$ and $\overset{\mathbf{.. }}{\lambda }_{k,l}(\theta )= (\overset{\mathbf{.. }}{\lambda }_{i,k,l}(\theta ))_{i\ge 1}$ such that

$$\begin{aligned} \frac{\partial \epsilon _t(\theta )}{\partial \theta _k}&=\sum _{i=1}^{\infty } \overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta \right) \epsilon _{t-i} \end{aligned}$$

(32)

$$\begin{aligned} \frac{\partial ^2\epsilon _t(\theta )}{\partial \theta _k\partial \theta _{l}}&=\sum _{i=1}^{\infty }\overset{\mathbf{.. }}{\lambda }_{i,k,l}\left( \theta \right) \epsilon _{t-i} . \end{aligned}$$

(33)

Of course it holds that $\overset{\mathbf{. }}{\lambda }_{k}(\theta )=\frac{\partial \gamma (\theta )}{\partial \theta _k}*\eta (\theta _0)$ and $\overset{\mathbf{.. }}{\lambda }_{k,l}( \theta )=\frac{\partial ^2\gamma (\theta )}{\partial \theta _k\partial \theta _{l}}*\eta (\theta _0)$.

Similarly we have

$$\begin{aligned} {\tilde{\epsilon }}_t(\theta )&=\sum _{i=0}^{\infty }\lambda _i^t \left( \theta \right) \epsilon _{t-i}, \end{aligned}$$

(34)

$$\begin{aligned} \frac{\partial {\tilde{\epsilon }}_t(\theta )}{\partial \theta _k}&=\sum _{i=1}^{\infty }\overset{\mathbf{. }}{\lambda }_{i,k}^t\left( \theta \right) \epsilon _{t-i}, \end{aligned}$$

(35)

$$\begin{aligned} \frac{\partial ^2{\tilde{\epsilon }}_t(\theta )}{\partial \theta _k \partial \theta _{l}}&=\sum _{i=1}^{\infty }\overset{\mathbf{.. }}{\lambda }_{i,k,l}^t\left( \theta \right) \epsilon _{t-i}, \end{aligned}$$

(36)

where $\lambda ^t(\theta ) = \gamma ^t(\theta )*\eta (\theta _0)$, $\overset{\mathbf{. }}{\lambda }^t_{k}(\theta )=\frac{\partial \gamma ^t(\theta )}{\partial \theta _k}*\eta (\theta _0)$ and $\overset{\mathbf{.. }}{\lambda }^t_{k,l}( \theta )=\frac{\partial ^2\gamma ^t(\theta )}{\partial \theta _k\partial \theta _{l}}*\eta (\theta _0)$.

In order to handle the truncation error $\epsilon _t(\theta )-{{\tilde{\epsilon }}}_t(\theta )$, one needs information on the sequence $\lambda (\theta )-\lambda ^t(\theta )$. This is the purpose of the following lemma.

Lemma 10

For $2\le r\le \infty$ and $1\le k,l \le p+q+1$, we have

$$\begin{aligned}&\parallel \lambda \left( \theta \right) -\lambda ^t\left( \theta \right) \parallel _{\ell ^r} \ =\mathrm {O}\left( t^{-1+\frac{1}{r}-(d-max(d_0,0))} \right) , \\&\parallel \overset{\mathbf{. }}{\lambda }_k\left( \theta \right) -\overset{\mathbf{. }}{\lambda }_k^t\left( \theta \right) \parallel _{\ell ^r} \ =\mathrm {O}\left( t^{-1+\frac{1}{r}-(d-max(d_0,0))}\right) \end{aligned}$$

and

$$\begin{aligned} \parallel \overset{\mathbf{.. }}{\lambda }_{k,l}\left( \theta \right) -\overset{\mathbf{.. }}{\lambda }_{k,l}^t\left( \theta \right) \parallel _{\ell ^r} \ =\mathrm {O}\left( t^{-1+\frac{1}{r}-(d-max(d_0,0))}\right) \end{aligned}$$

for any $\theta \in \varTheta _{\delta }$ if $d_0\le 0$ and for $\theta$ with non-negative memory parameter d if $d_0>0$.

Proof

In view of (27), $\eta (\theta _0)\in \ell ^{r_2}$ for $r_2\ge 1$ when $d_0<0$. If $d_0=0$, $\eta (\theta _0)$ is the sequence of coefficients of the power series $a^{-1}_{\theta _0}(z) b_{\theta _0}(z)$, so it belongs to $\ell ^{r_2}$ for all $r_2\ge 1$ since in this case $|\eta _j(\theta _0)|=\mathrm {O}(\rho ^j)$ for some $0<\rho <1$ (see Francq and Zakoïan (1998)). Thanks to (26), when $d_0\le 0$, Young’s inequality for convolution yields that for all $r\ge 2$

$$\begin{aligned} \parallel \lambda \left( \theta \right) -\lambda ^t\left( \theta \right) \parallel _{\ell ^r}&\le K\parallel \gamma (\theta )-\gamma ^t(\theta ) \parallel _{\ell ^r}\\&\le K\left( \sum _{i=t}^{\infty }\left| \gamma _i(\theta ) \right| ^r\right) ^{1/r}\\&\le K\left( \sum _{i=t}^\infty \frac{1}{i^{r+rd}}\right) ^{1/r}\\&\le K\left( \int _{t}^{\infty }\frac{1}{x^{r+rd}}\mathrm {dx} +\frac{1}{t^{r+rd}}\right) ^{1/r}\\&\le \frac{K}{t^{1-\frac{1}{r}+d}}. \end{aligned}$$

If $d_0>0$, the sequence $\eta (\theta _0)$ belongs to $\ell ^{r_2}$ for any $r_2>1/(1-d_0)$. Young’s inequality for convolution implies in this case that for all $r\ge 2$

$$\begin{aligned} \parallel \lambda \left( \theta \right) -\lambda ^t\left( \theta \right) \parallel _{\ell ^r} \ \le \parallel \gamma (\theta )-\gamma ^t(\theta ) \parallel _{\ell ^{r_1}}\parallel \eta (\theta _0)\parallel _{\ell ^{r_2}} \end{aligned}$$

(37)

with $r_2=(1-(d_0+\beta ))^{-1}>1/(1-d_0)$ and $r_1=r/(1+r(d_0+\beta ))$, for some $\beta >0$ sufficiently small. Thus there exists K such that $\parallel \eta (\theta _0)\parallel _{\ell ^{r_2}}\le K$. Similarly as before, we deduce when $d\ge 0$ that

$$\begin{aligned} \parallel \lambda \left( \theta \right) -\lambda ^t\left( \theta \right) \parallel _{\ell ^r}&\le K\parallel \gamma (\theta )-\gamma ^t(\theta ) \parallel _{\ell ^{r_1}}\\&\le K\left( \sum _{i=t}^\infty \frac{1}{i^{r_1+r_1d}}\right) ^{1/r_1}\\&\le \frac{K}{t^{1-\frac{1}{r_1}+d}}=\frac{K}{t^{1-\frac{1}{r}+(d-d_0)-\beta }}, \end{aligned}$$

the conclusion follows by tending $\beta$ to 0. The second and third points of the lemma are shown in the same way as the first. This is because from (26), the coefficients $\partial \gamma _j(\theta )/\partial \theta _k$ and $\partial ^2\gamma _j(\theta )/\partial \theta _k\partial \theta _l$ are $\mathrm {O}(j^{-1-d+\zeta })$ for any small enough $\zeta > 0$. The proof of the lemma is then complete.

$\square$

Remark 11

The above lemma implies that the sequence $\overset{\mathbf{. }}{\lambda }_k\left( \theta _0\right) -\overset{\mathbf{. }}{\lambda ^t}_k\left( \theta _0\right)$ is bounded and more precisely there exists K such that

$$\begin{aligned} \sup _{j\ge 1} \left| \overset{\mathbf{. }}{\lambda }_{j,k}\left( \theta _0\right) -\overset{\mathbf{. }}{\lambda ^t}_{j,k}\left( \theta _0\right) \right|&\le \frac{K}{t^{1+\min (d_0,0)}} \end{aligned}$$

(38)

for any $t\ge 1$ and any $1\le k\le p+q+1$.

Remark 12

In order to prove our asymptotic results, it will be convenient to give an upper bound for the norms of the sequences introduced in Lemma 10 valid for any $\theta \in \varTheta _{\delta }$. Since $d_1-d_0>-1/2$, Estimation (31) entails that for any $r\ge 2$,

$$\begin{aligned} \parallel \lambda \left( \theta \right) -\lambda ^t\left( \theta \right) \parallel _{\ell ^r} \ =\mathrm {O}\left( t^{-1+\frac{1}{r}-(d_1-d_0)} \right) , \ \ \ \forall \theta \in \varTheta _{\delta }. \end{aligned}$$

This can easily be seen since $\parallel \lambda (\theta )-\lambda ^t(\theta )\parallel _{\ell ^r}\le K(\sum _{i\ge t}i^{-r-r(d_1-d_0)})^{1/r}\le Kt^{-1+1/r-(d_1-d_0)}$. As in Hallin et al. (1999), the coefficients $\overset{\mathbf{. }}{\lambda }_{j,k}(\theta )$ and $\overset{\mathbf{.. }}{\lambda }_{j,k,l}(\theta )$ are $\mathrm {O}(j^{-1-(d-d_0)+\zeta })$ for any small enough $\zeta >0$, so we have

$$\begin{aligned} \parallel \overset{\mathbf{. }}{\lambda }_k\left( \theta \right) -\overset{\mathbf{. }}{\lambda }_k^t\left( \theta \right) \parallel _{\ell ^r} \ =\mathrm {O}\left( t^{-1+\frac{1}{r}-(d_1-d_0)+\zeta }\right) \end{aligned}$$

and

$$\begin{aligned} \parallel \overset{\mathbf{.. }}{\lambda }_{k,l}\left( \theta \right) -\overset{\mathbf{.. }}{\lambda }_{k,l}^t\left( \theta \right) \parallel _{\ell ^r} \ =\mathrm {O}\left( t^{-1+\frac{1}{r}-(d_1-d_0)+\zeta }\right) \end{aligned}$$

for any $r\ge 2$, any $1\le k,l\le p+q+1$ and all $\theta \in \varTheta _{\delta }$.

One shall also need the following lemmas.

Lemma 13

For any $2\le r\le \infty$, $1\le k \le p+q+1$ and $\theta \in \varTheta$, there exists a constant K such that we have

$$\begin{aligned} \parallel \overset{\mathbf{. }}{\lambda }_k^t\left( \theta \right) \parallel _{\ell ^r} \le K. \end{aligned}$$

Proof

The proof follows the same arguments as those developed in Remark 12.

$\square$

Lemma 14

There exists a constant K such that we have

$$\begin{aligned} \left| \overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta _0\right) \right| \le \frac{K}{i}. \end{aligned}$$

(39)

Proof

For $1\le k \le p+q+1$, the sequence $\overset{\mathbf{. }}{\lambda }_{k}(\theta )= (\overset{\mathbf{. }}{\lambda }_{i,k}(\theta ))_{i\ge 1}$ is in fact the sequence of the coefficients in the power series of

$$\begin{aligned} \frac{\partial }{\partial \theta _k }\left( b_\theta ^{-1}(z) a_{\theta }(z)(1-z)^{d-d_0} a_{\theta _0}^{-1}(z)b_{\theta _0}(z)\right) \ . \end{aligned}$$

Thus $\overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta _0\right)$ is the $i-$th coefficient taken in $\theta =\theta _0$. There are three cases.

$\diamond$:

$k=1,\dots ,p$: Since

$$\begin{aligned} \frac{\partial }{\partial \theta _k }\left( b_\theta ^{-1}(z) a_{\theta }(z)(1-z)^{d-d_0} a_{\theta _0}^{-1}(z)b_{\theta _0}(z) \right) = -b_\theta ^{-1}(z) z^k (1-z)^{d-d_0} a_{\theta _0}^{-1}(z)b_{\theta _0}(z)\ , \end{aligned}$$

we deduce that $\overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta _0\right)$ is the $i-$th coefficient of $-z^k a_{\theta _0}^{-1}(z)$ which satisfies $\overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta _0\right) \le K \rho ^i$ for some $0<\rho <1$ (see Francq and Zakoïan (1998) for example).

$\diamond$:

$k=p+1,\dots ,p+q$: We have

$$\begin{aligned} \frac{\partial }{\partial \theta _k } \left( b_\theta ^{-1}(z) a_{\theta }(z)(1-z)^{d-d_0} a_{\theta _0}(z)b_{\theta _0}(z)\right) = \left( \frac{\partial }{\partial \theta _k } b_\theta ^{-1}(z)\right) a_{\theta }(z) (1-z)^{d-d_0} a_{\theta _0}^{-1}(z)b_{\theta _0}(z) \end{aligned}$$

and consequently $\overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta _0\right)$ is the $i-$th coefficient of $(\frac{\partial }{\partial \theta _k } b_{\theta _0}^{-1}(z) ) b_{\theta _0}(z)$ which also satisfies $\overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta _0\right) \le K \rho ^i$ (see Francq and Zakoïan (1998)).

The last case will not be a consequence of the usual works on ARMA processes.

$\diamond$:

$k=p+q+1$: In this case, $\theta _k=d$ and so we have

$$\begin{aligned} \frac{\partial }{\partial \theta _k } \left( b_\theta ^{-1}(z) a_{\theta }(z)(1-z)^{d-d_0} a_{\theta _0}^{-1}(z)b_{\theta _0}(z)\right) = b_\theta ^{-1}(z)a_{\theta }(z) \mathrm {ln}(1-z)(1-z)^{d-d_0} a_{\theta _0}^{-1}(z)b_{\theta _0}(z) \end{aligned}$$

and consequently $\overset{\mathbf{. }}{\lambda }_{i,k}\left( \theta _0\right)$ is the $i-$th coefficient of $\mathrm {ln}(1-z)$ which is equal to $-1/i$.

The three above cases imply the expected result. $\square$

6.2 Proof of Theorem 1

Consider the random variable $\mathrm {W}_n(\theta )$ defined for any $\theta \in \varTheta$ by

$$\begin{aligned} \mathrm {W}_n(\theta )=\mathrm {V}(\theta )+Q_n(\theta _0)-Q_n(\theta ), \end{aligned}$$

where $V(\theta )\!=\!{\mathbb {E}}[O_n(\theta )]-{\mathbb {E}}[O_n(\theta _0)]$. For $\beta >0$, let $S_\beta =\{\theta : \Vert \theta -\theta _0\Vert \le \beta \}$, ${\overline{S}}_\beta =\{\theta \in \varTheta _\delta : \theta \notin S_\beta \}$. It can readily be shown that

$$\begin{aligned} {\mathbb {P}}\left( \left\| {\hat{\theta }}_n-\theta _0\right\| >\beta \right)&\le {\mathbb {P}}\left( {\hat{\theta }}_n\in {\overline{S}}_\beta \right) \nonumber \\&\le {\mathbb {P}}\left( \inf _{\theta \in {\overline{S}}_\beta } \left\{ Q_n(\theta )-Q_n(\theta _0)\right\} \le 0\right) \nonumber \\&\le {\mathbb {P}}\left( \sup _{\theta \in \varTheta _\delta } \left| \mathrm {W}_n(\theta )\right| \ge \inf _{\theta \in {\overline{S}}_\beta } \mathrm {V}(\theta )\right) \nonumber \\&\le {\mathbb {P}}\left( \sup _{\theta \in \varTheta _\delta } \left| Q_n(\theta )-{\mathbb {E}}\left[ O_n(\theta )\right] \right| \ge \frac{1}{2}\inf _{\theta \in {\overline{S}}_\beta } \mathrm {V}(\theta )\right) . \end{aligned}$$

(40)

Since $d_1-d_0>-1/2$, one has

$$\begin{aligned} \sup _{\theta \in \varTheta _\delta }{\mathbb {E}}\left[ \epsilon _t^2(\theta ) \right]&=\sup _{\theta \in \varTheta _\delta }\sum _{i=0}^\infty \sum _{j=0}^\infty \lambda _i(\theta )\lambda _j(\theta ){\mathbb {E}}\left[ \epsilon _{t-i} \epsilon _{t-j}\right] =\sigma _{\epsilon }^2\sup _{\theta \in \varTheta _\delta } \sum _{i=0}^\infty \lambda _i^2(\theta )\nonumber \\&\le \sigma _{\epsilon }^2+K\sigma _{\epsilon }^2\sum _{i=1}^\infty i^{-2-2(d_1-d_0)}<\infty . \end{aligned}$$

(41)

We can therefore use the same arguments as those of Francq and Zakoïan (1998) to prove under (A1) and (A2) that for any ${\overline{\theta }}\in \varTheta _\delta \setminus \{\theta _0\}$, there exists a neighbourhood $\mathrm {N}({\overline{\theta }})$ of ${\overline{\theta }}$ such that $\mathrm {N}({\overline{\theta }})\subset \varTheta _\delta$ and

$$\begin{aligned} \liminf _{n\rightarrow \infty }\inf _{\theta \in \mathrm {N}({\overline{\theta }})}O_n(\theta )>\sigma ^2_{\epsilon }, \quad \text { a.s}. \end{aligned}$$

(42)

Note that ${\mathbb {E}}[O_n(\theta _0)]=\sigma _\epsilon ^2$. It follows from (42) that

$$\begin{aligned} \inf _{\theta \in {\overline{S}}_\beta }\mathrm {V}(\theta )>K \end{aligned}$$

for some positive constant K.

In view of (40), it is then sufficient to show that the random variable $\sup _{\theta \in \varTheta _\delta }|Q_n(\theta )-{\mathbb {E}}[O_n(\theta )]|$ converges in probability to zero to prove Theorem 1. We use Corollary 2.2 of Newey (1991) to obtain this uniform convergence in probability. The set $\varTheta _\delta$ is compact and $({\mathbb {E}}[O_n(\theta )])_{n\ge 1}$ is a uniformly convergent sequence of continuous functions on a compact set so it is equicontinuous. We consequently need to show the following two points to complete the proof of the theorem:

• For each $\theta \in \varTheta _\delta$, $Q_n(\theta )-{\mathbb {E}}[O_n(\theta )]=\mathrm {o}_{{\mathbb {P}}}(1).$

• There is $B_n$ and $h: [0,\infty )\rightarrow [0,\infty )$ with $h(0)=0$ and h continuous at zero such that $B_n=\mathrm {O}_{{\mathbb {P}}}(1)$ and for all $\theta _1, \theta _2\in \varTheta _\delta$, $|Q_n(\theta _1)-Q_n(\theta _2)|\le B_nh(\Vert \theta _1-\theta _2\Vert )$.

6.2.1 Pointwise convergence in probability of $Q_n(\theta )-{\mathbb {E}}[O_n(\theta )]$ to zero

For any $\theta \in \varTheta _\delta$, Remark 12, the Cauchy–Schwarz inequality and (41) yield that

$$\begin{aligned} {\mathbb {E}}\left| Q_n(\theta )-O_n(\theta )\right|&\le \frac{1}{n} \sum _{t=1}^n{\mathbb {E}}\left| {\tilde{\epsilon }}_t^2(\theta ) -\epsilon _t^2(\theta )\right| \nonumber \\&\le \frac{1}{n}\sum _{t=1}^n{\mathbb {E}}\left( \epsilon _t(\theta ) -{\tilde{\epsilon }}_t(\theta )\right) ^2+\frac{2}{n}\sum _{t=1}^n{\mathbb {E}} \left| \epsilon _t(\theta )-{\tilde{\epsilon }}_t(\theta )\right| \left| \epsilon _t(\theta )\right| \nonumber \\&\le \frac{\sigma _\epsilon ^2}{n}\sum _{t=1}^n\left\| \lambda _i(\theta ) -\lambda _i^t(\theta )\right\| _{\ell ^2}^2+\frac{2\sigma _\epsilon }{n} \sum _{t=1}^n\left\| \lambda _i(\theta )-\lambda _i^t(\theta )\right\| _{\ell ^2} \sqrt{{\mathbb {E}}\left[ \epsilon _t^2(\theta )\right] }\nonumber \\&\le \frac{\sigma _\epsilon ^2}{n}\sum _{t=1}^nt^{-1-2(d_1-d_0)} +\frac{2K\sigma _\epsilon }{n}\sum _{t=1}^nt^{-1/2-(d_1-d_0)}\xrightarrow [n\rightarrow \infty ]{} 0. \end{aligned}$$

(43)

We use the ergodic theorem and the continuous mapping theorem to obtain

$$\begin{aligned} \left| O_n(\theta )-{\mathbb {E}}\left[ O_n(\theta )\right] \right| \xrightarrow [n\rightarrow \infty ]{\mathrm {a.s.}} 0. \end{aligned}$$

(44)

Combining the results in (43) and (44), we deduce that for all $\theta \in \varTheta _\delta$,

$$\begin{aligned} Q_n(\theta )-{\mathbb {E}}\left[ O_n(\theta )\right] \xrightarrow [n\rightarrow \infty ]{\mathrm {{\mathbb {P}}}} 0. \end{aligned}$$

6.2.2 Tightness characterization

Observe that for any $\theta _1, \theta _2\in \varTheta _\delta$, there exists $\theta ^\star$ between $\theta _1$ and $\theta _2$ such that

$$\begin{aligned} \left| Q_n(\theta _1)-Q_n(\theta _2)\right| \le \left( \frac{1}{n}\sum _{t=1}^n\left\| \frac{\partial {\tilde{\epsilon }}_t^2(\theta ^\star )}{\partial \theta } \right\| \right) \left\| \theta _1-\theta _2\right\| . \end{aligned}$$

As before, the uncorrelatedness of the innovation process $(\epsilon _t)_{t\in {\mathbb {Z}}}$ and Remark 12 entail that

$$\begin{aligned} {\mathbb {E}}\left[ \frac{1}{n}\sum _{t=1}^n\left\| \frac{\partial {\tilde{\epsilon }}_t^2(\theta ^\star )}{\partial \theta } \right\| \right]&\le {\mathbb {E}}\left[ \frac{2}{n}\sum _{t=1}^n\sum _{i=1}^{p+q+1} \left| {\tilde{\epsilon }}_t(\theta ^\star ) \frac{\partial {\tilde{\epsilon }}_t(\theta ^\star )}{\partial \theta _i} \right| \right] <\infty . \end{aligned}$$

Thanks to Markov’s inequality, we conclude that

$$\begin{aligned} \frac{1}{n}\sum _{t=1}^n\left\| \frac{\partial {\tilde{\epsilon }}_t^2(\theta ^\star )}{\partial \theta }\right\| =\mathrm {O}_{{\mathbb {P}}}(1). \end{aligned}$$

The proof of Theorem 1 is then complete.

6.3 Proof of Theorem 2

By a Taylor expansion of the function $\partial Q_n(\cdot )/ \partial \theta$ around $\theta _0$ and under (A3), we have

$$\begin{aligned} 0=\sqrt{n}\frac{\partial }{\partial \theta }Q_n({\hat{\theta }}_n) =\sqrt{n}\frac{\partial }{\partial \theta }Q_n(\theta _0) +\left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) \right] \sqrt{n}\left( {\hat{\theta }}_n-\theta _0\right) , \end{aligned}$$

(45)

where the $\theta ^*_{n,i,j}$’s are between ${\hat{\theta }}_n$ and $\theta _0$. The Eq. (45) can be rewritten in the form:

$$\begin{aligned}&\sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0)-\sqrt{n} \frac{\partial }{\partial \theta }Q_n(\theta _0)= \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0) +\left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) \right] \sqrt{n}\left( {\hat{\theta }}_n-\theta _0\right) . \end{aligned}$$

(46)

Under the assumptions of Theorem 2, it will be shown respectively in Lemmas 15 and 17 that

$$\begin{aligned} \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0)-\sqrt{n} \frac{\partial }{\partial \theta }Q_n(\theta _0)=\mathrm {o}_{{\mathbb {P}}}(1), \end{aligned}$$

and

$$\begin{aligned} \left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) \right] - J(\theta _0)=\mathrm {o}_{{\mathbb {P}}}(1). \end{aligned}$$

As a consequence, the asymptotic normality of $\sqrt{n}( {\hat{\theta }}_n-\theta _0)$ will be a consequence of the one of $\sqrt{n}\partial /\partial \theta O_n(\theta _0)$.

Lemma 15

For $1\le k\le p+q+1$, under the assumptions of Theorem 2, we have

$$\begin{aligned} \sqrt{n}\left( \frac{\partial }{\partial \theta _k}Q_n(\theta _0) -\frac{\partial }{\partial \theta _k}O_n(\theta _0)\right) =\mathrm {o}_{{\mathbb {P}}}(1). \end{aligned}$$

(47)

Proof

Throughout this proof, $\theta =(\theta _1,\ldots ,\theta _{p+q},d)'\in \varTheta _\delta$ is such that $\max (d_0,0)<d\le d_2$ where $d_2$ is the upper bound of the support of the long-range dependence parameter $d_0$.

The proof is quite long so we divide it in several steps.

$\diamond$ Step 1: preliminaries

For $1\le k \le p+q+1$ we have

$$\begin{aligned} \sqrt{n}\frac{\partial }{\partial \theta _k}Q_n(\theta _0)&=\frac{2}{\sqrt{n}}\sum _{t=1}^n{\tilde{\epsilon }}_t(\theta _0) \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0)\nonumber \\&=\frac{2}{\sqrt{n}}\sum _{t=1}^n\left( {\tilde{\epsilon }}_t(\theta _0) -{\tilde{\epsilon }}_t(\theta )\right) \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0)+\frac{2}{\sqrt{n}}\sum _{t=1}^n \left( {\tilde{\epsilon }}_t(\theta )-\epsilon _t(\theta )\right) \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0)\nonumber \\&\qquad +\frac{2}{\sqrt{n}}\sum _{t=1}^n\left( \epsilon _t(\theta ) -\epsilon _t(\theta _0)\right) \frac{\partial }{\partial \theta _k} {\tilde{\epsilon }}_t(\theta _0) +\frac{2}{\sqrt{n}}\sum _{t=1}^n\epsilon _t(\theta _0)\left( \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0)-\frac{\partial }{\partial \theta _k}\epsilon _t(\theta _0)\right) \nonumber \\&\qquad +\frac{2}{\sqrt{n}}\sum _{t=1}^n\epsilon _t(\theta _0) \frac{\partial }{\partial \theta _k}\epsilon _t(\theta _0)\nonumber \\&=\varDelta _{n,1}^k(\theta )+\varDelta _{n,2}^k(\theta )+\varDelta _{n,3}^k(\theta ) +\varDelta _{n,4}^k(\theta _0)+\sqrt{n}\frac{\partial }{\partial \theta _k}O_n(\theta _0), \end{aligned}$$

(48)

where

$$\begin{aligned} \varDelta _{n,1}^k(\theta )&=\frac{2}{\sqrt{n}}\sum _{t=1}^n \left( {\tilde{\epsilon }}_t(\theta _0)-{\tilde{\epsilon }}_t(\theta ) \right) \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0),\\ \varDelta _{n,2}^k(\theta )&=\frac{2}{\sqrt{n}}\sum _{t=1}^n \left( {\tilde{\epsilon }}_t(\theta )-\epsilon _t(\theta )\right) \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0),\\ \varDelta _{n,3}^k(\theta )&=\frac{2}{\sqrt{n}}\sum _{t=1}^n \left( \epsilon _t(\theta )-\epsilon _t(\theta _0)\right) \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0) \end{aligned}$$

and

$$\begin{aligned} \varDelta _{n,4}^k(\theta _0)&=\frac{2}{\sqrt{n}}\sum _{t=1}^n \epsilon _t(\theta _0)\left( \frac{\partial }{\partial \theta _k} {\tilde{\epsilon }}_t(\theta _0)-\frac{\partial }{\partial \theta _k} \epsilon _t(\theta _0)\right) . \end{aligned}$$

Using (32) and (35), the fourth term $\varDelta _{n,4}^k(\theta _0)$ can be rewritten in the form:

$$\begin{aligned} \varDelta _{n,4}^k(\theta _0)=\frac{2}{\sqrt{n}}\sum _{t=1}^n\sum _{j=1}^{\infty } \left\{ \overset{\mathbf{. }}{\lambda }^t_{j,k}\left( \theta _0\right) -\overset{\mathbf{. }}{\lambda }_{j,k}\left( \theta _0\right) \right\} \epsilon _t\epsilon _{t-j}. \end{aligned}$$

(49)

Therefore, if we prove that the three sequences of random variables $( \varDelta _{n,1}^k(\theta )+\varDelta _{n,3}^k(\theta ))_{n\ge 1}$, $( \varDelta _{n,2}^k(\theta ))_{n\ge 1}$ and $( \varDelta _{n,4}^k(\theta _0))_{n\ge 1}$ converge in probability to 0, then (47) will be true.

$\diamond$ Step 2: convergence in probability of $( \varDelta _{n,4}^k(\theta _0))_{n\ge 1}$ to 0

For simplicity, we denote in the sequel by $\overset{\mathbf{. }}{\lambda }_{j,k}$ the coefficient $\overset{\mathbf{. }}{\lambda }_{j,k}(\theta _0)$ and by $\overset{\mathbf{. }}{\lambda }_{j,k}^t$ the coefficient $\overset{\mathbf{. }}{\lambda }_{j,k}^t(\theta _0)$. Let $\varrho (\cdot ,\cdot )$ be the function defined for $1\le t,s\le n$ by

$$\begin{aligned} \varrho (t,s)=\sum _{j_1=1}^{\infty }\sum _{j_2=1}^{\infty }\left\{ \overset{\mathbf{. }}{\lambda }_{j_1,k}-\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right\} \left\{ \overset{\mathbf{. }}{\lambda }_{j_2,k}-\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right\} {\mathbb {E}}\left[ \epsilon _t\epsilon _{t-j_1} \epsilon _s\epsilon _{s-j_2}\right] . \end{aligned}$$

For all $\beta >0$, using the symmetry of the function $\varrho (t,s)$, we obtain that

$$\begin{aligned} {\mathbb {P}}\left( \left| \varDelta _{n,4}^k(\theta _0)\right| \ge \beta \right)&\le \frac{4}{n\beta ^2}{\mathbb {E}}\left[ \left( \sum _{t=1}^n \sum _{j=1}^{\infty }\left\{ \overset{\mathbf{. }}{\lambda }_{j,k} -\overset{\mathbf{. }}{\lambda }_{j,k}^t\right\} \epsilon _t\epsilon _{t-j}\right) ^2\right] \\&\le \frac{4}{n\beta ^2}\sum _{t=1}^n\sum _{s=1}^n\sum _{j_1=1}^{\infty } \sum _{j_2=1}^{\infty }\left\{ \overset{\mathbf{. }}{\lambda }_{j_1,k} -\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right\} \left\{ \overset{\mathbf{. }}{\lambda }_{j_2,k}-\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right\} {\mathbb {E}}\left[ \epsilon _t \epsilon _{t-j_1} \epsilon _s\epsilon _{s-j_2}\right] \\&\le \frac{8}{n\beta ^2}\sum _{t=1}^n\sum _{s=1}^t\sum _{j_1=1}^{\infty } \sum _{j_2=1}^{\infty }\left\{ \overset{\mathbf{. }}{\lambda }_{j_1,k}-\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right\} \left\{ \overset{\mathbf{. }}{\lambda }_{j_2,k}-\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right\} {\mathbb {E}}\left[ \epsilon _t\epsilon _{t-j_1} \epsilon _s\epsilon _{s-j_2}\right] . \end{aligned}$$

By the stationarity of $(\epsilon _t)_{t\in {\mathbb {Z}}}$ which is assumed in (A2), we have

$$\begin{aligned} {\mathbb {E}}\left[ \epsilon _t\epsilon _{t-j_1} \epsilon _s\epsilon _{s-j_2}\right]&= \mathrm {cum}\left( \epsilon _0,\epsilon _{-j_1}, \epsilon _{s-t},\epsilon _{s-t-j_2}\right) +{\mathbb {E}}\left[ \epsilon _0\epsilon _{-j_1}\right] {\mathbb {E}} \left[ \epsilon _{s-t}\epsilon _{s-t-j_2}\right] \\&+{\mathbb {E}} \left[ \epsilon _0\epsilon _{s-t}\right] {\mathbb {E}}\left[ \epsilon _{-j_1} \epsilon _{s-t-j_2}\right] \\&+{\mathbb {E}}\left[ \epsilon _0\epsilon _{s-t-j_2}\right] {\mathbb {E}} \left[ \epsilon _{-j_1}\epsilon _{s-t}\right] . \end{aligned}$$

Since the noise is not correlated, we deduce that ${\mathbb {E}}\left[ \epsilon _0\epsilon _{-j_1}\right] =0$ and ${\mathbb {E}}\left[ \epsilon _0\epsilon _{s-t-j_2}\right] =0$ for $1\le j_1, j_2$ and $s\le t$. Consequently we obtain

$$\begin{aligned} {\mathbb {P}}\left( \left| \varDelta _{n,4}^k(\theta _0)\right| \ge \beta \right)&\le \frac{8}{n\beta ^2}\sum _{t=1}^n\sum _{s=1}^t\sum _{j_1=1}^{\infty } \sum _{j_2=1}^{\infty }\sup _{j_1\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{j_1,k}-\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right| \left| \overset{\mathbf{. }}{\lambda }_{j_2,k}-\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right| \nonumber \\&\quad \left| \mathrm {cum}\left( \epsilon _0, \epsilon _{-j_1}, \epsilon _{s-t},\epsilon _{s-t-j_2}\right) \right| \nonumber \\&\quad +\frac{8}{n\beta ^2}\sum _{t=1}^n\sum _{s=1}^t\sum _{j_1=1}^{\infty } \sum _{j_2=1}^{\infty }\left| \overset{\mathbf{. }}{\lambda }_{j_1,k}-\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right| \left| \overset{\mathbf{. }}{\lambda }_{j_2,k} -\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right| \nonumber \\&\quad \left| {\mathbb {E}}\left[ \epsilon _0\epsilon _{s-t}\right] {\mathbb {E}}\left[ \epsilon _{-j_1}\epsilon _{s-t-j_2}\right] \right| . \end{aligned}$$

(50)

If

$$\begin{aligned} \sum _{s=1}^t\sum _{j_1=1}^{\infty }\sum _{j_2=1}^{\infty }\sup _{j_1\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{j_1,k}-\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right| \left| \overset{\mathbf{. }}{\lambda }_{j_2,k} -\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right| \left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-j_1}, \epsilon _{s-t},\epsilon _{s-t-j_2}\right) \right| \xrightarrow [t\rightarrow \infty ]{} 0,\nonumber \\ \end{aligned}$$

(51)

Cesàro’s Lemma implies that the first term in the right hand side of (50) tends to 0. Thanks to Lemma 10 applied with $r=\infty$ (or see Remark 11) and Assumption (A4’) with $\tau =4$, we obtain that

$$\begin{aligned} \sum _{s=1}^t\sum _{j_1=1}^{\infty }\sum _{j_2=1}^{\infty }\sup _{j_1\ge 1} \left| \overset{\mathbf{. }}{\lambda }_{j_1,k}-\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right|&\left| \overset{\mathbf{. }}{\lambda }_{j_2,k} -\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right| \left| \mathrm {cum} \left( \epsilon _0,\epsilon _{-j_1}, \epsilon _{s-t},\epsilon _{s-t-j_2}\right) \right| \\&\le \frac{K}{t^{1+\min (d_0,0)}}\sum _{s=1}^t\sum _{j_1=1}^{\infty } \sum _{j_2=1}^{\infty } \left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-j_1}, \epsilon _{s-t},\epsilon _{s-t-j_2}\right) \right| \\&\le \frac{K}{t^{1+\min (d_0,0)}}\sum _{s=-\infty }^{\infty }\sum _{j_1 =-\infty }^{\infty }\sum _{j_2=-\infty }^{\infty } \left| \mathrm {cum}\left( \epsilon _0,\epsilon _{s}, \epsilon _{j_1},\epsilon _{j_2}\right) \right| \xrightarrow [t\rightarrow \infty ]{} 0 \ , \end{aligned}$$

hence (51) holds true. Concerning the second term of right hand side of the inequality (50), we have

$$\begin{aligned} \frac{8}{n\beta ^2}\sum _{t=1}^n\sum _{s=1}^t\sum _{j_1=1}^{\infty } \sum _{j_2=1}^{\infty }&\left| \overset{\mathbf{. }}{\lambda }_{j_1,k} -\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right| \left| \overset{\mathbf{. }}{\lambda }_{j_2,k}-\overset{\mathbf{. }}{\lambda }_{j_2,k}^s\right| \left| {\mathbb {E}}\left[ \epsilon _0\epsilon _{s-t}\right] {\mathbb {E}} \left[ \epsilon _{-j_1}\epsilon _{s-t-j_2}\right] \right| \\&\quad = \frac{8\sigma _{\epsilon }^2}{n\beta ^2}\sum _{t=1}^n \sum _{j_1=1}^{\infty }\sum _{j_2=1}^{\infty }\left| \overset{\mathbf{. }}{\lambda }_{j_1,k}-\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right| \left| \overset{\mathbf{. }}{\lambda }_{j_2,k}-\overset{\mathbf{. }}{\lambda }_{j_2,k}^t\right| \left| {\mathbb {E}}\left[ \epsilon _{-j_1} \epsilon _{-j_2}\right] \right| \\&\quad = \frac{8\sigma _{\epsilon }^4}{n\beta ^2}\sum _{t=1}^n \sum _{j_1=1}^{\infty }\left| \overset{\mathbf{. }}{\lambda }_{j_1,k} -\overset{\mathbf{. }}{\lambda }_{j_1,k}^t\right| ^2 \\&\quad =\frac{8\sigma _{\epsilon }^4}{n\beta ^2}\sum _{t=1}^n \left\| \overset{\mathbf{. }}{\lambda }_{k}-\overset{\mathbf{. }}{\lambda }_{k}^t\right\| _{\ell ^2}^2\\&\quad \le \frac{K}{\beta ^2} \frac{1}{n}\sum _{t=1}^n\frac{1}{t^{1+2\min (d_0,0)}}\xrightarrow [n\rightarrow \infty ]{}0 \end{aligned}$$

where we have used the fact that the noise is not correlated, Lemma 10 with $r=2$ and Cesàro’s Lemma. This ends Step 2.

$\diamond$ Step 3: $(\varDelta _{n,2}^k(\theta ))_{n\ge 1}$ converges in probability to 0

For all $\beta >0$, we have

$$\begin{aligned} {\mathbb {P}}\left( \left| \varDelta _{n,2}^k(\theta )\right| \ge \beta \right)&\le \frac{2}{\beta \sqrt{n}}\sum _{t=1}^n\left\| {\tilde{\epsilon }}_t(\theta ) -\epsilon _t(\theta )\right\| _{{\mathbb {L}}^2}\left\| \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0)\right\| _{{\mathbb {L}}^2}. \end{aligned}$$

First, using Lemma 13, we have

$$\begin{aligned} \left\| \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0) \right\| ^2_{{\mathbb {L}}^2}&={\mathbb {E}}\left[ \left( \sum _{i=1}^{\infty }\overset{\mathbf{. }}{\lambda }_{i,k}^t \left( \theta _0\right) \epsilon _{t-i}\right) ^2 \right] \nonumber \\&=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }\overset{\mathbf{. }}{\lambda }_{i,k}^t\left( \theta _0\right) \overset{\mathbf{. }}{\lambda }_{j,k}^t \left( \theta _0\right) {\mathbb {E}}\left[ \epsilon _{t-i} \epsilon _{t-j} \right] \nonumber \\&=\sigma _{\epsilon }^2\sum _{i=1}^{\infty }\left\{ \overset{\mathbf{. }}{\lambda }_{i,k}^t\left( \theta _0\right) \right\} ^2 \nonumber \\&\le K . \end{aligned}$$

(52)

In view of (29), (34) and (52), we may write

$$\begin{aligned} {\mathbb {P}}\left( \left| \varDelta _{n,2}^k(\theta )\right| \ge \beta \right)&\le \frac{K}{\beta \sqrt{n}}\sum _{t=1}^n \left( {\mathbb {E}}\left[ \left( {\tilde{\epsilon }}_t(\theta ) -\epsilon _t(\theta )\right) ^2\right] \right) ^{1/2}\\&\le \frac{K}{\beta \sqrt{n}}\sum _{t=1}^n\left( \sum _{i \ge 0}\sum _{j\ge 0}\left( \lambda ^t_i(\theta )-\lambda _i(\theta )\right) \left( \lambda ^t_j(\theta )-\lambda _j(\theta )\right) {\mathbb {E}} \left[ \epsilon _{t-i}\epsilon _{t-j}\right] \right) ^{1/2}\\&\le \frac{\sigma _{\epsilon }K}{\beta \sqrt{n}}\sum _{t=1}^n \left( \sum _{i\ge 0}\left( \lambda ^t_i(\theta )-\lambda _i(\theta ) \right) ^2\right) ^{1/2} \\&\le \frac{\sigma _{\epsilon }K}{\beta \sqrt{n}}\sum _{t=1}^n\left\| \lambda (\theta )-\lambda ^t(\theta )\right\| _{\ell ^2}. \end{aligned}$$

We use Lemma 10, the fact that $d>\max (d_0,0)$ and the fractional version of Cesàro’s Lemma² to obtain

$$\begin{aligned} {\mathbb {P}}\left( \left| \varDelta _{n,2}^k(\theta )\right| \ge \beta \right) \le \frac{\sigma _{\epsilon }K}{\beta }\, \frac{1}{\sqrt{n}}\sum _{t=1}^n\frac{1}{t^{1/2+(d-\max (d_0,0))}} \xrightarrow [n\rightarrow \infty ]{} 0. \end{aligned}$$

This proves the expected convergence in probability.

$\diamond$ Step 4: convergence in probability of $(\varDelta _{n,1}^k(\theta )+\varDelta _{n,3}^k(\theta ))_{n\ge 1}$ to 0

Note that, for all $n\ge 1$, we have

$$\begin{aligned} \varDelta _{n,1}^k(\theta )+\varDelta _{n,3}^k(\theta )&=\frac{2}{\sqrt{n}}\sum _{t=1}^n\Big \{ \left( \epsilon _t(\theta )-{\tilde{\epsilon }}_t(\theta )\right) -\left( \epsilon _t(\theta _0)-{\tilde{\epsilon }}_t(\theta _0)\right) \Big \} \frac{\partial }{\partial \theta _k}{\tilde{\epsilon }}_t(\theta _0). \end{aligned}$$

A Taylor expansion of the function $(\epsilon _t-{\tilde{\epsilon }}_t)(\cdot )$ around $\theta _0$ gives

$$\begin{aligned} \Big | ( \epsilon _t(\theta )-{\tilde{\epsilon }}_t(\theta ))-( \epsilon _t(\theta _0)-{\tilde{\epsilon }}_t(\theta _0))\Big |&\le \left\| \frac{\partial ( \epsilon _t-{\tilde{\epsilon }}_t)}{\partial \theta }(\theta ^\star )\right\| _{{\mathbb {R}}^{p+q+1}} \Vert \theta -\theta _0\Vert _{{\mathbb {R}}^{p+q+1}} \ , \end{aligned}$$

(53)

where $\theta ^\star$ is between $\theta _0$ and $\theta$. Following the same method as in the previous step we obtain

$$\begin{aligned} {\mathbb {E}} \Big |\left( \epsilon _t(\theta )-{\tilde{\epsilon }}_t(\theta )\right) -\left( \epsilon _t(\theta _0)-{\tilde{\epsilon }}_t(\theta _0)\right) \Big |^2&\le K\Vert \theta -\theta _0\Vert ^2_{{\mathbb {R}}^{p+q+1}}\sum _{k=1}^{p+q+1} {\mathbb {E}} \left[ \left| \frac{\partial ( \epsilon _t -{\tilde{\epsilon }}_t)}{\partial \theta _k}(\theta ^\star ) \right| ^2\right] \\&\le K\Vert \theta -\theta _0\Vert ^2_{{\mathbb {R}}^{p+q+1}}\sum _{k=1}^{p+q+1} \sigma _{\epsilon }^2\left\| (\overset{\mathbf{. }}{\lambda _k} -\overset{\mathbf{. }}{\lambda _k}^t)(\theta ^\star )\right\| _{\ell ^2}^2 . \end{aligned}$$

As in Hallin et al. (1999), it can be shown using Stirling’s approximation and the fact that $d^\star >d_0$ that

$$\begin{aligned} \left\| (\overset{\mathbf{. }}{\lambda _k}-\overset{\mathbf{. }}{\lambda _k}^t) (\theta ^\star )\right\| _{\ell ^2}\le K\frac{1}{t^{1/2+(d^\star -d_0)-\zeta }} \end{aligned}$$

for any small enough $\zeta >0$. We then deduce that

$$\begin{aligned} \Big \Vert \left( \epsilon _t(\theta )-{\tilde{\epsilon }}_t(\theta )\right) -\left( \epsilon _t(\theta _0)-{\tilde{\epsilon }}_t(\theta _0)\right) \Big \Vert _{{\mathbb {L}}^2}&\le K\Vert \theta -\theta _0\Vert _{{\mathbb {R}}^{p+q+1}}\frac{1}{t^{1/2+(d^\star -d_0) -\zeta }}. \end{aligned}$$

(54)

The expected convergence in probability follows from (52), (54) and the fractional version of Cesàro’s Lemma.

$\square$

We show in the following lemma the existence and invertibility of $J(\theta _0)$.

Lemma 16

Under Assumptions of Theorem 2, the matrix

$$\begin{aligned} J(\theta _0)=\lim _{n\rightarrow \infty }\left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}O_n(\theta _0)\right] \end{aligned}$$

exists almost surely and is invertible.

Proof

For all $1\le i,j \le p+q+1$, we have

$$\begin{aligned} \frac{\partial ^2}{\partial \theta _i\partial \theta _j}O_n(\theta _0)&=\frac{1}{n}\sum _{t=1}^n\frac{\partial ^2}{\partial \theta _i\partial \theta _j}\epsilon _t^2(\theta _0)=\frac{2}{n}\sum _{t=1}^n\left\{ \frac{\partial }{\partial \theta _i}\epsilon _t(\theta _0)\frac{\partial }{\partial \theta _j}\epsilon _t(\theta _0)+\epsilon _t(\theta _0) \frac{\partial ^2}{\partial \theta _i\partial \theta _j}\epsilon _t(\theta _0) \right\} . \end{aligned}$$

Note that in view of (32), (33) and Remark 12, the first and second order derivatives of $\epsilon _t(\cdot )$ belong to ${\mathbb {L}}^2$. By using the ergodicity of $(\epsilon _t)_{t\in {\mathbb {Z}}}$ assumed in Assumption (A2), we deduce that

$$\begin{aligned} \frac{\partial ^2}{\partial \theta _i\partial \theta _j}O_n(\theta _0) \underset{n\rightarrow \infty }{\overset{\text {a.s.}}{\longrightarrow }} 2{\mathbb {E}}\left[ \frac{\partial }{\partial \theta _i}\epsilon _t(\theta _0)\frac{\partial }{\partial \theta _j}\epsilon _t(\theta _0)\right] +2{\mathbb {E}}\left[ \epsilon _t(\theta _0)\frac{\partial ^2}{\partial \theta _i \partial \theta _j}\epsilon _t(\theta _0)\right] . \end{aligned}$$

By (29) and (32), $\epsilon _t$ and ${\partial \epsilon _t(\theta _0)}/{\partial \theta }$ are non correlated as well as $\epsilon _t$ and ${\partial ^2\epsilon _t(\theta _0)}/{\partial \theta \partial \theta }$. Thus we have

$$\begin{aligned} \frac{\partial ^2}{\partial \theta _i\partial \theta _j}O_n(\theta _0)\underset{n\rightarrow \infty }{\overset{\text {a.s.}}{\longrightarrow }}J(\theta _0)(i,j):= 2{\mathbb {E}} \left[ \frac{\partial }{\partial \theta _i}\epsilon _t(\theta _0)\frac{\partial }{\partial \theta _j}\epsilon _t(\theta _0)\right] . \end{aligned}$$

(55)

From (29) and (39) we obtain that

$$\begin{aligned} {\mathbb {E}}\left[ \frac{\partial }{\partial \theta _i}\epsilon _t(\theta _0) \frac{\partial }{\partial \theta _j}\epsilon _t(\theta _0)\right]&={\mathbb {E}} \left[ \left( \sum _{k_1\ge 1}\overset{\mathbf{. }}{\lambda }_{k_1,i} \left( \theta _0\right) \epsilon _{t-k_1}\right) \left( \sum _{k_2\ge 1} \overset{\mathbf{. }}{\lambda }_{k_2,j}\left( \theta _0\right) \epsilon _{t-k_2} \right) \right] \\&=\sum _{k_1\ge 1}\sum _{k_2\ge 1}\overset{\mathbf{. }}{\lambda }_{k_1,i} \left( \theta _0\right) \overset{\mathbf{. }}{\lambda }_{k_2,j}\left( \theta _0 \right) {\mathbb {E}}\left[ \epsilon _{t-k_1}\epsilon _{t-k_2}\right] \\&\le K\, \sigma _{\epsilon }^2\sum _{k_1\ge 1}\left( \frac{1}{k_1}\right) ^2 <\infty . \end{aligned}$$

Therefore $J(\theta _0)$ exists almost surely.

If the matrix $J(\theta _0)$ is not invertible, there exists some real constants $c_1,\dots ,c_{p+q+1}$ not all equal to zero such that ${\mathbf {c}}^{'}J(\theta _0){\mathbf {c}}=\sum _{i=1}^{p+q+1} \sum _{j=1}^{p+q+1}c_jJ(\theta _0)(j,i)c_i=0$, where ${\mathbf {c}}=(c_1,\dots ,c_{p+q+1})^{'}$. In view of (55) we obtain that

$$\begin{aligned} \sum _{i=1}^{p+q+1}\sum _{j=1}^{p+q+1}{\mathbb {E}}\left[ \left( c_j\frac{\partial \epsilon _t(\theta _0)}{\partial \theta _j}\right) \left( c_i\frac{\partial \epsilon _t(\theta _0)}{\partial \theta _i}\right) \right] = {\mathbb {E}}\left[ \left( \sum _{k=1}^{p+q+1}c_k\frac{\partial \epsilon _t(\theta _0)}{\partial \theta _k}\right) ^2 \right]&=0, \end{aligned}$$

which implies that

$$\begin{aligned} \sum _{k=1}^{p+q+1}c_k\frac{\partial \epsilon _t(\theta _0)}{\partial \theta _k}&=0 \ \ \mathrm {a.s.} \text { or equivalenty }\ \ {\mathbf {c}}'\frac{\partial \epsilon _t(\theta _0)}{\partial \theta }=0 \ \ \mathrm {a.s.} \end{aligned}$$

(56)

Differentiating the Eq. (1), we obtain that

$$\begin{aligned} {\mathbf {c}}'\frac{\partial }{\partial \theta }\left\{ a_{\theta _0}(L)(1-L)^{d_0}\right\} X_t={\mathbf {c}}'\left\{ \frac{\partial }{\partial \theta }b_{\theta _0}(L)\right\} \epsilon _t + b_{\theta _0}(L){\mathbf {c}}'\frac{\partial }{\partial \theta } \epsilon _t(\theta _0). \end{aligned}$$

and by (56) we may write that

$$\begin{aligned} {\mathbf {c}}^{'}\left( \frac{\partial }{\partial \theta }\left\{ a_{\theta _0}(L)(1-L)^{d_0}\right\} X_t-\left\{ \frac{\partial }{\partial \theta }b_{\theta _0}(L)\right\} \epsilon _t \right) =0 \ \ \mathrm {a.s.} \end{aligned}$$

It follows that (1) can therefore be rewritten in the form:

$$\begin{aligned} \left( a_{\theta _0}(L)(1-L)^{d_0}+{\mathbf {c}}^{'}\frac{\partial }{\partial \theta }\left\{ a_{\theta _0}(L)(1-L)^{d_0}\right\} \right) X_t = \left( b_{\theta _0}(L) +{\mathbf {c}}^{'}\frac{\partial }{\partial \theta }b_{\theta _0}(L)\right) \epsilon _t, \ \ \mathrm {a.s.} \end{aligned}$$

Under Assumption (A1) the representation in (1) is unique (see Hosking (1981)) so

$$\begin{aligned} {\mathbf {c}}^{'}\frac{\partial }{\partial \theta }\left\{ a_{\theta _0}(L)(1-L)^{d_0}\right\}&=0 \end{aligned}$$

(57)

and

$$\begin{aligned} {\mathbf {c}}^{'}\frac{\partial }{\partial \theta }b_{\theta _0}(L)&=0. \end{aligned}$$

(58)

First, (58) implies that

$$\begin{aligned} \sum _{k=p+1}^{p+q} c_k \frac{\partial }{\partial \theta _k}b_{\theta _0}(L) =\sum _{k=p+1}^{p+q} -c_k L^k =0 \end{aligned}$$

and thus $c_k = 0$ for $p+1\le k\le p+q$.

Similarly, (57) yields that

$$\begin{aligned} \sum _{k=1}^{p} c_k \frac{\partial }{\partial \theta _k}a_{\theta _0}(L) (1-L)^{d_0}+c_{p+q+1} a_{\theta _0}(L)\frac{\partial (1-L)^d}{\partial d} (d_0) =0 \ . \end{aligned}$$

Since $\partial (1-L)^d / \partial d= (1-L)^{d}\mathrm {ln}(1-L)$, it follows that

$$\begin{aligned} -\sum _{k=1}^{p} c_k L^k +c_{p+q+1} \sum _{k\ge 0} e_k L^k =0 \ , \end{aligned}$$

where the sequence $(e_k)_{k\ge 1}$ is given by the coefficients of the power series $a_{\theta _0}(L)\mathrm {ln} (1-L)$. Since $e_0=0$ and $e_1=-1$, we obtain that

$$\begin{aligned} c_1&=-c_{p+q+1}\\ c_k&=e_k c_{p+q+1} \ \text {for }k=2,\dots ,p \\ 0&= e_k c_{p+q+1} \ \text {for }k\ge p+1. \end{aligned}$$

Since the polynomial $a_{\theta _0}$ is not the null polynomial, this implies that $c_{p+q+1}=0$ and then $c_k$ for $1\le k\le p$. Thus ${\mathbf {c}}=0$ which leads us to a contradiction. Hence $J(\theta _0)$ is invertible.

$\square$

Lemma 17

For any $1\le i,j\le p+q+1$ and under the assumptions of Theorem 1, we have

$$\begin{aligned} \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) -J(\theta _0)(i,j)=\mathrm {o}_{{\mathbb {P}}}(1), \end{aligned}$$

(59)

where $\theta ^*_{n,i,j}$ is defined in (45).

Proof

For any $\theta \in \varTheta _\delta$, let

$$\begin{aligned} {J}_n(\theta )&=\frac{\partial ^2}{\partial \theta \partial \theta ^{'}}Q_n\left( \theta \right) =\frac{2}{n}\sum _{t=1}^n\left\{ \frac{\partial }{\partial \theta }{\tilde{\epsilon }}_t\left( \theta \right) \right\} \left\{ \frac{\partial }{\partial \theta ^{'}}{\tilde{\epsilon }}_t\left( \theta \right) \right\} +\frac{2}{n}\sum _{t=1}^n{\tilde{\epsilon }}_t(\theta ) \frac{\partial ^2}{\partial \theta \partial \theta ^{'}} {\tilde{\epsilon }}_t(\theta ) \end{aligned}$$

and

$$\begin{aligned} J_n^{*}(\theta )&=\frac{\partial ^2}{\partial \theta \partial \theta ^{'}}O_n \left( \theta \right) =\frac{2}{n}\sum _{t=1}^n\left\{ \frac{\partial }{\partial \theta }\epsilon _t\left( \theta \right) \right\} \left\{ \frac{\partial }{\partial \theta ^{'}}\epsilon _t\left( \theta \right) \right\} +\frac{2}{n}\sum _{t=1}^n\epsilon _t(\theta )\frac{\partial ^2}{\partial \theta \partial \theta ^{'}}\epsilon _t(\theta ). \end{aligned}$$

We have

$$\begin{aligned} \left| \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n \left( \theta ^*_{n,i,j}\right) -J(\theta _0)(i,j)\right|&\le \left| {J}_{n}(\theta ^*_{n,i,j})(i,j)-J_{n}^{*}(\theta ^*_{n,i,j})(i,j) \right| \nonumber \\&\quad +\left| J_{n}^{*}(\theta ^*_{n,i,j})(i,j)-J_{n}^{*}(\theta _0)(i,j) \right| \nonumber \\&\quad +\left| J_{n}^{*}(\theta _0)(i,j)-J(\theta _0)(i,j)\right| . \end{aligned}$$

(60)

So it is enough to show that the three terms in the right hand side of (60) converge in probability to 0 when n tends to infinity. Following the same arguments as the proof of Lemma 16 and applying the ergodic theorem, we obtain that

$$\begin{aligned} J_n^{*}(\theta _0)\underset{n\rightarrow \infty }{\overset{\text {a.s.}}{\longrightarrow }}2{\mathbb {E}}\left[ \frac{\partial }{\partial \theta }\epsilon _t(\theta _0)\frac{\partial }{\partial \theta ^{'}}\epsilon _t(\theta _0)\right] =J(\theta _0). \end{aligned}$$

Let us now show that the random variable $|J_{n}(\theta ^*_{n,i,j})(i,j)-J_{n}^{*}(\theta ^*_{n,i,j})(i,j)|$ converges in probability to 0. It can easily be seen that

$$\begin{aligned}&\frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _i} \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _j} -\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i} \frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _j}\\&\quad =\left( \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _i} -\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i} \right) \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _j}\\&\quad +\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i} \left( \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _j} -\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _j} \right) . \end{aligned}$$

Hence, by the Cauchy–Schwarz inequality and Remark 12 one has

$$\begin{aligned} {\mathbb {E}}\Big |\frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _i}\frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _j}&-\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i}\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _j}\Big |\\&\le \left( {\mathbb {E}}\left( \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _i}-\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i}\right) ^2{\mathbb {E}} \left( \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _j} \right) ^2\right) ^{1/2}\\&\qquad +\left( {\mathbb {E}}\left( \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _j}-\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _j}\right) ^2{\mathbb {E}}\left( \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _i}\right) ^2\right) ^{1/2}\\&\le \left( \sup _{\theta \in \varTheta _\delta }{\mathbb {E}} \left( \frac{\partial \epsilon _t(\theta )}{\partial \theta _i} -\frac{\partial {\tilde{\epsilon }}_t(\theta )}{\partial \theta _i}\right) ^2 \sup _{\theta \in \varTheta _\delta }{\mathbb {E}}\left( \frac{\partial \epsilon _t (\theta )}{\partial \theta _j}\right) ^2\right) ^{1/2}\\&\qquad +\left( \sup _{\theta \in \varTheta _\delta }{\mathbb {E}} \left( \frac{\partial \epsilon _t(\theta )}{\partial \theta _j} -\frac{\partial {\tilde{\epsilon }}_t(\theta )}{\partial \theta _j}\right) ^2 \sup _{\theta \in \varTheta _\delta }{\mathbb {E}}\left( \frac{\partial \epsilon _t (\theta )}{\partial \theta _i}\right) ^2\right) ^{1/2}\\&\le \sigma _\epsilon ^2\left( \sup _{\theta \in \varTheta _\delta } \left\| \overset{\mathbf{. }}{\lambda }_{i}(\theta )-\overset{\mathbf{. }}{\lambda }_{i}^t(\theta )\right\| _{\ell ^2}^2\sup _{\theta \in \varTheta _\delta } \sum _{k\ge 1}\left( \overset{\mathbf{. }}{\lambda }_{k,j}(\theta )\right) ^2 \right) ^{1/2}\\&\qquad +\sigma _\epsilon ^2\left( \sup _{\theta \in \varTheta _\delta } \left\| \overset{\mathbf{. }}{\lambda }_{j}(\theta )-\overset{\mathbf{. }}{\lambda }_{j}^t(\theta )\right\| _{\ell ^2}^2\sup _{\theta \in \varTheta _\delta } \sum _{k\ge 1}\left( \overset{\mathbf{. }}{\lambda }_{k,i}^t(\theta )\right) ^2 \right) ^{1/2}\\&\le K\frac{1}{t^{1/2+(d_1-d_0)-\zeta }}\xrightarrow [t\rightarrow \infty ]{} \, 0. \end{aligned}$$

Similar calculation can be done to obtain

$$\begin{aligned} {\mathbb {E}}\left| \epsilon _t(\theta ^*_{n,i,j})\frac{\partial ^2\epsilon _t (\theta ^*_{n,i,j})}{\partial \theta _i\partial \theta _j}-{\tilde{\epsilon }}_t (\theta ^*_{n,i,j})\frac{\partial ^2{\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i\partial \theta _j}\right| \xrightarrow [t\rightarrow \infty ]{} \, 0. \end{aligned}$$

It follows then using Cesàro’s Lemma that

$$\begin{aligned} {\mathbb {E}}\left| J_{n}(\theta ^*_{n,i,j})(i,j)-J_{n}^{*}(\theta ^*_{n,i,j}) (i,j)\right|&\le \frac{2}{n}\sum _{t=1}^n{\mathbb {E}} \left| \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _i} \frac{\partial \epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _j} -\frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i} \frac{\partial {\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _j} \right| \\&\qquad +\frac{2}{n}\sum _{t=1}^n{\mathbb {E}}\left| \epsilon _t(\theta ^*_{n,i,j}) \frac{\partial ^2\epsilon _t(\theta ^*_{n,i,j})}{\partial \theta _i \partial \theta _j}-{\tilde{\epsilon }}_t(\theta ^*_{n,i,j}) \frac{\partial ^2{\tilde{\epsilon }}_t(\theta ^*_{n,i,j})}{\partial \theta _i \partial \theta _j}\right| \\&\le \frac{K}{n}\sum _{t=1}^n\frac{1}{t^{1/2+(d_1-d_0)-\zeta }}\xrightarrow [n\rightarrow \infty ]{} \, 0, \end{aligned}$$

which entails the expected convergence in probability to 0 of $|J_{n}(\theta ^*_{n,i,j})(i,j)-J_{n}^{*}(\theta ^*_{n,i,j})(i,j)|$.

By a Taylor expansion of $J_n^{*}(\cdot )(i,j)$ around $\theta _0$, there exists $\theta _{n,i,j}^{**}$ between $\theta ^*_{n,i,j}$ and $\theta _0$ such that

$$\begin{aligned} \left| J_n^{*}(\theta ^*_{n,i,j})(i,j)-J_n^{*}(\theta _0)(i,j)\right|&=\left| \frac{\partial }{\partial \theta }J_n^{*}(\theta _{n,i,j}^{**})(i,j) \cdot (\theta ^*_{n,i,j}-\theta _0)\right| \nonumber \\&\le \left\| \frac{\partial }{\partial \theta }J_n^{*}(\theta _{n,i,j}^{**}) (i,j)\right\| \left\| \theta ^*_{n,i,j}-\theta _0\right\| \nonumber \\&\le \frac{2}{n}\sum _{t=1}^n\left\| \left. \frac{\partial }{\partial \theta } \left\{ \frac{\partial }{\partial \theta _i}\epsilon _t(\theta ) \frac{\partial }{\partial \theta _j}\epsilon _t(\theta ) \right\} \right| _{\theta =\theta _{n,i,j}^{**}}\right\| \left\| \theta ^*_{n,i,j}- \theta _0\right\| \nonumber \\&\qquad +\frac{2}{n}\sum _{t=1}^n\left\| \left. \frac{\partial }{\partial \theta } \left\{ \epsilon _t(\theta )\frac{\partial ^2}{\partial \theta _i\partial \theta _j}\epsilon _t(\theta ) \right\} \right| _{\theta =\theta _{n,i,j}^{**}}\right\| \left\| \theta ^*_{n,i,j}-\theta _0\right\| . \end{aligned}$$

(61)

Since $d_1-d_0>1/2$, it can easily be shown as before that

$$\begin{aligned} {\mathbb {E}}\left\| \left. \frac{\partial }{\partial \theta }\left\{ \frac{\partial }{\partial \theta _i}\epsilon _t(\theta ) \frac{\partial }{\partial \theta _j}\epsilon _t(\theta ) \right\} \right| _{\theta =\theta _{n,i,j}^{**}}\right\| <\infty \end{aligned}$$

(62)

and

$$\begin{aligned} {\mathbb {E}}\left\| \left. \frac{\partial }{\partial \theta }\left\{ \epsilon _t(\theta )\frac{\partial ^2}{\partial \theta _i\partial \theta _j}\epsilon _t(\theta ) \right\} \right| _{\theta =\theta _{n,i,j}^{**}}\right\| <\infty . \end{aligned}$$

(63)

We use (61), (62), (63), the ergodic theorem and Theorem 1 to deduce the convergence in probability of $|J_n^{*}(\theta ^*_{n,i,j})(i,j)-J_n^{*}(\theta _0)(i,j)|$ to 0.

The proof of the lemma is then complete. $\square$

The following lemma states the existence of the matrix $I(\theta _0)$.

Lemma 18

Under the assumptions of Theorem 2, the matrix

$$\begin{aligned} I(\theta _0)=\lim _{n\rightarrow \infty }Var\left\{ \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0)\right\} \end{aligned}$$

exists.

Proof

By the stationarity of $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ (remind that this process is defined in (7)), we have

$$\begin{aligned} Var\left\{ \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0) \right\}&=Var\left\{ \frac{1}{\sqrt{n}}\sum _{t=1}^nH_t(\theta _0) \right\} \\&=\frac{1}{n}\sum _{t=1}^n\sum _{s=1}^nCov\left\{ H_t(\theta _0),H_s (\theta _0)\right\} \\&=\frac{1}{n}\sum _{h=-n+1}^{n-1}\left( n-|h|\right) Cov\left\{ H_t(\theta _0),H_{t-h}(\theta _0)\right\} . \end{aligned}$$

By the dominated convergence theorem, the matrix $I(\theta _0)$ exists and is given by

$$\begin{aligned} I(\theta _0)=\sum _{h=-\infty }^{\infty }Cov\left\{ H_t(\theta _0),H_{t-h}(\theta _0)\right\} \end{aligned}$$

whenever

$$\begin{aligned} \sum _{h=-\infty }^{\infty }\Vert Cov\left\{ H_t(\theta _0),H_{t-h}(\theta _0)\right\} \Vert <\infty . \end{aligned}$$

(64)

For $s\in {\mathbb {Z}}$ and $1\le k\ \le p+q+1$, we denote $H_{s,k}(\theta _0)=2\epsilon _s(\theta _0)\frac{\partial }{\partial \theta _k}\epsilon _s(\theta _0)$ the $k-$th entry of $H_{s}(\theta _0)$. In view of (32) we have

$$\begin{aligned} \left| Cov\left\{ H_{t,i}(\theta _0),H_{t-h,j}(\theta _0)\right\} \right|&=4\left| Cov\left( \sum _{k_1\ge 1}\overset{\mathbf{. }}{\lambda }_{k_1,i}\left( \theta _0\right) \epsilon _t\epsilon _{t-k_1},\sum _{k_2\ge 1}\overset{\mathbf{. }}{\lambda }_{k_2,j}\left( \theta _0\right) \epsilon _{t-h}\epsilon _{t-h-k_2}\right) \right| \\ {}&\le 4\sum _{k_1\ge 1}\sum _{k_2\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{k_1,i}\left( \theta _0\right) \right| \left| \overset{\mathbf{. }}{\lambda }_{k_2,j}\left( \theta _0\right) \right| \left| {\mathbb {E}} \left[ \epsilon _t\epsilon _{t-k_1}\epsilon _{t-h}\epsilon _{t-h-k_2}\right] \right| \\&\le \sum _{k_1\ge 1}\sum _{k_2\ge 1}\frac{K}{k_1k_2}\left| {\mathbb {E}}\left[ \epsilon _t\epsilon _{t-k_1}\epsilon _{t-h}\epsilon _{t-h-k_2}\right] \right| \end{aligned}$$

where we have used Lemma 14. It follows that

$$\begin{aligned} \sum _{h=-\infty }^{\infty }\left| Cov\left\{ H_{t,i}(\theta _0),H_{t-h,j}(\theta _0)\right\} \right|&\le \sum _{h\in {\mathbb {Z}}\setminus \{0\}}\sum _{k_1\ge 1}\sum _{k_2\ge 1}\frac{K}{k_1k_2}\left| \mathrm {cum}\left( \epsilon _t,\epsilon _{t-k_1},\epsilon _{t-h},\epsilon _{t-h-k_2}\right) \right| \\&+\sum _{k_1\ge 1}\sum _{k_2\ge 1}\frac{K}{k_1k_2}\left| {\mathbb {E}}\left[ \epsilon _t\epsilon _{t-k_1}\epsilon _{t}\epsilon _{t-k_2}\right] \right| \ . \end{aligned}$$

Thanks to the stationarity of $(\epsilon _t)_{t\in {\mathbb {Z}}}$ and Assumption (A4’) with $\tau =4$ we deduce that

$$\begin{aligned} \sum _{h=-\infty }^{\infty }\left| Cov\left\{ H_{t,i}(\theta _0),H_{t-h,j}(\theta _0)\right\} \right|&\le \sum _{h\in {\mathbb {Z}}\setminus \{0\}}\sum _{k_1\ge 1}\sum _{k_2\ge 1} \frac{K}{k_1k_2}\left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-k_1}, \epsilon _{-h},\epsilon _{-h-k_2}\right) \right| \\&\quad +\sum _{k_1\ge 1}\sum _{k_2\ge 1}\frac{K}{k_1k_2} \left| {\mathbb {E}}\left[ \epsilon _0\epsilon _{-k_1}\epsilon _{0} \epsilon _{-k_2}\right] \right| \\&\le K \sum _{h,k,l\in {\mathbb {Z}}}\left| \mathrm {cum}\left( \epsilon _0, \epsilon _{k},\epsilon _{h},\epsilon _{l}\right) \right| \\&\quad +\sum _{k_1\ge 1}\sum _{k_2\ge 1}\frac{K}{k_1k_2} \Big ( \left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-k_1}, \epsilon _{0},\epsilon _{-k_2}\right) \right| \\&\quad +\sigma _{\epsilon }^2\left| {\mathbb {E}}\left[ \epsilon _{-k_1}\epsilon _{-k_2}\right] \right| \Big ) \\&\le \! K \sum _{h,k,l\in {\mathbb {Z}}}\left| \mathrm {cum}\left( \epsilon _0,\epsilon _{k},\epsilon _{h},\epsilon _{l}\right) \right| \!+\! K \sigma _{\epsilon }^4\sum _{k_1\ge 1}\left( \frac{1}{k_1}\right) ^2 \!\le \! K \end{aligned}$$

and we obtain the expected result. $\square$

Lemma 19

Under Assumptions of Theorem 2, the random vector $\sqrt{n}({\partial }/{\partial \theta })O_n(\theta _0)$ has a limiting normal distribution with mean 0 and covariance matrix $I(\theta _0)$.

Proof

Observe that for any $t\in {\mathbb {Z}}$

$$\begin{aligned}&{\mathbb {E}}\left[ \epsilon _t\frac{\partial }{\partial \theta } \epsilon _t(\theta _0)\right] =0 \end{aligned}$$

(65)

because ${\partial \epsilon _t(\theta _0)}/{\partial \theta }$ belongs to the Hilbert space ${\mathbf {H}}_{\epsilon }(t-1)$ generated by the family $(\epsilon _s)_{s\le t-1}$. Therefore we have

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathbb {E}}\left[ \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0)\right]&= \lim _{n\rightarrow \infty }\frac{2}{\sqrt{n}}\sum _{t=1}^{n}{\mathbb {E}} \left[ \epsilon _t\frac{\partial }{\partial \theta }\epsilon _t(\theta _0)\right] =0. \end{aligned}$$

For $i\ge 1$, we denote by ${\varLambda }_{i}\left( \theta _0\right) =(\overset{\mathbf{. }}{\lambda }_{i,1} \left( \theta _0\right) ,\dots , \overset{\mathbf{. }}{\lambda }_{i,p+q+1}\left( \theta _0\right) )'$ and we introduce for $r\ge 1$

$$\begin{aligned} H_{t,r}(\theta _0)=2\sum _{i= 1}^r{\varLambda }_{i}\left( \theta _0\right) \epsilon _t\epsilon _{t-i}\ \text { and } \ G_{t,r}(\theta _0)=2\sum _{i\ge r+1}{\varLambda }_{k}\left( \theta _0\right) \epsilon _t\epsilon _{t-i}. \end{aligned}$$

From (32) we have

$$\begin{aligned} \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0)=\frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t,r}(\theta _0)+\frac{1}{\sqrt{n}}\sum _{t=1}^{n} G_{t,r}(\theta _0) . \end{aligned}$$

Since $H_{t,r}(\theta _0)$ is a function of finite number of values of the process $(\epsilon _t)_{t\in {\mathbb {Z}}}$, the stationary process $(H_{t,r}(\theta _0))_{t\in {\mathbb {Z}}}$ satisfies a mixing property (see Theorem 14.1 in Davidson (1994), p. 210) of the form (A4). The central limit theorem for strongly mixing processes (see Herrndorf (1984)) implies that $({1}/{\sqrt{n}})\sum _{t=1}^{n}H_{t,r}(\theta _0)$ has a limiting ${\mathcal {N}}(0,I_r(\theta _0))$ distribution with

$$\begin{aligned} I_r(\theta _0)=\lim _{n\rightarrow \infty }Var\left( \frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t,r}(\theta _0)\right) . \end{aligned}$$

Since $\frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t,r}(\theta _0)$ and $\frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t}(\theta _0)$ have zero expectation, we shall have

$$\begin{aligned} \lim _{r\rightarrow \infty }Var\left( \frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t,r}(\theta _0)\right) =Var\left( \frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t}(\theta _0)\right) =Var\left\{ \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0)\right\} , \end{aligned}$$

as soon as

$$\begin{aligned} \lim _{r\rightarrow \infty }{\mathbb {E}}\left[ \left\| \frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t}(\theta _0) -\frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t,r}(\theta _0)\right\| ^2\right] =0 . \end{aligned}$$

(66)

As a consequence we will have $\lim _{r\rightarrow \infty }I_r(\theta _0)=I(\theta _0)$. The limit in (66) is obtained as follows:

$$\begin{aligned} {\mathbb {E}}&\left[ \left\| \frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t}(\theta _0) -\frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t,r}(\theta _0)\right\| _{{\mathbb {R}}^{p+q+1}}^2\right] ={\mathbb {E}} \left[ \left\| \frac{1}{\sqrt{n}}\sum _{t=1}^{n}G_{t,r}(\theta _0)\right\| _{{\mathbb {R}}^{p+q+1}}^2\right] \\&\quad \le \frac{4}{n}\sum _{l=1}^{p+q+1}{\mathbb {E}} \left[ \left( \sum _{t=1}^{n}\sum _{k\ge r+1}\overset{\mathbf{. }}{\lambda }_{k,l}\left( \theta _0\right) \epsilon _{t-k}\epsilon _t\right) ^2 \right] \\&\quad \le \frac{4}{n}\sum _{l=1}^{p+q+1}\sum _{t=1}^{n}\sum _{s=1}^{n}\sum _{k\ge r+1}\sum _{j\ge r+1}\left| \overset{\mathbf{. }}{\lambda }_{k,l}\left( \theta _0\right) \right| \left| \overset{\mathbf{. }}{\lambda }_{j,l}\left( \theta _0\right) \right| \left| {\mathbb {E}}\left[ \epsilon _{t-k}\epsilon _t\epsilon _{s-j}\epsilon _{s}\right] \right| , \end{aligned}$$

We use successively the stationarity of $(\epsilon _t)_{t\in {\mathbb {Z}}}$, Lemma 14 and Assumption (A4’) with $\tau =4$ in order to obtain that

$$\begin{aligned} {\mathbb {E}}&\left[ \left\| \frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t}(\theta _0) -\frac{1}{\sqrt{n}}\sum _{t=1}^{n}H_{t,r}(\theta _0)\right\| _{{\mathbb {R}}^{p+q+1}}^2\right] \\&\quad \le \frac{4}{n}\sum _{l=1}^{p+q+1}\sum _{h=1-n}^{n-1} \sum _{k\ge r+1}\sum _{j\ge r+1}\left| \overset{\mathbf{. }}{\lambda }_{k,l} \left( \theta _0\right) \right| \left| \overset{\mathbf{. }}{\lambda }_{j,l} \left( \theta _0\right) \right| \left( n-\left| h\right| \right) \left| {\mathbb {E}}\left[ \epsilon _{t-k}\epsilon _t\epsilon _{t-h-j} \epsilon _{t-h}\right] \right| \\&\quad \le 4\sum _{l=1}^{p+q+1}\sum _{h=-\infty }^{\infty }\sum _{k\ge r +1}\sum _{j\ge r+1}\left| \overset{\mathbf{. }}{\lambda }_{k,l}\left( \theta _0 \right) \right| \left| \overset{\mathbf{. }}{\lambda }_{j,l}\left( \theta _0 \right) \right| \left| {\mathbb {E}}\left[ \epsilon _{t-k}\epsilon _t \epsilon _{t-h-j}\epsilon _{t-h}\right] \right| \\&\quad \le \frac{K}{(r+1)^2}\sum _{h\ne 0}\sum _{k\ge r+1}\sum _{j= -\infty }^{\infty }\left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-k}, \epsilon _{-j},\epsilon _{-h} \right) \right| \\&\quad +\frac{K}{(r+1)^2}\sum _{k\ge r+1}\sum _{j\ge r+1}\left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-k},\epsilon _{-j}, \epsilon _{0} \right) \right| +K\sigma _{\epsilon }^4\sum _{k\ge r+1}\left( \frac{1}{k}\right) ^2 \end{aligned}$$

and we obtain the convergence stated in (66) when $r\rightarrow \infty$.

Using Theorem 7.7.1 and Corollary 7.7.1 of Anderson (see Anderson (1971), pp. 425–426), the lemma is proved once we have, uniformly in n,

$$\begin{aligned} Var\left( \frac{1}{\sqrt{n}}\sum _{t=1}^{n}G_{t,r}(\theta _0)\right) \xrightarrow [r\rightarrow \infty ]{} 0 \ . \end{aligned}$$

Arguing as before we may write

$$\begin{aligned} \left[ Var\left( \frac{1}{\sqrt{n}}\sum _{t=1}^{n}G_{t,r}(\theta _0) \right) \right] _{ij}&=\left[ Var\left( \frac{2}{\sqrt{n}} \sum _{t=1}^{n}\sum _{k\ge r+1}\varLambda _k(\theta _0)\epsilon _{t-k}\epsilon _t \right) \right] _{ij}\\&=\frac{4}{n}\sum _{t=1}^{n}\sum _{s=1}^{n}\sum _{k_1\ge r+1} \sum _{k_2\ge r+1}\overset{\mathbf{. }}{\lambda }_{k_1,i}\left( \theta _0 \right) \overset{\mathbf{. }}{\lambda }_{k_2,j}\left( \theta _0\right) {\mathbb {E}}\left[ \epsilon _{t-k_1}\epsilon _t\epsilon _{s-k_2}\epsilon _s \right] \\&\le 4\sum _{h=-\infty }^{\infty }\sum _{k_1,k_2\ge r+1} \left| \overset{\mathbf{. }}{\lambda }_{k_1,i}\left( \theta _0\right) \overset{\mathbf{. }}{\lambda }_{k_2,j}\left( \theta _0\right) \right| \left| {\mathbb {E}}\left[ \epsilon _{t-k_1}\epsilon _t\epsilon _{t-h-k_2} \epsilon _{t-h}\right] \right| .\\ \end{aligned}$$

and we obtain that

$$\begin{aligned}&\sup _n Var\left( \frac{1}{\sqrt{n}}\sum _{t=1}^{n}G_{t,r}(\theta _0) \right) \xrightarrow [r\rightarrow \infty ]{} 0 , \end{aligned}$$

(67)

which completes the proof. $\square$

No we can end this quite long proof of the asymptotic normality result.

Proof of Theorem 2

In view of Lemma 15, the Eq. (46) can be rewritten in the form:

$$\begin{aligned}&\mathrm {o}_{{\mathbb {P}}}(1)= \sqrt{n}\frac{\partial }{\partial \theta }O_n(\theta _0) +\left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) \right] \sqrt{n}\left( {\hat{\theta }}_n-\theta _0\right) . \end{aligned}$$

From Lemma 19$[({\partial ^2}/{\partial \theta _i\partial \theta _j})Q_n( \theta ^*_{n,i,j})]\sqrt{n}( {\widehat{\theta }}_n-\theta _0)$ converges in distribution to ${\mathcal {N}}(0,I(\theta _0))$. Using Lemma 17 and Slutsky’s theorem we deduce that

$$\begin{aligned} \left( \left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) \right] ,\left[ \frac{\partial ^2}{\partial \theta _i\partial \theta _j}Q_n\left( \theta ^*_{n,i,j}\right) \right] \sqrt{n}( {\hat{\theta }}_n-\theta _0)\right) \end{aligned}$$

converges in distribution to $(J(\theta _0),Z)$ with ${\mathbb {P}}_{Z}={\mathcal {N}}(0,I)$. Consider now the function $h:{\mathbb {R}}^{(p+q+1)\times (p+q+1)}\times {\mathbb {R}}^{p+q+1}\rightarrow {\mathbb {R}}^{p+q+1}$ that maps (A, X) to $A^{-1}X$. If $D_h$ denotes the set of discontinuity points of h, we have ${\mathbb {P}}((J(\theta _0),Z)\in D_h)=0$. By the continuous mapping theorem

$$\begin{aligned} h\left( \left[ ({\partial ^2}/{\partial \theta _i\partial \theta _j})Q_n( \theta ^*_{n,i,j}) \right] ,\left[ ({\partial ^2}/{\partial \theta _i\partial \theta _j})Q_n( \theta ^*_{n,i,j}) \right] \sqrt{n}( {\hat{\theta }}_n-\theta _0)\right) \end{aligned}$$

converges in distribution to $h(J(\theta _0),Z)$ and thus $\sqrt{n}( {\hat{\theta }}_n-\theta _0)$ has a limiting normal distribution with mean 0 and covariance matrix $J^{-1}(\theta _0)I(\theta _0)J^{-1}(\theta _0)$. The proof of Theorem 2 is then completed.

6.4 Proof of the convergence of the variance matrix estimator

We show in this section the convergence in probability of ${\hat{\varOmega }}:={\hat{J}}_n^{-1}{\hat{I}}_n^{SP}{\hat{J}}_n^{-1}$ to $\varOmega$, which is an adaptation of the arguments used in Boubacar Mainassara et al. (2012).

Using the same approach as that followed in Lemma 17, we show that ${\hat{J}}_n$ converges in probability to J. We give below the proof of the convergence in probability of the estimator ${\hat{I}}_n^{SP}$, obtained using the approach of the spectral density, to I.

We recall that the matrix norm used is given by $\left\| A\right\| =\sup _{\left\| x\right\| \le 1}\left\| Ax\right\| =\rho ^{1/2}( A^{'}A)$, when A is a ${\mathbb {R}}^{k_1\times k_2}$ matrix, $\Vert x\Vert ^2=x^{'}x$ is the Euclidean norm of the vector $x\in {\mathbb {R}}^{k_2}$, and $\rho (\cdot )$ denotes the spectral radius. This norm satisfies

$$\begin{aligned} \left\| A\right\| ^2\le \sum _{i=1}^{k_1}\sum _{j=1}^{k_2}a_{i,j}^2, \end{aligned}$$

(68)

with $a_{i,j}$ the entries of $A\in {\mathbb {R}}^{k_1\times k_2}$. The choice of the norm is crucial for the following results to hold (with e.g. the Euclidean norm, this result is not valid).

We denote

$$\begin{aligned} \varSigma _{H,\underline{H_r}}={\mathbb {E}}H_t{\underline{H}}_{r,t}^{'}, \ \ \varSigma _{H}={\mathbb {E}}H_tH_t^{'}, \ \ \varSigma _{\underline{H_r}}={\mathbb {E}}{\underline{H}}_{r,t} {\underline{H}}_{r,t}^{'} \end{aligned}$$

where $H_t:=H_t(\theta _0)$ is definied in (7) and $\underline{{H}}_{r,t}=({H}_{t-1}^{'},\dots ,{H}_{t-r}^{'}) ^{'}$. For any $n\ge 1$, we have

$$\begin{aligned} {\hat{I}}_n^{\mathrm {SP}}&={\hat{\varPhi }}_r^{-1}(1) {\hat{\varSigma }}_{{\hat{u}}_r}{\hat{\varPhi }}_r^{'-1}(1) \\&=\left( {\hat{\varPhi }}_r^{-1}(1)-\varPhi ^{-1}(1)\right) {\hat{\varSigma }}_{{\hat{u}}_r}{\hat{\varPhi }}_r^{'-1}(1)+\varPhi ^{-1}(1) \left( {\hat{\varSigma }}_{{\hat{u}}_r}-\varSigma _u\right) {\hat{\varPhi }}_r^{'-1}(1)\\&\quad +\varPhi ^{-1}(1)\varSigma _u\left( {\hat{\varPhi }}_r^{'-1}(1)-\varPhi ^{'-1}(1)\right) +\varPhi ^{-1}(1)\varSigma _u\varPhi ^{'-1}(1). \end{aligned}$$

We then obtain

$$\begin{aligned} \left\| {\hat{I}}_n^{\mathrm {SP}}-I(\theta _0)\right\|&\le \left\| {\hat{\varPhi }}_r^{-1}(1)-\varPhi ^{-1}(1)\right\| \left\| {\hat{\varSigma }}_{{\hat{u}}_r}\right\| \left\| {\hat{\varPhi }}_r^{'-1} (1)\right\| +\left\| \varPhi ^{-1}(1)\right\| \left\| {\hat{\varSigma }}_{{\hat{u}}_r} -\varSigma _u\right\| \left\| {\hat{\varPhi }}_r^{'-1}(1)\right\| \nonumber \\&\quad +\left\| \varPhi ^{-1}(1)\right\| \left\| \varSigma _u\right\| \left\| {\hat{\varPhi }}_r^{'-1}(1)-\varPhi ^{'-1}(1)\right\| \nonumber \\&\le \left\| {\hat{\varPhi }}_r^{-1}(1)-\varPhi ^{-1}(1)\right\| \left( \left\| {\hat{\varSigma }}_{{\hat{u}}_r}\right\| \left\| {\hat{\varPhi }}_r^{'-1}(1)\right\| +\left\| \varPhi ^{-1}(1)\right\| \left\| \varSigma _u\right\| \right) \nonumber \\&\quad +\left\| {\hat{\varSigma }}_{{\hat{u}}_r}-\varSigma _u\right\| \left\| {\hat{\varPhi }}_r^{'-1}(1)\right\| \left\| \varPhi ^{-1}(1) \right\| \nonumber \\&\le \left\| {\hat{\varPhi }}_r^{-1}(1)\right\| \left\| \varPhi (1) - {\hat{\varPhi }}_r(1)\right\| \left\| \varPhi ^{-1}(1)\right\| \left( \left\| {\hat{\varSigma }}_{{\hat{u}}_r}\right\| \left\| {\hat{\varPhi }}_r^{'-1} (1)\right\| +\left\| \varPhi ^{-1}(1)\right\| \left\| \varSigma _u\right\| \right) \nonumber \\&\quad +\left\| {\hat{\varSigma }}_{{\hat{u}}_r}-\varSigma _u\right\| \left\| {\hat{\varPhi }}_r^{'-1}(1)\right\| \left\| \varPhi ^{-1}(1)\right\| . \end{aligned}$$

(69)

In view of (69), to prove the convergence in probability of ${\hat{I}}_n^{\mathrm {SP}}$ to $I(\theta _0)$, it suffices to show that ${\hat{\varPhi }}_r(1)\rightarrow \varPhi (1)$ and ${\hat{\varSigma }}_{{\hat{u}}_r}\rightarrow \varSigma _u$ in probability. Let the $r\times 1$ vector $\mathbb {1}_r=(1,\dots ,1)^{'}$ and the $r(p+q+1)\times (p+q+1)$ matrix ${\mathbf {E}}_r={I}_{p+q+1}\otimes \mathbb {1}_r$, where $\otimes$ denotes the matrix Kronecker product and ${I}_m$ the $m\times m$ identity matrix. Write ${\underline{\varPhi }}^{*}_r=(\varPhi _1,\dots ,\varPhi _r)$ where the $\varPhi _i$’s are defined by (8). We have

$$\begin{aligned} \left\| {\hat{\varPhi }}_r(1)-\varPhi (1)\right\|&=\left\| \sum _{k=1}^r{\hat{\varPhi }}_{r,k}-\sum _{k=1}^r\varPhi _{r,k}+\sum _{k=1}^r \varPhi _{r,k}-\sum _{k=1}^{\infty }\varPhi _k\right\| \nonumber \\&\le \left\| \sum _{k=1}^r\left( {\hat{\varPhi }}_{r,k} -\varPhi _{r,k}\right) \right\| +\left\| \sum _{k=1}^r\left( \varPhi _{r,k}-\varPhi _{k} \right) \right\| +\left\| \sum _{k=r+1}^{\infty }\varPhi _k\right\| \nonumber \\&\le \left\| \left( \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}_r \right) {\mathbf {E}}_r\right\| + \left\| \left( {\underline{\varPhi }}^{*}_r -{\underline{\varPhi }}_r\right) {\mathbf {E}}_r\right\| +\left\| \sum _{k=r+1}^{\infty }\varPhi _k\right\| \nonumber \\&\le \sqrt{p+q+1}\sqrt{r}\left( \left\| \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}_r\right\| + \left\| {\underline{\varPhi }}^{*}_r-{\underline{\varPhi }}_r\right\| \right) +\left\| \sum _{k=r+1}^{\infty }\varPhi _k\right\| . \end{aligned}$$

(70)

Under the assumptions of Theorem 5 we have

$$\begin{aligned} \left\| \sum _{k=r+1}^{\infty }\varPhi _k\right\| \le \sum _{k=r+1}^{\infty }\left\| \varPhi _k\right\| \xrightarrow [n\rightarrow \infty ]{} 0 . \end{aligned}$$

Therefore it is enough to show that $\sqrt{r}\Vert \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}_r\Vert$ and $\sqrt{r}\Vert {\underline{\varPhi }}^{*}_r-{\underline{\varPhi }}_r\Vert$ converge in probability towards 0 in order to obtain the convergence in probability of ${\hat{\varPhi }}_r(1)$ towards $\varPhi (1)$. From (9) we have

$$\begin{aligned} H_t(\theta _0)={\underline{\varPhi }}_r{\underline{H}}_{r,t}(\theta _0)+u_{r,t}, \end{aligned}$$

(71)

and thus

$$\begin{aligned} \varSigma _{u_r}=\mathrm {Var}(u_{r,t}) ={\mathbb {E}}\left[ u_{r,t}\left( H_t(\theta _0)-{\underline{\varPhi }}_r{\underline{H}}_{r,t}(\theta _0)\right) ^{'} \right] . \end{aligned}$$

The vector $u_{r,t}$ is orthogonal to ${\underline{H}}_{r,t}(\theta _0)$. It follows that

$$\begin{aligned} \mathrm {Var}(u_{r,t})&={\mathbb {E}}\left[ \left( H_t(\theta _0) -{\underline{\varPhi }}_r{\underline{H}}_{r,t}(\theta _0)\right) H_t^{'} (\theta _0)\right] \\&=\varSigma _{H}-{\underline{\varPhi }}_r\varSigma _{H,{\underline{H}}_r}^{'}. \end{aligned}$$

Consequently the least squares estimator of $\varSigma _{u_r}$ can be rewritten in the form:

$$\begin{aligned} {\hat{\varSigma }}_{{\hat{u}}_r}={\hat{\varSigma }}_{{\hat{H}}} -\underline{{\hat{\varPhi }}}_r{\hat{\varSigma }}^{'}_{{\hat{H}}, \underline{{\hat{H}}}_r}, \end{aligned}$$

(72)

where

$$\begin{aligned} {\hat{\varSigma }}_{{\hat{H}}}=\frac{1}{n} \sum _{t=1}^n{\hat{H}}_t{\hat{H}}_t^{'}. \end{aligned}$$

(73)

Similar arguments combined with (8) yield

$$\begin{aligned} \varSigma _u ={\mathbb {E}}\left[ u_t u_t^{'}\right]&={\mathbb {E}}\left[ u_t H^{'}_t(\theta _0)\right] \\&={\mathbb {E}}\left[ H_t(\theta _0)H_t^{'}(\theta _0)\right] -\sum _{k=1}^{r}\varPhi _k{\mathbb {E}}\left[ H_{t-k}(\theta _0)H^{'}_t(\theta _0) \right] -\sum _{k=r+1}^{\infty }\varPhi _k{\mathbb {E}} \left[ H_{t-k}(\theta _0)H^{'}_t(\theta _0)\right] \\&=\varSigma _{H}-{\underline{\varPhi }}^{*}_r\varSigma ^{'}_{H,{\underline{H}}_r} -\sum _{k=r+1}^{\infty }\varPhi _k{\mathbb {E}}\left[ H_{t-k}(\theta _0)H^{'}_t(\theta _0)\right] . \end{aligned}$$

By (72) we obtain

$$\begin{aligned} \left\| {\hat{\varSigma }}_{{\hat{u}}_r}-\varSigma _u\right\|&=\left\| {\hat{\varSigma }}_{{\hat{H}}} -\underline{{\hat{\varPhi }}}_r{\hat{\varSigma }}^{'}_{{\hat{H}}, \underline{{\hat{H}}}_r}-\varSigma _{H} +{\underline{\varPhi }}^{*}_r\varSigma ^{'}_{H,{\underline{H}}_r} +\sum _{k=r+1}^{\infty }\varPhi _k{\mathbb {E}}\left[ H_{t-k} (\theta _0)H^{'}_t(\theta _0)\right] \right\| \nonumber \\&=\left\| {\hat{\varSigma }}_{{\hat{H}}}-\varSigma _{H} -\left( \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}^{*}_r\right) {\hat{\varSigma }}^{'}_{{\hat{H}},\underline{{\hat{H}}}_r} -{\underline{\varPhi }}^{*}_r\left( {\hat{\varSigma }}^{'}_{{\hat{H}}, \underline{{\hat{H}}}_r}-\varSigma ^{'}_{H,{\underline{H}}_r}\right) \right. \nonumber \\&\left. +\sum _{k=r+1}^{\infty }\varPhi _k{\mathbb {E}}\left[ H_{t-k} (\theta _0)H^{'}_t(\theta _0)\right] \right\| \nonumber \\&\le \left\| {\hat{\varSigma }}_{{\hat{H}}}-\varSigma _{H}\right\| +\left\| \left( \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}^{*}_r \right) \left( {\hat{\varSigma }}^{'}_{{\hat{H}},\underline{{\hat{H}}}_r} -\varSigma ^{'}_{H,{\underline{H}}_r}\right) \right\| +\left\| \left( \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}^{*}_r\right) \varSigma ^{'}_{H,{\underline{H}}_r} \right\| \nonumber \\&\quad +\left\| {\underline{\varPhi }}^{*}_r\left( {\hat{\varSigma }}^{'}_{{\hat{H}},\underline{{\hat{H}}}_r} -\varSigma ^{'}_{H,{\underline{H}}_r}\right) \right\| +\left\| \sum _{k=r+1}^{\infty }\varPhi _k{\mathbb {E}}\left[ H_{t-k}(\theta _0)H^{'}_t(\theta _0)\right] \right\| . \end{aligned}$$

(74)

From Lemma 18 and under Assumptions of Theorem 5 we deduce that

$$\begin{aligned} \left\| \sum _{k=r+1}^{\infty }\varPhi _k{\mathbb {E}}\left[ H_{t-k} (\theta _0)H^{'}_t(\theta _0)\right] \right\|&\le \sum _{k=r+1}^{\infty } \left\| \varPhi _k\right\| \left\| {\mathbb {E}}\left[ H_{t-k} (\theta _0)H^{'}_t(\theta _0)\right] \right\| \\&\le K \sum _{k=r+1}^{\infty }\frac{1}{k^2}\xrightarrow [n\rightarrow \infty ]{} 0. \end{aligned}$$

Observe also that

$$\begin{aligned} \left\| {\underline{\varPhi }}^{*}_r\right\| ^2\le \sum _{k\ge 1}\mathrm {Tr}\left( \varPhi _k\varPhi _k^{'}\right) <\infty . \end{aligned}$$

Therefore the convergence ${\hat{\varSigma }}_{{\hat{u}}_r}$ to $\varSigma _u$ will be a consequence of the four following properties:

• $\Vert {\hat{\varSigma }}_{{\hat{H}}}-\varSigma _{H}\Vert =\mathrm {o}_{{\mathbb {P}}}(1)$,

• ${\mathbb {P}}-\lim _{n\rightarrow \infty }\Vert \underline{{\hat{\varPhi }}}_r -{\underline{\varPhi }}^{*}_r\Vert =0$,

• ${\mathbb {P}}-\lim _{n\rightarrow \infty }\Vert {\hat{\varSigma }}^{'}_{{\hat{H}}, \underline{{\hat{H}}}_r}-\varSigma ^{'}_{H,{\underline{H}}_r} \Vert =0$ and

• $\Vert \varSigma ^{'}_{H,{\underline{H}}_r} \Vert =\mathrm {O}(1)$.

The above properties will be proved thanks to several lemmas that are stated and proved hereafter. This ends the proof of Theorem 5. For this, consider the following lemmas:

Lemma 20

Under the assumptions of Theorem 5, we have

$$\begin{aligned} \sup _{r\ge 1}\max \left\{ \left\| \varSigma _{H,{\underline{H}}_r}\right\| , \left\| \varSigma _{{\underline{H}}_r}\right\| ,\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| \right\} <\infty . \end{aligned}$$

Proof

See Lemma 1 in the supplementary material of Boubacar Mainassara et al. (2012). $\square$

Lemma 21

Under the assumptions of Theorem 5 there exists a finite positive constant K such that, for $1\le r_1,r_2\le r$ and $1 \le m_1,m_2\le p+q+1$ we have

$$\begin{aligned} \sup _{t\in {\mathbb {Z}}}\sum _{h=-\infty }^{\infty }\left| \mathrm {Cov} \left\{ H_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2}(\theta _0),H_{t-r_1-h,m_1} (\theta _0)H_{t-r_2-h,m_2}(\theta _0) \right\} \right| <K. \end{aligned}$$

Proof

We denote in the sequel by $\overset{\mathbf{. }}{\lambda }_{j,k}$ the coefficient $\overset{\mathbf{. }}{\lambda }_{j,k}(\theta _0)$ defined in (30).

Using the fact that the process $(H_t(\theta _0))_{t\in {\mathbb {Z}}}$ is centered and taking into consideration the strict stationarity of $(\epsilon _t)_{t\in {\mathbb {Z}}}$ we obtain that for any $t\in {\mathbb {Z}}$

$$\begin{aligned} \sum _{h=-\infty }^{\infty }\Big |&\mathrm {Cov}\big ( H_{t-r_1,m_1} (\theta _0)H_{t-r_2,m_2}(\theta _0) ,H_{t-r_1-h,m_1}(\theta _0)H_{t-r_2-h,m_2} (\theta _0) \big ) \Big |\\&= \sum _{h=-\infty }^{\infty }\Big |{\mathbb {E}}\left[ H_{t-r_1,m_1} (\theta _0)H_{t-r_2,m_2}(\theta _0)H_{t-r_1-h,m_1}(\theta _0)H_{t-r_2-h,m_2} (\theta _0)\right] \\&\quad -{\mathbb {E}}\left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2} (\theta _0)\right] {\mathbb {E}}\left[ H_{t-r_1-h,m_1}(\theta _0)H_{t-r_2-h,m_2} (\theta _0)\right] \Big |\\&\le \sum _{h=-\infty }^{\infty } \Big |\mathrm {cum}\big ( H_{t-r_1,m_1} (\theta _0),H_{t-r_2,m_2}(\theta _0),H_{t-r_1-h,m_1}(\theta _0),H_{t-r_2-h,m_2} (\theta _0)\big ) \Big |\\&\quad +\sum _{h=-\infty }^{\infty }\left| {\mathbb {E}} \left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_1-h,m_1}(\theta _0)\right] \right| \left| {\mathbb {E}}\left[ H_{t-r_2,m_2}(\theta _0)H_{t-r_2-h,m_2} (\theta _0)\right] \right| \\&\quad +\sum _{h=-\infty }^{\infty }\left| {\mathbb {E}} \left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_2-h,m_2}(\theta _0)\right] \right| \left| {\mathbb {E}}\left[ H_{t-r_2,m_2}(\theta _0)H_{t-r_1-h,m_1} (\theta _0)\right] \right| \\&\le \sum _{h=-\infty }^{\infty }\sum _{i_1,j_1,k_1,\ell _1\ge 1} \left| \overset{\mathbf{. }}{\lambda }_{i_1,m_1}\overset{\mathbf{. }}{\lambda }_{j_1,m_2}\overset{\mathbf{. }}{\lambda }_{k_1,m_1} \overset{\mathbf{. }}{\lambda }_{\ell _1,m_2}\right| \\&\quad \left| \mathrm {cum}\right. \left. \left( \epsilon _{0}\epsilon _{-i_1},\epsilon _{r_1-r_2}\epsilon _{r_1-r_2-j_1}, \epsilon _{-h}\epsilon _{-h-k_1},\epsilon _{r_1-r_2-h}\epsilon _{r_1-r_2-h -\ell _1}\right) \right| \\&\quad +T_{r1,m_1,r_2,m_2}^{(1)}+T_{r1,m_1,r_2,m_2}^{(2)}, \end{aligned}$$

where

$$\begin{aligned} T_{r1,m_1,r_2,m_2}^{(1)}&=\sum _{h=-\infty }^{\infty }\left| {\mathbb {E}}\left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_1-h,m_1}(\theta _0)\right] \right| \left| {\mathbb {E}}\left[ H_{t-r_2,m_2}(\theta _0)H_{t-r_2-h,m_2} (\theta _0)\right] \right| \end{aligned}$$

and

$$\begin{aligned} T_{r1,m_1,r_2,m_2}^{(2)}&=\sum _{h=-\infty }^{\infty }\left| {\mathbb {E}}\left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_2-h,m_2}(\theta _0)\right] \right| \left| {\mathbb {E}}\left[ H_{t-r_2,m_2}(\theta _0)H_{t-r_1-h,m_1} (\theta _0)\right] \right| . \end{aligned}$$

Thanks to Lemma 14 one may use the product theorem for the joint cumulants ( Brillinger (1981)) as in the proof of Lemma A.3. in Shao (2011) in order to obtain that

$$\begin{aligned}&\sum _{h=-\infty }^{\infty }\sum _{i_1,j_1,k_1,\ell _1\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{i_1,m_1}\overset{\mathbf{. }}{\lambda }_{j_1,m_2}\overset{\mathbf{. }}{\lambda }_{k_1,m_1} \overset{\mathbf{. }}{\lambda }_{\ell _1,m_2}\right| \\&\quad \left| \mathrm {cum} \left( \epsilon _{0}\epsilon _{-i_1},\epsilon _{r_1-r_2}\epsilon _{r_1-r_2-j_1}, \epsilon _{-h}\epsilon _{-h-k_1},\epsilon _{r_1-r_2-h}\epsilon _{r_1-r_2-h -\ell _1}\right) \right| \\&<\infty \end{aligned}$$

where we have used the absolute summability of the k-th $(k=2,\dots ,8)$ cumulants assumed in (A4’) with $\tau =8$.

Observe now that

$$\begin{aligned} T_{r1,m_1,r_2,m_2}^{(1)}&=\sum _{h=-\infty }^{\infty }\left| {\mathbb {E}} \left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_1-h,m_1}(\theta _0)\right] \right| \left| {\mathbb {E}}\left[ H_{t-r_2,m_2}(\theta _0)H_{t-r_2-h,m_2} (\theta _0)\right] \right| \\&\le \sup _{h\in {\mathbb {Z}}}\left| {\mathbb {E}}\left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_1-h,m_1}(\theta _0)\right] \right| \sum _{h=-\infty }^{\infty }\left| {\mathbb {E}}\left[ H_{t-r_2,m_2} (\theta _0)H_{t-r_2-h,m_2}(\theta _0)\right] \right| . \end{aligned}$$

For any $h\in {\mathbb {Z}}$, from (29) we have

$$\begin{aligned} \left| {\mathbb {E}}\left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_1-h,m_1} (\theta _0)\right] \right|&\le \sum _{i,j\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{i,m_1}\right| \left| \overset{\mathbf{. }}{\lambda }_{j,m_1}\right| \left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-i},\epsilon _{-h}, \epsilon _{-h-j}\right) \right| \\&\quad +\sum _{i,j\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{i,m_1} \right| \left| \overset{\mathbf{. }}{\lambda }_{j,m_1}\right| \Bigg \{ \left| {\mathbb {E}}\left[ \epsilon _0\epsilon _{-i}\right] {\mathbb {E}} \left[ \epsilon _{-h}\epsilon _{-h-j}\right] \right| \\&\quad +\left| {\mathbb {E}}\left[ \epsilon _0 \epsilon _{-h}\right] {\mathbb {E}}\left[ \epsilon _{-i}\epsilon _{-h-j} \right] \right| +\left| {\mathbb {E}}\left[ \epsilon _0\epsilon _{-h-j} \right] {\mathbb {E}}\left[ \epsilon _{-i}\epsilon _{-h}\right] \right| \Bigg \} \\&\quad \le \sum _{i,j\ge 1}\left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-i},\epsilon _{-h}, \epsilon _{-h-j}\right) \right| +\sigma _{\epsilon }^4\sum _{i\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{i,m_1}\right| ^2 . \end{aligned}$$

Under Assumption (A4’) with $\tau =4$ and in view of Lemma 14 we may write that

$$\begin{aligned} \sup _{h\in {\mathbb {Z}}}\left| {\mathbb {E}}\left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_1-h,m_1}(\theta _0)\right] \right|&\le \sup _{h\in {\mathbb {Z}}}\sum _{i,j\ge 1}\left| \mathrm {cum}\left( \epsilon _0,\epsilon _{-i},\epsilon _{-h}, \epsilon _{-h-j}\right) \right| \\&\quad +\sigma _{\epsilon }^4\sum _{i\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{i,m_1}\right| ^2 <\infty . \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \sum _{h=-\infty }^{\infty }\left| {\mathbb {E}}\left[ H_{t-r_2,m_2} (\theta _0)H_{t-r_2-h,m_2}(\theta _0)\right] \right|&\le \sum _{h=-\infty }^{\infty }\sum _{i,j\ge 1}\left| \mathrm {cum} \left( \epsilon _0,\epsilon _{-i},\epsilon _{-h},\epsilon _{-h-j}\right) \right| \\&+\sigma _{\epsilon }^4\sum _{i\ge 1}\left| \overset{\mathbf{. }}{\lambda }_{i,m_1}\right| ^2\\&<\infty . \end{aligned}$$

Consequently $T_{r1,m_1,r_2,m_2}^{(1)}<\infty$ and the same approach yields that $T_{r1,m_1,r_2,m_2}^{(2)}<\infty$ and the lemma is proved. $\square$

Let ${\hat{\varSigma }}_{{\underline{H}}_r}$, ${\hat{\varSigma }}_{H}$ and ${\hat{\varSigma }}_{H,{\underline{H}}_r}$ be the matrices obtained by replacing ${\hat{H}}_t$ by $H_t(\theta _0)$ in ${\hat{\varSigma }}_{\underline{{\hat{H}}}_r}$, ${\hat{\varSigma }}_{{\hat{H}}}$ and ${\hat{\varSigma }}_{{\hat{H}},\underline{{\hat{H}}}_r}$.

Lemma 22

Under the assumptions of Theorem 5, $\sqrt{r}\Vert {\hat{\varSigma }}_{{\underline{H}}_r}-\varSigma _{{\underline{H}}_r}\Vert$, $\sqrt{r}\Vert {\hat{\varSigma }}_{H,{\underline{H}}_r} -\varSigma _{H,{\underline{H}}_r}\Vert$ and $\sqrt{r}\Vert {\hat{\varSigma }}_{H}-\varSigma _{H}\Vert$ tend to zero in probability as $n\rightarrow \infty$ when $r=\mathrm {o}(n^{1/3})$.

Proof

For $1\le m_1,m_2 \le p+q+1$ and $1\le r_1,r_2 \le r$, the $( \lbrace (r_1-1)(p+q+1)+m_1\rbrace ,\lbrace (r_2-1)(p+q+1)+m_2\rbrace )-$th element of ${\hat{\varSigma }}_{{\underline{H}}_r}$ is given by:

$$\begin{aligned} \frac{1}{n}\sum _{t=1}^nH_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2}(\theta _0). \end{aligned}$$

For all $\beta >0$, we use (68) and we obtain

$$\begin{aligned} {\mathbb {P}}\left( \sqrt{r}\left\| {\hat{\varSigma }}_{{\underline{H}}_r} -\varSigma _{{\underline{H}}_r}\right\| \ge \beta \right)&\le \frac{r}{\beta ^2}{\mathbb {E}}\left\| {\hat{\varSigma }}_{{\underline{H}}_r} -\varSigma _{{\underline{H}}_r}\right\| ^2\\&\le \frac{r}{\beta ^2}{\mathbb {E}}\left\| \frac{1}{n}\sum _{t=1}^n {\underline{H}}_{r,t}{\underline{H}}_{r,t}^{'}-{\mathbb {E}} \left[ {\underline{H}}_{r,t}{\underline{H}}_{r,t}^{'}\right] \right\| ^2\\&\le \frac{r}{\beta ^2}\sum _{r_1=1}^r\sum _{r_2=1}^r\sum _{m_1=1}^{p+q+1} \sum _{m_2=1}^{p+q+1}{\mathbb {E}}\Bigg (\frac{1}{n}\sum _{t=1}^nH_{t-r_1,m_1} (\theta _0)H_{t-r_2,m_2}(\theta _0) \\&\quad -{\mathbb {E}}\left[ H_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2}(\theta _0)\right] \Bigg )^2. \end{aligned}$$

The stationarity of the process $\left( H_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2}(\theta _0)\right) _{t\in {\mathbb {Z}}}$ and Lemma 21 imply

$$\begin{aligned} {\mathbb {P}}&\left( \sqrt{r}\left\| {\hat{\varSigma }}_{{\underline{H}}_r} -\varSigma _{{\underline{H}}_r}\right\| \ge \beta \right) \\ {}&\le \frac{r}{\beta ^2}\sum _{r_1=1}^r\sum _{r_2=1}^r \sum _{m_1=1}^{p+q+1}\sum _{m_2=1}^{p+q+1}\mathrm {Var} \left( \frac{1}{n}\sum _{t=1}^nH_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2} (\theta _0) \right) \\&\le \frac{r}{(n\beta )^2}\sum _{r_1=1}^r\sum _{r_2=1}^r \sum _{m_1=1}^{p+q+1}\sum _{m_2=1}^{p+q+1}\sum _{t=1}^n\\&\sum _{s=1}^n\mathrm {Cov}\left( H_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2} (\theta _0),H_{s-r_1,m_1}(\theta _0)H_{s-r_2,m_2}(\theta _0) \right) \\&\le \frac{r}{(n\beta )^2}\sum _{r_1=1}^r\sum _{r_2=1}^r \sum _{m_1=1}^{p+q+1}\sum _{m_2=1}^{p+q+1}\sum _{h=1-n}^{n-1}(n-|h|)\\&\mathrm {Cov}\left( H_{t-r_1,m_1}(\theta _0)H_{t-r_2,m_2}(\theta _0), H_{t-h-r_1,m_1}(\theta _0)H_{t-h-r_2,m_2}(\theta _0) \right) \\&\le \frac{r}{n\beta ^2}\sum _{r_1=1}^r\sum _{r_2=1}^r \sum _{m_1=1}^{p+q+1}\sum _{m_2=1}^{p+q+1}\sup _{t\in {\mathbb {Z}}} \sum _{h=-\infty }^{\infty }\\&\left| \mathrm {Cov}\left( H_{t-r_1,m_1}(\theta _0) H_{t-r_2,m_2}(\theta _0),H_{t-h-r_1,m_1}(\theta _0)H_{t-h-r_2,m_2}(\theta _0) \right) \right| \\&\le \frac{C(p+q+1)^2r^3}{n\beta ^2}. \end{aligned}$$

Consequently we have

$$\begin{aligned} {\mathbb {E}}\left[ r\left\| {\hat{\varSigma }}_{H}-\varSigma _{H}\right\| ^2\right]&\le {\mathbb {E}}\left[ r\left\| {\hat{\varSigma }}_{H,{\underline{H}}_r}-\varSigma _{H,{\underline{H}}_r} \right\| ^2\right] \\&\le {\mathbb {E}}\left[ r\left\| {\hat{\varSigma }}_{{\underline{H}}_r} -\varSigma _{{\underline{H}}_r}\right\| ^2\right] \\&\le \frac{C(p+q+1)^2r^3}{n}\xrightarrow [n\rightarrow \infty ]{} 0 \end{aligned}$$

when $r=\mathrm {o}(n^{1/3})$. The conclusion follows. $\square$

We show in the following lemma that the previous lemma remains valid when we replace $H_t(\theta _0)$ by ${\hat{H}}_t$.

Lemma 23

Under the assumptions of Theorem 5, $\sqrt{r}\Vert {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}-\varSigma _{{\underline{H}}_r}\Vert$, $\sqrt{r}\Vert {\hat{\varSigma }}_{{\hat{H}},\underline{{\hat{H}}}_r}-\varSigma _{H,{\underline{H}}_r}\Vert$ and $\sqrt{r}\Vert {\hat{\varSigma }}_{{\hat{H}}}-\varSigma _{H}\Vert$ tend to zero in probability as $n\rightarrow \infty$ when $r=\mathrm {o}(n^{(1-2(d_0-d_1))/5})$.

Proof

As mentioned in the end of the proof of the previous lemma, we only have to deal with the term $\sqrt{r}\Vert {\hat{\varSigma }}_{\underline{{\hat{H}}}_r} -\varSigma _{{\underline{H}}_r}\Vert$.

We denote ${\hat{\varSigma }}_{{\underline{H}}_{r,n}}$ the matrix obtained by replacing ${\tilde{\epsilon }}_t({\hat{\theta }}_n)$ by $\epsilon _t({\hat{\theta }}_n)$ in ${\hat{\varSigma }}_{\underline{{\hat{H}}}_{r}}$. We have

$$\begin{aligned} \sqrt{r}\left\| {\hat{\varSigma }}_{\underline{{\hat{H}}}_r} -\varSigma _{{\underline{H}}_r}\right\|&\le \sqrt{r}\left\| {\hat{\varSigma }}_{\underline{{\hat{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\| +\sqrt{r}\left\| {\hat{\varSigma }}_{{\underline{H}}_{r,n}}-{\hat{\varSigma }}_{{\underline{H}}_r} \right\| +\sqrt{r}\left\| {\hat{\varSigma }}_{{\underline{H}}_r} -\varSigma _{{\underline{H}}_r}\right\| . \end{aligned}$$

By Lemma 22, the term $\sqrt{r}\Vert {\hat{\varSigma }}_{{\underline{H}}_r}-\varSigma _{{\underline{H}}_r}\Vert$ converges in probability. The lemma will be proved as soon as we show that

$$\begin{aligned} \sqrt{r}\left\| {\hat{\varSigma }}_{\underline{{\hat{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\|&= \mathrm {o}_{{\mathbb {P}}}(1)\quad \text { and } \ \end{aligned}$$

(75)

$$\begin{aligned} \sqrt{r}\left\| {\hat{\varSigma }}_{{\underline{H}}_{r,n}} -{\hat{\varSigma }}_{{\underline{H}}_r}\right\|&=\mathrm {o}_{{\mathbb {P}}}(1), \end{aligned}$$

(76)

when $r=\mathrm {o}(n^{(1-2(d_0-d_1))/5})$. This is done in two separate steps.

Step 1: proof of (75). For all $\beta >0$, we have

$$\begin{aligned} {\mathbb {P}}\left( \sqrt{r}\left\| {\hat{\varSigma }}_{\hat{{\underline{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\| \ge \beta \right)&\le \frac{\sqrt{r}}{\beta }{\mathbb {E}}\left\| {\hat{\varSigma }}_{\hat{{\underline{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\| \\&\le \frac{\sqrt{r}}{\beta }{\mathbb {E}}\left\| \frac{1}{n}\sum _{t=1}^n \hat{{\underline{H}}}_{r,t}\hat{{\underline{H}}}_{r,t}^{'} -\frac{1}{n}\sum _{t=1}^n {\underline{H}}_{r,t}^{(n)} {\underline{H}}_{r,t}^{(n) '} \right\| \\&\le \frac{K\sqrt{r}}{\beta }\sum _{r_1=1}^r\sum _{r_2=1}^r\sum _{m_1=1}^{p+q+1} \sum _{m_2=1}^{p+q+1}{\mathbb {E}}\left| \frac{1}{n}\sum _{t=1}^n {\hat{H}}_{t-r_1,m_1}{\hat{H}}_{t-r_2,m_2}\right. \\&\quad \left. -\frac{1}{n} \sum _{t=1}^nH^{(n)}_{t-r_1,m_1}H_{t-r_2,m_2}^{(n)}\right| , \end{aligned}$$

where

$$\begin{aligned} H_{t,m}^{(n)}=2\epsilon _t({\hat{\theta }}_n)\frac{\partial }{\partial \theta _m}\epsilon _t({\hat{\theta }}_n)\quad \text { and }\quad {\underline{H}}_{r,t}^{(n)}=\left( H_{t-1}^{(n) '},\dots ,H_{t-r}^{(n) '} \right) ^{'} \ . \end{aligned}$$

It is follow that

$$\begin{aligned} {\mathbb {P}}\left( \sqrt{r}\left\| {\hat{\varSigma }}_{\hat{{\underline{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\| \ge \beta \right) \nonumber \\&\le \frac{4K\sqrt{r}}{n\beta }\sum _{r_1=1}^r\sum _{r_2=1}^r \sum _{m_1=1}^{p+q+1}\sum _{m_2=1}^{p+q+1} \nonumber \\&\quad {\mathbb {E}}\Bigg |\sum _{t=1}^n{\tilde{\epsilon }}_{t-r_1} ({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}} {\tilde{\epsilon }}_{t-r_1}({\hat{\theta }}_n){\tilde{\epsilon }}_{t-r_2} ({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}} {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n) \nonumber \\&\quad -\epsilon _{t-r_1}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1}({\hat{\theta }}_n)\epsilon _{t-r_2} ({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2} ({\hat{\theta }}_n)\Bigg |. \end{aligned}$$

(77)

Observe now that

$$\begin{aligned}&{\tilde{\epsilon }}_{t-r_1}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}}{\tilde{\epsilon }}_{t-r_1}({\hat{\theta }}_n) {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}}{\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)-\epsilon _{t-r_1} ({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} ({\hat{\theta }}_n)\epsilon _{t-r_2}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}({\hat{\theta }}_n)\\&\quad =\left( {\tilde{\epsilon }}_{t-r_1}({\hat{\theta }}_n) -\epsilon _{t-r_1}({\hat{\theta }}_n)\right) \frac{\partial }{\partial \theta _{m_1}}{\tilde{\epsilon }}_{t-r_1}({\hat{\theta }}_n) {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}}{\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)\\&\quad +\epsilon _{t-r_1}({\hat{\theta }}_n) \left( \frac{\partial }{\partial \theta _{m_1}}{\tilde{\epsilon }}_{t-r_1} ({\hat{\theta }}_n)-\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} ({\hat{\theta }}_n)\right) {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n) \frac{\partial }{\partial \theta _{m_2}}{\tilde{\epsilon }}_{t-r_2} ({\hat{\theta }}_n)\\&\quad +\epsilon _{t-r_1}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1}({\hat{\theta }}_n) \left( {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)-\epsilon _{t-r_2} ({\hat{\theta }}_n)\right) \frac{\partial }{\partial \theta _{m_2}} {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)\\&\quad +\epsilon _{t-r_1}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1}({\hat{\theta }}_n)\epsilon _{t-r_2} ({\hat{\theta }}_n)\left( \frac{\partial }{\partial \theta _{m_2}} {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)-\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}({\hat{\theta }}_n)\right) . \end{aligned}$$

We replace the above identity in (77) and we obtain by Hölder’s inequality that

$$\begin{aligned} {\mathbb {P}}\left( \sqrt{r}\left\| {\hat{\varSigma }}_{\hat{{\underline{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\| \ge \beta \right)&\le \frac{4K\sqrt{r}}{n\beta }\sum _{r_1=1}^r\sum _{r_2=1}^r\sum _{m_1=1}^{p+q+1} \sum _{m_2=1}^{p+q+1}\left( T_{n,1}+T_{n,2}+T_{n,3}+T_{n,4}\right) \end{aligned}$$

(78)

where

$$\begin{aligned} T_{n,1}&=\sum _{t=1}^n\left\| {\tilde{\epsilon }}_{t-r_1}({\hat{\theta }}_n) -\epsilon _{t-r_1}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2} \left\| \frac{\partial }{\partial \theta _{m_1}}{\tilde{\epsilon }}_{t-r_1} ({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6}\left\| {\tilde{\epsilon }}_{t-r_2} ({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6}\left\| \frac{\partial }{\partial \theta _{m_2}}{\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6},\\ T_{n,2}&=\sum _{t=1}^n\left\| \epsilon _{t-r_1}({\hat{\theta }}_n) \right\| _{{\mathbb {L}}^6}\left\| \frac{\partial }{\partial \theta _{m_1}} {\tilde{\epsilon }}_{t-r_1}({\hat{\theta }}_n)-\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2} \left\| {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6} \left\| \frac{\partial }{\partial \theta _{m_2}}{\tilde{\epsilon }}_{t-r_2} ({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6},\\ T_{n,3}&=\sum _{t=1}^n\left\| \epsilon _{t-r_1}({\hat{\theta }}_n) \right\| _{{\mathbb {L}}^6}\left\| \frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6} \left\| {\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)-\epsilon _{t-r_2} ({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2}\left\| \frac{\partial }{\partial \theta _{m_2}}{\tilde{\epsilon }}_{t-r_2}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6}, \\ T_{n,4}&=\sum _{t=1}^n\left\| \epsilon _{t-r_1}({\hat{\theta }}_n) \right\| _{{\mathbb {L}}^6}\left\| \frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6}\left\| \epsilon _{t-r_2}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^6}\left\| \frac{\partial }{\partial \theta _{m_2}}{\tilde{\epsilon }}_{t-r_2} ({\hat{\theta }}_n)-\frac{\partial }{\partial \theta _{m_2}} \epsilon _{t-r_2}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2}. \end{aligned}$$

For all $\theta \in \varTheta _{\delta }$ and $t\in {\mathbb {Z}}$, in view of (29) and Remark 12, we have

$$\begin{aligned} \left\| {\tilde{\epsilon }}_{t}({\hat{\theta }}_n)-\epsilon _{t} ({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2}&=\left( {\mathbb {E}} \left[ \left\{ \sum _{j\ge 0}\left( \lambda ^{t}_j({\hat{\theta }}_n) -\lambda _j({\hat{\theta }}_n)\right) \epsilon _{t-j}\right\} ^2\right] \right) ^{1/2}\\&\le \sup _{\theta \in \varTheta _{\delta }}\left( {\mathbb {E}}\left[ \left\{ \sum _{j\ge 0}\left( \lambda ^{t}_j({\theta }) -\lambda _j({\theta })\right) \epsilon _{t-j}\right\} ^2\right] \right) ^{1/2}\\&\le \sigma _{\epsilon }\sup _{\theta \in \varTheta _{\delta }}\left\| \lambda (\theta ) -\lambda ^{t}(\theta )\right\| _{\ell ^2}\\&\le K\frac{1}{t^{1/2+(d_1-d_0)}}. \end{aligned}$$

It is not difficult to prove that ${\tilde{\epsilon }}_t(\theta )$ and $\partial {\tilde{\epsilon }}_t(\theta )/\partial \theta$ belong to ${\mathbb {L}}^6$. The fact that $\epsilon _t(\theta )$ and $\partial \epsilon _t(\theta )/\partial \theta$ have moment of order 6 can be proved using the same method than in Lemma 21 using the absolute summability of the k-th $(k=2,\dots ,8)$ cumulants assumed in (A4’) with $\tau =8$. We deduce that

$$\begin{aligned} T_{n,1}\le K\sum _{t=1}^n\left\| {\tilde{\epsilon }}_{t-r_1} ({\hat{\theta }}_n)-\epsilon _{t-r_1}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2}&\le K \sum _{t=1-r}^0\left\| \epsilon _{t}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2} +K\sum _{t=1}^{n}\left\| {\tilde{\epsilon }}_{t}({\hat{\theta }}_n) -\epsilon _{t}({\hat{\theta }}_n)\right\| _{{\mathbb {L}}^2}\\&\le K\left( r+\sum _{t=1}^{n}\frac{1}{t^{1/2+(d_1-d_0)}}\right) . \end{aligned}$$

Then we obtain

$$\begin{aligned} T_{n,1}&\le K\left( r+ n^{1/2-(d_1-d_0)}\right) . \end{aligned}$$

(79)

The same calculations hold for the terms $T_{n,2}$, $T_{n,3}$ and $T_{n,4}$. Thus

$$\begin{aligned} T_{n,1}+T_{n,2}+T_{n,3}+T_{n,4}\le K\left( r+ n^{1/2-(d_1-d_0)}\right) \end{aligned}$$

(80)

and reporting this estimation in (78) implies that

$$\begin{aligned} {\mathbb {P}}\left( \sqrt{r}\left\| {\hat{\varSigma }}_{\hat{{\underline{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\| \ge \beta \right)&\le \frac{Kr^{5/2}(p+q+1)^2}{n\beta }\left( r+n^{1/2-(d_1-d_0)}\right) \\&\le K\left( \frac{r^{7/2}}{n}+\frac{r^{5/2}}{n^{1/2+(d_1-d_0)}}\right) . \end{aligned}$$

Since $2/7>(1+2(d_1-d_0))/5$, the sequence $\sqrt{r}\left\| {\hat{\varSigma }}_{\hat{{\underline{H}}}_r} -{\hat{\varSigma }}_{{\underline{H}}_{r,n}}\right\|$ converges in probability to 0 as $n\rightarrow \infty$ when $r=r(n)=\mathrm {o}(n^{(1-2(d_0-d_1))/5})$.

Step 2: proof of (76). First we follow the same approach than in the previous step. We have

$$\begin{aligned} \left\| {\hat{\varSigma }}_{{\underline{H}}_{r,n}} -{\hat{\varSigma }}_{{\underline{H}}_r}\right\| ^2&=\left\| \frac{1}{n}\sum _{t=1}^n {\underline{H}}_{r,t}^{(n)} {\underline{H}}_{r,t}^{(n) '}-\frac{1}{n}\sum _{t=1}^n{\underline{H}}_{r,t} {\underline{H}}_{r,t}^{'} \right\| ^2\\&\le \sum _{r_1=1}^r\sum _{r_2=1}^r\sum _{m_1=1}^{p+q+1} \sum _{m_2=1}^{p+q+1}\left( \frac{1}{n}\sum _{t=1}^nH^{(n)}_{t-r_1,m_1} H_{t-r_2,m_2}^{(n)}-\frac{1}{n}\sum _{t=1}^nH_{t-r_1,m_1}H_{t-r_2,m_2} \right) ^2\\&\le 16\sum _{r_1=1}^r\sum _{r_2=1}^r\sum _{m_1=1}^{p+q+1} \sum _{m_2=1}^{p+q+1}\left( \frac{1}{n}\sum _{t=1}^n\epsilon _{t-r_1} ({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} ({\hat{\theta }}_n)\epsilon _{t-r_2}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}({\hat{\theta }}_n)\right. \\&\quad \left. -\epsilon _{t-r_1}(\theta _0)\frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}(\theta _0)\epsilon _{t-r_2}(\theta _0)\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}(\theta _0)\right) ^2. \end{aligned}$$

Since

$$\begin{aligned}&\epsilon _{t-r_1}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1}({\hat{\theta }}_n)\epsilon _{t-r_2} ({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2} ({\hat{\theta }}_n)-\epsilon _{t-r_1}(\theta _0)\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1}(\theta _0)\epsilon _{t-r_2}(\theta _0) \\&\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}(\theta _0)\\&\quad =\left( \epsilon _{t-r_1}({\hat{\theta }}_n)-\epsilon _{t-r_1}(\theta _0) \right) \frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} ({\hat{\theta }}_n)\epsilon _{t-r_2}({\hat{\theta }}_n) \frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}({\hat{\theta }}_n)\\&\quad +\epsilon _{t-r_1}(\theta _0)\left( \frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}({\hat{\theta }}_n)-\frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}(\theta _0)\right) \epsilon _{t-r_2}({\hat{\theta }}_n) \frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}({\hat{\theta }}_n)\\&\quad +\epsilon _{t-r_1}(\theta _0)\frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}(\theta _0)\left( \epsilon _{t-r_2}({\hat{\theta }}_n) -\epsilon _{t-r_2}(\theta _0)\right) \frac{\partial }{\partial \theta _{m_2}} \epsilon _{t-r_2}({\hat{\theta }}_n)\\&\quad +\epsilon _{t-r_1}(\theta _0)\frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}(\theta _0)\epsilon _{t-r_2}(\theta _0) \left( \frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2} ({\hat{\theta }}_n)-\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2} (\theta _0)\right) , \end{aligned}$$

one has

$$\begin{aligned} \left\| {\hat{\varSigma }}_{{\underline{H}}_{r,n}} -{\hat{\varSigma }}_{{\underline{H}}_r}\right\| ^2&\le 16\sum _{r_1=1}^r\sum _{r_2=1}^r\sum _{m_1=1}^{p+q+1}\sum _{m_2=1}^{p+q+1} \left( U_{n,1}+U_{n,2}+U_{n,3}+U_{n,4}\right) ^2 \end{aligned}$$

(81)

where

$$\begin{aligned} U_{n,1}&=\frac{1}{n}\sum _{t=1}^n\left| \epsilon _{t-r_1} ({\hat{\theta }}_n)-\epsilon _{t-r_1}(\theta _0)\right| \left| \frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} ({\hat{\theta }}_n)\right| \left| \epsilon _{t-r_2}({\hat{\theta }}_n) \right| \left| \frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2} ({\hat{\theta }}_n)\right| ,\\ U_{n,2}&=\frac{1}{n}\sum _{t=1}^n\left| \epsilon _{t-r_1} (\theta _0)\right| \left| \frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}({\hat{\theta }}_n)-\frac{\partial }{\partial \theta _{m_1}} \epsilon _{t-r_1}(\theta _0)\right| \left| \epsilon _{t-r_2}({\hat{\theta }}_n) \right| \left| \frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2} ({\hat{\theta }}_n)\right| ,\\ U_{n,3}&=\frac{1}{n}\sum _{t=1}^n\left| \epsilon _{t-r_1}(\theta _0) \right| \left| \frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} (\theta _0)\right| \left| \epsilon _{t-r_2}({\hat{\theta }}_n)-\epsilon _{t-r_2} (\theta _0)\right| \left| \frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2} ({\hat{\theta }}_n)\right| \\ U_{n,4}&=\frac{1}{n}\sum _{t=1}^n\left| \epsilon _{t-r_1}(\theta _0) \right| \left| \frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} (\theta _0)\right| \left| \epsilon _{t-r_2}(\theta _0)\right| \left| \frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}({\hat{\theta }}_n) -\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}(\theta _0)\right| . \end{aligned}$$

Taylor expansions around $\theta _0$ yield that there exists ${\underline{\theta }}$ and ${\overline{\theta }}$ between ${\hat{\theta }}_n$ and $\theta _0$ such that

$$\begin{aligned} \left| \epsilon _{t}({\hat{\theta }}_n)-\epsilon _{t}(\theta _0)\right|&\le w_t\left\| {\hat{\theta }}_n-\theta _0\right\| \end{aligned}$$

and

$$\begin{aligned} \left| \frac{\partial }{\partial \theta _{m}}\epsilon _{t}({\hat{\theta }}_n) -\frac{\partial }{\partial \theta _{m}}\epsilon _{t}(\theta _0)\right|&\le q_t\left\| {\hat{\theta }}_n-\theta _0\right\| \end{aligned}$$

with $w_t=\left\| {\partial \epsilon _t({\underline{\theta }})}/{\partial \theta ^{'}}\right\|$ and $q_t=\left\| {\partial ^2\epsilon _t({\overline{\theta }})}/{\partial \theta ^{'}\partial \theta _m}\right\|$. Using the fact that

$$\begin{aligned} {\mathbb {E}}\left| w_{t-r_1}\frac{\partial }{\partial \theta _{m_1}}\epsilon _{t-r_1} ({\hat{\theta }}_n)\epsilon _{t-r_2}({\hat{\theta }}_n)\frac{\partial }{\partial \theta _{m_2}}\epsilon _{t-r_2}({\hat{\theta }}_n)\right| <\infty \end{aligned}$$

and that $(\sqrt{n}( {\hat{\theta }}_n-\theta _0))_n$ is a tight sequence (which implies that $\Vert {\hat{\theta }}_n-\theta _0\Vert =\mathrm {O}_{{\mathbb {P}}}(1/\sqrt{n})$), we deduce that

$$\begin{aligned} U_{n,1}=\mathrm {O}_{{\mathbb {P}}}\left( \frac{1}{\sqrt{n}}\right) . \end{aligned}$$

The same arguments are valid for $U_{n,2}$, $U_{n,3}$ and $U_{n,4}$. Consequently $U_{n,1}+U_{n,2}+U_{n,3}+U_{n,4}=\mathrm {O}_{{\mathbb {P}}}(1/\sqrt{n})$ and (81) yields

$$\begin{aligned} \left\| {\hat{\varSigma }}_{{\underline{H}}_{r,n}} -{\hat{\varSigma }}_{{\underline{H}}_r}\right\| ^2&=\mathrm {O}_{{\mathbb {P}}}\left( \frac{r^2}{n}\right) . \end{aligned}$$

When $r=\mathrm {o}(n^{1/3})$ we finally obtain $\sqrt{r}\Vert {\hat{\varSigma }}_{{\underline{H}}_{r,n}} -{\hat{\varSigma }}_{{\underline{H}}_r}\Vert =\mathrm {o}_{{\mathbb {P}}}(1)$.

$\square$

Lemma 24

Under the assumptions of Theorem 5, we have

$$\begin{aligned} \sqrt{r}\left\| {\underline{\varPhi }}_r^{*}-{\underline{\varPhi }}_r\right\| =\mathrm {o}_{{\mathbb {P}}}(1)\quad \text { as }r\rightarrow \infty . \end{aligned}$$

Proof

Recall that by (8) and (71) we have

$$\begin{aligned} H_t(\theta _0)={\underline{\varPhi }}_r{\underline{H}}_{r,t}+u_{r,t} ={\underline{\varPhi }}_r^{*}{\underline{H}}_{r,t}+\sum _{k=r+1}^{\infty } \varPhi _kH_{t-k}(\theta _0)+u_t:={\underline{\varPhi }}_r^{*}{\underline{H}}_{r,t} +u_{r,t}^{*}. \end{aligned}$$

By the orthogonality conditions in (8) and (71), one has

$$\begin{aligned}&\varSigma _{u_r^{*},{\underline{H}}_r}:={\mathbb {E}}\left[ u_{r,t}^{*}{\underline{H}}_{r,t}^{'}\right] ={\mathbb {E}}\left[ \left( H_t(\theta _0)-{\underline{\varPhi }}_r^{*}{\underline{H}}_{r,t} \right) {\underline{H}}_{r,t}^{'}\right] \\&={\mathbb {E}}\left[ \left( {\underline{\varPhi }}_r{\underline{H}}_{r,t} +u_{r,t}-{\underline{\varPhi }}_r^{*}{\underline{H}}_{r,t} \right) {\underline{H}}_{r,t}^{'}\right] =\left( {\underline{\varPhi }}_r- {\underline{\varPhi }}_r^{*}\right) \varSigma _{{\underline{H}}_r} , \end{aligned}$$

and consequently

$$\begin{aligned} {\underline{\varPhi }}_r^{*}-{\underline{\varPhi }}_r=-\varSigma _{u_r^{*}, {\underline{H}}_r}\varSigma _{{\underline{H}}_r}^{-1}. \end{aligned}$$

(82)

Using Lemmas 20 and 21, (82) implies that

$$\begin{aligned}&{\mathbb {P}}\left( \sqrt{r}\left\| {\underline{\varPhi }}_r^{*} -{\underline{\varPhi }}_r\right\| \ge \beta \right) \le \frac{\sqrt{r}}{\beta } \left\| \varSigma _{u_r^{*},{\underline{H}}_r}\right\| \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| \\&\le \frac{K\sqrt{r}}{\beta }\left\| {\mathbb {E}}\left[ \left( \sum _{k \ge r+1}\varPhi _kH_{t-k}(\theta _0)+u_t\right) {\underline{H}}_{r,t}^{'} \right] \right\| \\&\le \frac{K\sqrt{r}}{\beta } \sum _{k\ge r+1}\left\| \varPhi _k\right\| \left\| {\mathbb {E}}\left[ H_{t-k}(\theta _0){\underline{H}}_{r,t}^{'} \right] \right\| \\&\le \frac{K\sqrt{r}}{\beta } \sum _{\ell \ge 1}\left\| \varPhi _{\ell +r} \right\| \left\| {\mathbb {E}}\left[ H_{t-\ell -r}(\theta _0)\left( H^{'}_{t-1} (\theta _0),\dots , H^{'}_{t-r}(\theta _0)\right) \right] \right\| \\&\le \frac{K\sqrt{r}}{\beta } \sum _{\ell \ge 1}\left\| \varPhi _{\ell +r} \right\| \left( \sum _{j=1}^{p+q+1}\sum _{k=1}^{p+q+1}\sum _{r_1=1}^{r} \left| {\mathbb {E}}\left[ H_{t-r-\ell ,j}(\theta _0) H_{t-r_1,k}(\theta _0) \right] \right| ^2\right) ^{1/2}\\&\le \frac{K\sqrt{r}}{\beta } \sum _{\ell \ge 1}\left\| \varPhi _{\ell +r} \right\| \left( \sum _{j=1}^{p+q+1}\sum _{k=1}^{p+q+1}\sum _{r_1=1}^{r} {\mathbb {E}}\left[ H_{t-r-\ell ,j}^2(\theta _0) \right] {\mathbb {E}}\left[ H_{t-r_1,k}^2(\theta _0) \right] \right) ^{1/2}\\&\le \frac{K(p+q+1)r}{\beta } \sum _{\ell \ge 1}\left\| \varPhi _{\ell +r}\right\| . \end{aligned}$$

Under Assumptions of Theorem 5, $r\sum _{\ell \ge 1}\left\| \varPhi _{\ell +r}\right\| =\mathrm {o}(1)$ as $r\rightarrow \infty$. The proof of the lemma follows. $\square$

Lemma 25

Under the assumptions of Theorem 5, we have

$$\begin{aligned} \sqrt{r}\left\| {\hat{\varSigma }}^{-1}_{\underline{{\hat{H}}}_r} -\varSigma ^{-1}_{{\underline{H}}_r}\right\| =\mathrm {o}_{{\mathbb {P}}}(1) \end{aligned}$$

as $n\rightarrow \infty$ when $r=\mathrm {o}(n^{(1-2(d_0-d_1))/5})$ and $r\rightarrow \infty$.

Proof

We have

$$\begin{aligned} \left\| {\hat{\varSigma }}^{-1}_{\underline{{\hat{H}}}_r} -\varSigma ^{-1}_{{\underline{H}}_r}\right\|&\le \left( \left\| {\hat{\varSigma }}^{-1}_{\underline{{\hat{H}}}_r} -\varSigma ^{-1}_{{\underline{H}}_r}\right\| +\left\| \varSigma ^{-1}_{{\underline{H}}_r}\right\| \right) \left\| \varSigma _{{\underline{H}}_r}- {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| , \end{aligned}$$

and by induction we obtain

$$\begin{aligned} \left\| {\hat{\varSigma }}^{-1}_{\underline{{\hat{H}}}_r} -\varSigma ^{-1}_{{\underline{H}}_r}\right\| \le \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| \sum _{k=1}^{\infty } \left\| \varSigma _{{\underline{H}}_r}- {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| ^k\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| ^k. \end{aligned}$$

We have

$$\begin{aligned}&{\mathbb {P}}\Big ( \sqrt{r}\big \Vert {\hat{\varSigma }}^{-1}_{\underline{{\hat{H}}}_r} - \varSigma ^{-1}_{{\underline{H}}_r}\big \Vert>\beta \Big ) \\&\le {\mathbb {P}}\left( \sqrt{r}\left\| \varSigma _{{\underline{H}}_r}^{-1} \right\| \sum _{k=1}^{\infty }\left\| \varSigma _{{\underline{H}}_r} - {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| ^k\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| ^k>\beta \right) \\&\le {\mathbb {P}}\left( \sqrt{r}\left\| \varSigma _{{\underline{H}}_r}^{-1} \right\| \sum _{k=1}^{\infty }\left\| \varSigma _{{\underline{H}}_r} - {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| ^k\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| ^k>\beta \text { and } \left\| \varSigma _{{\underline{H}}_r}- {\hat{\varSigma }}_{\underline{{\hat{H}}}_r} \right\| \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| <1\right) \\&+{\mathbb {P}}\left( \sqrt{r}\left\| \varSigma _{{\underline{H}}_r}^{-1} \right\| \sum _{k=1}^{\infty }\left\| \varSigma _{{\underline{H}}_r} - {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| ^k\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| ^k>\beta \text { and } \left\| \varSigma _{{\underline{H}}_r}- {\hat{\varSigma }}_{\underline{{\hat{H}}}_r} \right\| \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| \ge 1\right) \\&\le {\mathbb {P}}\left( \sqrt{r}\frac{\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| ^2\left\| \varSigma _{{\underline{H}}_r} - {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| }{1-\left\| \varSigma _{{\underline{H}}_r}- {\hat{\varSigma }}_{\underline{{\hat{H}}}_r} \right\| \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| }>\beta \right) +{\mathbb {P}}\left( \sqrt{r} \left\| \varSigma _{{\underline{H}}_r} - {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| \ge 1\right) \\&\le {\mathbb {P}}\left( \sqrt{r}\left\| \varSigma _{{\underline{H}}_r} - {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| >\frac{\beta }{\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| ^2+\beta r^{-1/2}\left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| }\right) \\&+{\mathbb {P}}\left( \sqrt{r} \left\| \varSigma _{{\underline{H}}_r}- {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}\right\| \ge \left\| \varSigma _{{\underline{H}}_r}^{-1}\right\| ^{-1}\right) . \end{aligned}$$

Lemmas 20 and 23 imply the result. $\square$

Lemma 26

Under the assumptions of Theorem 5, we have

$$\begin{aligned} \sqrt{r}\left\| \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}_r\right\| =\mathrm {o}_{{\mathbb {P}}}(1) \quad \text { as }r\rightarrow \infty \text { and }r=\mathrm {o}(n^{(1-2(d_0-d_1))/5}). \end{aligned}$$

Proof

Lemmas 20 and 25 yield

$$\begin{aligned} \left\| {\hat{\varSigma }}^{-1}_{\underline{{\hat{H}}}_r}\right\| \le \left\| {\hat{\varSigma }}^{-1}_{\underline{{\hat{H}}}_r} -\varSigma ^{-1}_{{\underline{H}}_r}\right\| +\left\| \varSigma ^{-1}_{{\underline{H}}_r}\right\| =\mathrm {O}_{{\mathbb {P}}}(1). \end{aligned}$$

(83)

By (71), we have

$$\begin{aligned} 0&={\mathbb {E}}\left[ u_{r,t}{\underline{H}}_{r,t}^{'} \right] ={\mathbb {E}}\left[ \left( H_t(\theta _0) -{\underline{\varPhi }}_r{\underline{H}}_{r,t} \right) {\underline{H}}_{r,t}^{'} \right] =\varSigma _{H,{\underline{H}}_r}-{\underline{\varPhi }}_r \varSigma _{{\underline{H}}_r}, \end{aligned}$$

and so we have ${\underline{\varPhi }}_r=\varSigma _{H,{\underline{H}}_r} \varSigma _{{\underline{H}}_r}^{-1}$. Lemmas 20,  23,  25 and (83) imply

$$\begin{aligned} \sqrt{r}\left\| \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}_r\right\|&=\sqrt{r}\left\| {\hat{\varSigma }}_{{\hat{H}},\underline{{\hat{H}}}_r} {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}^{-1}-\varSigma _{H,{\underline{H}}_r} \varSigma _{{\underline{H}}_r}^{-1}\right\| \\&=\sqrt{r}\left\| \left( {\hat{\varSigma }}_{{\hat{H}}, \underline{{\hat{H}}}_r}-\varSigma _{H,{\underline{H}}_r}\right) {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}^{-1}+\varSigma _{H,{\underline{H}}_r} \left( {\hat{\varSigma }}_{\underline{{\hat{H}}}_r}^{-1} -\varSigma _{{\underline{H}}_r}^{-1}\right) \right\| \\&=\mathrm {o}_{{\mathbb {P}}}(1) , \end{aligned}$$

and the lemma is proved. $\square$

6.5 Proof of Theorem 5

Since by Lemma 23 we have $\Vert {\hat{\varSigma }}_{{\hat{H}}}-\varSigma _{H}\Vert =\mathrm {o}_{{\mathbb {P}}}(r^{-1/2})=\mathrm {o}_{{\mathbb {P}}}(1)$ and $\Vert {\hat{\varSigma }}_{{\hat{H}},\underline{{\hat{H}}}_r}-\varSigma _{H,{\underline{H}}_r} \Vert =\mathrm {o}_{{\mathbb {P}}}(r^{-1/2})=\mathrm {o}_{{\mathbb {P}}}(1)$, and by Lemma 24$\Vert \underline{{\hat{\varPhi }}}_r-{\underline{\varPhi }}^{*}_r\Vert =\mathrm {o}_{{\mathbb {P}}}(r^{-1/2})=\mathrm {o}_{{\mathbb {P}}}(1)$, Theorem 5 is then proved.

6.6 Invertibility of the normalization matrix $P_{p+q+1,n}$

The following proofs are quite technical and are adaptations of the arguments used in Boubacar Maïnassara and Saussereau (2018).

To prove Proposition 6, we need to introduce the following notation.

We denote $S_t$ the vector of ${\mathbb {R}}^{p+q+1}$ defined by

$$\begin{aligned} S_t=\sum _{j=1}^tU_j=\sum _{j=1}^t-2J^{-1}H_j=-2J^{-1}\sum _{j=1}^t \epsilon _j\frac{\partial }{\partial \theta }\epsilon _j(\theta _0) \end{aligned}$$

and $S_t(i)$ its $i-$th component. We have

$$\begin{aligned} S_{t-1}(i)&=S_t(i)-U_t(i). \end{aligned}$$

(84)

If the matrix $P_{p+q+1,n}$ is not invertible, there exists some real constants $d_1,\dots ,d_{p+q+1}$ not all equal to zero, such that ${\mathbf {d}}^{'}P_{p+q+1,n}{\mathbf {d}}=0$, where ${\mathbf {d}}=(d_1,\dots ,d_{p+q+1})^{'}$. Thus we may write that $\sum _{i=1}^{p+q+1}\sum _{j=1}^{p+q+1}d_jP_{p+q+1,n}(j,i)d_i=0$ or equivalently

$$\begin{aligned} \frac{1}{n^2}\sum _{t=1}^n\sum _{i=1}^{p+q+1}\sum _{j=1}^{p+q+1}d_j \left( \sum _{k=1}^t( U_k(j)-{\bar{U}}_n(j))\right) \left( \sum _{k=1}^t( U_k(i)-{\bar{U}}_n(i))\right) d_i&=0 . \end{aligned}$$

Then

$$\begin{aligned} \sum _{t=1}^n\left( \sum _{i=1}^{p+q+1}d_i\left( \sum _{k=1}^t( U_k(i)-{\bar{U}}_n(i))\right) \right) ^2&=0, \end{aligned}$$

which implies that for all $t\ge 1$

$$\begin{aligned} \sum _{i=1}^{p+q+1}d_i\left( \sum _{k=1}^t( U_k(i)-{\bar{U}}_n(i))\right) =\sum _{i=1}^{p+q+1}d_i\left( S_t(i) -\frac{t}{n}S_n(i)\right)&=0. \end{aligned}$$

So we have

$$\begin{aligned} \frac{1}{t}\sum _{i=1}^{p+q+1}d_iS_t(i)&=\sum _{i=1}^{p+q+1}d_i \left( \frac{1}{n}S_n(i)\right) . \end{aligned}$$

(85)

We apply the ergodic theorem and we use the orthogonality of $\epsilon _t$ and $(\partial /\partial \theta )\epsilon _t(\theta _0)$ in order to obtain that

$$\begin{aligned} \sum _{i=1}^{p+q+1}d_i\left( \frac{1}{n}\sum _{k=1}^nU_k(i)\right) \xrightarrow [n\rightarrow \infty ]{\text {a.s.}} \sum _{i=1}^{p+q+1}d_i{\mathbb {E}}\left[ U_k(i) \right] =-2\sum _{i,j=1}^{p+q+1}d_iJ^{-1}(i,j){\mathbb {E}} \left[ \epsilon _k\frac{\partial \epsilon _k}{\partial \theta _j} \right] =0 \ . \end{aligned}$$

Reporting this convergence in (85) implies that $\sum _{i=1}^{p+q+1}d_iS_t(i)=0$ a.s. for all $t\ge 1$. By (84), we deduce that

$$\begin{aligned} \sum _{i=1}^{p+q+1}d_iU_t(i)=-2\sum _{i=1}^{p+q+1}d_i \sum _{j=1}^{p+q+1}J^{-1}(i,j)\left( \epsilon _t\frac{\partial \epsilon _t}{\partial \theta _j} \right) =0, \ \ \ \mathrm { a.s.} \end{aligned}$$

Thanks to Assumption (A5), $(\epsilon _t)_{t\in {\mathbb {Z}}}$ has a positive density in some neighborhood of zero and then $\epsilon _t\ne 0$ almost-surely. So we would have ${\mathbf {d}}^{'}J^{-1}\frac{\partial \epsilon _t}{\partial \theta }=0$ a.s. Now we can follow the same arguments that we developed in the proof of the invertibility of J (see Proof of Lemma 16 and more precisely (56)) and this leads us to a contradiction. We deduce that the matrix $P_{p+q+1,n}$ is non singular.

6.7 Proof of Theorem 7

The arguments follows the one in Boubacar Maïnassara and Saussereau (2018) in a simpler context.

Recall that the Skorohod space ${\mathbb {D}}^{\ell }[ 0{,}1]$ is the set of ${\mathbb {R}}^{\ell }-$valued functions on [0, 1] which are right-continuous and has left limits everywhere. It is endowed with the Skorohod topology and the weak convergence on ${\mathbb {D}}^{\ell } [ 0{,}1]$ is mentioned by $\xrightarrow []{{\mathbb {D}}^{\ell }}$. The integer part of x will be denoted by $\lfloor x\rfloor$.

The goal at first is to show that there exists a lower triangular matrix T with nonnegative diagonal entries such that

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{t=1}^{\lfloor nr\rfloor }U_t \xrightarrow [n\rightarrow \infty ]{{\mathbb {D}}^{p+q+1}} \ (TT^{'})^{1/2} B_{p+q+1}(r), \end{aligned}$$

(86)

where $(B_{p+q+1}(r))_{r\ge 0}$ is a $(p+q+1)-$dimensional standard Brownian motion. Using (29), $U_t$ can be rewritten as

$$\begin{aligned} U_t=\left( -2\left\{ \sum _{i=1}^{\infty }\overset{\mathbf{. }}{\lambda }_{i,1}\left( \theta _0\right) \epsilon _t\epsilon _{t-i},\dots ,\sum _{i=1}^{\infty } \overset{\mathbf{. }}{\lambda }_{i,p+q+1}\left( \theta _0\right) \epsilon _t\epsilon _{t-i}\right\} J^{-1 '} \right) ^{'}. \end{aligned}$$

The non-correlation between $\epsilon _t$’s implies that the process $(U_t)_{t\in {\mathbb {Z}}}$ is centered. In order to apply the functional central limit theorem for strongly mixing process, we need to identify the asymptotic covariance matrix in the classical central limit theorem for the sequence $(U_t)_{t\in {\mathbb {Z}}}$. It is proved in Theorem 2 that

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{t=1}^nU_t\xrightarrow [n\rightarrow \infty ]{\text {in law}} {\mathcal {N}}\left( 0,\varOmega =:2\pi f_U(0)\right) , \end{aligned}$$

where $f_U(0)$ is the spectral density of the stationary process $(U_t)_{t\in {\mathbb {Z}}}$ evaluated at frequency 0. The existence of the matrix $\varOmega$ has already been discussed (see the proofs of Lemmas 16 and 18 ).

Since the matrix $\varOmega$ is symmetric positive definite, it can be factorized as $\varOmega =TT^{'}$ where the $(p+q+1)\times (p+q+1)$ lower triangular matrix T has real positive diagonal entries. Therefore, we have

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{t=1}^n(TT^{'})^{-1/2}F_t \xrightarrow [n\rightarrow \infty ]{\text {in law}} \ {\mathcal {N}}\left( 0,I_{p+q+1}\right) , \end{aligned}$$

where $I_{p+q+1}$ is the identity matrix of order $p+q+1$.

As in the proof of the asymptotic normality of $(\sqrt{n}({\hat{\theta }}_n-\theta _0))_{n\ge 1}$, the distribution of $n^{-1/2}\sum _{t=1}^nU_t$ when n tends to infinity is obtained by introducing the random vector $U_t^k$ defined for any positive integer k by

$$\begin{aligned} U_t^k=\left( -2\left\{ \sum _{i=1}^{k}\overset{\mathbf{. }}{\lambda }_{i,1}\left( \theta _0\right) \epsilon _t\epsilon _{t-i},\dots ,\sum _{i=1}^{k}\overset{\mathbf{. }}{\lambda }_{i,p+q+1}\left( \theta _0\right) \epsilon _t\epsilon _{t-i}\right\} J^{-1 '} \right) ^{'}. \end{aligned}$$

Since $U_t^k$ depends on a finite number of values of the noise process $(\epsilon _t)_{t\in {\mathbb {Z}}}$, it also satisfies a mixing property (see Theorem 14.1 in Davidson (1994), p. 210). The central limit theorem for strongly mixing process of Herrndorf (1984) shows that its asymptotic distribution is normal with zero mean and variance matrix $\varOmega _k$ that converges when k tends to infinity to $\varOmega$ (see the proof of Lemma 19):

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{t=1}^nU_t^k \xrightarrow [n\rightarrow \infty ]{\text {in law}} \ {\mathcal {N}}\left( 0,\varOmega _k\right) . \end{aligned}$$

The above arguments also apply to matrix $\varOmega _k$ with some matrix $T_k$ which is defined analogously as T. Consequently, we obtain

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{t=1}^n(T_kT_k^{'})^{-1/2}U_t^k \xrightarrow [n\rightarrow \infty ]{\text {in law}} {\mathcal {N}}(0,I_{p+q+1}). \end{aligned}$$

Now we are able to apply the functional central limit theorem for strongly mixing process of Herrndorf (1984) and we obtain that

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{t=1}^{\lfloor nr\rfloor }(T_kT_k^{'})^{-1/2}U_t^k \xrightarrow [n\rightarrow \infty ]{{\mathbb {D}}^{p+q+1}} B_{p+q+1}(r). \end{aligned}$$

Since

$$\begin{aligned} (TT^{'})^{-1/2}U_t^k=\left( (TT^{'})^{-1/2}-(T_kT_k^{'})^{-1/2}\right) U_t^k +(T_kT_k^{'})^{-1/2}U_t^k, \end{aligned}$$

we may use the same approach as in the proof of Lemma 19 in order to prove that $n^{-1/2}\sum _{t=1}^{n}((TT^{'})^{-1/2}-(T_kT_k^{'})^{-1/2})U_t^k$ converges in distribution to 0. Consequently we obtain that

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{t=1}^{\lfloor nr\rfloor }(TT^{'})^{-1/2}U_t^k \xrightarrow [n\rightarrow \infty ]{{\mathbb {D}}^{p+q+1}}B_{p+q+1}(r). \end{aligned}$$

In order to conclude that (86) is true, it remains to observe that uniformly with respect to n it holds that

$$\begin{aligned} {\tilde{Y}}_n^k(r):=\frac{1}{\sqrt{n}}\sum _{t=1}^{\lfloor nr\rfloor }(TT^{'})^{-1/2}{\tilde{Z}}_t^k \xrightarrow [n\rightarrow \infty ]{{\mathbb {D}}^{p+q+1}} \ 0, \end{aligned}$$

(87)

where

$$\begin{aligned} {\tilde{Z}}_t^k=\left( -2\left\{ \sum _{i=k+1}^{\infty }\overset{\mathbf{. }}{\lambda }_{i,1} \left( \theta _0\right) \epsilon _t\epsilon _{t-i},\dots ,\sum _{i=k+1}^{\infty }\overset{\mathbf{. }}{\lambda }_{i,p+q+1}\left( \theta _0\right) \epsilon _t\epsilon _{t-i}\right\} J^{-1 '} \right) ^{'}. \end{aligned}$$

By (67), one has

$$\begin{aligned} \sup _{n}\mathrm {Var}\left( \frac{1}{\sqrt{n}}\sum _{t=1}^{n}{\tilde{Z}}_t^k \right) \xrightarrow [n\rightarrow \infty ]{} 0 \end{aligned}$$

and since $\lfloor nr\rfloor \le n$,

$$\begin{aligned} \sup _{0\le r\le 1}\sup _n\left\{ \left\| {\tilde{Y}}_n^k(r)\right\| \right\} \xrightarrow [n\rightarrow \infty ]{} \ 0. \end{aligned}$$

Thus (87) is true and the proof of (86) is achieved.

By (86) we deduce that

$$\begin{aligned}&\frac{1}{\sqrt{n}}\left( \sum _{j=1}^{\lfloor nr \rfloor } (U_j-{\bar{U}}_n)\right) \xrightarrow [n\rightarrow \infty ]{{\mathbb {D}}^{p+q+1}}(TT^{'})^{1/2} \left( B_{p+q+1}(r)-rB_{p+q+1}(1)\right) . \end{aligned}$$

(88)

One remarks that the continuous mapping theorem on the Skorohod space yields

$$\begin{aligned} P_{p+q+1,n}&\xrightarrow [n\rightarrow \infty ]{\text {in law}} (TT^{'})^{1/2}\left[ \int _0^1\left\{ B_{p+q+1}(r) -rB_{p+q+1}(1)\right\} \left\{ B_{p+q+1}(r)-rB_{p+q+1}(1) \right\} ^{'}\mathrm {dr}\right] \\&\quad (TT^{'})^{1/2}\\ =&\quad (TT^{'})^{1/2}V_{p+q+1}(TT^{'})^{1/2}. \end{aligned}$$

Using (86), (88) and the continuous mapping theorem on the Skorohod space, one finally obtains

$$\begin{aligned}&n \big ({\hat{\theta }}_{n}-\theta _0\big )^{'}P_{p+q+1,n}^{-1} \big ({\hat{\theta }}_{n}-\theta _0\big ) \\&\quad \xrightarrow [n\rightarrow \infty ]{{\mathbb {D}}^{p+q+1}} \left\{ (TT^{'})^{1/2}B_{p+q+1}(1)\right\} ^{'}\left\{ (TT^{'})^{1/2}V_{p+q+1}(TT^{'})^{1/2}\right\} ^{-1} \left\{ (TT^{'})^{1/2}B_{p+q+1}(1)\right\} \\&\quad =B_{p+q+1}^{'}(1)V_{p+q+1}^{-1}B_{p+q+1}(1):={\mathcal {U}}_{p+q+1}. \end{aligned}$$

The proof of Theorem 7 is then complete.

6.8 Proof of Theorem 8

In view of (14) and (17), we write ${{\hat{P}}}_{p+q+1,n}=P_{p+q+1,n}+ Q_{p+q+1,n}$ where

$$\begin{aligned} Q_{p+q+1,n}&= \big ( J(\theta _0)^{-1}-{{{\hat{J}}}}_n^{-1} \big )\frac{1}{n^2}\sum _{t=1}^n\left( \sum _{j=1}^t( H_j-{\frac{1}{n} \sum _{k=1}^n H_k})\right) \left( \sum _{t=1}^n( H_j-{\frac{1}{n} \sum _{k=1}^n H_k})\right) ^{'} \\&\quad + {{{\hat{J}}}}_n^{-1} \frac{1}{n^2} \sum _{t=1}^n \Bigg \{ \left( \sum _{j=1}^t( H_j-{\frac{1}{n} \sum _{k=1}^n H_k})\right) \left( \sum _{t=1}^n( H_j-{\frac{1}{n} \sum _{k=1}^n H_k})\right) ^{'} \\&\quad - \left( \sum _{j=1}^t( {{\hat{H}}}_j-{\frac{1}{n} \sum _{k=1}^n {{\hat{H}}}_k})\right) \left( \sum _{t=1}^n( {{\hat{H}}}_j-{\frac{1}{n} \sum _{k=1}^n {{\hat{H}}}_k})\right) ^{'} \Bigg \} . \end{aligned}$$

Using the same approach as in Lemma 17, ${\hat{J}}_n$ converges in probability to J. Thus we deduce that the first term in the right hand side of the above equation tends to zero in probability.

The second term is a sum composed of the following terms

$$\begin{aligned} q_{s,t}^{i,j,k,l} = \epsilon _s(\theta _0)\epsilon _{t}(\theta _0)\frac{\partial {\epsilon }_{s}(\theta _0)}{\partial \theta _i} \frac{\partial \epsilon _{t}(\theta _0)}{\partial \theta _{j}} - {\tilde{\epsilon }}_s({{\hat{\theta }}}_n){\tilde{\epsilon }}_{t} ({{\hat{\theta }}}_n)\frac{\partial {\tilde{\epsilon }}_{s}({{\hat{\theta }}}_n)}{\partial \theta _k} \frac{\partial {\tilde{\epsilon }}_{t}({{\hat{\theta }}}_n)}{\partial \theta _l}. \end{aligned}$$

Using similar arguments done before (see for example the use of Taylor’s expansion in Sect. 6.4, we have $q_{s,t}^{i,j,k,l} = \mathrm {o}_{{\mathbb {P}}}(1)$ as n goes to infinity and thus $Q_{p+q+1,n}= \mathrm {o}_{{\mathbb {P}}}(1)$. So one may find a matrix $Q^*_{p+q+1,n}$ that tends to the null matrix in probability and such that

$$\begin{aligned} n\, \left( {\hat{\theta }}_{n}-\theta _0\right) ^{'}{{\hat{P}}}_{p+q+1,n}^{-1} \left( {\hat{\theta }}_{n}-\theta _0\right)&= n\, \left( {\hat{\theta }}_{n}-\theta _0\right) ^{'} \left( P_{p+q+1,n}+ Q_{p+q+1,n}\right) ^{-1}\left( {\hat{\theta }}_{n}-\theta _0\right) \\&= n\, \left( {\hat{\theta }}_{n}-\theta _0\right) ^{'}P_{p+q+1,n}^{-1} \left( {\hat{\theta }}_{n}-\theta _0\right) \\ {}&\qquad + n\, \left( {\hat{\theta }}_{n}-\theta _0\right) ^{'}Q_{p+q+1,n}^*\left( {\hat{\theta }}_{n}-\theta _0\right) . \end{aligned}$$

Thanks to the arguments developed in the proof of Theorem 7, $n ({\hat{\theta }}_{n}-\theta _0)^{'} P_{p+q+1,n}^{-1}({\hat{\theta }}_{n}-\theta _0)$ converges in distribution. So $n ({\hat{\theta }}_{n}-\theta _0)^{'}Q_{p+q+1,n}^*({\hat{\theta }}_{n}-\theta _0)$ tends to zero in distribution, hence in probability. Then $n ({\hat{\theta }}_{n}-\theta _0)^{'}{{\hat{P}}}_{p+q+1,n}^{-1}({\hat{\theta }}_{n}-\theta _0)$ and $n ({\hat{\theta }}_{n}-\theta _0)^{'} P_{p+q+1,n}^{-1}({\hat{\theta }}_{n}-\theta _0)$ have the same limit in distribution and the result is proved.