1 Introduction

Civil, structural and mechanical engineering students will, at some point in their undergraduate studies, come across the name Euler (1707–1783). It tends to crop up in a number of places: in mathematics, fluids and solid mechanics. For an extensive but by no means exhaustive list of mathematical terms, theorems, functions and formulae bearing his name, see Burckhardt (1983). But most likely, for an engineer, it is the Euler Buckling Formula (EBF) for which his name is best remembered. This formula, one of the first examples of the application of the calculus to engineering design, gives the critical value of the compressive end force required to buckle a long slender straight rod. The EBF first appeared in 1744, in an Appendix to a treatise on the calculus of variations: Treatise on Isoperimeters. The appendix has the title De Curvis Elasticis, which freely translates “Concerning Elastic Curves”. This work has drawn the attention of a variety of scientists, engineers and mathematicians. Structural engineers are interested in EBF for its application to design. Dynamicists are curious in EBF as (perhaps the first) example of the analysis of a phenomenon known as a bifurcation (from the Latin furca, to fork). Their curiosity may also be aroused by the mathematical analogy between the problem of the elastica and the dynamics of a pendulum. Historians of mathematics are interested in the analysis which leads to EBF—for its association with the early foundations of the calculus of variations and its connections with the development of elliptic functions. We can also mention that the problem of determining the configuration of an elastic line under terminal forces, i.e. the problem of the elastica, illuminates some important principles which underlie mechanics and scientific methodology. In particular it sheds light on the search for unifying principles of mechanics and its connection with experimental work. It follows that the problem of the elastica presents enormous potential as an interesting historical case study and can be viewed from a number of perspectives. Taken together, they also provide the student with a rare overview of mechanics. Our aim is to examine these themes from a unified perspective.

Anyone who bothers to open the pages of De Curvis Elasticis will quickly realise that the derivation of EBF is not its central theme, but is encountered serendipitously. Euler discovered it whilst engaged in the task of solving the equations of equilibrium which describe the post-buckled configurations of elastica. Figure 1 shows a photograph of a length of nickel–titanium alloy wire which has buckled from its natural stress-free straight configuration by displacing the ends towards each other. But the variety of possible configurations includes rods bent into a “U”, a ring, a figure-of-eight, and a knot. Euler proposes a classification scheme for these shapes some of which are shown in Fig. 2. Before we continue, we note that the post-buckled rod is not simply a mathematical curiosity, but finds wide applications in engineering and the physical sciences: in deep-sea cable and pipe-laying operations (Coyne 1990), tangling in cable–buoy systems (Berteaux 1976), mechanism design (Sönmez 2006), the textile industry (Hearle 2000), and in many areas of biology, notably as a model for the writhing of DNA (Balaeff et al. 2006; Travers and Thompson 2004).

Fig. 1
figure 1

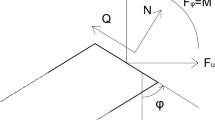
Photograph of a bent nickel–titanium alloy rod clamped at its ends. The rod is 1 mm diameter and 350 mm long. A coordinate system is superimposed, also showing the loading from an end force P and a bending moment M. This configuration of elastica falls within Species 2 of Euler’s classification scheme

Full size image
Fig. 2
figure 2

Euler’s drawings of some of the nine “species” of elastica. These are defined in terms of the ratio \(\frac{c^2}{a^2}\), a load parameter. Not shown here are Species 1 which is the straight rod with \(\frac{c}{a}=0\), Species 2 with \(0\, < \frac{c^2}{a^2}\, < 1\), (see Fig. 1), Species 3 with a = c which is the “rectangular elastica”, and Species 9 which is a ring given by \(\frac{c}{a}=\infty\) and where the end force vanishes

Full size image

We have talked enough about applications and it is time to return to one of our central themes: the connection between the theory of the elastica and experiments on “physical rods”. This connection can be portrayed as the link between the branch of engineering analysis known as “strength of materials” and the branch of mathematics referred to as elasticity theory. The former composes a body of knowledge assembled from a variety of sources, one of which is elasticity theory, but others may be empirical. The latter, however, is a self contained rational theory. The development of elasticity theory was largely achieved by finding the solution to some simple problems, at first isolated, but later linked together to construct the general theory from which more complicated problems could be solved. Euler’s De Curvis Elasticis is one of these simple problems. We pause here to contemplate Love’s remark in the Historical Introduction to his classical work The Mathematical Theory of Elasticity:

Most of the men by whose researches it [elasticity theory] has been founded and shaped have been more interested in Natural Philosophy than in material progress, in trying to understand the world than in trying to make it more comfortable. (Love 1927, p. 30)

This remark captures the motivation of Euler and that of his contemporaries as they grappled with the task of unraveling the elastica problem. Euler was not, however, completely removed from the affairs of the real world: when he stumbled across EBF, he suggests that it “can be put to use especially for wooden columns, since they are subject to bending”. The extent of its applicability to real-world engineering is an issue which has concerned engineers since Euler’s time to the present:

The story of the column formula is a unique one with a continuity over a 239 period. It needs retelling from time to time to revive attention to some lesser known facets and to bring it up to date. At the same time it must be recognised that it concerns an unattainable limit of “perfection” that does not exist for columns in real structures. (Johnson 1983)

The connection between EBF and the design of real structures is a manifestation of two different methods of scientific discovery—one mathematical, the other experimental. We introduce Euler’s studies of the phenomenon of buckling in Sect. 2. Then in Sect. 3 we take a look at the experimental approach to the problem. In Sect. 4 we draw attention to some of the debates, which preceded Euler’s work, on how scientific enquiry should proceed. By tracing the problem of the elastic curve back to the study of curves in general, in Sects. 5 and 6, Euler’s De Curvis Elasticis is set firmly within the context of the mathematical approach, the one so succinctly depicted by Love. The mathematical model also has a curious static–dynamic analogy, which is the focus of Sect. 7. The significance of Euler’s De Curvis Elasticis, as a corner stone in elasticity theory, and the quest for unifying principles of mechanics is alluded to in Sect. 8. We remark here that some of these topics may well lie on the margins of an undergraduate engineering programme of study. Nevertheless, merely by bringing the main concepts to the attention of a student can provide for a deeper appreciation of the subject area. Note though, it is not our intension to review Euler’s De Curvis Elasticis. This has been done in detail elsewhere, see Frasier (1991) and Truesdell (1960). In any case, it is worthwhile reading the translation of Euler’s work (1744).

2 The Buckling Phenomenon

The EBF gives the critical load P c at which a straight rod buckles:

$$ P_{c} = n\lambda\frac{\pi ^{2}B}{L^{2}}, $$
(1)

where L is the length of the rod, B is its flexural stiffness (sometimes referred to as rigidity) and is a property of the cross section of the rod which accounts for both the material it is made from and the geometry of its cross sectional, n is an integer which depicts the mode of buckling, and the value of λ depends on boundary conditions (the manner by which the ends of the rod are fixed). As we mentioned above, Euler does not dwell for long in De Curvis Elasticis to ponder the significance of (1), nevertheless something or someone must have prompted him to revisit it. In 1757, thirteen years later, Euler wrote a paper titled On the Strength of Columns, in which he refocuses attention on the EBF:

When I developed elastic curves in the supplement to my Treatise on Isoperimeters, I drew from them a conclusion in regard to the strength of columns that strikes me as very remarkable. It concerns the loads that a column can support without buckling. (Euler 1947)

He continues with a contemplation of the phenomenon of buckling:

At first glance it would seem that such a force [the end force P], no matter how large, would never cause the column to bend; because there would be no reason why the column should bend in either one sense or another. (Euler 1947)

Buckling involves an exchange of stability: the trivial solution (the straight configuration) loses stability and the rod moves to a new bent state which is stable. If we restrict our analysis to deflection in the plane (a rod with a flat cross section will tend to only buckle in the plane) then the rod can bend in only two directions: either to the left or the right. Thus, at P c there is a bifurcation—two equilibrium states which are mirror images of each other emerge from the point at which the straight configuration loses stability. A characteristic of buckling is that it is sensitive to the presence of small imperfections. In the case of the rod, an imperfection is often the factor which determines the direction a rod will buckle in. The role of imperfections did not escape Euler’s perceptive mind:

But the slightest variation in the dimensions or in the slightest force applied, no matter from what side, would furnish sufficient cause, to induce buckling in a special direction. (Euler 1947)

But this raises a paradox: an end force applied laterally, no matter how small in magnitude, causes a deflection, whereas for values P < P c , an end force applied axially causes no defection whatsoever. Euler can only “explain” the paradox by appealing to mathematics, for which he had absolute confidence:

… in order to explain this paradox, we have but to say that so long as the loads supported by the column are less than the quantity ππEkk/aa [i.e. P c ], the bending is imaginary, and it remains = 0, until the load attains this limit, and when this limit is exceeded the bending becomes real and increases with force. Since this is in agreement with the principle of calculus, which, being based on continuity, should not result in anything that contradicts this principle, we are without question obliged to accept this explanation; and we may conclude as a general principle, that the results of mathematical analysis always furnish the most reliable rules, which we must follow in our reasoning based on the principle of continuity. (Euler 1947)

Evidentally Euler is struck by the fact that each of the nine species he had described in De Curvis Elasticis evolves smoothly from one species to the next, whereas in the case of a straight rod nothing happens until the critical load is reached. That nothing happens is not strictly intuitive and due to the likely presence of the aforementioned imperfections, is not necessarily consistent with experience, though in a carefully controlled experiment it is readily observable.

3 Experimental Investigations into Buckling

The starting point for an experimental investigation into the buckling of slender rods may well proceed by first of all identifying the critical parameters. These can be listed as follows:

  • The length of the rod,

  • The material the rod is made of,

  • The geometry of the cross section (e.g., circular, rectangular),

  • The details of how the ends are fixed (e.g., sliding grips, hinged, clamped ends),

  • The load—its direction and magnitude and the manner in which it is applied.

The next step would be to work out which of these parameters can be measured, which can be controlled, and which can be held constant. A parameter which the experimentalist can control could then be either assigned as an independent or a dependent variable. In an experiment the value of the independent variable would be adjusted, the dependent variable measured, and other parameters held constant. Once an experimental procedure has subsequently been established a set of experimental data would be collected and a best-fit line drawn between the data points, from which a rule could be derived which expresses quantitatively the dependence of one parameter upon another. Intriguingly, an experimental procedure similar to that outlined above had already been followed some fifteen years before the appearance of De Curvis Elasticis. In 1729 Pieter van Musschenbroek (1693–1761), a Dutch professor based at the University of Utrecht and later Leiden, carried out a systematic and accurate sets of experiments on a wide range of structural materials. His apparatus was well designed and permitted proper control of parameters. However he was not so complimentary of the tensile testing rig designed by the French physicist and experimentalist Edmé Mariotte (1620–1684), remarking:

In this method I noticed the inconvenience that the feet of him who performs the experiment are always exposed to danger of injury when the weight falls. (Quoted in Truesdell 1960, p. 151)

Van Musschenbroek’s experiments were on long strips of wood of rectangular cross section. His experimental data led him to deduce the following quantitative rule:

Parallelepipeds of the same wood…, compressed along their lengths, exert forces of resistance which vary inversely as the square of the length, directly as the thickness of the side that is not bent, and directly as the square of the side that is bent. [Van Musschenbroek Physicae experimentales et geometricae 1729. (Quoted in Truesdell 1960, p. 153)

i.e.

$$P_{c}=\frac{b d ^2}{L^2}, $$
(2)

which has the same dependence upon the length L as (1), though the correct dependence on the geometry of the cross section is the second moment of area I. For a rectangular cross section \(I=\frac{bd^3}{12}\), where d = depth and b = thickness. We note that Euler was also unsure of the dependence of buckling on the geometry of the cross section. He may have realised that his one-dimensional theory cannot directly give this dependence (the elastic curve strictly has no cross section but has an overall flexural stiffness B) and in his “On the Strength of Columns” he proposes an experimental programme for investigating this dependence:

In the meantime it would be desirable if we made numerous experiments with various specimens, bending them by means of a force F in numerous directions, in order to learn more exactly in what manner the stiffness moment [=bending stiffness] is affected by the width as by the thickness. (Euler 1947)

Clearly Euler could see a positive role for experimental methodology, though not as a substitute for mathematics, rather as a means for taking the research further once mathematical methods were exhausted. Sometimes experimentation can achieve this role and sometimes it is reversed. But in an experiment the nature of the research can also change. So Van Musschenbroek did not see any problem with extending his experimental study to fracture (which lies outside the domain of elastic behaviour). He was consequently able to additionally conclude that the rod “breaks in the middle where it is bent the most”. Another contribution of Van Musschenbroek was to show that failure in compression is entirely different to failure in tension. Bell says of him:

If a man of his excellence had been interested in pre-rupture constitutive equations, the impact of experimental solid mechanics upon theory and interpretation might have been considerable even in the mid-eighteenth century. (Bell 1973, p. 162)

It is interesting though, that Van Musschenbroek did not share Euler’s confidence in mathematics:

The doctrine of resistance [elasticity] is always too problematic for the insight of mathematicians. [Van Musschenbroek Physicae experimentales et geometricae 1729. Quoted in (Benvenuto 1991, p. 282).]

Euler either did not know of Musschenbroek’s work, or simply chose to ignore it. We suggest here that if he had made reference to Musschenbroek’s experimental result (2) then, apart from not being able to claim to be the first to discover EBF, his work would have attracted interest from beyond the realm of Natural Philosophers. Though the Musschenbroek–Euler connection gradually became known, it was to be at least a century before EBF found its way into undergraduate text books on the mechanics of materials. That it took so long is probably because the structural materials in common use in Euler’s time were stone, cast iron and wood. Of course, timber construction has thousands of years of empirical wisdom to fall upon, so it is not surprising that EBF was not widely discussed amongst eighteenth century structural engineers. Their attention was only really drawn to Euler’s work when new materials started to be mass produced (mild steels around the 1850s, and structural aluminium alloys around the 1900s), and there emerged a growing demand for guidelines for design against buckling.

In the year 1811, the French engineer A.J.C.B. Duleau (dates unknown but died in 1830), carried out a comprehensive set of experimental investigations into structures, which included many buckling experiments. Their historical significance is noted by Bell:

the experiments of Duleau became the primary basis for discussion and criticism, both with respect to matters of further experimentation and in the later development of the linear theory of elasticity, throughout the entire first half of the 19th Century. (Bell 1973, p. 196)

One of Duleau’s set of experiments involved varying the slenderness ratio L/r (where L is the length and r is an average measure of the cross section (r = the radius in the case of a rod with a circular cross section) from 200 to 24 and found an average ratio of 1.16 of experimental to theoretical buckling load. He was not sure why his experiments on buckling deviated from EBF but, as Bell remarks:

Duleau pointed out in those first definitive measurements what every modern experimentalist knows too well, namely that friction and the manner of holding the specimen make the experiments extremely difficult to perform. (Bell 1973, p. 202)

In a footnote Bell adds that Cauchy (1789–1857) and Poisson (1781–1840), two individuals who played crucial roles in the development of elasticity theory during the nineteenth century, studied Duleau’s results:

The two famous theorists thought that the difference also could be attributed to the fact that Euler’s formula applied to the situation was in some sense an approximation and suggested that the experiments indicated that it did indeed give too weak a result. (Bell 1973, p. 202)

Engineers like formulae because they know they work, irrespective of whether they are founded on sound mathematical principles or not. Consequently, when EBF did not give a good match with experimental data, it wasn’t long before some engineers dismissed it out of hand. For example, the experimentalist Peter Barlow (1776–1862) had this to say:

[Euler’s works are] too delicate to operate successfully upon the materials to which they have been applied; so that whilst they exhibit under the strongest point of view, the immense resources of analysis, and the transcendent talents of their author, they unfortunately furnish but little, very little, useful information. (An Essay on the Strength and Stress of Timber (1817) Quoted in Timoshenko 1953, p. 99)

Later, in 1822, further criticism came from J. Robinson, who described Euler’s work as follows:

… a dry mathematical discourse, proceeding on assumptions which (to speak favourably) are extremely gratuitous … his theory of the strength of columns is one of the strongest evidences of this wanton kind of proceedings … (Quoted in Timoshenko 1953, p. 99)

It is evident that in the course of these early experimental investigations, engineers were finding different results from those predicted by EBF, and were generally not very impressed by it. In his definitive historical treatise on experimental mechanics (Bell 1973), Bell draws attention to the basic difficulty encountered in experimental studies on the buckling of rods:

Beginning from the early eighteenth century experimental studies of Van Musschenbroek on the buckling of compressed struts and the classical theoretical studies of Euler on the same subject, an enormous literature on experiment has grown which has described the complex buckling of all manner of geometrical shapes. However unlike the boundary value problems in the field of vibration, for which many precise experiments in the 19th and 20th centuries led to truly striking correlations between prediction and observation, the experimental data in the field of elastic stability has been beset from the first small deformation measurements of Alphonse Duleau in 1812 to the present, with basic difficulties. The widely variable experimental data have arisen from the fact that buckling behaviour is keenly sensitive to small details in matters of load application, alignment, and local peculiarities in the specimens. (Bell 1973, p. 4)

It was not until 1889 that the validity of EBF was established; at the Polytechnic Institute of Munich by its first director Johann Bauschinger (1833–1893). He took great care to avoid eccentricity in application of the load and to ensure that the end conditions were satisfied (Timoshenko and Gere 1961). We note that nearly all experimental investigations into the mechanics of rods concern the buckling phenomenon and the applicability of EBF. This is obviously a consequence of the engineer’s requirement to avoid buckling when designing structures. However, many physical problems also require a knowledge of structures undergoing large deflections. For a study of post-buckling experiments see (Goss et al. 2005).

4 Scientific Methodology

By the time Bauschinger performed his experiments, the experimental procedures, specifications and the techniques of measurement had greatly improved since Musschenbroek’s early experiments. It should also be pointed out that the notion that experimentation is a reliable means of scientific discovery had become firmly established. This acceptance owes much to the writings of the English lawyer Francis Bacon (1561–1626). Bacon advocated a completely new approach to scientific discovery, one based firmly on experience and experiment. He was keen to outline a scientific method which would arrive at truth by means of rational steps which were transparent and could be checked and reviewed on a collective basis. He also considered that experiment was the most effective strategy for eliminating false laws. This new approach was to replace what he saw as a corrupted scientific methodology:

Natural Philosophy is not yet to be found sincere, but is infected and corrupted: in the school of Aristotle by Logic; in the school of Plato, by Natural Theology; in the second school of Plato, that of Proclus and others, by Mathematics, which ought to limit natural Philosophy, and not generate or originate it. But from a Natural Philosophy, pure and unmixed, better things are to be hoped. (Bacon 1620/1902, p. 285, Novum Organum)

Bacon was also skeptical of a scientific methodology which starts out from a preconceived premise and which is supported by insufficient evidence:

… in preparing the subject-matter of Philosophy, men either draw a great deal from a few instances, or a little from a great number; so that, in either case, Philosophy is founded on too narrow a basis of experience and natural history, and dogmatises on too insufficient evidence. (Bacon 1620/1902, p. 265, Novum Organum)

For Bacon, knowledge and understanding of the natural world can be determined with absolute conviction by pursuing a programme of careful observation combined with cleverly devised experiments. It should be pointed out that experimentation was not a new method of finding things out, either to Bacon or his contemporaries; it can be traced back to the Classical Greeks. However, Bacon was writing at a time when astrology, alchemy and mysticism were considered valid means of scientific enquiry and theology was upheld as a source of absolute truth,

Nor is the fact to be passed by, that Natural Philosophy has in all ages found a troublesome and difficult enemy: I mean superstition, and a blind and immoderate zeal about religion. (Bacon 1620/1902, Novum Organum, p. 281)

By not appealing to the authority of theology, Bacon effectively separated religion from science—at the time a radical and crucial step. Perhaps it was the Protestant influence which declares that you do not have to be a monk or a priest in order to follow a devout and religious life which made Bacon a keen advocate of the idea that science was something which anyone could do. Just so long as the correct procedures were followed. Of significance too is Bacon’s belief that scientific knowledge should be put to good use—to improve the material welfare of mankind. In coining the phrase “knowledge is power” he captures England’s emerging industrial classes’ thirst for scientific knowledge as a means for driving technological progress.

By the mid 1640s Bacon’s ideas on science were being widely discussed and it was not to be long before the idea of a college with the sole purpose of promoting science along Baconian lines was conceived. In 1662, with the declared aim of the “Improvement of Natural Knowledge”, and motto “Nullius in verba” (“take nobody’s word for it” or “Nothing by mere authority”), the Royal Society of London for Improving Natural Knowledge was founded in London, later to be called The Royal Society. The founding members of the Royal Society had fought on both sides of the English Civil war. But they were united in the quest to establish a program of scientific discovery along Baconian lines.

The first president of the Royal Society was Robert Boyle (1627–1691). Managing to keep out of the Civil War, Boyle had devoted his life to the pursuit of scientific knowledge. He was a keen experimentalist (Sargant 1989), but had also traveled across Europe as a boy and studied the works of the Italian Galileo Galilei (1564–1642) and the Frenchman René Descartes (1596–1650). In addition to his investigations into the behaviour of gases, for which he is renowned, Boyle showed, for the first time, that a feather and a lump of lead land together when released from the same height, which Galileo had asserted using “thought experiments”. Boyle appointed Robert Hooke (1635–1703) as the Royal Society’s Curator of Experiments. Born in the Isle of White and initially trained as an artist, Hooke was a skilled draftsman, instrument maker, mathematician and experimentalist and has been dubbed “London’s Leonardo” by (Bennett et al. 2003). He was also a keen supporter of the notion that science be based on experimental evidence:

The truth is, the science of Nature has already been too long made only a work of the brain and the fancy. It is now high time that it should return to the plainness and soundness of observations on material and obvious things. (Hooke 1665/2006, p. 5, Micrographia)

In 1676 Hooke reported on the results of an extensive experimental investigation into how materials respond when loaded by a tensile force. He found that a wide variety of materials “whether metal, wood, stones, baked earth, hair, horns, silk, bones, sinews, glass and the like” undergo extension according to a linear law. This law is known today as Hooke’s Law. It is a constitutive relation, connecting the geometry of deformation of a material with an applied load. We remark here that constitutive relations are of fundamental importance in the theory of elasticity, but to this day they can only be determined from experiments. Whilst Hooke’s Law describes a linear relationship, which greatly simplifies the analysis, we note of course, that if the loads and strains are small enough, then any nonlinear response can be approximated by a linear one.

The scientific methodology of Boyle and Hooke was very close to the scheme advocated by Bacon: scientific enquiry should progress in an encyclopedic fashion, by the accumulation of lots of facts based on observation and experimentation. However, a rather different methodology in which logical argument takes precedence had been suggested in the works of Descartes. Noting that things in Nature can change form (Descartes used the example of a piece of wax which can melt when heated) he assumed that knowledge based on the senses (seeing, hearing, smelling, tasting) is intrinsically unreliable. It seemed to follow, therefore, that the process of discovery should proceed by a process of logic, not by the senses. Whilst this approach was opposed by Bacon, there are significant similarities. First of all we can mention that both shared an optimism with respect to discovery: they were convinced that anyone can achieve certainty about the underlying workings of Nature so long as their methodology is correct. They also sought to separate scientific study from theology. Descartes argued that mind and matter are two separate substances and therefore required separate treatment. Furthermore, even though they supported the idea that science should be used for the common good, they also held the fundamental belief that the ultimate aim of science should be to determine the causes of natural phenomena. It is at this point that we introduce a rather different approach to scientific methodology, one which was promoted by a contemporary of Descartes’ and which he criticised:

I find in general that [Galileo] philosophizes much better than common people insofar as he avoids as much as possible the errors of the Scholastics, and attempts to examine physical matters by means of mathematical reasons. In that I agree entirely with him, and hold that there is no other means to discover truth. But it seems to me that he is greatly deficient in that he digresses continually and that he does not stop to explain fully any subject; this shows that he has not examined any in orderly fashion, and that he has sought for the reasons of some particular effects without having considered the first causes of nature, and that thus, he has built without foundation. But, to the extent that his method of philosophizing is closer to the true one, we can more easily know his faults, in the same way that we can more easily recognize of those who sometimes follow the right path that they have strayed away, than we can of those who never follow the right path. (Quoted in Ariew 1986)

Rather than seek the underlying causes of observed natural phenomena, Galileo concentrated on the task of formulating a quantitative description of it. The first step in this approach is to identify the significant physical parameters, and where possible to measure them. The next step is to determine mathematical relationships, i.e, treat the parameters as mathematical variables. Guided by careful observation and experimentation, Galileo was above all else concerned to gain absolute certainty about the relationships between the parameters involved.

In his early work Le Mechaniche, estimated to have been written in 1593, we find what is essentially a text book for a course Galileo delivered on the mechanics of machines. He delivered this course whilst employed at the University of Padua in the years 1597–1598. Evidentally the course was delivered to engineers as well as to individuals (“natural philosophers”) who were motivated by curiosity (Ceccarelli 2006). In his descriptions of the kinematics of levers, pulleys, lathes, screws, and other machines, Galileo formulates quantitative relationships and although he does not write any mathematical equations, he was convinced that mathematics is the key to understanding how these machines work.

Galileo was to later extrapolate this idea to Nature, as can be seen from his famous statement of 1610:

Philosophy [nature] is written in this enormous book which is continually open before our eyes (I mean the universe), but it cannot be understood unless one first understands the language and recognises the characters with which it is written. It is written in a mathematical language, and its characters are triangles, circles, and other geometric figures. Without knowledge of this medium it is impossible to understand a single word of it; without this knowledge it is like wandering hopelessly through a dark labyrinth. (Galilei 1623, p. 232)

Galileo’s knowledge of machines extended to the latest contemporary instruments of observation: he invented a microscope and when he first heard of the telescope, he immediately set about constructing one. His telescopic observations of the surface of the Moon instilled in him the idea that Nature is not an immobile, unchanging, unalterable place. Consequently, he turned his attention to the task of interpreting change and movement on a grander scale than engineering machines. It was at this point that he caught the unwelcome attention of the Catholic clergy. In 1633 he was placed under house arrest for his advocacy of the Copernican theory (that the Sun is at the centre of the Solar System rather than the Earth). During his time of incarceration Galileo pursued further studies into mechanics (but not Solar System mechanics). These studies helped to establish a modern scientific approach to discovery; one which describes natural phenomena by means of quantities such as force, mass and acceleration—quantities which we do necessarily see, but which are measurable and which can be abstracted from observations of the natural world. Galileo’s methodology can be described as hypothetico-deductive: we deduce statements about how things must occur based on a hypothesis and then observations and experiments can be used to test and confirm/disconfirm the hypothesis. This constituted a new approach, and is the basis for modern scientific methodology. Its synthesis can be found in the work of Isaac Newton (1642–1727), born the same year Galileo died and following closely in his footsteps. Newton’s Principia and Optiks had respectively established mathematics and experimentation at the forefront of scientific methodology:

Newton’s achievements as far as scientific method is concerned, then, was to identify and use a method which gave scope for emphasis upon the use of mathematical results, as in Principia, and for emphasis upon experimental evidence as in the Opticks, but its essential features are the same in both treatises. (Gower 1997, p. 79)

Musschenbroek’s experiments and Euler’s De Curvis Elasticis are the legacy of Newton’s pioneering work. They represent two parallel methods of scientific discovery, experimentation and rational thought (through mathematics). We can think of these two methodologies as experiments in two different worlds—the physical world and the mathematical world. An experiment on a physical three-dimensional rod permits phenomena to be explored which falls outside of the rules set out by the one-dimensional mathematical model. For example, the dependence of buckling upon the variety of cross sections, the nature of imperfections, the behaviour of materials with complex nonlinear constitutive relations and the study of non-elastic behaviour may all be encountered during the course of an experiment. On the other hand, in the mathematical world an “experiment” on a rod will give exactly the same result today as it did yesterday. Since solutions are not limited by the constraints of the physical world, they can be found over the entire domain in which the independent variable is defined. So even though not all the species of elastica depicted in Fig. 2 may be readily observable in the physical world, it does not imply that they are impossible. The mathematical model can also guide us in which experiments to carry out and the most effective experimental procedure. It follows that if we wish to use the mathematical model for guidance then the specification for an experiment should be as close a copy to the mathematical model as is physically possible. In fact it was only when this approach was adopted, by Bauschinger, that EBF was finally “accepted” by engineers.

5 Flexible Curves and the Catenary

The formulation of the mathematical model for the elastica and its subsequent solution constitutes a corner stone in our understanding of the mechanics of long slender structures, i.e. the development of rod theory. At the heart of rod theory is the concept of a “material point”—just as in Euclidian geometry we find the concept of the geometric point. A “rod” is an elastic line or curve consisting of a set of material points. In rod theory a particular rod is characterised by its constitutive relations. For planar problems these relations depict the response to a bending moment (flexural stiffness), to a shearing force, (“shearability”) and to an axially applied end force (compressibility/extensibility), which is Hooke’s Law. In the case of the elastica, the rod is inextensible, cannot suffer shear, but bends in response to a bending moment M according to a law given by a linear constitutive relation, i.e. \(M=B\kappa\), where B is the flexural stiffness and \(\kappa\) is the curvature. A rod which offers no resistance to bending is called a “string”. It is completely flexible. The string model finds applications in the study of long slender structural members such as cables, where an external load dominates the mechanics and the rod’s flexural stiffness is negligible. For example, the problem of the catenary is to determine the shape of a chain suspended between two points and sagging under its own weight. Other classical problems are the suspension bridge problem (constant vertical loading intensity per horizontal distance), the valeria or sail (where the force is a normal pressure of constant intensity) and the linteria (where the normal pressure varies linearly with depth). It is the problem of the catenary which is of interest to us here. But before we introduce the catenary, we step back to reflect upon the concept of a “material curve”—a concept which underlies all rod theory. This concept emerged as a consequence of the injection of analysis into geometry.

One of the important contributions of Descartes to the development of mathematics was to connect algebra with geometry. He realised that every point on a piece of paper can be located by means of two mutually perpendicular lines intersecting at that point. The extension of this idea to the representation of a point by means of two numbers, marked along these lines, led him to write a treatise on geometry, La Géométrie, in which geometric curves are represented by algebraic equations. The study of curves was recognised by the seventeenth and eighteenth century natural philosophers as being a particularly worthwhile pursuit. For example, Kepler’s discovery that planetary orbits follow more accurately the path of an ellipse than a circle, and Galileo’s discovery that the trajectory of an arrow is approximately described by a parabola, were widely recognised as key steps in revealing Nature’s hidden workings.

In La Géométrie, Descartes also discusses curves which he characterises as being generated by “two separate movements whose relation does not admit of exact determination” (Descartes 1954, p. 44). For example, the cycloid is the curve traced out by a point on the rim of a circle rolling along a straight line, see Fig. 3. Descartes neglected to study these curves because he lacked the necessary mathematical tools. However, within 20 years of his death a new calculating method, the calculus, was invented, which partly evolved from his own work. The calculus greatly simplifies the procedure for computing tangents, normals, curvatures and stationary points along a curve and it was not long before it was applied to the task of unraveling the mysteries of the curves which had eluded Descartes.

Fig. 3
figure 3

Two important curves connected to the development of mathematics, the Cycloid (left) and the Lemniscate of Bernoulli (right). The Cycloid is the curve traced by a point on a rolling circle

Full size image

Amongst the many varieties of curves which were probed by the calculus are those exhibiting the property that a particular quantity is minimised (or maximised). The most famous of these “extremum curves” is the cycloid, see Fig. 3. This curve is the solution to the brachistochrone problem, which is to determine the curve down which a particle will slide from one point to another in the quickest time. Some Natural Philosophers thought that the extremum principle is intrinsic to the way that Nature works—a point we will return to later. However, an extremum problem which is of particular interest here is that of the catenary; which is to find the shape of a hanging chain, the extremum principle being that the centre of gravity is lowest, see Fig. 4.

Fig. 4
figure 4

The catenary, showing the coordinates and the end tension T

Full size image

Perhaps Galileo was seeing parabolas everywhere, when in 1638, thinking that he had solved the problem of the catenary, he wrote that the shape of the hanging chain is parabolic (Galilei 1638/1988). However, in 1646, a few years after Galileo’s death, a 17-year-old Dutchman, Huygens (1629–1695), proved that the parabola only arises for the case that equal weights are suspended at equal horizontal intervals along the chain (the suspension bridge problem). Huygens effectively placed the catenary back on the list of unsolved problems. However it was not until 1690 that James Bernoulli (1654–1705), a professor at the University of Basel in Switzerland, formally challenged the community of Natural Philosophers to solve the problem. His challenge appeared in Acta Eruditorum, an academic journal founded by Leibniz (1646–1716). The following year three solutions were published; the authors being Huygens, Leibniz and James Bernoulli’s younger brother John (1667–1748). Huygens, who never fully mastered the calculus, used a rather unwieldy proof relying on geometry. His solution was cast into the shadows by those of the other two authors, particularly John Bernoulli’s, where the problem was formulated as a differential equation:

$$ \frac{{\rm {d}}y}{{\rm {d}}x} = \frac{1}{\sqrt{x^2-a^2}}, $$
(3)

where a is a constant which equals the ratio of the weight per unit length to the horizontal component of the tension T (this component remains constant along the entire length). This was as far as John Bernoulli could take the solution, though today we recognise (3), upon separation of variables, as being a standard integral leading to an inverse hyperbolic function. John Bernoulli’s use of a differential equation as a mathematical model for describing mechanical phenomena marks an important step away from a reliance upon purely geometric proofs. Always proud of his discovery, John wrote later:

The efforts of my brother [James] were without success; for my part I was more fortunate, for I found the skill (I say it without boasting, why should I conceal the truth?) to solve it in full……. I ran to my brother, who was still struggling miserably with this Gordian knot without getting anywhere, always thinking like Galileo that the catenary was a parabola. Stop! Stop! I say to him, don’t torture yourself any more to try to prove the identity of the catenary with the parabola, since it is entirely false. The parabola indeed serves in the construction of the catenary, but the two curves are so different that one is algebraic, the other is transcendental…. Letter to P. Remond de Montmort 29/9/1718, quoted in Kline 1972, p. 473)

Nevertheless, in later years James Bernoulli presented an overview of the various approaches to solving the problem. His studies culminated in the derivation of a set of equilibrium equations for a string loaded by any distribution of tangential (W t ) and normal (W n ) forces, see Benvenuto 1991. These equations can written as follows:

$$ \frac{{\rm{d}}T}{{\rm{d}}s}=-W_t,\quad T \kappa =W_n. $$
(4)

Today, we recognise (4) as a first step towards the discovery of a more general system of differential equations governing the equilibrium of long slender rods—both flexible rods and elastic.

6 Elastic Curves, the Supreme Creator and Elliptic Integrals

In the same issue of Acta Eruditorum in which the solutions to the catenary appeared, James Bernoulli posed “an equally interesting problem”:

… [to determine] the inflection or of the curving of beams, of bows, or elastic elements of every kind, because of their own weight or of a weight applied to them or of any other acting force. (Quoted in Benvenuto 1991, p. 273)

Three years later he declared “…I cannot longer deny to the public the golden theorem…” and published his findings. As with the problem of the catenary, James Bernoulli derives a differential equation for the rod’s curvature \(\kappa\), but he additionally equates \(\kappa\) to some function f of the bending moment M. These relations can be expressed as follows:

$$ \kappa =-\frac{\hbox{d}\theta}{\hbox{d}s},\quad\hbox{and}\quad\kappa = f(M). $$
(5)

As with Hooke’s Law, (5) relates the geometry of deformation to an applied load. In this case the load is a bending moment and the deformation is curvature. James Bernoulli proceeds in his analysis to focus attention on the case of a rod which is bent into a U shape such that the two ends of the rod are parallel, called the rectangular elastica. Using cartesian coordinates, he derives the following equation:

$$ \hbox{d}y=\frac{x^2\rm d x}{\sqrt{a^4-x^4}}, $$
(6)

where a 2 is a constant equal to the ratio of the applied force P to the bending rigidity B (i.e. \(a^2=\frac{B}{P}\)). James Bernoulli was unable to solve (6) and rather wearily remarked

I have heavy grounds to believe that the construction of our curve depends neither on the quadrature nor on the rectification of any conic section…. (Quoted in Truesdell 1960, p. 95)

which prompted Huygens to remark:

And even now all he has found seems no use to me, but only such very beautiful and subtle pastimes as one finds when one has nothing on which to employ mathematics more fruitfully. (Quoted in Truesdell 1960, p. 97)

However, James Bernoulli did suggest that a way forwards was to expand the radical in (6) as a series and proceed by integrating the resultant expression term by term. There was one individual who was particulary gifted in the manipulation of infinite series, and that was Leonard Euler, a pupil of James’ brother John. Euler was prompted into tackling the problem of the elastica by John’s son, Daniel Bernoulli (1700–1782):

I should like to know if your Worship could not solve the curvature of the elastic band in the case that a band of given length be fixed at two points and that also the tangents at these points be given… Since no one has perfected the isoperimetric method as much as you, you will easily solve this problem of rendering \(\int \frac {ds}{r^2}\) a minimum. [r is the radius of curvature (Truesdell 1960) Letter from Daniel Bernoulli to Euler dated 20th October 1742]

The “isoperimetric method” is the term used to describe what we now call the calculus of variations. In this method, the integral of the product of mass, velocity and distance traveled is set to an extreme (maximised or minimised) and an “optimal condition” is obtained. The idea that Nature has a tendency to economise had been formulated into a general principle, the Principle of Least Action, by the head of the Academy in Berlin, Pierre Maupertuis (1698–1759) where Euler was employed (1741–1766). Maupertuis propounded this principle for theological reasons (see Kline 1972, Chap. 24) and Euler, also a devout Christian, set about formulating this as an exact dynamical theorem. His work culminated in the treatise of which De Curvis Elasticis is an appendix, and where he expounds his theological viewpoint in the opening paragraph:

For since the fabric of the universe is most perfect and the work of a wise Creator, nothing at all takes place in the universe in which some rule of the maximum or minimum does not appear. (Euler 1744, p. 2)

It is curious that Euler was keen to explain the causes for natural phenomena at a time when Galileo’s and Newton’s work had received international acclaim. The Principle of Least Action echoes the tradition passed down from the Ancient Greek philosophers, who set the core task of natural philosophy to be the search for underlying causes for everyday observed effects. It is interesting to note that whilst Galileo, Bacon, Descartes and Newton had managed in their own ways to steer scientific enquiry along a route free from religious dogma, they were themselves deeply religious people and many of the leading Natural Philosophers who followed in their wake (including Musschenbroek) also held strong religious convictions. This was certainly true of Euler, who was from a Calvinist background and firmly believed that Nature was a consequence of God’s design. Euler denounced atheism in many of his philosophical works, though they were remarked upon for not being in the same league as his science (see Fellmann 2007, p. 75)

In the case of the elastica the minimisation principle involves the bending strain energy, supplied by Daniel Bernoulli. Euler expresses the problem as follows:

That among all curves of the same length, which not only pass through the points A and B, [the ends of the rod] but also are tangent to given straight lines at these points, that curve be determined in which the value \(\int \frac {ds}{r^2}\) is a minimum. (Euler 1744, p. 79)

Following James Bernoulli’s advice, Euler uses the binomial theorem to expand the radical in (6) as an infinite series and integrates the resultant expression term by term. This enables him to sketch the elastica. His nine “Species” are obtained by varying a load parameter, see Fig. 5, and for further details refer to Euler (1744), Frasier (1991), and Truesdell (1960). Today we recognise (6) as an elliptic integral, a name attached to them due to their connection with the arc length of an ellipse. The general form of an elliptic integral is \(\int R[t,\sqrt{p(t)}]dt,\)where R is a rational function and p is a third of fourth degree polynomial. They cannot be evaluated in terms of the elementary functions (algebraic, trigonometric, logarithmic of exponential), and it was to take many decades of research before they were properly understood. However, it was in the course of their investigations into curves, including the elastica, that the eighteenth century natural philosophers took the first steps in finding things out about them.

Fig. 5
figure 5

Euler’s Species 2. Euler starts his analysis with an arc length AM, origin at A, and line of action of the force P is along AD downwards. Consequently the bending moment vanishes at A, which is an inflection point. The x axis is along AP and the y axis along AD. Noting that “if x and y are both made negative, the form of the equation is not changed”, Euler deduces that the curve on both sides of A has similar branches AMC and amc. He finds humps (local maxima) at C, and therefore at c, from which he deduces that “the whole curve will be contained between the extreme ordinates EC and ec”. Beyond these humps, Euler uses a translation of coordinates showing the periodicity of the elastica CNB and cnb

Full size image

A major step towards our understanding of elliptic integrals is in connection with a curve which is named in honour of James Bernoulli. The arc length of the Lemniscate of Bernoulli, see Fig. 3, is given by an elliptic integral of the form \(\int_0^x dt/\sqrt{1-t^4}\) , which was recognised as being remarkably similar to that defining the inverse sine, i.e. \( \arcsin x = \int_0^x dt/\sqrt{1-t^2}\) . There was strong sense that there was further work to be done with respect to this integral. But no one knew how. That is, until in 1751, when Euler came across the work of an amateur mathematician, Count Giulio Carlo de’ Toshi di Fagnano (1682–1766). Euler immediately saw a connection between some addition properties relating to the lemniscate’s arc length which Fagnano had discovered and the elliptic integral. He used Fagnano’s results as the basis for some addition theorems relating to elliptic integrals. These theorems constitute the platform for all later work on elliptic integrals, see Kline (1972) and Stillwell (1989). The corresponding elliptic functions (cn, dn sn) were later discovered to possess identities and addition theorems in a similar manner to the trigonometric and hyperbolic functions. They were also found to be doubly periodic and, when certain elliptic parameters are set to their extreme values, to collapse into the trigonometric and hyperbolic functions. With respect to the planar elastica, the case where the elliptic function degeneratesinto a trigonometric function corresponds to Euler's Species 1. It is from here that we derive EBF. At the other extreme, where we obtain a hyperbolic function, the center point of the rod is “curved to a knot” and the loose ends stretch out to infinity either side. This case is Species 7, see Fig. 2, and has been used as the basis for the study of loop formation in cables and pipelines, see for example (Coyne 1990). Euler expresses the shape of this curve by means of the logarithmic function.

7 Rods and Pendulums

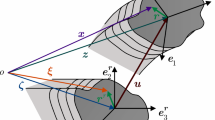
One of the interesting properties of the elastica is symmetry, a property which is reflected in the periodicity of elliptic functions. The symmetry can easily be seen with respect to cuts from an infinitely long elastica, as depicted in Fig. 6. The cuts at ABCDEFGG′ represent various boundary conditions: pinned, clamped, and free. Figure 6 also depicts the static–dynamic analogy between the elastica and a pendulum. This analogy is obtained through the mathematics. The period T of a simple pendulum (in polar coordinates) is given by the following elliptic integral:

$$ T=\frac{l}{g}\int\nolimits^{\pi/2}_0 \frac{d\phi}{\sqrt{1-k^2\sin^2 \phi}} $$
(7)
Fig. 6
figure 6

The phase plane, which can be used to study both the statics of the planar elastica and the dynamics of a pendulum. The diagram is symmetric about both the θ and \(\kappa\) axes and repeats with period 2π along the θ axis. The angle θ denotes the angular position for a pendulum and in the case of the elastica it is the angle of slope the rod makes with the line of action of the end force P. For a pendulum \(\kappa\) is the derivative of θ with respect to time (the angular velocity) and for the elastica it is the derivative of θ with respect to arc length s (the curvature). The oval-like curve called the separatrix denotes the infinitely long period of a pendulum which starts from and returns to the upside-down equilibrium state, which is unstable. This corresponds to Euler’s Species7. Curves within the separatrix pass through \(\kappa=0\) signifying the existence of an inflection point, e.g. at B and D, and correspond to an oscillating pendulum. Phase curves lying outside the separatrix can never cross this axis and are called noninflectional (revolving pendulum)

Full size image

where ϕ and k are parameters and l is the pendulum length and g the acceleration due to gravity. A curious feature of (7) is that if we substitute \(\sqrt{B/P}\) for l/g then (7) gives the length L of elastica. In other words the problem of the elastica is mathematically analogous to that of the pendulum. In the dynamics problem the independent variable is time and in the statics it is the arc length s.

In the dynamics problem, there are two states which deserve special attention. The first is where the pendulum hangs vertically down and the second is the inverted state where it is “upside down”, see Fig. 6. Both are equilibrium states. If left undisturbed, a pendulum will remain in these positions for ever. But there is an important difference: give the upside-down pendulum a small nudge and it will fall away from this position, never to return. However, for the vertically down case, a small nudge only results in small oscillations about the equilibrium state, and if there were friction present then these oscillations would, after some time, die away and the pendulum would come back to rest in its equilibrium position. It follows that the vertically down equilibrium state is stable and the vertically-up state is unstable. Furthermore, two qualitatively different types of motion are observable in a moving pendulum. The first type of motion involves oscillations to and fro about the stable equilibrium state. The second type of motion involves revolutions in one direction or the other. A diagram called the phase plane, where the angular velocity \(\kappa\) is plotted against the angular position θ, illustrates these qualitatively different types of motion—revolutions and oscillations—in one picture, see Fig. 6. The demarcation between them is given by the phase path called the separatrix. This path is intimately connected with the unstable equilibrium position.

The phase plane also offers a straightforward illustration of a classification scheme for the planar elastica, which can be traced to A.E.H. Love (1863–1940). In a section of his definitive treatise The Mathematical Theory of Elasticity, under the heading Classification of the forms of the elastica §263 (Love 1927), Love defines just two classes of elastica. The first class encompasses all those configurations where “the flexural couple vanishes, so that the rod can be held in the form of an inflectional elastica by terminal force alone” (Love 1927, p. 402). The inflectional elastica corresponds to an oscillating pendulum and embraces Euler’s Species 1–7. The second class, the non-inflectional elastica, corresponds to the revolving pendulum. It has no inflection points and is depicted by Euler’s Species 8, depicted in Fig. 2 and Species 9, which is the case where the elastica is bent into a ring.

It is not entirely clear when the analogy between the pendulum and the elastica was established, but certainly Gustav Kirchhoff (1824–1887) established the analogy within the context of his study of a spinning top and a twisted rod (Kirchhoff 1859). The top and twisted rod are respectively three-dimensional generalisations of the pendulum and elastica, and do not concern us here.

The static–dynamic analogy highlights the important differences between an initial value problem and a boundary value problem. In the former, the analyst need only specify a set of appropriate initial conditions. These are usually stipulated at time zero and with respect to the dynamics of a pendulum, the initial position θ and angular velocity \(\kappa\) are specified. In the case of the elastica the boundary conditions specify the details of how the ends of the rod are fixed and/or loaded. Typical conditions are welded, hinged and free. In the case of the pendulum, for a given set of initial conditions, there is just one unique solution. However, in the case of the elastica, there are an infinite number of solutions which satisfy a given set of boundary conditions. So the question immediately arises as to what an infinite number of solutions means with respect to a bent rod. The first person to address this question was Lagrange (1736–1813).

By restricting his analysis to the study of small deflections (a characteristically engineering approach), Lagrange (1770) employs the approximation dx≈ ds and subsequently obtains a linear second order differential equation:

$$ Py+B\frac{d^2y}{dx^2}=0. $$
(8)

Lagrange solves (8) for the case that the deflection and bending moment at the ends are zero (i.e. the ends are hinged). The solution is given by

$$ y(x)=A\sin \left( \sqrt{\frac{P}{B}}x\right), $$
(9)

where A is a constant representing the undetermined amplitude of the deflection at the mid point. Equation (9) implies that the condition y(L) = 0 can be satisfied by either A = 0, in which case the elastica is straight or by \(\sin \left( \sqrt{\frac{P}{B}}L\right)=0\), in which case \(\sqrt{\frac{P}{B}}L=n\pi\) where n = 0,1,2,3,…. Since n = 0 is also trivial, it follows that the condition for buckling is given by \(P_{c}=\frac{\pi^2nB}{L^2}\) . Thus Lagrange showed the existence of a multiplicity of buckling modes, or put another way, an infinite number of solutions to (9). In an uncharacteristic departure from his generally figure-less publications, Lagrange included in his paper some drawings of the buckled shapes for the cases n = 2 and n = 3 (see Fig. 7). The case n = 1 is the primary mode, discovered by Euler.

Fig. 7
figure 7

Lagrange’s Figures 3 and 4 of Lagrange (1770, p. 130), showing the second and third buckling modes of the planar elastica with hinged ends

Full size image

8 The Mathematisation of Nature

Lagrange first came to Euler’s attention in 1750; when at the age of nineteen he presented a scheme for tackling isoperimetric problems. Lagrange’s scheme involved a systematic procedure based on analytical techniques. It had the benefit that it could be applied to many of the various problems being studied at that time. Lagrange was to later apply this approach to mechanics. The search for unifying principles of mechanics and attempts to unify the various problems in mechanics was a major concern for both Lagrange and Euler.

The general principles governing the mechanics of elastic materials were only laid down when the concept of stress was formulated (mathematically) by Cauchy in 1822, (see Truesdell 1968). This was 78 years before Euler’s De Curvis Elasticis. Euler was able to solve the problem of the elastica without a concept of stress because the elastica is a one-dimensional problem: the equilibrium of forces and moments take the role of the stress equations. Nevertheless, in 1744 Euler did not have at his disposal a systematic methodology for tackling one-dimensional problems. In fact, the two important one-dimensional problems which had been successfully solved were the catenary and the elastica, but these were solved independently of each other. It was not clear to Euler, at least for most of his life, what underlying principles unifies these two problems.

It is not difficult to see today that both the catenary and the elastica problems concern long thin bodies i.e. they are both “rods”. As mentioned above, the catenary problem involves a special kind of rod—one which offers no resistance to bending. Some years prior to De Curvis Elasticis, in 1728, Euler had shown how the catenary and the elastica equations can be derived by the application of balance of moments (Truesdell 1968). However, it bothered him that whilst the catenary can also be derived from equilibrium of forces, this was not the case with the elastica. Evidentally this was a problem which he grappled with for many years:

… he was unsatisfied with the statical foundation of the theory of the elastica and sought for most of his lifetime, in repeated trials, to establish the equations of the elastica, like those of the catenary, directly from the balance of forces acting on a portion of the curve. That this is impossible, is one of the major pieces of evidence that led him, finally, to perceive that the balance of moments is a mechanical law independent, in general, of the balance of forces. (Truesdell 1968, p. 232)

At the age of 64 and having completely lost his eyesight, Euler took the crucial step which unified the catenary with the elastica: he separated the constitutive relations from the equilibrium equations. By subsequently decomposing the force vector into a shear force, N and an axial force T, he established a set of differential equations which express the balance of forces and the balance of moments M for a section of rod (in a plane):

$$ \frac{{\rm{d}}T}{{\rm{d}}s}+N\frac{{\rm{d}}\theta}{{\rm{d}}s}=-W_t,\quad\frac{{\rm{d}}N}{{\rm{d}}s}-T\frac{{\rm{d}}\theta}{{\rm{d}}s}=-W_n,\quad\frac{{\rm{d}}M}{{\rm{d}}s}-N=0, $$
(10)

where θ is the slope angle. Euler showed how all previous results involving elastic rods and strings can be derived from (10), which constitute one-dimensional versions of the general stress equations.

Euler’s unification of the elastica with the catenary was part of a grander scheme which he had being pursuing all his working life. It is succinctly expressed in a footnote to a paper on mechanics, Mechanica, which he wrote in 1736:

Firstly we will examine infinitesimal bodies, i.e. those that can regarded as points. We will then deal with bodies having a finite size—those that are rigid, not allowing their shape to be changed. Thirdly, we will discuss flexible bodies. Fourthly, we will discuss bodies that allow of tension and compression. Fifthly, we will investigate the motion of many separate bodies, one of which is preventing the others from executing motions in the way they are inclined to do. Sixthly, the flow of fluid bodies will be examined. In relation to these bodies, we will not only examine how, left to themselves, they continue to flow, but also investigate how external factors, i.e., forces, act on these bodies. (Quoted in Mikhailov and Stepanov 2007)

Euler’s Mechanica is recognised today as a landmark in the history of the development the general principles and formal procedures for the analysis of problems in mechanics (Truesdell 1968; Mikhailov and Stepanov 2007). It was also acknowledged as such by Euler’s contemporaries John Bernoulli and Maupertuis. It was almost certainly an inspiration for Lagrange’s quest to establish mechanics as a branch of analysis; a quest epitomised in the often quoted introduction to his definitive work The Mechanique Analytique:

To reduce the theory of mechanics, and the art of solving the associated problems, to general formulae, whose simple development provides all the equations necessary for the solution of each problem… No diagrams will be found in this work. The methods that I explain in it require neither constructions nor geometrical or mechanical arguments, but only the algebraic operations inherent to a regular and uniform process. Those who love Analysis will, with joy, see mechanics become a branch of it and will be grateful to me for thus having extended its field. (Quoted in Dugas 1955, p. 333)

If for Euler the role of mathematics is a tool for modeling problems which arise in mechanics (the models generally taking the form of ordinary and partial differential equations); then for Lagrange it was something deeper. Lagrange was seeking to place the whole of mechanics upon an axiomatic-deductive framework; an approach which follows closely in Descartes’ footsteps. But we should not interpret this as an attempt to divorce mechanics from its connection to the physical world. More likely, Lagrange was convinced, like the Pythagorean brotherhood before him, that Nature was inherently mathematical. Nevertheless, it would seem to be the case that other approaches to scientific enquiry (in particular experimentation) do not, for Lagrange, play a fundamental role. Lagrange also appears to have been more concerned with the formal procedures, the codification of problems, than with solving new ones; whereas Euler’s works reveals that he placed more value on physical principles than Lagrange. We note that by the time Lagrange wrote Mechanique Analytique, elementary geometry had been completely underpinned by the theory of equations (Stillwell 1989). With this in mind, Lagrange’s Mechanique Analytique can be interpreted as extending this mathematisation to mechanics. For this contribution Lagrange remains celebrated:

Lagrange’s advancement in the foundations of science can be hardly overemphasised. In the history of science, the birth of Lagrange’s Mechanics constitutes a milestone, as it was correctly perceived by subsequent scientists. Indeed, Lagrange’s Mechanics started a new epoch for the history of the whole science; in this new epoch, a whole field of scientific phenomena, such as mechanical phenomena, can be managed in a synthetic and straightforward way. (Capechhi and Drago 2005)

Some historians of science and mechanics are less impressed. Clifford Truesdell (1919–2000) writes scathingly of Lagrange’s The Mechanique Analytique

Unlike Newton’s Principia, it contains scarcely any examples, applications, interpretations in physical contexts, or new results. It omits all problems not easily amenable to Lagrange’s methods…… Its effect upon subsequent conceptions of the history of mechanics was largely unfortunate, first because, concentrating upon facile algebra, it failed to mention the deepest work done in the eighteenth century, and second because Lagrange included historical sketches which are so capriciously lacunary as to lie in effect even if not in fact. (Truesdell 1984)

The quest to set mechanics upon an axiomatic basis continued into the twentieth Century. In 1900, the mathematician David Hilbert (1862–1943) delivered a lecture at the International Congress of Mathematicians in Paris. He presented a series of problems for mathematicians to strive to solve. “Problem 6” was as follows:

To treat in the same manner, by means of axioms, those physical sciences in which mathematics plays an important part; in the first rank are the theory of probabilities and mechanics. (Hilbert 1900)

In 1957, Walter Noll (1925) in a series of papers, set out axioms of mechanics which have been proclaimed as a “the true turning point in the history of the axiomatisation of mechanics” (Benvenuto 1991). Noll’s approach was adopted by Truesdell and others who founded a branch of mechanics called “rational mechanics”. We remark here that Antman’s treatise (1995) on rod theory is firmly identified with rational mechanics. The value of this work, and others like it, to engineers is perhaps most widely felt with respect to computational work, where correct problem formulation is important. Thus we find in Antman (1995) a systematic codification of boundary value problems and mathematical descriptions of a wide range of boundary conditions, such as welded, hinged, and ball and socket joints: conditions which are of practical importance in engineering design.

9 Discussion

A “rod” is something of a hybrid—a mathematical curve made up of “material points”. It has no cross section, yet it has stiffness. It can weigh nothing or it can be heavy. We can twist it, bend it, stretch it and shake it, but we cannot break it, it is completely elastic. Of course, it is a mathematical object, and does not exist in the physical world; yet it finds wide application in structural (and biological) mechanics: columns, struts, cables, thread, and DNA have all been modeled with rod theory.

It is precisely its ability to transgress the realms of physical experience which provides the elastica with its power and versatility. In this respect we can think of the mathematical model as an experimental laboratory where we can perform experiments on an idealised Platonic object. The physical objects which we observe in our everyday lives which resemble a rod are therefore imperfect copies of the “real” thing. The planar elastica is essentially a simple model: as well as being a one-dimensional representation of a three-dimensional object, it additionally assumes that the rod is isotropic, homogeneous, and has a linearly elastic response to end loads. It is also integrable. The benefit to engineers of this simple model lies in its provision of a straightforward benchmark both for the study of more complex mathematical models and for experiments on “imperfect physical rods”. The principles of mechanics were for the most part forged by finding solutions to simple problems, such as the catenary and elastica. As we have seen, these problems were solved in the absence of any general scheme for one-dimensional elasticity, let alone the concept of stress. But the unification of the problems was a major step towards establishing the general theory.

In his lecture titled The Role of Experiments in Mechanics, K. Ravi-Chandar states that “The role of experiments is very clear: it has to do with discovery, characterisation, and verification” (Ravi-Chandar 2005). Discovery starts with observation, though before we carry out an experiment we must be equipped with a theory, a notion of the underlying principles and physics. Without this, we would be unable to recognise the significance of what we observe. The process of characterisation involves qualitative and quantitative descriptions of our observations. Ravi-Chandar defines verification as the determination of the physical and mathematical limitations of the discovery. Engineering students, may well follow similar steps during laboratory sessions. In addition to helping the student see how knowledge is reached and verified, practical laboratory work provides an opportunity for the student to acquire key experimental skills. These skills are useful because an experiment can assist students to bridge the gap between the theories of engineering mechanics and real-world engineering—a key learning outcome from an engineering undergraduate course. This combination of experimentation and mathematical modeling constitutes the basis of other similarly useful investigations into everyday phenomena, see for example Lyons and Brader (2004). Sometimes everyday phenomena require complicated mathematical models, and this is certainly the case for the large deflections of an elastic rod. A related case involves the vibrations of a car antenna, which can be modeled as a beam and leads us to construct a fourth order partial differential equation (Newburgh and Newburgh 2000). We may not expect a first year undergraduate student to be equipped with the mathematical skills required for solving these problems, however there is much pedagogic value to seeing the relationship between the everyday observation and the complicated mathematical model and in following the steps taken towards formulating the model.

Many studies point to history as a means of encouraging students to think more deeply about their discipline, to develop enquiring, critical minds and formulate innovative ideas (Schecker 1992; Speiser 2003). The story of the elastica offers a number of different avenues for exploring these themes. Perhaps the most important is the connections between mathematics and engineering. Experience indicates that students of engineering and the sciences often find it difficult to fully grasp the connections between mathematical analysis and engineering practise. Engineering students are not usually attracted to engineering for the reason of doing mathematics. On the contrary, mathematics is often something which they do in a perfunctory manner. This attitude can prevent them from thinking deeply about their subject matter. A closer look at rod theory, however, reveals a world of underlying symmetry. The symmetry which one finds in the mathematics is mirrored in the configuration of the elastica. Furthermore, since these configurations are equilibrium states of minimal energy, we can establish an intimate connection with Euler’s isoperimetric method and the calculus of variations. Concepts of perfect form, so essential in the arts, are also important for engineers. That this appreciation of mathematics is often missed in the sciences is at least partly a consequence of an education which emphasises mathematical technique.

The related issues of equilibrium and stability, crucial in engineering practise, arise within the context of both the statics of a straight rod and the dynamics of the inverted pendulum. The latter case can only be encountered by studying the nonlinear mathematical model. The use of computers makes it easier for the undergraduate engineering student to learn about nonlinear mechanics, without the requirement to study a lot of new mathematics (such as elliptic functions). The computer also permits an easy-enough examination of the dynamic–static analogy by means of the phase plane, which has applications beyond rod theory. It opens a door to a world which the engineering undergraduate rarely glimpses and may not even know exists, even though the student may observe nonlinear dynamics/post-buckling in the physical world. Mostly engineers are concerned to avoid any deflections, hence small deflection linear models. However, large deflection problems are not simply the focus of curiosity, but continue to find new applications in engineering and the physical sciences. The static–dynamic analogy also presents the student with a clear means of understanding the difference between initial value and boundary value problems. And we note that students engaged in a wide variety of engineering disciplines will come across both the pendulum and buckling during the course of their studies. We have also mentioned the analogy between a spinning top and three-dimensional configurations of a twisted rod. It is unlikely that the student identifies a twisted bar with a gyroscope. But knowledge of these concepts and the various associated classification schemes (e.g., Euler’s Species and Love’s inflectional/noninflectional forms) encourages the student to identify further analogies (see Kipnis 2005), to synthesise and to seek order and simplicity.

It is common practise for students to learn the principles of mechanics by means of mathematical analysis and by experiments in the laboratory—the same scientific methodology established by Galileo and Newton. However, this can sometimes be denigrated to the study of an arid desert of scientific “facts”, laws, axioms, techniques and procedures. These the student are expected to learn without question, to systematically apply to the solution of various problems, and most importantly (for the student) to regurgitate a few months later during a 3 h examination. Whilst this depressing picture is obviously an exaggeration, unfortunately it is all too often the perceived view of what learning science and engineering is all about. Furthermore, it has been pointed out that this idea of science does not provide for real world scientific practise and does not reflect what goes on in scientific research (Metz et al. 2007). It is no wonder though, against such a popular misconception of engineering and science that it is the social sciences and the arts which tend to attract the more critical and independent-minded students into their ranks. Nevertheless, with increasing public awareness of the huge social responsibility which engineers have with respect to the environment, it has become increasingly evident to professional bodies and employers that engineers need to take account of the wider implications of their activities. Historical studies can help to provide this awareness.