A tractable method to measure utility and loss aversion under prospect theory

Abstract

This paper provides an efficient method to measure utility under prospect theory. Our method minimizes both the number of elicitations required to measure utility and the cognitive burden for subjects, being based on the elicitation of certainty equivalents for two-outcome prospects. We applied our method in an experiment and were able to replicate the main findings on prospect theory, suggesting that our method measures what it is intended to. Our data confirmed empirically that risk seeking and concave utility can coincide under prospect theory. Utility did not depend on the probability used in the elicitation, which offers support for the validity of prospect theory.

Traditionally, utility measurement has assumed that people behave according to expected utility. Then a decision maker’s utility can be measured by eliciting a few equivalences between prospects. Evidence abounds, however, that people violate expected utility in systematic ways (Starmer 2000) and that utility measurements based on expected utility give inconsistent results (Hershey and Schoemaker 1985; Bleichrodt et al. 2001; Abdellaoui et al. 2007). An obvious danger of basing utility measurement on a theory that is descriptively invalid is that the obtained utilities will be biased and that recommendations are made that are not in the decision maker’s best interests.

Two important causes of violations of expected utility are probability weighting, the nonlinear evaluation of probabilities, and loss aversion, the finding that people evaluate outcomes as gains and losses relative to a reference point and are more sensitive to losses than to gains (e.g. Diecidue and Wakker 2001; Tversky and Kahneman 1992). Both probability weighting and loss aversion are modeled by prospect theory. A difficulty in measuring utility under risk, assuming prospect theory, is that the methods that are commonly used to measure utility, such as the probability, certainty equivalence, and lottery equivalence methods (Farquhar 1984; McCord and de Neufville 1986) are no longer valid because they do not take account of probability weighting and loss aversion.

Tversky and Kahneman (1992) measured utility under prospect theory by imposing parametric forms for utility and probability weighting. Gonzalez and Wu (1999) observed, however, that the parametric form for the probability weighting function that was adopted by Tversky and Kahneman (1992) did not fit the data of their subjects. An important improvement in measuring utility under prospect theory was made by Wakker and Deneffe (1996). Their trade-off method for measuring utility is robust to probability weighting when all outcomes are of the same sign. The trade-off method can measure utility on the domain of gains and on the domain of losses separately, but it cannot handle loss aversion and, hence, it cannot be used to measure utility on the entire domain of gains and losses without making additional parametric assumptions. This problem was solved by Abdellaoui, Bleichrodt, and Paraschiv (2007). They derived a method that allows to completely measure utility under prospect theory without imposing any assumptions on utility, probability weighting, or loss aversion. Nonparametric measurements offer three important advantages over parametric measurements. First, the measurements are not confounded by assumptions about the shape of utility or probability weighting. Second, the measurements provide insight in the psychological processes underlying the measurements because there is a direct link between choices and utilities. Third, the direct link between choices and utilities allows solving inconsistencies in utility measurement, which is important for prescriptive decision making. Observed inconsistencies can be directly related to particular choices and solving these inconsistencies will give new insights into the decision maker’s preferences. Under parametric assumptions there is no direct link between choices and utilities.

A drawback of nonparametric measurements compared to parametric measurements is that they are generally more susceptible to response error and are less efficient, in the sense that more questions are needed. The relative lack of efficiency can be a problem in applied decision analysis and, in particular, in neuroeconomics where efficient methods are highly desirable given the high cost of running subjects. The purpose of this paper is to propose a new method to measure utility under prospect theory that seeks to achieve a balance between the advantages of nonparametric and parametric measurements. Our method is the most efficient method to measure utility under prospect theory [and models that coincide with it for two-outcome prospects such as rank-dependent utility and Gul’s (1991) theory of disappointment aversion] that is currently available. Accounting for response error, the elicitation of utility on the full domain requires about 10–12 elicitations, which can be performed in about 15 min. Our method uses only parametric assumptions that are widely supported in the literature. The key insight behind our method is that only the decision weight of one probability needs to be known to measure utility. This insight reduces the number of measurements and thereby enhances the scope for application of prospect theory. Because we only need the weight of one probability our method requires no assumptions about probability weighting. The method is based on the elicitation of certainty equivalents of prospects involving just two outcomes, a widely used method in applied research and decision analysis. The certainty equivalence method in which an outcome for sure is compared with a two-outcome prospect is generally perceived as easier than methods that compare two risky prospects such as the trade-off method, which is used in step 1 of the method of Abdellaoui, Bleichrodt, and Paraschiv (2007). Hence, our method minimizes the cognitive burden for subjects. The different certainty equivalents are not linked and, hence, not susceptible to error propagation. For utility, we adopt a parametric specification. Our method works for various parametric specifications but we will mainly focus on the power specification. Previous findings indicate that the power function provides an excellent fit to utility measurements (for an overview see Stott 2006). In particular, Abdellaoui, Bleichrodt, and Paraschiv (2007) observed that the power function fitted their data very well.

We applied our method in an experiment. Our data confirmed most previous findings on prospect theory, which we interpret as support for our method. A novel finding that we observed is the coexistence of concave utility and risk seeking behavior for losses. This observation shows that the one-to-one relationship between risk aversion and utility curvature that exists under expected utility no longer holds under prospect theory. Chateauneuf and Cohen (1994, Corollary 4) derived theoretically that risk seeking behavior and concave utility can coincide under prospect theory. To the best of our knowledge, we are the first to observe this empirically and, hence, our finding can be interpreted as the empirical counterpart to Chateauneuf and Cohen (1994).

The paper proceeds as follows. Section 1 reviews prospect theory and previous empirical evidence on utility, probability weighting and loss aversion under prospect theory. Section 2 describes our method for eliciting prospect theory. Section 3 describes the design of an experiment in which our method was applied. Section 4 describes the results of our experiment and Section 5 concludes.

1 Prospect theory

Let (x, p; y) denote the binary prospect that results in outcome x with probability p and in outcome y with probability 1 − p. Throughout the paper we will only use binary prospects. For binary prospects, original prospect theory (Kahneman and Tversky 1979) and new (or cumulative) prospect theory (Tversky and Kahneman 1992) coincide and all our results are valid under both theories.

Let ≽ denote the decision maker’s preference relation over binary prospects. The relations of strict preference and indifference are denoted by ≻ and ∼. Outcomes are real numbers, they are money amounts in the experiment reported in Section 3. Higher numbers are always preferred. If x = y or p = 0 or p = 1 the prospect is riskless, otherwise it is risky. Outcomes are expressed as changes with respect to the status quo or reference point, i.e. as gains and losses. Throughout the paper, we assume that the reference point is 0. Hence, gains are outcomes larger than 0 and losses outcomes less than 0. A gain prospect involves no losses, a loss prospect no gains. A mixed prospect involves both a gain and a loss. For gain [loss] prospects, the notation (x, p; y) implies that x ≥ y ≥ 0 [x ≤ y ≤ 0]. For mixed prospects, it implies that x > 0 > y.

1.1 Utility and probability weighting for gains and losses

The individual evaluates each prospect and chooses the prospect that offers the highest overall utility. The overall utility of a prospect is expressed in terms of three functions: a probability weighting function w ⁺ for gains, a probability weighting function w ⁻ for losses, and a utility function U.

Under prospect theory, gain prospects (x, p; y) are evaluated as

$$w^ + \left( p \right)\left( {U\left( x \right) - U\left( y \right)} \right) + U\left( y \right),$$

(1a)

and loss prospects as

$$w^ - \left( p \right)\left( {U\left( x \right) - U\left( y \right)} \right) + U\left( y \right).$$

(1b)

The probability weighting functions w⁺ and w⁻ are strictly increasing and satisfy w ⁺(0) = w ⁻(0) = 0 and w ⁺(1) = w ⁻(1) = 1. The utility function U is strictly increasing and satisfies U(0) = 0. U is a ratio scale, i.e. we can arbitrarily choose the unit of the function. The intuition behind Eq. 1a [1b] is that the decision maker gains [loses] at least U(y), regardless of how the uncertainty is resolved, and may gain [lose] an additional w ^s(p)(U(x) − U(y)), s = +, −.

The utility of a mixed prospect (x, p; y) is equal to

$$w^ + \left( p \right)U\left( x \right) + w^ - \left( {1 - p} \right)U\left( y \right).$$

(2)

Expected utility is the special case of prospect theory where w ⁺(p) = w ⁻(p) = p.

Tversky and Kahneman (1992) assumed that the utility function and the probability weighting functions w ⁺ and w ⁻ exhibit diminishing sensitivity. This leads to an S-shaped utility function, concave for gains and convex for losses and to inverse S-shaped probability weighting functions, overweighting small probabilities and underweighting moderate and high probabilities. Taken together, S-shaped utility and inverse S-shaped probability weighting imply a fourfold pattern of risk attitudes: risk aversion for small-p losses and larger-p gains and risk seeking for larger-p losses and small-p gains. Loss aversion predicts strong risk aversion for mixed prospects. Empirical evidence supports both the fourfold pattern and strong risk aversion for mixed prospects (e.g. Laughhunn et al. 1980; Payne et al. 1980, 1981; Schoemaker 1990; Myagkov and Plott 1997; Heath et al. 1999).

Most empirical studies on probability weighting observed inverse S-shaped probability weighting both for gains and for losses (Tversky and Kahneman 1992; Tversky and Fox 1995; Wu and Gonzalez 1996; Gonzalez and Wu 1999; Abdellaoui 2000; Bleichrodt and Pinto 2000). The point where the probability weighting function changes from overweighting probabilities to underweighting probabilities lies around 1/3.

Measurements of the shape of utility for gains and for losses have generally confirmed prospect theory’s assumption of concave utility for gains and convex utility for losses. This holds both at the aggregate and at the individual level. The available evidence is stronger for gains than for losses. When the power specification was assumed, the estimated power coefficients generally varied between 0.70 and 0.90 for gains and between 0.85 and 0.95 for losses.

1.2 Loss aversion

Many empirical studies have observed qualitative support for loss aversion both at the individual and at the aggregate level. Few studies have, however, performed quantitative estimations of loss aversion. To measure loss aversion the utility for gains and losses must be measured simultaneously and, as mentioned before, until recently no method existed to perform such a measurement without imposing additional assumptions. An additional complication in the measurement of loss aversion is that there is no agreed-upon definition of loss aversion. Abdellaoui, Bleichrodt, and Paraschiv (2007) compared several definitions that have been proposed in the literature and concluded that the definitions proposed by Kahneman and Tversky (1979) and Köbberling and Wakker (2005) were most satisfactory in the sense that they were able to classify most subjects according to their attitude towards losses. Kahneman and Tversky (1979) suggested that loss aversion be defined by −U(−x) > U(x) for all x > 0. This implies that a loss aversion coefficient can be defined as the mean or median of $- \frac{{U\left( { - x} \right)}}{{U\left( x \right)}}$ over relevant x. Tversky and Kahneman (1992) implicitly used $- \frac{{U\left( { - \$ 1} \right)}}{{U\left( {\$ 1} \right)}}$ as an index of loss aversion. This index has become popular in the empirical literature and many studies have taken Tversky and Kahneman’s (1992) estimate of 2.25 as the value of the index for loss aversion. Köbberling and Wakker (2005) defined the loss aversion coefficient as, $\frac{{U'_ \downarrow \left( 0 \right)}}{{U'_ \downarrow \left( 0 \right)}}$ where ${\text{U'}}_ \uparrow \left( 0 \right)$ stands for the left and $U'_ \downarrow \left( 0 \right)$ for the right derivative of U at the reference point. This definition can be considered the limiting case of Kahneman and Tversky’s (1979) definition for x approaching 0. A similar definition was suggested by Benartzi and Thaler (1995). In this paper we will employ the definition of Tversky and Kahneman (1992). This follows from our adoption of the power specification for utility. If a different specification for utility is used, our method can easily quantify the Köbberling and Wakker’s (2005) index as well.

2 Elicitation method

Our elicitation method consists of three stages. In the first stage utility is elicited on the gain domain, in the second stage utility is elicited on the loss domain, and in the third stage the utility on the gain domain and on the loss domain are linked.

Like Köbberling and Wakker (2005), we assume that observable utility U is a composition of a loss aversion coefficient λ > 0, reflecting the different processing of gains and losses, and a basic utility u that reflects the intrinsic value of outcomes. Formally, this assumption means that

$$U\left( x \right) = \left\{ {\begin{array}{*{20}l} {u\left( x \right)} \hfill & {if} \hfill & {x \geqslant 0} \hfill \\ {\lambda u\left( x \right)} \hfill & {if} \hfill & {x <0.} \hfill \\ \end{array} } \right.$$

(3)

The exact definition of loss aversion depends on the specification of u. We will return to this issue later.

2.1 Elicitation of utility on the domain of gains and on the domain of losses

Consider first the elicitation of utility on the gain domain. We start by selecting a probability p_g that is kept fixed throughout the elicitation of the utility function on the gain domain. We choose a series of gain prospects (x _i , p _g ; y _i ), i = 1,…,k. and elicit their certainty equivalents G _i . By Eqs. 1a and 3 it follows that

$$u\left( {G_i } \right) = \delta ^ + \left( {u\left( {x_i } \right) - u\left( {y_i } \right)} \right) + u\left( {y_i } \right)$$

(4)

or

$$G_i = u^{ - 1} \left( {\delta ^ + \left( {u\left( {x_i } \right) - u\left( {y_i } \right)} \right) + u\left( {y_i } \right)} \right),$$

(5)

where δ ⁺ = w ⁺(p _g ). The advantage of keeping the probability p _g fixed is that only one point of the probability weighting function plays a role in the process of utility elicitation. The probability weight δ ⁺ can just be taken to be one additional parameter that has to be estimated in the utility elicitation exercise. In fact, if we adopt a parametric specification for utility, then Eq. 5 can easily be estimated through nonlinear least squares.¹ In the experiment described below we adopted the most widely used parametric specification, the power function $u\left( x \right) = x^\alpha$. Then

$$G_i = \left( {\delta ^ + \left( {x_i^\alpha - y_i^\alpha } \right) + y_i^\alpha } \right)^{{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha }} ,$$

(6)

where α and δ ⁺ are the parameters to be estimated. The parameter α reflects the curvature of the utility function and δ ⁺ reflects the impact of probability weighting at probability p _g . Under expected utility we only need to measure α. Note that the adoption of a power function implies the scaling u(1) = 1.

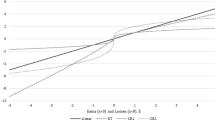
Figure 1 shows the impact of probability weighting on utility measurement when δ ⁺ < p _g , i.e. when probabilities are underweighted. The figure shows that underweighting of probabilities will exert a downward impact on the elicited utilities compared with expected utility, the case in which there is no probability weighting. Because utility is unique up to unit and location we can fix the utility of two outcomes. In the figure, we have fixed the utility of the outcomes x _i and y _i . Expected utility then posits that the utility of G _i is equal to $p_g \left( {u\left( {x_i } \right) - u\left( {y_i } \right)} \right) + u\left( {y_i } \right)$. This exceeds $\delta ^ + \left( {u\left( {x_i } \right) - u\left( {y_i } \right)} \right) + u\left( {y_i } \right)$, the utility of G _i under prospect theory, when probabilities are underweighted. Consequently, analyzing the data under expected utility theory will overestimate the concavity of utility on the gain domain when probabilities are underweighted. A similar analysis reveals that expected utility will underestimate the concavity of utility on the gain domain when probabilities are overweighted. Figure 1 also shows that if the underweighting of probabilities is strong enough then risk aversion can co-exist with linear or even convex utility. In the figure the utility function under expected utility is concave indicating risk aversion. However, if δ⁺ is sufficiently low then the utility function can be convex under prospect theory. Hence, the one-to-one relationship between risk aversion and concave utility, which exists under expected utility, no longer exists under prospect theory. This observation was formally proved by Chateauneuf and Cohen (1994).

Fig. 1

The impact of probability weighting on utility measurement

The procedure to elicit utility on the domain of losses is largely similar to the procedure described above for gains. We select $p_\ell = 1 - p_g$ and a series of prospects (x _i , $p_\ell$, y _i ) for which 0 ≥ y _i  > x _i , i = 1, …, k and elicit their certainty equivalents L _i . The reason we set $p_\ell = 1 - p_g$ is that this equality is crucial in the estimation of loss aversion. By Eqs. 1a, 1b and 3 it follows that

$$L_{i} = u^{{ - 1}} {\left( {\delta ^{ - } {\left( {u{\left( {x_{i} } \right)} - u{\left( {y_{i} } \right)}} \right)} + u{\left( {y_{i} } \right)}} \right)},$$

(7)

where $\delta ^ - = w^ - \left( {p_\ell } \right)$. By adopting a parametric specification for u we can estimate Eq. 7 by nonlinear least squares. Underweighting of probabilities now entails that expected utility will underestimate the concavity of utility on the loss domain and overweighting of probabilities entails that expected utility overestimates the concavity of utility on the loss domain.

Because we only use the weight of one probability we do not have to make assumptions regarding probability weighting in the estimation of Eqs. 5 and 7. Moreover, Eqs. 5 and 7 can be estimated at the individual level and, hence, individual heterogeneity in probability weighting is taken into account.

2.2 Measuring loss aversion

The third stage of our elicitation procedure serves to establish the link between the utility for gains and the utility for losses and, hence, measures the loss aversion coefficient λ. This can be done through the elicitation of a single indifference. Select a gain G* from within (0, x _k ], the interval for which u was determined in the first stage and determine the loss L* for which (G*, p _g ; L*) ~ 0. It follows from Eqs. 2, 3 and $p_\ell = 1 - p_g$ that

$$\delta ^ + u\left( {G^ * } \right) + \delta ^ - \lambda u\left( {L^ * } \right) = u\left( 0 \right) = 0.$$

(8)

Because δ ⁺, u(G*), δ ⁻, and u(L*) are known from the estimation of Eqs. 5 and 7, Eq. 8 uniquely determines λ. Our procedure imposes no constraints on λ and both loss aversion (λ > 1) and gain seeking (λ < 1) are possible.

3 Experiment

3.1 Subjects

Subjects were 48 (25 female) graduate students in economics and mathematics at the Ecole Normale Supérieure, Antenne de Bretagne, France. They were paid €10 for their participation. In addition, one subject was randomly selected to play out one of the gain questions with the actual payment divided by 10. We chose this incentive scheme for the following reason. On the one hand, and as discussed in Abdellaoui, Barrios and Wakker (2007), it is desirable to implement real incentives. On the other hand, utility measurements are typically of interest only for significant amounts of money: utility is close to linear for moderate amounts of money (Rabin 2000; Savage 1954, p. 60). Therefore, we adopted a “mixed” strategy using significant amounts of money (up to €10,000 for gains) along with the random selection of one subject to play out one of the gain questions with the actual payment divided by 10. This incentive mechanism makes feasible the maximum amount at stake (€1,000) for the experimentalist while keeping the attractiveness of the outcomes for subjects. The random lottery selection procedure is common in experimental economics and previous research observed that it gives similar results as a procedure in which each question is played out for real (Starmer and Sugden 1991; Cubitt et al. 1998). Division of large amounts is also not uncommon in experimental economics (e.g. Andersen et al. forthcoming). For ethical and feasibility reasons, we could not play out for real one of the loss questions or one of the mixed questions. Section 5 of this paper will further discuss our incentive procedure in light of recent experimental results on utility elicitation and the impact of real incentives on certainty equivalent elicitation for gains and losses.

3.2 Procedure

The experiment was run on a computer. Responses were collected in personal interview sessions. Subjects were told that there were no right or wrong answers and that they were allowed to take a break at any time during the session. The responses were entered into the computer by the interviewer, so that the subjects could focus on the questions. Before the experiment started subjects were given several practice questions. The experiment lasted 60 min on average, including 15 min for explanation of the tasks and practice questions.

All indifferences were elicited through a series of binary choices. Each binary choice corresponded to an iteration in a bisection process, which is described in Appendix 2. After each choice the subject was asked to confirm his choice. We used a choice-based elicitation procedure because previous studies have found that inferring indifferences from a series of choices leads to fewer inconsistencies than asking subjects directly for their indifference values (Bostic, Herrnstein, and Luce 1990). In each choice a subject was faced with two prospects, labeled A and B, where prospect A was always riskless. Prospects were displayed as pie charts with the sizes of the slices of the pie corresponding to the probabilities. Appendix 1 gives two examples of the way the experimental questions were displayed. To control for response errors, we repeated the first iteration after the final iteration. The iteration process was started anew when a subject changed his choice in the repeat of the first iteration.

3.3 Stimuli

We used six certainty equivalence questions to elicit the utility function for gains and six certainty equivalence questions to elicit the utility function for losses. The prospects for which we determined the certainty equivalents are displayed in Table 1. We used substantial money amounts to be able to detect curvature of utility; for small amounts utility is approximately linear (Wakker and Deneffe 1996). We used round money amounts, multiples of €1,000, to facilitate the task for the subjects.

Table 1 Questions asked to determine the utility for gains and the utility for losses

Our method also allows examining the validity of prospect theory with utility equal to Eq. 3. As a first test, we elicited utility using two different values of p _g , p _g  = 1/2 and p _g  = 2/3 and, consequently, $p_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ and $p_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$ for losses. Under prospect theory we should observe no systematic differences between the utility elicited with p _g  = 1/2 and the utility elicited with p _g  = 2/3. For losses no difference should be observed between the utility elicited with $p_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ and the utility elicited with $p_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$.

The order in which the 24 certainty equivalents were elicited was random, except that we always elicited first six certainty equivalents for gains, then six certainty equivalents for losses, then six certainty equivalents for gains, and finally six certainty equivalents for losses. We learned from the pilot sessions that subjects found it easier to start with questions involving only gains than to start with questions involving only losses. At the end of the elicitation of the utility for gains and the elicitation for losses we repeated the third iteration for eight questions, four for gains (two for p _g  = 1/2 and two for p _g  = 2/3) and four for losses (two for $p_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ and two for $p_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$). The questions that were repeated were determined randomly.

To determine the loss aversion coefficients, we selected $G_1^ * , \ldots G_6^ *$ and determined $L_j^ *$ such that $\left( {G_j^ * ,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2};\;L_j^ * } \right) \sim 0,j = 1, \ldots ,6$. Our method only needs one indifference to elicit the loss aversion coefficient λ. We used six questions to have another test of the validity of prospect theory with Eq. 3. Under prospect theory with Eq. 3, the six values of the loss aversion coefficients that we observed should be equal. The order in which these questions were asked was random. We repeated the third iteration of two randomly determined questions to test for consistency.

3.4 Analysis

As mentioned before, we used a power specification for utility. To test the robustness of our findings we also explored two other parametric specifications: exponential, and expo-power. The power and exponential specification are widely used in economics and decision analysis. The expo-power family was proposed by Abdellaoui, Barrios, and Wakker (2007). The goodness of fit, as measured by the sum of squared errors, did not differ significantly between the three families (p = 0.100). Convergence of the estimations was better for power and expo-power than for exponential. The results based on expo and expo-power were similar to the results for the power family. The results were also similar when we took for each subject the family that best fitted his data.

The power family for gains is defined by ${\text{x}}^\alpha$ and for losses by $- \left( { - {\text{x}}} \right)^\beta$ with α,β > 0. For gains (losses), the power function is concave if α < 1 (β > 1), linear if α = 1 (β = 1), and convex if α > 1 (β < 1). For the power family the loss aversion coefficient λ is defined as $\frac{{ - {\text{U}}\left( { - 1} \right)}}{{{\text{U}}\left( 1 \right)}}$. This is the definition implicitly adopted by Tversky and Kahneman (1992).

Based on the obtained estimates for the power coefficient we could classify individuals according to the shape of their utility for gains and the shape of their utility for losses. We used two classifications. In the first classification, a subject was classified as concave (convex) for gains if the power estimate for gains was less than (greater than) 1. For losses a subject was classified as convex (concave) if the power estimate for losses was less than (greater than) 1. In the second classification, which was included to examine the robustness of the first classification, we only counted the number of subjects for whom the power coefficient differed statistically significantly from 1 based on the standard error that resulted from the nonlinear least squares estimation. This second classification led to similar conclusions as the first and, hence, these data are not reported separately.

In each question, a subject was risk averse if the certainty equivalent was less than the expected value of the prospect, risk neutral if the certainty equivalent was equal to the expected value of the prospect, and risk seeking if the certainty equivalent exceeded the expected value of the prospect. To account for response error, we classified a subject as risk averse for gains (losses) if at least 8 out of 12 certainty equivalence questions involving gains (losses) produced a risk averse answer. Similarly, a subject was classified as risk neutral (seeking) if at least 8 out of 12 questions produced a risk neutral (seeking) answer.

For loss aversion we computed for each subject the median of the six elicited loss aversion coefficients. A subject was classified as loss averse if this median exceeded 1 and as gain seeking if it was less than 1.

We will focus on the medians in what follows. The results for the means were similar. Significance of differences was tested by the Wilcoxon test and by the Friedman test (for comparisons between more than two variables). The binomial test was used to test for differences between proportions.

4 Results

4.1 Reliability

One subject was excluded because she did not understand the task. This left 47 subjects in the final analysis. In the analysis of loss aversion we excluded another five subjects because they were not willing to trade any loss for a gain regardless how small the loss.

The reliability of the responses was good. In 95.6% of the cases, the replication of the first iteration led to the same choice as the first iteration. In 66% of the cases, the replication of the third iteration led to the same choice. The lower reliability in the third iteration is not surprising because the stimulus value was generally close to the certainty equivalent in the third iteration. The reliability in the repeat of the third iteration was comparable to the reliability observed in previous studies (for an overview see Table 1 in Stott 2006). In the repeat of the first iteration the reliability was much better, as expected given that this involved choices for which most subjects had a clear preference for one of the two options.

4.2 Consistency

The consistency tests supported prospect theory. We neither observed significant differences between the utility for gains elicited using p_g = 1/2 and the utility for gains elicited using p_g = 2/3 (p = 0.492) nor between the utility for losses elicited using ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ and the utility for losses elicited using ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}\left( {{\text{p}} = 0.320} \right)$. Because utility did not depend on the probability used in the elicitation, we will mainly focus on the results for ${\text{p}}_{\text{g}} = {\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ in what follows.

Table 2 shows the median loss aversion coefficients elicited from the six mixed prospects. Although there is some variation in the medians, we could not reject the null hypothesis that the 6 elicited loss aversion coefficients were equal (p = 0.96). This is consistent with prospect theory and Eq. 3 and we will henceforth pool the observations from the six loss aversion questions.

Table 2 Elicited loss aversion coefficients from the six mixed prospects

4.3 Median certainty equivalents and risk attitude

Table 3 shows the median responses to the 24 certainty equivalence questions used to elicit the utility for gains and the utility for losses and their interquartile ranges. The table shows that the dominant pattern was risk aversion for gains and risk seeking for losses, but for losses subjects were closer to being risk neutral than for gains. For gains, the certainty equivalent of a prospect is always lower than its expected value, consistent with risk aversion. Overall, 74% of the choices were consistent with risk aversion for p_g = 1/2 and 81% for p_g = 2/3. For losses and ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$, there is risk seeking in 4 out of 6 questions (the expected value is smaller than the certainty equivalent). For ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$, there is risk seeking in 3 questions and risk aversion in the other 3. Overall, 59% of the choices were consistent with risk seeking for ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$, but only 46% for ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$. The difference between the certainty equivalent and the expected value was generally larger for gains than for losses.

Table 3 Median elicited certainty equivalents (absolute values)

Table 4 shows the classification of the subjects in terms of their risk attitude for gains and for losses. Risk aversion was dominant for gains, the difference between risk averse and risk seeking was highly significant (p < 0.001). The proportion of risk averse subjects that we observed was comparable to the proportion observed in previous studies (Schoemaker 1990; Tversky and Kahneman 1992; Fennema and van Assen 1998; Abdellaoui 2000; Abdellaoui et al. 2007; Baucells and Villasis 2006). For losses the picture was more varied. Risk seeking was most common but the difference between the proportion of risk seeking subjects and the proportion of risk averse subjects was not significant (p = 0.617). The proportion of risk seeking subjects that we observed was generally lower than in previous studies, the exception being Booij and van de Kuilen (2007). When we combine risk attitudes for gains and for losses, the most common pattern is risk aversion both for gains and for losses. The proportion of subjects who were risk averse both for gains and for losses was, however, not significantly different from the proportion of subjects who were risk averse for gains and risk seeking for losses (p = 0.424).

Table 4 Classification of subjects in terms of risk attitude

Consistent with previous studies we observed strong risk aversion in the mixed prospects. Table 5 shows the median results in the mixed prospects. The size of the loss that established indifference was typically around half the size of the corresponding gain. Overall, 80.5% of choices were risk averse. At the individual level, the degree of risk aversion was comparable to the degree of risk aversion in the gains prospects: 36 subjects were risk averse, 9 risk seeking, and 2 were classified as mixed.

Table 5 Median results in the mixed prospects

4.4 Utility for gains and losses

Figure 2 displays the elicited utility function based on the median data. The estimated parameters are given in Table 6. The elicited utility function was not entirely consistent with the conjecture of Kahneman and Tversky (1979) that utility is S-shaped. For gains the function was concave. The median power coefficient of 0.86 differed significantly from 1 (p = 0.041) and was close to and not significantly different from the power coefficients found in most previous studies. The interquartile range for the power coefficient indicated considerable variation at the individual level.

Fig. 2

The elicited utility function based on the median data

Table 6 Estimation results

For losses, however, we did not observe convexity, but slight concavity. The median power estimate of 1.06 differed significantly from 1 (p = 0.015). Our median estimate was also significantly different from the medians found in earlier studies that estimated the utility for losses (p < 0.001).

To compare our experimental results with other measurement approaches, we also estimated the model with pooled data. Because each subject gave multiple responses, we corrected for the clustered nature of the standard errors. We observed significant concavity both for gains and for losses. The power parameter for gains was equal to 0.81 (standard error 0.06), which is comparable to the parameter based on the individual estimations. For losses the pooled estimate was higher (1.19, standard error 0.07), indicating more concavity. In order to detect a possible gender effect, we estimated the pooled data with the assumption that each parameter is gender-dependent. We found no significant difference in utility curvature for both the gain domain (p = 0.14) and the loss domain (p = 0.80).

Appendix 3 displays the estimates for each individual separately. Table 7 shows the classification of subjects based on their power estimates. The most common pattern was concave utility for gains and concave utility for losses. The proportion of subjects with an everywhere concave utility function was, however, not significantly different from the proportion of subjects with an S-shaped utility function (p = 0.487). For gains, concave utility was clearly the dominant pattern and the proportion of concave subjects was significantly different from the proportion of convex subjects (p = 0.008). For losses, concave utility was also the most common pattern, but the proportion of concave subjects was not significantly different from the proportion of convex subjects (p = 0.243).

Table 7 Classification of subjects according to the shape of their utility function

It is of interest to compare the findings of Tables 5 and 7. In Table 5 we observed that for losses most subjects were risk seeking. In Table 7 we observed that most subjects had concave utility for losses. These findings illustrate that there is no one-to-one relationship between risk aversion and concave utility under prospect theory and that concave utility and risk seeking behavior can and in fact do occur simultaneously. These results provide empirical evidence for the theoretical results derived by Chateauneuf and Cohen (1994).

4.5 Loss aversion

We found clear evidence of loss aversion. Table 6 shows the median of the individual loss aversion coefficients. It differed significantly from 1 (p = 0.000), the case of no loss aversion. It was comparable to the findings of Abdellaoui, Bleichrodt, and Paraschiv (2007) (p = 0.116). The interquartile range showed considerable variation at the individual level. The pooled estimate of the loss aversion coefficient was lower, 1.60, but it still differed significantly from 1 (p < 0.001). There was no gender effect of loss aversion (p = 0.47).

Loss aversion was clearly the dominant pattern at the individual level. Thirty-six subjects (76.6%) had a median loss aversion coefficient that exceeded 1 and were classified as loss averse. Only 6 subjects had a median loss aversion coefficient less than 1 and were classified as gain seeking. For 5 subjects all loss aversion coefficients exceeded 10 and they were not classified. The proportion of loss averse subjects was significantly different from the proportion of gain seeking subjects (p = 0.000). The support for loss aversion that we observed at the individual level is comparable with the findings of Abdellaoui, Bleichrodt, and Paraschiv (2007).

4.6 Probability weighting

Recall that our estimation procedure also yielded some information on probability weighting. Table 8 summarizes our estimations. The table shows that our, admittedly limited, results were broadly consistent with inverse S-shaped probability weighting. For a probability of 1/3 we observe no probability weighting for losses (p = 0.710). For probability 1/2 there is small but significant underweighting of probability both for gains (p = 0.030) and for losses (p = 0.003). There is more pronounced underweighting of 2/3 for gains (p = 0.000). The results were similar to those obtained in earlier studies. For example, Abdellaoui (2000) found that w⁻(1/3) = 0.35, w⁻(1/2) = 0.46, w⁺(1/2) = 0.39, and w⁺(2/3) = 0.50. Only w⁺(1/2) differed significantly from Abdellaoui (2000) (p = 0.006, the other p values all exceeded 0.40).

Table 8 Results on probability weighting

We could not reject the null hypothesis that w⁺(1/2) = w⁻(1/2) (p = 0.35). Hence, we could not reject the hypothesis that the degree of probability weighting was the same for gains and for losses for a probability of 1/2. We observed no gender effects for probability weighting either.

4.7 Comparison with expected utility

Table 9 shows the obtained power estimates under expected utility, i.e. when we assume that people do not transform probabilities. The table clearly illustrates that the existence of probability weighting implies that expected utility leads to distorted utilities. First, the power coefficients under expected utility were indeed generally different from those obtained under prospect theory. For gains, they are both significantly lower than under prospect theory (p = 0.041 when probability 1/2 was used in the elicitation and p < 0.001 when probability 2/3 was used in the elicitation) showing that expected utility overestimates the degree of concavity of utility for gains when subjects underweight probabilities. A second indication that expected utility leads to biased utilities is that the power coefficients for p_g = 1/2 and p_g = 2/3 were significantly different (p < 0.001). The dependence of utility on the probability used in the elicitation entails another violation of expected utility.

Table 9 Power estimates under expected utility

For losses, the power coefficient was significantly different from the power coefficient under prospect theory for probability 1/2 (p = 0.009) but not for probability 1/3 (p = 0.860). The power coefficients for ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$ and ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ did not differ significantly (p = 0.08). That utility for losses under prospect theory did not differ significantly from utility under expected utility when the elicitation was performed with ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$ is consistent with the observed absence of probability weighting for ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$. A similar finding was reported by Abdellaoui, Barrios, and Wakker (2007). For ${\text{p}}_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ expected utility overestimated the degree of convexity of the utility for losses consistent with the observed underweighting of 1/2. In fact, under expected utility the utility for losses was convex whereas under prospect theory it was slightly concave. This finding suggests that previous measurements under expected utility that observed convex utility for losses and that typically used a probability of 1/2 in the elicitations were biased towards convexity of utility.

5 Discussion

This paper has proposed a new method to measure utility and loss aversion under prospect theory. The main strength of our method is its efficiency. Allowing for response error, only 10–12 elicitations are required to measure prospect theory’s utility function on the entire domain. To compare, the method of Abdellaoui, Bleichrodt, and Paraschiv (2007) requires 18–20 measurements. An additional advantage of our method is that it minimizes the cognitive burden for subjects by only using certainty equivalents for two-outcome prospects. The method may be used at the individual level to measure directly a decision maker’s risk preferences, but also at the aggregate level by pooling the data. We hope that the provision of such a tractable method will foster the use of prospect theory in applications.

Our experimental results were broadly consistent with previous findings on prospect theory. As we mentioned in the introduction, this is a desirable conclusion. If we would have obtained significantly different findings, there would have been reason for concern that the method was not measuring what it was supposed to. We also obtained two novel findings. First, by performing our elicitations for different probabilities we tested the validity of prospect theory. We found that our measurements were robust, offering support for prospect theory. A second novel finding of our study is that we found evidence of the coexistence of concave utility and risk seeking behavior. To the best of our knowledge, this has not been observed before.

Our method has several drawbacks. First, by making parametric assumptions about utility it inherits the disadvantages of using parametric measurements. We do not believe that the assumption of power utility will confound the results as there is a lot of support for power utility in the literature. Moreover, adopting different parametric specifications did not affect our conclusions. A more serious problem for prescriptive measurements is that there is no direct link between choices and utilities as there is in the method of Abdellaoui, Bleichrodt, and Paraschiv (2007). Hence, if inconsistencies arise it is not immediately possible to resolve these by our method. Let us emphasize that we do not intend our method to replace the method of Abdellaoui, Bleichrodt, and Paraschiv (2007). The methods are useful in different decision contexts and are complementary. The method of this paper is particularly useful in decision contexts where time is limited, for example in many medical decision contexts where extensive measurements are too demanding for patients.

A possible danger of estimating the parameter of the utility function through nonlinear least squares is that the outcome of the analysis is not unique but that there is a range of values for which the goodness of fit is broadly similar. For example, risk seeking for losses can be explained both by a less elevated probability weighting function and by convex utility for losses. We tested the results of our analysis by different statistical algorithms and found that the results were stable, however, suggesting that our method is not susceptible to convergence problems and interactions between the parameters.

In our experimental study, we did not have real incentives for losses and for the mixed questions. Several studies have addressed the effects of incentives, but the results are different. Beattie and Loomes (1997), Camerer and Hogarth (1999), and Abdellaoui, Baillon, and Wakker (2007) found little or no systematic effects of incentives for the kinds of tasks that we performed. Holt and Laury (2002) on the other hand observed that real incentives led to more risk aversion. All these studies used gains. In a recent paper, Etchart-Vincent and l’Haridon (2008) studied the effects of real incentives for losses at the individual level. They compared three incentive schemes in the loss domain, namely hypothetical losses, real losses with an initial endowment and real losses without an initial endowment and concluded that there were no systematic differences between these three treatments. We conclude that our incentive scheme is unlikely to have caused problems.

Our finding of concave utility for losses may appear surprising in light of previous evidence suggesting (slightly) convex utility for losses. Like previous studies, we do not observe much curvature of utility for losses at the aggregate level. Combining the available evidence, it seems safe to conclude that utility for losses is closer to linearity than utility for gains and that curvature of utility for losses does not contribute much to observed risk attitudes. For all practical purposes, to take utility for losses linear does not seem to lead to substantial distortions. Of course, this conclusion only holds at the aggregate level. At the individual level the picture is much more diverse. For individual decisions, individual prospect theory parameters must be elicited. It is here that our method can prove particularly useful.

Appendices

Appendix 1

1.1 Illustration of questions

Fig. 3

Illustration of a task in the gain domain

Fig. 4

Illustration of a task in the mixed domain

Appendix 2

2.1 Explanation of the bisection method

The bisection method used to generate the iterations is illustrated in Table 10 for L ₁ for $p_\ell = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$ and the elicitation of $L_6^ *$ for $p_g = p_\ell = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$. The prospect that is chosen is printed in bold. Starting values in the iterations were always chosen so that prospects had equal expected value. Depending on the choice made, the certain outcome was increased or decreased. The size of the change was always half the size of the change in the previous question with the restriction that numbers should always be a multiple of 10. When a number was not a multiple of 10 it was rounded downwards. The method resulted in an interval within which the indifference value should lie. The midpoint of this interval was taken as the indifference value. For example, in Table 10 the indifference value for $L_6^ *$ should lie between −3,960 and −3,680. Then we took as the indifference value −3,820. In the elicitation of utility on the gain and loss domains, the certainty equivalents were elicited in five iterations. In the elicitation of the loss aversion coefficients, we used six iterations. We used one additional iteration in the elicitation of the loss aversion coefficients because the intervals $G_j^ * - L_j^ *$ were larger than the intervals |x _j  − y _j |.

Table 10 An illustration of the bisection method

Appendix 3

Table 11 Overview of the individual results (standard errors are in parentheses)