Abstract
We consider the valuation of collateralized derivative contracts such as interest rate swaps or forward FX contracts. We allow for posting securities or cash in different currencies. In the latter case, we focus on using overnight index rates on the interbank market. Using time varying haircuts, we provide an intuitive way to derive the basic discounting results, keeping in line with the most standard theoretical and market views. In a number of cases associated with margining with major central counterparties, pricing rules for collateralized trades remain linear, thus the use of (multiple) discount curves. We also show how to deal with partial collateralization, involving haircuts, asymmetric CSA, counterparty risk and funding costs. We therefore intend to provide a unified view. Mathematical or legal details are not dealt with and we privilege financial insights and easy to grasp concepts and tools.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The pricing of collateralized OTC contracts, such as swaps ruled by numerous CSA involved in ISDA master agreements or cleared on LCH.Clearnet, ICE, CME, etc. has become a subject of great importance. It concerns the pricing of new trades, of novation trades and the backload of older trades to a clearinghouse.
The aim of this paper is to provide an intuitive approach to the main results, some of them such as OIS discounting routinely used by market practitioners, an understanding of the (strong) assumptions involved and, on the other hand, to emphasize the wide range of applications. A number of results are connected to the recursive approach introduced by Cvitanić and Karatzas (1993), Duffie and Huang (1996), Duffie et al. (1996), Karoui et al. (1997), which allows a comprehensive treatment of different lending and borrowing rates. The use of time varying haircuts and collateral sets encompasses the standard features of collateralization schemes.
Among academic papers that deal with the valuation of collateralized derivative contracts, Johannes and Sundaresan (2007) can be seen as pioneering while the papers by Fujii et al. provide a deep investigation of many pricing issues. Bianchetti (2010), Kenyon (2010), Bielecki et al. (2011), Brigo et al. (2011), Castagna (2013), Crépey (2011, 2012a, b), Pallavicini et al. (2012), Kan and Pedersen (2011), Piterbarg (2010, 2012) also deal with various aspects of the valuation of collateralized trades within the new financial architecture. This field of research is still in progress, a number of issues such as the impact of funding costs, optimal posting of collateral, gap (or slippage) risks and the impact of initial margin may not be matter of consensus.
The paper is organized as follows:
Section 2 presents the theoretical pricing framework, where we allow for different lending and borrowing default-free rates. This can be of importance when considering partial collateralization schemes where trades need to be funded in the market. Comparisons with outstanding methodologies within that context are recalled.
Section 3 provides a simplified framework regarding the expected rate of return of posted collateral including bonds and foreign currencies. For simplicity, we have restricted ourselves to the case where no haircut is applied to posted bonds, corresponding to the case of major government issues.
Section 4 relates variation margins to collateral accounts, introduces settlement prices for collateralized trades and provides a general additive formula, i.e. a corrective term to uncollateralized prices.
Section 5 deals with various collateralization schemes in an integrated framework. This is achieved through the notion of local haircuts applied at CSA level. This leads to a recursive discounting pricing formula that applies both to collateralized and uncollateralized prices. We recall the standard cases of OIS discounting, futures’ pricing, costless collateral. The optimal choice of posted securities is investigated.
Section 6 provides a general approach to multiple discount curves in the context of swaps or of forward contracts. Suitable changes of measure are introduced leading to simple pricing formulas and generic convexity adjustments. Standard examples, involving easy to bootstrap collateralized discount factors, are investigated. It is noticeable that, in the above setting, we remain in a linear pricing framework, thus the existence of discount factors.
Section 7 broadens the view by considering imperfect collateralization schemes, different lending and borrowing rates and CVA effects altogether. Though the CVA approach used here is not identical to market practice, it can be thought of as a first-order approximation. Above all, it provides an integrated and easy to grasp pricing framework.
Section 8 deals with trade contributions in a non linear pricing framework. We provide some results that connect the stochastic discount factor to marginal pricing at book level and easy to compute trade contributions, some topics of great practical importance.
2 Pricing default-free uncollateralized contracts with different lending and borrowing rates
\(r(t)\) will denote the usual default-free short rate at time \(t\) as in the standard Heath–Jarrow–Morton case. This is taken as a starting point to keep in line with the standard mathematical finance framework and thus simplifying the exposition.
Overnight “rates” such as Eonia, Sonia or the effective Fed funds rates are related to unsecured interbank loans. Piterbarg (2010, Eq. 1) or Morini and Prampolini (2010) assimilate \(r(t)\) and overnight rates (denoted by \(r_C (t)\) in Piterbarg), which can be associated with the assumption that bank defaults can be foreseen over a 1 day time-horizon. On the other hand, Afonso et al. (2011), Pallavicini et al. (2012) state that there is a default component in overnight rates. Apart from periods of market stress, this default component is likely to be small, though difficult to assess, given that \(r(t)\) is not directly observable. As mentioned in Pallavicini et al. (2012), \(r(t)\) can be seen as an instrumental variable that eventually vanishes in a number of cases.
Bergman (1995) introduces a (default-free) lending short rate \(r(t)\) and a borrowing short rate \(R(t)\), with \(r(t) \le R(t)\). The difference \(R(t)-r(t)\)corresponds to the (funding) liquidity premium \(\gamma _X \) in Castagna (2011) or to the (default-free) liquidity basis in Morini and Prampolini (2010), i.e. the spread over the risk-free rate \(r(t)\) at which a default-free entity would borrow in the market. This also corresponds to \(s_t^F \) in Castagna (2012), Castagna (2013) or \(l^{\pm }\), the liquidity bases in Pallavicini et al. (2012). Bergman considers a savings account \(\beta \) and a borrowing account \(L\), such that \(\beta \left( t \right) =\exp \int \nolimits _0^t {r(s)ds} \) and \(L\left( t \right) =\exp \int \nolimits _0^t {R(s)ds} \). To preclude arbitrage opportunities, one cannot borrow and lend simultaneously. Such constraints on account holdings are convex and are dealt with in Cvitanić and Karatzas (1993). Crépey (2012a) defines two external investing and funding assets, the funding asset jumping downwards at default time of the pricing entity. As stated in Fries (2010), the above approaches reflect the benefit, at the entity level, of cancelling a fraction of outstanding debt at default time. In Fries terminology, this corresponds to the third party (or mark-to-market) liquidation view. As a consequence, there is no own credit risk term when discounting receivables (positive cash-flows) as in Burgard and Kjaer (2011). We refer to Hull and White (2012) for further discussion on this controversial issue.
Within Bergman setting, extending results from Korn (1992), Cvitanić and Karatzas (1993) consider a model with \(d\)—primary traded assets driven by a \(d\)—dimensional Brownian motion and an invertible volatility matrix. Going along standard lines, they construct through Girsanov theorem a \(Q^{\beta }\)—measure such that prices of primary (hedging) assets discounted by \(\beta (t)\) are \(Q^{\beta }\)—martingales. The existence of such a measure is postulated in Johannes and Sundaresan (2007), Piterbarg (2010, Eq. 1), Fries (2010); Fujii et al. (2010), Fujii and Takahashi (2011), Castagna (2013). We will thereafter assume that the set of traded assets is large enough for \(Q^{\beta }\) to be uniquely defined, a common feature in HJM models.
One interesting outcome of the above approach is that a large class of contingent claims, including call options, is replicable. The replication price of an uncollateralized contract \(p^{U}(t)\) is obtained as the unique solution of the following backward stochastic differential equation (BSDE, see also Karoui et al. 1997):
where the BSDE generator \(g\left( p \right) =Rp^{+}+rp^{-}\) is a key tool. In such a default-free setting, given a terminal payoff \(X(T)\), we get:
Such equations are well known in finance. They have been considered in a CVA context by Duffie and Huang (1996) and Duffie et al. (1996) and more recently by Crépey (2011), Fujii and Takahashi (2012) and Henry-Labordère (2012). We also refer to Cesari et al. (2010), Burgard and Kjaer (2011) for closely related approaches.
Equation (2.2) actually provides the opposite of the replication price of \(-X(T)\). A dealer holding an amount \(X(T)\) can cancel out his position by replicating \(-X(T)\). As a consequence, a pure asset cash-flow \((X(T)>0)\) is discounted at the high rate \(R(t)\), while a pure liability cash-flow (\(X(T)<0)\) is discounted at the low rate \(r(t)\). We think that this convention is more meaningful and conservative on financial grounds than considering the replication price of \(X(T)\) [that would involve switching \(R(t)\) and \(r(t)]\).
Equation (2.2) provides a standalone replication price. When considering a trade within a portfolio, the condition \(\left\{ {p^{U}(s)>0} \right\} \) should be replaced by a positivity condition on the value of the portfolio. This is dealt with at this end of this paper when addressing trade contributions.
Similarly, if the hedging instruments have some cash impacts, the positivity condition needs to cope with the total cash balance. The simplest case would correspond to hedging with forward contracts of the same maturity as the derivative to be priced, since no impact on the cash balance would occur.
One could think of borrowing on the cash market at the low rate \(r(t)\) and lend at the high rate \(R(t)\). This would correspond to the case where a derivatives dealer is a liquidity provider rather than a liquidity taker. As above, we have rather chosen a conservative approach though it would need to be adapted to individual cases.
Equation (2.2) is consistent with Eq. (34) in Castagna (2013), when \(\gamma =0\) (no collateralization scheme). The positivity condition in the quoted paper is put on the cash account, which inverts signs when using the price of the derivative.
Piterbarg (2010) introduces a funding rate \(r_F (t)\) which is meant to include a default component. However, in his framework, counterparty default is ignored and in further computations (see for example, Eq. 3), \(r_F (t)\) acts as a default free borrowing and lending rate in the cash market (with equality between these two rates) and is de facto equal to \(r(t)\), while the rate \(r_C (t)\) is further assimilated with the rate of cash collateral \((c(t)\) in our notations).
While the pricing framework can cope with different borrowing and lending rates, to ease the exposition, we will keep tied to a unique default-free cash rate, i.e. \(r(t)=R(t)\), until we consider asymmetric CSAs.
Piterbarg (2012) or Macey (2011) directly derive no arbitrage restrictions among settlement prices of fully collateralized derivatives under different CSAs, from which a risk-neutral measure is constructed. Thus, there is no a priori use of the theoretical default-free short rate \(r(t)\). However, when it comes up to partially collateralized derivatives, we need to introduce some rate for lending or borrowing cash, which acts as default-free short rate. Eventually, as mentioned in Piterbarg (2010), we may end-up with the same pricing measure for collateralized and uncollateralized contracts, which actually appears to be \(Q^{\beta }\).
3 Collateral assets
3.1 Cash in different currencies and securities posted as collateral
Quite often, cash is used as collateral. We will denote by \(c(.)\) the rate (with continuous compounding) paid on the collateral account, typically EONIA or fed fund rate. We will also consider the cases where \(c(.)=0\) and \(c(.)=r(.)\).
To cope with various netting agreements, we need to enlarge the cash collateral setting. Let us denote by \(A(t)\), the price at time \(t\) of the posted asset, which may be a bond or some currency. For simplicity, we will assume that \(A(.)\) is a positive semimartingale admitting the decomposition:
where \(M_A \) is a \(Q^{\beta }\) - martingale. We assume that the price can actually be observed and that the market for the security \(A\) is frictionless, i.e. no bid-ask spread and constant unit price. For simplicity, we will thereafter consider a single collateral asset though the results readily extend to a portfolio of collateral assets.
As is the case in a standard bilateral CSA or when margining through a CCP, we will assume that the collateral rate does not change when a party switches from collateral giver to receiver.
3.2 Posting bonds
In the repo market, a large set of securities can be posted, quite often bonds. We show that the short-term repo rate can be seen as the expected rate of return of the bond under \(Q^{\beta }\). This holds under assumptions detailed and discussed below. The core point is that a short-term repo contract with no haircut can also be seen as an “instantaneous” forward bond contract and the repo rate is then related to a default-free forward bond price. This result is a key point in subsequent analysis related to optimal choice of collateral and discounting results.
Let us consider a short-term repo contract, say between dates \(t\) and \(t+dt\). As above \(A(t)\) denotes the bond price at date \(t\) and no coupon is to be paid between \(t\) and \(t+dt\). Let us assume that no haircut is applicable.Footnote 1 Thus, the repo contract turns out to be a (short-term) forward contract, with no payment at inception and a payment equal to \(A\left( {t+dt} \right) -\left( {1+\hbox {repo}_A (t)dt} \right) A(t)\). If the payment is made for sure, i.e. none of the parties is in default at date \(t+dt\), we have \(E_t^{Q^{\beta }} \left[ {A(t+dt)-\left( {1+\hbox {repo}_A (t)dt} \right) A(t)} \right] =0\) and thus:
The above result is related to Barden (2009) or Piterbarg (2010).
If defaults can occur but are predictable, then one can state whether or not the parties will be in default at date \(t+dt\). Clearly, there is no reason why a trade would occur with one of parties going to default with certainty at \(t+dt\) and we will not further investigate this unlikely case.
There are a number of cases where defaults can occur, yet \(\left( {1+\hbox {repo}_A (t)dt} \right) A(t)\) can still be seen as a default-free forward price.
The first one corresponds to cancellationFootnote 2 of the deal at default. We denote by \(\lambda (t)dt\), the probability of the deal to be cancelledFootnote 3, due to default of one of the parties. If occurrence of defaults and changes in collateral asset are independent, the pricing equation becomes:
Thus, we still have \(r_A (t)dt=E_t^{^{Q^{\beta }}} \left[ {\frac{dA(t)}{A(t)}} \right] =\hbox {repo}_A (t)dt\). Let us consider the case where the payment to the non defaulted party is of the form \(\delta \max \big ( A(t+dt)-\big ( 1+\hbox {repo}_A (t)dt \big )A(t),0 \big )\) and \(\delta \) is a recovery rate. Provided that the two parties have the same recovery rate and default probability, \(E_t^{^{Q^{\beta }}} \left[ {\frac{dA(t)}{A(t)}} \right] =\hbox {repo}_A (t)dt\) still holds. This symmetry between the parties would occur if “tier-one” or “prime” banks are to trade together.
Eventually, if we assume that \(A\) is driven by a Brownian motion or that its jump component is independent of the default counting processes of the two involved parties, then \(E_t^{^{Q^{\beta }}} \left[ {\frac{dA(t)}{A(t)}} \right] =\hbox {repo}_A (t)dt\) is still valid and CVA/DVA terms can be neglected when computing the instantaneous forward price of a bond. This corresponds to a “no gap risk” at default assumption.
In our simplified setting regarding counterparty and operational risks, the repo rate \(\hbox {repo}_A (t)\) is thus only related to security \(A\), without consideration of the parties identity.Footnote 4
Let us remark that a short-term repo contract with no haircut can be seen as a perfectly collateralized trade. We are considering buying a security deliverable at date \(t+dt\), the transaction being secured with cash and the cash collateral rate being equal to \(\hbox {repo}_A (t)\). In other words, the repo rate can also be seen as a cash collateral rate. The term \(A(t+dt)-\left( {1+\hbox {repo}_A (t)dt} \right) A(t)\)corresponds to the variation margin to be paid on an open repo (see below regarding the computation of variation margins).
As already mentioned, the repo rate is tied to the instantaneous forward price of a bond. We emphasize that we directly consider a forward market and related forward prices without refereeing to lending cash between \(t\) and \(t+dt\). This is purposeless since there are no cash-flows being exchanged at date \(t\) and no need for transferring funds across time. As a consequence, the default-free forward price is primitive and is not derived from a borrowing and lending cash market as in the standard cash and carry approach.
3.3 Posting foreign currencies
In the case of cash-collateral paid in the base currency (say USD), the collateral account typically earns the effective fed funds rate, thus \(r_A \equiv c^{\$ }\) and the settlement price of a collateralized trade is computed by discounting the terminal cash-flow (expressed in USD) at the collateral rate under the usual risk-neutral probability, \(Q^{\beta ^{\$ }}\) associated with the USD savings account numeraire.
We may need to consider collateral accounts in different currencies. As an example, we could consider a cash-collateral account in a foreign currency, for instance  , where
, where  corresponds to the spot exchange rate and
corresponds to the spot exchange rate and  to the Eonia. As for bonds, we will have:
to the Eonia. As for bonds, we will have:  being a \(Q^{\beta ^{\$}}\) martingale, and we need to determine
being a \(Q^{\beta ^{\$}}\) martingale, and we need to determine  .
.
For this purpose, we can go along the same lines as for bonds. Let us introduce an instantaneous forward FX contract that is assumed to be default-free and denote by  , the forward exchange rate, where
, the forward exchange rate, where  is the interest differential between USD and EUR. As for the repo contract, we have:
is the interest differential between USD and EUR. As for the repo contract, we have:

Thus,  and
and  leads to:
leads to:

The counterparty risk issues associated with the instantaneous forward FX contract are the same as the ones already discussed in the repo case. In the simplest cases of no gap risk, the CVA/DVA terms can be neglected, as if the instantaneous forward FX contract was default-free. This instantaneous forward FX contract approach is being used in Macey (2011) or Piterbarg (2012).
In the standard mathematical finance framework, we would have:  , where
, where  are the instantaneous USD and EUR default-free rates and we then get a result similar to Fujii et al. (2010), Eq. (3.13) or Castagna (2012), Eq. (11). As for calibration issues, the interest rate differential
are the instantaneous USD and EUR default-free rates and we then get a result similar to Fujii et al. (2010), Eq. (3.13) or Castagna (2012), Eq. (11). As for calibration issues, the interest rate differential  can be directly inferred from the FX market, while separate calibration of \(r^{\$ }(t)\) and
can be directly inferred from the FX market, while separate calibration of \(r^{\$ }(t)\) and  can be problematic.
can be problematic.
4 Variation margins, collateral accounts, settlement prices and the additive formula
4.1 Variation margins paid on a collateral account
The computation of variation margins involves a collateral account. We will denote by \(V(s)\) the amount at date \(s\) of the collateral account. The amount of the collateral account is the market value of the securities being posted as collateral. If \(V(s)>0\), the pricing entity receives collateral, if \(V(s)<0\), the pricing entity gives collateral.
At time \(s,\, t\le s\le T\), the number of securities posted on the collateral account is equal to \(\frac{V(s)}{A(s)}\). The value of the posted collateral at \(s+ds\) is then equal to \(\frac{V(s)}{A(s)}\times A\left( {s+ds} \right) \).Footnote 5
As a consequence, the variation margin for the time interval between \(s\) and \(s+ds\) is equal to:
Since \(dV(s)=V(s)\times \frac{dA(s)}{A(s)}+dVM(s)\), the term \(V(s)\times \frac{dA(s)}{A(s)}\) corresponds to the self-financed part. The variation margin \(dVM(s)\)corresponds to the inflow in the collateral account.
In the case of cash collateral with rate \(c\left( . \right) \), \(\frac{A(s+ds)}{A(s)}=1+c(s)ds\) and the variation margin equals \(dVM(s)=dV(s)-V(s)c(s)ds\) (see Piterbarg 2012) and is basically an extension of the future’s case where \(dVM(s)=dV(s)\).
4.2 Settlement prices and the additive formula
We will consider a collateralized trade with single maturity \(T\). This readily extends to multiple payment dates as in the case of interest rate swaps.
The contractual payoff at date \(T\) paid in the base currency, say USD, will be denoted by \(X(T)\). As stated before, we do not take into account immediately the possibility of default. Apart from interest rate swaps, we could think of forward FX contracts, securities lending and repo transactions as other examples involved in collateralized transactions.
\(p^{S}(t)\) will denote the settlement price at time \(t\) of a collateralized trade with maturity \(T\) (in the same base currency) and our purpose is the computation of such a settlement price. \(p^{S}(t)\) will play a key role in margining, either for the computation of variation margins or regarding the collateral account amount. The settlement price will converge at time \(T\) to the contractual cash-flow \(X(T)\), thus the same notation. For simplicity, we implicitly assume that the contract is cash-settled.
Let us detail the various cash-flows at hand. The net cash-flow at inception date \(t\) is equal to \(-p^{S}(t)+V(t)\), where \(p^{S}(t)\) is the settlement or collateralized price and \(V(t)\) is the value of the posted collateral. The net cash-flow at expiration of the contract is \(X(T)-V(T)\). The pricing equation also takes into account the collateral cash-flows, most notably the variation margins paid between \(t\) and \(T\). Using the pricing framework stated in Sect. 2, and assuming same borrowing and lending default-free rates leads to:
where \(p^{U}(t)\) is the uncollateralized price, \(V(s),\, t\le s\le T\) is the value of the collateral account at time \(s\) and \(dVM(s)\) is the variation margin. Let us remark that that \(V(.)\) is not self-financed since there are some inflows or outflows, i.e. the variation margins.
It is interesting to consider the present value of the variation margins in isolation and consider the difference between uncollateralized and collateralized prices.
Using the above results, the time \(t\) present value of cash-flows associated with managing the collateral account can be written as:
The present value of cash-flows associated with the management of the collateral account is the additive correcting term to switch from an uncollateralized PV to a collateralized PV. It is worth noting that this holds for all collateralization schemes as only the value \(V\left( t \right) \) of the collateral account is involved and not the settlement price \(p^{S}\left( t \right) \). The present value of collateral cash-flows can eventually be written as:Footnote 6
In the case of cash-collateral, with collateral rate \(c(.)\), \(\frac{dA(s)}{A(s)}=c(s)ds\) and the latter expression actually simplifies to \(E_t^{Q^{\beta }} \left[ {\int \nolimits _t^T {\left( {r(s)-c(s)} \right) V(s)e^{-\int \nolimits _t^s {r(u)du} }ds} } \right] \) (see Eq. 3 in Piterbarg 2010 or Eq. (26) in Castagna 2013). Unsurprisingly, the present value of collateral cash-flows equals the present value of the margins (accrued interest point of view) as is standard with any cash account. Obviously, in the case where the collateral rate \(c\left( . \right) \) equals the risk free rate \(r\left( . \right) \), the present value of collateral cash-flows is equal to zero since there is no net margin associated with the collateral amount (“costless collateral”).
Though the clearing house is assumed to be default-free (in our theoretical setting), clearing members are lending to that clearing house at a different rate. From the point of view of clearing members, \(r(s)-c(s)\) is the convenience yield associated with the collateral account and \(\left( {r(s)-c(s)} \right) V(s)ds\) is simply the margin associated with the management of the collateral account, between \(s\) and \(s+ds\).
5 Recursive pricing formulas and collateralization schemes
5.1 Collateralization schemes
A collateralization scheme relates settlement prices \(p^{S}\left( t \right) \) and the value of the collateral account \(V\left( t \right) \). For instance, in the so-called perfect collateralization case, at any point in time, the value of the collateral is equal to the settlement price: \(V(s)=p^{S}(s)\), for all \(s,t\le s\le T\). For an asymmetric CSA, we would have \(V\left( s \right) =\max \left( {p^{S}\left( s \right) ,0} \right) \) or \(V\left( s \right) =\min \left( {p^{S}\left( s \right) ,0} \right) \).
We provide a comprehensive treatment of collateralization schemes by introducing some haircut ratios. When a security is being posted in a collateral agreement, some haircut is usually applied. Given potential “runs on repos”, it makes sense to deal with time varying haircuts. Let us denote by \(\frac{1}{\alpha _A (s)}\) the haircut ratio at time \(s\) associated with security \(A\). At time \(s,t\le s\le T\), the amount of collateral account is then equal to \(V(s)=\alpha _A (s)p^{S}(s)\) and the number of posted securities is given by \({\alpha _A (s)p^{S}(s)}/{A(s)}\). For an asymmetric CSA, \(\alpha _A (t)=0,1\) depending on the sign of \(p^{S}(t)\).
5.2 The basic discounting result
Let us focus on the changes in the variation margins with such collateralization features. Using the ongoing notations, the variation margin \(dVM(t)=V(t+dt)-\frac{V(t)}{A(t)}A(t+dt)\) becomes:
Let us consider a trade initiated at time \(t\) and unsettled at \(t+dt\). The net cash-flow at time \(t\) is given by: \(V(t)-p^{S}(t)=\left( {\alpha _A (t)-1} \right) p^{S}(t)\). The net cash-flow at \(t+dt\) is provided by:
In the simplified setting where no defaults occurs at \(t+dt\), the previous cash-flow is paid for sure. The net expected (under \(Q^{\beta }\)) present value is equal to zero; This can be written as:
This leads to the pricing equation (not accounting for CVA/DVA effects, i.e. default-free counterparties entering a collateralized trade):
An intuitive way to look at this drift restriction is to consider that \(\alpha _A \left( t \right) p^{S}\left( t \right) \) is invested in the collateral account with expected rate of return \(r_A \left( t \right) \). The remaining part \(\left( {1-\alpha _A \left( t \right) } \right) p^{S}\left( t \right) \) corresponds to a cash-flow invested in the cash market at expected rate of return \(r\left( t \right) \). Equation (5.3) corresponds to Eq. (6) of Piterbarg (2010) (remembering that his funding rate \(r_F \) is actually a default-free short rate for cash lending or borrowing). When there is a unique borrowing and lending short rate \(r\left( t \right) \), our result is also consistent with Castagna (2013), Eq. (29).
In the case where \(X(T)\)is a function of an underlying asset \(S(T)\), further results can be stated. If we assume that the underlying asset is repoable (with no haircut), the drift under \(Q^{\beta }\) of this asset is equal to the repo rate (minus the continuous dividend rate). This is consistent with Eq. (49) in Castagna (2013) or Eq. (4) in Piterbarg (2010). When the asset is not repoable, we need to use the short rate \(r(t)\) instead of the repo rate as in Eq. (29) in Castagna (2013). This is of course more problematic from a calibration point of view, since we cannot get rid of unobserved \(r(t)\).
Equation (5.3) can be restated through the simple discounting formula:
The most common market feature consists in using haircut ratios below 1 (overcollateralization) and is associated with \(\alpha _A (t)>1\). \(0\le \alpha _A (t)<1\) corresponds to under-collateralization, i.e. the amount of collateral is only a fraction of the value of the settlement price (or PV) of the trade. If \(\alpha _A (t)=0\), no collateral is being posted and provided that the counterparties are default-free, we are led back to the standard discounting at the default-free rate \(r(.)\).
5.3 The basic discounting result with perfect collateralization
With perfect collateralization, the variation margins paid throughout the life of the trade perfectly match the potential loss in case of default of one of the parties. This corresponds to the case where \(\alpha _A (t)=1\). Thus:
Under perfect collateralization, the settlement price is obtained by discounting the terminal payoff at the risk-neutral expected rate of return of the collateral. This contrasts with using the default-free rate for uncollateralized trades. The pricing measure remains the usual one, associated with the default free savings account.
Pricing equation (5.5) also extends already known results for futures contracts (see Duffie 1989). Actually, the pricing of futures contracts corresponds to cash collateral and collateral rate set to zero: \(c(.)\equiv 0\). The settlement price is then a \(Q^{\beta }\) - martingale.
Let us remark that when \(r_A =r\) and \(A(t)=\beta (t)=\exp \left( {\int \nolimits _0^t {r(s)ds} } \right) \), there is no difference with the ordinary pricing equation for default-free uncollateralized trades: In both cases, discounting is done at the short-term default-free rate \(p^{S}(t)=E_t^{Q^{\beta }} \left[ {X(T)\exp \left( {-\int \nolimits _t^T {r(s)ds} } \right) } \right] \). This corresponds to “costless collateral” according to Johannes and Sundaresan (2007) terminology. Thus, when the collateral rate equals the short-rate, uncollateralized prices are equal to (perfectly) collateralized prices.
A simple case corresponds to the use of USD cash collateral. We then have: \(\frac{dA(t)}{A(t)}=\frac{dC^{\$ }(t)}{C^{\$ }(t)}=c^{\$ }(t)dt\), where \(c^{\$ }(t)\) is the effective fed funds rate and the USD settlement price is provided by \(p^{S}(t)=E_t^{Q^{\beta }} \left[ {X(T)\exp \left( {-\int \nolimits _t^T {c^{\$ }(s)ds} } \right) } \right] \), i.e. the so-called “OIS discounting” (see for example Eq. (3.5) in Fujii et al. 2010).
On technical grounds, let us remark that the general discounting formula with partial collateralization (Eq. (5.4)) is actually embedded in the simplest case of perfect collateralization: We can write the margin associated with managing the collateral account [see Eq. (4.4)] as \(\left( {r(s)-r_A (s)} \right) V(s)=\left( {r(s)-r_A^*(s)} \right) p^{S}(s)\) with \(r_A^*(s)=\left( {1-\alpha _A (s)} \right) r(s)+\alpha _A (s)r_A (s)\). The PV of variation margins can be computed under the assumption of perfect collateralization and a modified expected rate of return on the collateral \(r_A^*(s)\). Equation (5.5) then turns out to be identical to Eq. (5.4).
5.4 Optimal choice of posted securities
We assume that a set of eligible securities and cash currencies \(\left\{ {1,\ldots ,I} \right\} \) can be posted in the collateral account. To ease the exposition, let us assume that \(p^{S}\left( t \right) <0\). The pricing entity is thus collateral giver. We assume that the collateral giver chooses the posted collateral and that the collateral pool can be wholly substituted at any time. We follow the same line of reasoning as in Sect. (5.1) with minor adaptation. The collateral giver chooses the collateral asset such that the expected (under \(Q^{\beta }\)) net present value is maximized. For such a choice, the expected net present value is equal to zero. If collateral \(i\) is posted, following Eqs. (5.2) and (5.3), the expected NPV is equal to \(E_t^{Q^{\beta }} \left[ {dp^{S}(t)} \right] -\left( {\left( {1-\alpha _{A_i } (t)} \right) r(t)+\alpha _{A_i } (t)r_{A_i } (t)} \right) p^{S}\left( t \right) dt\). The posted collateral thus maximizes \(\left( {1-\alpha _{A_i } (t)} \right) r(t)+\alpha _{A_{i}} (t)r_{A_{i}} (t)\) and the pricing equation becomes:
As a consequence the previous discounting result is extended to:
The optionality in the collateral choice magnifies the discount rate to \(\max _{i\in \left\{ {1,\ldots ,I} \right\} } \big ( 1-\alpha _{A_i} (s) \big )r(s)+\alpha _{A_i } (s)r_{A_i} (s)\) but the pricing rule relating terminal cash-flow \(X(T)\) to settlement price \(p^{S}(t)\) remains linear (provided that default-free lending and borrowing rates are equal). Equation (5.7) corresponds to and extends Eq. (21) in Fujii and Takahashi (2011) (see also Fujii et al. 2010).
A CSA (or another collateral agreement as in a tri-party repo) provides the set of assets that can be posted. The settlement price is specific to the CSA and there are thus many potential settlement prices depending upon the collateral pools. Thus novation trades or the backload of ISDA CSA trades to LCH.Clearnet, which may involve changes in the collateral pool, are rather intricate.
6 Multiple curves
An important application of the above techniques is the pricing of interest rate swaps or forward FX contracts under the perfect collateralization scheme. In a market where lending and borrowing rates are equal, pricing rules are linear, leading to the use of specific discount factors. Suitable changes of measures are introduced and connected to such collateralized discount factors. In the case of cash collateral paying overnight rate index (i.e. EONIA or fed fund rate), settlement prices of collateralized trades are obtained by discounting with the overnight rate. Convexity adjustments are derived when dealing with swaps associated with different collateral rates.
It is worth mentioning that a number of papers, including Kijima et al. (2009), Henrard (2009), Mercurio (2009, 2010a, b), Bianchetti (2010) have considered a decoupling between discount factors and forward rates, with important applications to the pricing of Libor derivatives or cross-currency swaps. Though our main concern is the pricing of collateralized swaps, we hopefully end-up with similar results.
6.1 Changes of measure and further notations
We will define a set of measures, equivalent to \(Q^{\beta }\), denoted as \(Q_T^A \) associated with the collateral account by their density:
\(Q_T^A \) is named “collateralized forward measure” by Fujii et al. (2010).Footnote 7 The density process of \(Q_T^A \) (with respect to \(Q^{\beta }\)) is defined as usual by: \(\xi _T^A \left( t \right) =E_t^{Q^{\beta }} \left[ {\frac{dQ_T^A }{dQ^{\beta }}} \right] \). Let us further denote:
\(B_A \left( {t,T} \right) \) is the date \(t\) - settlement price of a cash-flow of 1 paid at date \(T\) collateralized with \(A\). It can then be considered as a \(A\)-collateralized discount bond price. For instance, \(B_{C^{\$}} \left( {t,T} \right) =E_t^{Q^{\beta }} \left[ {\exp \left( {-\int \nolimits _t^T {c^{\$ }(s)ds} } \right) } \right] \) corresponds to the settlement price of a zero-coupon collateralized with cash remunerated at fed funds rate.
We can write the density process as:
The usual forward measure \(Q_T^\beta \) is defined as:
under the standard notation: \(B\left( {t,T} \right) =E_t^{Q_T^\beta } \left[ {\exp \left( {-\int \nolimits _t^T {r(s)ds}}\right) }\right] \). The measure with density \({\exp \left( {-\int \nolimits _0^T{r_A^*(s)} } \right) }/{E^{Q^{\beta }}\left[ {\exp \left( {-\int \nolimits _0^T {r_A^*(s)} } \right) } \right] }\) and \(r_A^*(s)=\left( {1-\alpha _A (s)} \right) r(s)+\alpha _A (s)r_A (s)\) encompasses the collateralized forward measure and the usual forward measure: The former corresponding to a perfect collateralization scheme, the latter to a non collateralized framework. While we could actually account for partial collateralization, let us for simplicity go back to the perfect collateralization scheme. The change of measure technique leads to writing the settlement price \(p_A^S (t)\) as:
Since we have considered different collaterals, it is interesting to switch from one to another. Let us denote by \(A,B\) two kinds of collateral assets and \(r_A,r_B \) the corresponding \(Q^{\beta }\)- expected rates of return. We then have:
We denote by \(\xi _T^{B,A} \left( t \right) =E_t^{Q_T^A } \left[ {{dQ_T^B }/{dQ_T^A }} \right] \) the density process of \(Q_T^B \) (with respect to \(Q_T^A\)). It can be shown that \(\xi _T^{B,A} \left( t \right) ={\xi _T^B \left( t \right) }/{\xi _T^A \left( t \right) }\).
6.2 Generic convexity adjustments
We can think of comparing two derivatives assets, with same terminal payoff, perfect collateralization, but different collaterals. A typical example would involve a Eurodollar future (collateral rate equal to zero) and a FRA collateralized at effective Fed funds rate.
For a given payoff \(X(T)\) collateralized with \(A\), its \(T\)- forward settlement price \(p_{A,T} (t)\) is equal to \(p_{A,T} (t)=E_t^{Q_T^A } \left[ {X(T)} \right] \). Indeed,\(0=B_A \left( {t,T} \right) \times E_t^{Q_T^A } \left[ {X(T)-p_{A,T} (t)} \right] \). Thus we are to compare \(E_t^{Q_T^A} \left[ {X(T)} \right] \)and \(E_t^{Q_T^B } \left[ {X(T)} \right] \). This involves a covariance term between the payoff and the spread between (expected) rates of return on the two collaterals:
We refer to the “Appendix” for proofs, computations and further details in a Brownian filtration setting. Let us remark that one can extend the approach to partially collateralized deals, thus providing an integrated framework as already mentioned in the previous subsection (see Piterbarg 2010).
6.3 Linear pricing rules and (perfectly collateralized) discount factors
Let us first remind that within a perfect collateralization framework as defined above, there is no gap risk when unwinding a trade, thus no independent amount or initial margin based on non linear measures of risk and thus no resulting portfolio effect.
In a number of cases, the expected rate of return of the posted collateral, \(r_A (.)\) is not independent of \(X\left( T \right) \). This may lead to a number of quanto effects. However, this does not change the point that in a perfect collateralization framework and provided that the collateral rate does not depend on the sign of the PV, the pricing rule remains linear. If one considers the pricing of a collateralized terminal cash-flow \(X_1 (T)+X_2 (T)\), then the cash-flows associated with the variation margins will be the sum of those associated with \(X_1 (T)\) and \(X_2 (T)\) considered independently. As a consequence, after discounting these variation-margin cash-flows at the default-free short rate under \(Q^{\beta }\), we will have that the settlement price at time \(t\) of the collateralized terminal payoff \(X_1 (T)+X_2 (T)\), is simply \(p_1^S (t)+p_2^S (t)\). Similarly, the settlement price at time \(t\) of the collateralized terminal payoff \(\alpha \times X(T)\), where \(\alpha \) is a real number, is \(\alpha \times p^{S}(t)\).
If we consider square integrable payoffs, from Riesz representation theorem, we can write \(p^{S}(0)=E^{Q^{\beta }}\left[ {\xi \times X(T)} \right] \) for some square-integrable random variable \(\xi \). Taking \(X(T)=1\), we get \(B_A (0,T)=E^{Q^{\beta }}\left[ \xi \right] \). Then, we can define a new probability measure \(Q_T^A \) from its density: \({dQ_T^A }/{dQ^{\beta }}=\xi /{E^{Q^{\beta }}\left[ \xi \right] }\). As a consequence, the pricing rule \(p^{S}(0)=B_A \left( {0,T} \right) E^{Q_T^A }\left[ {X(T)} \right] \), where \(B_A (0,T)\) is the collateralized discount factor, is not surprising but a direct consequence of the linear structure of cash-flows in perfect collateral schemes.
6.4 OIS contracts with cash collateral
We will first focus on the simplest payoff, a stylized (with continuous compounding) overnight indexed swap, where:
where \(t_0\) is the trade date, \(T\) the maturity date of the trade. \(y\) is the (continuously compounded) fixed rate of the collateralized overnight indexed swap, while \(c^{\$ }(t)\) is the cash collateral rate, say the effective Fed funds rate.
The settlement price \(p^{S}(t),\, t_0 \le t\le T\), is provided by:
It is worth noting that the compounding and discounting rates are equal leading to simplifications. Under our standing notations, \(B_{C^{\$ }} (t,T)=E_t^{Q^{\beta }} \left[ {\exp \left( {-\int \nolimits _t^T {c^{\$ }(s)ds} } \right) } \right] \). Thus,
It can be seen that \(B_{C^{\$}} (t,T)\) acts as a discount factor.
Let us consider a par trade at inception, i.e. \(t=t_0 \) and settlement price equal to 0. Then, the par rate, at date \(t\), of such a collateralized OIS contract with maturity date \(T,\, y^{\$}\left( {t,T} \right) \), is derived from:
Let us remark that the discount factors \(B_{C^{\$}} \left( {t,t+\delta } \right) \) are directly related to market observables, i.e. par rates of collateralized OIS. As a consequence, we can readily write settlement prices of collateralized OIS contracts in a model free setting (up to interpolation schemes).
6.5 Libor swaps
Let us denote by \(L\left( {T,T+\delta } \right) \) the Libor (or Euribor rate) at time \(T\) for maturity \(\delta \). The case of a Libor FRA contract is such that \(h(T+\delta )=\delta \times \left( {FRA-L(T,T+\delta )} \right) \) where \(\delta \) is the coverage factor and \(FRA\) is the contractual FRA rate. We then have:
The par rate \(L_A \left( {t,T,T+\delta } \right) \) is the FRA rate such that the settlement price at date \(t\) equals zero. \(L_A \left( {t,T,T+\delta } \right) \) is a forward collateralized (with \(A\)) Libor rate. We have:
The forward Libor curve depends upon the collateral choice. For instance, one might think of using LCH.Clearnet type contracts, where cash-collateral is posted in the same currency as the one of the interest rate swap contract and earns the corresponding reference overnight rate. We would then have \(L_{C^{\$ }} \left( {t,T,T+\delta } \right) =E_t^{Q_{T+\delta }^{C^{\$ }} } \left[ {L\left( {T,T+\delta } \right) } \right] \). Such OIS discounting corresponds to Kijima et al. (2009) or Mercurio (2009). If we were to think of Eurodollar futures, the (collateralized) forward Libor rate would be different, since the latter case, the collateral rate equals zero and not the reference overnight rate.
We can then write the settlement price of a collateralized FRA contract as:
which involves market observables or quantities that can be derived from market observables. From this and the linearity property of settlement prices, we can compute the present value of Libor swaps collateralized at overnight rates of the LCH.Clearnet type.
6.6 Collateralized forward FX contracts
The contractual payoff is such that:  where, for simplicity,Footnote 8 we state that:
where, for simplicity,Footnote 8 we state that:

Let us assume that the collateral is posted in cash USD and earns the effective fed funds rate \(c^{\$ }\). Then, applying the pricing equation: \(p^{S}(t)=E_t^{Q^{\beta ^{\$ }}} \Big [ X(T)\exp \Big ( -\int \nolimits _t^T {c^{\$ }(s)ds} \Big ) \Big ]\), we obtain:

Let us remark that the discount factors \(E_t^{Q^{\beta ^{\$ }}} \left[ {\exp \left( {-\int \nolimits _t^T {c^{\$ }(s)ds} } \right) } \right] =B_{C^{\$ }} \left( {t,T} \right) \) can be obtained from the quotes on the USD interest swaps collateralized at effective fed funds rate. Thus, from the quotes of the collateralized forward FX contracts, we can derive more discount factors. More precisely, let us denote by  , the collateralized (in cash USD) forward price of one euro. It is such that:
, the collateralized (in cash USD) forward price of one euro. It is such that:  . Thus, we can compute the discount factor
. Thus, we can compute the discount factor  from quoted forward FX contracts. As for a non par collateralized contract, with contractual payoff
from quoted forward FX contracts. As for a non par collateralized contract, with contractual payoff  , the settlement price at time \(t\) is simply provided by
, the settlement price at time \(t\) is simply provided by  .
.
We can then compute settlement prices of cross-currency swaps as a simple extension of forward FX contracts.
7 Asymmetric CSA, CSA with thresholds
7.1 No default risk
In a typical asymmetric CSA framework, no collateral is to be posted if the settlement price is above zero while the value of posted collateral equals the settlement price is negative if it is negative. Thus, \(V(t)=\min \left( {0,p^{S}\left( t \right) } \right) =\left( {0\times 1_{\left\{ {p^{S}\left( t \right) >0} \right\} } +1\times 1_{\left\{ {p^{S}\left( t \right) \le 0} \right\} }} \right) p^{S}(t)\). This corresponds to a haircut being set to \(\alpha _A (t)=0\) if \(p^{S}(t)>0\) and \(\alpha _A (t)=1\), if \(p^{S}(t)\le 0\). Thus, going into the same lines as in Sects. 2 and 5, the applicable discount rate is \(R(t)1_{\left\{ {p^{S}(t)>0} \right\} } +r_A (t)1_{\left\{ {p^{S}(t)\le 0} \right\} }\) where \(R\) is the default-free borrowing rate. We obtain the pricing formula for default-free counterparties and asymmetric CSA as a special case of pricing with haircuts:
7.2 CVA and asymmetric CSA
In an asymmetric CSA, only one party is protected against the default of the other, thanks to posted collateral. One could either consider that the party that is not posting collateral is default-free and the pricing formula stated in previous sub-section is valid. However, in most cases, one would need to take into account the price impact of counterparty risk.
As outlined by Brigo and Morini (2010), setting-up the closeout payment in case of default is an intricate issue. The easiest way to go is to compute so called “risk-free”Footnote 9 present values, either by discounting at overnight rates, as in the computation of the settlement price of a perfectly collateralized trade, collateralized at overnight rate or by using an uncollateralized swap curve. The previous approach is questionable in our asymmetric CSA case. Using a recovery based upon settlement price in the spirit of Duffie and Huang (1996) is simpler and provides useful guidance: we can derive a settlement price coping both with CVA and collateral valuation adjustments.
First, let us recall that we only deal with the default risk of one party due to one one-side counterparty risk protection. Thus, depending on the party’s point of view, the settlement price is free of CVA or DVA. We can take the point of view of a dealer, typically an investment bank, involved in trades with a sovereign counterparty and thus exposed to that sovereign default. We do not detail the resolution process of sovereign default on derivatives contracts and assume that sovereign default intensity process, \(\lambda \) and recovery rate \(\delta \) are given. We chose here a fractional recovery of market value approach, as in Duffie and Huang (1996), a route which is not privileged by market practitioners, but which is meaningful in our context. Then, the loss in case of default, which occurs between \(t\) and \(t+dt\) with conditional probability \(\lambda \left( t \right) dt\) is simply equal to \(\left( {1-\delta } \right) p^{S}(t)1_{\left\{ {p^{S}\left( t \right) >0} \right\} } \). By considering, as before, the expected change in the settlement price, prior to default, we readily get:
As above, we focused on the generator of the BSDE, which now takes the form \(g\left( p \right) =\left( {R+\lambda \left( {1-\delta } \right) } \right) p^{+}+r_A p^{-}\) and therefore remains piecewise linear. The pre-default portfolio value is simply written as:
where the term \(\lambda \left( {1-\delta } \right) \) accounts for the counterparty risk adjustment.
8 Trade contributions in a non-linear setting
It is interesting to go back to the BSDE stated in Eq. (7.3). The terminal value is \(X\left( T \right) \) corresponding to contractual payoff and the generator \(g\left( p \right) =\left( {R+\lambda (1-\delta )} \right) p^{+}+r_A p^{-}\), with \(p^{+}=\max \left( {p,0} \right) \) and \(p^{-}=\min \left( {p,0} \right) \). We recall that in a Brownian filtration setting, such BSDE is a standard mathematical finance tool (Karoui et al. 1997) and admits a unique solution. \(p^{S}\left( t \right) \) is also known as the conditional \(g-\)expectation of \(X\left( T \right) \) (see Peng 2004). Let us remark that the collateralization scheme is embedded in the shape of the generator of the BSDE. Moreover, properties of the generator translate to the price functional (Peng 2006). For instance, in an asymmetric CSA, the generator is positively homogeneous. Thus, the price functional is also positively homogenous: for a positive real number \(\lambda \), the price at time \(t\) of \(\lambda X\left( T \right) \) is equal to \(\lambda p^{S}\left( t \right) \). If \(R+\lambda \left( {1-\delta } \right) \ge r_A \), the generator is concave and thus the functional associating the contractual payoff (terminal value) \(X\left( T \right) \) to current settlement price \(p^{S}\left( t \right) \) is also concave.Footnote 10 Non linearity is associated with portfolio effects: under the assumption that \(R+\lambda \left( {1-\delta } \right) \ge r_A\), the present value of a portfolio of two trades \(X_1 \left( T \right) +X_2 \left( T \right) \) is greater than the sum of the present values of the two trades considered in isolation.
In such a non-linear context, one needs to consider pricing at portfolio level and the settlement price has to be understood as the present value of a portfolio of trades against a given counterparty (possibly a CCP) and under a specific CSA.
Two issues need to be addressed, marginal pricing and trade contributions. As will be shown these two issues are closely connected and are quite intuitive on a financial point of view.
Regarding marginal pricing, we consider the present value impact of a small trade with payoff \(\varepsilon Z,\, \varepsilon \in \mathrm{R}\) being a scaling factor. Thus the portfolio payoff translates from \(X\left( T \right) \) to \(X\left( T \right) +\varepsilon Z\). Let us denote by \(\left( {p^{S}+\varepsilon Z} \right) \left( t \right) \) the settlement price after inception of the new trade. The generator \(g\left( p \right) =\left( {R+\lambda (1-\delta )} \right) p^{+}+r_A p^{-}\) is differentiable with respect to \(p\), except for \(p=0\), which actually deserves a specific treatment.Footnote 11 Thanks to Proposition 2.4 of Karoui et al. (1997), \(\varepsilon \rightarrow \left( {p^{S}+\varepsilon Z} \right) (t)\) is differentiable with derivative at \(\varepsilon =0\) is given by:
The previous term is known as the directional derivative of the price functional around the current portfolio in the direction of the new trade \(Z\). Marginal pricing is based on the first order expansion:
The deflator (or stochastic discount factor) \(\exp \big ( -\int \nolimits _t^T \big ( \big ( {R+\lambda (1-\delta )} \big )\left( s \right) 1_{\left\{ {p^{S}\left( s \right) >0} \right\} } +r_A \left( s \right) 1_{\left\{ {p^{S}\left( s \right) >0} \right\} } \big )ds \big )\) is the functional derivative (or Fréchet derivative) of the price with respect to terminal payoff. The important point is that the first order term is linear in \(Z\), thus leading to standard pricing methods.
We have already noticed that, in the case of an asymmetric CSA, the settlement price is positively homogenous with respect to terminal payoff. Thus, (functional) Euler’s equation holds and can be written as:
where \(\exp \left( {-\int \nolimits _t^T {\left( {\left( {R+\lambda (1-\delta )} \right) \left( s \right) 1_{\left\{ {p^{S}\left( s \right) >0} \right\} } +r_A \left( s \right) 1_{\left\{ {p^{S}\left( s \right) \le 0} \right\} } } \right) ds} } \right) \) is the derivative of the price. By connecting the already stated pricing formula to Euler’s equation, we can use standard risk allocation techniques to compute the trade contributions. Let the portfolio payoff \(X\left( T \right) \) be the sum of \(J\) individual trades \(X\left( T \right) =X_1 \left( T \right) +\cdots +X_J \left( T \right) \). Then according to Euler’s allocation rule, the trade contribution of \(X_j \left( T \right) \) to portfolio present value \(p^{S}\left( t \right) \) is provided by:
This is not to be confused with the standalone present value:
Euler’s allocation rule is totally additive, i.e. the sum of trade contributions is equal to the portfolio present value. Unlike the standalone present values, the trade contributions involve a standard (linear) expectation.
It can be seen that the trade contributions and marginal prices are computed quite similarly. Let us once again emphasize that the collateralization scheme is embedded in the shape of the generator and thus in the stochastic discount factor \(\exp \left( {-\int \limits _t^T {\left( {\left( {R+\lambda (1-\delta )} \right) (s)1_{\left\{ {p^{S}(s)>0} \right\} } +r_A (s)1_{\left\{ {p^{S}(s)\le 0} \right\} }} \right) ds} } \right) \).
In the perfect collateralization case, we introduced the suitable collateralized forward measures. This can readily be extended to locally proportional haircuts and therefore to asymmetric CSA. We can introduce a CSA and portfolio specific change of measure:
Let us further denote by \(B_{X,CSA} \left( {t,T} \right) = E_t^{Q^{\beta }} \big [ \exp \big ( -\int \nolimits _t^T \big ( \left( {R+\lambda (1-\delta )} \right) (s) 1_{\left\{ {p^{S}(s)>0} \right\} } +r_A (s)1_{\left\{ {p^{S}(s)\le 0} \right\} } \big )ds \big ) \big ]\), the collateralized discount bond price. Then, the trade contribution or the marginal price of \(X_j \left( T \right) \) can simply be written as \(B_{X,CSA} \left( {t,T} \right) E_t^{Q_T^{X,CSA} } \left[ {X_j \left( T \right) } \right] \). Let us eventually remark that the changes of measure and the pricing formulas mimic and extends those stated in Sect. 6 for the perfect collateralization scheme.
9 Conclusion
In this paper, we kept as closely as possible to mainstream mathematical finance. It has been shown that well known concepts and tools can be used with minor adaptation to the collateralized pricing issues: On one hand, we used Cvitanić and Karatzas (1993) framework to cope with different default-free borrowing and lending rates. On the other hand, we used varying haircuts to provide a generic discounting approach that applies to a wide range of contracts, with perfect or partial collateralization. Within that framework, we provided suitable changes of measure to compute prices or trade contributions.
Though we dealt comprehensively with various kinds of collateral and collateralization schemes, we left aside the pricing impacts of initial margins. This is an important topic but the rules governing the computations of initial margins are not yet stabilized. We did not investigate the numerical issues associated with solving BSDE in the asymmetric CSA case and the connections with the standard approaches to the computations of CVA. This is left for future research.
Notes
One could think of Treasury GC as a proxy.
In such a framework, the claim on default for a repo contract would differ from the claim associated with other OTC trades, such as interest rate swaps. We may relate cancellation to fails-to-deliver without penalty.
Default times of the counterparties are then assumed to be totally inaccessible. \(\lambda (t)\) is here the intensity of the first to default-time.
If the bond \(A\) is special, the corresponding repo rate is lower.
\(\frac{V(s)}{A(s)}\times A\left( {s+ds} \right) \) can be seen as the value of the collateral account, prior to the variation margin payment.
Define \(\zeta (s)=V(s)e^{-\int \nolimits _t^s {r(u)du} }\). \(d\zeta (s)=e^{-\int \nolimits _t^s {r(u)du} }dV(s)-r(s)\zeta (s)ds\). Thus, the present value of the collateral cash-flows equals: \(E_t^{Q^{\beta }} \left[ {\zeta (t)+\int \nolimits _t^T {d\zeta (s)+\left( {r(s)ds-\frac{dA(s)}{A(s)}} \right) \zeta (s)ds} -\zeta (T)} \right] \), which can be simplified as: \(E_t^{Q^{\beta }} \left[ {\int \nolimits _t^T {\left( {r(s)ds-\frac{dA(s)}{A(s)}} \right) V(s)e^{-\int \nolimits _t^s {r(u)du} }} } \right] \), which leads to the stated expression.
This illustrative example, where
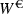 is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.
is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.“Risk-free” means that an uncollateralized swap curve or overnight rates in the interbank market are to be used in the discounting process. While this can be understood from an historical perspective, when the default component in effective fed funds rates or EONIA was neglected or when swaps contracts were deemed default-free and CVA/DVA effects could be neglected, the market terminology is misleading. “Recovery of swap”, similarly to “recovery of Treasury” would be more explicit.
Actually, if \(R+\lambda (1-\delta )\ge r_A \), the generator is super-additive and the price functional, associated with an asymmetric CSA, too. Conversely, if \(R+\lambda (1-\delta )\le r_A \), the generator is sub-additive and the price functional is sub-additive and thus convex, thanks to positive homogeneity. Concavity or convexity are useful properties, since when the price functional is not differentiable with respect to terminal payoff, we can still consider a non-empty subdifferential and deal with left and right Gâteaux derivatives, which stills allows for simple one-sided first order expansions.
When \(p=0\), the first-order expansion is readily derived and leads to different left and right derivatives.
References
Afonso, G., Kovner, A., & Schoar, A. (2011). Stressed not frozen: The federal funds market in the financial crisis. Journal of Finance, 66(4), 1109–1139.
Barden, P. (2009). Equity forward prices in the presence of funding spreads. In ICBI conference, Rome.
Bergman, Y. (1995). Option pricing with differential interest rates. Review of Financial Studies, 8(2), 475–500.
Bianchetti, M. (2010). Two curves, one price. Risk magazine, 23(8), 66–72.
Bielecki, T., Cialenco, I., & Iyigunler, I. (2011). Counterparty risk and the impact of collateralization in CDS contracts, working paper, Illinois Institute of Management.
Brigo, D., & Morini, M. (2010). Dangers of bilateral counterparty risk: The fundamental impact of closeout conventions, working paper, department of mathematics, King’s College.
Brigo, D., Capponi, A., Pallavicini, A., & Papatheodorou, V. (2011). Collateral margining in arbitrage-free counterparty valuation adjustment including re-hypothecation and netting, working paper, department of mathematics, King’s College.
Burgard, C., & Kjaer, M. (2011). Partial differential equation representations of derivatives with bilateral counterparty risk and funding costs. The Journal of Credit Risk, 7(3), 75–93.
Castagna, A. (2011). Funding, liquidity, credit and counterparty risk: Links and implications, working paper.
Castagna, A. (2012). Pricing of collateralized derivatives contracts when more than one currency are involved: Liquidity and funding value adjustments, working paper.
Castagna, A. (2013). Pricing of derivatives contracts under collateral agreements: Liquidity and funding value adjustments, working paper.
Cesari, G., Aquilina, J., Charpillon, N., Filipovic, Z., Lee, G., & Manda, I. (2010). Modelling, pricing, and hedging counterparty credit exposure, a technical guide. Springer.
Cox, J. C., Ingersoll, J, Jr, & Ross, S. A. (1981). The relation between forward prices and futures prices. Journal of Financial Economics, 9(4), 321–346.
Crépey, S. (2011). A BSDE approach to counterparty risk under funding constraints, working paper, University of Evry.
Crépey, S. (2012a). Bilateral counterparty risk under funding constraints part I: Pricing. Mathematical Finance. doi:10.1111/mafi.12004.
Crépey, S. (2012b). Bilateral counterparty risk under funding constraints part II: CVA. Mathematical Finance. doi:10.1111/mafi.12005.
Cvitanić, J., & Karatzas, I. (1993). Hedging contingent claims with constrained portfolios. Annals of Applied Probability, 3, 652–681.
Duffie, D. (1989). Futures markets. Englewood Cliffs: Prentice Hall.
Duffie, D., & Huang, M. (1996). Swaps rates and credit quality. Journal of Finance, 51(3), 921–948.
Duffie, D., Schroder, M., & Skiadas, C. (1996). Recursive valuation of defaultable securities and the timing of resolution of uncertainty. Annals of Applied Probability, 6(4), 1075–1090.
El Karoui, N., Peng, S., & Quenez, M.-C. (1997). Backward stochastic differential equations in finance. Mathematical Finance, 7(1), 1–71.
Fries, C. P. (2010). Discounting revisited. Valuation under funding costs, counterparty risk and collateralization, working paper.
Fujii, M., Shimada, Y., & Takahashi, A. (2009). A survey on modeling and analysis of basis spreads, CARF working paper.
Fujii, M., Shimada, Y., & Takahashi, A. (2009). A market model of interest rates with dynamic basis spreads in the presence of collateral and multiple currencies, CIRJE discussion paper.
Fujii, M., Shimada, Y., & Takahashi, A. (2010). A note on construction of multiple swap curves with and without collateral, working paper, University of Tokyo.
Fujii, M., & Takahashi, A. (2011). Choice of collateral currency. Risk, 24(1), 120–125.
Fujii, M., & Takahashi, A. (2011). Collateralized CDS and default dependence, working paper, University of Tokyo.
Fujii, M., & Takahashi, A. (2012). Perturbative expansion techniques for non-linear FBSDEs with interacting particle method, working paper, University of Tokyo.
Fujii, M., & Takahashi, A. (2013). Derivative pricing under asymmetric and imperfect collateralization and CVA. Quantitative Finance, 13(5), 749–768.
Geman, H., El Karoui, N., & Rochet, J.-C. (1995). Changes of numéraire, changes of probability measure and option pricing. Journal of Applied Probability, 32(2), 443–458.
Henrard, M. (2009). The irony in the derivatives discounting part II: The crisis, working paper, Dexia Bank, Brussels.
Henry-Labordère, P. (2012). Cutting CVA’s complexity. RISK, 25(7), 67–73.
Hull, J., & White, A. (2012). The FVA debate. Risk 25th anniversary issue, July 2012.
ISDA - International Swap and Derivatives Association (2010). Best practices for the OTC derivatives collateral process, technical document, June 30, 2010.
Johannes, M., & Sundaresan, S. (2007). The impact of collateralization on swap rates. Journal of Finance, 62(1), 383–410.
Kan, Y. H. & Pedersen, C. (2011). The impact of margin interest on the valuation of credit default swaps, working paper, Columbia University and Barclays Capital.
Kenyon, C. (2010). Post-shock short rate pricing. Risk, 23(11), 83–87.
Kijima, M., Tanaka, K., & Wong, T. (2009). A multi-quality model of interest rates. Quantitative Finance, 9(2), 133–145.
Korn, R. (1992). Option pricing in a model with a higher interest rate for borrowing than for lending, working paper.
Macey, G. (2011). Pricing with standard CSA defined by currency buckets, working paper, HSBC.
Mercurio, F. (2009). Interest rates and the credit crunch: New formulas and market models, working paper.
Mercurio, F. (2010a). Modern LIBOR market models: Using different curves for projecting rates and for discounting. International Journal of Theoretical and Applied Finance, 13, 1–25.
Mercurio, F. (2010b). A LIBOR market model with stochastic basis. Available at http://ssrn.com/abstract=1583081.
Morini, M., & Prampolini, A. (2010). Risky funding: A unified framework for counterparty and liquidity charges, working paper, Banca IMI.
Pallavicini, A., Perini, D., & Brigo, D. (2012). Funding, collateral and hedging: Uncovering the mechanics and the subtleties of funding valuation adjustments, working paper.
Peng, S. (2004). Nonlinear expectations, nonlinear evaluations and risk measures. Stochastic methods in finance. Lecture notes in mathematics, vol. 1856. Springer (pp. 243–256).
Peng, S. (2006). Modelling derivatives pricing mechanisms with their generating function, working paper.
Piterbarg, V. (2010). Funding beyond discounting: Collateral agreements and derivatives pricing. Risk Magazine, 23(2), 97–102.
Piterbarg, V. (2012). Cooking with collateral. Risk, 25(8), 58–63.
Schroder, M. (1999). Change of numeraire for pricing futures, forwards, and options. The Review of Financial Studies, 12(5), 1143–1163.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors are indebted to many people within the Fixed Income, Treasury and ALM departments of BNP Paribas. They thank participants to the FEBS—Labex RéFi conference on Financial Regulation & Systemic Risk, The French Banking Association “Rencontre des Chaires” and the Sorbonne Finance seminars in Paris and to the French Finance Association conference in Lyon for helpful comments. They also thank the referee for numerous and helpful remarks. The authors take the sole responsibility for any error within this document. Jean-Paul Laurent acknowledges support from the Fixed Income and Research Strategies Team (FIRST) of BNP Paribas and from the BNP Paribas Cardif chair “management de la modélisation”. The views expressed in this paper are authors own.
Appendix: Convexity adjustments
Appendix: Convexity adjustments
\(E_t^{Q_T^B } \left[ {X(T)} \right] ={E_t^{Q_T^A } \left[ {\frac{dQ_T^B }{dQ_T^A }X(T)} \right] }/{E_t^{Q_T^A } \left[ {\frac{dQ_T^B }{dQ_T^A }} \right] }\). Thus,
It can easily be shown that: \(E_t^{Q_T^A } \left[ {\exp \left( {-\int \limits _t^T {\left( {r_B -r_A } \right) (s)ds} } \right) } \right] =\frac{B_B \left( {t,T} \right) }{B_A \left( {t,T} \right) }\). Thus,
which involves a covariance term between the payoff \(X(T)\) and the stochastic spread terms \(r_B -r_A \).
Let us consider the special case associated with a Brownian filtration. Since \(\xi _T^A \) is a positive \(Q^{\beta }\)- martingale, we have: \(\frac{d\xi _T^A (t)}{\xi _T^A (t)}=\sigma _A \left( {t,T} \right) dW_A^\beta (t),\, \xi _T^A (t)=\varepsilon \left( {\int \nolimits _0^t {\sigma _A \left( {s,T} \right) dW_A^\beta (s)} } \right) \) where \(W_A^\beta \) is a \(Q^{\beta }\)- Brownian motion. Since \(\xi _T^{B,A} \left( t \right) =\frac{\xi _T^B \left( t \right) }{\xi _T^A \left( t \right) }\) is a \(Q_T^A \) - martingale and using Girsanov theorem, we have:
where \(W_B^{A,T},W_A^{A,T} \) are \(Q_T^A \) - Brownian motions.
\(\sigma _A \left( {t,T} \right) \) is related to collateralized discount bond prices since from \(B_A \left( {t,T} \right) =B_A \left( {0,T} \right) \xi _T^A \left( t \right) \exp \left( {\int \limits _0^t {r_A (s)ds} } \right) \), we get \(\frac{dB_A (t,T)}{B_A (t,T)}=r_A (t)dt+\sigma _A \left( {t,T} \right) dW_A^\beta (t)\).
Let us assume that \(X(T)>0\), thus \(p_{A,T} (t)>0\). \(\frac{dp_{A,T} (t)}{p_{A,T} (t)}=\sigma _X \left( {t,T} \right) dW_A^{X,T} (t)\), where \(W_A^{X,T}\) is a \(Q_T^A \)- martingale and \(X(T)\!=\!E_t^{Q_T^A } \left[ {X(T)} \right] \varepsilon \left( {\int \limits _t^T \!{\sigma _X \left( {s,T} \right) dW_A^{X,T} (s)} } \right) \). This leads to the following relation between forward prices under collaterals \(A,B\):
Rights and permissions
About this article
Cite this article
Laurent, JP., Amzelek, P. & Bonnaud, J. An overview of the valuation of collateralized derivative contracts. Rev Deriv Res 17, 261–286 (2014). https://doi.org/10.1007/s11147-014-9098-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11147-014-9098-8





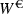 is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.
is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.